Древо чисел как составить

Числословное древо (расширенный вариант)

 24.10.2007 02:17 Обновлено 03.07.2012 19:23 Автор: КАА

А. А. КорнеевЧислословное древо (расширенный вариант)

Для начала надо понять: А что же такое – “ЧИСЛОСЛОВНОЕ ДЕРЕВО” (ДРЕВО)?       Числословное Древо – это итоговая графическая схема результатов  многократных преобразований набора некоторых ИСХОДНЫХ ЧИСЕЛ (или даже одиночных Цифр) в числительные, которые затем превращаются (побуквенно!) в уникальные суммы цифр, соответствующих порядковым номерам (для каждой из букв этих числительных); Далее, вычисленные таким способом, суммарные число ВНОВЬ записываются в своей словесной форме (т.е. в виде новых числительных), а затем, в итоге,  …  вся процедура повторяется снова и снова, пока….

Вот именно! …. Пока что?!!

Перед началом этого эксперимента первым ощущением было то, что такая процедура – бесконечна; т.е. что мы никогда не дойдём до какого-либо “логического конца”.

А значит, это будет бессмысленный эксперимент…Но, потом мне, почему то, подумалось, что, возможно, некоторые числа в результате этой процедуры может быть и будут иметь окончание.

Однако, в итоге мы получим только отдельные наборы кодовых цепочек, никак не связанных друг с другом, либо имеющих редкие пересечения… И, что это нам даст??!И, наконец, пришла третья, спасительная мысль о том, что для начала можно ограничиться только одними лишь Первоцифрами, так как все остальные числа (какие бы они ни были) могут быть сведены к ним обычным нумерологическим сложением.

МЕТОДИКА ПОСТРОЕНИЯ ЧИСЛОСЛОВНОГО ДРЕВА

Шаги

Расчёты элементов Древа Первоцифр

Элементы графического образа Древа

1

Берём одну из 9 (девяти) Первоцифр, например цифру «3»

2

Произносим и пишем Первоцифру в форме Слова числительного (часть речи) «3» –ТРИ. Такие элементы будут венчать верхние концы строящегося у нас числословного Древа

Исходное слово, обозначающее Первоцифру ТРИ

3

Все числительные будем обозначать здесь в виде Числа, но в специальных угловых скобках <3>

Под словом ТРИ можно написать словесную форму данного числительного: <3>или опустить её

4

Начнём расчёт числительных слов (у нас это – ТРИ) для чего используем таблицу числовых соответствий между буквами. В порядке следования букв в русском Алфавите: А = 1; Б=2; В=3; …. И т.д. до Я=33;

Эти расчёты «числовой кальки» в графическом отображении Древа опускаются

5.

Получаем последовательность (код) из чисел /цифр/, которые надо затем просуммировать: Т(20); Р(18); И(10) /В круглых скобках – порядковый номер буквы алфавита/. Такая процедура называется «снятием числовой кальки» со Слова. У нас – это числительное, но это может быть числовая калька с любого иного слова.

Этот этап не отображается в Древе

6

Производим суммирование цифр (чисел) «числовой кальки» слова ТРИ, т.е порядковых номеров соответствующих букв слова.: (20)+(18)+(10) = «48». «48» – это число (!) Оно записано в кавычках.. А если мы произнесём это число («3»), то получим числительное: СОРОК ВОСЕМЬ или(в наших обозначениях <48> – смотрите п.3 выше.

В древо, под слово ТРИ (или под <3>. Мы записываем Только конечный результат этапа 6, т.е. Обозначение <48>

7.

Таким образом, у нас есть первое новое числительное (<48>) после изначального числительного <3>. Цикл замкнулся и мы можем повторять описанную выше манипуляцию столько, сколько это будет возможно

Вносим <48> в рисунок Древа

8

Цикл 2

Новый цикл, естественно, мы начнём с нового (ранее вычисленного) числительного, т.е. с <48>

Новый цикл.

9

Числительное <48> трансформируем в словесную форму, т.е. в слово «СОРОК ВОСЕМЬ»

Этап не отображается

10

Формируем «числовую кальку» слова <48>: С(19)_О(16)_Р(18)_О(16)_К(12)_В(3)_О(16)_С(19)_Е(6)_ М(14)_Ь(30)

Этап не отображается

11

Суммируем порядковые номера всех букв «числовой кальки»: /19+16+18+16+12/ + /3+16+19+6+14+30/ = 169

Этап не отображается

12

«169»

– это промежуточное расчётное число.

Вносим обозначение Числительного <169> в рисунок Древа

13

Число «169» превращаем в числительное слово:СТО ШЕСТЬДЕСЯТ ДЕВЯТЬ, и обозначаем его как <169>

Внесена ячейка цепи <169>

14

<169> – это очередной элемент наших расчётов и графиков. Именно такие числительные, отображаемые в условной числовой форме вида <3>, <48>, <169> и так далее являются узлами цепочек каждой ветки (или ствола) Древа.

Этап не отображается

15

Числительное <169> – очередной этап построения Древа.

Этап не отображается

16.

Снова снимаем числовую кальку этого числительного:

Этап не отображается

17

Снова считаем сумму букв в числовой кальке

Этап не отображается

18

Снова получаем новое число «Х»

Этап не отображается

19

Снова пишем число «Х» в форме слова (числительного)

Этап не отображается

20

Снова обозначаем вычисленное числительное в условно-числовой форме <Х> для отображения в дереве

Данные <X> для отображения вносим в Древо

21

Начинаем новый цикл, используя в качестве исходного слова полученное выше числительное…..

Этап не отображается

Графический образ “Числословного Древа” (слова ” ТРИ”) см. ниже:

Итак, я взялся за дело, вручную выписывая и складывая цифры и буквы, числительные (и им соответствующие суммы). Работа потребовала большого количества внимания, времени и терпения. Одна ошибка по ходу перекодировок отбрасывала назад всё работу…    Тем не менее в итоге получилось ЧИСЛОСЛОВНЕЕ ДРЕВО, представленное на главном рисунке (см. выше), в котором на самом верху СЛОВОМ или цифрой ( в кавычках и в ОВАЛЕ) показаны Исходные Цифры и Числа, для которых и проводилась упомянутая выше процедура многократных перекодировок.    В кружках, которые опускаются (от ОВАЛОВ) всё ниже и ниже – в кружках представлены в виде чисел результаты цифровой кодировки числительного, которое для экономии места – не писалось, но таким способом отображалось.    На самом же деле, каждое из таких чисел (в малых кружках) писалось отдельно в виде числительного, а вместо букв в нём ставились цифры и числа, и затем их сумма снова вписывалась в малый кружок (Число – вместо числительного). И… процедура повторялась вновь и вновь…

—–ХХХ——

    Когда всё было сведено в один рисунок, стали проявляться удивительные картинки и напрашиваться странные выводы:1. Практически все Первоцифры и большое число Чисел (кроме «6» и ряда Чисел !?) вписалось – таки в числословное дерево в виде индивидуальных «веточек» на общем стволе.2. Удивительным оказался «корень» числословного Дерева, представленный совершенно конкретной ТРОЙКОЙ чисел (или числительных): 232, 200 и 63, которые ВКРУГОВУЮ превращаются только друг в друга???! 3. Такой «корень» или «ЯДРО» числословного дерева вызывает законный1 вопрос: «А почему именно эти числительные, числа или эквивалентные им (в числовом исчислении) слова являются центром всего этого, столь сложного строения? Случайность ли это? Что за этим стоит?4. Встретилось явление «ОТПАВШИХ ЛИСТЬЕВ», когда некая цифра или Число сразу (или через небольшое число этапов) «окукливаются и НЕ ВХОДЯТ(!) в структуру Числового Дерева, существуя отдельно: Это, в частности, цифра «6», числа «13», «33», «369»… Кстати, не в этом ли неприязнь людей к некоторым конкретным числам. Не исключено, что люди просто чувствуют это!5. Естественно, что одному и тому же числительному (числу) могут соответствовать в русском языке разные СЛОВА, связь и общность которых ещё надо проверять… Например, сразу выявилось, что числу «97» соответствуют эквиваленты {9}, {302}; А числу «285» – эквивалентные числительные {66}, {811} и {990}; Числу «192» соответствуют эквивалентные числительные {52}, {403}, {68}, {304}…6. Проще говоря, на числовом дереве обнаружились «ТОЧКИ ВЕТВЛЕНИЯ», представляющие несомненный семантический интерес

—–ХХХ——

В отношении Числословного Дерева можно выдвинуть некоторую гипотезу, которая состоит в том, что, по крайней мере, достаточное количество чисел в своём словесном обличии (в виде числительных) могут быть эквивалентны как между собой, так и просто соответствующему ЧИСЛУ.Можно также предположить, что несовпадения имеют место только для тех числительных, где сумма порядковых номеров букв, из которых состоит данное числительное, не равна формальному числу «Х», так как нарушен порядок букв в алфавите. В этом случае расчётом интересно было бы установить истинный порядок и конкретные буквы алфавита, которые задействованы в дереве Числослова и которые могли бы снять несоответствия расчётов.    Тем не менее, по крайней мере, для некоторых узловых точек Дерева такая эквивалентность, почему-то, соблюдается.    Рассмотрим для примера число «Х =285» ~ Двести восемьдесят пять – {285};    Здесь и далее будем иметь ввиду, что фигурные скобки { } – это условная, цифровая запись числа 285 в виде числительного.    В чём идея моего эксперимента?ИСХОДНОЕ число – 285 мы попытаемся представить в виде сумм нескольких (фиксированных) слагаемых чисел, для которых нам известны их числительные имена.    Далее, подразумевая, и тем самым, косвенно проверяя Алфавит, произведём переход в формально-числовую форму, где сложению (вычитанию) нами подвергаются уже словесные формы: {Х} + {Y}.    Результат будет являть собой некое «синтетическое» сложение числительных: {X} +{Y} = {{X+Y}} = {{Z}}.. результат которого во всех формах своего представления (ПО ИДЕЕ!) должен быть равен исходному числу «285».    Выпишем несколько комбинаций, как подтверждающих идентичный результат, так и отрицающих его:    (285) = {66} — {60}+{6} — (184 + 101) = 285!    {811} — {800} + {11} — (143 + 142) =285!    {811} — {810} + {1} — ( 256 + 46) = 302?!!    {811} — {801} + {10} — ( 189+113) = 302?!!    {990} — (900} + {90} — 152 + 133 = 285!    {199} — {100} + {99} — 55 + 230 = 285!    {199} — {100} + {90} + {9} — 55 + 133 + 97 = 285!    {199} — {190} + {9} — 188 + 97 = 285!    {199} — {109} + {10} — 152 + 133 = 285!{337} — {300} +{30} + {7} — (88+128+69) = 285!    {337} — {330} + {7} — (216+69) = 285!    {337} — {300} + {37} — (88+197) = 285!    {337} — {307} +{30} — (157+128) = 285!Таким образом, найдено, например, что эквивалентность числа и слова могут давать, например, такие соответствия числительных:    285 = {66} = {811} = {990} = {199} = {337}…    Однако, не все (выбранные мною) числительные дают аналогичный результат.     Действительно, число 285, например, можно представить себе по–разному:     Посмотрим варианты – А, В, С и D:    А). 285 = (69 +48) + (9 +159), откуда следует сложение числительных:     ({7} + {3}) + ({2} +{104}) = {10} + (106} = (113 + 156) = 269;Или же:    В). 285 = (163 – 46) + (113 + 55), откуда следует сложение числительных:     ({204} – {1}) + ({10} + {100}) = (167 + 168) = 335;    Или же:    C). 285 = (69 + 48) + ( 104 + 64); откуда следует сложение числительных :    ({7} +{3}) + ({4} + {102}) = (113 + 156) = 269;    Или же:    D). 285 = (69 + 48) + (113 +55); откуда вытекает сложение числительных :     ({7} +{3}) + ({10} + {100}) = {7} + {3} = {110} — (69 + 18 +168) = 285!     Можно понять, что от комбинаций слагаемых {Xi} результаты очень даже зависят, хотя можно получить и правильные результаты, т.е. зависимость (точность) здесь весьма неоднозначная, ХОТЯ ОНА И ВСТРЕЧАЕТСЯ! НО, ПОЧЕМУ ЭТО ТАК?!!Сказанное выше даёт мне основания предполагать, в частности, что:1. Древний русский алфавит, который ныне не вполне достоверно известен, мог быть раньше – другим, а именно: точно и однозначно СЧИСЛИМЫМ математически, 2. СЧИСЛИМЫЙ математически алфавит – на сегодняшний день МОЖЕТ БЫТЬ, в принципе, синтезирован и ИСКУССТВЕННО, если применить к этому мою методику числословного Древа, программирование и компьютерную технику!—–ХХХ——А пока приходится, кроме всего прочего, констатировать, что результаты моих экспериментов непонятным образом зависят и от перестановок, демонстрируя таким образом, что математика СЛОВ и математика Цифр, к сожалению, не всегда совпадают… Это иллюстрирует, например, ещё один проведённый мной расчётный эксперимент, который представлен ниже:

—–ХХХ——

Рассмотрим сложение, например, такой последовательности:{7} + {3} + {10} + {100} = ???, (Здесь в фигурных скобках даны (в форме цифр!) – «слова–числительные», для которых мы будем искать полные суммы цифр, соответствующих буквам этих числительных…)1. {7+3}+ {10} +{100} — (69 +48) + (113) + (55) = 281;2. {7 +10} + {3} +{100} — 135 +48 + + 55 = 238;3. {7+100} + {3 + 10} — 124 +144 = 268;4. {7 + 100} +{3} + {10} — 124 + 48 + 113 = 285;5. {7+10+100} + {3} — 190 + 48 = 238;6. {3+10+100} + {7} — 199+69 = 268;7. {3+100} + {7+10} — 103 + 135 = 238;Получились, увы, весьма неоднозначные результаты…ОСТАЁТСЯ ТОЛЬКО РАЗМЫШЛЯТЬ И ИСКАТЬ причины того, что именно есть общего между теми комбинациями, которые дают идентичные (правильные) результаты и что именно отсутствует и порождает в них отличия (не правильность результата)?!!!К сожалению, такие исследование ещё не закончены…1. Числословное дерево, тем не менее, уже сейчас можно использовать для исследования не только вопросов синхронизированности (идентичности) сложения собственно чисел и их числительных (на предмет выявления роли алфавита в проблеме СЧИСЛЕНИЯ ИСТИНЫ), но и анализировать сами числа…2. Например, возможно построить числословные деревья для особых чисел, например, для чисел из строк магических квадратов, включая прямое (привычное) прочтение цифр этих чисел, а также зеркальные написания тех же цифр исследуемых чисел.3. Можно использовать числословные деревья и для изучения семантических проблем, переходя с их помощью в плоскость анализа эквивалентных числовых форм представления изучаемых словесных форм.4. Числословные деревья могут также служить инструментом исследования экспериментально полученных чисел, когда конечной целью будет нахождение эквивалентных (числам) – словесных форм, а также для окончательного анализа нужных СЛОВЕСНЫХ форм представления, например, с рекламных позиций.К слову сказать, на основании уже имеющегося у меня словаря (~25000 слов) представляет немалый интерес прочтение словесных эквивалентов чисел, лежащих в основе, (в «корне», в «ядре») Числословного Древа (и / или чисел непосредственно примыкающих к этой ЗАГАДОЧНОЙ Тройке Чисел – 63, 200, 232). —–ХХХ——Вот некоторые из них (без комментариев).

ЧИСЛО

«63»

[9]

ЧИСЛО

«200»

[2]

ЧИСЛО

«232»

[7]

Лицо

План Божий,

Будда, Майя-Шакти, Тарх, Дажьбог, Адонай, Господь.

Египет

Семь разумов планет,

Триграммы, Иероглифы,

Бхагават Гита, Пурана.

СЫН

Первосвященник,

Дерево Сефирот, Квадратура круга,Первопричина,

Целем

Держательница Мира,

Цари Питри, Волны жизни, Молекула ДНК,

Девонгари

Деяния апостолов, Мари, Матфей, Лука, Иоанн Симон Маг,

Сады Гисперит, Иешуа Мессия,

Радогост

Колесо фортуны, Кали-юга, Цель,

Инволюция

Батый

Пандора, Конец, Исход, Сарос, Саркофаг,

Усоньша, Щада,

Черномор, Обида,

ЗОРИ

Как пламень огненный,

Гог и Магог,

Первоэлемент,

Ретра

Византийская Русь, Руника русская

Великое колесо

вращения жизни

Топаз

Капище, Царь, Чистота души и тела

…И ноги подобны

хальколивану

Вахабизм

Тридевять земель, Дмитрий Пожарский,

Тамплиеры,

Гомункулус,

Баить

Хорошая Доля, Гадья,

…Не мстите за себя

Возлюбленные.

Никогда

Лунный месяц

Книга мёртвых

Звать

Нечёт, Дуализм, Коралл,

Треугольник,

Золотой вурф

Новая нумерологияДалее даётся большая выписка из трудов В. И. Пьянова, которая касается новейшей практики обращения с числовыми образами слов русского языка. Эта практика имеет свою специфику, но мы не видим причин, которые могли бы помешать объединению методики В. И Пьянова с нашей Методикой исследований при помощи построения числословных деревьев отдельных (важных) слов, выражений и других частей речи русского языка.Итак, Методика В. И Пьянова допускает следующие манипуляции:Замена букв слова их порядковыми номерами в алфавите современного русского языка выявляет дифференциальную числовую характеристику слова. Создатель учения о логарифмах шотландский математик Джон Непер (1550 – 1617) предложил термин “логарифм”, трактуя перевод этого слова, как специфическое “отношение чисел”. При расшифровке сценария оказалось, что обычное деление (определение отношения) двух чисел, являющихся дифференциальными числовыми кальками слов, так же как и логарифмирование числовых калек слов, является эффективным способом познания эзотерического содержания чисел и слов. Вместе с использованием буквенно-числового кода, связывающего слово и число употребимы, в частности, операции логарифмирования, извлечения корня, деления и умножения, которые позволяют получить информацию о скрытом.    В традиционной нумерологии для познания тайной сущности числа допускается:

1.  перестановка цифр в числе (аналог для слова – использование анаграмм), произвольное использование “плавающей” запятой,
2. выполнение арифметических действий с числами,
3. сложение цифр числа,
4. возведение числа в степень, в том числе дробную.
5. В нумерологии путем сложения цифр числа оно сводится к интегральной характеристике и нумерологии делают вывод о тайной сущности числа.

Мною (В.И. Пьяновым) предложено (в дополнение к традиционным приемам нумерологии):

1. логарифмировать числа и ставить между цифрами числа точку (точки), что позволяет читать в числах даты в общепринятом обозначении.
2. принимать группы стоящих рядом цифр или отдельные цифры в числе за то или иное обозначение дня года
3. осуществлять замену одного обозначения дня на эквивалентное другое (принцип эквивалентности).
4. отсчитывать порядковый номер дня в году как от начала года, так и от конца, (при этом сумма двух дополняющих друг друга обозначений дня равна длительности года в сутках (365 или 366).
5. Заменять порядковый номер дня на дополняющий номер дня – (принцип дополнительности).
6. Использовать при расшифровке принцип эквивалентности и принцип дополнительности последовательно.
7. Год в шифре обозначается 2-х, 3-х или 4-х значными числами.
8. Совместив начало и конец числа или слова, можно получить кольцевую запись.
9. Чтение кольцевой записи чисел, слов или составляющих их частей в обоих направлениях корреспондируется с отсчетом времени в календарных системах, состоящих из вложенных циклов различной длительности (год, месяц, неделя, день), так как движение во времени к концу цикла вместе с тем является движением к началу аналогичного цикла.
10. При “обратном” (справа налево) чтении числа его тайный смысл, как правило, меняется на противоположный.
11.  Если по шифру сценария 52 – война, то 25 – мир, если 18 – рождение, то 81 – смерть.

—–ХХХ——

  Так как история человечества представляет собой совокупность событий, происходящих во времени, а точные временные координаты событий – суть числа, то параллельно с событийным сценарием, описываемым словами, а скорее и до него, небесный сценарист должен был разработать числовой сценарий мировой истории, объединив в итоге Слово (logos) и Число (arithmos).   Все, что было и будет сказано, написано, открыто и создано людьми, изначально содержится в численно-событийном сценарии М Р.Замена букв слова их порядковыми номерами в алфавите современного русского языка выявляет дифференциальную числовую характеристику слова. Создатель учения о логарифмах шотландский математик Джон Непер (1550 – 1617) предложил термин “логарифм”, трактуя перевод этого слова, как “отношение специфических чисел”. Обычное деление двух чисел, являющихся дифференциальными числовыми кальками слов (определение отношения специфических чисел), так же как и логарифмирование числовых калек слов, является эффективным способом познания эзотерического содержания чисел и слов.

—–ХХХ——

    На Руси на старославянском – «В начале было Слово, и Слово было у Бога, и Слово было Бог» (гл.1 ст. 1).     В течение двух тысячелетий сокровенный эзотерический смысл Слова Божьего оставался “тайной за семью печатями”. Покажем, что за дифференциальным цифровым представлением Слова скрывается слово Число. Заменив в слове Число первые две буквы их порядковыми номерами в современном русском алфавите, получим:     2510CЛО.Цифры 5 и 1 в комбинированной записи слова число соответствуют буквам Д и А. Цифра 2 соответствует букве Б русского алфавита, по звучанию совпадающей со второй буквой латиницы В, идентичной по написанию с третьей буквой кириллицы В. В старославянской кириллице В как цифра обозначает 2. Все эти буквы (Б, В, B) произошли от буквы ? греческого алфавита, что в итоге предопределяет взаимозаменяемость букв Б и В и цифр 2 и 3 в коде. Замены Б-В и 2-3 являются наиболее употребительными. Так как цифра 0 в написании идентична букве О, то после перестановок (прием эзотерической нумерологии) с учетом исходного слова можем написать:

ДА, СЛОВО – ЧИСЛО и (1)СЛОВО ДА ЧИСЛО

Существует слово, объединяющее слово и число. Это слово – ЛОГАРИФМ (СЛОВО – logos, ЧИСЛО – arithmos). Полученные расшифровки, по сути, являются подсказкой: для того, чтобы познать тайную сущность СЛОВА, необходимо прологарифмировать числовой аналог СЛОВА.  Чтобы узнать, какое же число было в НАЧАЛЕ, вновь учтем, что буква О идентична по написанию цифре 0, а слово логарифм объединяет корни двух указанных греческих слов и прологарифмируем числовое представление слова СЛОВО, предположив, что операция логарифмирования позволяет выявить связь между СЛОВОМ и ЧИСЛОМ:lg1913030 = 6,281722.Чтобы у дешифровщика не возникло сомнений, что в логарифме СЛОВА 6,28 – это первых три цифры значения 2?, за первыми тремя знаками 2? следует 17 – порядковый номер буквы p кириллицы, идентичной в письме букве ? греческого алфавита, от которой она и происходит и цифра 2. В итоге 1722 (2 17 2 после перестановки) может быть прочитано, как «2? дважды». Так как цифра 6 соответствует букве е кириллицы, а цифры 2 и 3 по шифру взаимозаменяемы, то начало (6-е) и конец (3) логарифма СЛОВА означают «e трижды». Чтобы дешифровщик понял, что буква e соответствует общепринятому обозначению основания натуральных логарифмов (ОНЛ), в кольцевой записи логарифма СЛОВА после «e трижды» читаются первые 5 знаков (2,7182) значения e. Бог, у которого “было СЛОВО”, умел логарифмировать и знал значения Пи и е?Христиане считают Богом Иисуса Христа, рожденного смертной женщиной Марией. Я не буду останавливаться на вызывающих сомнение догматах непорочного зачатия и воскрешения. Отмечу неподлежащее сомнению. У Иисуса были земные родители и 2000 лет назад люди понятия не имели ни о логарифмах, ни об основании натуральных логарифмов. В настоящее время обучение логарифмированию, числа ? и е служат элементами школьного образования. И надо полагать, что СЛОВО намного древнее Иисуса, а Знание, заключенное в СЛОВЕ Бога (Мирового Разума), должно быть существенно сложнее школьного знания ныне живущих.На многочисленных примерах можно показать, что не только е и ?, но и другие, используемые сейчас общепринятые в науке символы для обозначения математических и физических величин, изначально заданы в сценарии и используются для этих же целей. Так, таинственные Алфа(?) и Омега(?) в Апокалипсисе Иоанна Богослова обозначают: ? – мировые физические константы (постоянную тонкой структуры и константу гравитационного взаимодействия), а ? – угловые скорости вращательных движений Земли и угловую скорость вращения Вселенной [2]. С учетом вышеизложенного числовую кальку слова СЛОВО – 1913030 в буквенном виде можно представить как А3 АБ ОВО и Аз АБ ОВО. В первом варианте АЗ является аббревиатурой словосочетания Абсолютное Знание, во втором читается как старославянское Аз (личное местоимение Я). На слух последние 5 букв воспринимаются как широко известное латинское выражение ab ovo (от яйца, с самого начала ), поэтому с учётом идентичности звучания бывшее в начале всего сущего СЛОВО означает:      Абсолютное Знание от начала начал;      Я от начала начал.Подставив эти расшифровки в (1), получим:Да, Абсолютное Знание от начала начал – ЧИСЛО; Да, Я от начала начал – ЧИСЛО. (2) Так как согласно Иоанну Богослову ‘‘Слово было у Бога, и Слово было Бог’’, то из (2) следует, что Бог – изначальное Абсолютное Знание, выраженное в числах и словах.Под Абсолютным Знанием Бога необходимо подразумевать не только научное физическое знание об устройстве мироздания, строении материи и мировых константах [1], но и эзотерическое знание о будущем, предопределенным так называемыми Планами Господними.

—–ХХХ——

Корнеев А. А. Москва, 1992 г.

Задание 14. . Какие трёхзначные числа можно составить из цифр 0, 1, 2? Решите задачу, достроив дерево возможных вариантов.

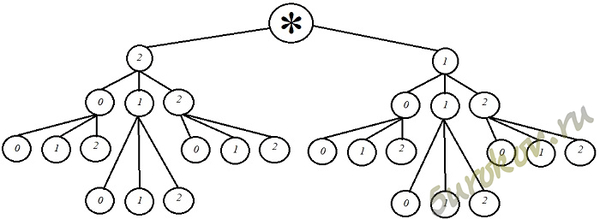
Из цифр 0, 1 и 2 можно составить 18 трёхзначных чисел: 100, 101, 102, 110, 111, 112, 120, 121, 122, 200, 201, 202, 210, 211, 212, 220, 221 и 222.
Ответ: 100, 101, 102, 110, 111, 112, 120, 121, 122, 200, 201, 202, 210, 211, 212, 220, 221 и 222

Скачать материал

без ожидания

Скачать материал

без ожидания

Дерево решений является одним из наиболее часто используемых и эффективных графических представлений возможных результатов связанных выборов. Используя дерево решений, человек может взвешивать действия на основе решения, которое он принимает. Кроме того, дерево решений может помочь вам принять наиболее важное решение, которое вы принимаете. Однако многие люди задаются вопросом, какое приложение можно использовать для создания дерева решений. И если вы не знаете, Microsoft Excel — это приложение, которое вы можете использовать для создания дерева решений. Microsoft Excel — это не просто приложение для работы с электронными таблицами, с его помощью вы также можете создать дерево решений. Итак, прочитайте эту статью полностью, чтобы узнать как сделать дерево решений в экселе.

• Часть 1. Как создать дерево решений с помощью Excel
• Часть 2. Плюсы и минусы использования Excel для построения дерева решений
• Часть 3. Лучшая альтернатива Excel при создании дерева решений
• Часть 4. Часто задаваемые вопросы о том, как сделать дерево решений в Excel

Часть 1. Как создать дерево решений с помощью Excel

Microsoft Excel — это приложение, которое использует электронные таблицы для упорядочивания чисел и данных, касающихся формул и функций. Многие профессионалы используют Microsoft Excel для бизнес-приложений для форматирования и вычисления данных, необходимых для определенной цели. Он широко используется в бизнесе, школах и многих других профессиях. А ниже мы покажем вам, как создать дерево решений с помощью Excel.

Следуя описанным выше шагам, вы можете легко построить дерево решений с помощью Excel.

Часть 2. Плюсы и минусы использования Excel для построения дерева решений

Как и другие инструменты или приложения, Microsoft Excel имеет свои преимущества и недостатки при создании дерева решений.

Часть 3. Лучшая альтернатива Excel при создании дерева решений

Если вы предпочитаете использовать стандартный конструктор дерева решений, у нас есть лучшая альтернатива. Microsoft Excel позволяет составить дерево решений; однако существует множество ограничений, с которыми вы можете столкнуться. Итак, в этой части мы покажем вам еще одно приложение для построения дерева решений.

MindOnMap — одно из лучших приложений для создания дерева решений. Это приложение позволяет вам легко составить дерево решений, используя блок-схему, TreeMap или опцию Right Map. Кроме того, вы можете делать множество вещей, таких как организационные диаграммы, интеллект-карты, блок-схемы, древовидные карты и многое другое. Он также имеет готовые шаблоны, которые вы можете использовать для создания дерева решений. А с помощью этого приложения вы можете делать заметки в режиме реального времени во время занятий, чтобы эффективно просматривать уроки.
Кроме того, вы можете использовать уникальные и удивительные значки, чтобы добавить больше остроты в ваше дерево решений. Что еще фантастического в этом приложении, так это то, что вы можете поделиться ссылкой со своими друзьями или коллегами для работы с вашим деревом решений. Кроме того, вы можете экспортировать свой проект в различные выходные форматы, такие как PNG, JPG, SVG, PDF и другие. Следуйте приведенным ниже инструкциям, если вы предпочитаете использовать MindOnMap для создания дерева решений.

Как составить дерево решений с помощью MindOnMap

Часть 4. Часто задаваемые вопросы о том, как сделать дерево решений в Excel