Содержание:
- § 1 Понятие алгебраической дроби
- § 2 Допустимые значения переменных алгебраической дроби
§ 1 Понятие алгебраической дроби
Алгебраической дробью называют выражение
![]()
где Р и Q —многочлены; Р — числитель алгебраической дроби, Q — знаменатель алгебраической дроби.
Вот примеры алгебраических дробей:
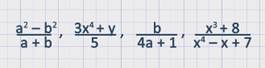
Любой многочлен – это частный случай алгебраической дроби, потому что любой многочлен можно записать в виде
![]()
Например:
![]()
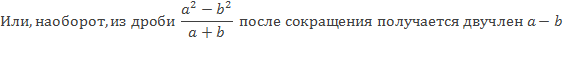
Значение алгебраической дроби зависит от значения переменных.
Например, вычислим значение дроби
![]()
1)![]()
2)![]()
В первом случае получаем:
![]()
Заметим, данную дробь можно сократить:
![]()
Таким образом, вычисление значения алгебраической дроби упрощается. Воспользуемся этим.
Во втором случае получим:
![]()
Как видно, с изменением значений переменных изменилось значение алгебраической дроби.
§ 2 Допустимые значения переменных алгебраической дроби
Рассмотрим алгебраическую дробь
![]()
Значение x = –1 является недопустимым для данной дроби, т.к. знаменатель дроби при таком значении х обращается в нуль. При этом значении переменной алгебраическая дробь не имеет смысла.
Таким образом, допустимыми значениями переменных алгебраической дроби являются такие значения переменных, при которых знаменатель дроби не обращается в нуль.
Решим несколько примеров.
Пример 1:
При каких значениях переменной не имеет смысла алгебраическая дробь:
![]()
Решение:
Для нахождения недопустимых значений переменных знаменатель дроби приравнивается к нулю, и находятся корни соответствующего уравнения.
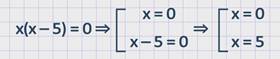
Ответ:
![]()
Пример 2:
При каких значениях переменной равна нулю алгебраическая дробь:
![]()
Решение:
Дробь равна нулю, если числитель равен нулю. Приравняем к нулю числитель нашей дроби и найдем корни получившегося уравнения:
![]()
Далее следует найти недопустимые значения переменной х. Действуем как в предыдущем примере, приравниваем к нулю знаменатель алгебраической дроби и решаем получившееся уравнение:
![]()
Таким образом, при x = 0 и x= 3 данная алгебраическая дробь не имеет смысла, а значит, мы должны исключить эти значения переменной из ответа.
Ответ:
![]()
Итак, на этом уроке Вы изучили основные понятия алгебраической дроби: числитель и знаменатель дроби, а также допустимые значения переменных алгебраической дроби.
Список использованной литературы:
- Мордкович А.Г. «Алгебра» 8 класс. В 2 ч. Ч.1 Учебник для общеобразовательных учреждений / А.Г. Мордкович. – 9-е изд., перераб. – М.: Мнемозина, 2007. – 215 с.: ил.
- Мордкович А.Г. «Алгебра» 8 класс. В 2 ч. Ч.2 Задачник для общеобразовательных учреждений / А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская. – 8-е изд., – М.: Мнемозина, 2006 – 239с.
- Алгебра. 8 класс. Контрольные работы для учащихся образовательных учреждений Л.А. Александрова под ред. А.Г. Мордковича 2-е изд., стер. – М.: Мнемозина 2009. – 40с.
- Алгебра. 8 класс. Самостоятельные работы для учащихся образовательных учреждений: к учебнику А.Г. Мордковича, Л.А. Александрова под ред. А.Г. Мордковича. 9-е изд., стер. – М.: Мнемозина 2013. – 112с.
Содержание:
Вы уже знакомы с целыми рациональными выражениями, то есть с выражениями, которые не содержат деления на выражение с переменной, например:
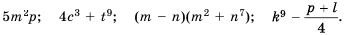
Любое целое выражение можно представить в виде многочлена стандартного вида, например:
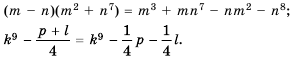
В отличие от целых выражений, выражения
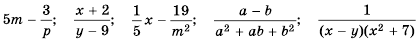
содержат деление на выражение с переменной. Такие выражения называют дробными рациональными выражениями. Целые рациональные и дробные рациональные выражения называют рациональными выражениями.
Рациональные выражения — это математические выражения, содержащие действии сложения, вычитания, умножения, деления и возведения в степень с целым показателем.
Определение рациональной дроби
Рациональное выражение вида 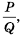 , где
, где 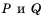 – выражения, содержащие числа или переменные, называют дробью. Выражение
– выражения, содержащие числа или переменные, называют дробью. Выражение 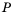 – ее числитель, a
– ее числитель, a 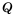 – знаменатель. Если
– знаменатель. Если 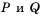 в дроби – многочлены, то дробь называют рациональной дробью.
в дроби – многочлены, то дробь называют рациональной дробью.
Целое рациональное выражение имеет смысл при любых значениях входящих в него переменных, так как при нахождении его значения выполняют действия сложения, вычитания, умножения и деления на число, отличное от нуля, что всегда выполнимо.
Рассмотрим дробное рациональное выражение — 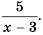 . Его значение можно найти для любого
. Его значение можно найти для любого 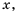 кроме
кроме 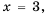 так как при
так как при 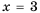 знаменатель дроби обращается в нуль. В этом случае говорят, что выражение
знаменатель дроби обращается в нуль. В этом случае говорят, что выражение 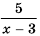 имеет смысл при всех значениях переменной
имеет смысл при всех значениях переменной 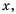 кроме
кроме 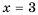 (или же при
(или же при 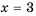 не имеет смысла).
не имеет смысла).
Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных в выражении.
Эти значения образуют область определения выражения, или область допустимых значений переменных в выражении.
Пример:
Найдите допустимые значения переменной в выражении:
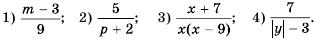
Решение:
1) Выражение имеет смысл при любых значениях переменной 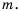 2) Допустимые значения переменной
2) Допустимые значения переменной 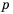 – все числа, кроме числа
– все числа, кроме числа 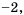 так как это число обращает знаменатель дроби в нуль. 3) Знаменатель дроби
так как это число обращает знаменатель дроби в нуль. 3) Знаменатель дроби 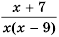 обращается в нуль при
обращается в нуль при 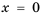 или
или 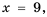 поэтому допустимые значения переменной
поэтому допустимые значения переменной 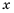 – все числа, кроме чисел 0 и 9. 4) Допустимые значения переменной
– все числа, кроме чисел 0 и 9. 4) Допустимые значения переменной 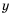 – все числа, кроме 3 и -3.
– все числа, кроме 3 и -3.
Кратко ответы можно записать следующим образом: 1) 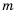 – любое число;
– любое число; 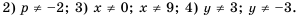
Рассмотрим условие равенства дроби нулю. Так как 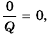 если
если 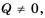 то можно сделать вывод, что дробь
то можно сделать вывод, что дробь 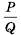 равна нулю тогда и только тогда, когда числитель
равна нулю тогда и только тогда, когда числитель 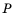 равен нулю, а знаменатель
равен нулю, а знаменатель 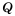 не равен нулю, то есть
не равен нулю, то есть 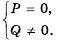
Пример:
При каких значениях переменной равно нулю значение дроби:
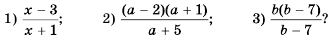
Решение:
1) Числитель дроби равен нулю при 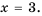 Это значение переменной не обращает знаменатель в нуль, поэтому число 3 является значением переменной, при котором данная дробь равна нулю. 2) Числитель дроби равен нулю при
Это значение переменной не обращает знаменатель в нуль, поэтому число 3 является значением переменной, при котором данная дробь равна нулю. 2) Числитель дроби равен нулю при 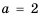 или
или  Для каждого из этих значений знаменатель дроби нулю не равен. Поэтому числа 2 и -1 – те значения переменной, при которых данная дробь равна нулю. 3) Числитель дроби равен нулю, если
Для каждого из этих значений знаменатель дроби нулю не равен. Поэтому числа 2 и -1 – те значения переменной, при которых данная дробь равна нулю. 3) Числитель дроби равен нулю, если 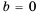 или
или 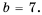 При
При 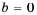 знаменатель дроби нулю не равен, а при
знаменатель дроби нулю не равен, а при 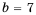 знаменатель дроби обращается в нуль, то есть такой дроби не существует. Следовательно, данная дробь равна нулю только при
знаменатель дроби обращается в нуль, то есть такой дроби не существует. Следовательно, данная дробь равна нулю только при 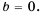
Ответ. 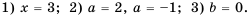
А еще раньше
Древнегреческий математик Диофант (прибл.  в. н. э.) рассмотрел рациональные дроби и действия с ними в своей работе «Арифметика». В частности, на страницах этой книги можно встретить доказательство тождеств
в. н. э.) рассмотрел рациональные дроби и действия с ними в своей работе «Арифметика». В частности, на страницах этой книги можно встретить доказательство тождеств
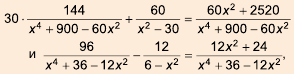
записанных символикой того времени.
Выдающийся английский ученый Исаак Ньютон (1643-1727) в своей монографии «Универсальная арифметика» (1707 г.) определяет дробь следующим образом: «Запись одной из двух величин под другой, ниже которой между ними проведена черта, означает часть или же величину, возникающую при делении верхней величины на нижнюю». В этой работе Ньютон рассматривает не топько обычные дроби, но и рациональные.
Определение: Дробь, числитель и знаменатель которой — многочлены, называется рациональной дробью.
Например, выражения 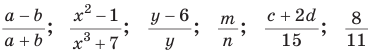
являются рациональными дробями.
Рациональная дробь является рациональным выражением. Выражения, составленные из чисел, переменных с помощью действий сложения, вычитания, умножения, деления, возведения в натуральную степень, называют рациональными выражениями.
Если рациональное выражение не содержит деления на выражение с переменными, то оно называется целым рациональным выражением.
Рассмотрим задачу: Туристы в первый день проплыли на лодке по течению реки 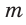 км, а во второй — на 6 км больше. Сколько времени продолжалось все путешествие, если собственная скорость лодки равна
км, а во второй — на 6 км больше. Сколько времени продолжалось все путешествие, если собственная скорость лодки равна 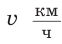 , а скорость течения реки —
, а скорость течения реки — 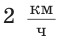 ?
?
Решение:
Так как за два дня туристы преодолели 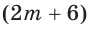 км по течению реки, а скорость движения лодки по течению реки равна
км по течению реки, а скорость движения лодки по течению реки равна 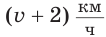 , то время, затраченное на весь путь, ч равно
, то время, затраченное на весь путь, ч равно 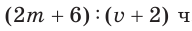 . Частное
. Частное 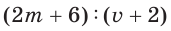 можно записать в виде дроби
можно записать в виде дроби 
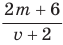 .
.
Ответ: 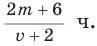
При решении этой задачи получили дробь, в числителе и знаменателе которой записаны многочлены. Такая дробь называется рациональной.
Целые рациональные выражения
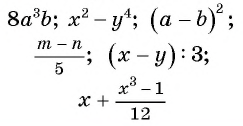
Например, выражения 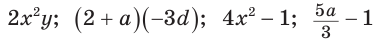 являются целыми рациональными выражениями.
являются целыми рациональными выражениями.
Рациональное выражение, содержащее деление на выражение с переменными, называют дробным рациональным выражением.
Дробные рациональные выражения
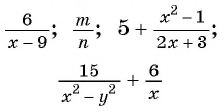
Например, выражения 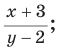
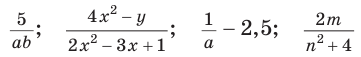 являются дробными рациональными выражениями, поскольку содержат (кроме действий сложения, вычитания, умножения) деление на выражение с переменными.
являются дробными рациональными выражениями, поскольку содержат (кроме действий сложения, вычитания, умножения) деление на выражение с переменными.
Связь между понятиями «рациональная дробь», «целое рациональное выражение» и «дробное рациональное выражение» иллюстрирует рисунок 1.
Целые рациональные выражения имеют смысл при любых значениях входящих в них переменных.
Например, областью определения выражения 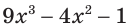 является множество всех действительных чисел.
является множество всех действительных чисел.
Рациональные выражения:
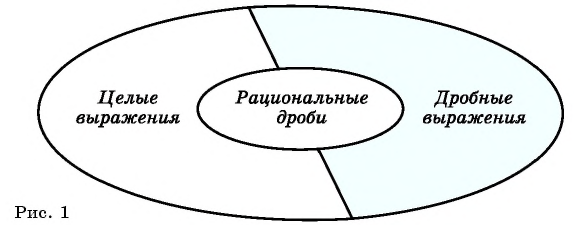
Дробные рациональные выражения имеют смысл при всех значениях переменных, кроме тех, которые обращают знаменатели дробей в нуль.
Например, выражение 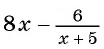 при
при 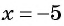 не имеет смысла, так как при
не имеет смысла, так как при 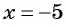 знаменатель дроби
знаменатель дроби 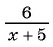 обращается в нуль. Значит, данное выражение имеет смысл при всех значениях переменной, кроме
обращается в нуль. Значит, данное выражение имеет смысл при всех значениях переменной, кроме 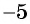 .
.
Рациональная дробь  имеет смысл при любых значениях переменной, кроме чисел
имеет смысл при любых значениях переменной, кроме чисел 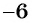 и
и 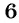 , так как при
, так как при 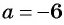 и при
и при 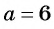 знаменатель дроби обращается в нуль.
знаменатель дроби обращается в нуль.
Областью определения рациональной дроби является множество всех значений входящих в нее переменных, кроме тех, которые обращают ее знаменатель в нуль.
Пример №1
Найдите область определения рациональной дроби:
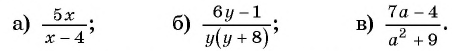
Решение:
а) Областью определения рациональной дроби 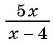 является множество всех действительных чисел, кроме числа
является множество всех действительных чисел, кроме числа 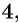 так как при
так как при 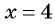 знаменатель дроби обращается в нуль. Можно записать:
знаменатель дроби обращается в нуль. Можно записать: 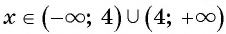 .
.
б) Найдем, при каких значениях переменной знаменатель дроби 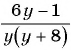 обращается в нуль. Для этого решим уравнение
обращается в нуль. Для этого решим уравнение 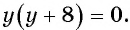 Корнями данного уравнения являются числа
Корнями данного уравнения являются числа 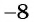 и
и 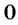 . Значит, областью определения дроби
. Значит, областью определения дроби 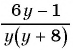 является множество всех действительных чисел, кроме чисел
является множество всех действительных чисел, кроме чисел 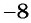 и
и 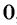 , т. е.
, т. е. 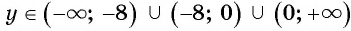 .
.
в) Поскольку выражение 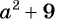 является положительным числом при любых значениях переменной, то нет таких значении переменной, при которых знаменатель дроби
является положительным числом при любых значениях переменной, то нет таких значении переменной, при которых знаменатель дроби 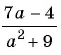 был бы равен нулю. Значит, рациональная дробь имеет смысл при любых значениях переменной, т. е. областью определения дроби является множество всех действительных чисел,
был бы равен нулю. Значит, рациональная дробь имеет смысл при любых значениях переменной, т. е. областью определения дроби является множество всех действительных чисел, 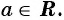
Рациональные выражения:
Пример №2
Какие из следующих выражений:
а) 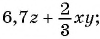
б) 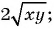
в) 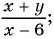
г) 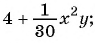
д) 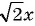 — являются рациональными?
— являются рациональными?
Решение:
Выражения а), в), г) и д) являются рациональными, так как составлены из чисел, переменных и содержат действия сложения, вычитания, умножения и деления. Выражение б) не является рациональным, так как содержит действие извлечения корня из выражения с переменными.
Пример №3
Какие из следующих выражений:
а) 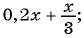
б) 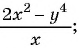
в) 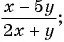
г) 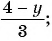
д) 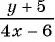 — являются дробными рациональными?
— являются дробными рациональными?
Решение:
Выражения б), в), д) являются дробными рациональными, так как составлены из чисел, переменных, натуральных степеней переменных с помощью действий сложения, вычитания, умножения и содержат действие деления на рациональное выражение с переменными.
Пример №4
Какие из следующих выражений:
а) 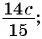
б) 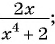
в) 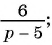
г) 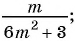
д) 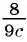 являются рациональными дробями?
являются рациональными дробями?
Решение:
Выражения а) — д) являются рациональными дробями, так как каждое из них представляет собой дробь, числитель и знаменатель которой являются многочленами.
Пример №5
Найдите значение выражения:
а) 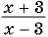 при
при 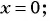
б) 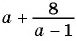 при
при 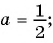
в) 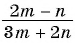 при
при 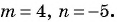
Решение:
а) Подставим 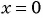 в выражение
в выражение 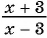 , и получим:
, и получим: 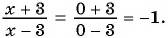
б) При 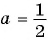 имеем:
имеем:
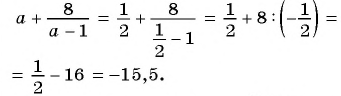
в) Если 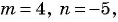 то
то 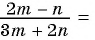
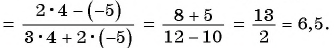
Область определения рациональной дроби
Пример №6
Найдите область определения рациональной дроби:
а) 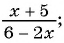
б) 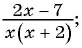
в) 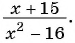
Решение:
а) Найдем, при каком значении переменной знаменатель дроби обращается в нуль. Для этого решим уравнение 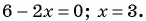 Областью определения данной дроби является множество всех действительных чисел, кроме числа 3, т. е.
Областью определения данной дроби является множество всех действительных чисел, кроме числа 3, т. е. 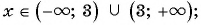
б) 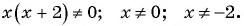 Областью определения данной дроби является множество всех действительных чисел, кроме чисел
Областью определения данной дроби является множество всех действительных чисел, кроме чисел 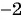 и
и 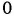 , т. е.
, т. е. 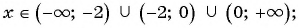
в) 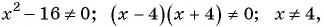
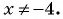 Областью определения данной дроби является множество всех действительных чисел, кроме чисел
Областью определения данной дроби является множество всех действительных чисел, кроме чисел 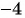 и
и 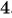 . Значит,
. Значит, 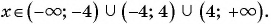
Пример №7
Найдите область определения рационального выражения:
а) 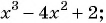
б) 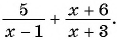
Решение:
а) Выражение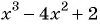 является целым рациональным, его областью определения является множество всех действительных чисел, т. е.
является целым рациональным, его областью определения является множество всех действительных чисел, т. е. 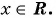
б) Знаменатель первой дроби обращается в нуль при 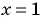 , а знаменатель второй дроби равен нулю при
, а знаменатель второй дроби равен нулю при 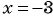 . Значит, областью определения данного выражения является множество всех действительных чисел, кроме чисел
. Значит, областью определения данного выражения является множество всех действительных чисел, кроме чисел 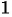 и
и 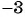 . Таким образом,
. Таким образом, 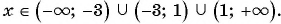
Основное свойство рациональной дроби
Действия с рациональными дробями выполняются по тем же правилам, что с обыкновенными дробями. Так, согласно основному свойству обыкновенных дробей, если числитель и знаменатель дроби умножить или разделить на одно и то же число, не равное нулю, то получится дробь, равная данной.
Например, 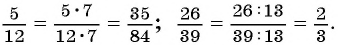
Аналогичное свойство можно сформулировать для рациональных дробей.
Если числитель и знаменатель дроби умножить или разделить на одно и то же выражение, не равное нулю, то получится дробь, тождественно равная данной.
Это свойство называют основным свойством дроби.
Для любой рациональной дроби 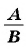 справедливо тождество
справедливо тождество 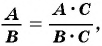 где
где 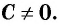
Умножим числитель и знаменатель дроби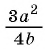 на одночлен
на одночлен 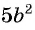 и получим:
и получим: 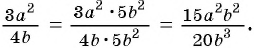 В этом случае говорят, что дробь
В этом случае говорят, что дробь 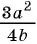 привели к новому знаменателю
привели к новому знаменателю 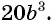
Пример №8
Приведите дробь:
а) 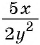 к знаменателю
к знаменателю 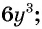
б) 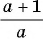 к знаменателю
к знаменателю 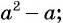
в) 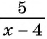 к знаменателю
к знаменателю 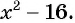
Решение:
а) 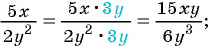
б) 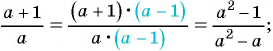
в) 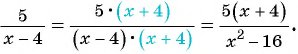
Если основное свойство дроби записать справа налево, то получится равенство
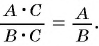
Это равенство позволяет дробь 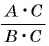 заменить на тождественно равную ей дробь
заменить на тождественно равную ей дробь 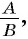 разделив числитель и знаменатель дроби
разделив числитель и знаменатель дроби 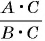 на множитель
на множитель 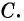
Например, разделим числитель и знаменатель дроби 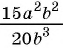 на одночлен
на одночлен 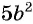 и получим:
и получим: 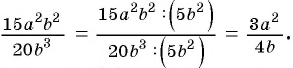 В этом случае говорят, что дробь
В этом случае говорят, что дробь 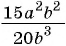 сократили на множитель
сократили на множитель 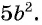 .
.
Сократить рациональную дробь — это значит числитель и знаменатель дроби разделить на их общий множитель.
Например, сократим дробь 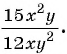 Для этого нужно найти множитель, на который можно разделить числитель и знаменатель дроби. Одночлены
Для этого нужно найти множитель, на который можно разделить числитель и знаменатель дроби. Одночлены 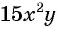 и
и 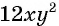 имеют общий множитель
имеют общий множитель 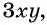 на который можно сократить данную дробь:
на который можно сократить данную дробь:
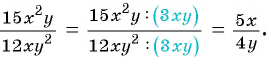
Чтобы сократить рациональную дробь, нужно:
- Разложить (если возможно) числитель и знаменатель дроби на множители.
- Определить общий множитель числителя и знаменателя дроби.
- Разделить числитель и знаменатель данной дроби на общий множитель.
Сократите дробь 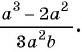
(1) 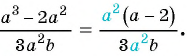
(2) 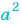 — общий множитель числителя и знаменателя дроби.
— общий множитель числителя и знаменателя дроби.
(3) 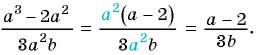
Пример №9
Сократите дробь:
а) 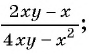
б) 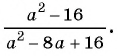
Решение:
а)
- (1) Разложим числитель и знаменатель дроби на множители:
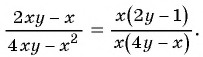
- (2) Числитель и знаменатель дроби имеют общий множитель
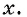
- (3) Разделим числитель и знаменатель данной дроби на общий множитель, т. е. сократим дробь:
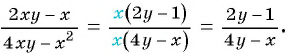
б)
Из основного свойства дроби следует, что 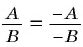 и
и 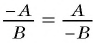 (и в том и в другом случае вторая дробь получена из первой умножением числителя и знаменателя на
(и в том и в другом случае вторая дробь получена из первой умножением числителя и знаменателя на 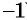 ).
).
Пример №10
Приведите дробь 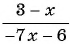 к знаменателю
к знаменателю 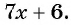
Решение:
Воспользуемся равенством 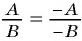 и получим:
и получим: 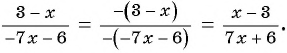
Пример №11
Сократите дробь:
а) 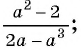
б) 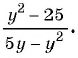
Решение:
а) Разложим знаменатель дроби на множители и получим:
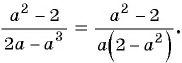
Выражения 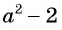 и
и 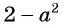 отличаются только знаками. Чтобы сократить дробь, поменяем знаки одного из множителей
отличаются только знаками. Чтобы сократить дробь, поменяем знаки одного из множителей 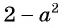 или
или 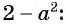
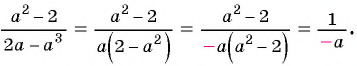
Полученный ответ можно записать в виде 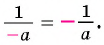 В этом случае говорят, что знак «минус» поставили перед дробью.
В этом случае говорят, что знак «минус» поставили перед дробью.
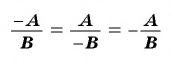
б) Разложим числитель и знаменатель дроби на множители и получим:
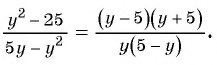
Поменяем знаки одного из множителей 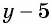 или
или 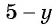 и поставим знак «минус» перед дробью:
и поставим знак «минус» перед дробью:
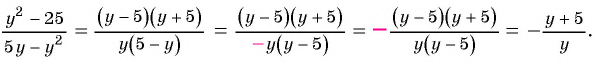
Пример №12
Приведите дробь 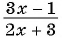 к знаменателю:
к знаменателю:
а) 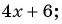
б) 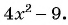
Решение:
а) Умножим числитель и знаменатель дроби на 2 и получим:
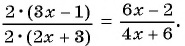
б) Умножим числитель и знаменатель дроби на 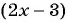 и получим:
и получим: 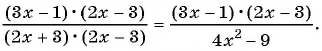
Разберём лекцию подробно:
Вспомним основное свойство обыкновенной дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получим дробь, равную данной. Иначе говоря, для любых натуральных чисел 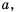
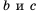 справедливо равенство:
справедливо равенство:
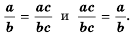
Докажем, что эти равенства являются верными не только для натуральных значений 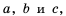 но и для любых других значений при условии
но и для любых других значений при условии 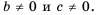
Докажем сначала, что 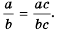
Пусть 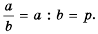 Тогда по определению частного
Тогда по определению частного 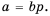 Умножим обе части этого равенства на
Умножим обе части этого равенства на 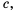 получим:
получим: 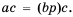 Используя переставное и сочетательное свойства умножения, приходим к равенству:
Используя переставное и сочетательное свойства умножения, приходим к равенству: 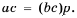 Так как
Так как 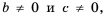 то и
то и 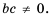 Из последнего равенства (по определению частного) имеем:
Из последнего равенства (по определению частного) имеем: 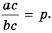 Поскольку
Поскольку 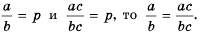
Это равенство является тождеством, следовательно, можем поменять в нем левую и правую части местами:
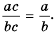
Это тождество дает возможность заменить дробь 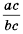 на дробь
на дробь 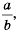 , то есть сократить дробь
, то есть сократить дробь 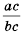 на общий множитель
на общий множитель 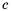 числителя и знаменателя.
числителя и знаменателя.
Свойство дроби, выраженное равенствами 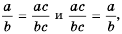 называют основным свойством рациональной дроби.
называют основным свойством рациональной дроби.
Если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля выражение, то получим дробь, равную данной.
Рассмотрим примеры применения этого свойства для дробей на их области допустимых значений переменной.
Пример №13
Сократите дробь 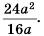
Решение:
Представим числитель и знаменатель этой дроби в виде произведений, содержащих одинаковый (общий) множитель 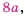 и сократим дробь на это выражение:
и сократим дробь на это выражение:
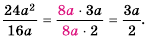
Ответ: 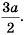
Пример №14
Сократите дробь 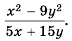
Решение:
Разложим на множители числитель и знаменатель дроби: 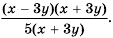 Сократим дробь на
Сократим дробь на 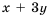 – общий множитель числителя и знаменателя:
– общий множитель числителя и знаменателя: 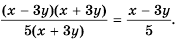
Ответ: 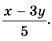
Таким образом, чтобы сократить дробь, нужно:
- разложить на множители числитель и знаменатель дроби, если это необходимо;
- выполнить деление числителя и знаменателя на их общий множитель и записать ответ.
Тождество 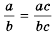 дает возможность приводить дроби к заданному другому (новому) знаменателю.
дает возможность приводить дроби к заданному другому (новому) знаменателю.
Пример №15
Приведите дробь 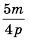 к знаменателю
к знаменателю 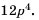
Решение:
Поскольку 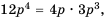 то, умножив числитель и знаменатель дроби
то, умножив числитель и знаменатель дроби 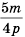 на
на 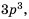 получим дробь со знаменателем
получим дробь со знаменателем 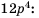
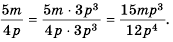
Множитель 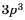 называют дополнительным множителем числителя и знаменателя дроби
называют дополнительным множителем числителя и знаменателя дроби 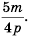
Ответ: 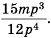
Пример №16
Приведите дробь 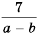 к знаменателю
к знаменателю 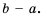
Решение:
Поскольку 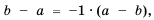 то, умножив числитель и знаменатель дроби
то, умножив числитель и знаменатель дроби 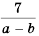 на -1, получим дробь со знаменателем
на -1, получим дробь со знаменателем 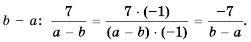
Дробь 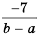 можно заменить тождественно равным ему выражением
можно заменить тождественно равным ему выражением 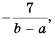 так как изменение знака перед дробью приводит к изменению знака в числителе или знаменателе.
так как изменение знака перед дробью приводит к изменению знака в числителе или знаменателе.
Поэтому 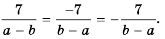
Ответ. 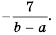
Аналогично, например, 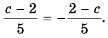 Следовательно,
Следовательно,
- если изменить знак в числителе (или знаменателе) дроби одновременно со знаком перед дробью, то получим дробь, тождественно равную данной.
Это правило можно записать с помощью тождества:
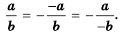
Пример №17
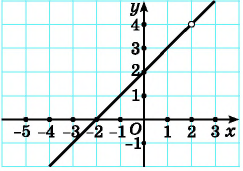
Найдите область определения функции 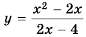 и постройте ее график.
и постройте ее график.
Решение:
Область определения функции – все числа, кроме тех, которые обращают знаменатель 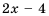 в нуль. Так как
в нуль. Так как 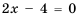 при
при 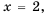 то область определения функции все числа, кроме числа 2. Упростим дробь
то область определения функции все числа, кроме числа 2. Упростим дробь 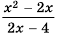 путем сокращения:
путем сокращения: 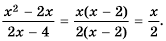 Следовательно, функция
Следовательно, функция 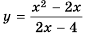 имеет вид
имеет вид 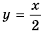 при условии
при условии 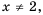 а ее графиком является прямая
а ее графиком является прямая 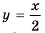 точки с абсциссой 2, то есть без точки (2; 1). Такую точку называют «выколотой» и обязательно исключают ее из графика, изображая «пустой».
точки с абсциссой 2, то есть без точки (2; 1). Такую точку называют «выколотой» и обязательно исключают ее из графика, изображая «пустой».
График функции 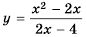 представлен на рисунке 1.
представлен на рисунке 1.
Сокращение рациональных дробей
Пример №18
Сократите дробь 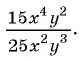
Решение:
Дробь можно сократить на 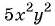 — общий множитель числителя и знаменателя дроби:
— общий множитель числителя и знаменателя дроби:
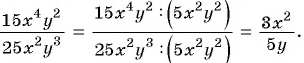
Пример №19
Сократите дробь:
а) 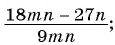
б) 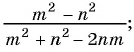
в) 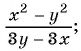
г) 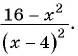
Решение:
а) Разложим на множители числитель дроби и сократим дробь:
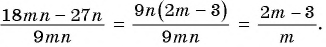
б) С помощью формул сокращенного умножения разложим на множители числитель и знаменатель дроби и получим:
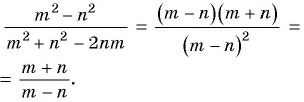
в) Разложим на множители числитель и знаменатель дроби:
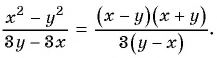
Множители 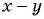 и
и 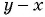 отличаются только знаками. Поменяем знаки одного из множителей
отличаются только знаками. Поменяем знаки одного из множителей 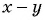 или
или 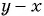 и поставим знак «минус» перед дробью:
и поставим знак «минус» перед дробью:
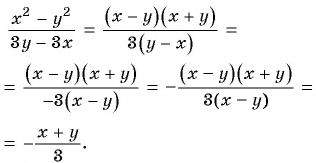
г) После разложения на множители числителя дроби имеем:
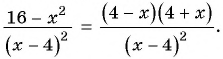
Воспользуемся тем, что 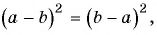 т. е.
т. е. 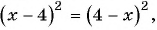 и получим:
и получим:
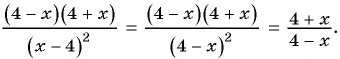
Пример №20
Сократите дробь:
а) 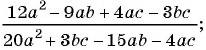
б) 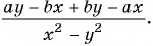
Решение:
а) С помощью способа группировки разложим числитель и знаменатель дроби на множители и сократим дробь:
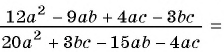
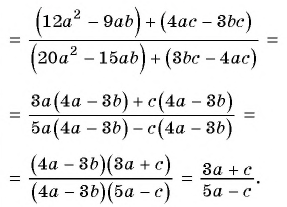
б) 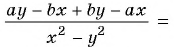
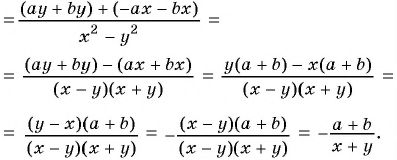
Пример №21
Сократите дробь:
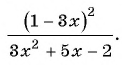
Решение:
Для разложения на множители знаменателя дроби воспользуемся формулой разложения квадратного трехчлена на множители: 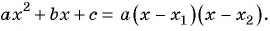 Найдем корни квадратного трехчлена
Найдем корни квадратного трехчлена 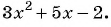 Для этого решим квадратное уравнение
Для этого решим квадратное уравнение 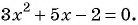
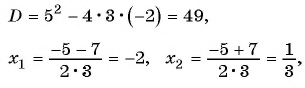
тогда 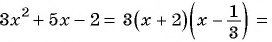
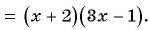
Сократим дробь:
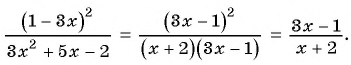
Пример №22
Упростите выражение 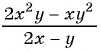 и найдите его значение при
и найдите его значение при 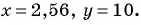
Решение:
Упростим выражение, сократив дробь:
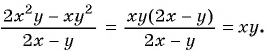
Подставим 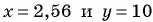 в выражение
в выражение 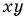 и получим
и получим 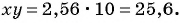
Пример №23
Из данных рациональных дробей выберите дробь, тождественно равную дроби 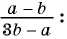
а) 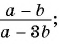
б) 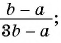
в) 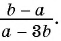
Решение:
Выполним преобразования:
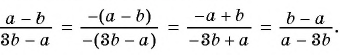
Дроби 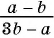 тождественно равна дробь в).
тождественно равна дробь в).
Пример №24
Приведите дробь:
а) 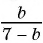 к знаменателю
к знаменателю 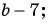
б) 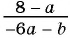 к знаменателю
к знаменателю 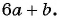
Решение:
Умножим числитель и знаменатель дроби на 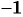 и получим:
и получим:
а) 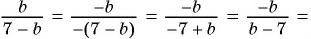
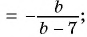
б) 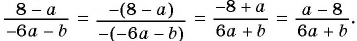
Пример №25
Постройте график функции 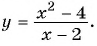
Решение:
Областью определения данной функции является множество всех действительных чисел, кроме числа 2.
Сократим дробь 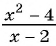 и получим:
и получим:
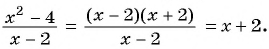
Необходимо построить график функции 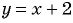 при
при 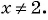 Графиком данной функции является прямая
Графиком данной функции является прямая 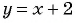 без точки (2; 4).
без точки (2; 4).
Сложение и вычитание рациональных дробей
Вспомним, как складывают и вычитают обыкновенные дроби. Например:
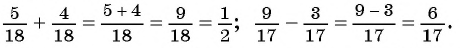
Сложение и вычитание рациональных дробей выполняются по таким же правилам, что сложение и вычитание обыкновенных дробей.
Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тем же.
Затем, если возможно, следует сократить полученную дробь.
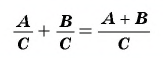
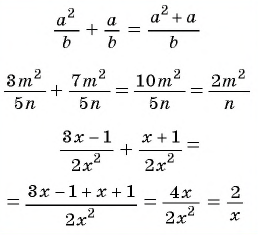
Пример №26
Найдите сумму рациональных дробей:
а) 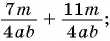
б) 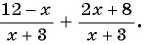
Решение:
а) 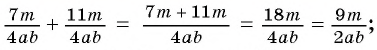
б) 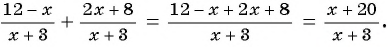
Чтобы вычесть дроби с одинаковыми знаменателями, нужно из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тем же. Затем, если возможно, следует сократить полученную дробь.
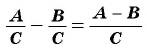
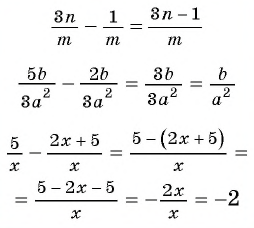
Пример №27
Найдите разность рациональных дробей:
а) 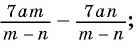
б) 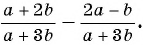
Решение:
а) 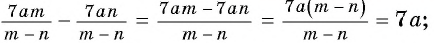
б) 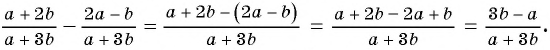
При сложении и вычитании обыкновенных дробей с разными знаменателями их приводят к общему знаменателю (например, 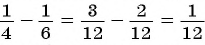 ).
).
Для того чтобы выполнить сложение или вычитание рациональных дробей с разными знаменателями, их также нужно привести к общему знаменателю.
Чтобы привести рациональные дроби к общему знаменателю, нужно:
- Разложить знаменатель каждой дроби на множители (если это необходимо) и определить общий знаменатель дробей.
- Умножить числитель и знаменатель каждой дроби на недостающие множители из общего знаменателя дробей.
Приведите к общему знаменателю рациональные дроби 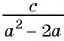 и
и 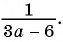
(1) 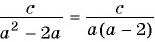 и
и 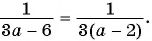
Общий знаменатель 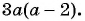
(2) 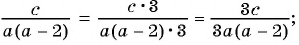
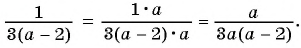
Пример №28
Приведите к общему знаменателю дроби: а) 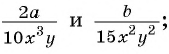
б) 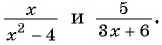
Решение:
а) Общим знаменателем данных дробей является одночлен 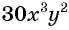 , поскольку НОК (10, 15) = 30 и переменные
, поскольку НОК (10, 15) = 30 и переменные 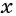 и
и 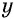 взяты с наибольшим показателем степени.
взяты с наибольшим показателем степени.
Умножим числитель и знаменатель первой дроби на 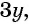 а числитель и знаменатель второй дроби на
а числитель и знаменатель второй дроби на 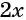 и приведем дроби к общему знаменателю:
и приведем дроби к общему знаменателю:
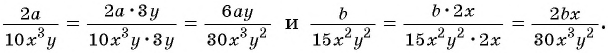
б) Разложим на множители знаменатель каждой дроби и получим:
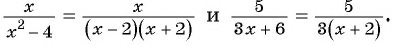
Умножим числитель и знаменатель первой дроби на 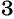 , а числитель и знаменатель второй дроби на
, а числитель и знаменатель второй дроби на 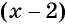 и приведем дроби к общему знаменателю:
и приведем дроби к общему знаменателю:
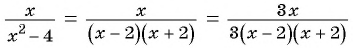
и
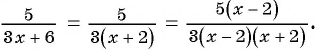
Чтобы выполнить сложение (вычитание) рациональных дробей с разными знаменателями, нужно:
- Привести дроби к общему знаменателю.
- Применить правила сложения (вычитания) дробей с одинаковыми знаменателями.
Найдите сумму рациональных дробей 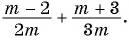
(1) 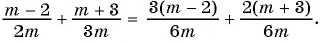
(2) 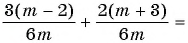
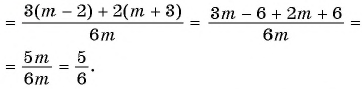
Пример №29
Найдите разность рациональных дробей
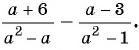
Решение:
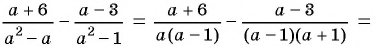
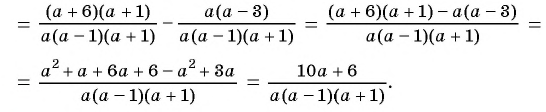
Сложение и вычитание дробей с одинаковыми знаменателями
Вспомним, как сложить дроби с одинаковыми знаменателями. Нужно сложить их числители, а знаменатель оставить тот же. Например:
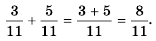
Запишем это правило в виде формулы:
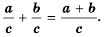
Это равенство справедливо для любых дробей. Докажем его (при условии 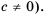
Пусть 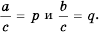 Тогда по определению частного
Тогда по определению частного 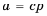
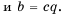 Имеем:
Имеем: 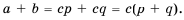 Поскольку
Поскольку 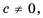 то по определению частного
то по определению частного 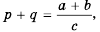
следовательно, 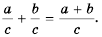
Сформулируем правило сложения дробей с одинаковыми знаменателями:
чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.
Пример №30
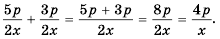
Аналогично можно доказать тождество
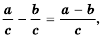
при помощи которого записывают правило вычитания дробей с одинаковыми знаменателями.
Сформулируем правило вычитания дробей с одинаковыми знаменателями:
чтобы вычесть дроби с одинаковыми знаменателями, нужно от числителя уменьшаемого отнять числитель вычитаемого, а знаменатель оставить тот же.
Пример №31
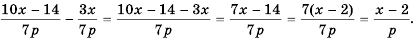
Рассмотрим еще несколько примеров.
Пример №32
Найдите сумму и разность дробей
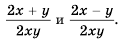
Решение:
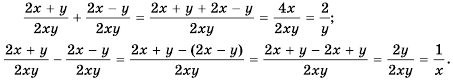
Ответ.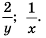
Пример №33
Упростите выражение
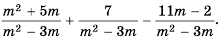
Решение:
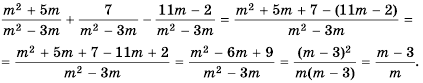
Ответ: 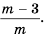
Пример №34
Найдите сумму 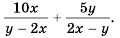
Решение:
Так как 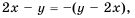 то второе слагаемое можно записать с тем же знаменателем, что и в первом слагаемом:
то второе слагаемое можно записать с тем же знаменателем, что и в первом слагаемом:
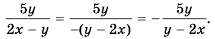
Тогда
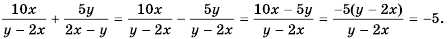
Ответ: 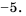
Если в тождествах 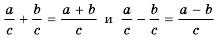 поменять местами левые и правые части, то получим тождества:
поменять местами левые и правые части, то получим тождества:
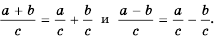
С помощью этих тождеств дробь, числитель которой является суммой или разностью нескольких выражений, можно записать в виде суммы или разности нескольких дробей.
Пример №35
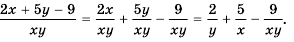
Пример №36
Запишите дробь в виде суммы или разности целого выражения и дроби: 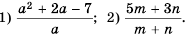
Решение:
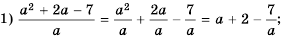
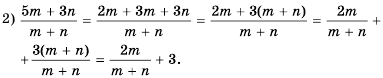
Ответ. 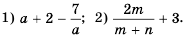
Пример №37
Выполните сложение рациональных дробей:
а) 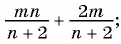
б) 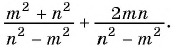
Решение:
а) 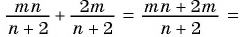
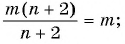
б) 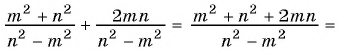
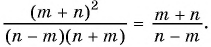
Пример №38
Найдите разность рациональных дробей:
а) 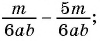
б) 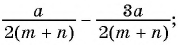
в) 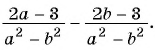
Решение:
а) 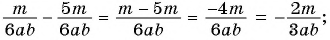
б) 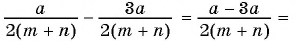
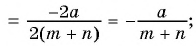
в) 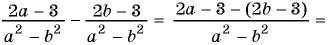
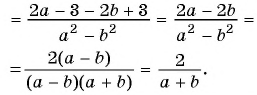
Пример №39
Выполните действия:
а) 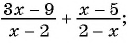
б) 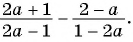
Решение:
а) Знаменатели дробей отличаются только знаком. Поменяем знак в знаменателе второй дроби и перед этой дробью и получим:
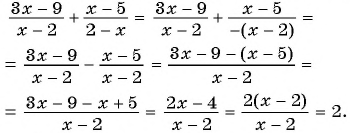
б) 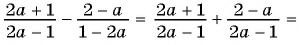
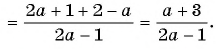
Пример №40
Выполните действия:
а) 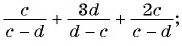
б) 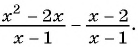
Решение:
а) 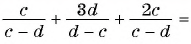
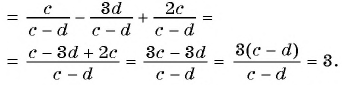
б) 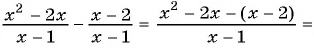
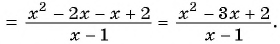
Разложим на множители квадратный трехчлен в числителе дроби и сократим дробь:
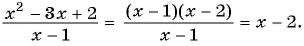
Сложение и вычитание дробей с разными знаменателями
Если дроби имеют разные знаменатели, то их, как и обычные дроби, сначала приводят к общему знаменателю, а потом складывают или вычитают по правилу сложения или вычитания дробей с одинаковыми знаменателями.
Рассмотрим, как прибавить дроби 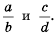 Приведем эти дроби к их общему знаменателю
Приведем эти дроби к их общему знаменателю 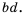 Для этого числитель и знаменатель дроби
Для этого числитель и знаменатель дроби 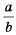 умножим на
умножим на 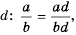 числитель и знаменатель дроби
числитель и знаменатель дроби 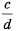 умножим на
умножим на 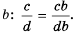 Дроби
Дроби 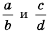 привели к общему знаменателю
привели к общему знаменателю 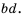 Напомним, что
Напомним, что 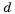 называют дополнительным множителем числителя и знаменателя дроби —
называют дополнительным множителем числителя и знаменателя дроби — 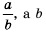 дополнительным множителем числителя и знаменателя дроби
дополнительным множителем числителя и знаменателя дроби 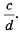
Описанную последовательность действий для сложения дробей с разными знаменателями можно записать так:
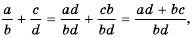
или сокращенно:
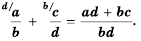
Аналогично выполняют и вычитание дробей с разными знаменателями:
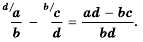
Пример №41
Выполните действие: 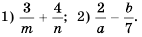
Решение:
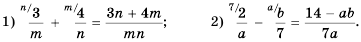
Общим знаменателем двух или более дробей может быть не только произведение их знаменателей. Вообще у дробей есть бесконечно много общих знаменателей. Часто при сложении и вычитании дробей с разными знаменателями удается найти более простой общий знаменатель, чем произведение знаменателей этих дробей. В таком случае говорят о простейшем общем знаменателе (аналогично наименьшему общему знаменателю числовых дробей).
Рассмотрим пример, где знаменатели дробей – одночлены.
Пример №42
Выполните сложение 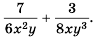
Решение. Общим знаменателем данных дробей можно считать одночлен 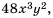 который является произведением знаменателей дробей, но в данном случае он не будет простейшим общим знаменателем. Попробуем найти простейший общий знаменатель, что для дробей, знаменатели которых являются одночленами, будет также одночленом. Коэффициент этого одночлена должен делиться и на 6, и на 8. Наименьшим из таких чисел будет 24. В общий знаменатель каждая из переменных должна входить с наибольшим из показателей степени, которые содержат знаменатели дробей. Таким образом, простейшим знаменателем будет одночлен
который является произведением знаменателей дробей, но в данном случае он не будет простейшим общим знаменателем. Попробуем найти простейший общий знаменатель, что для дробей, знаменатели которых являются одночленами, будет также одночленом. Коэффициент этого одночлена должен делиться и на 6, и на 8. Наименьшим из таких чисел будет 24. В общий знаменатель каждая из переменных должна входить с наибольшим из показателей степени, которые содержат знаменатели дробей. Таким образом, простейшим знаменателем будет одночлен 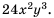 Тогда дополнительным множителем для первой дроби станет выражение
Тогда дополнительным множителем для первой дроби станет выражение 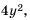 так как
так как 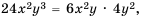 а для второй – выражение
а для второй – выражение 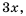 так как
так как 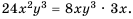 Следовательно, имеем:
Следовательно, имеем:
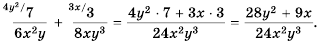
Ответ: 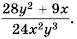
Обратите внимание, что в примере 2 при приведении дробей к общему знаменателю дополнительные множители 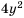 и
и 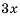 не содержали ни одного общего множителя, отличного от единицы. Это означает, что мы нашли простейший общий знаменатель дробей.
не содержали ни одного общего множителя, отличного от единицы. Это означает, что мы нашли простейший общий знаменатель дробей.
Рассмотрим пример, в котором знаменателями дробей являются многочлены.
Пример №43
Выполните вычитание
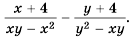
Решение:
Чтобы найти общий знаменатель, разложим знаменатели на множители:
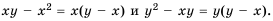
Простейшим общим знаменателем дробей будет выражение 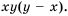 Тогда дополнительным множителем для первой дроби станет
Тогда дополнительным множителем для первой дроби станет 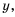 а для второй –
а для второй – 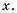 Выполним вычитание:
Выполним вычитание:
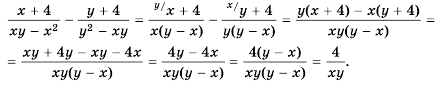
Ответ. 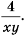
Таким образом, чтобы выполнить сложение или вычитание дробей с разными знаменателями, нужно:
- разложить на множители знаменатели дробей, если это необходимо;
- найти общий знаменатель, лучше простейший;
- записать дополнительные множители;
- найти дробь, которая является суммой или разницей данных дробей;
- упростить эту дробь и получить ответ.
Аналогично выполняют сложение и вычитание целого выражения и дроби.
Пример №44
Упростите выражение 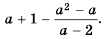
Решение:
Запишем выражение 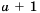 в виде дроби со знаменателем 1 и выполним вычитание:
в виде дроби со знаменателем 1 и выполним вычитание:
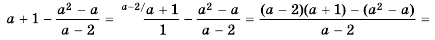
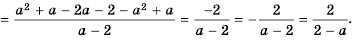
Ответ: 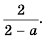
Пример №45
Выполните сложение рациональных дробей:
а) 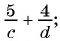
б) 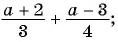
в) 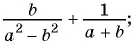
г) 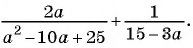
Решение:
а) 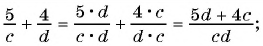
б) 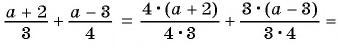
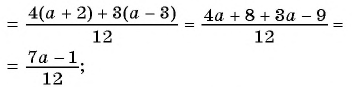
в) 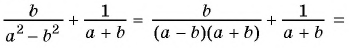
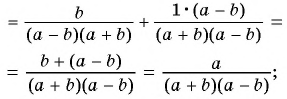
г) 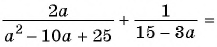
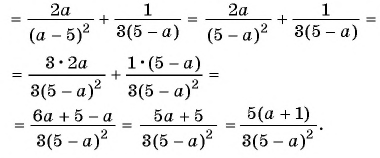
Пример №46
Выполните вычитание:
а) 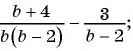
б) 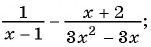
в) 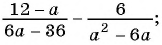
г) 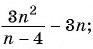
д) 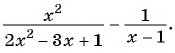
Решение:
а) 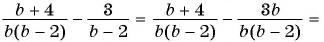
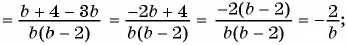
б) 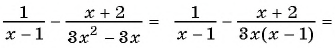
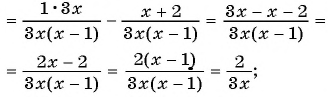
в) 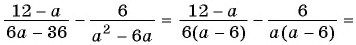
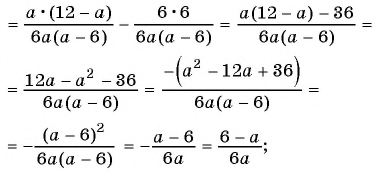
г) 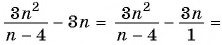
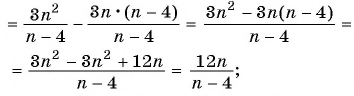
д) Разложим на множители квадратный трехчлен в знаменателе первой дроби и получим:
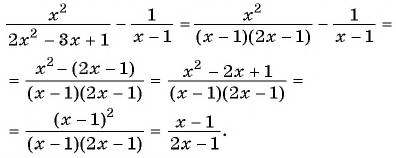
Пример №47
Представьте в виде дроби выражение
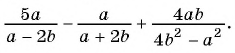
Решение:
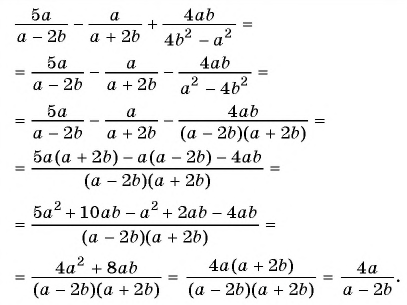
Умножение и деление рациональных дробей
Вспомним, как умножают и делят обыкновенные дроби.
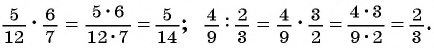
Правила умножения и деления рациональных дробей аналогичны правилам умножения и деления обыкновенных дробей.
Произведение рациональных дробей равно дроби, числитель которой равен произведению числителей данных дробей, а знаменатель равен произведению знаменателей данных дробей. 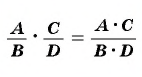
Чтобы найти произведение рациональных дробей, нужно:
- Произведение числителей данных дробей записать в числителе новой дроби, а произведение знаменателей данных дробей записать в знаменателе новой дроби.
- Сократить полученную дробь, если это возможно.
Найдите произведение рациональных дробей 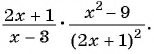
(1) 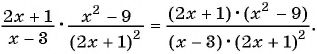
(2) 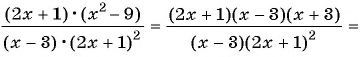
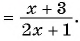
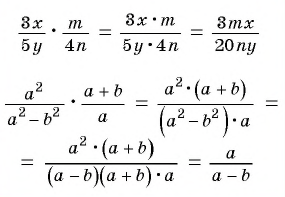
Пример №48
Найдите произведение рациональных дробей:
а) 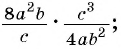
б) 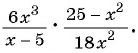
Решение:
а) 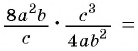
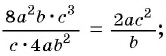
б) 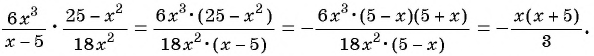
Правило умножения рациональных дробей можно использовать при возведении рациональной дроби в степень. Например:
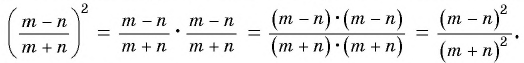
Обобщим этот прием и получим правило:
Чтобы возвести рациональную дробь в степень, нужно возвести в эту степень числитель дроби и полученный результат записать в числителе новой дроби, возвести в эту степень знаменатель дроби и полученный результат записать в знаменателе новой дроби.
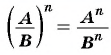
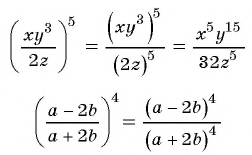
Пример №49
Возведите в степень дробь:
а) 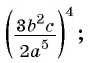
б) 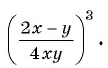
Решение:
а) 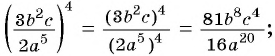
б) 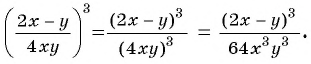
Чтобы разделить одну рациональную дробь на другую, нужно делимое умножить на дробь, обратную делителю.
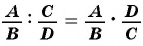
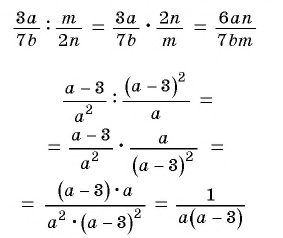
Пример №50
Найдите частное:
а) 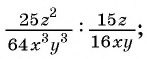
б) 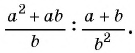
Решение:
а) 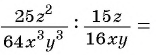
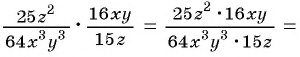
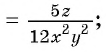
б) 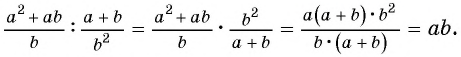
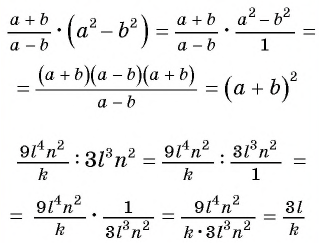
Пример №51
Представьте в виде дроби рациональное выражение:
а) 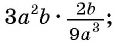
б) 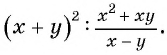
Решение:
а) Представим множитель 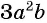 в виде рациональной дроби:
в виде рациональной дроби: 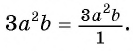
Выполним умножение дробей:
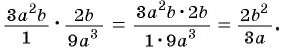
б) Представим выражение 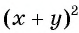 в виде рациональной дроби
в виде рациональной дроби 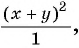 получим:
получим: 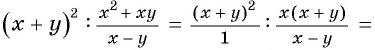
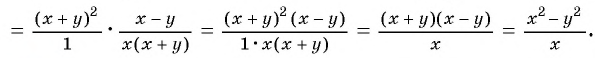
Пример №52
Выполните умножение рациональных дробей:
а) 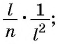
б) 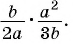
Решение:
а) 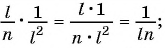
б) 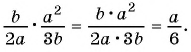
Пример №53
Представьте в виде рациональной дроби произведение:
а) 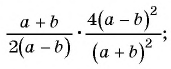
б) 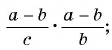
в) 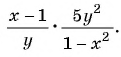
Решение:
а) 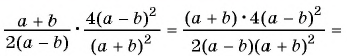
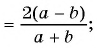
б) 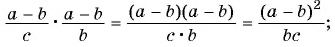
в) 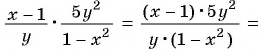
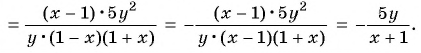
Пример №54
Представьте в виде рациональной дроби выражение:
а) 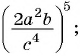
б) 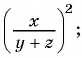
в) 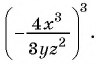
Решение:
а) 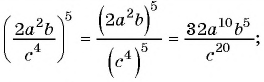
б) 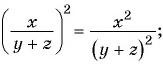
в) 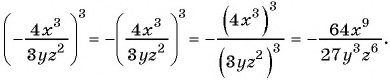
Пример №55
Представьте в виде степени рациональную дробь:
а) 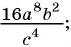
б) 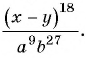
Решение:
а) 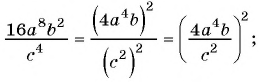
б) 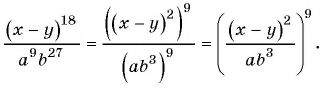
Пример №56
Выполните деление рациональных дробей:
а) 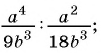
б) 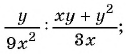
в) 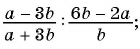
г) 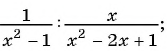
д) 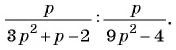
Решение:
а) 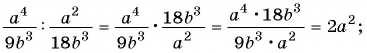
б) 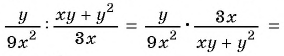
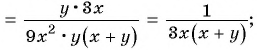
в) 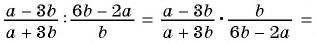
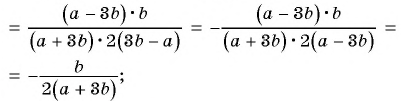
г) 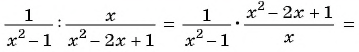
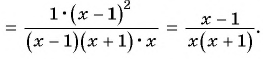
д) Воспользуемся формулой разложения квадратного трехчлена на множители и получим: 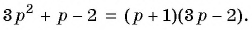
Тогда
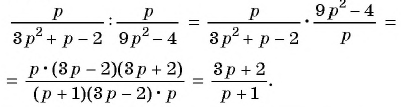
Пример №57
Выполните действия:
а) 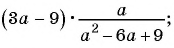
б) 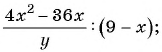
в) 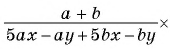
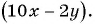
Решение:
а) 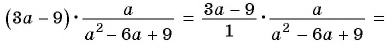
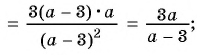
б) 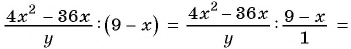
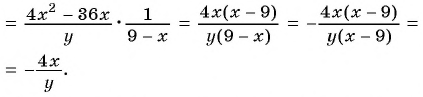
в) Разложим на множители многочлен, применив способ группировки:
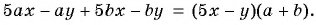
Тогда 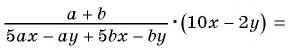
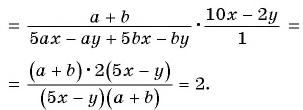
Пример №58
Найдите значение выражения
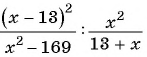
при 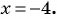
Решение:
Выполним деление:
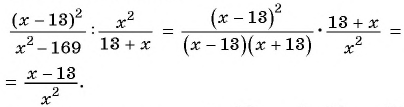
При 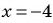 получим:
получим: 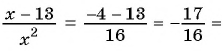
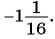
Пример №59
Найдите значение выражения 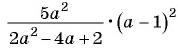
при 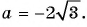
Решение:
Выполним умножение:
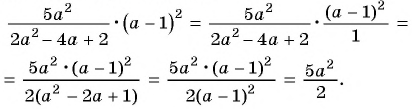
При 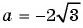 имеем:
имеем:
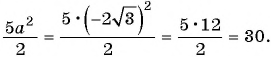
Умножение дробей
Напомним, что произведением двух обыкновенных дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей данных дробей:
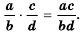
Докажем, что это равенство является тождеством для любых значений 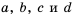 при условии, что
при условии, что 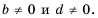
Пусть 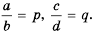 Тогда по определению частного
Тогда по определению частного 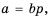
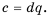 Поэтому
Поэтому 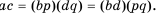 Так как
Так как 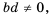 то, снова учитывая определение частного, получим:
то, снова учитывая определение частного, получим: 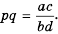 следовательно, если
следовательно, если 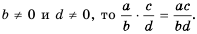
Сформулируем правило умножения дробей.
Чтобы умножить дробь на дробь, нужно перемножить отдельно числители и отдельно знаменатели сомножителей и записать первый результат в числителе, а второй – в знаменателе произведения дробей.
Пример №60
Выполните умножение 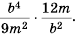
Решение:
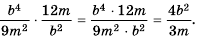
Ответ: 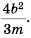
Пример №61
Найдите произведение
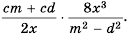
Решение.
Используем правило умножения дробей и разложим на множители числитель первой дроби и знаменатель второй:
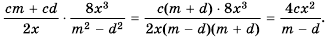
Ответ.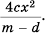
Обратите внимание, что в примерах 1 и 2 при умножении дробей мы не находили сразу же результат умножения числителей и знаменателей. Сначала мы записали произведения в числителе и в знаменателе по правилу умножения дробей, потом сократили полученную дробь, так как она оказалась сократимой, а уже затем выполнили умножение в числителе и в знаменателе и записали ответ. Целесообразно это учитывать и в дальнейшем.
Пример №62
Умножить дробь 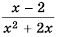 на многочлен
на многочлен 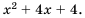
Решение:
учитывая, что 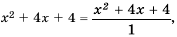 имеем:
имеем:
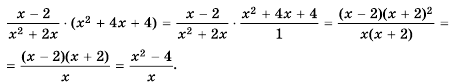
Ответ. 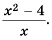
Правило умножения дробей можно распространить на произведение трех и более множителей.
Пример №63
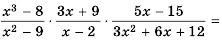
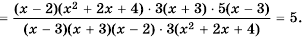
Возведение дроби в степень
Рассмотрим возведение дроби 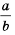 в степень
в степень 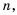 где
где 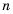 – натуральное число.
– натуральное число.
По определению степени и правилу умножения дробей имеем:
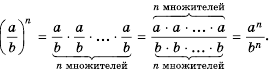
Следовательно:
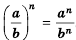
Сформулируем правило возведения дроби в степень.
Чтобы возвести дробь в степень, нужно возвести в эту степень числитель и знаменатель и первый результат записать в числитель, а второй – в знаменатель дроби.
Пример №64
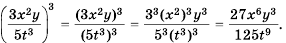
Пример №65
Представьте выражение 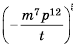 в виде дроби.
в виде дроби.
Решение:
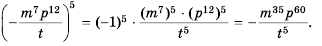
Ответ: 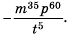
Деление дробей
Напомним, чтобы найти частное двух обыкновенных дробей, нужно делимое умножить на дробь, обратную делителю:
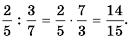
Формулой это можно записать так:
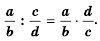
Докажем, что это равенство является тождеством для любых значений 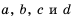 при условии, что
при условии, что 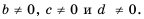
Так как: 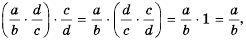
то по определению частного имеем: 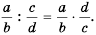
Следовательно, если 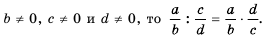
Дробь 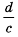 называют обратной дроби
называют обратной дроби 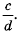
Сформулируем правило деления дробей.
Чтобы разделить одну дробь на другую, нужно первую дробь у множить на дробь, обратную второй.
Пример №66
Разделите дробь 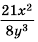 на дробь
на дробь 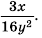
Решение:
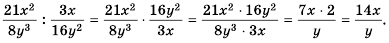
Ответ. 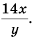
Пример №67
Выполните деление 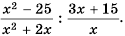
Решение:
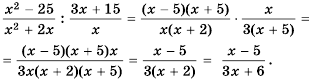
Ответ: 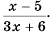
Пример №68
Упростите выражение: 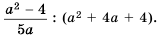
Решение:
Так как 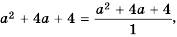 то:
то:
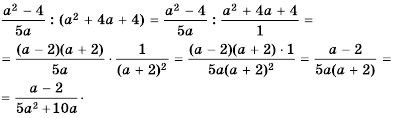
Ответ: 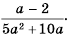
Преобразования рациональных выражений
При решении многих задач требуется упрощать рациональные выражения, приводя их к рациональным дробям. Для этого выполняют преобразования рациональных выражений.
Чтобы преобразовать рациональное выражение, нужно:
- Установить порядок действий в выражении.
- Выполнить действия по порядку, используя правила сложения, вычитания, умножения и деления рациональных дробей.
Упростите выражение:
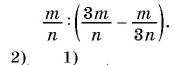
(1) 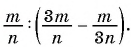
(2) 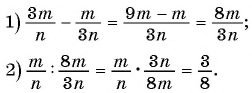
Пример №69
Представьте выражение 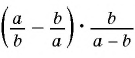 в виде рациональной дроби.
в виде рациональной дроби.
Решение:
(1) Сначала необходимо выполнить вычитание выражений, стоящих в скобках, а затем выполнить умножение.
(2) 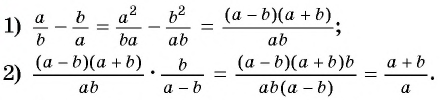
Преобразование рационального выражения можно выполнить не по действиям, а “цепочкой”. В данном случае получим:
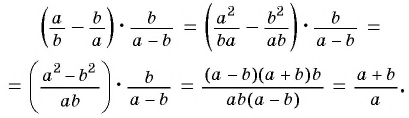
Пример №70
Найдите значение выражения
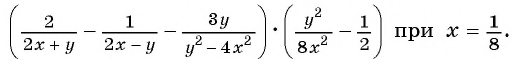
Решение:
Упростим выражение, выполнив действия по порядку:
1) 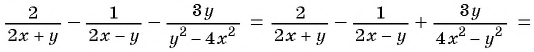
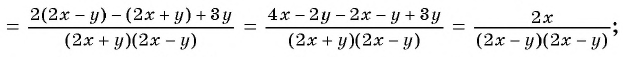
2) 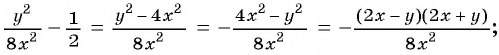
3) 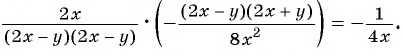
При 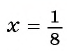 получим:
получим: 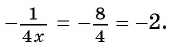
Преобразования рациональных выражений можно выполнять наряду с другими, ранее изученными преобразованиями.
Пример №71
Упростите выражение 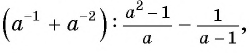 приведя его к рациональной дроби.
приведя его к рациональной дроби.
Решение:
1) 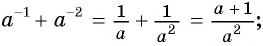
2) 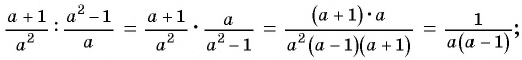
3) 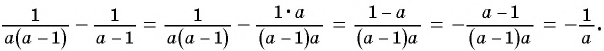
Правила преобразования рациональных выражений можно использовать и для преобразования выражений, содержащих корни.
Пример №72
Сократите дробь:
а) 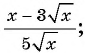
б) 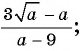
в) 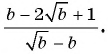
Решение:
а) 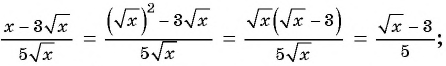
б) 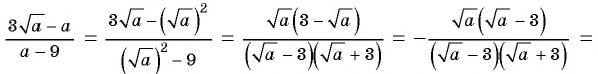
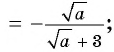
в) 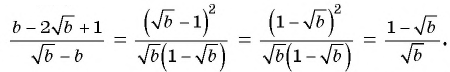
Пример №73
Упростите выражение 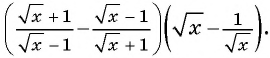
Решение:
1) 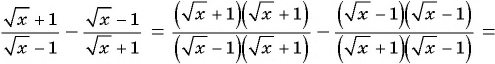
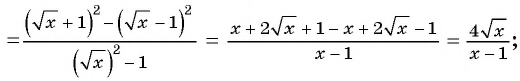
2) 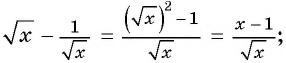
3) 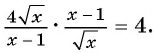
Пример №74
Представьте выражение 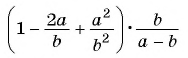 в виде дроби.
в виде дроби.
Решение:
1) 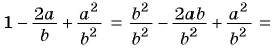
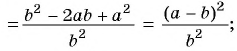
2) 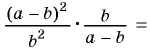
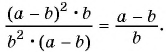
Пример №75
Найдите значение выражения 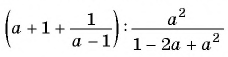 при
при 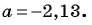
Решение:
Преобразуем данное выражение “цепочкой”:
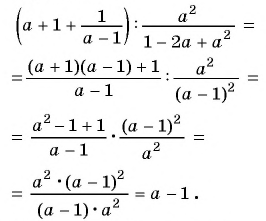
При 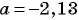 получим:
получим: 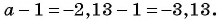
Пример №76
Упростите выражение
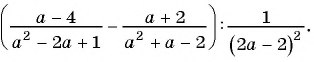
Решение:
1) Корнями квадратного трехчлена 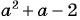 являются числа
являются числа 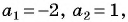 значит,
значит, 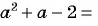
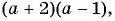 тогда:
тогда:
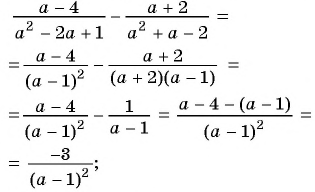
2) 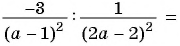
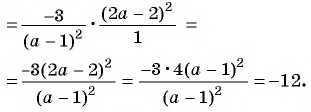
Пример №77
Докажите, что значение выражения
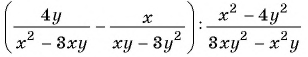
не зависит от значений переменных.
Решение:
Значение выражения при различных значениях переменных из области его определения можно найти, предварительно упростить его:
1) 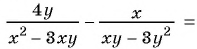
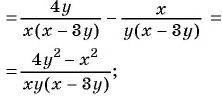
2) 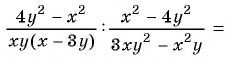
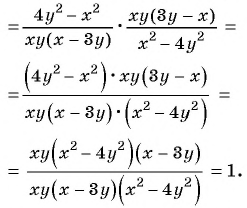
Получили, что результат упрощения равен числу 1, значит при любых значениях переменных из области определения значение данного выражения равно 1, т. е. не зависит от значений переменных.
Пример №78
Упростите выражение
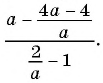
Решение:
Запишем дробь в виде частного и получим: 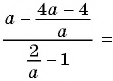
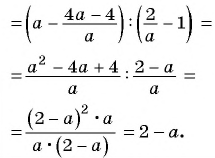
Пример №79
Упростите выражение
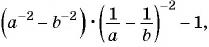 приведя его к несократимой дроби.
приведя его к несократимой дроби.
Решение:
1) 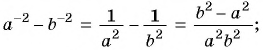
2) 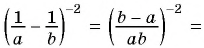
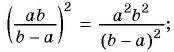
3) 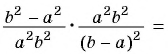
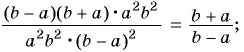
4) 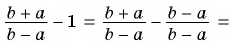
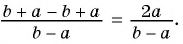
Пример №80
Примените к выражению алгоритм сокращения рациональной дроби:
а) 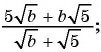
б) 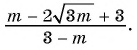
Решение:
а) 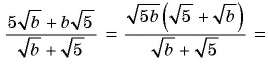
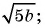
б) 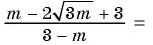
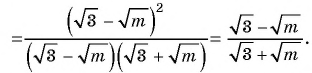
Пример №81
Упростите выражение
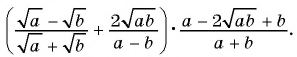
Решение:
1) 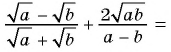
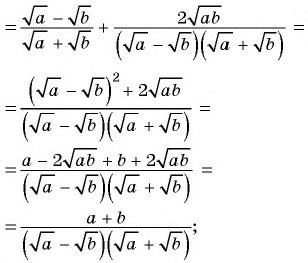
2) 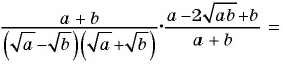
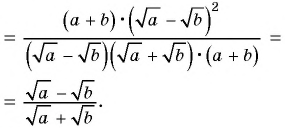
Пример №82
Найдите значение выражения 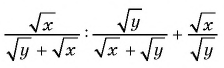 при
при 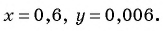
Решение:
Упростим данное выражение:
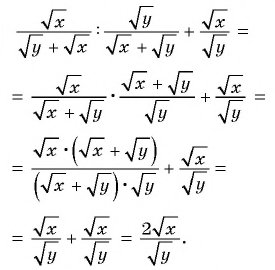
При 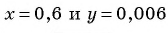 получим:
получим:
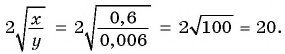
- Заказать решение задач по высшей математике
Тождественные преобразования рациональных выражений
Рассмотрим примеры преобразований рациональных выражений.
Пример №83
Докажите тождество 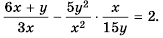
Решение:
Упростим левую часть равенства:
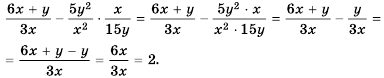
С помощью тождественных преобразований мы привели левую часть равенства к правой. Следовательно, равенство является тождеством.
Пример №84
Упростите выражение
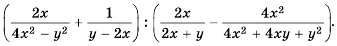
Решение:
Сначала выполним действие в каждой из скобок, а потом – действие деления:
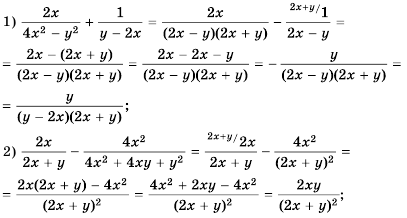
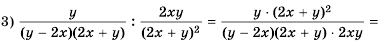
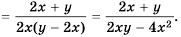
Ответ: 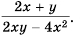
Решение можно было записать и в виде «цепочки»:
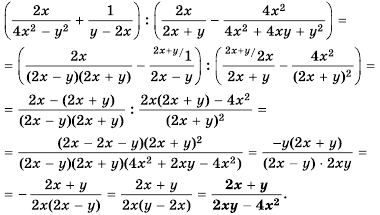
Каждое выражение, содержащее сумму, разность, произведение и частное рациональных дробей, можно представить в виде рациональной дроби.
Пример №85
Докажите, что при всех допустимых значениях переменных значение дроби 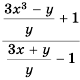 неотрицательно.
неотрицательно.
Решение:
Можно представить эту дробь в виде частного 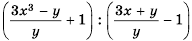 и далее преобразовать ее, как предложено в примере 2.
и далее преобразовать ее, как предложено в примере 2.
А можно, используя основное свойство дроби, умножить числитель и знаменатель данной дроби на их общий знаменатель, то есть на 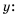
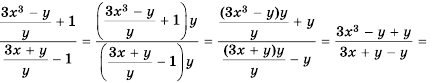
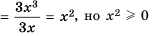 при любом значении
при любом значении 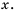
- Функция в математике
- Наибольшее и наименьшее значения функции
- Раскрытие неопределенностей
- Дробно-рациональные уравнения
- Система показательных уравнений
- Непрерывные функции и их свойства
- Правило Лопиталя
- Вычисления в Mathematica с примерами
|
Алгебраическая дробь имеет смысл только в случае неравенства своего знаменателя нулю. Ведь делить на ноль, как известно, нельзя. При необходимости определить для дроби те значения, когда она смысл имеет, надо записать значение числового ряда за исключеним тех чисел, которы получаются при решении уравнения при приравнивании знаменателя нулю. модератор выбрал этот ответ лучшим
Алсу – Ш 6 лет назад Напомню некоторые сведения, касающиеся алгебраических дробей, а также их допустимых значений. Авторы верно ответили на вопрос о том, что дробь имеет смысл только тогда, когда знаменатель ее не равен нулю. Так как речь идет об алгебраических дробях, можно добавить: знаменатель не равен нулю при каждом допустимом значении переменных. Одинаковый смысл имеют типы заданий: Чтобы выполнить любое из данных заданий, нужно найти множество допустимых значений переменных, для этого исключить недопустимые. Мы приравниваем к 0 знаменатель дроби (знак равенства часто перечеркивают), решаем полученное уравнение (обычно со знаком перечеркнутого равенства), корни его исключаем из множества значений переменных (перечеркнутые значения переменных – это и есть исключенные корни из множества значений переменных). Таким образом, в ответе запишутся все значения переменных, за исключением найденных. Пример:
В представленной картинке даны алгебраические дроби. Если в знаменателе дан многочлен, который ни при каких значениях переменных не обращается в нуль, то дробь будет иметь смысл на всей числовой прямой, т.е. на множестве действительных чисел (см. 2-й пример на картинке ниже), если в задаче дополнительно не указывается другое конкретное множество значений переменных, на котором задана дробь, например, рациональных чисел. Пример.
Одним из основных свойств алгебраических дробей, знакомых еще математикам античности, является запрет деления на 0. Когда в знаменатели дроби возникает это “пустое” число” дробь теряет смысл. В школьной программе часто можно встретить разнообразные задания, в которых спрашивается когда выражение или дробь не имеет смысла, при каком значении переменной Х. При этом знаменатель дроби представлен неким выражением, например 8х-4 или х+5. Для нахождения ответа таких заданий знаменатель приравнивается к нули и решается как уравнение. Удовлетворяющие этому уравнению значения Х делают дробь не имеющей смысла. В данных примерах дробь с любым числителем не имеет смысла если в первом примере Х= 0.5, а во втором Х=-5.
Дробь имеет смысл при условии, что ее знаменатель отличен от нуля. В школьной математике важно, чтобы и числитель был строго больше минус бесконечности и строго меньше плюс бесконечности, иначе даже при ненулевом знаменателе дробь все так же “скатится” в бесконечность.
Nelli4ka 6 лет назад Проще было бы ответить на вопрос: когда она не имеет смысла? Тогда бы мы ответили, что тогда, когда знаменатель в дроби равен нулю. Ведь на ноль делить нельзя, как мы помним еще со школы, ибо он все обращает в ноль. На ваш же вопрос можно ответить таким образом: когда в знаменателе не ноль (будь-то положительные числа, будь-то отрицательные), дробь существует и несет при этом определенный смысл.
moreljuba 6 лет назад Говоря о дробях важно понимать, что используя знак дроби (то есть черту), мы подразумеваем процесс деления. А так как нам всем известно, что деление на ноль проводить нельзя согласно правил, то можно точно сказать, что алгебраическая дробь имеет смысл в том случае, когда значение её знаменателя отлично от нуля.
Помощни к 6 лет назад Также мне кажется, что алгебраическая дробь, или написание числа в виде дроби, не имеет смысла, если числитель равен знаменателю. В таком случае можно написать выражение гораздо проще. К примеру, вместо “1/1” лучше написать просто “1”. Ну, а по правилам, главное чтобы снизу дроби не был “0”.
Александр Ветров 6 лет назад Насколько мне известно, алгебраическая дробь не имеет смысла, когда её знаменатель равняется нулю, поскольку на него делить нельзя. Таким образом, во всех остальных случаях алгебраическая дробь имеет смысл, и её можно смело использовать для различных расчётов. По моему дробь имеет смысл всегда, за исключением случая, когда в знаменателе стоит ноль, так как мы помним, что на ноль делить нельзя. Другое дело в высшей математике, там и но ноль делят, получая математические пределы и т.д.
Про100 й 8 лет назад При любом значении числа дробь имеет смысл,кроме одного случая, если только знаменатель не равен нулю, так как на ноль делить нельзя. Дробь не имеет смысла если знаменатель равен нулю. Как то так помню со школы.
Алгебраическая дробь имеет смысл только тогда, когда её знаменатель не равен нулю. В противном случае, когда знаменатель равен нулю, алгебраическая дробь не имеет смысла, так как делить на ноль нельзя. mat033 10 лет назад В рамках школьной программы, смысл имеет дробь с отличным от нуля знаменателем 😉 Ну, если актуально большие числа и прочая экзотика не вошла, за эти годы, в школьную программу. Знаете ответ? |
Определение и примеры алгебраических дробей
Рациональные выражения делятся на целые и дробные выражения.

Определение. Рациональная дробь – дробное выражение вида ![]() , где
, где ![]() – многочлены.
– многочлены. ![]() – числитель,
– числитель, ![]() – знаменатель.
– знаменатель.
Примеры рациональных выражений: ![]() – дробные выражения;
– дробные выражения; ![]() – целые выражения. В первом выражении, к примеру, в роли числителя выступает
– целые выражения. В первом выражении, к примеру, в роли числителя выступает ![]() , а знаменателя –
, а знаменателя – ![]() .
.
Значение алгебраической дроби, как и любого алгебраического выражения, зависит от численного значения тех переменных, которые в него входят. В частности, в первом примере значение дроби зависит от значений переменных ![]() и
и ![]() , а во втором только от значения переменной
, а во втором только от значения переменной ![]() .
.
Вычисление значения алгебраической дроби и две основные задачи на дроби
Рассмотрим первую типовую задачу: вычисление значения рациональной дроби при различных значениях входящих в нее переменных.
Пример 1. Вычислить значение дроби ![]() при а)
при а) ![]() , б)
, б) ![]() , в)
, в) ![]()
Решение. Подставим значения переменных в указанную дробь: а) ![]() , б)
, б) ![]() , в)
, в) ![]() – не существует (т. к. на ноль делить нельзя).
– не существует (т. к. на ноль делить нельзя).
Ответ: а) 3; б) 1; в) не существует.
Как видим, возникает две типовые задачи для любой дроби: 1) вычисление дроби, 2) нахождение допустимых и недопустимых значений буквенных переменных.
Определение. Допустимые значения переменных – значения переменных, при которых выражение имеет смысл. Множество всех допустимых значений переменных называется ОДЗ или область определения.
Допустимые (ОДЗ) и недопустимые значения переменных в дробях с одной переменной
Значение буквенных переменных может оказаться недопустимым, если знаменатель дроби при этих значениях равен нулю. Во всех остальных случаях значение переменных являются допустимыми, т. к. дробь можно вычислить.
Пример 2. Установить, при каких значениях переменной не имеет смысла дробь ![]() .
.
Решение. Чтобы данное выражение имело смысл, необходимо и достаточно, чтобы знаменатель дроби не равнялся нулю. Таким образом, недопустимыми будут только те значения переменной, при которых знаменатель будет равняться нулю. Знаменатель дроби ![]() , поэтому решим линейное уравнение:
, поэтому решим линейное уравнение:
![]() .
.
Следовательно, при значении переменной ![]() дробь не имеет смысла.
дробь не имеет смысла.
Ответ: -5.
Из решения примера вытекает правило нахождения недопустимых значений переменных – знаменатель дроби приравнивается к нулю и находятся корни соответствующего уравнения.
Рассмотрим несколько аналогичных примеров.
Пример 3. Установить, при каких значениях переменной не имеет смысла дробь![]() .
.
Решение. ![]() .
.
Ответ. ![]() .
.
Пример 4. Установить, при каких значениях переменной не имеет смысла дробь ![]() .
.
Решение.![]() .
.
Встречаются и другие формулировки данной задачи – найти область определения или область допустимых значений выражения (ОДЗ). Это означает – найти все допустимые значения переменных. В нашем примере – это все значения, кроме ![]() . Область определения удобно изображать на числовой оси.
. Область определения удобно изображать на числовой оси.
Для этого на ней выколем точку ![]() , как это указано на рисунке:
, как это указано на рисунке:

Рис. 1
Таким образом, областью определения дроби будут все числа, кроме 3.
Ответ.![]() .
.
Пример 5. Установить, при каких значениях переменной не имеет смысла дробь ![]() .
.
Решение.![]() .
.
Изобразим полученное решение на числовой оси:

Рис. 2
Ответ.![]() .
.
Графическое представление области допустимых (ОДЗ) и недопустимых значений переменных в дробях
Пример 6. Установить, при каких значениях переменных не имеет смысла дробь ![]() .
.
Решение.![]() . Мы получили равенство двух переменных, приведем числовые примеры:
. Мы получили равенство двух переменных, приведем числовые примеры: ![]() или
или ![]() и т. д.
и т. д.
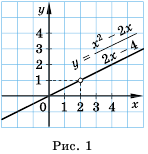
Изобразим это решение на графике в декартовой системе координат:

Рис. 3. График функции ![]()
Координаты любой точки, лежащей на данном графике, не входят в область допустимых значений дроби.
Ответ. ![]() .
.
Случай типа “деление на ноль”
В рассмотренных примерах мы сталкивались с ситуацией, когда возникало деление на ноль. Теперь рассмотрим случай, когда возникает более интересная ситуация с делением типа ![]() .
.
Пример 7. Установить, при каких значениях переменных не имеет смысла дробь ![]() .
.
Решение.![]() .
.
Получается, что дробь не имеет смысла при ![]() . Но можно возразить, что это не так, потому что:
. Но можно возразить, что это не так, потому что: ![]() .
.
Может показаться, что если конечное выражение равно 8 при ![]() , то и исходное тоже возможно вычислить, а, следовательно, имеет смысл при
, то и исходное тоже возможно вычислить, а, следовательно, имеет смысл при ![]() . Однако, если подставить
. Однако, если подставить ![]() в исходное выражение, то получим
в исходное выражение, то получим ![]() – не имеет смысла.
– не имеет смысла.
Ответ.![]() .
.
Чтобы подробнее разобраться с этим примером, решим следующую задачу: при каких значениях ![]() указанная дробь равна нулю?
указанная дробь равна нулю?
![]() (дробь равна нулю, когда ее числитель равен нулю)
(дробь равна нулю, когда ее числитель равен нулю) ![]() . Но необходимо решить исходное уравнение с дробью, а она не имеет смысла при
. Но необходимо решить исходное уравнение с дробью, а она не имеет смысла при ![]() , т. к. при этом значении переменной знаменатель равен нулю. Значит, данное уравнение имеет только один корень
, т. к. при этом значении переменной знаменатель равен нулю. Значит, данное уравнение имеет только один корень ![]() .
.
Правило нахождения ОДЗ
Таким образом, можем сформулировать точное правило нахождения области допустимых значений дроби: для нахождения ОДЗ дроби необходимо и достаточно приравнять ее знаменатель к нулю и найти корни полученного уравнения.
Мы рассмотрели две основные задачи: вычисление значения дроби при указанных значениях переменных и нахождение области допустимых значений дроби.
Рассмотрим теперь еще несколько задач, которые могут возникнуть при работе с дробями.
Разные задачи и выводы
Пример 8. Докажите, что при любых значениях переменной дробь ![]() .
.
Доказательство. Числитель – число положительное. ![]() . В итоге, и числитель, и знаменатель – положительные числа, следовательно, и дробь является положительным числом.
. В итоге, и числитель, и знаменатель – положительные числа, следовательно, и дробь является положительным числом.
Доказано.
Пример 9. Известно, что ![]() , найти
, найти ![]() .
.
Решение. Поделим дробь почленно ![]() . Сокращать на
. Сокращать на ![]() мы имеем право, с учетом того, что
мы имеем право, с учетом того, что ![]() является недопустимым значением переменной для данной дроби.
является недопустимым значением переменной для данной дроби.
Ответ.![]() .
.
На данном уроке мы рассмотрели основные понятия, связанные с дробями. На следующем уроке мы рассмотрим основное свойство дроби.
Список литературы
- Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
- Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Фестиваль педагогических идей (Источник).
- Старая школа (Источник).
Домашнее задание
- №4, 7, 9, 12, 13, 14. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
- Запишите рациональную дробь, областью определения которой является: а) множество
 , б) множество
, б) множество  , в) вся числовая ось.
, в) вся числовая ось. - Докажите, что при всех допустимых значениях переменной
 значение дроби
значение дроби  неотрицательно.
неотрицательно. - Найдите область определения выражения
 . Указание: рассмотреть отдельно два случая: когда знаменатель нижней дроби равен нулю и когда знаменатель исходной дроби равен нулю.
. Указание: рассмотреть отдельно два случая: когда знаменатель нижней дроби равен нулю и когда знаменатель исходной дроби равен нулю.
Содержание материала
- Понятие алгебраической дроби
- Видео
- Алгебраические дроби и их решение
- Умножение и деление дробей
- Сложение и вычитание дробей
- Наибольший общий делитель (НОД) и наименьшее общее кратное (НОК)
- Более сложные случаи сложения и вычитания дробей
- Сложные дроби
- Все действия с дробями. Расположенные многочлены в числителе и знаменателе дроби. Выделение целой части из неправильной дроби
Понятие алгебраической дроби
Начнем с определения. Под алгебраической дробью понимается выражения P/Q, где P является числителем, а Q – знаменателем. Под буквенной записью может скрываться число, числовое выражение, численно-буквенное выражение.
Прежде чем задаваться вопросом, как решать алгебраические дроби, для начала нужно понимать, что подобное выражение – часть целого.
Как правило, целое – это 1. Число в знаменателе показывает, на сколько частей разделили единицу. Числитель необходим для того, чтобы узнать, сколько элементов взято. Дробная черта соответствует знаку деления. Допускается запись дробного выражения в качестве математической операции «Деление». В таком случае числитель – делимое, знаменатель – делитель.
Алгебраические дроби и их решение
Если алгебраическое выражение, составленное из букв и чисел, содержит, кроме трех первых действий— сложения, вычитания и умножения, — также еще и деление (на буквенное выражение), то такое выражение называют дробным. Примером могут служить выражения:  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Если последнее действие, указываемое выражением, есть деление, то такое выражение называется просто «дробью (алгебраической дробью). При этом, если, кроме этого последнего действия, делений больше производить не нужно, дробь называется простой, в противном случае — сложной. Так, среди предыдущих примеров только последний нельзя назвать дробью (это сумма двух дробей); предпоследний есть сложная дробь, четыре предыдущих — простые дроби.
К сложным дробям мы обратимся несколько позднее; сначала же будем заниматься только простыми.
Простая алгебраическая дробь есть отношение двух целых алгебраических выражений, являющихся числителем и знаменателем дроби.
Мы знаем, что существует число, которое ни в коем случае не может быть знаменателем дроби: это — нуль; поэтому, если знаменатель про стой алгебраической дроби оказывается тождественное равным нулю, то сама дробь не имеет смысла ни при каких значениях входящих букв. Примером служит дробь  . Очень часто встречается другой случай, когда знаменатель дроби тождественно не равен нулю, однако обращается в нуль при некоторых значениях входящих букв. При этих значениях букв дробь «теряет смысл» — не имеет никакого числового значения. По этому, написав дробь, всегда подразумевают, что числовые значения, придаваемые входящим буквам, таковы, что не обращают знаменатель в нуль.
. Очень часто встречается другой случай, когда знаменатель дроби тождественно не равен нулю, однако обращается в нуль при некоторых значениях входящих букв. При этих значениях букв дробь «теряет смысл» — не имеет никакого числового значения. По этому, написав дробь, всегда подразумевают, что числовые значения, придаваемые входящим буквам, таковы, что не обращают знаменатель в нуль.
Иногда это отмечают и в явной форме: например,  .
.
В дальнейшем, говоря о данной дроби, мы всегда будем подразумевать, что буквам даются лишь такие значения, которые не обращают знаменатель в нуль. Что касается числителя дроби, то исключать из рассмотрения те случаи, когда он обращается в нуль, излишне. Напомним, что если числитель дроби равен нулю, то и сама дробь равна нулю. Обратно, если дробь равна нулю, то непременно числитель равен нулю. Итак, простая алгебраическая дробь обращается в нуль при тех и только при тех значениях входящих букв, при которых ее числитель обращается в нуль.
Из арифметики отлично известно основное свойство дроби (частного); дробь (частное) не изменяется, если числитель (делимое) и знаменатель (делитель) умножить или разделить на одно и то же число  . Например, дробь
. Например, дробь  не изменяется, если ее числитель и знаменатель умножить или разделить на
не изменяется, если ее числитель и знаменатель умножить или разделить на  :
:  .
.
Число  может также быть дробным: если, допустим,
может также быть дробным: если, допустим,  равно
равно  ,то умножить на
,то умножить на  — значит сначала умножить на
— значит сначала умножить на  и затем разделить на
и затем разделить на  . Оно может быть и отрицательным: при умножении числителя и знаменателя на отрицательное число знаки числителя и знаменателя меняются, а знак дроби остается неизменным. Оно не может быть только равным нулю: понятно — почему.
. Оно может быть и отрицательным: при умножении числителя и знаменателя на отрицательное число знаки числителя и знаменателя меняются, а знак дроби остается неизменным. Оно не может быть только равным нулю: понятно — почему.
В виде формулы основное свойство дроби записывается следующим образом:  (1).
(1).
Основное свойство дроби можно выразить следующими словами; если некоторое выражение входит множителем в числитель и в знаменатель алгебраической дроби, то при условии, что оно не равно нулю, можно на него «сократить» данную дробь: значение дроби при этом не меняется. И, напротив, можно умножить числитель и знаменатель алгебраической дроби на произвольное выражение при условии, что оно не обращается в нуль.
Примечание:
Равенство (1), выражающее основное свойство дроби, считается тождеством, несмотря на то, что его левая часть теряет смысл при  , и на то, что обе его части теряют смысл при
, и на то, что обе его части теряют смысл при  .
.
Вообще за равенством двух алгебраических выражений принято сохранять наименование тождества и в том случае, если одно из этих выражений или оба теряют смысл при некоторых исключительных значениях входящих букв. Такое расширенное понимание тождества, между прочим, позволяет относить сокращение дроби на буквенное выражение к числу тождественных преобразований.
Руководствуясь основным свойством дроби, можно сокращать алгебраическую дробь (как и арифметическую) на буквенные или числовые множители, входящие одновременно в ее числитель и в ее знаменатель.
Если таких множителей нет, дробь называют несократимой.
Например, дробь  можно сократить на
можно сократить на  :
:  .
.
Левая и правая часть равенства тождественно равны (хотя левая теряет смысл при  , и обе — при
, и обе — при  ).
).
Мы переходим дальше к изучению действий над алгебраическими дробями — сложения, вычитания, умножения и деления. Выполнить одно из этих действий над данными простыми дробями — значит не только соединить эти дроби соответственным знаком, но также и произвести над полученным выражением тождественные преобразования, целью которых является представить это выражение в виде простой дроби (или целого выражения). Производя действия над дробями, стараются вместе с тем сокращать дробь на общие множители числителя и знаменателя.
При изучении действий над дробями мы начнем с более легких — умножения и деления, а затем перейдем к более трудным — сложению и вычитанию. Те случаи, когда какие-нибудь из данных выражений оказываются целыми, мы не будем рассматривать отдельно, так как всякое целое выражение можно представить в виде дробного, именно, подписывая под ним в качестве знаменателя единицу.
Умножение и деление дробей
Правило умножения арифметических дробей выражается формулой:  (*) и словами может быть прочитано следующим образом: произведение двух дробей равно дроби, у которой числитель равен произведению числителей, а знаменатель — произведению знаменателей.
(*) и словами может быть прочитано следующим образом: произведение двух дробей равно дроби, у которой числитель равен произведению числителей, а знаменатель — произведению знаменателей.
Написанная выше формула справедлива не только в том случае, если входящие буквы имеют целые положительные значения, но и в том случае, если эти значения — дробные; она справедлива также и в том случае, если некоторые из входящих букв имеют отрицательные значения. Значение нуль, конечно, исключено для знаменателей, но не исключено для числителей.
Но раз равенство (*) имеет место при всех значениях входящих букв (кроме тех исключительных, при которых знаменатели дробей обращаются в нуль), то оно является тождеством.
Таким образом, правило умножения алгебраических дробей выражается той же формулой и формулируется теми же словами, что и правило умножения арифметических дробей.
В алгебре вместо того, чтобы вычесть некоторое число, можно прибавить число, противоположное по знаку:  .
.
Таким же образом вместо того, чтобы разделить на некоторое число (не равное нулю), достаточно умножить на величину, обратную этому числу:  .
.
Действительно, следуя правилу умножения, мы получаем:  .
.
Так как величина, обратная дроби  есть дробь
есть дробь  , то правило деления дроби на дробь (подобное арифметическому) дается формулой:
, то правило деления дроби на дробь (подобное арифметическому) дается формулой:  (2).
(2).
Чтобы разделить на дробь, достаточно умножить на величину, ей обратную («разделить на числитель и умножить на знаменатель).
Сложение и вычитание дробей
Сложить две алгебраические дроби означает — представить их сумму в виде одной алгебраической дроби; то же — для вычитания.
Если данные дроби имеют один и тот же знаменатель, то, чтобы сложить их — в алгебре, как и в арифметике, — достаточно составить дробь с тем же знаменателем и с числителем, равным сумме числителей:  .
.
Это — распределительный закон деления, справедливый при любом  , не равном нулю.
, не равном нулю.
Если же складываемые дроби имеют различные знаменатели, то в алгебре, как и в арифметике, необходимо предварительно привести дроби к общему знаменателю. При этом пользуются основным свойством дроби — основным тождеством (*) , в котором мы теперь поменяем местами правую и левую части:  .
.
Желая сложить две дроби  и
и  , мы всегда можем умножить числитель и знаменатель первой дроби на
, мы всегда можем умножить числитель и знаменатель первой дроби на  , а числитель и знаменатель второй — на
, а числитель и знаменатель второй — на  . и тогда получим:
. и тогда получим:  , дальше достаточно сложить числители:
, дальше достаточно сложить числители:  . Итак, мы получаем тождество:
. Итак, мы получаем тождество:  (3).
(3).
Подобным же образом, ссылаясь на распределительный закон деления и на основное свойство дроби, выведите общую формулу вычитания дробей:  (4).
(4).
При действиях с дробями часто приходится пользоваться важным частным случаем основного свойства дроби (*)  именно, тем случаем, когда
именно, тем случаем, когда  равно
равно  . В этом случае мы получаем:
. В этом случае мы получаем:  .
.
Таким образом, значение дроби не меняется при одновременном изменении знаков числителя и знаменателя.
Так как  , то можно заключить: при изменении знака только числителя или только знаменателя знак дроби меняется.
, то можно заключить: при изменении знака только числителя или только знаменателя знак дроби меняется.
Отсюда следует: если мы меняем знак знаменателя, то, чтобы значение дроби не изменилось, достаточно еще изменить знак, или числителя или самой дроби; если мы меняем знак числителя, то, чтобы значение дроби не изменилось, достаточно еще изменить знак или знаменателя или самой дроби. Например, .
.
Наибольший общий делитель (НОД) и наименьшее общее кратное (НОК)
В арифметике указывается правило для нахождения наибольшего общего делителя (НОД) и наименьшего общего кратного (НОК) нескольких целых чисел.
Пусть даны числа  ,
,  и
и  . Разложим их на простые множители:
. Разложим их на простые множители:  ,
,  ,
,  .
.
Составим новое число из данных чисел следующим образом: возьмем каждый встречающийся множитель в наименьшей из степеней, в которых он встречается, и затем перемножим:  .
.
Полученное число  есть НОД данных чисел: частные от деления этих чисел на
есть НОД данных чисел: частные от деления этих чисел на  уже не имеют общих делителей, отличных от
уже не имеют общих делителей, отличных от  .
.
Составим другое число из данных чисел, отбирая каждый встречающийся множитель в наибольшей из степеней, в которых он встречается, и перемножая:  . Полученное число
. Полученное число  есть НОК данных чисел; частные от деления числа
есть НОК данных чисел; частные от деления числа  на эти числа уже не имеют общих делителей, отличных от
на эти числа уже не имеют общих делителей, отличных от  .
.
Таким же образом можно составлять НОД и НОК алгебраических одночленных выражений с целыми коэффициентами, обращаясь при этом с буквами как с целыми числами (хотя буквы могут иметь какие угодно, в том числе и дробные, значения). Так, если даны выражения  ,
,  и
и  , то их наибольший общий делитель равен
, то их наибольший общий делитель равен  , а их наименьшее общее кратное равно
, а их наименьшее общее кратное равно  . После деления данных выражений на их НОД получаются частные
. После деления данных выражений на их НОД получаются частные  ,
,  ,
,  , уже не имеющие общих множителей. После деления НОК на данные числа получаются частные
, уже не имеющие общих множителей. После деления НОК на данные числа получаются частные  ,
,  и
и  , также не имеющие общих множителей.
, также не имеющие общих множителей.
Наибольший общий делитель двух чисел может быть полезен в арифметике при сокращении дробей: найдя НОД числителя и знаменателя и сократив на него, мы сразу получаем несократимую дробь. При этом нахождение НОД стоит некоторого труда, так как не всегда очевидно с первого взгляда, каковы простые множите ли данного числа и в каких степенях они входят.
В алгебре же такого рода применение НОД излишне, так как буквенные множители выписываются явно.
Если, например, дана дробь  то НОД числителя и знаменателя равен
то НОД числителя и знаменателя равен  ; сокращая на него, получим
; сокращая на него, получим  . Но и без наибольшего общего делителя можно сократить сначала, например, на
. Но и без наибольшего общего делителя можно сократить сначала, например, на  , потом на
, потом на  .
.
Зато в алгебре НОД приносит больше пользы при вынесении за скобку общих множителей много членных выражений. Пусть дано выражение  .
.
Мы видим сразу, что НОД всех членов равен  , и, вынося его за скобку, получаем:
, и, вынося его за скобку, получаем:  .
.
Что касается наименьшего общего кратного, то мы увидим дальше, что в алгебре, как и в арифметике, оно позволяет значительно упрощать записи при сложении и вычитании дробей.
Более сложные случаи сложения и вычитания дробей
При сложении и вычитании дробей удобно пользоваться приемом составления общего знаменателя посредством перемножения знаменателей данных дробей только в том случае, если каждые два, попарно взятые, знаменателя не имеют общих — ни буквенных, ни числовых — множителей. В других случаях употребление этого приема, хотя и дает верный результат, однако, ни коим образом не может быть рекомендовано, так как ведет к лишним записям и потере времени. Общее правило таково: в качестве общего знаменателя нескольких дробей следует брать НОК знаменателей всех данных дробей. Предварительно необходимо каждый знаменатель представить как про изведение отдельных множителей; в частности, если данный знаменатель — многочлен, нужно общие числовые и буквенные множители его членов выносить за скобку. Если встречаются многочленные множители, отличающиеся только знаком, то знак нужно менять, пользуясь уже известными приемами.
После того как общий знаменатель найден, необходимо выяснить, на какой один и тот же «дополнительный множитель» придется умножить знаменатель и числитель каждой дроби для того, чтобы ее знаменатель стал равным выбранному общему знаменателю.
Дальше, раз уже дроби приведены к общему знаменателю, сделать сложение или вычитание не представляет труда.
Пример:

Произведение знаменателей равно  . Однако есть возможность в качестве общего знаменателя взять более простое выражение, именно НОК знаменателей, равное
. Однако есть возможность в качестве общего знаменателя взять более простое выражение, именно НОК знаменателей, равное  . Дополнительным множителем для первой дроби является
. Дополнительным множителем для первой дроби является  , для второй
, для второй  , для третьей
, для третьей  :
:  ,
,  ,
,  .
.
Итак, 
Пример:
 .
.
HOK знаменателей равно  . Для первой дроби дополнительный множитель равен
. Для первой дроби дополнительный множитель равен  , для второй
, для второй  . Итак,
. Итак,  .
.
Пример:

Принимая во внимание, что  и что
и что  , мы можем переписать данное выражение в следующем виде:
, мы можем переписать данное выражение в следующем виде:  .
.
Теперь ясно, что наименьшее общее кратное знаменателей равно  . Дополнительные множители трех дробей соответственно равны
. Дополнительные множители трех дробей соответственно равны  ,
,  и
и  . Итак, мы получаем сумму
. Итак, мы получаем сумму  или же, после упрощений в числителе и сокращения на
или же, после упрощений в числителе и сокращения на  ,
,  .
.
Сложные дроби
Если приходится выполнять деление над выражениями, уже содержащими дроби, то, записывая частное в виде дроби (с чертой), мы получаем сложную дробь. Для облегчения записи в таких случаях иногда пользуются знаком двоеточия, но смысл получаемого от этого, конечно, не изменяется. Например, если  требуется разделить на
требуется разделить на  , то результат можно записать в виде
, то результат можно записать в виде  или
или  .
.
Сложную дробь всегда можно преобразовать в простую. Для этого достаточно выполнить все действия в том порядке, как они указаны: сначала числитель и знаменатель сложной дроби записать в виде простых дробей и затем разделить дробь на дробь, согласно правилу деления. Так, в нашем примере мы получим:
Однако такой способ преобразования сложной дроби в простую практически менее удобен, чем следующий. Пользуясь основным свойством дроби, умножим в нашем примере числитель и знаменатель на  ; тогда получим прежний результат:
; тогда получим прежний результат:  .
.
В качестве множителя, на который умножаются и числитель и знаменатель данной сложной дроби, следует, конечно, выбирать НОК знаменателей всех дробей, содержащихся в числителе и знаменателе данной дроби.
Всякое дробное алгебраическое выражение содержит лишь конечное число делений. Поэтому, сколько бы ни было «этажей» о сложной дроби, такую дробь всегда можно преобразовать в простую, постепенно уничтожая «этажи». Отсюда следует, что дробное алгебраическое выражение всегда может быте представлено в виде отношения двух целых алгебраических выражений.
Все действия с дробями. Расположенные многочлены в числителе и знаменателе дроби. Выделение целой части из неправильной дроби
Выполняя указанные действия над данными, простыми или сложными, алгебраическими дробями, мы получаем в результате простую алгебраическую дробь.
Если числители и знаменатели данных дробей — многочлены, расположенные по степеням одной и той же буквы, то числитель и знаменатель дроби, получающейся в результате выполнения действий, также представляются в виде многочленов, расположенных по степеням той же буквы.
После этого, если удастся в числителе и знамена теле обнаружить общие множители, на них следует сокращать полученную дробь.
Простая дробь, у которой числитель и знаменатель — многочлены, расположенные по степеням одной и той же буквы, называется: правильной, если степень числителя меньше, чем степень знаменателя; неправильной, если степень числителя больше или равна степени знаменателя.
Если дробь — неправильная, то ее всегда можно представить в виде суммы многочлена и правильной дроби. Это делается посредством деления числителя на знаменатель.
Неправильная дробь равна сумме: 1) частного, получающегося при делении числителя на знаменатель, и 2) правильной дроби, у которой числитель равен остатку при этом делении, а знаменатель — знаменателю данной дроби.
Например, деля многочлен  на двучлен
на двучлен  , получаем:
, получаем:  ; значит,
; значит,  .
.
Описанное выше преобразование напоминает выделение целой части из неправильной арифметической дроби; сравните хотя бы с таким примером: 
По указанной причине это преобразование называется выделением целой части из неправильной алгебраической дроби.




