Двойная звезда как найти большую полуось

На прошлом уроке мы с вами узнали, что звёзды отличаются
большим разнообразием. И при первом знакомстве со звёздным небом обращает на
себя внимание тот факт, что звёзды разнятся по цвету. Гораздо сильнее это
заметно при рассмотрении их спектров. С учётом видов спектральных линий и их
интенсивности строится спектральная классификация звёзд, которая отражает
уменьшение температуры атмосферы звезды от класса О к
классу М.

Однако не только цветом и температурой могут отличаться
звёзды. Как показали наблюдения, многие из них образуют пары или являются
членами сложных систем. При этом только в нашей Галактике примерно половина
всех звёзд принадлежит к двойным системам.

Двойными звёздами называют близко расположенные пары
звёзд.

Среди звёзд, которые видны на небе рядом, различают оптические
двойные и физические двойные. В первом случае две звезды
проецируются на небесную сферу рядом друг с другом. Хотя в действительности они
могут располагаться на огромном расстоянии друг от друга.

А вот физические двойные звёзды действительно расположены в
пространстве рядом друг с другом. Они не только связаны между собой силами
тяготения, но и обращаются около общего центра масс.

Впервые идея о существовании двойных звёзд была выдвинута
английским учёным и священником Джоном Мичеллом в 1767 году. А наблюдательные
подтверждения этой гипотезы были опубликованы в 1802 году Уильямом Гершелем.

Первая известная ещё с древности звёздная пара — это Мицар и
Алькор, наблюдаемые в ручке «ковша» Большой Медведицы. Эта звёздная пара —
хороший пример оптической двойной звезды, так как Алькор отстоит от Мицара
примерно на 12 угловых минут.

Но, если посмотреть на Мицар в телескоп, то легко можно
заметить, что он состоит из двух очень близко расположенных звёзд, названных
Мицаром А и Мицаром В. Эта звёздная пара — пример физической двойной звезды.

Когда число звёзд в системе, связанных взаимным тяготением,
оказывается больше двух, то их называют кратными. Существуют звёзды
тройные, четверные и даже более высокой кратности. Примером кратных звёзд может
служить тройная звезда α Центавра. Причём, что интересно, одна из компонентов — Проксима — является ближайшей к
Земле звездой после Солнца.

К кратным звёздам принято причислять звёзды, имеющие менее 10
компонентов. Если же в системе
насчитывается большее количество звёзд, то её называют звёздным скоплением.
Классическим примером служит рассеянное скопление Плеяд, видное на ночном небе
невооружённым глазом.

Физические двойные звёзды, в зависимости от способа их
наблюдения, принято делить на несколько классов. Рассмотрим их поподробнее.

Визуально-двойные звёзды — это двойные звёзды,
компоненты которых можно увидеть раздельно (в телескоп или сфотографировать).
Возможность наблюдать звезду как визуально-двойную определяется разрешающей
способностью телескопа. Поэтому все известные визуально-двойные звёзды
расположены в окрестностях Солнца с очень большим периодом обращения (вплоть до
нескольких тысяч лет). А их орбиты сравнимы по размерам с орбитами
планет-гигантов нашей Солнечной системы. В связи с этим, из свыше 110 000 таких
объектов менее чем у сотни орбиты определены с большой точностью.

Оказалось, что относительное видимое движение компонентов
совершается по эллипсу и удовлетворяет закону площадей. Следовательно, в
двойных системах обращения звёзд вокруг общего центра масс происходят в
соответствии с законами Кеплера и подчиняются закону всемирного тяготения
Ньютона.

Из этого следует, что при известном расстоянии до этих систем
использование третьего обобщённого закона Кеплера позволяет определить их
массу. Для этого достаточно сравнить движение спутника звезды с движением Земли
вокруг Солнца.

Приняв массу Солнца равной единице большую полуось земной
орбиты равной одной астрономической единице и пренебрегая массой Земли по
сравнению с массой Солнца, получим соотношение, по которому можно определить
суммарную массу двойной системы, выраженную в массах Солнца:

Если же необходимо вычислить массу каждого компонента
звёздной пары, то надо изучить движение каждой из них и вычислить их расстояния
от общего центра масс:

Тогда отношение масс компонентов звёздной пары будет обратно
пропорционально отношению больших полуосей их орбит:

Для примера давайте с вами определим сумму масс и массу звёзд
двойной звезды, годичный параллакс которой составляет 0,08’’. Будем считать,
что период обращения компонентов равен 56 годам, а большая полуось видимой
орбиты равна 3’’. Компоненты звезды отстоят от центра масс на расстояниях,
относящихся как 1 : 7.

Наблюдения за двойными звёздами и оценка их масс для
различных типов показали, что:

·                  
массы звёзд колеблются в пределах 0,03—60 масс Солнца. Причём наибольшее
количество звёзд имеет массу от 0,4 до 3 масс Солнца;

·                  
существует зависимость между массами звёзд и их светимостями, что даёт
возможность оценивать массы одиночных звёзд. Так, если масса звезды лежит в
интервале от 0,5 до 10 масс Солнца, то её светимость пропорциональна 4 степени
массы. Если же масса звезды больше 10 масс Солнца, — то 2 степени.

Второй класс двойных систем составляют затменно-двойные
или затменно-переменные звёзды. Они представляют собой тесные пары,
обращающиеся с периодом от нескольких часов до нескольких суток по орбитам,
большая полуось которых сравнима с самими звёздами. Это приводит к тому, что
угловое расстояние между звёздами очень мало. Поэтому мы не можем увидеть
компоненты системы по-отдельности.

Однако судить о том, что система действительно является
двойственной, можно по периодическим колебаниям её блеска. Предположим, что
плоскости орбит звёзд по лучу зрения практически совпадают. Тогда при обращении
звёздной пары, когда один из компонентов оказывается впереди или сзади другого,
наблюдаются затмения.

Разность звёздных величин в минимуме и максимуме блеска
называется амплитудой. А промежуток времени между двумя
последовательными наименьшими минимумами — периодом переменности.

Классическим примером затменно-переменной звезды является
звезда β Персея (Алголь). Она каждые 2,567 суток затмевается на девять 9,6
часа.

Пока известно около 4000 затменно-двойных звёзд.

Следующий класс представляют спектрально-двойные звёзды.
Это такие звёзды, двойственность которых устанавливается лишь на основании
спектральных наблюдений.

Представьте, у нас есть две звезды: одна массивная и яркая А,
вторая — менее яркая и массивная В. Обе они обращаются вокруг общего центра
масс системы, то приближается к наблюдателю, то удаляется от него.

Вследствие эффекта Доплера в первом случае линии в спектре
звезды будут смещаться в фиолетовую область спектра, а во втором — в красную.
Причём период этих смещений будет равен периоду обращения звёзд.

Интересно, что благодаря этому методу в 1995 году у звезды 51
Пегаса был обнаружен спутник, масса которого составляла около половины массы
Юпитера. Так была найдена первая экзопланета (так называют планеты,
находящиеся вне Солнечной системы).

На середину октября 2017 года спектральным методом достоверно
подтверждено существование 3672 экзопланет в 2752 планетных системах.

И последний класс двойственных систем представляют астрометрически-двойные
звёзды. Они представляют собой очень тесные звёздные пары, в которых одна
из звёзд или очень мала по размерам, или имеет низкую светимость.

Двойственность такой звезды можно обнаружить лишь по
отклонениям яркой компоненты от прямолинейной траектории то в одну, то в другую
сторону. Вычисления показали, что такие возмущения пропорциональны массе
спутника.

Среди близких к Солнцу звёзд обнаружено около 20
астрометрически-двойных систем.

Массы
и размеры звезд

1.
Двойные звезды

Массы звезд. Как мы убедились на примере Солнца, масса звезды
является той важнейшей характеристикой, от которой зависят физические условия в
ее недрах. Прямое определение массы возможно лишь для двойных звезд.

Двойные звезды называются визуально-двойными, если их
двойственность может быть замечена при непосредственных наблюдениях в телескоп.

Примером визуально-двойной звезды, видимой даже невооруженным
глазом, является с, Большой Медведицы, вторая звезда с конца “ручки”
ее “ковша”. При нормальном зрении совсем близко от нее видна вторая
слабая звездочка. Ее заметили еще древние арабы и назвали Алькор (Всадник).
Яркой звезде они дали название Мицар. Мицар и Алькор отстоят друг
от друга на небе на 11′. В бинокль таких звездных пар можно найти немало.

Системы с числом звезд n≥З называются кратными. Так, в
бинокль видно, что ε Лиры состоит из двух одинаковых звезд 4-й звездной
величины с расстоянием между ними 3′. При наблюдении в телескоп ε Лиры –
визуально-четверная звезда. Однако некоторые звезды оказываются лишь оптически-двойными,
т. е. близость, таких двух звезд является результатом случайной проекции их на
небо. На самом деле в пространстве они далеки друг от друга. Если же при
наблюдении звезд выясняется, что они образуют единую систему и обращаются под
действием сил взаимного притяжения вокруг общего центра масс, то их
называют физическими двойными.

Множество двойных звезд открыл и изучил известный русский ученый
В. Я. Струве. Самые короткие из известных периодов обращения визуально-двойных
звезд – несколько лет. Изучены пары с периодами обращения в десятки лет, а пары
с периодами в сотни лет изучат в будущем. Ближайшая к нам звезда а Центавра
является двойной. Период обращения ее составляющих (компонентов) 70 лет. Обе
звезды в этой паре по массе и температуре сходны с Солнцем.

Рис. 73 Орбита спутника двойной вокруг главной звезды, расстояние которой от
нас составляет 10 пк. (Точки отмечают измеренные положения спутника в указанные
годы. Их отклонения от эллипса вызваны погрешностями наблюдений.)

Главная звезда обычно не находится в фокусе видимого эллипса,
описываемого спутником, потому что мы видим его орбиту в проекции искаженной
(рис. 73). Но знание геометрии позволяет восстановить истинную форму орбиты и
измерить ее большую полуось а в секундах дуги. Если известно расстояние D до
двойной звезды в парсеках и большая полуось орбиты звезды-спутника в секундах
дуги, равная а”, то в астрономических единицах она будет равна:

так как D_пк=¹/_р” .

Сравнивая движение спутника звезды с движением Земли вокруг Солнца
(для которой период обращения Т=1 год,
а большая полуось орбиты а=1 а.
е.), мы по III зэкону Кеплера можем написать:

где m₁ и m₂ – массы компонентов в
паре звезд, Ми М –
массы Солнца и Земли, а T – период обращения пары в годах. Пренебрегая массой
Земли в сравнении с массой Солнца, мы получаем сумму масс звезд, составляющих
пару, в массах Солнца:

Чтобы определить массу каждой звезды, надо изучить движение
компонентов относительно окружающих звезд и вычислить их расстояния А₁ и
А₂ от общего центра масс. Тогда получим второе уравнение m₁:m₂=А₂:А₁ и
из системы двух уравнений найдем обе массы отдельно.

Двойные звезды в телескоп нередко представляют собой красивое
зрелище: главная звезда желтая или оранжевая, а спутник белый или голубой.

Если компоненты двойной звезды при взаимном обращении подходят
близко друг к другу, то даже в самый сильный телескоп их нельзя видеть
раздельно. В этом случае двойственность может быть определена по спектру. Такие
звезды будут называться спектрально-двойными. Из-за эффекта Доплера
линии в спектрах звезд будут смещаться в противоположные стороны (когда одна
звезда удаляется от нас, другая приближается). Смещение линий меняется с
периодом, равным периоду обращения пары. Если яркости и спектры звезд,
составляющих пару, сходны, то в спектре двойной звезды наблюдается
периодически повторяющееся раздвоение спектральных линий (рис. 74).
Пусть компоненты занимают положения А₁ и В₁ или
A₃ и В₃, тогда один из них движется к наблюдателю, а
другой – от него (рис. 74, I, III). В этом случае наблюдается раздвоение
спектральных линий. У приближающейся звезды спектральные линии сместятся к синему
концу спектра, а у удаляющейся – к красному. Когда же компоненты двойной звезды
занимают положения А₂ и В₂ или A₄ и
В₄ (рис. 74, II, IV), то оба они движутся под прямым углом к
лучу зрения и раздвоения спектральных линий не получится.

Рис. 74. Объяснение раздвоения, или колебания, линий в спектрах
спектрально-двойных звезд

Если одна из звезд светится слабо, то будут видны линии только
другой звезды, смещающиеся периодически.

Компоненты спектрально-двойной звезды могут при взаимном обращении
поочередно загораживать друг друга. Такие звезды называются затменно-двойными
или алголями, по названию своего типичного представителя β Персея. Во время
затмений общая яркость пары, компонентов которой мы по отдельности не видим,
будет ослабевать (положения В и D рис. 75.) В остальное же время в промежутках
между затмениями она почти постоянна (положения А и С) и тем дольше, чем короче
длительность затмений и чем больше радиус орбиты. Если спутник большой, но сам
дает мало света, то когда яркая звезда затмевает его, суммарная яркость системы
будет уменьшаться лишь ненамного.

Рис. 75. Изменения видимой яркости р Лиры и схема движения ее спутника. (Форма
звезд, близко расположенных друг к другу, вследствие их приливного воздействия
может сильно отличаться от сферической.)

Древние арабы назвали β Персея Алголем (испорченное
эль гуль), что означает “дьявол”. Возможно, что они заметили ее
странное поведение: в течение 2 дней 11 ч яркость Алголя постоянна, затем за 5
ч она ослабевает от 2,3 до 3,5 звездной величины, а затем за 5 ч яркость ее
возвращается к прежнему значению.

Анализ кривой изменения видимой звездной величины в функции
времени позволяет установить размеры и яркость звезд, размеры орбиты, ее форму
и наклон к лучу зрения, а также массы звезд. Таким образом, затменно-двойные
звезды, наблюдаемые также и в качестве спектрально-двойных, являются наиболее
хорошо изученными системами. К сожалению, таких систем известно пока
сравнительно мало.

Периоды известных спектрально-двойных звезд и алголей в основном
короткие – около нескольких суток.

В общей сложности двойственность звезд очень распространенное
явление. Статистика показывает, что до 30% всех звезд, вероятно, являются
двойными.

Определенные описанными методами массы звезд различаются гораздо
меньше, чем их светимости: примерно от 0,1 до 100 масс Солнца. Очень большие
массы встречаются крайне редко. Обычно звезды обладают массой меньше пяти масс
Солнца.

Именно масса звезд обусловливает их существование и природу как
особого типа небесных тел, для которых характерна высокая температура недр
(свыше 10⁷ К) – Происходящие при такой температуре ядерные
реакции превращения водорода в гелий являются у большинства звезд источником
излучаемой ими энергии. При меньшей массе температура внутри небесных тел не достигает
тех значений, которые необходимы для протекания термоядерных реакций.

Эволюция химического состава вещества во Вселенной происходила и
происходит в настоящее время главным образом благодаря звездам. Именно в их
недрах идет необратимый процесс синтеза более тяжелых химических элементов из
водорода.

Пример
решения задачи

Задача. У двойной звезды период обращения 100 лет. Большая полуось
видимой орбиты а = 2,0″, а параллакс ρ = 0,05″. Определите сумму масс
и массы звезд в отдельности, если звезды отстоят от центра масс на расстояниях,
относящихся как 1:4.

Упражнение
21

1. Определите сумму масс двойной звезды Капеллы, если большая
полуось ее орбиты равна 0,85 а. е., а период обращения составляет 0,285 года.

2. Если бы по орбите Земли двигалась звезда с такой же массой, как
у Солнца, каков был бы период ее обращения?

3. По рисунку 73 оцените период обращения спутника, большую
полуось орбиты и вычислите сумму масс компонентов. Считать, что большая полуось
орбиты лежит в плоскости рисунка.

2.
Размеры звезд. Плотность их вещества

Покажем на простом примере, как можно сравнить размеры звезд
одинаковой температуры, например Солнца и Капеллы (α Возничего). Эти звезды
имеют одинаковые спектры, цвет и температуру, но светимость Капеллы в 120 раз
превышает светимость Солнца. Так как при одинаковой температуре яркость единицы
поверхности звезд тоже одинакова, то, значит, поверхность Капеллы больше, чем
поверхность Солнца, в 120 раз, а диаметр и радиус ее больше солнечных в  раз.

Определить размеры других звезд позволяет знание законов
излучения.

Так, в физике установлено, что полная энергия, излучаемая в
единицу времени с 1 м² поверхности нагретого тела, равна: i =
σТ⁴, где σ – коэффициент пропорциональности, а T – абсолютная
температура^*. Относительный линейный диаметр звезд, имеющих
известную температуру Т, находят из формулы

^* (Закон
Стефана – Болыдмана установлен австрийскими физиками Й. Стефаном
(экспериментально) и Л. Больцманом. )

где r – радиус звезды, i – излучение единицы поверхности звезды, r, i, T относятся
к Солнцу, a L= l. Отсюда

в радиусах Солнца.

Результаты таких вычислений размеров светил полностью подтвердились,
когда стало возможным измерять угловые диаметры звезд при помощи особого
оптического прибора (звездного интерферометра).

Звезды очень большой светимости называются сверхгигантами. Красные
сверхгиганты оказываются такими и по размера (рис. 76). Бетельгейзе и Антарес в
сотни раз больше Солнца по диаметру. Более далекая от нас VV Цефея настолько
велика, что внутри нее поместилась бы Солнечная система с орбитами планет до
орбиты Юпитера включительно! Между тем массы сверхгигантов больше солнечной всего
лишь в 30-40 раз. В результате даже средняя плотность красных сверхгигантов в
тысячи раз меньше, чем плотность комнатного воздуха.

Рис. 76. Сравнительные размеры Солнца и звезд разных типов (масштабы в двух
частях рисунка различны)

При одинаковой светимости размеры звезд тем меньше, чем эти звезды
горячее. Самыми малыми среди обычных звезд являются красные карлики. Массы их и
радиусы – десятые доли солнечных, а средние плотности в 10-100 раз выше, чем
плотность воды. Еще меньше красных белые карлики – но это уже необычные звезды.

У близкого к нам и яркого Сириуса (имеющего радиус примерно вдвое
больше солнечного) есть спутник, обращающийся вокруг него с периодом 50 лет.
Для этой двойной звезды расстояние, орбита и массы хорошо известны. Обе звезды
белые, почти одинаково горячие. Следовательно, поверхности одинаковой площади
излучают у этих звезд одинаковое количество энергии, но по светимости спутник в
10 000 раз слабее, чем Сириус. Значит, его радиус меньше в √10000= 100 раз, т.
е. он почти такой же, как Земля. Между тем масса у него почти как у Солнца!
Следовательно, белый карлик имеет громадную плотность – около 10⁹ кг/м³.
Существование газа такой плотности было объяснено следующим образом: обычно
предел плотности ставит размер атомов, являющихся системами, состоящими из ядра
и электронной оболочки. При очень высокой температуре в недрах звезд и при
полной ионизации атомов их ядра и электроны становятся независимыми друг от
друга. При колоссальном давлении вышележащих слоев это “крошево” из
частиц может быть сжато гораздо сильнее, чем нейтральный газ. Теоретически
допускается возможность существования при некоторых условиях звезд с
плотностью, равной плотности атомных ядер.

Мы еще раз видим на примере белых карликов, как астрофизические исследования
расширяют представления о строении вещества; пока создать в лаборатории такие
условия, какие есть внутри звезд, еще нельзя. Поэтому астрономические
наблюдения помогают развитию важнейших физических представлений. Например, для
физики громадное значение имеет теория относительности Эйнштейна. Из нее
вытекает несколько следствий, которые можно проверить по астрономическим
данным. Одно из следствий теории состоит в том, что в очень сильном поле
тяготения световые колебания должны замедляться и линии спектра смещаться к
красному концу, причем это смещение тем больше, чем сильнее поле тяготения
звезды. Красное смещение было обнаружено в спектре спутника Сириуса. Оно
вызвано действием сильного поля тяготения на его поверхности. Наблюдения
подтвердили это и ряд других следствий теории относительности. Подобные примеры
тесной взаимосвязи физики и астрономии характерны для современной науки.

Пример
решения задачи

Задача. Во сколько раз Арктур больше Солнца, если светимость
Арктура 100, а температура 4500 К?

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 7 июля 2020 года; проверки требуют 6 правок.

Функция масс двойных звёзд (англ. Binary mass function) — функция, создающая ограничения для массы ненаблюдаемого компонента (звезды или экзопланеты) в спектрально-двойных звёздах или планетных системах с одной линией. Значение определяется по наблюдаемым характеристикам: по орбитальному периоду двойной системы и пику лучевой скорости наблюдаемой звезды. Скорость одного компонента двойной и орбитальный период двойной системы предоставляют частичную информацию о расстоянии и гравитационном взаимодействии между компонентами, что даёт сведения о массах объектов.

Введение[править | править код]

Функция масс двойных систем опирается на третий закон Кеплера, в который вводится лучевая скорость наблюдаемого компонента.^[1] Третий закон Кеплера описывает движения двух тел, обращающихся вокруг одного центра масс. Он связывает период обращения (время, необходимое для совершения полного оборота), расстояние между двумя объектами и сумму их масс. При заданном расстоянии между телами в случае большей суммы масс системы орбитальные скорости также будут выше. С другой стороны, при заданной массе больший период обращения подразумевает большее расстояние и большие скорости на орбите.

Поскольку период обращения и скорости на орбите в двойной системе связаны с массами компонентов двойной, то измерение данных параметров предоставляет некоторые сведения о массе одного или обоих объектов.^[2] Но, поскольку настоящую орбитальную скорость в общем случае определить невозможно, то получаемая информация весьма ограничена.^[1]

Лучевая скорость является компонентом орбитальной скорости вдоль луча зрения наблюдателя. В отличие от истинной орбитальной скорости, лучевую скорость можно определить методами доплеровской спектроскопии спектральных линий в излучении звезды^[3] или по вариациям времени приёма импульсов от радиопульсара.^[4] В том случае, когда наблюдается спектральная линия только одного компонента, можно определить нижнюю границу для массы второго компонента.^[1]

Истинные значения массы и орбитальной скорости нельзя определить по данным о лучевой скорости, поскольку наклонение орбиты относительно картинной плоскости чаще всего неизвестно (наклонение орбиты с точки зрения наблюдателя связывает лучевую скорость и орбитальную^[1]). Это приводит к зависимости оценки массы от наклона орбиты.^[5][6] Например, если измеренная скорость мала, это может означать либо малую орбитальную скорость (что означает малые массы объектов) и большое наклонение (орбита видна практически с ребра), либо высокую орбитальную скорость (и большие массы компонентов) при малом наклонении (орбита видна практически плашмя).

Вывод соотношений для круговых орбит[править | править код]

Пик лучевой скорости является половиной амплитуды кривой лучевых скоростей, как показано на рисунке. Орбитальный период определяется по периодичности кривой лучевой скорости. Эти величины необходимо определить по наблюдательным данным для вычисления функции масс двойной системы.^[2]

Наблюдаемый объект и его параметры обозначим индексом 1, ненаблюдаемый объект — индексом 2.

Пусть и — массы объектов, представляет полную массу двойной системы, и — орбитальные скорости, и — расстояния от объектов до центра масс системы. — большая полуось двойной системы.

Запишем третий закон Кеплера, здесь — орбитальная частота, — гравитационная постоянная.

По определению центра масс, ,^[1] запишем

Подставляя данное выражение для в третий закон Кеплера, получим

что можно переписать в виде

Пик лучевой скорости объекта 1, , зависит от наклонения орбиты (наклонение 0° соответствует орбите, видимой плашмя, при наклонении 90° орбита видна с ребра). Для круговой орбиты (эксцентриситет равен 0) определяется соотношением^[7]

После подстановки получаем соотношение

Функция масс двойной системы имеет вид^{[8][7][2][9][1][6][10]}

Для оценки или предположения о массе наблюдаемого объекта 1 можно определить минимальную массу ненаблюдаемого объекта 2 в предположении . Истинное значение массы зависит от наклонения орбиты. Наклонение обычно неизвестно, но с некоторой точностью его можно определить из наблюдений затмений,^[2] ограничить по ненаблюдаемости прохождений^[8][9] или моделировать с использованием эллипсоидальных вариаций (несферическая форма звезды в двойной системе приводит к изменениям блеска при обращении по орбите, зависящим от наклонения системы).^[11]

Ограничения[править | править код]

В случае (например, когда ненаблюдаемый объект является экзопланетой^[8]) функция масс приводится к виду

В случае (например, если ненаблюдаемый объект является массивной чёрной дырой), функция масс имеет вид^[2]

и при для функция массы даёт нижний предел для массы ненаблюдаемого объекта 2.^[6]

В общем случае для любого и

Орбита с ненулевым эксцентриситетом[править | править код]

В случае, когда орбита обладает ненулевым эксцентриситетом , функция массы имеет вид^[7][12]

.

Применение[править | править код]

Рентгеновские двойные звёзды[править | править код]

Если объект-аккретор в рентгеновской двойной звезде обладает минимальной массой, превосходящей предел Оппенгеймера — Волкова (наибольшая возможная масса нейтронной звезды), то объект, вероятно, является чёрной дырой. Такова ситуация с источником Лебедь X-1, для которого была измерена скорость звезды-компаньона.^[13][14]

Внесолнечные планеты[править | править код]

Наличие экзопланеты приводит к движению звезды по малой орбите вокруг центра масс системы звезда-планета. Такие колебания могут наблюдаться, если лучевая скорость звезды достаточно высока. Похожим образом проводится метод детектирования экзопланет по лучевым скоростям.^[5][3] Используя функцию масс и лучевую скорость родительской звезды, можно определить минимальную массу экзопланеты.^{[15][16]:9[12][17]} Применение данного метода к наблюдениям Проксимы Центавра, ближайшей звезды к Солнцу, привело к обнаружению Проксимы Центавра b, экзопланеты земного типа с минимальной массой 1.27 M_⊕.^[18]

Планеты около пульсаров[править | править код]

Пульсарные планеты обращаются вокруг пульсаров, несколько подобных планет было открыто при анализе интервалов времени между вспышками. Изменения лучевой скорости пульсара определяются по меняющимся промежуткам времени между приёмом сигнала от импульсов.^[4] Первые экзопланеты открыты таким методом в 1992 году вокруг миллисекундного пульсара PSR 1257+12.^[19] Другим примером является PSR J1719-1438, миллисекундный пульсар, чьим компаньоном является PSR J1719-1438 b, обладает минимальной массой примерно как у Юпитера, согласно функции масс.^[8]

Примечания[править | править код]

Лекция 16, 17.
Внутреннее строение и эволюция звезд

Общие характеристики
двойных систем

Двойные звезды
весьма часто встречаются в природе,
поэтому их изучение существенно не
только для выяснения природы самих
звезд, но и для космогонических проблем
происхождения и эволюции звезд.

Чтобы убедиться
в том, что данная пара звезд физически
связана и не является оптически двойной,
необходимо произвести длительные
наблюдения, позволяющие заметить
орбитальное движение одной из звезд
относительно другой. С большой степенью
вероятности физическая двойственность
звезд может быть обнаружена по их
собственным движениям: звезды, образующие
физическую пару (компоненты двойной
звезды), имеют почти одинаковое собственное
движение. Иногда видна только одна из
звезд, совершающих взаимное орбитальное
движение. В этом случае ее путь на небе
выглядит волнистой линией.

В настоящее время
известны десятки тысяч тесных визуально
двойных звезд. Из них только 10% уверенно
обнаруживают относительные орбитальные
движения и лишь для 1% (примерно для 500
звезд) оказывается возможным надежно
вычислить орбиты.

Движение компонентов
двойных звезд происходит в соответствии
с законами Кеплера оба компонента
описывают в пространстве подобные (т.е.
с одинаковым эксцентриситетом)
эллиптические орбиты вокруг общего
центра масс. Таким же эксцентриситетом
обладает орбита звезды-спутника
относительно главной звезды, если
последнюю считать неподвижной. Большая
полуось орбиты относительного движения
спутника вокруг главной звезды равна
сумме больших полуосей орбит движения
обеих звезд относительно центра масс.
С другой стороны, величины больших
полуосей этих двух эллипсов обратно
пропорциональны массам звезд. Таким
образом, если из наблюдений известна
орбита относительного движения, то
можно определить сумму масс компонентов
двойной звезды. Если же известны отношения
полуосей орбит движения звезд относительно
центра масс, то можно найти еще отношение
масс и, следовательно, массу каждой
звезды в отдельности. В этом также
заключается огромная роль изучения
двойных звезд в астрономии: оно позволяет
определить важную характеристику звезды
— массу, знание которой необходимо, как
мы видели, для исследования внутреннего
строения звезды и ее атмосферы.

Для определения
элементов орбиты двойной звезды
рассмотрим движение спутника S₂
относительно главной звезды S₁
(рисунок). Она является эллипсом с большой
полуосью а
= а₁
+ а₂,
где а₁
и а₂
— большие
полуоси эллипсов, описываемых каждой
звездой вокруг общего центра масс.
Главная звезда находится в фокусе этого
эллипса. Точка орбиты спутника, ближайшая
к главной звезде, называется периастром
(П),
противоположная
— апоастром
(А).

Движение спутника
относительно главной звезды характеризуется
элементами
орбиты:
величина орбиты определяется длиной
большой полуоси а;
форма — эксцентриситетом
орбиты е;
положение плоскости орбиты относительно
наблюдателя — углом
наклонения плоскости орбиты i,
т.е.
углом, который она составляет с
перпендикулярной к лучу зрения картинной
плоскостью; движение спутника
характеризуется периодом
обращения Р,
обычно выражаемым в годах; положение
спутника в любой момент времени легко
определить, если задать момент
прохождения спутника через периастр
Т.

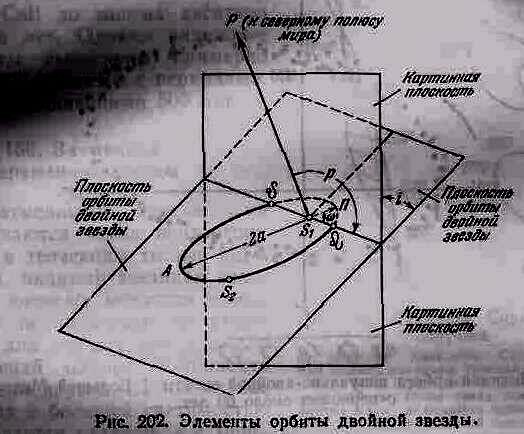
К этим пяти основным
элементам следует добавить еще два,
характеризующие положение большой оси
эллипса орбиты в пространстве. Углы в
плоскости орбиты отсчитываются от
одного из ее узлов.
Узлами <
и >
называются точки пересечения орбиты с
картинной плоскостью. Угол в плоскости
орбиты от узла до периастра называется
долготой
периастра
().
В картинной плоскости положение узла
определяется позиционным
углом р,
отсчитываемым от направления на полюс
мира до узла. Таким образом добавляется
еще два элемента: р
— позиционный
угол узла орбиты (берется всегда меньше
180°); 
— долгота периастра.

Визуально-двойные звезды

Двойные звезды,
двойственность которых обнаруживается
при непосредственных наблюдениях в
телескоп, называются визуально-двойными.
Видимую орбиту звезды-спутника
относительно главной звезды находят
по длительным рядам наблюдений,
выполненным в различные эпохи. С точностью
до ошибок наблюдений эти орбиты всегда
оказываются эллипсами (рис. 203). В некоторых
случаях на основании сложного собственного
движения одиночной звезды относительно
звезд фона можно судить о наличии у нее
спутника, который невидим либо из-за
близости к главной звезде, либо из-за
своей значительно меньшей светимости
(темный спутник). Именно таким путем
были открыты первые белые карлики —
спутники Сириуса и Проциона, впоследствии
обнаруженные визуально.

Видимая орбита
визуально-двойной звезды является
проекцией истинной орбиты на картинную
плоскость. Поэтому для определения всех
элементов орбиты прежде всего необходимо
знать угол наклонения i.
Этот угол можно найти, если видны обе
звезды. Его определение основано на
том, что в проекции на плоскость,
перпендикулярную лучу зрения, главная
звезда оказывается не в фокусе эллипса
видимой орбиты, а в какой-то другой его
внутренней точке. Положение этой точки
однозначно определено углом наклонения
i
и долготой периастра .
Таким образом, определение элементов
i
и ,
а также эксцентриситета е
является чисто геометрической задачей.
Элементы Р,
Т и р
получаются непосредственно из наблюдений.
Наконец, истинное значение большой
полуоси орбиты а
и видимое а’
связаны очевидным соотношением

а’ = a cos i.

Из наблюдений а’
и, следовательно, а
получаются в угловой мере. Только зная
параллакс звезды, можно найти значение
большой полуоси в астрономических
единицах (а.е.).

В настоящее время
зарегистрировано свыше 60 000 визуально-двойных
систем. Примерно у 2000 из них удалось
обнаружить орбитальные движения с
периодами от наименьшего 2,62 года у 
Ceti
до многих десятков тысяч лет. Однако
надежные орбиты вычислены примерно для
500 объектов с периодами, но превышающими
500 лет.

Затменные переменные звезды

Затменными
переменными называются такие неразрешимые
в телескопы тесные пары звезд, видимая
звездная величина которых меняется
вследствие периодически наступающих
для земного наблюдателя затмений одного
компонента системы другим. В этом случае
звезда с большей светимостью называется
главной, а с меньшей — спутником.
Типичными примерами звезд этого типа
являются звезды Алголь 
Персея) и 
Лиры. Вследствие регулярно происходящих
затмений главной звезды спутником, а
также спутника главной звездой суммарная
видимая звездная величина затменных
переменных звезд меняется периодически.

График, изображающий
изменение потока излучения звезды со
временем, называется кривой
блеска.
Момент времени, в который звезда имеет
наименьшую видимую звездную величину,
называется эпохой максимума, а наибольшую
— эпохой минимума.

Разность звездных
величин в минимуме и максимуме называется
амплитудой,
а промежуток времени между двумя
последовательными максимумами или
минимумами — периодом
переменности. У Алголя, например, период
переменности равен 2^d
20^h
49^m,
а у 
Лиры — 12^d
21^h
48^m.

По характеру кривой
блеска затменной переменной звезды
можно найти элементы орбиты одной звезды
относительно другой, относительные
размеры компонентов, а в некоторых
случаях даже получить представление
об их форме. На рисунке показаны кривые
блеска некоторых затменных переменных
звезд вместе с полученными на их основании
схемами движения компонентов. На всех
кривых заметны два минимума: глубокий
(главный, соответствующий затмению
главной звезда спутником), и слабый
(вторичный), возникающий, когда главная
звезда затмевает спутник.

На основании
детального изучения кривых блеска можно
получить следующие данные о компонентах
затменных переменных звезд:

1. Характер затмений
(частное, полное или центральное)
определяется наклонением i
и размерами звезд. Когда i
= 90°, затмение центральное, как у 
Лиры (см. рис. 203). В тех случаях, когда
диск одной звезды полностью перекрывается
диском другой, соответствующие области
кривой блеска имеют характерные плоские
участки (как у IH
Кассиопеи), что говорит о постоянстве
общего потока излучения системы в
течение некоторого времени, пока меньшая
звезда проходит перед или за диском
большей. В случае только частных затмений
минимумы острые (как у RX
Геркулеса или 
Персея).

2. На основании
продолжительности минимумов находят
радиусы компонентов R₁
и R₂
,
выраженные в долях большой полуоси
орбиты, так как продолжительность
затмения пропорциональна диаметрам
звезд.

3. Если затмение
полное, то по отношению глубин минимумов
можно найти отношение светимостей, а
при известных радиусах, — также и
отношение эффективных температур
компонентов.

4. Отношение
промежутков времени от середины главного
минимума до середины вторичного минимума
и от вторичного минимума до следующего
главного минимума зависит от эксцентриситета
орбиты е
и долготы периастра .
Точнее, фаза наступления вторичного
минимума зависит от произведения е
cos
.
Если вторичный минимум лежит посередине
между двумя главными минимумами (как у
RX
Геркулеса), то орбита симметрична
относительно луча зрения и, в частности,
может быть круговой. Асимметрия положения
вторичного минимума позволяет найти
произведение е
cos
.

5. Наклон кривой
блеска, иногда наблюдаемый между
минимумами, позволяет количественно
оценить эффект отражения одной звездой
излучения другой, как, например, у 
Персея.

6. Плавное изменение
кривой блеска, как, например, у 
Лиры, говорит об эллипсоидальности
звезд, вызванной приливным воздействием
очень близких компонентов двойных
звезд. К таким системам относятся звезды
типа 
Лиры и W
Большой Медведицы. В этом случае по
форме кривой блеска можно установить
форму звезд.

7. Детальный ход
кривой блеска в минимумах иногда
позволяет судить о законе потемнения
диска звезды к краю. Выявить этот эффект,
как правило, очень трудно. Однако, в
отличие от Солнца, это единственный
имеющийся в настоящее время метод
изучения распределения яркости по
дискам звезд.

В итоге на основании
вида кривой блеска затменной переменной
звезды в принципе можно определить
следующие элементы и характеристики
системы:

i
— наклонение орбиты; Р
— период; Т
— эпоха
главного минимума; е
— эксцентриситет орбиты; 
— долгота периастра; R₁
и R₂
— радиусы
компонентов, выраженные в долях большой
полуоси; для звезд типа 
Лиры — эксцентриситеты эллипсоидов,
представляющих форму звезд; L₁/L₂
— отношение
светимостей компонентов или их температур
T₁/T₂
.

Для некоторых
особых типов звезд (например, Вольфа —
Райе), если они затменные, удается найти
ряд дополнительных характеристик.

Задача определения
всех этих величин весьма сложна и далеко
не всегда может быть решена до конца.
Обычно по общему виду кривой блеска
сначала грубо определяют тип и поименную
ориентацию орбиты, после чего точно
вычисляются элементы орбиты.

В настоящее время
известно свыше 4000 затменных переменных
звезд различных типов. Минимальный
известный период — менее часа, наибольший
— 57 лет. Информация о затменных звездах
становится более полной и надежной при
дополнении фотометрических наблюдений
спектральными.

Соседние файлы в папке Лекции

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #