Единичный отрезок 3 класс как найти

Урок
по математике в 3 классе

Учитель:
Титарева Елена Яковлевна

Тема раздела: «Числовой
(координатный) луч» -13 часов

Тема урока:
Единичный отрезок и его выбор- 5 урок

Цель:
Способствовать введению понятия «единичный отрезок»

Ожидаемый
результат:

– оперирует
понятием «единичный отрезок»,

– находит
единичный отрезок на числовом луче,

– строит числовой
луч с заданным единичным отрезком,

– устанавливает
причинно-следственные связи между длиной единичного отрезка и    расположением
изображаемых чисел,

– принимает и
сохраняет учебную задачу,

– планирует
собственную деятельность,

– осуществляет
самоконтроль и самооценку.

Этапы урока	Деятельность учителя	Деятельность ученика
I. Эмоциональный настрой	Сегодня необычный урок. Вы уже знаете, что урок будет вести группа учителей. Кроме нас еще гости. Повернитесь и поприветствуйте их. Спасибо. Настраиваемся на работу. Откройте тетради, запишите дату, классная работа.	Приветствуют, записывают
II.Постановка учебной задачи 1. Актуализация знаний	– Ребята, мы приехали вчера и узнали, что вы уже изучаете тему «Числовой луч». У нас нет такой темы. Мы вообще это  не проходили. Помогите нам разобраться. – Что вы можете сказать про числовой луч? (Заполняет кластер) (Вариант: Ой, на столе еще остались карточки с записями. Кто поможет разобраться?) – Постройте числовой луч в тетради. – Покажите готовность. – Кто желает начертить свой луч на доске? – Отнеситесь к ответу ребят. – Итак: (чертит на доске две шкалы), я поняла, что вы знакомы с понятием «числовой луч» и умеете его строить.	– у числового луча есть начало, но нет конца, он бесконечен – у числового луча есть стрелка для указания направления – у числового луча начало обозначено нулем – у числового луча на одинаковом расстоянии отмечены точки,  которым соответствуют натуральные числа, идущие по порядку, увеличиваясь на один – умеем строить числовой луч – строят  в тетрадях числовые лучи – чертят лучи (3 ученика) на доске …. мнения
2. Проблематизация	– Молодцы! Вы хорошо объяснили и показали, как строить числовой луч. – У меня появился  вопрос: «А можно ли на числовом луче найти единичный отрезок?» (Прикрепляется карточка «Единичный отрезок») …………………. (Просит 3-х уч-ся найти единичный отрезок на числовых лучах) – Отнеситесь к тому, что сказали ребята. ………..	……мнения – Предлагают свои варианты
-Что происходит? Каких знаний не хватает? Фиксирует на доске проблему детей ( единичный отрезок -?)	– Не знаем, что такое единичный отрезок Фиксируют проблему в тетради
3. Целеполагание	-Так какая задача перед нами стоит? Записывает тему урока ( Что такое единичный отрезок?)	– Узнать, что такое единичный отрезок и как его найти на числовом луче. Записывают тему урока.
III. Решение учебной задачи. 1. Открытие знаний	– Вопрос есть. Что будете делать? ………….. – Сколько времени вам нужно для этой работы?	….. мнения Предложения детей.
(Раздать листы А 4) – Время. Покажите готовность групп.	Индивидуально-групповая работа.
– Что смогли найти? Расскажите.	Предъявляют результаты работы
2. Первичное закрепление	– Кто помнит, какой вопрос я задавала? – А теперь можете показать на числовом луче единичный отрезок? – Ребята, давайте обобщим. Продолжите мою фразу: «Единичный отрезок-это ……» – Выделите ключевые слова в этой формулировке.	Подходят к доске, показывают. – Мерка, которую выбирают для построения числового луча. -Мерка, построение.
3. Применение полученных знаний	Потренируемся в построении числового луча с заданным единичным отрезком. Раздает карточки с дифференцированным заданием. Задания. 1.     Постройте числовой луч с единичным отрезком 5 мм. Отметьте на числовом луче точку, соответствующую числу 6.  2.     Отметьте на числовом луче точку, соответствующую числу 7.    0	Работают в парах.
– Покажите готовность. –  Кто выполнял первое задание? – Кто выполнял второе задание?	Пара предъявляет результаты работы.
IV. Итоговая рефлексия	– Итак, какое открытие мы сделали? – Кого бы вы хотели похвалить? – Кто хотел бы похвалить себя?	– Узнали, что такое единичный отрезок

1. Главная
2. Справочники
3. Справочник по математике для начальной школы
4. Виды линий
5. Отрезок. Луч
6. Числовой отрезок

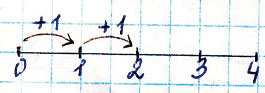
Советуем посмотреть:

Точка. Кривая. Прямая линия

Отрезок. Луч

Ломаная линия

Длиннее. Короче. Уже. Шире. Одинаковые по длине и ширине

Виды линий

Правило встречается в следующих упражнениях:

1 класс

Страница 59. Урок 36,
Петерсон, Учебник, часть 1

Страница 2. Урок 2,
Петерсон, Учебник, часть 2

Страница 5. Урок 3,
Петерсон, Учебник, часть 2

Страница 11. Урок 6,
Петерсон, Учебник, часть 2

Страница 39. Урок 20,
Петерсон, Учебник, часть 3

Страница 61. Урок 31,
Петерсон, Учебник, часть 3

2 класс

Страница 13. Урок 4,
Петерсон, Учебник, часть 2

Страница 22. Урок 7,
Петерсон, Учебник, часть 2

---

Буравова Елена Юрьевна

учитель начальных классов

ГБОУ гимназия №1 г. Новокуйбышевск

Класс 3. Программа «Школа России»

Тема: Числовой  луч

Задачи  урока:

предметные

• дать понятие о  единичном отрезке и его величине на  числовом луче;
• развивать умение решать задачи без соотнесения  с ранее знакомыми;
• развивать геометрические представления при решении задач на нахождение расстояния;
• развивать творческое математическое мышление посредством введения эвристических вопросов;
• рассмотреть  несколько  вариантов решения задачи;
• расширить знания   по окружающему миру и стимулировать  к поиску новых знаний.

метапредметные:

формировать УУД:

• интерес к новому учебному материалу,
• основы гражданской идентичности личности в форме осознания «Я» как гражданин России,
• воспитание интереса к предмету через познание родного края,
• воспитание интереса к путешествию по родному краю,
• умение учитывать выделенные учителем ориентиры действия в новом учебном материале,
• умение ориентироваться в разнообразии способов решения задачи,
• умение формулировать собственное мнение, контролировать действия партнёра,
• развитие мышления через умение сравнивать, анализировать и обобщать полученные результаты.

Слайд № 3  Создание учебной мотивации.

Учитель:

– Здравствуйте, тихо сели! Урок математики! А пройдёт он у нас сегодня необычно.

Вначале мне хотелось бы узнать, а кто из вас любит путешествия?  (Конечно, все!)        Слайд

Учитель

– И сегодня мы отправимся в путешествие по необъятным просторам нашей великой страны, которая называется ….. РОССИЯ.              Слайд

На каком виде транспорта мы сможем побывать в разных уголках России?             Слайд

– Ребята, а чтобы быть обычным или успешным  путешественником, мы должны к нему хорошо подготовиться. В этом нам помогут многие уроки математики, в том числе и этот урок.

– Открываем тетрадь – это на сегодня маршрутный лист нашего путешествия. Записываем число, классная работа. Итак, мы отправляемся в путь 2 февраля.

Запись числа классной работы.

Слайд № 4

Учитель:

– Внимание на экран. Перед вами 3 последовательности чисел.

 1. Повторение знаний об отрезке и натуральном ряде чисел  

• 0   1   2   3   4   5   6 …
• 1  2  3  4  5   6  7  ….
• 1   2  3  4  5  6  7                            Слайд

Учитель.  Запишите эти последовательности чисел

 – Что вы можете о них  сказать?

Дети. №1 – числовой ряд, потому что начинается  с 0 ,

          № 2 – натуральный ряд чисел,

          № 3 – отрезок натурального  ряда чисел

-Где мы используем числовой ряд?

          Запись № 1 используют для измерения длины, такая числовая последовательность – на линейке,  если добавить наименования                      Слайд

–Какие знаете единицы измерения длины?            Слайд

Учитель.  Внесите необходимые изменения в 1 ряд чисел.

(Дети самостоятельно работают в тетради). 

Последующая проверка.

Слайд № 5

На слайде  представлены все  варианты выполнения  задания

Учитель.   Как можно назвать эти записи?                  Слайд

Дети. Единицы измерения длины. Линейные единицы измерений.

Учитель.  Подумайте, какие задания будут на уроке?

Дети.  

• Выполнять действия с этими величинами, 

• переводить одни измерения в другие.
• Решать задачи с такими величинами.
• Находить города и дороги на карте.

Учитель. (Сообщение для учащихся  темы и целей урока).

• Мы будем строить числовой луч и на нем будем обозначать величины;
• решать задачи  с помощью числового луча простые и более сложные.
• вернемся к решению задачи на нахождение расстояния между  деревнями и решим её другим способом.
• И, конечно, будем знакомиться с новыми знаниями об окружающем мире, как  настоящие путешественники.

Слайд № 6.

Повторение материала прошлого урока  и введения нового понятия (на материале № 293  учебника)

Учитель.

– Внимание на экран. Рассмотрите  рисунок.  Что вы можете сказать?

Дети.    

• Это луч, и на нем точки на одинаковом расстоянии друг от друга.
• Лягушка прыгает одинаковыми прыжками.

Учитель 

– Кто видел, как прыгает лягушка?  Мы вместе  сможем это увидеть  в электронном пособии «Коллекция фото и видеоизображений. Биология»

           Что показывают числа 1  2  3?

Дети. Количество прыжков лягушки.

Учитель   Какое число надо поставить у начала луча?                 Слайд

Дети. .0, потому что  это начало первого прыжка

Учитель Рассмотрите  следующий  рисунок.  Что вы можете сказать?              Слайд

Дети

• Это луч, и на нем точки на одинаковом расстоянии друг от друга.
• Кузнечик  прыгает одинаковыми прыжками.
• Каждый прыжок больше прыжка лягушки
• -Что должно стоять в начале луча?
• В начале луча должен стоять 0    

Учитель Что вы можете сказать о третьем рисунке?            Слайд

• Это тоже  луч, и на нем точки тоже на одинаковом расстоянии друг от друга,
• Заяц  прыгает одинаковыми прыжками, большими, чем у лягушки, но меньшими, чем у  кузнечика.

Учитель  Что напоминают эти лучи?

Дети     Линейки с разными мерками.

Учитель

– Больше об этих животных мы узнаем на уроке окружающего мира, а  поможет нам  в этом электронная  энциклопедия Кирилл и Мефодий.

– Все ли животные сделали одинаковое кол-во прыжков? Если нет, то почему?

Дети Нет, разная длина прыжка

Учитель – А знаете ли вы длину прыжка  каждого животного?

– Выберите из предложенных мерок  мерку для каждого животного

(На доске 100см, 50 см; 180 см)

Учитель. Мерка, которая выбрана  вами для каждого животного, называется единичным отрезком. (Появление на слайде этого построения)

Слайд № 7.   Устный счет

Учитель. Рассмотрите эти математические ситуации и предложите одноклассникам свои вопросы.  

Дети. Найдите расстояние, которое пропрыгала  лягушка?

50х5=250(см)  (250 см=25дм)

Учитель. Как узнали? Запишите в тетради  полученную величину и переведите ее в более крупные единицы измерения.

Дети      Какова длина всех прыжков кузнечика?   180х2=360 (см) (360см)

Учитель Как узнали? Выполните в тетради операцию перевода  в более крупные единицы    

Дети       Какое расстояние пробежал заяц? 100х3=300(см) (300 см)

Учитель  Как узнали?  Переведите эту величину в дм

Дети     .На ск. меньше прыжок лягушки, чем прыжок  кузнечика? 180-50=130 (см) На 130 см

Дети     Во ск. раз больше прыжок зайца, чем лягушки?  100:50=2 (раза) (В 2 раза)

Итог 1 этапа.

Учитель  Кратко расскажите, что мы сейчас делали, что нового узнали?

Дети    

• Строили числовые лучи и  узнали про  единичный отрезок.
• Решали  задачи, находили расстояние нескольких прыжков и  разницу величины прыжков.

Слайд № 8.

ФИЗМИНУТКА

Учитель проговаривает команды для движений, которые должны показать дети, а сам может выполнять другие движения. Команды: воздух (руки вверху), вода (руки впереди), огонь (руки крутим перед собой), земля (руки вниз).

Слайд № 9.

Учитель: Переходим к решению задач.

Задача № 294 (текст из  учебника)

Деревни Ивановка, Марьино  и Аксинино расположены на одной дороге. От Ивановки до Марьино 7 км, а от Марьино  до  Аксинино в 3 раза дальше. Сколько км от Ивановки до Аксинино?

Учитель Как вы поняли  условие задачи, что деревни  находятся на одной дороге?  

                Переведите текстовую информацию в графическую.

                Как геометрически представили эту дорогу на чертеже?

Дети  (пошаговое восстановление предыдущей работы). Задача  решена на  предыдущем уроке.

• Построили  числовой луч.

• Обозначили буквами  И – Ивановку,  затем М – Марьино,  А – Аксинино по порядку –слева-направо.
• Написали  данные; 7 км, «в 3 раза дальше»
• Объединили скобкой расстояние от Ивановки до Аксинино, которое надо найти.

Учитель Что вы можете сказать о  единичном отрезке?

Дети  Единичный отрезок – 7 км. Потом он повторяется 3 раза

Учитель  Расскажите план решения по  буквенным выражениям

Дети  Надо найти расстояние ИА   которое состоит из ИМ и МА. Это сумма расстояний. Нам известно, что  ИМ – 7 км.  МА можно найти, т.к. это расстояние  в 3 раза дальше, чем ИМ, значит, ИМх3.

 (Проверка оформления решения по щелчку мыши).

Слайд № 10. « В зоне ближайшего развития» . Повышенный уровень трудности.  Это решение спланировано. Такой способ решения в учебниках появится гораздо позже. Но эта пропедевтическая работа поможет решать задачи из следующей темы «Дробные числа».

Учитель  А теперь попробуем решить эту задачу другим способом.

                 Выполните построение числового луча, как мы с вами только что повторили (алгоритм на листе) – комментирование????

                 Назовите искомое расстояние

Дети  От Ивановки до Аксинино  (ИА)      Слайд

 Учитель Рассмотрим составляющие это расстояние отрезки.

Дети  Единичный отрезок и еще 3 таких же отрезка от  Марьино до Аксинино

Учитель  Вспомните начало урока, как мы решали задачи про прыжки животных.

                 Как можно представить это  расстояние? 

Дети  Как 4 прыжка

           Как 4 отрезка

            1+3 = 4

Учитель  Найдите искомое расстояние, используйте знакомый уже способ нахождения расстояния прыжков животных.

Выполните запись решения самостоятельно. Индивидуальная помощь

(Проверка с появлением слайдов по щелчку мыши)

Слайд № 11. (по пункту № 3 этой задачи) Возникновение противоречия

Учитель Внимание на экран. При решении этой задачи Костя получил ответ 28 км, а Вася – 14 км. Что вы скажете об ответах мальчиков?

Дети  Ответ Кости – 28 км  как у нас, а ответ Васи,  наверное, неправильный.

Учитель   Кто  считает, что ответ Васи неверный?

Учитель Давайте исследуем эту ситуацию и разрешим проблему. Сравните эти расстояния.

Слайд № 12.

 Второе решение задачи, связанное с неполным условием о расположении объектов

Дети  14 км  в 2 раза меньше, чем 28 км

Учитель  Как так может быть? Посмотрите на наш чертеж, может быть можно его изменить?

Дети  Надо поставить Ивановку в середину

          Поставить Ивановку на расстоянии  2 отрезков от Аксинино

(по щелчку мыши выполняется это действие).

Учитель  Назовите искомое расстояние

Дети  От  Ивановки до Аксинино (ИА).

Учитель  Назовите данные

Дети   Расстояние от Марьино до Ивановки 7 км

            Это единичный отрезок

           Расстояние от Марьино до  Аксинино – в 3 раза дальше (МИ  взять 3 раза)

Учитель Как найти искомое расстояние (ИА)

Дети  Надо из всего расстояния вычесть МИ (от Марьино до Аксинино)

Выполнение решения  (Появление решения на слайде. «Сильные» учащиеся решали самостоятельно)

Слайд № 13. Самостоятельная работа.  

Оказание индивидуальной помощи 5 учащимся.         Чертеж для решения показать.

Действие по щелчку мыши для проверки решения

Слайд № 14. (работа в парах)

Учитель Можно ли  решить эту задачу, представив расстояние в частях, как мы решили предыдущую вторым способом?

Можно советоваться, решать в парах, обернуться к следующей паре, но помни правила дружной работы:

• Внимательно слушай товарища.
• Говори вполголоса.
• Исправляй товарища так, чтобы его не обидеть.
• Береги каждую минуту.

(проверка решения по щелчку мыши на слайде)

Учитель Все ли убедились в том, что так же верен ответ 14 км?

Дети  (Да – ответ жестом согласия – рука).

1. Д.М. Контроль и самоконтроль

Работа с тестами.

– Ну а теперь пришло время проверить, как вы усвоили тему предыдущих уроков. Перед вами лежат листочки, в которых выполнено внетабличное умножение и деление. Ваша задача, проверить правильность выполненных действий. Если задание выполнено верно, то рядом, в пустой клеточке, вы ставите “+”, а если неверно, то ставите знак “–”.

14х2=28		60:2=30
48х2=80		120:3=4
32х3=96		800:4=200
19х4=72		900:3=30
30х3=900		90:3=30

– Вижу, что вы справились с заданием. А сейчас поменяйтесь листочками друг с другом для взаимопроверки. У меня на доске даны ответы. Сверьте их с теми, которые получились у вас и оцените своего товарища.

Подведение итогов:

Итак, урок подошёл к концу.

Слайд № 15 .Применение знаний  в окружающем мире

Учитель  Где нам пригодятся знания о расположении населенных пунктов, о нахождении расстояния?             Слайд

Дети  Когда едем на машине, надо знать, сколько километров между городами

            Надо знать расстояние, чтобы хватило бензина до  заправки.

            Какая дорога короче, какая длиннее.

           Нужно уметь находить расстояния по карте.

Слайд № 16. Домашнее задание

1. Построй числовой луч. (Помощь в  № 293-6).

• Подбери  персонаж, который будет двигаться по лучу.
• Выбери  мерку – единичный отрезок.    
• Обозначь его величину.

2. Задача № 294  Выбери вариант выполнения:

А) составь и реши подобную задачу;

Б) составь обратную задачу

В) Какое уточнение нужно внести в  задачу, чтобы у неё было только одно решение (№ 294, пункт5)

Учитель:  

– Мне сегодня было очень комфортно с вами на уроке. Спасибо вам.

Продолжи фразу:

Я узнал (а) …
Я повторил (а) …
Я научился (лась) …

Рефлексия.

– Ну, а теперь мне хотелось бы узнать, как вы сами оцениваете свою работу на уроке. У каждого из вас, на парте, лежит пассажир, ожидающий поезд. Но это необычный поезд. У него разные вагоны: веселые-красные и грустные-синие. Вы должны посадить своего пассажира в тот вагон, который соответствует вашему настроению от сегодняшнего урока.

5.1. Координатный луч. Единичный отрезок

Натуральные числа можно изображать на луче. Построим луч с началом в точке О, направив его слева – направо, направление отметим стрелкой.

Началу луча (точке О) поставим в соответствие число 0 (ноль). Отложим от точки О отрезок ОА произвольной длины. Точке А поставим в соответствие число 1 (один). Длину отрезка ОА будем считать равной 1 (единице). Отрезок АВ = 1 называется единичным отрезком. Отложим от точки А в направлении луча отрезок АВ = ОА. Поставим точке В в соответствие число 2. Заметим, что точка В находится от точки О на расстоянии  в два раза большем, чем точка А. Значит, длина отрезка ОВ равна 2 (двум единицам). Продолжая откладывать в направлении луча отрезки, равные единичному, будем получать точки, которым соответствуют числа 3, 4, 5, и т.д. Данные точки удалены от точки О соответственно на 3, 4, 5, и т.д. единиц.

Луч, построенный таким способом, называется координатным или числовым. Начало числового луча, точка О, называется точкой отсчета. Числа, поставленные в соответствие точкам на этом луче, называются координатами этих точек (отсюда: координатный луч). Пишут: О(0), А(1), В(2), читают: «точка О с координатой 0 (ноль), точка А с координатой 1 (один), точка В с координатой 2 (два)» и т.д.

Любое натуральное число n можно изобразить на координатном луче, при этом соответствующая ему точка P будет удалена от точки О на n единиц. Пишут: ОP = n и P(n) – точка P (читают: “пэ”) с координатой n (читают: “эн”). Например, чтобы отметить на числовом луче точку К(107), необходимо от точки О отложить 107 отрезков, равных единичному. В качестве единичного можно выбрать отрезок любой длины. Часто длину единичного отрезка выбирают такой, чтобы было возможно в пределах рисунка изобразить на числовом луче необходимые натуральные числа. Рассмотрите пример

5.2. Шкала

Важным применением числового луча являются шкалы и диаграммы. Они используются в измерительных приборах и устройствах, при помощи которых измеряют различные величины. Одним из основных элементов измерительных приборов является шкала. Она представляет собой числовой луч, нанесенный на металлическое, деревянное, пластиковое, стеклянное или другое основание. Часто шкала выполнена в виде окружности или части окружности, которые разделены штрихами на равные части (деления-дуги) подобно числовому лучу. Каждому штриху на прямой или круговой шкале поставлено в соответствие определенное число. Это значение измеряемой величины. Например, числу 0 на шкале термометра соответствует температура 0⁰С, читают: «ноль градусов Цельсия». Это температура, при которой начинает таять лед (или начинает замерзать вода).

Используя измерительные приборы и инструменты со шкалами, определяют значение измеряемой величины по положению указателя на шкале. Чаще всего указателем служат стрелки. Они могут перемещаться вдоль шкалы, отмечая значение измеряемой величины (например, стрелка часов, стрелка весов, стрелка спидометра – прибора для измерения скорости, рисунок 3.1.). Подобна смещающейся стрелке граница столбика ртути или подкрашенного спирта в термометре (рисунок 3.1). В некоторых приборах движется не стрелка вдоль шкалы, а шкала перемещается относительно неподвижной стрелки (метки, штриха), например, в напольных весах. В некоторых инструментах (линейка, рулетка) указателем служат границы самого измеряемого предмета.

Промежутки (части шкалы) между соседними штрихами шкалы называются деления. Расстояние между соседними штрихами, выраженное в единицах измеряемой величины, называется ценой деления (разность чисел, которым соответствуют соседние штрихи шкалы.) Например, цена деления спидометра на рисунке 3.1. равна 20 км/ч (двадцать километров в час), а цена деления комнатного термометра на рисунке 3.1. равна 1⁰С (один градус Цельсия).

      Диаграмма

Для видимого изображения величин используют линейные, столбчатые или круговые диаграммы. Диаграмма состоит из числового луча-шкалы, направленного слева – направо или снизу – вверх. Кроме того на диаграмме помещены отрезки или прямоугольники (столбцы), изображающие сравниваемые величины. При этом длина отрезков или столбцов в единицах шкалы равна соответствующим величинам. На диаграмме возле числового луча-шкалы подписывают название единиц измерения, в которых отложены величины. На рисунке 3.2. изображена столбчатая диаграмма, а на рисунке 3.3 линейная.

3.2.1. Величины и приборы для их измерения

В таблице приведены названия некоторых величин, а также  приборов и инструментов, предназначенных для их измерения. (Жирным шрифтом выделены основные единицы Международной системы единиц).

5.2.2. Термометры. Измерение температуры

На рисунке 3.4 приведены термометры, в которых использованы разные температурные шкалы: Реомюра (°R), Цельсия (°С) и Фаренгейта (°F).В них использован один и тот же температурный интервал – разность температур кипения воды и плавления льда. Этот интервал разделён на различное число частей: в шкале Реомюра – на 80 частей, шкале Цельсия – на 100 частей, в шкале Фаренгейта – на 180 частей. При этом в шкалах Реомюра и Цельсия температуре таяния льда соответствует число 0 (ноль), а в шкале Фаренгейта –          число 32. Единицы температуры в этих термометрах: градус по Реомюру, градус по Цельсию, градус по Фаренгейту. В устройстве термометров используется свойство жидкостей (спирта, ртути) расширяться при нагревании. При этом различные жидкости по-разному расширяются при нагревании, что видно на рисунке 3.5, где штрихи для столбика спирта и ртути не совпадают при одинаковой температуре.

5.2.3. Измерение влажности воздуха

Влажность воздуха зависит от количества в нём водяных паров. Например, летом в пустыне воздух сухой, влажность его низкая, так как в нём содержится мало паров воды. В субтропиках, например, в Сочи влажность высокая, в воздухе много водяных паров. Измерить влажность можно с помощью двух термометров. Один из них обычный (сухой термометр). У второго шарик обёрнут влажной тканью (влажный термометр). Известно, что при испарении воды температура тела понижается. (Вспомните озноб при выходе из моря после купания). Поэтому влажный термометр показывает более низкую температуру. Чем суше воздух, тем больше разность показаний двух термометров. Если показания термометров одинаковы (разность равна нулю), то влажность воздуха равна 100 %. В этом случае выпадает роса. Прибор, измеряющий влажность воздуха, называется психрометром (рисунок 3.6). Он снабжён таблицей, в которой приведены: показания сухого термометра, разность показаний двух термометров, влажность воздуха в процентах. Чем ближе влажность к 100%, тем более влажный воздух. Нормальная влажность в помещениях должна быть равна около 60%.

               

Блок 3.3. Самоподготовка

5.3.1. Заполните таблицу

Отвечая на вопросы таблицы, заполняйте свободную колонку («Ответ»). При этом используйте рисунки приборов в блоке «Дополнительный».

 

760 мм. рт. ст. считается нормальным. На рисунке 3.11 показано изменение атмосферного давления при подъёме на самую высокую гору Эверест.

Постройте линейную диаграмму изменения давления, отложив на вертикальном луче высоту над уровнем моря, а по горизонтали давление.

Блок 5.4. Проблемный

Построение числового луча с единичным отрезком заданной длины

Для решения этой учебной проблемы работайте по плану, приведенному в левой колонке таблицы, при этом правую колонку рекомендуется закрыть листом бумаги. Ответив на все вопросы, сопоставьте свои выводы с приведёнными решениями.

Блок 5.5. Фасетный тест

Числовой луч, шкала, диаграмма

В задачах фасетного теста использованы рисунки из таблицы. Все задачи начинаются так: «ЕСЛИ числовой луч представлен на рисунке …., то…»   

ЕСЛИ: числовой луч представлен на рисунке…                               Таблица

ТО:

1. Количество единиц между соседними штрихами числового луча.
2. Координаты точек А, В, С, D.
3. Длина (в сантиметрах) отрезков АВ, ВС, АD, ВD соответственно.
4. Длина (в метрах) отрезков АВ, ВС, АD, ВD соответственно.
5. Натуральные числа, расположенные на числовом луче левее точки D.
6. Натуральные числа, расположенные на числовом луче между точками А и С.
7. Количество натуральных чисел, лежащих на числовом луче между точками А и D.
8. Количество натуральных чисел, лежащих на числовом луче между точками В и С.
9. Цена деления шкалы прибора.
10. Скорость автомобиля в км/ч, если стрелка спидометра указывает на точки А, В, С, D соответственно.
11. Величина (в км/ч), на которую увеличилась скорость автомобиля, если стрелка спидометра переместилась из точки В в точку С.
12. Величина скорости автомобиля после того, как водитель уменьшил скорость на        84 км/ч (перед уменьшением скорости стрелка спидометра указывала на точку D).
13. Масса груза на весах в центнерах, если стрелка – указатель весов – расположена напротив  точек А, В, С соответственно.
14. Масса груза на весах в килограммах, если стрелка – указатель весов – расположена напротив точек А, В, С соответственно.
15. Масса груза на весах в граммах, если стрелка – указатель весов – расположена напротив  точек А, В, С соответственно.
16. Количество учеников в 5 классе.
17. Разность между количеством учеников, успевающих на «4», и количеством учеников, успевающих на «3».
18. Отношение количества учеников, успевающих на «4» и «5», к количеству учеников, успевающих на «3».

РАВНО (равна, равны, это):

 а) 10   б) 6,12,3,3     в) 1   г) 99,102,106,104   д) 2   е) 201,202    ж) 49   з) 3500,3000,8000,4500

 и) 5,2,1,4   к) 599   л) 6,3,3,9   м) 10,4,16,7   н) 100   о) 4 км/ч   п) 65,85,105,115   р) 7,2,4,6      с) 20,20,50,30   т) 0   у) 700,600,1600,900   ф) 1,2,3,4,5,6   х) 25,10,5,20   ц) 3,4,5,2   ч) 203,197,200,206   ш) 15,20,25,10   щ) 1599   ы) 11,12,13,14,15   э) 30,60,15,15  ю) 0,700,1300,1600   я) 100,100,250,150   аа) 30,15,15,45  бб) 4   вв) 1,2,3,4,5   гг) 17  дд) 500 кг   ее) 19    жж) 80   зз) 100,101,102,103,104,105   ии)5,6   кк) 28,64,100,164   лл) 1500000,3000000,4500000   мм) 11   нн) 36   оо) 1500,3000,4500   пп) 7   рр) 24  сс) 15,30,45

Блок 5.6. Учебная мозаика

В заданиях мозаики использованы приборы из блока «Дополнительный». Ниже приведено поле мозаики. На нём указаны названия приборов. Кроме того для каждого прибора обозначены: измеряемая величина (В), единица измерения величины (Е), показание прибора (П), цена деления шкалы (Ц). Далее помещены ячейки мозаики. Прочитав ячейку, вы должны сначала определить прибор, к которому она относится, и поставить в окружность ячейки номер прибора. Затем надо догадаться, о чём эта ячейка. Если речь идёт об измеряемой величине, надо к номеру приписать букву В. Если это единица измерения – поставить букву Е, если показание прибора – букву П, если цена деления – букву Ц. Таким образом надо обозначить все ячейки мозаики. Если ячейки вырезать и расположить так, как на поле, то можно систематизировать сведения о приборе. В компьютерном варианте мозаики при правильном расположении ячеек создаётся рисунок.