Единица
совокупности – первичный элемент
статистической совокупности (одна
фирма, семья).
Вариация
признака – различие индивидуальных
значений признака внутри изучаемой
совокупности.
–
атрибутивные
– выраж-ся смысловым понятием (пол
человека, цвет волос);
–
альтернативные
– если атрибут-ые пр-ки применяют только
одно из 2-х противоположных знач-ий;
–
колич-ые
– выраж-ся числовым значением (возраст,
рост, з/п);
–
варьирующие
– приз-ки, применяющие различ. знач-ия
у отдельных ед-ц изуч-го явл-ия (объем
товарооборота у различ-ых магазинов).
Также
различают:
–
основные
– опред-ют главное содер-ие изуч-го
явл-ия;
–
второстепенные
– не связаны непосредственно с основным
их содерж-ем.
Признак
– качественная особенность в ед.
совокуп-ти.
Вариация
– измен-ие цифровых значений признака.
Статистический
показатель – отображает количественные
характеристики, соотношение признаков
общественных явлений.
–
учетно-оценочные
– хар-ют размеры колич-но определенных
соц.-эк. явл. В конкретных усл-ях места
и вр. Могут отображ-ть объемы распростр-ия
показателей в пространстве или достигнутые
на опред-ые моменты (даты) ур-ни развития.
–
аналитические
– применяются для анализа стат. инф-ии
и характер-ют особенности развития
изуч-го явл-ия. В их кач-ве примен-ся
относит-ый и ср. величины, показатели
вариации и динамики, тесноты связи и
пр.
4. Система государственной статистики в рф.
Главным
статистическим органом является
федеральная служба гос. Статистики РФ
(Росстат).Система органов государственной
статистики образована в соответствии
с государственным устройством и
административно-территориальным
делением страны.
Росстат
→ Республиканские комитеты по статистике
→ Комитеты государственной статистики
автономных областей, округов, краев,
областей, городов Москва и С.-Петербург
→ Управления (отделы) гос.статистики
районов (городов).
Во
главе Федеральной службы стоит
Председатель, который несет персональную
ответственность за ее работу.
В
соответствии с Конституцией РФ руководство
статистикой осуществляет Росстат как
федеральный орган исполнительной
власти.
Формы
и методы сбора и обработки статистических
данных, установленные Росстатом являются
статистическими стандартами РФ. В основе
деятельности Росстата лежат федеральные
статистические программы, которые
финансируются из гос.бюджета.
5. Задачи и пр-пы орг-ии гос.Учета. Стат.Станд-ты рф.
Задачи:
–
всестороннее иссл-ие происходящих в
стране глубоких преобраз-ий эк. и соц.
процессов;
–
обобщение и прогноз-ие тенденций развития
различ. отраслей и эк. РФ в целом;
–
выявление имеющихся резервов развития
эк.;
–
своевременное обеспеч-ие надежной
информацией гос-ых, хоз-ых и эк-их органов.
Система
органов
стат. образована в соот-ии с гос.
устройством и админ.-терр. делением
страны.
Формы
и методы сбора и обработки стат. данных
устан-ся Росстатом и явл-ся стат-ми
стандартами.
6. Функции органов гос.Статистики. Современные технологии организации статистического учета.
Основные
функции Федеральной службы:
1)
организует проведение гос.статистических
наблюдений;
2) обеспечивает
функционирование ЕГРПО (единого
гос.регистра предприятий и организаций);
3)
обеспечивает сбор, обработку, хранение,
защиту статистической информации;
соблюдение государственной и коммерческой
тайны;
4) сопоставляет основные
социально-экономические показатели
России с аналогичными показателями
других стран.
Для
вычислительных систем, работающих на
промышленном производстве, таких,
например, как большие корпоративные
компьютерные системы, разрабатывается
специальное программное обеспечение.
Эти приложения, как правило, поддерживают
возможности группового доступа к
системе, а также совместимы с корпоративными
хранилищами данных.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Понятие статистики мы уже рассмотрели в прошлом уроке, и поняли, что она знает многое, кто не понял, забыл или прошел мимо, может перейти по ссылке и освежить свои знания)). Но в теории статистики есть еще одно очень интересное изречение. В мире есть три вида лжи – ложь, наглая ложь и… СТАТИСТИКА!!!
Совершенно противоречивое утверждение другое – статистика знает все. Но отчасти в нем есть доля правды. Все дело в данных, которые были собраны для обработки.
Но об этом поговорим позже…

Однако вернемся к статистическим категориям. Категории или основные статистические термины важная часть науки. И дело здесь в том, что эти термины регулярно употребляются в процессе обработки и анализа данных. Именно в этом кроется их такая важность для статистической науки.
Статистическая совокупность – это группа социально-экономических объектов или явлений общественной жизни объединенных общей связью, но отличающихся друг от друга отдельными признаками. Это наиболее часто встречающее определение совокупности. Включает в себя ее особенности, и что очень важно и другие статистические категории. Попытаемся упростить или понять, что же такое совокупность на примере.
Совокупность это некоторое объединение элементов или явлений или людей и т.п. Мало того что в совокупности как правило много частей или элементом (всегда больше одного), так еще все они в чем-то похожи. Так вот эта похожесть и есть признак, по которому объединили эти элементы. Общее у элементов одно, и масса других характеристик отличающихся.

Вот небольшой такой пример. На картинке у нас изображены условно люди. Это совокупность людей – по этому признаку их и объединили в совокупность. Однако все мы разные и у нас масса признаков, которые отличают нас друг от друга – пол, возраст, образование, семейное положение, уровень доходов, место жительства и так далее.
Вообще в совокупность можно объединить разные элементы, лишь бы было что изучать:
— совокупность школьников – общее учатся в школе, а различия пол, возраст, класс, место учебы и многое другое;
— совокупность деревьев в лесу – общее это деревья, различия возраст, разновидность дерева, высота и т.п.;
— совокупность предприятий – общее предприятия, различия, отрасль, число работников, объем выпуска, объем прибыли и др.
И таких примеров можно привести огромное количество.
Задание. Предположим на картинке представлена совокупность студентов. Опишите ее, почему она является совокупностью, какие есть признаки у студентов. Нет ли на картинке лишних элементов, не относящихся к данной совокупности?

 Единица статистической совокупности – это первичный элемент статистической совокупности, являющийся носителем признаков подлежащих регистрации.
Единица статистической совокупности – это первичный элемент статистической совокупности, являющийся носителем признаков подлежащих регистрации.
И снова упростим это определение. Единица совокупности это то, из чего состоит наша совокупность, но в единственном числе, то на что она делится. Значит единица это один единственный элемент совокупности. Если вернуться к нашей совокупности людей, единице совокупности будет один человек, допустим, что это красный человечек!
В других наших примерах единицей совокупности будет:
— совокупность школьников – один школьник;
— совокупность деревьев в лесу – одно дерево;
— совокупность предприятий – одно предприятие.
Признак единицы статистической совокупности – это качественная или количественная особенность, которая может быть изучена. О признаках упоминалась в двух предыдущих определениях и примеры мы уже привели. Однако действительно признак это то, что мы изучаем у каждой единицы совокупности.
Задание. Приведите примеры признаков, которые могут быть интересны для статистического изучения для следующих единиц совокупности – ребенок, собака, дом, машина, яблоко.
Статистический показатель – это количественная (чаще) или качественная (реже) характеристика признака статистической совокупности.
По сути, статистические показатели это те данные, которые мы собираем или то результаты исследования, которые мы получаем. И недаром он имеет название ПОКАЗАТЕЛЬ – показывает он нам что-то.
Можно говорить, что показатель бывает индивидуальным, это когда мы собрали данные по одной единице совокупности, или расчетным (что вернее) он получается после обработки данных (суммирование, усреднение и т.п.)
Качественная сторона статистического показателя определяется признаком, который подлежит изучению и отражается в названии показателя, количественная сторона — в численном значении показателя.
Еще одной особенностью статистических показателей является то, что они всегда привязаны к конкретным обстоятельствам места и времени.
Например, мы узнали возраст 4 человек – 24, 38, 28, 19. Можно сказать, что для каждого человека из обследованных это будет индивидуальный показатель возраста. Из этих данных мы можем получить и расчетный показатель среднего возраста – 27 лет. Вот 27 нам показывает, что средний возраст обследованной группы людей 27 лет.

И последний очень важный термин вариация!
Вариация – это колебания признака статистической совокупности. В статистике говорят – признак колеблется или ВАРЬИРУЕТСЯ.
Вариация признака это основа статистической науке. Не было бы вариации, не было бы статистики. Именно потому что признаки изменяются и происходит их изучении. Если не было бы изменений и отличий и все было одинаковым, то изучать было бы нечего и статистики не было.
 А дальше мы перейдем к статистическому наблюдению. Но прежде домашние задания.
А дальше мы перейдем к статистическому наблюдению. Но прежде домашние задания.
Контрольное задание. Приведите примеры двух трех совокупностей, выделите в них единицы совокупности и охарактеризуйте их признаками. Приведите пример статистических показателей и вариации признака.
Доклад – Органы государственной статистики в РФ – функции, задачи, структура. – Федеральная служба государственной статистики — http://ya-prepod.ru/www.gks.ru/
Может еще поучимся? Загляни сюда!

Методы прикладной математической статистики активно применяются в технических исследованиях, экономике, теории и практике управления (менеджмента), социологии, медицине, геологии, истории и т. д. С результатами наблюдений, измерений, испытаний, опытов, с их анализом имеют дело специалисты во всех отраслях практической деятельности, почти во всех областях теоретических исследований.
Прикладная математическая статистика нацелена на решение реальных задач. Поэтому в ней возникают новые постановки математических задач анализа статистических данных, развиваются и обосновываются новые методы. Обоснование часто проводится математическими методами, то есть путем доказательства теорем. Большую роль играет методологическая составляющая — как именно ставить задачи, какие предположения принять с целью дальнейшего математического изучения. Велика роль современных информационных технологий, в частности, компьютерного эксперимента.
Здравствуйте на этой странице я собрала примеры решения задач по предмету статистика с решением по каждой теме, чтобы вы смогли освежить знания!
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Статистика
Статистика изучает массовые общественно-экономические явления в конкретных обстоятельствах места и времени.
Предметом статистики выступают размеры и количественные соотношения массовых общественных явлений в неразрывной связи с их качественной стороной с целью выявления закономерностей их развития.
Статистика является важным элементом плана подготовки специалистов высшей экономической квалификации. Знание статистики необходимо современному специалисту для принятия решений в условиях, когда анализируемые явления подвержены влиянию случайностей, для анализа элементов рыночной экономики, прогнозирования и разработки сценариев поведения экономических систем при изменении условий их функционирования
Основные понятия и формы статистического наблюдения
Всякое статистическое исследование делится на три последовательных этапа: статистическое наблюдение, сводка и группировка материалов, полученных в результате наблюдения; вычисление обобщающих показателей, всесторонне характеризующих изучаемое явление и их анализ.
Таким образом, статистическое наблюдение (СН) является исходным этапом статистического исследования и состоит в планомерном, научно-организованном собирании массовых данных о явлениях и процессах общественной жизни. Целью СН является регистрация элементов, составляющих изучаемое массовое явление, по заранее установленным наиболее существенным признакам. Это означает, что СН должно быть организовано как планомерное, массовое и систематическое.
Планомерность статистического наблюдения заключается в том, что оно подготавливается и осуществляется по заранее подробно разработанному плану и программе, которые охватывают все вопросы методологии, организации и техники сбора информации. В программно-методологическую часть плана статистического наблюдения включаются вопросы определения цели, объекта наблюдения, единицы наблюдения и единицы совокупности.
Объектом статистического наблюдения называется совокупность единиц изучаемого явления, подлежащих статистическому изучению (совокупность предприятий, лиц, магазинов, фермерских хозяйств и др.).
Единицей наблюдения называется первичная ячейка совокупности, которая является источником информации.
Единицей совокупности называется элемент единицы наблюдения, служащий основой счета и обладающий признаками, подлежащими регистрации.
Каждая единица наблюдения и единица совокупности должны характеризоваться совокупностью признаков, которые по форме и содержанию делятся на количественные, т. е. выражающиеся числом (возраст, заработная плата и т. д.) и атрибутивные, характеризующие качественное состояние данного явления и не имеющие количественного выражения (пол, специальность, образование и пр.). В свою очередь и те и другие могут быть факторными, т. е. характеризующими условия, определяющие размер того или иного явления, и результативными, являющимися результатом действия факторных признаков (например, стаж работы факторный признак, производительность труда результативный признак).
Массовый характер статистического наблюдения означает, что оно организовано и направлено на охват возможно большего, массового числа случаев проявления данного явления или процесса
Систематичность статистического наблюдения определяется тем, что оно производится не стихийно, а регулярно или непрерывно.
Статистическое наблюдение осуществляется в двух формах: путем представления отчетности и проведения специально организованного статистического наблюдения, причем основной формой СН является представление отчетности.
Возможно эта страница вам будет полезна:
Виды и способы статистического наблюдения
Статистическое наблюдение различается по видам и способам проведения. Их можно классифицировать следующим способом:
I. По степени охвата единиц исследуемой совокупности.
По этому классификационному признаку СН подразделяется на два способа:
1. Сплошное наблюдение, т.е. когда охватываются все единицы совокупности (например, перепись населения, текущая отчетность предприятии).
2. Несплошное (частичное) наблюдение — обследованием охватывается определенная часть изучаемой совокупности. Несплошное наблюдение занимает очень важное место в статистике и подразделяется на следующие виды:
а) метод основного массива (наблюдение наиболее важных объектов) заключается в том, что обследованию подвергается та часть совокупности, у которой величина изучаемого признака является определяющей во всем объеме. Например, отслеживания объема реализации и динамики цен на колхозных рынках в России проводились в 264 крупных городах, составляющих менее 5% всех городов, но в которых проживало более 50% всего городского населения.
б) монографическое наблюдение состоит в подробном описании небольшого числа или отдельных единиц совокупности (описание работы передового или отстающего предприятия и т. д.);
в) суть анкетного вида несплошного наблюдения заключается в рассылке и сборе анкет;
г) случайный отбор определенного количества единиц из совокупности (выборочный метод).
В свою очередь он может выполняться следующими способами:
— при собственно-случайном отборе, отбор единиц для выборочной совокупности осуществляется случайным образом по жребию;
— сущность механического отбора состоит в том, что единицы изучаемой совокупности предварительно располагают в определенном порядке (например, по возрастанию или убыванию), а потом механическим путем выбирают необходимое количество единиц (например, берут каждую 4-ю, каждую 10-ю единицу и пр.);
— типологическому отбору предшествует распределение единиц изучаемой совокупности на группы по типичному признаку, затем внутри каждой группы проводится тот или иной отбор (собственно-случайный, механический или любой другой);
— серийный отбор предполагает образование выборочной совокупности не из отдельных единиц, а из целых серий, причем серии выбираются путем механического или собственно-случайного отбора, а внутри каждой серии проводится сплошное наблюдение.
Все способы случайного отбора могут выполняться по двум схемам:
— повторный отбор (схема возвращенного шара) — после выбора какой-либо единицы она вновь возвращается в исходную совокупность и может быть выбрана снова;
— бесповторный отбор (схема невозвращенного шара) — отобранная единица обратно в совокупность не возвращается и не может быть выбрана снова.
II. В зависимости от времени статистическое наблюдение может быть непрерывным (текущим), периодическим и единовременным.
1. Непрерывным или текущим наблюдением называется такое, которое проводится непрерывно, по мере возникновения явлений, например, учет выпуска продукции на предприятии;
2. Если наблюдение проводится через определенные промежутки времени, то оно называется периодическим (сессия в вузах);
3. Единовременное наблюдение проводится по мере необходимости, например, перепись населения.
Установление времени наблюдения является очень важным, и в статистике различают, объективное и субъективное время и критический момент.
Объективным временем называется время, к которому относятся данные наблюдения. Оно характеризует тот момент или период времени, по состоянию на который были собраны и зарегистрированы данные. Например, данные о выпуске продукции, размерах потребления и т.д. можно получить только за определенный период. Сведения же о численности населения, числе больничных коек и т. д. можно собрать только по состоянию на определенную дату.
Если наблюдение приурочено к определенному моменту, то этот момент называется критическим.
Субъективное время наблюдения — это время производства наблюдения, т.е. период, в течение которого проводится регистрация единиц совокупности. В целях обеспечения точности наблюдения субъективное время должно измеряться возможно более коротким периодом. Когда наблюдение основано на документальных данных, длительность субъективного времени не имеет значения.
III. В зависимости от источников собираемых данных различают:
4) Непосредственное наблюдение, т.е. наблюдение лично регистратором — снятие товарных остатков, изучение и замер норм времени и т. д.;
5) Документальное наблюдение, когда используются различного рода документы;
6) Наблюдение базируется на опросе заинтересованных лиц и получение данных в форме ответов.
IV. По способу организации наблюдения различают:
1) Наблюдение, заключающееся в обработке отчетных данных — отчетность, наиболее распространен в практике работы.
2) Экспедиционный способ — к каждой единице совокупности посылается специальное лицо, которое в соответствующих формулярах фиксирует необходимые сведения;
3) Саморегистрация — заполнение специально выданных бланков;
4) Анкетный способ — рассылка анкет и их обработка.
Наиболее распространенной формой статистического наблюдения является представление отчетности. Виды статистической отчетности делятся на типовую и специализированную; по периодичности различают недельную, двухнедельную, месячную, квартальную и годовую отчетность; в зависимости от установленного порядка прохождения отчетность делится на централизованную (наиболее распространенную) и децентрализованную.
Пример №1.
На заводе ведется учет выполнения норм выработки. Укажите виды наблюдения по времени проведения, охвату единиц совокупности и источника данных.
Так как наблюдению подвергаются все, без исключения, рабочие, то по степени охвата единиц наблюдение сплошное; наблюдение непрерывное, так как проводится по мере возникновения явления; источником данных служат документы.
Пример №2.
Проведено обследование части школьных буфетов в городе. Укажите вид наблюдения по степени охвата единиц и способу проведения.
Так как наблюдалась только часть буфетов, то наблюдение несплошное и, повидимому, был применен экспедиционный способ, т.е. в каждый проверяемый буфет посылался специальный человек, который и фиксировал необходимую информацию.
Пример №3.
Первая Всесоюзная перепись населения 1926 г. проводилась по состоянию на 12 ч. ночи с 16 на 17 декабря и продолжалась в городах 7 дней, а в сельской местности — 14 дней. Укажите объективное и субъективное время и критический момент наблюдения.
Объективное время — 12 ч. ночи с 16 на 17 декабря. Этот же момент является критическим. Субъективное время: в городах — 7 дней; в сельской местности — 14 дней.
Пример №4.
Срок представления годовых отчетов за 1995 год — 1-25 января 1996 г. Укажите объективное и субъективное время и критический момент наблюдения.
Объективное время — 1995 год, т.к. данные наблюдения относятся именно к этому периоду; субъективное время — 1-25 января 1996 г., так как в это время составляется отчет, собираются данные; критический момент отсутствует.
Пример №5.
Проводится перепись художественной литературы в библиотеках области. Укажите объект, единицу наблюдения и единицу совокупности.
Объектом наблюдения являются библиотеки области, единицей наблюдения здесь будет фонд художественной литературы, так как другие ее виды не учитываются, а единицей наблюдения является каждая конкретная книга, так как она обладает признаками, подлежащими регистрации.
Ошибки наблюдения и их контроль
Ошибкой называется расхождение между результатом наблюдения и истинным значением исследуемой величины.
Все ошибки статистического наблюдения можно классифицировать:
1. По характеру ошибок:
а) случайные ошибки, которые вызываются самыми разными причинами. Так как искажение может быть как в ту, так и в другую сторону, то случайные ошибки могут не очень влиять на общий результат;
б) систематические ошибки, которые искажают явление только в одну сторону более опасны и, как правило, вызываются действием систематического фактора (например, тяготение к круглым цифрам вносит большие осложнения при собирании сведений о возрасте населения).
2. По стадии возникновения:
а) ошибки регистрации;
б) ошибки при подготовке данных к обработке;
в) ошибки при обработке.
3. По причинам возникновения:
а) свойственные только выборочному методу и связанные с неправильным выбором части совокупности ошибки репрезентативности (представительности);
б) непреднамеренные ошибки, совершаются неумышленно, непреднамеренно, т. е. не имеют целью исказить результаты наблюдения;
в) преднамеренные ошибки возникают в результате умышленного искажения фактов. Все преднамеренные ошибки являются систематическими.
Для исключения ошибок статистические данные проверяются арифметическим и логическим контролем.
Логический контроль состоит в сопоставлении ответов на взаимосвязанные между собой вопросы программы наблюдения.
Счетный и арифметический контроль сводится к проверке общих и групповых цифровых итогов и сопоставлений; задача его обнаружить и исправить неверные итоги числовых показателей.
Пример №6.
В сводку завода о выпуске продукции за февраль была включена и продукция, выпущенная 1 и 2 марта. Укажите характер допущенной ошибки и причины возникновения.
Ошибка систематическая и преднамеренная, так как были сознательно искажены действительные результаты для получения определенных материальных выгод.
Пример №7.
В переписном листе записано: «лет-, месяцев — 11» вместо «лет — 11, месяцев-». Укажите характер и причину ошибки.
Ошибка случайная (описка) и непреднамеренная.
Пример №8.
Проведите логический контроль правильности заполнения переписного листа Всесоюзной переписи населения 1970 г. В ответах на какие вопросы допущены ошибки?
Переписной лист № 4
1. Фамилия имя и отчество — Антонова Мария Павловна.
2. Пол -женский.
3. Отношение к главе семьи -внучка.
4. Возраст (число исполнившихся лет) -4.
5. Состоит ли в браке в настоящее время -да.
6. Образование -не имеет начального.
Логика ответов подсказывает, что ошибка в 5 вопросе. Должно быть — «нет».
Сводка и группировка статистических данных. Сводка и группировка. Виды группировок
В результате статистического наблюдения получают сведения о каждой единице совокупности в отдельности. Чтобы на основе этих данных сделать определенные выводы, необходимо провести сводку полученных материалов, т.е. в узком смысле сводка -это подсчет или подведение итогов.
Однако в более широком смысле под статистической сводкой понимают сложную операцию научной обработки первичных статистических данных, которая включает группировку материала, разработку системы показателей для характеристики типичных групп и подгрупп, подсчет (подведение) итогов по группам и по совокупности в целом и изображение сгруппированных данных в виде статистических таблиц.
Статистическая группировка — расчленение общей совокупности единиц по одному или нескольким существенным признакам на однородные группы, различающиеся между собой в качественном и количественном отношении и позволяющие выделить социальноэкономические типы, изучить структуру совокупности или проанализировать связи между отдельными признаками. Группировка проводится только для целей конкретного исследования.
В соответствии с решаемыми задачами все группировки подразделяются на типологические, структурные и аналитические.
1.Расчленение разнородной совокупности на качественные однородные группы, выделение качественно однородных экономических групп или типов общественных явлений осуществляется при помощи типологических группировок.
Таблица 2.1
Распределение промышленной продукции, произведенной в различных формах хозяйствования за отчетный период
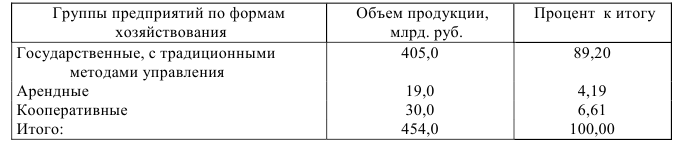
Приведенные данные характеризуют социально-экономический состав промышленной продукции (выделены типы явления), а также свидетельствуют о возникших в последнее время новых формах хозяйствования.
2. Группировка, цель которой расчленение совокупности единиц на группы, характеризующие структуру по определенным признакам, называется структурной группировкой.
Приведенная в табл. 2.2 группировка, содержит систему показателей, характеризующих структуру изучаемой совокупности по ряду признаков, а также концентрацию торгово-закупочного процесса, нашедшего свое выражение в укрупнении магазинов по величине товарооборота.
Таблица 2.2
Группировка торговых предприятий района по объему товарооборота (в процентах к итогу)
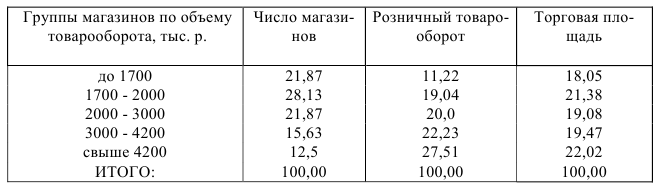
3. Группировка, целью которой является установление взаимосвязей между изучаемыми явлениями, называется аналитической. Примером аналитической группировки могут служить данные табл.2.3.
Таблица 2.3
Зависимость урожайности зерновых культур от количества внесенных удобрений по группе совхозов
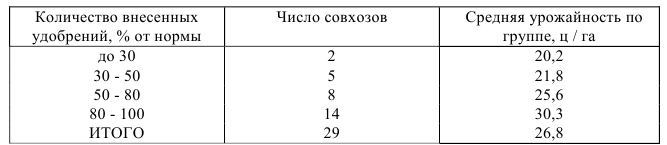
Данные показывают, что увеличение количества внесенных удобрений (факторный признак) приводит при прочих равных условиях к повышению урожайности (результативный признак).
Возможно эта страница вам будет полезна:
Группировочные признаки
Признаки в статистике — это свойства, характерные черты или особенности явлений, которые можно выразить рядом статистических величин. Признаки, положенные в основание группировки, называются группировочными.
Группировки по одному признаку называются простыми. Когда же для выделения групп берутся два более признака, т. е. группы, образованные по одному признаку, подразделяются на подгруппы по другому, а полученные в результате этого подгруппы подразделяются (каждая в отдельности) еще на подгруппы и т. д., то такие группировки называются комбинационными.
Различают четыре вида группировочных признаков: атрибутивные, количественные, признаки пространства и признаки времени.
2. Атрибутивным называется признак, который характеризует свойство, качество данного явления и не имеет количественного выражения. При группировке по атрибутивным (качественным) признакам статистическая совокупность разбивается на столько групп, сколько разновидностей имеет признак (по полу — на две группы, по национальному составу — на столько групп, сколько имеется национальностей и т.д.).
Разновидностью атрибутивных признаков являются альтернативные, т.е. такие признаки, которыми одни единицы совокупности обладают, а другие -нет. Например, одни работники имеют высшее образование, а другие не имеют и т. д.
3. Количественным называется признак, характеризующий размеры, величину изучаемой совокупности и дающий возможность расчленить её на группы по величине индивидуальных значений группировочного признака.
4. Признак пространства -это адресный признак (адрес предприятия и пр.). Группировки по признаку пространства применяются для изучения пространственных (географических) закономерностей.
5. Признак времени позволяет установить хронологию событий, и его применяют для изучения изменений явлений во времени.
Признаки бывают первичные и вторичные. Первичные признаки характеризуют абсолютные размеры изучаемых явлений (например, численность рабочих), вторичные являются производными от первичных и показывают структуру группируемых явлений (фондовооруженность, себестоимость и т. д.).
Предварительные сведения о рядах распределения
Ряд цифровых показателей, представляющий распределение единиц совокупности по одному признаку, разновидности которого расположены в определенной последовательности, называется рядом распределения.
Ряд распределения -это первичная характеристика массовой статистической совокупности, в которой находят количественное выражение закономерности массовых явлений и процессов.
Ряды распределения могут быть построены как по атрибутивному признаку — атрибутивные ряды распределения, так и по количественному — вариационные ряды распределения.
Числовые значения количественного признака в вариационном ряду называются вариантами и располагаются в определенном порядке; численность единиц в каждой группе называется частотой, а если частоты выражены в процентах, то они называются частостями. Рассмотрим табл.2.4.
Таблица 2.4
Распределение рабочих завода по уровню месячной заработной платы
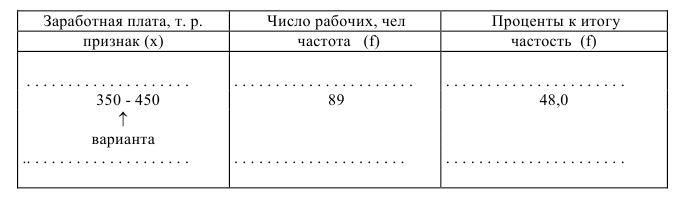

В данной таблице уровень заработной платы является вариантой, а число рабочих — частотой, показывающей, сколько раз повторяется данная варианта (т.е. сколько рабочих получают заработную плату, лежащую в пределах от 350 до 450 тыс. руб.). Частота, выраженная в процентах (в данном примере — 48,0) — это частость. Сумма всех частот называется объемом ряда распределения или его численностью (в данном случае было обследовано 180 рабочих).
Вариация признака может быть дискретной (прерывной) или непрерывной. При дискретной вариации признака значение вариантов отличается друг от друга на вполне определенную величину, и варианты обычно выражаются целыми числами (например, число членов семьи — 1, 2, 3, 4 и т. д.). Такие ряды называются вариационными дискретными рядами.
При непрерывной вариации признака его величина может принимать любые значения в определенном интервале (интервальные ряды распределения), например, рост человека, урожайность, заработная плата и т.д. Построение интервального ряда основано на принципах статистической группировки.
Интервалы могут быть неравными, поэтому сравнивать частоты и судить о степени заполнения разных интервалов нельзя. В целях сравнения заполненности интервалов рассчитывается показатель, называемый плотностью распределения, — т.е. число единиц совокупности, приходящееся в среднем на одну единицу ширины интервала (ширина интервала — разность между его границами). Если плотность определяется с помощью частот, она называется абсолютной, если с помощью частостей — относительной.
Для облегчения анализа рядов распределения их изображают при помощи графиков.
При дискретной вариации анализа признака графиком вариационного ряда служит полигон распределения. Он представляет собой замкнутый многоугольник, абсциссами вершин которого являются значения варьирующего признака, а ординатами — соответствующие им частоты или частости. Для примера рассмотрим построение полигона распределения по следующим данным (таблица 2.5). Полигон распределения приведен на рис.2.1.
Таблица 2.5
Распределение квартир жилого дома по числу проживающих в них лиц

Для иллюстрации рядов распределения часто используется кумулятивная кривая или кумулята, построенная по накопленным частотам. Накопленная частота показывает, какое число единиц имеет величину варианта не большую данной и находится путем последовательного суммирования частот (строка 3 в табл.2.5), например из табл.2.5 видно, что в 10 квартирах проживают семьи, состав которых не превышает 2 человек, в 78 квартирах проживают семьи, состав которых не превышает 4 человек и т. д. Кумулята приведена на рис.2.2.
Если при построении кумуляты поменять местами значения признака и частоты (т.е. на оси ординат отложить значения признака, а на оси абсцисс — частоты) то получим кривую, называемую огивой.
Для иллюстрации интервального ряда распределения применяют график, называемый гистограммой распределения. Гистограмма представляет собой ряд смежных столбиков, основание каждого равно величине соответствующего интервала, а высота — частоте (правильнее — пропорциональна частоте). Пример гистограммы приведен на рис.2.3.
Разновидностью кумулятивной кривой является график Лоренца или кривая концентрации. Например, необходимо дать характеристику уровня концентрации производства в промышленности России по числу рабочих (см. табл. 2.6). График приведен на рис. 2.4. Если бы численность рабочих распределялась равномерно по числу предприятий, т.е. процесс концентрации отсутствовал полностью, график представлял бы собой прямую линию. При неравномерном распределении линия концентрации отходит от прямой, причем, чем выше уровень концентрации, тем больше ее кривизна.
Таблица 2.6
Группировка промышленных предприятий по численности рабочих за 19__г.
Возможно эта страница вам будет полезна:
Абсолютные и относительные величины
Абсолютные величины
Абсолютной величиной называется статистический показатель, выражающий абсолютные размеры изучаемого явления.
По способу выражения размеров изучаемых явлений абсолютные величины подразделяются на индивидуальные, которые отражают абсолютные размеры каждой отдельной единицы совокупности, и суммарные (групповые), которые получаются суммированием индивидуальных абсолютных величин.
Абсолютные величины — всегда числа именованные, имеющие определенную размерность, единицу измерения. В зависимости от различных причин и целей анализа применяют натуральные, условно-натуральные, трудовые и стоимостные единицы измерения.
Натуральные измерители в большинстве своем соответствуют природным или потребительским свойствам предмета изучения и выражаются в физических мерах веса, длины и т. д. Учет в натуральных единицах измерения называется натуральным учетом. Иногда применяется составная единица измерения (например, тоннокилометры — ткм и т. д.).
Однородная, но неодинаковая продукция измеряется в условно-натуральных единицах измерения. Такие единицы получают, приводя различные натуральные единицы к одной, принятой за базу, например, в консервной продукции емкость банки в 354,4 см3 принята за условную и вся продукция пересчитывается в этих условных банках. Аналогично производится пересчет в условно-натуральные измерители и в других отраслях (топливной, текстильной и пр.).
Показатели, отражающие результаты труда, измеряются в трудовых единицах измерения, а наиболее распространенные – в стоимостных (или денежных) единицах измерения.
Относительные величины: сущность, виды, единицы измерения
Статистические показатели, выражающие относительные размеры изучаемого явления, называются относительными величинами.
Относительные величины получаются в результате деления одной величины на другую, принимаемую за базу сравнения (или основание относительной величины). Причем следует иметь в виду, что в числителе всегда находится показатель, отражающий то явление, которое изучает, т.е. сравнимый показатель, а в знаменателе — показатель, с которым производится сравнение.
База сравнения выступает в качестве своеобразного измерителя. Если значение базы принимается за единицу (производится простое деление двух величин), то относительная величина выражается в коэффициенте (например, темпы роста), если основание (база) — 100%, то относительная величина выражается в процентах.
Иногда за базу принимают 1000 (при расчете коэффициентов рождаемости или смертности, естественного или механического прироста показателя, в фармации и т. д.). Такие единицы измерения называются промилле и обозначаются %0.
Все относительные величины делятся на относительные величины выполнения плана и планового задания (в настоящее время лучше говорить о выполнении договорных обязательств), динамики, структуры, координации, интенсивности, сравнения, уровня экономического развития.
Относительная величина выполнения плана (ОВВП) — соотношение величины показателя, достигнутое за какое-то время или какому-либо моменту, и величины его, установленной по плану за это же время:
ОВВП = Факт(95)/План(95)
— факт (95) — фактическое выполнение за 1995 г.;
— план (95) — плановое значение за 1995 г.
Относительная величина планового задания (ОВПЗ) — соотношение плановой величины показателя к его фактически достигнутому уровню в предыдущем периоде (или в периоде, принятом за базу):
ОВПЗ = Факт(94)/План(95)
— факт (94) — фактическое выполнение за 1994 г.
Произведение этих двух величин дает относительную величину динамики (см. ниже): ОВД = ОВВП — ОВПЗ;
Относительная величина динамики (ОВД) — соотношение величины показателя за данное время и величины его за какое-либо аналогичное предшествующее время, принятое за базу сравнения. Относительная величина динамики характеризует степень, скорость изменения показателя во времени, в частности, темпы роста. Она выражается в виде краткого отношения (коэффициента) или в процентах. Если имеется ряд динамики (ряд во времени) абсолютных величин, то ОВД может исчисляться как отношение величины показателя за каждое последующее время к величине его за непосредственно предшествующее ему время или как отношение к величине его за одно и то же время, принятое за базу сравнения. В первом случае относительная величина динамики называется ОВД с переменной базой или цепная, во втором — с постоянной базой сравнения или базисная.
Если уровни ряда обозначить через 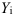 , то ОВД вида:
, то ОВД вида:
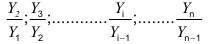 называются цепными, а вида:
называются цепными, а вида: 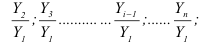 базисными (более подробно эта тема раскрывается в разделе рядов динамики).
базисными (более подробно эта тема раскрывается в разделе рядов динамики).
Относительная величина структуры характеризует состав изучаемой совокупности и показывает какой удельный вес (какую долю) в общем итоге составляет каждая ее часть. Она получается в результате деления значения каждой части совокупности на их общий итог, принятой за базу.
Относительная величина координации характеризует соотношение отдельных частей целого, одна из которых принимается за базу сравнения и является дополнением к относительной величине структуры. Например, число сельских жителей, приходящихся на 100 городских и т. д.
Относительная величина интенсивности (степени) показывает степень распространенности данного явления в определенной среде. Обычно это отношение двух разноименных абсолютных величин (плотность населения на квадратный километр; производство сельскохозяйственной продукции на 1 га сельхозугодий и пр.).
Относительная величина сравнения характеризуют соотношение одноименных показателей, относящихся к различным объектам или территориям, но за один и тот же период времени.
Относительная величина уровня экономического развития – обычно соотношение величины важнейших экономических показателей (страны, региона, отрасли) и численности населения (так называемые показатели на душу населения).
Возможно эта страница вам будет полезна:
Пример №9.
Мыловаренный завод произвел за отчетный период следующее количество продукции, т.:
мыло хозяйственное 40%-ное – 25,0;
мыло туалетное – 20,0;
мыло хозяйственное 60%-ное – 22,0; порошок стиральный – 55,0.
Определите общий выпуск продукции в пересчете на условное 40%-ное мыло по следующим переводным коэффициентам: мыло 60%-ное и туалетное – 1,75, порошок стиральный – 0,5.
Решение:
Перемножив фактический выпуск продукции на коэффициенты пересчета в условное 40%-ное мыло, получим:
25·1.0 + 22.0·1.75 + 20.0·1.75 + 55.0·0.5 = 126 тыс. т условного 40%-ного мыла.
Пример №10.
По плану предусматривалось собрать по 30 ц пшеницы с гектара, а собрано по 33 ц. Определить выполнение плана по урожайности.
Решение:
Поделим фактическую урожайность на плановую и получим:
(33·100)/30 = 110%
План по урожайности выполнен на 110%, или перевыполнен на 10%.
Пример №11.
Планом предприятия предусматривалось повысить производительность труда на 5% и снизить затраты на 2%. Фактически производительность труда возросла на 6%, затраты были снижены на 4%. Определите выполнение плана по росту производительности труда и снижению затрат.
Решение:
Степень выполнения плана по повышению производительности труда равна отношению достигнутого уровня — 106% (100% + 6%) к показателю плана — 105% (100% +5%) в процентах:
(106 ·100)/105 = 101%
Аналогично, фактическое снижение затрат — 96% (100% — 4%), а плановое — 98% (100% — 2%) их отношение дает 98%, т.е. план по снижению затрат перевыполнен на 2%.
Пример №12.
Плановое задание по выпуску продукции на 1995 г. составило 04%, а выполнено на 105%. Определить относительную величину динамики.
Решение:
Здесь 104% — это относительная величина планового задания, а 105%- это относительная величина выполнения плана, а так как ОВД = ОВВП · ОВПЗ, то (104 ·105)/100 = 109,2%, т.е. выпуск продукции в 1995 г. составил по сравнению с 1994 годом 109,2% или увеличился на 9,2%.
Пример №13.
По данным переписи населения 1970 г. в СССР проживало в возрасте 100 лет и старше 19304 чел., из них мужчин — 4252 чел., женщин — 15052. Определите структуру долгожителей по полу и относительную величину координации, приняв число мужчин за базу, равную 100.
Решение:
Для вычисления относительных величин структуры нужно разделить значение каждой части на общий итог, принимаемый за целое (100%). Количество мужчин и 18 женщин в возрасте 100 лет и старше надо поделить на общее их число или исчислить удельный вес мужчин, а затем отнять его от 100%:
(4250 ·100)/19304 = 22% мужчин
женщин — 78% (100%-22%).
Относительные величины координации характеризуют соотношение отдельных частей совокупности. В задаче требуется вычислить соотношение между численностью мужчин и женщин в возрасте 100 лет и старше. Для этого, приняв число мужчин за базу сравнения, равную 100, поделим численность женщин на численность мужчин и получим
(15052·100)/4252 = 354
Это значит, что на каждые 100 мужчин в возрасте 100 лет и старше приходится 354 женщины в том же возрасте.
Средние величины
Средней величиной называется показатель, который дает обобщенную характеристику варьирующего признака единиц однородной совокупности.
Средняя отражает то общее, что скрывается в каждой единице совокупности, улавливает общие черты, общую тенденцию, закономерность, присущую данному распределению, она является равнодействующей, потому что в ней находит свое отражение, суммируется и синтезируется влияние всей совокупности факторов, под воздействием которых формируется ряд распределения. Средняя дает также характеристику центра распределения.
Средняя арифметическая
Обозначив индивидуальные значения признака через
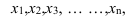
их количество — через n, можно записать:
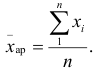
Исчисленная таким образом средняя называется средней арифметической простой, т.е. она равна частному от деления суммы индивидуальных значений признака на их количество.
Средняя арифметическая простая применяется в тех случаях, когда каждое индивидуальное значение признака встречается один, или одинаковое количество раз, т. е. когда средняя рассчитывается по не сгруппированным данным.
В том случае, когда мы имеем дискретный ряд распределения, т. е. когда значение признака встречается несколько раз, применяют среднюю арифметическую взвешенную, рассчитываемую по формуле: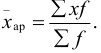
Таблица 4.1

По данным таблицы средняя заработная плата рассчитывается:
(1002+2005+30020+40030+50015+60010+7005) / 87 = 36200 / 87 = 416 тыс.руб.
Таким образом, средняя арифметическая взвешенная равна сумме произведений индивидуальных значений признака x на их частоты или веса f, поделенной на сумму частот ∑f.
Довольно часто в статистике приходится вычислять среднюю арифметическую в интервальном ряду, среднюю из групповых средних и среднюю из относительных величин.
При вычислении средней интервального ряда необходимо найти середину каждого интервала, и, взяв ее за значение признака использовать формулу средней арифметической взвешенной.
При вычислении средней из групповых (или частных) средних (например, при вычислении средней заработной платы по отрасли, когда имеется средняя заработная плата по предприятиям этой отрасли), в качестве индивидуальных значений признака берется соответствующая групповая средняя и рассчитывается по формуле средней арифметической взвешенной.
При вычислении средней из относительных величин в качестве весов (или частот) берут основание относительной величины, а в качестве значения признака — соответствующую этому основанию относительную величину.
Свойства средней арифметической
1) Средняя арифметическая суммы варьирующих величин равна сумме средних арифметических этих величин.
2) Алгебраическая сумма отклонений индивидуальных значений признака от средней равно нулю.
3) Если все варианты ряда (значения признака) изменить на одно и то же число a или изменить в A раз, то и средняя изменится на a или в A раз соответственно.
4) Если все частоты ряда изменить в A раз, то средняя не изменится.
Средняя гармоническая
Во многих статистических исследованиях приходится сталкиваться с таким положением, когда известны значения индивидуального признака — x и произведения x · f, т.е. действительные значения весов (частот) неизвестны. В этом случае расчет средней производится с использованием средней гармонической взвешенной, которая определяется по формуле: ,
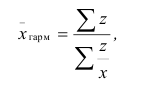
где Z=x·f, т.е. произведению значения признака на частоту.
В тех случаях, когда произведения x·f одинаковы или равны единице
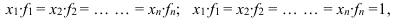
применяется средняя гармоническая простая, определяемая по формуле:
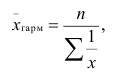
где x — отдельные варианты (значения признака);
n— число наблюдений (общее число признаков или вариант).
Таким образом, средняя гармоническая представляет собой особый вид средней, которая применяется в тех случаях, когда известны варианты x и произведения вариантов на частоты — x·f , при отсутствии действительных весов.
Средняя геометрическая
В некоторых случаях приходится вычислять средний коэффициент роста в единицу времени. Коэффициент роста характеризует скорость изменения статистических показателей и представляет собой отношение величины показателя за два периода времени, как правило, за ряд смежных лет (табл. 4.2).
Таблица 4.2
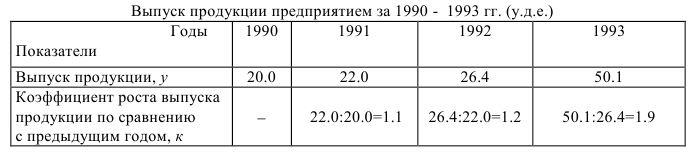
Средняя, которая отражает средний коэффициент роста показателя за определенный период называется средней геометрической, которая равна корню степени m из произведений коэффициентов роста (m — число коэффициентов роста),
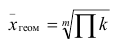
Средний коэффициент роста (среднюю геометрическую) можно определить и по значениям первого и последнего членов динамического ряда. Если первый уровень ряда обозначить 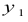 , а последний —
, а последний — 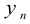 , то
, то  , где n — число членов ряда (число лет).
, где n — число членов ряда (число лет).
Средняя квадратическая
В тех случаях, когда осреднению подлежат величины, выраженные в виде квадратных функций, применяется средняя квадратическая. Средние диаметры колес, труб, стволов, средние стороны квадратов и т.д. определяются при помощи средней квадратической.
Средняя квадратическая простая вычисляется путем извлечения квадратного корня из частного от деления суммы квадратов отдельных значений признака на их число:
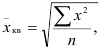
Соотношение между различными видами средних (мажорантность средних)
Все выше рассмотренные виды средних величин можно получить из формулы степенной средней вида 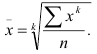
При различных значениях показателя получаются различные средние, средняя арифметическая, гармоническая, геометрическая и квадратическая.
Мажорантность средних состоит в том, что средняя некоторого вида всегда больше средней некоторого другого вида (для признака, не могущего иметь отрицательных значений). В частности, если для одной совокупности вычислить средние гармоническую, геометрическую, арифметическую и квадратическую, то по численному значению они расположатся в возрастающем порядке. Порядок возрастания этих средних определяет показатель степени k в формуле степенной средней, т.е. чем больше k, тем больше средняя (табл.4.3).
Таблица 4.3

Подробно общее условие мажорантности т.е. соотношения между различными видами средних было сформулировано А. Я. Боярским. Проиллюстрируем правило мажорантности геометрически (см. рисунок).
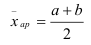
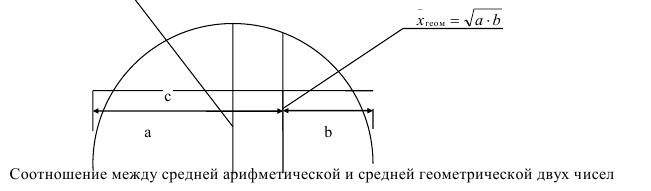
Опишем на отрезке c = a + b, как на диаметре, полукруг и восстановим из общей точки отрезка a и b перпендикуляр, длина которого будет равна. 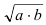 . Восстановим также перпендикуляр из центра полукруга, длина которого будет равна (a + b)/2. Из рисунка видно, что средняя геометрическая меньше средней арифметической. При этом, чем меньше отличаются отрезки а и b друг от друга, тем меньше разница между средними.
. Восстановим также перпендикуляр из центра полукруга, длина которого будет равна (a + b)/2. Из рисунка видно, что средняя геометрическая меньше средней арифметической. При этом, чем меньше отличаются отрезки а и b друг от друга, тем меньше разница между средними.
Возможно эта страница вам будет полезна:
Мода и медиана
Кроме средних в статистике для описательной характеристики величины варьирующего признака пользуются показателями моды и медианы.
Мода — это наиболее часто встречающийся вариант ряда. Мода применяется, например при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей, наиболее распространенной цены на тот или иной товар и пр.
Модой в дискретном ряду называется варианта (значение признака), имеющая наибольшую частоту (повторяющаяся самое большое количество раз), например: имеем данные о продаже магазином обуви по размерам (табл.4.4):
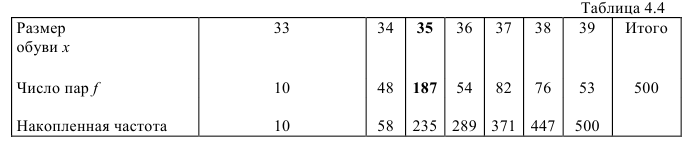
В этом примере модой является 35-й размер, так как обуви такого размера продано больше всего — 187 пар.
Если мы имеем интервальный ряд, то для определения моды необходимо сначала определить модальный интервал, причем, если интервалы равны, то модальный интервал определяется по наибольшей частоте, а если неравны, то по наибольшей плотности. При равных интервалах мода внутри модального интервала может определяться по формуле:
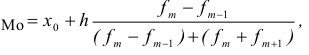
где 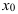 — нижняя граница модального интервала;
— нижняя граница модального интервала;
h — величина (ширина) интервала; 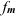 — частота модального интервала;
— частота модального интервала; 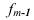 — частота интервала, предшествующего модальному;
— частота интервала, предшествующего модальному; 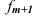 — частота интервала, следующего за модальным.
— частота интервала, следующего за модальным.
Мода является наиболее распространенной и в этом смысле типичной величиной в распределении. Но мода и средняя величина по разному характеризуют совокупность. Мода определяет непосредственно размер признака, свойственный хотя и значительной части, но все же не всей совокупности. Поэтому мода по своему обобщающему значению уступает средней, которая характеризует совокупность в целом, так как складывается под воздействием всех без исключения элементов совокупности.
При наличии одной моды распределение называют унимодальным, при двух модах — бимодальным, при трех и более модах — мультимодальным.
Медианой называется варианта, которая приходится на середину ряда, расположенного в порядке возрастания или убывания численных значений признака. Медиана делит ряд на две равные части.
Если в совокупности нечетное число единиц, т. е. 2m+1, то значение признака у (m+1)-ой единицы будет медианным. Если в совокупности четное число, т.е. 2∙m единиц, то медиана равна средней арифметической из двух серединных значений вариантов.
Для определения медианы в дискретном ряду при наличии частот сначала вычисляют полусумму частот, а затем определяют, какое значение признака приходится на нее. В примере с размером обуви (см. табл.4.4) медианой является 35-й размер, так как именно он приходится на полусумму частот (500:2=250). Это значит, что 35-й размер делит ряд на две равные части.
При вычислении медианы для интервального вариационного ряда вначале определяют медианный интервал, т.е. первый интервал, накопленная частота которого принимает полусумму частот, а затем приближенное значение медианы по формуле:
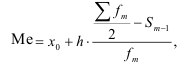
где 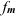 — сумма частот;
— сумма частот; 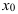 — нижняя граница медианного интервала;
— нижняя граница медианного интервала;
h — ширина интервала; 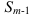 — сумма накопленных частот интервалов, предшествующих медианному;
— сумма накопленных частот интервалов, предшествующих медианному; 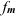 — частота медианного интервала.
— частота медианного интервала.
Главное свойство медианы состоит в том, что сумма абсолютных отклонений вариантов от медианы меньше, чем от любой другой величины (в том числе и от средней арифметической):
∑|x-Ме|= min.
Медиану, являющуюся описательной характеристикой вариационного ряда, иногда называют непараметрической средней. Медиана меньше, чем средняя арифметическая, зависит от формы распределения признака. Она не зависит ни от амплитуды колебаний ряда, ни от распределения частот в пределах двух равных частей ряда. Вот почему в медиане не находят отражения важные свойства совокупности и она используется обычно для решения некоторых частных задач, связанных с определением оптимума, совпадающего с вариантой, приходящейся на середину ряда.
Мода и медиана являются описательными характеристиками совокупностей с количественно варьирующими признаками и не могут заменить среднюю обобщающую величину. Величина моды и медианы, как правило, отличается от величины средней, совпадая с ней только в случае симметрии вариационного ряда.
Пример №14.
По следующим данным определите средний стаж рабочего (табл.4.5):

Решение:
Признаком в данной задаче является общий стаж рабочего, а частотами соответственно количество рабочих, имеющих тот или иной стаж. Ряд распределения — интервальный, причем первый и последний интервал — открытые.
Если интервалы открыты, то по правилам принимаем величину первого интервала равной второму, а последнего предпоследнему. Так как имеются и значения признака и частоты, то средний стаж находим по формуле средней арифметической взвешенной. А так как ряд интервальный, то в качестве значения признака в каждой группе берём середины интервала
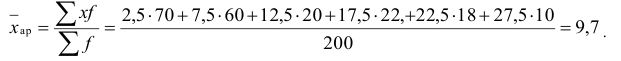
Пример №15.
Все частоты уменьшились в два раза, а все варианты увеличились на две единицы. Что произойдет со средней?
Решение:
Согласно свойствам средней арифметической, если все частоты ряда уменьшить или увеличить в одинаковое количество раз, то средняя не изменится, т.е. с точки зрения частот средняя не изменится. Если все варианты увеличить или уменьшить на одно и то же число, то и средняя изменится на это же число. В нашем случае средняя увеличится на две единицы.
Пример №16.
Двое рабочих в течение 8-часового рабочего дня изготовляют одни и те же детали. Первый из них тратит на изготовление детали 30 мин., второй — 40 мин. Вычислите среднюю затрату времени на изготовление одной детали.
Решение:
В этой задаче явно даны только значения признака затраты времени, а частоты, которыми является количество изготовленных каждым рабочим деталей, в явном виде не присутствуют. Однако произведения значений признака на частоты дает количество проработанного времени — 8 час. Так как произведения признака на частоту равны, то средняя определяется по формуле средней гармонической простой:
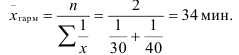
Пример №17.
Автомобиль проехал 1000 км, из них 480 км он прошел со скоростью 60 км/час, 320 — со скоростью 80 км/час и 200 км — со скоростью 50 км/час. Определите среднюю скорость, с которой совершался рейс.
Решение:
В этой задаче опять известны только значения признака, а значения частот (время) не даны, однако имеются данные о пройденном расстоянии, которое является произведением признака на частоту. В этом случае средняя рассчитывается по формуле средней гармонической взвешенной:
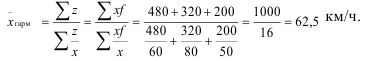
Пример №18.
Определите среднегодовой темп роста выпуска продукции на заводе, если в 1990 г. было произведено продукции на 21,15 у.д.е., а в 1995 г. было запланировано произвести продукции на 35 у.д.е.
Решение:
Для определения средних темпов роста применяется средняя геометрическая. Когда имеются данные о первом периоде (в нашем случае — выпуск продукции в 1990 г. на сумму 21,15 у.д.е.) и в последнем периоде (в задаче — выпуск продукции по плану в 1995 г. на сумму 35 у.д.е.), среднегодовой темп роста определяется по формуле:
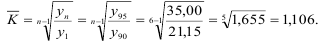
Пример №19.
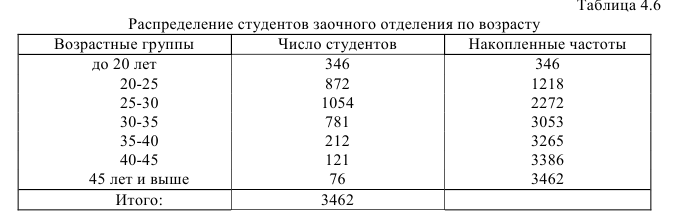
Определить моду и медиану по следующим данным (табл. 4.6):
Решение:
Для определения моды определяем модальный интервал. Им является интервал 25-30 лет, так как его частота наибольшая (1054), тогда
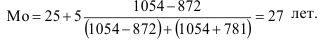
Для определения медианы тоже необходимо определить медианный интервал. Медианным интервалом является интервал 25-30, так как он является первым интервалом, накопленная частота которого превышает полусумму частот (3462:2=1731). Тогда медиана определится как:
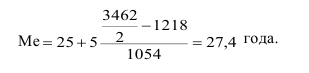
Показатели вариации и другие характеристики рядов распределения. Понятие о вариации
При изучении процессов и явлений общественной жизни статистика встречается с разнообразной вариацией признаков, характеризующей отдельные единицы совокупности. Величина признака изменяется, колеблется под влиянием различных причин и условий. Чем разнообразнее условия, влияющие на размер данного признака, тем больше его вариация.

Одна и та же средняя может характеризовать совокупность, в которой размеры вариации признака существенно отличаются друг от друга (табл.5.1). Как видно, средняя дневная выработка в обеих бригадах одинакова, хотя в первой бригаде средняя значительно меньше отличается от индивидуальных значений признака, чем во второй.
Следовательно, для всесторонней характеристики рядов распределения необходимы показатели, определяющие меру, степень колеблемости отдельных значений признака от средней, т.е. степень вариации, а также форму (тип) распределения, характеризующую ее закономерности.
Показатели вариации и способы их расчета
а) Размах вариации является наиболее простой мерой колеблемости значений признака и представляет собой разность между максимальным и минимальным значением признака: R = Хmax — Хmin.
Размах вариации имеет недостаток, проявляющийся в том, что при вычислении R используется только крайние значения ряда распределения, и он не всегда правильно характеризует колеблемость признака.
В связи с тем, что каждое индивидуальное значение признака отклоняется от средней на определенную величину, мерой вариации может служить средняя из отклонений каждой отдельной варианты от их средней.
Такими показателями являются среднее линейное отклонение, дисперсия, среднее квадратическое отклонение.
б) Среднее линейное отклонение представляет собой среднюю из абсолютных значений отклонений индивидуальных значений признаков от их средней:
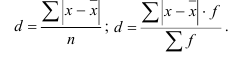
Недостаток среднего линейного отклонения в том, что оно берется без учета знака. Поэтому в статистике чаще используют дисперсию и среднее квадратическое отклонение.
в) Дисперсия и среднее квадратическое отклонение. Дисперсией называется средний квадрат отклонений индивидуальных значений признака от их средней величины

Дисперсия имеет очень большое значение в анализе. Однако ее применение как меры вариации в ряде случаев бывает не совсем удобным, потому что размерность дисперсии равна квадрату размерности изучаемого признака. Поэтому вычисляют среднее квадратическое отклонение, равное корню квадратному из суммы квадратов отклонений индивидуальных значений признака от их средней, т.е. из дисперсии
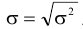
Сопоставление линейных или средних квадратических отклонений по нескольким совокупностям дает возможность определять степень их однородности в отношении того или иного признака. Чем меньше: 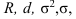 тем совокупность более однородна, тем более типичной будет средняя величина.
тем совокупность более однородна, тем более типичной будет средняя величина.
г) Коэффициент вариации. Так как дисперсия и среднее квадратическое отклонение характеризуют абсолютный размер отклонений, то представляет интерес сопоставить среднее квадратическое отклонение с его средней величиной. Такой показатель называется коэффициентом вариации
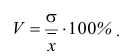
Если взять отношение среднего линейного отклонения к средней арифметической, то получим линейный коэффициент вариации 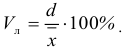
Отношение размаха вариации к средней арифметической называется коэффициентом осцилляции: 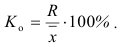
Взаимосвязь показателей вариации
В нормальном ряду распределения между показателями вариации имеются следующие примерные соотношения: 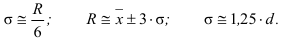
Основные свойства дисперсии
1. Если все значения признака уменьшить или увеличить на какое-то постоянное число а, то дисперсия не изменится.
2. Если все значения признака уменьшить или увеличить в К раз, то дисперсия изменится в К 2 раз.
3. Сумма квадратов отклонений индивидуальных значений признака x от их средней x меньше суммы квадратов отклонений индивидуальных значений признака от любого числа а, при условии, что 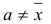
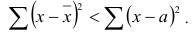
4. Дисперсия признака равна разности между средним квадратом значения признака и квадратом их средней:
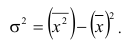
Дисперсия альтернативного признака
В ряде случаев возникает необходимость измерить вариацию альтернативного признака, то есть такого, который может принимать только два значения. Обозначив отсутствие интересующего нас признака через 0, его наличие через 1, долю единиц, обладающих данным признаком — через р, не обладающих — через q, дисперсию этого признака можно определить как
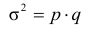
Например, если 64% работников предприятия имеют высшее образование р, то дисперсия будет равна:
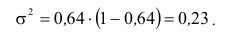
Правило сложения дисперсий
На вариацию признака влияют различные причины и факторы, которые делятся на случайные и систематические. Поэтому и вариация может быть случайной, вызванной действием случайных причин и систематической, обусловленной воздействием постоянных причин и факторов. В связи с этим возникает необходимость в определении случайной систематической составляющей и её роли в общей вариации. Общую дисперсию мы уже рассматривали. Она характеризует общую вариацию признака под влиянием всех условий, всех причин, вызывающих эту вариацию и исчисляется по формуле:
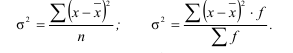
Для определения влияния постоянного фактора на величину вариации пользуются аналитической группировкой. Вариация, обусловленная фактором, положенным в основание группировки, называется межгрупповой вариацией. Размеры ее определяются при помощи дисперсии групповых средних или межгрупповой дисперсии, которая характеризует колеблемость групповых или частных средних 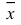 около их общей средней:
около их общей средней:
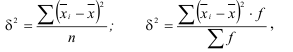
где 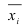 — средняя по каждой отдельной группе;
— средняя по каждой отдельной группе; 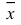 — средняя по всей совокупности;
— средняя по всей совокупности;
n — число единиц совокупности;
f — частоты или веса.
Таким образом, межгрупповая дисперсия (дисперсия групповых средних) равна средней арифметической из квадратов отклонений частных средних от общей средней. Она характеризует систематическую вариацию, которая возникает под влиянием фактора, признака, положенного в основание группировки.
Для определения влияния случайных факторов и их роли в общей вариации определяют дисперсию в пределах каждой группы, т.е. внутригрупповую дисперсию, а затем и среднюю из внутригрупповых дисперсий: 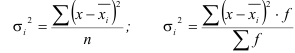
где x — индивидуальные значения признака;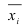 — групповые или частные средние:
— групповые или частные средние: 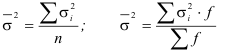
В математической статистике доказано, что общая дисперсия признака равна сумме межгрупповой дисперсии и средней из внутригрупповых дисперсий.
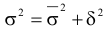
Это правило называется правилом сложения дисперсий.
Ряды распределения и их моделирование
а) Моменты распределения
Одной из важных задач анализов рядов распределения является выявление закономерности распределения, определение ее характера и количественного выражения. Эта задача решается при помощи показателей, характеризующих форму, тип распределения.
Кроме рассмотренных выше важной характеристикой рядов распределения являются моменты распределения.
Моментом распределения 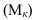 называется средняя арифметическая из отклонений значений признака x от некоторой постоянной величины а в степени к:
называется средняя арифметическая из отклонений значений признака x от некоторой постоянной величины а в степени к:
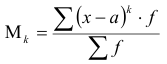
Величина к определяет порядок момента. В зависимости от величины а различают начальные, центральные и условные моменты (табл. 5.2).
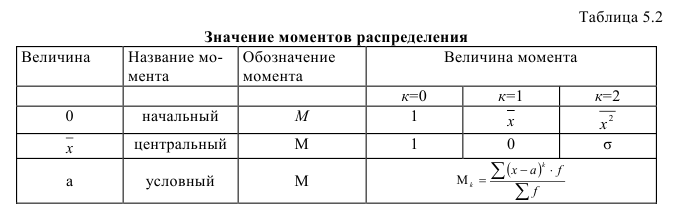
Условные моменты используются для определения дисперсий высоких степеней. Практически используются моменты первых четырех порядков. Если в качестве весов взять не частоты, а вероятности, то получим теоретические моменты распределения.
б) Кривые распределения
Для обобщенной характеристики особенностей формы распределения применяются кривые распределения, которые выражают закономерность распределения единиц совокупности по величине варьирующего признака.
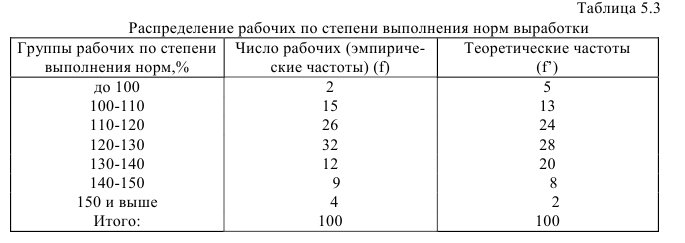
Эмпирическая кривая — это фактическая кривая, полученная по данным наблюдения, в которой отражаются как общие, так и случайные условия, определяющие распределение (кривая 1, рис.5.3)
Теоретическая кривая распределения — это кривая, выражающая функциональную связь между изменением варьирующего признака и изменением частот и характеризующая определенный тип распределения (кривая 2, рис.5.3).
По форме кривые распределения бывают симметричными и асимметричными. В зависимости от того, какая ветвь кривой вытянута, различают правостороннюю асимметрию и левостороннюю асимметрию (рис.5.1). Кривые распределения также могут иметь различную островершинность (рис.5.2).
Для характеристики степени асимметрии кривой используют коэффициент асимметрии, который представляет собой отношение центрального момента третьего порядка к среднему квадратическому отклонению в кубе
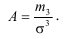
Если А > 0, то асимметрия правосторонняя, а если А < 0, то асимметрия левосторонняя, в симметричном распределении — А=0. Кроме этого коэффициента для характеристики асимметрии применяют и соотношение между 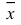 и модой или медианой по отношению к среднеквадратическому отклонению.
и модой или медианой по отношению к среднеквадратическому отклонению.
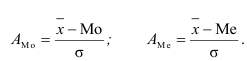
Он менее точен по сравнению с коэффициентом асимметрии и применяется реже.
Для характеристики островершинности кривой распределения применяют коэффициент эксцесса, который равен отношению центрального момента четвертого порядка к дисперсии в квадрате
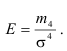
В нормальном распределении Е=3, поэтому, если Е>3, то эксцесс выше нормального (островершинная кривая), Е<3, эксцесс ниже нормального (плосковершинная кривая).
в) Моделирование рядов распределения
Все рассмотренные выше показатели характеризуют отдельные свойства совокупности. Общую характеристику ряда распределения можно представить аналитически, в виде функции, характеризующей зависимость между изменениями признака и частотами. Если имеется эмпирический ряд распределения, то необходимо найти функцию распределения, т. е. подобрать такую теоретическую кривую, которая наиболее полно бы раскрывала закономерность распределения.
Нахождение функции кривой распределения называется моделированием.
Для аппроксимации (выравнивания) эмпирических кривых распределения в статистике часто пользуются нормальным распределением, функция которого
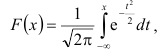
где F(x) — интегральная функция распределения;
t — нормированное отклонение;
e — основание натуральных логарифмов.
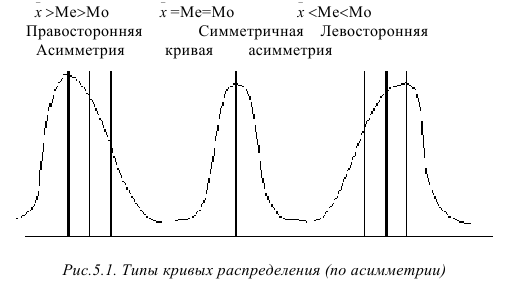
Эмпирическое и теоретическое распределение рабочих по степени выполнения норм приведено в табл.5.3 и на рис.5.3.
г) критерии согласия
Для оценки близости эмпирического и теоретического распределения используются специальные показатели, которые называются критериями согласия. Критерии согласия как правило тем или иным способом оценивают степень расхождения между эмпирическими и теоретическими частотами.
Наиболее часто используется критерий, который называется хи-квадрат Пирсона и рассчитывается 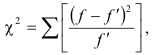
где f’ — теоретические частоты, f — эмпирические частоты.
Чем меньше значение 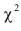 , тем лучше теоретическое распределение отражает реальное положение в совокупности и наоборот. Если
, тем лучше теоретическое распределение отражает реальное положение в совокупности и наоборот. Если 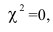 то расхождение между f и f’ отсутствует.
то расхождение между f и f’ отсутствует.
Для проверки согласия с помощью 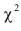 рассчитанное значение
рассчитанное значение 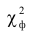 сравнивают с табличным и при условии
сравнивают с табличным и при условии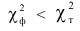 можно с определенной вероятностью сказать, что расхождение теоретического и эмпирического распределения случайно, и наоборот.
можно с определенной вероятностью сказать, что расхождение теоретического и эмпирического распределения случайно, и наоборот.
Также применяется и критерий согласия Колмогорова 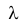 , который равен
, который равен 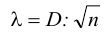 , где D — максимальная разность накопленных частот (без учета знака), n — объем совокупности.
, где D — максимальная разность накопленных частот (без учета знака), n — объем совокупности.
Вычислив фактический критерий 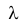 , по специальной таблице находят вероятность достижения критерием этого значения. Если вероятность значительна, то расхождение между эмпирическим и теоретическим распределением можно считать случайным.
, по специальной таблице находят вероятность достижения критерием этого значения. Если вероятность значительна, то расхождение между эмпирическим и теоретическим распределением можно считать случайным.
В явлениях общественной жизни асимметричные распределения встречаются гораздо чаще, чем симметричные. Некоторые асимметричные распределения могут быть приведены к симметричному путем преобразования признака Х, например логарифмированием. В этом случае распределение называется логарифмически нормальным. Такое преобразование производится, как правило, для сильно асимметричных распределений.
Пример №20.
Проверка пряжи на крепость в лаборатории дала следующие результаты (табл. 5.4):

Вычислить все показатели вариации.
Решение:
В задаче значения признака имеют различную численность, поэтому значения, 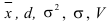 должны вычисляться как средние взвешенные величины. Для вычисления показателей вариации проводим дополнительные расчеты (табл. 5.5)
должны вычисляться как средние взвешенные величины. Для вычисления показателей вариации проводим дополнительные расчеты (табл. 5.5)


Средняя крепость пряжи определяется по формуле
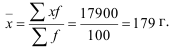
Размах вариации
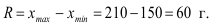
Среднее линейное отклонение вычисляется по формуле
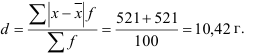
Дисперсия, взвешенная по частоте вариантов, равна
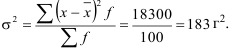
Среднее квадратичное отклонение равно:
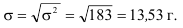
коэффициент вариации составляет
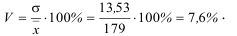
Пример №21.
На предприятии 64% работников имеют среднее и высшее образование. Определить дисперсию доли рабочих, имеющих среднее и высшее образование.
Решение:
Дисперсия альтернативного признака определяется как 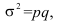 где p – доля единиц совокупности, обладающих данным признаком, а q=1-p – доля единиц совокупности, не обладающих данным признаком, следовательно:
где p – доля единиц совокупности, обладающих данным признаком, а q=1-p – доля единиц совокупности, не обладающих данным признаком, следовательно: 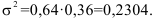
Пример №22.
Имеются следующие данные (табл.5.6):

Вычислить: среднюю месячную заработную плату для каждой группы и для всех рабочих; групповые дисперсии; среднюю из внутригрупповых дисперсий; межгрупповую дисперсию; общую дисперсию; проверить правило сложения дисперсий и сделать выводы.
Решение:
В задаче требуется определить, как влияют на изменение заработной платы рабочих постоянные причины, положенные в основание группировки (в данном случае различия в профессии), и случайные причины. Для этого необходимо определить систематическую и случайную вариации и их роль в общей вариации. Для решения задачи и вычисления заданных показателей, построим вспомогательную таблицу (табл.5.7).
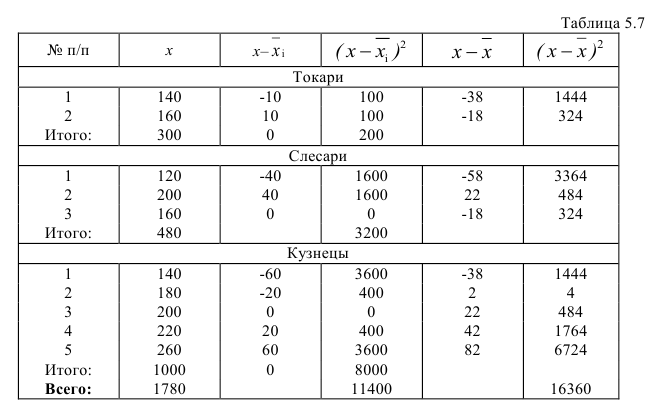
Среднюю заработную плату по каждой группе и для всех рабочих определяем по формуле средней арифметической простой:
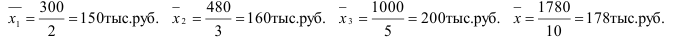
Внутригрупповые дисперсии вычисляем по формуле:
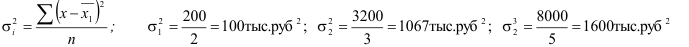
Средняя из внутригрупповых дисперсий равна:
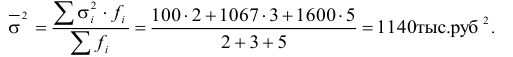
Межгрупповая дисперсия определяется как:
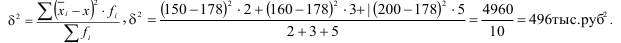
Общая дисперсия равна: 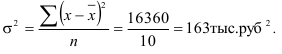
По правилу сложения дисперсий общая дисперсия равна сумме средней внутригрупповых и межгрупповой дисперсии: 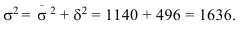
Пример №23.
Средняя успеваемость студентов экономического факультета 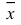 =4 балла, Мо=4,8 балла, Ме=4,2 балла. Указать, симметричным или асимметричным является распределение студентов по успеваемости. Если асимметричным, то с какой асимметрией (левосторонней или правосторонней).
=4 балла, Мо=4,8 балла, Ме=4,2 балла. Указать, симметричным или асимметричным является распределение студентов по успеваемости. Если асимметричным, то с какой асимметрией (левосторонней или правосторонней).
Решение:
В симметричном распределении 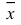 =Мо=Ме. В нашей задаче такого равенства нет. Следовательно, распределение асимметрично, а так как
=Мо=Ме. В нашей задаче такого равенства нет. Следовательно, распределение асимметрично, а так как 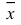 <Ме<Мо, то разности между
<Ме<Мо, то разности между 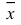 –Ме и
–Ме и 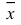 –Мо отрицательные и асимметрия левосторонняя.
–Мо отрицательные и асимметрия левосторонняя.
Пример №24.
Урожайность сахарной свеклы в сельхозпредприятиях области характеризуется следующими показателями: 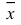 =300 ц/га,
=300 ц/га, 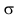 =120 ц/га, Мо=240 ц/га, а урожайность зерновых —
=120 ц/га, Мо=240 ц/га, а урожайность зерновых — 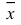 =30ц/га;
=30ц/га; 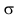 =10 ц/га, Мо=27 ц/га. Вычислить показатели асимметрии и указать где она больше. Каково направление асимметрии?
=10 ц/га, Мо=27 ц/га. Вычислить показатели асимметрии и указать где она больше. Каково направление асимметрии?
Решение:
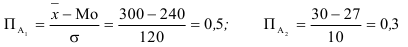
Асимметрия правосторонняя, так как 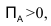 и больше в первом случае.
и больше в первом случае.
Пример №25.
Центральный момент третьего порядка 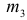 =34,56 при
=34,56 при 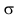 =12. Вычислить коэффициент асимметрии и сделать выводы; центральный момент четвертого порядка
=12. Вычислить коэффициент асимметрии и сделать выводы; центральный момент четвертого порядка 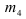 =64,32 при
=64,32 при 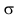 =2 . Вычислить коэффициент эксцесса и сделать выводы.
=2 . Вычислить коэффициент эксцесса и сделать выводы.
Решение:
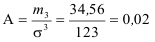
Асимметрия правосторонняя, так как A>0 , и незначительная
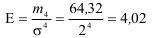
Эксцесс выше нормального, потому что E>3.
Выборочное наблюдение
Общие сведения о выборочном наблюдении
В связи с тем, что статистика имеет дело с массовыми совокупностями статистические исследования весьма трудоемки. Поэтому давно возникла мысль о замене сплошного наблюдения выборочным.
Выборочное наблюдение — это наиболее совершенный способ несплошного наблюдения, при котором обследуется не вся совокупность, а лишь ее часть, отобранная по определенным правилам выборки и обеспечивающая получение данных, характеризующих всю совокупность в целом.
При проведении выборочного наблюдения нельзя получить абсолютно точные данные. Как при сплошном, так как при выборочном наблюдении неизбежны ошибки, которые делятся на ошибки регистрации и ошибки репрезентативности. В свою очередь, ошибки репрезентативности бывают случайные и систематические.
Важнейшим условием применения выборочного метода является правильный отбор единиц совокупности, а именно:
а) строго объективный отбор единиц совокупности, при котором каждая из них получала бы абсолютно одинаковую возможность попасть в выборку;
б) достаточное количество отобранных единиц совокупности. При соблюдении этих условий выборка будет репрезентативной или представительной.
Вся совокупность единиц, из которой производится отбор, называется генеральной совокупностью и обозначается буквой N. Часть генеральной совокупности, попавшая в выборку, называется выборочной совокупностью и обозначается n.
Обобщающие показатели генеральной совокупности — средняя, дисперсная и доля — называются генеральными и соответственно обозначается 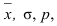 где p — доля или отношение числа единиц совокупности М, обладающих данным признаком ко всей численно- 36 сти генеральной совокупности, т.е.
где p — доля или отношение числа единиц совокупности М, обладающих данным признаком ко всей численно- 36 сти генеральной совокупности, т.е. 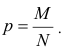 Те же обобщающие характеристики в выборочной совокупности обозначаются соответственно
Те же обобщающие характеристики в выборочной совокупности обозначаются соответственно 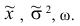
Теоретической основой выборочного метода является теорема П.Л.Чебышева, которая формулируется следующим образом: с вероятностью, сколь угодно близкой к единице (достоверности), можно утверждать, что при достаточно большом объеме выборки и ограниченной дисперсии генеральной совокупности разность между выборочной средней и генеральной средней будет сколь угодно мала:
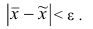
При практическом использовании теоремы Чебышева генеральную дисперсию 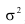 , которая неизвестна, заменяют выборочной дисперсией.
, которая неизвестна, заменяют выборочной дисперсией.
Виды и схемы отбора
Формирование выборочной совокупности из генеральной может осуществляться по-разному. Различают следующие виды отбора: собственно-случайный; механический; типический; серийный; комбинированный.
5. Собственно-случайный отбор. Он ориентирован на выборку единиц из генеральной совокупности без всякого расчленения ее на части или группы. Либо применяется жеребьевка, либо используются таблицы случайных чисел.
6. Механический отбор. Он состоит в том, что отбор единиц в выборочную совокупность производится из генеральной совокупности, разбитой на равные интервалы (группы), причем все единицы генеральной совокупности должны располагаться в определенном порядке. Размер интервала или группы равен обратной величине доли выборки (или количеству отбираемых единиц). Из каждой группы (интервала) берется только одна единица. Так, при 2%-ной выборке отбирается каждая 50-ая единица (1:0,02; или формируется 50 групп или интервалов), при 20%-ной выборке — каждая 5-я единица (1:0,2) и т. д.
7. Типический отбор. При его осуществлении вся генеральная совокупность делится на группы по типическому признаку, а затем в каждой группе проводится тот или иной отбор. Наиболее часто из каждой группы выбирается количество единиц, пропорциональное удельному весу группы в общей совокупности и как правило — механическим отбором. Такой отбор часто называют пропорциональным типическим отбором с механической выборкой.
8. Серийный отбор с равновеликими сериями состоит в выборке не отдельных единиц генеральной совокупности, а целых серий (гнезд). Попавшие в выборку серии подвергаются сплошному наблюдению. Сами серии могут формироваться различными методами и способами.
9. Комбинированный отбор. Все вышеперечисленные виды отбора комбинируются между собой.
Используя различные виды отбора, можно применить и различные схемы отбора: бесповторный отбор (схема невозвращенного шара) — после выбора какой-либо единицы она обратно в генеральную совокупность не попадает и не может быть выбрана снова; повторный отбор (схема возвращенного шара) — после выбора какой-либо единицы она вновь возвращается в генеральную совокупность и может быть выбрана снова.
Определение средних и предельных ошибок при различных видах отбора
Ошибка выборки 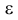 — разность между характеристиками выборочной и генеральной совокупности.
— разность между характеристиками выборочной и генеральной совокупности.
Если 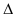 представляет собой предел, которого не превосходит абсолютная величина
представляет собой предел, которого не превосходит абсолютная величина 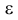 то
то 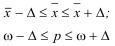
Ошибка выборки зависит от многих факторов, и, если из одной и той же генеральной совокупности можно сформировать бесконечное множество выборочных совокупностей, каждая из них даст и свою ошибку. Поэтому при выборочном наблюдении говорят о средней из возможных ошибок (средняя или стандартная ошибка выборки), которую обозначают как 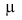 .
.
Величина 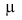 прямо пропорциональна корню квадратному из дисперсии и обратно пропорциональна квадратному корню из объема выборочной совокупности;
прямо пропорциональна корню квадратному из дисперсии и обратно пропорциональна квадратному корню из объема выборочной совокупности; 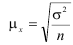 , для доли, соответственно
, для доли, соответственно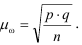 .
.
Эти формулы справедливы для повторной схемы отбора. При бесповторном отборе вводится поправочный коэффициент, равный
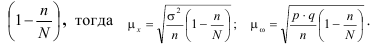
В тех случаях, когда выборка небольшая этим множителем можно пренебречь, так как его значение близко к единице (обычно при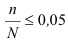 ).
).
Для решения практических задач важна не средняя ошибка выборки, а пределы, за которые она не выйдет, т.е. говорят о предельной ошибке выборки.
Предельная ошибка выборки связана со средней ошибкой соотношением 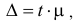 где t— коэффициент доверия, или t— статистика; t принимает значения 1, 2 или 3 и связан с вероятностью достижения заданного предела. Если t=1 это значит, что вероятность того, что ошибка выборки не превысит заданного значения, равна 0,683 или 68,3%. При t=2 — P=0,954 или 95,4%; t=3 — P=0,997 или 99,7%.
где t— коэффициент доверия, или t— статистика; t принимает значения 1, 2 или 3 и связан с вероятностью достижения заданного предела. Если t=1 это значит, что вероятность того, что ошибка выборки не превысит заданного значения, равна 0,683 или 68,3%. При t=2 — P=0,954 или 95,4%; t=3 — P=0,997 или 99,7%.
Таким образом, предельная ошибка выборки зависит от трех факторов: дисперсии 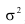 , объема выборки n, и коэффициента доверия t. Формулы для определения предельных ошибок при различных видах и схемах отбора приведены в табл. 6.1.
, объема выборки n, и коэффициента доверия t. Формулы для определения предельных ошибок при различных видах и схемах отбора приведены в табл. 6.1.
Таблица 6.1


Возможно эта страница вам будет полезна:
Определение необходимой численности выборки
При разработке выборочного наблюдения предполагают заранее заданными величину допустимой ошибки выборки и вероятность ответа (и t). Неизвестным, следовательно, остается тот минимальный объем выборки, который должен обеспечить требуемую точность. Из формулы 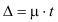 и формул предельных ошибок выборки устанавливаем необходимую численность выборки. Формулы для определения численности выборки n зависят от способа отбора (табл.6.2).
и формул предельных ошибок выборки устанавливаем необходимую численность выборки. Формулы для определения численности выборки n зависят от способа отбора (табл.6.2).
Таблица 6.2

Численность выборки можно выразить через отношение 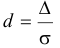 , т.е. предельную ошибку выборки выражают в единицах среднего квадратичного отклонения. Так, например, формула численности бесповторной собственно-случайной выборки для средней при t=3 примет вид
, т.е. предельную ошибку выборки выражают в единицах среднего квадратичного отклонения. Так, например, формула численности бесповторной собственно-случайной выборки для средней при t=3 примет вид 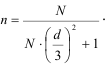
Для типического и серийного отбора объем выборки определяется по специальным формулам.
Пример №26.
Методом случайной повторной выборки было взято для проверки на вес 200 шт. деталей. В результате был установлен средний вес детали — 30 г при среднеквадратическом отклонении равном 4 г. С вероятностью 0,954 требуется определить предел, в котором находится средний вес детали в генеральной совокупности.
Решение:
Предельная ошибка средней при собственно-случайном отборе (повторная выборка) определится по формуле
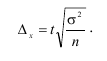
Нам известно, что t=2 (т.к. P=0.954); 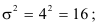 n=200, тогда
n=200, тогда
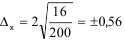
Следовательно, с вероятностью 0,954 можно утверждать, что средний вес детали в генеральной совокупности будет находиться в пределах
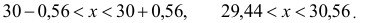
Пример №27.
Был проведен учет городского населения города А методом случайного бесповторного отбора. Из общей численности населения 500 тыс. человек было отобрано 500 тыс. и установлено, что 15% имеют возраст старше 60 лет. С вероятностью 0,683 определить предел, в котором находится доля жителей города А в возрасте старше 60 лет.
Решение:
Предельная ошибка доли при собственно-случайном бесповторном отборе определится как
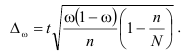
Здесь 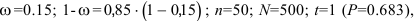 тогда подставляя эти данные в формулу получим:
тогда подставляя эти данные в формулу получим:
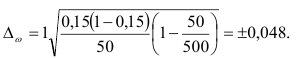
Следовательно, с вероятностью 0,683 можно утверждать, что доля жителей старше 60 лет находится в пределах:
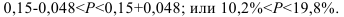
Пример №28.
Проведена 10%-ная типическая выборка пропорциональна численности отобранных групп (табл. 6.3).
Таблица 6.3

Требуется с вероятностью 0,954 определить пределы, в которых находится средний процент выполнения норм рабочими завода в целом. Выборка бесповторная.
Решение:
Вычислим общий средний процент выполнения норм выработки:
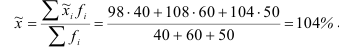
Далее определим среднюю из групповых дисперсий
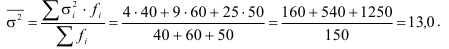
Рассчитаем предельную ошибку выработки для типического отбора
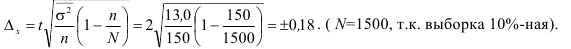
Таким образом, с вероятностью 0,954 можно утверждать, что средний процент выполнения норм рабочими завода в целом находится в пределах
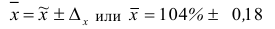
т.е. он не меньше 103,82% и не больше 104,18%.
Пример №29.
Для определения средней урожайности сахарной свеклы в области проведена 20%-ная серийная бесповторная выборка, в которую вошло 5 районов из 25. Средняя урожайность по каждому отобранному району составила: 250, 260, 275, 280, 300 ц/га. Определить с вероятностью 0,954 пределы, в которых будет находиться средняя урожайность сахарной свеклы по области.
Решение:
Найдем общую среднюю
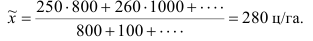
Определим межсерийную дисперсию по формуле
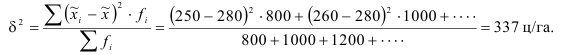
Рассчитаем предельную ошибку выборки при серийном бесповторном отборе
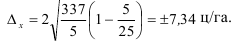
Следовательно, с вероятностью 0,954 можно утверждать, что средняя урожайность сахарной свеклы в области будет находиться в пределах от 272,66 до 287,34 ц/га.
Пример №30.
Предполагается, что партия деталей содержит 8 % брака. Определить необходимый объем выборки, чтобы с вероятностью 0,954 можно было установить долю брака с погрешностью не более 2% . Исследуемая партия содержит 5000 деталей.
Решение:
По условию задачи t=2 , доля бракованных деталей 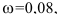
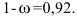 Предельная ошибка доли по условию равна
Предельная ошибка доли по условию равна 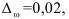 а N=5000. Подставляем эти данные в формулу и получим
а N=5000. Подставляем эти данные в формулу и получим
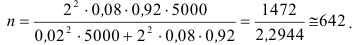
Чтобы с вероятностью 0,954 можно было утверждать, что предельная ошибка доли брака не превысит 2% , необходимо из 5000 деталей отобрать 642.
Пример №31.
Что произойдет с предельной ошибкой выборки, если:
а) дисперсия уменьшится в 4 раза;
б) численность выборки увеличить в 9 раз;
в) вероятность исчисления изменится с 0,683 до 0,997.
Решение:
Из формулы для расчета предельной ошибки выборки 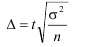 видно, что она:
видно, что она:
а) прямо пропорциональна корню квадратному из дисперсии. Следовательно, если дисперсия уменьшится в 4 раза, то предельная ошибка уменьшится в 2 раза;
б) обратно пропорциональна корню квадратному из численности выборки. Следовательно, если объем выборки увеличится в 9 раз, то предельная ошибка уменьшится в 3 раза;
в) прямо пропорциональна вероятности исчисления, т.е. при увеличении Р с 0,683 (t=1) до 0,997 (t=3) ошибка увеличится в 3 раза.
Статистическое изучение связи, виды и формы взаимосвязи между явлениями
Одной из важнейших задач статистики является изучение, измерение и количественное выражение взаимосвязи между явлениями общественной жизни, установленной на основе качественного анализа.
Различают два вида связей: функциональную и корреляционную, обусловленные двумя типами закономерностей: динамическими и статистическими.
Для явлений, в которых проявляются динамические закономерности, характерна жесткая, механическая причинность, которая может быть выражена в виде уравнения, четкой зависимости и т.д. Такая зависимость называется функциональной. При функциональной связи каждому значению одной величины (аргумента) соответствует одно или несколько вполне определенных значений другой величины (функции).
В общественных процессах, в которых проявляются статистические закономерности, нет строгой зависимости между причиной и результатом и обычно не представляется возможным выявить строгую зависимость.
Связь, при которой каждому значению аргумента соответствует не одно, а несколько значений функции и между аргументом и функциями нельзя установить строгой зависимости называется корреляционной. Корреляционная зависимость проявляется только в средних величинах и выражает числовое соотношение между ними в виде тенденции к возрастанию или убыванию одной переменной величины при возрастании или убывании другой.
По направлению различают прямую и обратную связи.
По аналитическому выражению корреляционная связь может быть прямолинейной и криволинейной.
Основные приемы изучения взаимосвязей
а) Метод параллельных рядов. Чтобы установить связь между явлениями достаточно расположить полученные в результате сводки и обработки материалы в виде параллельных рядов и сопоставить их между собой.
б) Балансовый метод. Для характеристики взаимосвязи между явлениями в статистике широко применяется балансовый метод. Сущность его заключается в том, что данные взаимосвязанных показателей изображаются в виде таблицы и располагаются таким образом, чтобы итоги между отдельными частями были равны, т.е. чтобы был баланс. Балансовый метод используется для характеристики взаимосвязи между производством и распределением продуктов, денежными доходами и расходами населения и т.д.
в) Метод аналитических группировок. При наличии массовых статистических данных для изучения и измерения взаимосвязей социально-экономических явлений широко пользуются методом аналитических группировок. Аналитические группировки позволяют установить наличие связи между двумя и более признаками и ее направление. Метод группировок сочетается с методом средних и относительных величин.
г) Дисперсионный анализ. Аналитические группировки при всей своей значимости не дают количественного выражения тесноты связи между признаками. Эта задача решается при помощи дисперсионного и корреляционного анализов.
Дисперсионный анализ дает, прежде всего, возможность определить роль систематической и случайной вариаций в общей вариации и, следовательно, установить роль изучаемого фактора в изменении результативного признака. Для этого пользуются правилом сложения дисперсий.
Корреляционный анализ. Определение формы связи
Изучение взаимосвязей между признаками статистической совокупности заключается в определении формы и количественной характеристики связи, а также степени тесноты связи. Корреляционный анализ и решает эти две основные задачи.
Первая задача заключается в определении формы связи, т.е. в установлении математической формы, в которой выражается данная связь.
Предварительный этап при установлении формы связи заключается в теоретическом анализе изучаемого явления, а также в представлении искомой связи графически. График, построенный по исходным данным, позволяет приблизительно определить: есть ли какая-то связь между явлениями; ее направление (прямая или обратная); примерную тесноту связи (естественно, что при графическом анализе используются только две переменные).
Применение методов корреляционного анализа дает возможность выражать связь между признаками аналитически — в виде уравнения — и придавать ей количественное выражение.
Другими словами необходимо найти зависимость вида y=f(x), причем в качестве функции f(x) могут быть
полином 1-го порядка — 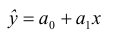
полином 2-го порядка — 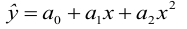
степенная функция — 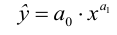
гиперболическая функция — 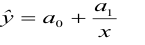
(могут быть использованы и другие виды функций).
Неизвестные параметры функций (аналитических уравнений связи) находятся методом наименьших квадратов, сущность которого в следующем: сумма квадратов отклонений фактических данных от выровненных должна быть наименьшей (см. рисунок):
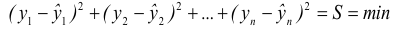
или
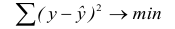
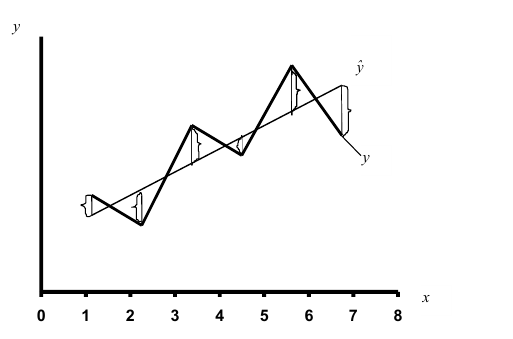
Отклонение фактических уровней от выровненных
Измерение тесноты связи
При изучении корреляционной связи важно выяснить не только форму, но и тесноту связи между факторным и результативным признаком. Для этого (при прямолинейной связи) рассчитывается показатель, называемый парным линейным коэффициентом корреляции 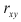 , вычисляемый по формуле
, вычисляемый по формуле
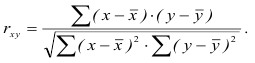
Коэффициент корреляции принимает значение от -1 до +1, причем если 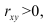 то корреляция прямая, если
то корреляция прямая, если 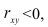 то корреляция обратная, а если
то корреляция обратная, а если 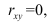 то корреляция отсутствует полностью. В зависимости от того, насколько
то корреляция отсутствует полностью. В зависимости от того, насколько 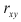 приближается к единице, различают связь слабую, умеренную, заметную, высокую, тесную и весьма тесную. Коэффициент корреляции может быть исчислен и по следующей формуле
приближается к единице, различают связь слабую, умеренную, заметную, высокую, тесную и весьма тесную. Коэффициент корреляции может быть исчислен и по следующей формуле
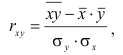
где 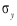 — среднее квадратическое отклонение результативного признака;
— среднее квадратическое отклонение результативного признака; 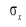 — среднее квадратическое отклонение факторного признака.
— среднее квадратическое отклонение факторного признака.
Зная линейный коэффициент корреляции, можно определить и параметры уравнения регрессии вида 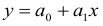 потому что:
потому что:
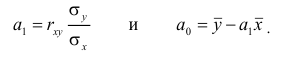
Коэффициент корреляции 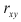 применяется только в тех случаях, когда между явлениями существует прямолинейная связь. Если же связь криволинейная, то пользуются коэффициентом корреляции, вычисляемым по формуле
применяется только в тех случаях, когда между явлениями существует прямолинейная связь. Если же связь криволинейная, то пользуются коэффициентом корреляции, вычисляемым по формуле
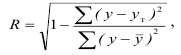
где y— исходные значения результативного показателя; 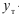 -теоретические значения;
-теоретические значения; 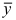 — среднее значение y.
— среднее значение y.
Имея среднее значение дисперсий, коэффициент корреляции можно вычислить как
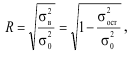
где 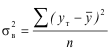 факторная (межгрупповая) дисперсия или дисперсия воспроизводимости;
факторная (межгрупповая) дисперсия или дисперсия воспроизводимости; 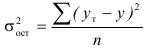 — случайная (средняя из внутригрупповых) дисперсия или остаточная дисперсия;
— случайная (средняя из внутригрупповых) дисперсия или остаточная дисперсия; 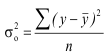 — общая дисперсия.
— общая дисперсия.
Коэффициент корреляции по своему абсолютному значению находится в пределах от 0 до 1.
Если коэффициент корреляции возвести в квадрат и выразить в процентах, получим показатель, называемый коэффициентом детерминации
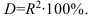
Он показывает, на сколько процентов изменение результативного фактора зависит от изменения факторного признака. Коэффициент детерминации является наиболее конкретным показателем, так как он отвечает на вопрос о том, какая доля в общем результате зависит от фактора, положенного в основании группировки.
Множественная корреляция
Определение формы и тесноты связи между тремя и более параметрами называется множественной корреляцией. При множественной корреляции определение формы связи аналогично определению формы связи при парной корреляции, а само уравнение регрессии ищется в виде (как правило)
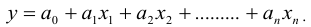
При определении тесноты связи есть свои особенности. Теснота связи измеряется множественным коэффициентом корреляции, вид которого аналогичен коэффициенту корреляции при парной связи
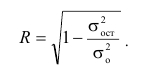
Если изучается взаимодействие только трех факторов y=f(x,z), то коэффициент множественной корреляции можно определить по формуле
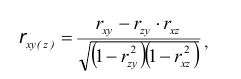
где 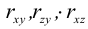 — парные коэффициенты корреляции.
— парные коэффициенты корреляции.
Множественный коэффициент корреляции находится в пределах от 0 до 1.
Множественный коэффициент детерминации, равный квадрату R, выраженному в процентах, характеризует долю вариации результативного признака Y под воздействием всех изучаемых факторных признаков.
Поскольку факторные признаки действуют не изолировано, а по взаимосвязи, то может возникнуть задача определения тесноты связи между результативным признаком и одним из факторных при постоянных значениях прочих факторов. Она решается при помощи частных коэффициентов корреляции. Например, при линейной связи y=f(x,z) частный коэффициент корреляции между x и y при постоянном z вычисляется по следующей формуле
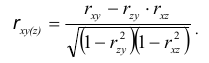
Частный коэффициент корреляции при изучении зависимости Y от Z при постоянном Х определяется по формуле
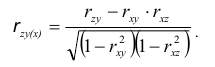
Парные коэффициенты корреляции, как правило, выше частных. Это объясняется тем, что факторы взаимно коррелируют между собой.
При значительном количестве факторов частный коэффициент корреляции можно получить по формуле
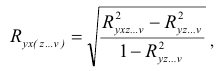
где 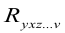 — коэффициент множественной корреляции;
— коэффициент множественной корреляции; 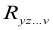 — коэффициент множественной корреляции результативного фактора (y) со всеми за исключением исследуемого.
— коэффициент множественной корреляции результативного фактора (y) со всеми за исключением исследуемого.
Простейшие методы измерения тесноты связи
Измерение тесноты связи между факторами с помощью корреляционно-регрессионного и дисперсионного анализов сопряжено с большими вычислительными трудностями. Для ориентировочной оценки степени тесноты связи существуют приближённые методы, не требующие трудоемких расчетов. К ним относятся: коэффициент корреляции знаков Фехнера, коэффициент корреляции рангов, коэффициент ассоциации и коэффициент взаимной сопряженности.
Коэффициент корреляции знаков
Основан на сопоставлении знаков отклонений от средней и подсчете числа случаев совпадения и несовпадения знаков Коэффициент корреляции знаков определяется по формуле
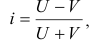
где U — число пар с одинаковыми знаками отклонений x и y от 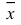 и
и 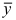 ; V- число пар с разными знаками отклонений x и y от
; V- число пар с разными знаками отклонений x и y от 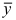 и
и 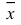 .
.
Коэффициент корреляции знаков колеблется от -1 до +1. Этот показатель исчисляется очень просто, но именно в силу этого он не очень точен.
Коэффициент корреляции рангов
Этот показатель вычисляется не по первичным данным, а по рангам (порядковым номерам ), которые присваиваются всем значениям изучаемых признаков,расположенным в порядке их возрастания. Если значения признака совпадают, то определяется средний ранг путем деления суммы рангов на число совпадающих значений.Коэффициент корреляции рангов определяется по формуле
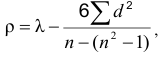
где 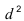 — квадрат разности рангов для каждой единицы d=x-y. Коэффициент корреляции рангов также колеблется в пределах от -1 до +1.
— квадрат разности рангов для каждой единицы d=x-y. Коэффициент корреляции рангов также колеблется в пределах от -1 до +1.
Коэффициент ассоциации
Коэффициент ассоциации применяется для установления меры связи между двумя качественными альтернативными признаками. Для его вычисления строится комбинационная 4-клеточная таблица:

которая выражает связь между двумя альтернативными явлениями. Коэффициент ассоциации рассчитывается по формуле
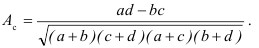
Коэффициент ассоциации тоже колеблется в пределах от -1 до +1.
Коэффициент взаимной сопряженности
В тех случаях, когда требуется установить связь между качественными признаками, каждый из которых состоит из трех и более групп, применяется коэффициент взаимной сопряженности. Для определения степени тесноты связи вычисляется специальный показатель, который называется коэффициентом взаимной сопряженности. Он определяется по формуле:
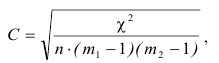
где n — число единиц совокупности; 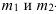 — число групп по первому и второму признаку;
— число групп по первому и второму признаку; 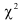 — показатель абсолютной квадратичной сопряженности Пирсона.
— показатель абсолютной квадратичной сопряженности Пирсона.
Методика применения всех четырех коэффициентов показана при решении типовых задач.
Пример №32.
По данным о месячной заработной плате 10 рабочих трех разных профессий (токарь, слесарь и кузнец) вычислены: общая дисперсия заработной платы 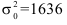 и средняя из внутригрупповых дисперсий
и средняя из внутригрупповых дисперсий 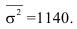 Вычислить корреляционное отношение.
Вычислить корреляционное отношение.
Решение:
Корреляционное отношение вычисляется по формуле
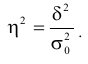
Следовательно, сначала необходимо найти межгрупповую дисперсию
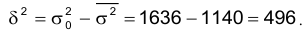
Подставляя это значение в вышеприведенную формулу, получим:
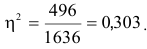
Пример №33.
Вычислено следующее уравнение множественной регрессии по сельскохозяйственным предприятиям области, характеризующее связь между размерами предприятия по посевной площади х га, числу коров z шт., доходами предприятия y млн. руб.: y=290+3,12x+0,65z. Требуется проанализировать параметры уравнения регрессии.
Решение:
Увеличение посевной площади на один гектар приводит к повышению доходов в среднем на 3,12 млн руб.; увеличение числа коров на 1 голову приводит к повышению доходов на 0,65 млн руб.
Пример №34.
По данным задачи №2 получены следующие парные коэффициенты корреляции
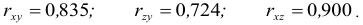
Вычислить коэффициент множественной корреляции и детерминации.
Решение:
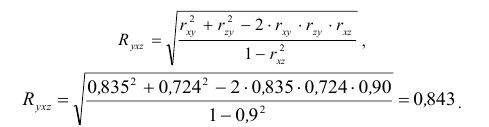
Таким образом, между доходами, посевной площадью и числом коров существует тесная связь. Коэффициент детерминации в нашем случае равен
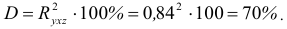
Это значит, что 70% всей вариации денежных доходов предприятий объясняется действием рассматриваемых факторов.
Пример №35.
По данным задачи №3 вычислите коэффициент корреляции между y и x и сделайте выводы.
Решение:
Частный коэффициент корреляции характеризует тесноту связи между результативным признаком и одним из факторных при постоянных значениях прочих факторов, т. е.
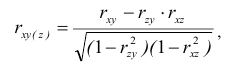
где 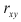 — парные коэффициенты корреляции.
— парные коэффициенты корреляции.
Подставляя в формулу их значения, получим:
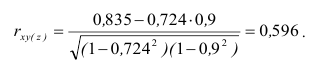
Следовательно, связь между денежными доходами и посевной площадью при исключении влияния других факторов заметная.
Этот же результат можно получить, используя общую формулу коэффициента частной корреляции
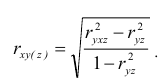
Подставляя имеющиеся значения, получим:
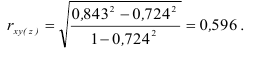
Пример №36.
По 10 предприятиям имеются следующие данные, млн руб. (табл.7.1).

Определите коэффициент корреляции знаков и сделайте выводы о тесноте связи.
Решение:
Для вычисления коэффициента корреляции знаков составим вспомогательную таблицу (табл. 7.2), из которой получим число совпадений знаков от средней. В нашем случае оно равно 8, число несовпадений знаков отклонений от средней — 2.
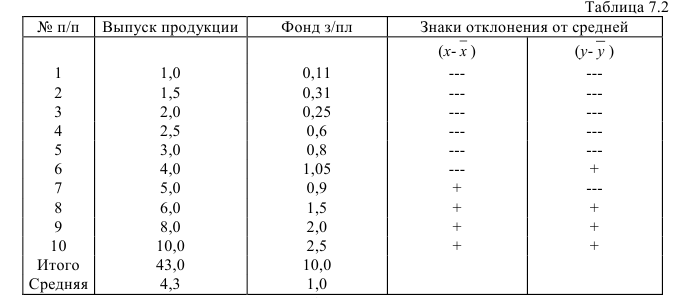
Подставляя эти значения в формулу коэффициента корреляции, получим:
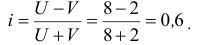
Связь между выпуском продукции и фондом заработной платы прямая и заметная.
Пример №37.
По 10 предприятиям имеются следующие данные (табл 7.3):

Решение:
Коэффициент корреляции рангов вычисляется по рангам (порядковым номерам), которые присваиваются всем единицам совокупности, расположенным в порядке возрастания признака. Для его вычисления составим вспомогательную таблицу (табл 7.4).
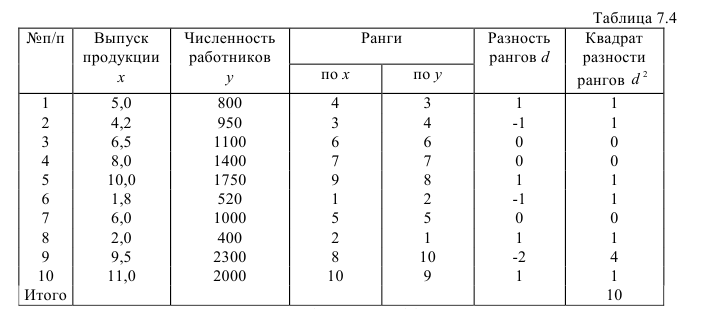
Подставляя соответствующие данные в формулу коэффициента, получим:
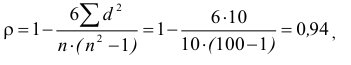
то есть связь между выпуском продукции и среднесписочной численностью работников весьма тесная.
Пример №38.
По данным табл. 7.5 вычислить коэффициент ассоциации.
Таблица 7.5

Решение:
Коэффициент ассоциации используется для установления степени тесноты связи между двумя качественными альтернативными признаками, состоящими из двух групп, и определяется по следующей формуле
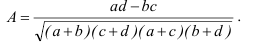
Подставим соответствующие данные из табл. 7.5 в формулу и получим:
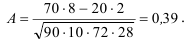
Как видно, между выполнением плана и наличием специальной подготовки существует прямая и заметная связь.
Ряды динамики, понятие о динамических рядах и их видах
Процессы и явления общественной жизни, которые изучаются статистикой, находятся в постоянном движении и изменении. В процессе развития меняются размеры, состав, объем, структура конкретных общественных явлений. Эти изменения статистика выражает при помощи различных статистических показателей.
Статистические данные, характеризующие изменения явлений во времени, называются динамическими (хронологическими или временными) рядами. Такие ряды имеют огромное значение для выявления и изучения складывающихся закономерностей в явлениях общественной жизни.
Довольно часто имеющиеся динамические ряды несопоставимы в силу изменения круга объектов учета, территориальных границ, изменения масштаба единиц измерения и т.д. В этом случае для преобразования несопоставимых динамических рядов в сопоставимые используют различные приемы, основные из которых следующие: прямой пересчет данных, пересчеты при помощи ключей и смыкание рядов.
В зависимости от характера изучаемых величин различают три вида динамических рядов: моментные, интервальные и ряды средних.
Моментными рядами называются ряды статистических величин, характеризующие размеры изучаемого явления на определенные даты или моменты времени. Примером могут служить данные о среднесписочной численности работающих по состоянию на первое число каждого месяца.
Отличительной особенностью моментных рядов является то, что они не подлежат суммированию.
Интервальными рядами называются ряды статистических показателей, характеризующих размеры изучаемого явления за определенные промежутки (периоды, интервалы) времени. Интервальные ряды можно суммировать.
Ряды средних величин — это ряды, характеризующие изменения средних уровней изучаемого явления во времени. Как и моментные, ряды средних величин не подлежат суммированию.
Вычисление средней динамического ряда
Средняя, вычисленная из уровней динамического ряда, называется хронологической средней. Способы ее расчета зависят от вида динамического ряда.
a) для интервальных рядов средняя исчисляется по формуле средней арифметической, причем при равных интервалах применяется средняя арифметическая простая, а при неравных — средняя арифметическая взвешенная.
б) для моментных рядов средняя рассчитывается по формуле
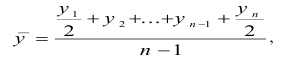
т.е. средняя хронологическая моментного ряда равна сумме всех уровней ряда, поделенной на число членов ряда без одного, причем первый и последний члены ряда берутся в половинном размере.
Если интервалы между периодами неравные, то применяется средняя арифметическая взвешенная, а в качестве весов берутся отрезки времени между датами, к которым относятся парные средние смежных значений уровня.
Основные показатели, используемые при анализе динамических рядов
Динамические ряды анализируются при помощи ряда показателей, определяющих характер, направление, интенсивность количественных изменений во времени. К ним относятся: уровень ряда, средний уровень, абсолютный прирост, темп роста, коэффициент роста, темп прироста, коэффициент опережения, абсолютное значение одного процента прироста.
Уровнем ряда называется абсолютная величина каждого члена динамического ряда. Различают начальный (величина первого члена ряда), конечный (последнего), средний уровень ряда.
Средний уровень определяется в зависимости от вида динамического ряда.
Абсолютный прирост характеризует размер увеличения или уменьшения изучаемого явления за определенный период времени. Он определяется как разность между данным уровнем и предыдущим или начальным. Уровень, который сравнивается, называется текущим, а уровень с которым производится сравнение, называется базисным. Если каждый уровень ряда сравнивается с предыдущим, то получаются цепные показатели. Если же все уровни ряда сравниваются с одним и тем же, первоначальным уровнем, то полученные показатели называются базисными.
Абсолютный прирост определяется по формулам;
цепной: 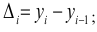 базисный:
базисный: 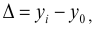
где 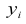 — текущий уровень ряда;
— текущий уровень ряда; 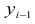 — уровень предшествующий;
— уровень предшествующий; 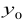 — начальный уровень ряда.
— начальный уровень ряда.
Темпом роста называется отношение данного уровня к предыдущему или начальному, выраженному в процентах. Темпы роста бывают цепными и базисными и вычисляются по формулам
цепной: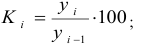 базисный: —
базисный: —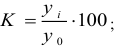
Если темпы роста выражены в виде простых отношений (база-1), то полученные показатели называются коэффициентами роста.
Темпом прироста называется отношение абсолютного прироста к предыдущему или начальному членам ряда, выраженным в процентах;
цепной: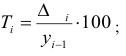 базисный
базисный 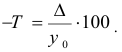
Темп прироста также может быть рассчитан как:
цепной: 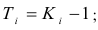 базисный
базисный 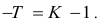
Для характеристики темпов роста и прироста в среднем за весь период вычисляют средний темп роста и прироста. Средний темп, коэффициент роста и прироста определяются по формулам средней геометрической.
Для определения средней из средних коэффициентов или темпов роста за неодинаковые промежутки времени применяется средняя геометрическая взвешенная
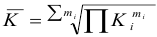
где m — продолжительность отрезков времени.
Коэффициентом опережения называется отношение базисных темпов роста двух динамических рядов за одинаковые отрезки времени
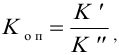
где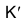 -базисные темпы роста первого ряда;
-базисные темпы роста первого ряда; 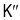 — базисные темпы роста второго ряда.
— базисные темпы роста второго ряда.
В тех случаях, когда темпы роста по двум сравниваемым рядам динамики неизвестны, а имеются средние темпы роста за одинаковый период времени, коэффициент опережения рассчитывается по формуле
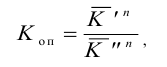
где 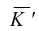 — средний темп роста первого ряда динамики,
— средний темп роста первого ряда динамики, 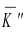 — второго, а n — число лет в периоде.
— второго, а n — число лет в периоде.
Отношение абсолютного прироста к темпу прироста представляет собой абсолютное значение одного процента прироста и определяется по формуле
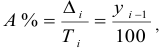
где A % — абсолютный прирост; 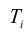 — цепной темп прироста;
— цепной темп прироста; 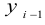 — уровень, предшествующий
— уровень, предшествующий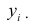 .
.
Из формулы видно, что абсолютное значение одного процента прироста равно одной сотой части предшествующего уровня.
Важнейшие приемы обработки и анализа динамических рядов
Существуют различные приемы обработки динамических рядов:
а) Приведение рядов к одному основанию.
Для выявления связи или различия в динамике двух или нескольких рядов их можно привести к одному основанию. Для этого показатели каждого ряда выражаются в процентах к первому или любому другому члену ряда.
б) Разбивка ряда на короткие периоды.
Для выявления тенденции данных колеблющихся рядов их разбивают на более короткие периоды, а затем определяют средний уровень по каждому периоду.
в) Сглаживание способом скользящих (подвижных) средних.
Сущность его заключается в том, что по конкретным уровням ряда рассчитываются сглаженные, скользящие средние, которые получаются из подвижных сумм путем последовательного сдвига на одну дату суммируемых показателей. Затем подвижные суммы делят на число дат, получая, таким образом, скользящие или подвижные средние. Например, складывают три первых члена ряда, а их среднюю относят ко второму периоду, затем складывают 2-й, 3-й и 4-й члены ряда, а их среднюю относят к третьему периоду и т.д.
г) Метод аналитического выравнивания динамических рядов.
Сущность метода состоит в том, что основная тенденция выражается в виде функции y=f(x), где за параметр х принимается время t .
Кстати готовые на продажу задачи тут, и там же теория из учебников может быть вам поможет она.
Корреляционный анализ и сезонные колебания в рядах динамики
Для изучения связи в рядах динамики применяется и корреляционный анализ. Однако его применение связано с определенными трудностями, потому что в динамических рядах уровни независимы друг от друга.
Зависимость между каждым предыдущим и последующим членами динамического ряда называется автокорреляцией. Корреляция между уровнями динамических рядов будет правильно отражать связь между явлениями только при условии устранения автокорреляции. Для этого существует ряд способов.
Первый способ состоит в том, что ищется связь не между уровнями рядов, а между первыми, вторыми и т. д. разностями (т. е. из каждого последующего уровня ряда вычитается значение предыдущего — первые разности и т. д.). В этом случае коэффициент корреляции вычисляется по формуле
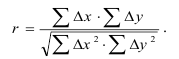
Второй способ исключения автокорреляции состоит в том, что сопоставляются отклонения от тренда (основной тенденции) по изучаемым рядам: для каждого динамического ряда проводится аналитическое выравнивание, затем находятся отклонения от найденной основной тенденции и уже потом, используя эти отклонения в качестве искомых переменных, определяют связь.
Для многих явлений общественной жизни характерны внутригодичные повторяющиеся колебания, которые называются сезонными. Они наблюдаются в различных отраслях народного хозяйства: при производстве большинства видов сельхозпродуктов, их переработки, в строительстве, транспорте, торговле и т. д.
Для выявления и измерения интенсивности сезонных колебаний пользуются индексами сезонности, причем индексы сезонности могут вычисляться по-разному.
14.Если средний годовой уровень сезонного явления остается от года к году относительно неизменным, применяется метод простых средних. Он состоит в определении простой средней за одни и те же месяцы всего изучаемого периода и в сопоставлении их со средней за весь изучаемый период.
15.Когда уровень явления проявляет тенденцию к росту или снижению, применяют метод помесячных отношений. Он заключается в том, что в начале вычисляются по каждому году процентные отношения между показателями за каждый данный и предшествующий месяцы, а затем из полученных отношений определяется среднеарифметическое.
Пример №39.
По следующим данным вычислить среднемесячные остатки материалов за полугодие (табл 8.1):

Решение:
В нашей задаче даны остатки материалов на определенные моменты в ремени (1/1, 1/2, и т.д.), промежутки между которыми равны. В этом случае средняя исчисляется по формуле средней хронологического ряда:
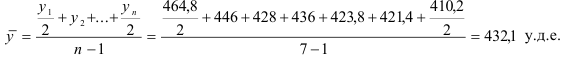
Пример №40.
По следующим данным определите среднее поголовье коров по совхозу за год (табл 8.2):

Решение:
В задаче дано поголовье коров за определенный момент, даты, причем интервалы между датами не равны (6, 4 и 2 месяца). В таких случаях средняя хронологическая моментного ряда рассчитывается как средняя арифметическая взвешенная, где в качестве весов применяются отрезки времени между датами, к которым относятся парные средние смежные значения уровня. Определим прежде всего средние смежные значения уровней.
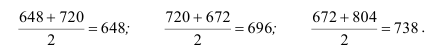
Взвесим их теперь на отрезке времени между датами
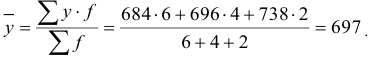
Пример №41.
Производство продукции по предприятию за 1990 1994 гг. характеризуется следующими данными (табл. 8.3):

Определить:
16.начальный, конечный и средний уровни ряда;
17.абсолютные приросты по годам, к 1990 г. и среднегодовой абсолютный прирост;
18.темп роста и прироста по годам и к 1990 г.;
19.абсолютное значение одного процента прироста;
20.среднегодовой темп роста и прироста за период 1990 1994 гг.
Решение:
1. Начальный уровень (величина первого члена ряда) — 4140, конечный — 5426. Средний уровень ряда определяется по формуле простой средней арифметической, так как ряд периодический
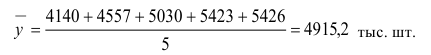
Вычисленные основные показатели данного динамического ряда сводим в таблицу 8.4.
2. Абсолютный прирост показывает, насколько изменился текущий уровень по сравнению с предыдущим или базисным и определяется как разность двух уровней
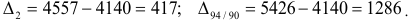
Среднегодовой абсолютный прирост исчисляется по формуле средней арифметической простой и равен
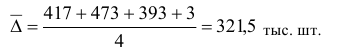
Среднегодовой абсолютный прирост можно вычислить и таким образом:
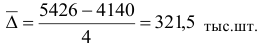
3. Темп роста показывает, во сколько раз текущий уровень больше предыдущего или базисного, и определяется как отношение двух уровней, выраженное в процентах:
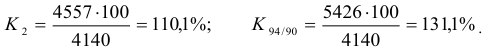
Темп прироста показывает, на сколько процентов увеличился текущий уровень по сравнению с текущим или базисным и определяется как разность соответствующего темпа роста и 100%:

Абсолютное значение 1% прироста определяется как отношение абсолютного прироста к темпу прироста:
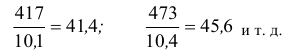
Среднегодовой темп роста рассчитывается по формуле средней геометрической
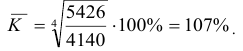
Среднегодовой темп прироста равен среднегодовому темпу роста минус 100%, т. е. 107% — 100% = 7%
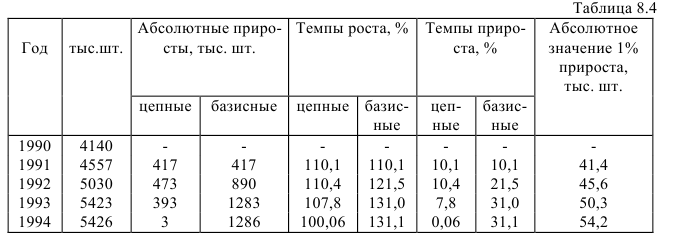
Пример №42.
Среднегодовой темп роста заработной платы рабочих завода за 1990-91 гг. составил 104%, а за 1992-1994 гг. -106%. Определить среднегодовой темп роста заработной платы на заводе за 1990 — 1994 гг.
Решение:
Средняя из средних темпов роста за неодинаковые промежутки времени рассчитывается по формуле средней геометрической взвешенной, причем весами являются сами промежутки времени, следовательно:
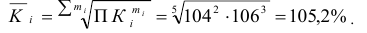
Задачи с решением по всем темам статистики
Статистика — отрасль общественных наук, имеющая целью сбор, упорядочение, анализ и сопоставление фактов, относящихся к самым разнообразным массовым явлениям.
Под предметом статистики понимается количественная сторона массовых общественных явлений в постоянной связи с их содержанием или количественной стороной, а также количественное выражение закономерностей общественного развития в конкретных условиях места и времени. Каждая отрасль имеет свою статистику. Статистика развивается как отдельная наука. Отраслевая статистика дополняет теорию статистики.
Теория статистики является основополагающей дисциплиной и служит фундаментом для применения статистического метода анализа для хозяйственных субъектов. На любом уровне и в любой сфере эффективность использования статистики во многом определяется качеством исходной информации.
Демографическая статистика, показатели численности и состава населения
Для развития национальной экономики в целом и для развития ее основных отраслей необходима статистическая информация о населении. Как статистическая категория население представляет собой совокупность людей, проживающих на данной территории. Оно непрерывно изменяется за счет рождения и смертей, а также миграции.
Информация о населении включает его естественный прирост, естественное движение, его профессиональный состав, возрастной состав, численность трудоспособного населения. Единицей наблюдения или единицей учета в статистике населения может быть как отдельный человек, так и семья, а также домохозяйство и населенный пункт.
Основным источником информации о населении является перепись. Она даёт наиболее подробные сведения о населении страны, включая его экономическую активность, жилищные условия, владение языками и т.д.
Главные принципы переписей населения, которые фактически действуют уже более полутора веков:
- периодичность (переписи проводятся в строгой периодичности, чтобы было возможно выявить тенденции в народонаселении страны и мира);
- сплошной характер (переписи подлежат все лица, независимо от гражданства находящиеся на территории данной страны, а также граждане данной страны, временно проживающие за рубежом. Исключение составляют иностранные дипломаты, сотрудники международных миссий и т.д.);
- индивидуальность регистрации (наблюдению подвергается каждый человек);
- одновременность (синхронность получения информации обо всех единицах наблюдения, что достигается введением критического момента переписи – такого момента времени, по состоянию на который регистрируются сведения).
Достоинством переписей является полнота информации о населении страны, однако такая форма наблюдения весьма затратная (по финансам и по времени), а также сложно организуемая. Поэтому переписи проводятся с 10-летней периодичностью. Сроки переписей в разных странах координирует ООН, чтобы обеспечить сопоставимость статических данных о демографических процессах в мире.
Альтернативой классическим переписям являются выборочные обследования. Они охватывают малую часть жителей, проводятся в более сжатые сроки, но они не могут дать полную картину о численности и составе населения всей страны.
При переписи населения учитываются две основные категории населения:
1) постоянное население (ПН) — лица, для которых данный населённый пункт является местом постоянного проживания, включая временно отсутствующих (ВО);
2) наличное население (НН) — лица, фактически находящиеся на момент переписи в данном населенном пункте, включая временно проживающих (ВП).
Рассмотрим более подробно две дополнительные категории населения – временно отсутствующие и временно проживающие. Временно отсутствующие (ВО) — это лица, имеющие постоянное место жительства в данном населённом пункте, которые на момент учёта отсутствуют. Их отсутствие не должно превышать 6 месяцев.
Временно проживающие (ВП) — это лица, находящиеся на момент учёта в данном населённом пункте, но имеющие постоянное место жительства в другом населённом пункте.
Взаимосвязь данных категорий населения:
ПН = НН – ВП + ВО, (1.1)
НН = ПН – ВО + ВП. (1.2)
В ходе статистического обследования населения определяется численность населения на момент проведения переписи. Сведения о наличном населении очень важны для населенных пунктов, где наблюдается сильное влияние сезонного фактора (курортные районы) или где используется рабочая сила вахтовым методом.
Указанные категории населения не связаны с временной или постоянной регистрацией (с пропиской) граждан РФ по месту пребывания и по месту жительства.
Численность населения – это моментный показатель, так как он рассчитывается на определённую дату. Для того чтобы охарактеризовать демографическую ситуацию за период (год, месяц и т.д.), необходим интервальный показатель – средняя численность населения  .
.
Формула расчёта зависит от исходных данных. Обычно Росстат публикует данные о населении на начало и конец периода. Следовательно, расчёт производится по средней арифметической простой формуле:

где  — численность населения на начало периода;
— численность населения на начало периода; 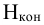 — численность населения на конец периода.
— численность населения на конец периода.
В других случаях необходимо обратиться к рассмотренному ранее материалу темы «Ряды динамики» в курсе «Теория статистики» [1, c. 18-23], где изучаются методы расчёта среднего уровня ряда динамики. Рассмотрим пример расчёта средней численности населения.
Задача с решением №1.1
Данные по трём городам о численности наличного населения (тыс. чел.):
ГОРОД «А»
1 января 2015 г. – 230; 1 января 2016 г. – 242.
ГОРОД «Б»
1 января 2015 г. – 148; 1 февраля – 147; 1 марта – 146; 1 апреля – 142; 1 мая – 145; 1 июня – 150; 1 июля – 155; 1 августа – 162; 1 сентября – 160; 1 октября – 153; 1 ноября – 155; 1 декабря – 154; 1 января 2016 г. – 150.
ГОРОД «В»
1 января 2015 г. – 87; 1 апреля – 93; 1 сентября – 95; 1 октября – 100. Рассчитать среднюю численность населения каждого города в 2015 году.
Решение
ГОРОД «А»
Есть данные на начало и конец периода. Расчёт производится по средней арифметической простой формуле:
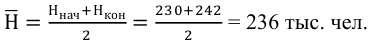
ГОРОД «Б»
Моментный ряд динамики с равными промежутками между датами. Расчёт ведётся по формуле средней хронологической:
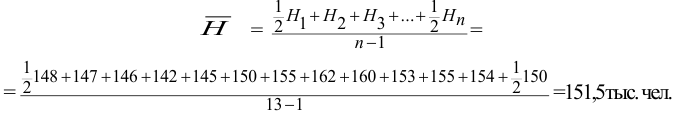
ГОРОД «В»
Моментный ряд динамики с неравными промежутками между датами. Расчёт ведётся по формуле средней арифметической взвешенной:
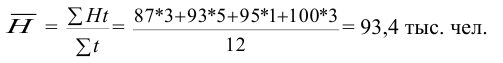
Напомним, что в числителе каждый уровень ряда (численность населения на определённую дату – Н) умножается на число месяцев, в течение которого он не менялся (t). В знаменателе — число месяцев в году.
Показатели движения населения
Движение населения – это изменение численности населения. В статистике различают:
1) естественное движение (рождаемость и смертность);
2) механическое движение (миграция).
Выделяют две группы показателей движения населения.
К первой группе относятся абсолютные показатели (единица измерения — чел.):
— число родившихся (Р), число умерших (У);
— естественный прирост (Δе) = Р – У;
— число прибывших (П), число выбывших (В);
— механический (миграционный) прирост, называемый также сальдо миграции (Δм) = П – В;
— общий прирост (Δобщ) = Δе + Δм.
Кроме того, общий прирост можно также вычислить как разность численности населения на конец и на начало периода. Показатели естественного, механического и общего прироста (Δе, Δм, Δобщ) могут иметь отрицательное значение, что говорит об уменьшении численности населения под влиянием тех или иных причин.
Задача с решением №1.2
Данные о численности населения региона, тыс. чел.:
НА 1 ЯНВАРЯ
Численность наличного населения – 2050,
из них — временно проживающих 113.
Численность временно отсутствующих 125.
В ТЕЧЕНИЕ ГОДА Родилось 27; умерло 36; прибыло на постоянное жительство из других городов 15; выехало на постоянное жительство из числа постоянного населения 11.
Рассчитать:
1) численность постоянного населения на начало и конец года;
2) естественный, механический и общий прирост населения.
Решение
1) Численность постоянного населения на начало года:
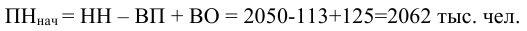
Численность постоянного населения на конец года определяется, исходя из численности на начало года, а также с учётом демографических процессов в течение года:
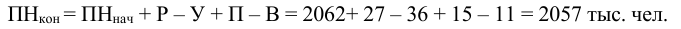
2) Естественный прирост (Δе) = Р – У = 27-36 = — 9 тыс. чел; Механический прирост (Δм) = П – В = 15 – 11 = 4 тыс. чел.;
Общий прирост (Δобщ) = Δе + Δм = -9 + 4 = -5 тыс. чел.
Проверка: 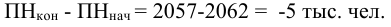
Вторая группа – относительные показатели (демографические коэффициенты). Традиционно большинство из них измеряется в промилле (‰). Эти показатели удобны при сравнении демографических процессов в регионах с разным числом жителей.
Общий коэффициент рождаемости (Кр) характеризует интенсивность деторождения по отношению к населению в целом (всех возрастов) и вычисляется как отношение числа родившихся живыми в течение года (Р) к среднегодовой численности населения 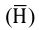 :
:

Коэффициент рождаемости показывает число родившихся в расчёте на 1000 жителей (измеряется в ‰).
Общий коэффициент смертности (Кс) представляет собой отношение общего числа умерших в течение года (У) к среднегодовой численности населения:

Коэффициент смертности показывает число умерших в расчёте на 1000 жителей (измеряется в ‰).
Коэффициент естественного прироста 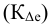 представляет собой разность между коэффициентом рождаемости и коэффициентом смертности и измеряется в ‰:
представляет собой разность между коэффициентом рождаемости и коэффициентом смертности и измеряется в ‰:
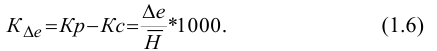
Коэффициент жизненности, или Индекс Покровского (Кж) показывает, сколько родившихся приходится на 1 умершего за период:

Если данный коэффициент более 1, это говорит о положительной демографической тенденции – превышении числа родившихся над числом умерших. Специальный коэффициент рождаемости 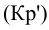 рассчитывается не по отношению ко всему населению, а к численности женщин репродуктивного (фертильного, детородного) возраста (15-49 лет):
рассчитывается не по отношению ко всему населению, а к численности женщин репродуктивного (фертильного, детородного) возраста (15-49 лет):
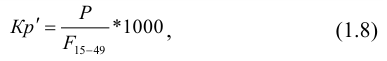
где 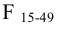 — среднегодовая численность женщин репродуктивного возраста. Этот показатель также измеряется в ‰.
— среднегодовая численность женщин репродуктивного возраста. Этот показатель также измеряется в ‰.
Коэффициент прибытия (Кп) представляет собой соотношение общего числа прибывших в течение года (П) к среднегодовой численности населения:

Коэффициент прибытия показывает число прибывших в расчёте на 1000 жителей (измеряется в ‰).
Коэффициент выбытия (Кв) есть соотношение общего числа выбывших в течение года (В) к среднегодовой численности населения:

Коэффициент выбытия показывает число выбывших в расчёте на 1000 жителей (измеряется в ‰).
Коэффициент механического прироста 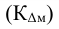 – это разность между коэффициентами прибытия и выбытия. Он измеряется в ‰:
– это разность между коэффициентами прибытия и выбытия. Он измеряется в ‰:
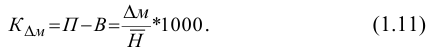
Коэффициент общего прироста 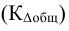 – итоговый показатель, представляющий собой сумму коэффициентов естественного и механического приростов (и измеряется в ‰):
– итоговый показатель, представляющий собой сумму коэффициентов естественного и механического приростов (и измеряется в ‰):
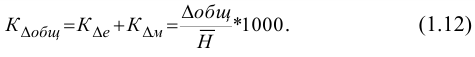
Относительные показатели естественного, механического и общего прироста 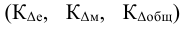 могут иметь отрицательное значение.
могут иметь отрицательное значение.
Задача с решением №1.3
Данные о населении Самарской области (тыс. чел.) за 2014 год: численность на начало года – 3211,2, на конец года – 3212,7; родилось 40,3, умерло 45,9.
Рассчитать относительные показатели естественного движения населения Самарской области в 2014 году.
Решение
Проведём предварительный расчёт, необходимый для вычисления демографических коэффициентов – рассчитаем среднюю численность населения за год. Так как имеются данные на начало и конец года, то применяем среднюю арифметическую простую формулу:
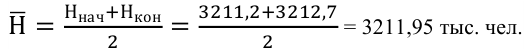
Далее рассчитаем показатели в соответствии с заданием.
Общий коэффициент рождаемости
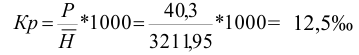 , то есть в расчёте на 1000 жителей в среднем рождалось 12,5 чел.
, то есть в расчёте на 1000 жителей в среднем рождалось 12,5 чел.
Общий коэффициент смертности
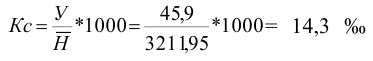 , то есть из каждой 1000 жителей в среднем умирает 14,3 чел.
, то есть из каждой 1000 жителей в среднем умирает 14,3 чел.
Коэффициент естественного прироста
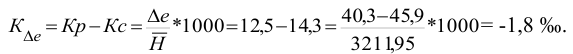
Коэффициент жизненности
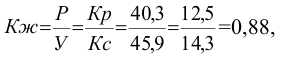 то есть на одного умершего в среднем приходится 0,88 родившихся (на 100 умерших – 88 родившихся, и т.д.).
то есть на одного умершего в среднем приходится 0,88 родившихся (на 100 умерших – 88 родившихся, и т.д.).
В отдельную группу можно выделить показатели, которые дают косвенную или дополнительную характеристику движения населения.
Средний возраст населения 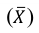 — примерная характеристика возрастной структуры населения. Его величина во многом является следствием таких демографических явлений, как смертность и миграция населения. Средний возраст вычисляется как средняя арифметическая путем деления общего числа человеко–лет (сумма произведений значений возраста на численность населения в этом возрасте) на общую численность населения.
— примерная характеристика возрастной структуры населения. Его величина во многом является следствием таких демографических явлений, как смертность и миграция населения. Средний возраст вычисляется как средняя арифметическая путем деления общего числа человеко–лет (сумма произведений значений возраста на численность населения в этом возрасте) на общую численность населения.
Расчет можно производить также исходя из данных о численности населения по возрастным группам; тогда значением возраста считается середина интервала. Средний возраст населения рассчитывается по формуле:
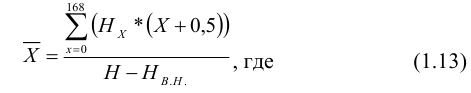
где Н – общая численность населения; 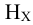 – численность лиц в возрасте «Х» лет;
– численность лиц в возрасте «Х» лет;
Х – число исполнившихся лет в годах, от 0 до 168;
0,5 – const; 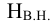 – численность лиц, не указавших возраст.
– численность лиц, не указавших возраст.
Задача с решением №1.4
Численность населения Самарской области в возрасте 25 лет – 50474 чел., в возрасте 26 лет – 49910 чел., 27 лет – 49636 чел. Определить средний возраст населения в возрастной группе 25 – 27 лет.
Решение
1) Определим число человеко-лет в каждом из данных возрастов:
(25+0,5) х 50474 = 1287087,
(26+0,5) х 49910 = 1322615,
(27+0,5) х 49636 = 1364990.
2) Определим общее число человеко-лет в данной возрастной группе:
1287087 + 1322615 + 1364990 = 3974692.
3) Определим численность населения в возрастной группе 25-27 лет:
50474 + 49910 + 49636 = 150020 чел.
4) Определим средний возраст в возрастной группе 25-27 лет — число человеко-лет данной возрастной группы разделим на численность населения в этой же возрастной группе:
3974692 : 150020 = 26,49 лет.
На основе распределений родившихся по очередности рождения можно, прежде всего, определить относительные показатели структуры (долю рождений у матерей разного возраста в общей численности родившихся, долю первых, вторых и более рождений в общей численности рождений) и средние величины (средняя очередность рождения ребенка у матери).
Средняя очерёдность рождения (l) ребенка у матери характеризует интенсивность рождаемости и определяется по формуле:

l – порядковый номер родов (1, 2, 3 и более);
V – число живорожденных у матери с данным порядковым номером родов.
Задача с решением №1.5
Число родившихся у женщин, не состоящих в зарегистрированном браке, по очередности рождения первыми составляет 5701 чел., вторыми – 2026 чел., третьими – 537 чел., четвертыми – 156 чел., пятыми – 63 чел. Определить среднюю очередность рождения.
Решение
1) Найдем сумму произведений числа родившихся на очередность их рождения:
1 * 5701 + 2 * 2026 + 3 * 537 + 4 * 156 +5 * 63 = 12303.
2) Определим число родившихся всех очередностей рождения:
5701 + 2026 + 537 + 156 + 63 = 8483.
3) Определим среднюю очередность рождения – сумму произведений числа родившихся на очередность их рождения разделим на число родившихся всех очередностей рождения:
12303 : 8483 = 1,45.
Возрастные коэффициенты смертности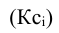 являются частными показателями по отношению к рассмотренному ранее общему коэффициенту смертности. Они характеризуют уровень 16 смертности населения определённой возрастной группы (например, 70-летних жителей или населения в возрасте 50-59 лет).
являются частными показателями по отношению к рассмотренному ранее общему коэффициенту смертности. Они характеризуют уровень 16 смертности населения определённой возрастной группы (например, 70-летних жителей или населения в возрасте 50-59 лет).
Эти коэффициенты рассчитываются как отношение числа умерших в данном возрасте 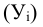 в течение календарного года к среднегодовой численности лиц данного возраста
в течение календарного года к среднегодовой численности лиц данного возраста 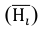 :
:

Младенческая смертность – это смертность детей на первом году жизни (0-12 мес.), важный статистический показатель состояния здравоохранения в стране (регионе). Расчет коэффициента младенческой смертности 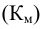 за год проводится по формуле:
за год проводится по формуле:
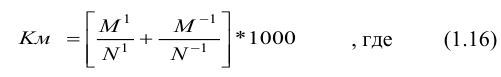
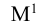 – число умерших в возрасте до 1 года из родившихся в том году, для которого вычисляется коэффициент;
– число умерших в возрасте до 1 года из родившихся в том году, для которого вычисляется коэффициент; 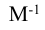 – число умерших в возрасте до 1 года из родившихся в предыдущем году;
– число умерших в возрасте до 1 года из родившихся в предыдущем году; 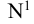 – число родившихся в том году, для которого вычисляется коэффициент;
– число родившихся в том году, для которого вычисляется коэффициент; 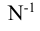 – число родившихся в предыдущем году.
– число родившихся в предыдущем году.
Коэффициент перинатальной смертности рассчитывается как отношение суммы мертворожденных и умерших в возрасте 0-6 дней в данном году к числу родившихся живыми и мертвыми в этом же году, или как сумма коэффициентов мертворождаемости и ранней неонатальной смертности.
Коэффициент мертворождаемости рассчитывается как отношение числа мертворожденных в данном году к числу родившихся живыми и мертвыми в том же году.
Коэффициент ранней неонатальной смертности рассчитывается как отношение числа умерших в возрасте 0-6 дней к числу родившихся живыми и мертвыми в том же году.
Коэффициенты смертности по причинам смерти рассчитываются как отношения чисел умерших от указанных причин смерти к среднегодовой численности населения;
Коэффициент младенческой смертности по основным классам причин смерти рассчитывается для групп причин смерти, (инфекционные и паразитарные болезни, болезни органов дыхания, болезни органов пищеварения, врожденные аномалии, состояния, возникающие в перинатальном периоде, другие причины) как произведение доли умерших от данной причины среди всех умерших в возрасте до 1 года на коэффициент младенческой смертности;
Коэффициенты смертности рассчитывают на 1000 населения, коэффициенты смертности по причинам — на 100000 населения; коэффициенты младенческой смертности рассчитываются на 1000 родившихся, по причинам смерти — на 10000 родившихся.
Для оценки эффективности миграции 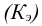 определяется отношение механического прироста
определяется отношение механического прироста 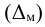 к объёму миграции, то есть к сумме прибывших (П) и выбывших (В):
к объёму миграции, то есть к сумме прибывших (П) и выбывших (В):
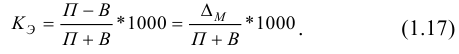
Отрицательное значение говорит о том, сколько выбывших приходится на 1000 общей численности мигрантов; положительное значение — о том, сколько прибывших приходится на 1000 общей численности мигрантов.
Показатели брачности и разводимости
Семейная организация общества статистически может быть исследована показателями брачности и разводимости.
Брачность — это процесс образования супружеских пар населения. В ходе опросов и переписей состояние в браке учитывается не только на основании соотвествующего свидетельства, выданного органом ЗАГС, но и на основании собственного представления о своём брачном статусе (например, люди, совместно проживающие, но не зарегистрировавшие свои отношения официально, так же могут признать себя состоящими в браке).
Разводимость – процесс распада супружеских пар вследствие официального или неофициального расторжения брака. Прекращение брака, вызванное овдовением, не относится к понятию «разводимость», так как в данном случае причиной является смерть одного из супругов.
Брачность и разводимость являются факторами естественного движения населения (прежде всего, рождаемости).
Показатели брачности и разводимости также делятся на два вида:
1) абсолютные (измеряемые в единицах) – число браков (Бр) и число разводов (Рв);
2) относительные (измеряемые в коэффициентах или в промилле). Рассмотрим их более подробно.
Общий коэффициент брачности (Кбр) — отношение числа заключённых браков на определённой территории (Бр) за некоторый период к среднегодовой численности населения 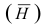 этой территории:
этой территории:

Общий коэффициент брачности показывает число зарегистрированных браков в расчёте на 1000 жителей (измеряется в ‰).
Общий коэффициент разводимости (Кразв) — отношение числа разводов (Рв) за данный период к средней численности населения 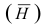 за этот же период:
за этот же период:

Общий коэффициент разводимости показывает число разводов в расчёте на 1000 жителей (измеряется в ‰).
Коэффициент соотношения браков и разводов (Кб/р) определяется по следующей формуле:
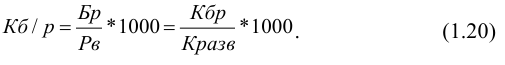
Этот показатель отражает число браков в расчёте на 1000 разводов. Если данный коэффициент более 1000, это говорит о превышении числа браков над числом разводов.
Обратная величина коэффициента соотношения браков и разводов — коэффициент неустойчивости браков (Кр/б). Он может быть определен на основе соотношения числа разводов и браков (или коэффициентов разводимости и брачности) и рассчитывается по формуле:
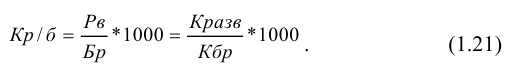
В данном случае определяется число разводов в расчёте на 1000 браков. Рост этого показателя говорит о нарастающей дезорганизации института семьи.
Задача с решением №1.6
Данные по Российской Федерации за 2014 год: среднегодовая численность населения 144 967 100 чел.; зарегистрировано браков 1225985, разводов 693730.
Рассчитать относительные показатели брачности и разводимости в РФ в 2014 году.
Решение
Общий коэффициент брачности
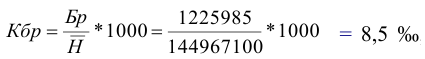 , то есть в расчёте на 1000 жителей в среднем заключалось 8,5 браков.
, то есть в расчёте на 1000 жителей в среднем заключалось 8,5 браков.
Общий коэффициент разводимости
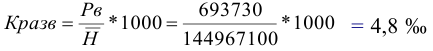 , то есть в расчёте на 1000 жителей в среднем регистрировалось 4,8 разводов.
, то есть в расчёте на 1000 жителей в среднем регистрировалось 4,8 разводов.
Коэффициент соотношения браков и разводов:
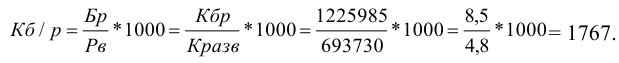
На 1000 разводов в среднем приходится 1767 браков.
Коэффициент неустойчивости браков:
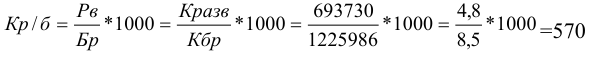
На 1000 браков в среднем приходится 570 разводов.
Коэффициенты брачности и разводимости зависят от возрастной и брачной структуры населения, так как число браков и разводов сопоставляется со всем населением, включая не состоящих в браке людей (в том числе детей). Это облегчает их расчёт и интерпретацию, однако при этом не всегда понятен экономический смысл результатов. Данный недостаток можно устранить расчётом частных коэффициентов (по отношению не к населению в целом, а к его определённой части).
Специальные коэффициенты брачности 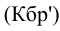 и разводимости
и разводимости 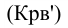 определяются для населения брачного возраста – от 15 лет (Н15+) — независимо от его брачного состояния:
определяются для населения брачного возраста – от 15 лет (Н15+) — независимо от его брачного состояния:
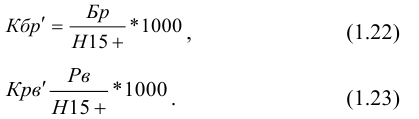
Эти коэффициенты отражают, соответственно, число браков и разводов в расчёте на 1000 жителей в возрасте от 15 лет (измеряются в ‰). Несмотря на то, что Семейный кодекс РФ (ст. 13) устанавливает наступление брачного возраста с 18 лет, тот же нормативный акт позволяет региональным властям разрешать снижение брачного возраста (до 16 лет) при наличии исключительных обстоятельств. Часть субъектов Федерации этим правом уже воспользовалась.
Демографические прогнозы
Для прогнозирования численности населения используются как стандартные статистические и эконометрические методы (например, прогнозирование на основе трендовых моделей), так и специфические, присущие только демографическим расчётам.
Рассмотрим два подобных метода:
1) прогнозирование на основе общего прироста;
2) возрастная передвижка (передвижка возрастов).
Прогнозирование на основе общего прироста
В основе прогнозирования лежит формула:
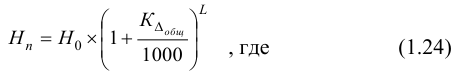
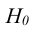 – численность населения на начало прогнозного периода;
– численность населения на начало прогнозного периода; 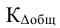 – коэффициент общего прироста населения;
– коэффициент общего прироста населения;
L – срок прогноза.
Эта формула представляет собой модификацию формулы прогнозирования на основе среднего темпа роста (см. тему «Ряды динамики» в курсе «Теория статистики») [1, c. 18-23]. Роль среднего темпа роста выполняет коэффициент общего прироста населения.
Задача с решением №1.7
Данные по региону:
Среднегодовая численность населения в 2015 году составила 2500 тыс. чел.
В последние годы в регионе смертность всего населения составила в среднем 19 ‰, рождаемость 12 ‰, прибытие 10 ‰, выбытие 8 ‰.
Вычислить перспективную численность населения региона в 2017 году.
Решение
Сделаем предварительный расчёт коэффициента общего прироста:
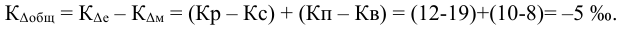
Нам известны: численность населения на начало прогнозного периода (2500 тыс. чел.), срок прогноза (2 года = 2017 – 2015). Рассчитаем перспективную численность населения региона в 2017 году:
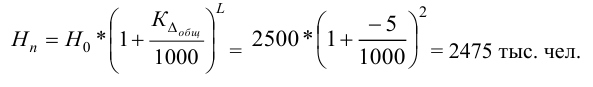
Возрастная передвижка
Метод основан на данных о вероятности людей возраста i дожить до возраста i+1. Для реализации метода требуется следующая информация по каждой возрастной группе населения:
1) возрастные коэффициенты смертности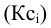 ;
;
2) возрастные коэффициент дожития 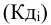 .
.
Эти показатели взаимодополняют друг друга до 1, то есть до 1000 ‰.
Задача с решением №1.7.1
Смертность 70-летних жителей региона составляет 35 ‰ (то есть вероятность умереть равна 0,035). Значит, коэффициент дожития будет равен 1000 ‰ — 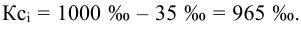 Таким образом, из каждой тысячи 70-летних жителей до возраста 71 год в среднем доживают 965 чел. (вероятность дожития составляет 0,965).
Таким образом, из каждой тысячи 70-летних жителей до возраста 71 год в среднем доживают 965 чел. (вероятность дожития составляет 0,965).
Общая формула для передвижки возрастов: 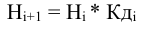 , где:
, где: 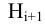 – численность населения в следующем году (в возрасте i+1).
– численность населения в следующем году (в возрасте i+1).
Данные о возрастной смертности содержатся в таблицах смертности, формируемых на основе многолетних наблюдений за уровнем смертности каждой возрастной группы на конкретной территории.
При прогнозировании населения важно знать, что коэффициенты смертности различаются не только по территориям и возрастам, но и по полу (у мужчин они значительно выше, чем у женщин).
Таблицы смертности – это таблица, содержащая информацию о смертности в определённой совокупности населения, точнее, порядок вымирания поколений людей при тех или иных заданных вероятностях умереть.
Для построения таблиц смертности необходимы сведения о численности возрастно-половых групп населения, количестве умерших по возрастным группам.
Задача с решением №1.8
Данные по городу: На 1 января 2016 года проживало 1700 чел. в возрасте 44 года. Известны данные о смертности:
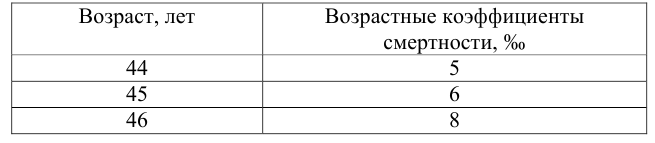
Определить вероятную численность 47-летних жителей на 1 января 2019 года.
Решение
Сделаем «передвижку» на один год вперёд, когда 44-летним жителям исполнится 45 лет. Для удобства и корректности расчётов коэффициенты выразим не в промилле, разделив их на 1000.
Рассчитаем численность 45-летних жителей на 1 января 2017 года:
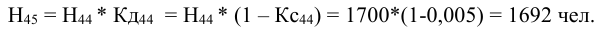
Сделаем ещё одну «передвижку» на один год вперёд, когда 45- летним жителям исполнится 46 лет.
Рассчитаем численность 46-летних жителей на 1 января 2018 года:
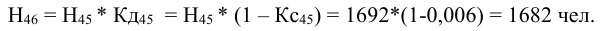
В итоге делаем ещё одну «передвижку» на один год вперёд, когда 46-летним жителям исполнится 47 лет.
Рассчитаем численность 47-летних жителей на 1 января 2018 года:
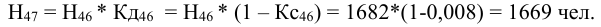
Все расчёты можно свести к следующей формуле:
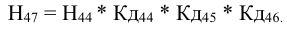
Информация о вероятности дожития имеет важное применение в таких сферах деятельности, как: пенсионная система, страхование жизни, оценка демографической ситуации и т.д.
Статистика рынка труда, показатели численности и состава трудовых ресурсов
Термин «трудовые ресурсы» появился в 1920-х годах в работах академика С.Г. Струмилина. Наибольшее распространение он получил именно в отечественной статистике.
Трудовые ресурсы — это часть населения, которая по возрасту и состоянию здоровья способна производить материальные и духовные блага, а также оказывать услуги [4, c. 101-102]. Трудовые ресурсы включают как занятых, так и незанятых, но способных работать. Таким образом, трудовые ресурсы состоят из населения, занятого фактически, а также потенциально занятого.
Основой для расчёта трудовых ресурсов является группировка населения по возрасту. Выделяют 3 возрастных группы населения.
1) Трудоспособный (рабочий) возраст – это женщины 16-54 лет (включительно), мужчины 16-59 лет (включительно).
2) Моложе трудоспособного возраста – лица обоего пола 0 – 15 лет.
3) Старше трудоспособного возраста (лица пенсионного возраста) — это женщины 55 лет и старше, мужчины 60 лет и старше.
Примечания:
— в зависимости от законодательно изменённых возрастных границ выхода на пенсию могут измениться и границы трудоспособного возраста;
— нижняя граница трудоспособного возраста (16 лет) не связана с законодательно разрешённым в РФ возрастом, когда подростки могут вступать в трудовые отношения (только по достижению 14 лет).
Среди лиц трудоспособного возраста по признаку состояния здоровья различают две группы населения – трудоспособные и нетрудоспособные.
В группу нетрудоспособных включаются: неработающие инвалиды I и II групп рабочего возраста, неработающие пенсионеры трудоспособного возраста, получающие пенсию на льготных условиях.
Для того чтобы рассчитать численность трудовых ресурсов, можно взять за основу общую численность населения трудоспособного возраста, к которой прибавляется число работающих пенсионеров и работающих подростков (моложе 16 лет) и исключается количество неработающих инвалидов I и II групп (рабочего возраста), а также численность пенсионеров трудоспособного возраста, получающих пенсию на льготных условиях.
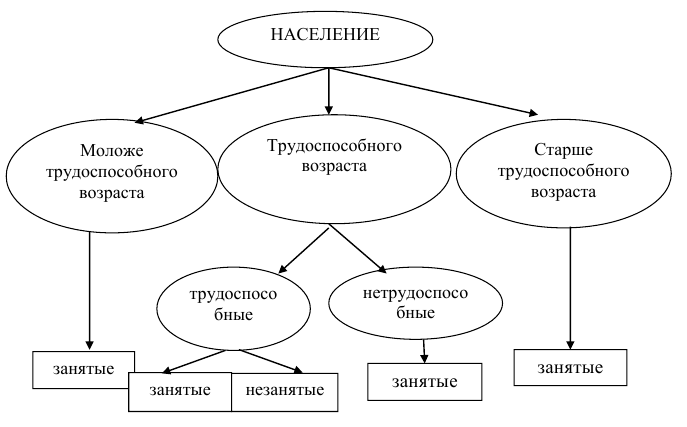
Рис. 2.1. Состав трудовых ресурсов
Задача с решением №2.1
Имеются следующие данные по региону на конец года, тыс. чел.:
Трудоспособные наёмные работники рабочего возраста 2040;
Трудоспособные лица рабочего возраста, занятые собственным делом 175;
Занятые инвалиды рабочего возраста 4;
Незанятые инвалиды рабочего возраста 36;
Занятые льготные пенсионеры рабочего возраста 17;
Незанятые льготные пенсионеры рабочего возраста 98;
Незанятые трудоспособные лица рабочего возраста 604;
Занятые подростки и пенсионеры 233.
Рассчитать (на конец года):
1. численность лиц рабочего возраста;
2. численность трудоспособных лиц рабочего возраста;
3. численность трудовых ресурсов.
Решение
1) Численность лиц рабочего возраста =
2040+175+4+36+17+98+604=2974 тыс. чел.
2) Численность трудоспособных лиц рабочего возраста =
2040+175+604=2819 тыс. чел.
3) Численность трудовых ресурсов =
2040+175+4+17+604+233=2840 тыс. чел.
Средняя численность трудовых ресурсов 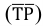 рассчитывается теми же методами, что и средняя численность населения (см. тему 1). Так, по данным на начало и конец года определяется по формуле средней арифметической простой:
рассчитывается теми же методами, что и средняя численность населения (см. тему 1). Так, по данным на начало и конец года определяется по формуле средней арифметической простой:
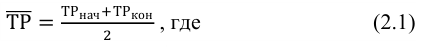
 — численность трудовых ресурсов на начало периода;
— численность трудовых ресурсов на начало периода;  — численность трудовых ресурсов на конец периода;
— численность трудовых ресурсов на конец периода;
по данным на определённые даты через равные промежутки времени между ними по формуле средней хронологической простой:
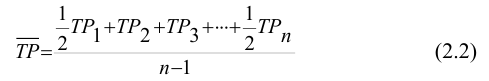
n – число уровней ряда динамики (дат).
Соотношение между отельными возрастными группами в структуре трудовых ресурсов дают показатели демографической нагрузки. Они характеризуют соотношение лиц того или иного возраста и лиц трудоспособного возраста.
Коэффициент пенсионной нагрузки (нагрузки пожилыми людьми)  рассчитывается как отношение числа лиц старше трудоспособного возраста
рассчитывается как отношение числа лиц старше трудоспособного возраста 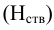 к численности лиц трудоспособного возраста
к численности лиц трудоспособного возраста 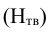 :
:
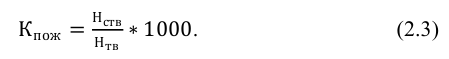
Он показывает, сколько лиц пенсионного возраста приходится в среднем на 1000 лиц трудоспособного возраста.
Коэффициент замещения трудовых ресурсов (нагрузки детьми) 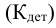 рассчитывается как отношение числа лиц моложе трудоспособного возраста
рассчитывается как отношение числа лиц моложе трудоспособного возраста 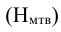 к численности лиц трудоспособного возраста
к численности лиц трудоспособного возраста 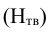 :
:

Он показывает, сколько лиц в возрасте моложе 16 лет приходится в среднем на 1000 лиц трудоспособного возраста.
Коэффициент общей (демографической) нагрузки 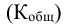 можно рассчитать суммированием двух предыдущих коэффициентов или соотношением числа лиц нетрудоспособных возрастов
можно рассчитать суммированием двух предыдущих коэффициентов или соотношением числа лиц нетрудоспособных возрастов 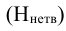 к численности лиц трудоспособного возраста:
к численности лиц трудоспособного возраста:
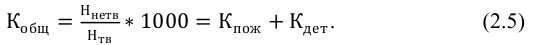
Результат показывает, сколько лиц нетрудоспособных возрастов приходится в среднем на 1000 лиц трудоспособного возраста.
Задача с решением №2.2
Данные о распределении населения Российской Федерации (на начало 2015 года), тыс. чел.:

Исчислить:
1) удельный вес отдельных возрастных групп в общей численности населения;
2) коэффициенты нагрузки детьми, пожилыми людьми;
3) общий коэффициент демографической нагрузки.
Решение
Сделаем предварительный расчёт – вычислим общую численность населения (Н) страны на начало 2015 года:
25689+85415+35163=146267 тыс. чел.
1) Удельный вес (доля) отдельных возрастных групп в общей численности населения – это относительная величина структуры (см. тему «Относительные величины» в курсе «Теории статистики»). Она представляет собой соотношение части и целого. При этом вся совокупность принимается равной 100 %.
Удельный вес населения моложе трудоспособного возраста = 17,6 %
Удельный вес населения трудоспособного возраста = 58,4 %
Удельный вес населения старше трудоспособного возраста = 24,0 %
Проверить правильность расчётов можно суммированием всех трёх полученных чисел. Сумма должна составить 100 %:
17,6 + 58,4 + 24 = 100 %.
2) Коэффициент нагрузки детьми = 301 ‰
На 1000 чел. трудоспособного возраста в среднем приходится 301 чел. моложе трудоспособного возраста.
Коэффициент нагрузки пожилыми людьми = 412 ‰
На 1000 чел. трудоспособного возраста в среднем приходится 412 чел. старше трудоспособного возраста.
3) Коэффициент общей нагрузки = 713 ‰
На 1000 чел. трудоспособного возраста в среднем приходится 713 чел. нетрудоспособных возрастов.
Показатели движения трудовых ресурсов
Движение трудовых ресурсов – это изменение численности трудовых ресурсов. По аналогии с демографической статистикой, различают 2 формы движения:
1) естественное (не связанное с процессом миграции);
2) механическое (миграция).
Выделяют две группы показателей движения трудовых ресурсов.
К первой группе относятся абсолютные показатели (единица измерения — чел.).
— естественное пополнение (Пе) – это пополнение численности трудовых ресурсов по следующим причинам: вступление в 30 трудоспособный возраст подростков; привлечение к занятости пенсионеров, инвалидов, а также лиц моложе 16 лет;
— естественное выбытие (Ве) – это выход из числа трудовых ресурсов по следующим причинам: смертность и переход на инвалидность трудовых ресурсов, выход на пенсию; прекращение занятости лиц моложе 16 лет.
— естественный прирост (Δе) = Пе – Ве;
— механическое пополнение (Пм) – это пополнение численности трудовых ресурсов по причине миграции (приезда из других регионов);
— механическое выбытие (Вм) – это выбытие из числа трудовых ресурсов по причине миграции (отъезда в другие регионы);
— механический (миграционный) прирост (Δм) = Пм – Вм;
— общий прирост (Δобщ) = Δе + Δм.
Кроме того, общий прирост можно также вычислить как разность численности трудовых ресурсов на конец и на начало периода.
Показатели естественного, механического и общего прироста (Δе, Δм, Δобщ) могут иметь отрицательное значение, что говорит об уменьшении численности трудовых ресурсов под влиянием тех или иных причин.
Для того чтобы рассчитать интенсивность изменения численности трудовых ресурсов, используются относительные показатели (коэффициенты), измеряемые в промилле (‰).
Коэффициент естественного пополнения 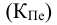 трудовых ресурсов рассчитывается как отношение числа вступивших в трудоспособный возраст и привлеченных к общественному труду пенсионеров и подростков к среднему количеству трудовых ресурсов за определённый период:
трудовых ресурсов рассчитывается как отношение числа вступивших в трудоспособный возраст и привлеченных к общественному труду пенсионеров и подростков к среднему количеству трудовых ресурсов за определённый период:

Коэффициент естественного выбытия 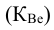 рассчитывается как отношение количества выбывших из состава трудовых ресурсов (по причине смертности, инвалидности, выхода на пенсию) к средней величине трудовых ресурсов:
рассчитывается как отношение количества выбывших из состава трудовых ресурсов (по причине смертности, инвалидности, выхода на пенсию) к средней величине трудовых ресурсов:

Коэффициент естественного прироста  рассчитывается как разность между коэффициентами пополнения и выбытия трудовых ресурсов:
рассчитывается как разность между коэффициентами пополнения и выбытия трудовых ресурсов:
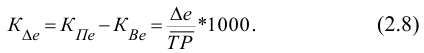
Коэффициент механического пополнения 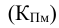 показывает число прибывших трудовых ресурсов в расчёте на 1000 человек трудовых ресурсов:
показывает число прибывших трудовых ресурсов в расчёте на 1000 человек трудовых ресурсов:
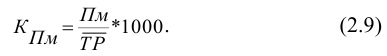
Коэффициент механического выбытия 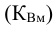 рассчитывается как отношение количества выбывших из состава трудовых ресурсов по причине миграции к средней величине трудовых ресурсов:
рассчитывается как отношение количества выбывших из состава трудовых ресурсов по причине миграции к средней величине трудовых ресурсов:

Коэффициент механического прироста 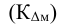 трудовых ресурсов рассчитывается как отношение миграционного прироста к средней величине трудовых ресурсов:
трудовых ресурсов рассчитывается как отношение миграционного прироста к средней величине трудовых ресурсов:
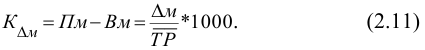
Коэффициент общего прироста 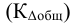 трудовых ресурсов рассчитывается как сумма коэффициентов естественного и механического прироста:
трудовых ресурсов рассчитывается как сумма коэффициентов естественного и механического прироста:
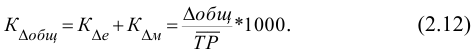
Относительные показатели естественного, механического и общего прироста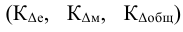 могут иметь отрицательное значение.
могут иметь отрицательное значение.
Задача с решением №2.3
Данные по региону, тыс. чел.:

Рассчитать:
1. численность трудовых ресурсов на начало и конец года;
2. среднегодовую численность трудовых ресурсов;
3. абсолютные показатели движения трудовых ресурсов;
4. относительные показатели движения трудовых ресурсов.
Решение
1) численность трудовых ресурсов на начало года (ТРнач):
ТРнач = 2800-480+215 = 2535 тыс. чел.
численность трудовых ресурсов на начало года (ТРкон):
ТРкон = 2535+198-252+20-16+67-47=2505 тыс. чел.
2) среднегодовая численность трудовых ресурсов 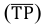
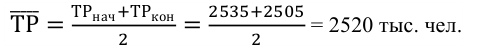
3) абсолютные показатели движения трудовых ресурсов
Естественное пополнение:
Пе = 198+20 = 218 тыс. чел.
Естественное выбытие:
Ве = 252 +16 = 268 тыс. чел.
Естественный прирост:
Δе = Пе — Ве = 218-268 = — 50 тыс. чел;
Механическое пополнение:
Пм = 67 тыс. чел.
Механическое выбытие:
Вм = 47 тыс. чел.
Механический прирост:
Δм = Пм – Вм = 67 – 47 = 20 тыс. чел.;
Общий прирост:
Δобщ = Δе + Δм = -50 + 20 = -30 тыс. чел.
Проверка: 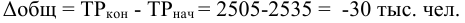
4) относительные показатели движения трудовых ресурсов
Коэффициент естественного пополнения:
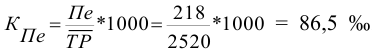 ,то есть на каждую 1000 человек трудовых ресурсов естественное пополнение составляет в среднем 86,5 чел.
,то есть на каждую 1000 человек трудовых ресурсов естественное пополнение составляет в среднем 86,5 чел.
Коэффициент естественного выбытия:
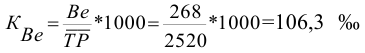 , то есть на каждую 1000 человек трудовых ресурсов естественное выбытие составляет в среднем 106,3 чел.
, то есть на каждую 1000 человек трудовых ресурсов естественное выбытие составляет в среднем 106,3 чел.
Коэффициент естественного прироста:
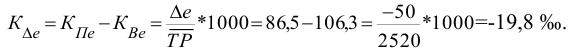
Коэффициент механического пополнения:
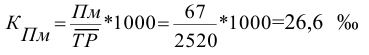 , то есть на каждую 1000 человек трудовых ресурсов механическое пополнение составляет в среднем 26,6 чел.
, то есть на каждую 1000 человек трудовых ресурсов механическое пополнение составляет в среднем 26,6 чел.
Коэффициент механического выбытия:
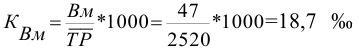 , то есть на каждую 1000 человек трудовых ресурсов механическое выбытие составляет в среднем 18,7 чел.
, то есть на каждую 1000 человек трудовых ресурсов механическое выбытие составляет в среднем 18,7 чел.
Коэффициент механического прироста:
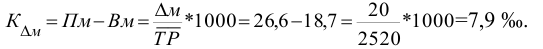
Коэффициент общего прироста:
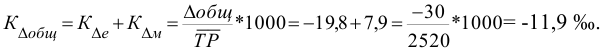
Показатели экономической активности населения
При изучении экономической активности населения статистика использует следующие источники информации:
— отчётность предприятий (о численности занятых);
— отчётность служб занятости (о численности зарегистрированных безработных);
— переписи населения;
— периодические выборочные обследования.
Отечественная статистическая методология исследования рынка труда во многом базируется на рекомендациях МОТ (Международной организации труда).
При исследовании рынка труда выделяют четыре основные категории населения: «занятые», «безработные», «экономически активное население» (ЭАН), «экономически неактивное население» (ЭНН). При этом объектом статистического наблюдения является население только в возрасте 15 – 72 лет.
С 2017 года Росстат заменяет две последние категории новыми, принятыми в международных стандартах – «рабочая сила» и «лица, не входящие в состав рабочей силы», а также планирует отменить верхнюю границу обследуемого возраста.
Занятые – это лица, которые в рассматриваемый период:
1) выполняли работу по найму за вознаграждение на условиях полного или неполного рабочего времени* (при этом не важно, присутствовал ли человек фактически на рабочем месте или находился, например, в отпуске); (*Неполное рабочее время – как минимум, один час в неделю)
2) самостоятельно обеспечивали себя работой (с использованием или без использования наёмной рабочей силы);
3) выполняли работу без оплаты на семейном предприятии.
Однако отметим, что в нашей стране не существует такой юридической формы предпринимательства, как «семейный бизнес».
К занятым также относятся:
— служители религиозных культов (духовенство),
— военнослужащие (в том числе срочной службы),
— лица, которые временно отсутствовали на работе (из-за болезни, ухода за больными, ежегодного отпуска и т.д.),
— лица, занятые в домашнем хозяйстве производством товаров и услуг для продажи или обмена.
К занятым не относятся учащиеся очных отделений трудоспособного возраста (школьники, студенты). Если данные категории населения вышли на работу, то они включаются в состав занятых.
В статистике выделяют несколько группировок занятого населения. Во-первых, оно группируется по основным социальнодемографическим характеристикам (по полу, возрасту, уровню образования и т.д.); во-вторых, по статусу занятости.
Различают два статуса занятости: наёмные работники и лица, работающие не по найму.
К наёмным работникам относятся:
а) лица, заключившие договор, контракт или устное соглашение с работодателем об условиях трудовой деятельности;
б) лица, избранные или назначенные на оплачиваемую должность.
Лица, работающие не по найму, включают следующие категории:
а) самозанятые – лица, работающие на индивидуальной основе (не использующие наёмный труд или использующие его нерегулярно);
б) работодатели (занятые на собственном предприятии и использующие труд наёмных работников на постоянной основе);
в) члены производственных кооперативов;
г) неоплачиваемые работники семейных предприятий.
В развитых странах с рыночной экономикой наёмные работники составляют в среднем более 90% всей рабочей силы.
Согласно методологии МОТ, к безработным относятся лица 15- 72 лет, которые в рассматриваемый период соответствовали трём критериям (одновременно):
а) не имели работы (доходного занятия);
б) занимались поиском работы (обращались в службу занятости, использовали или помещали объявления в печати, непосредственно обращались к работодателю, использовали личные связи, предпринимали шаги к организации собственного дела);
в) были готовы приступить к работе в настоящий момент (если появится возможность трудоустройства).
Обратим ваше внимание на то, что признание человека безработным может произойти и в случае, если он не обращался в службу занятости (государственную или коммерческую), а искал работу своими силами.
Учащиеся, студенты, пенсионеры и инвалиды учитываются в качестве безработных, если они занимались поиском работы и были готовы приступить к ней.
Таким образом, понятие «безработный» не тождественно понятию «незанятый». Первая категория является частью второй, так как не каждый незанятый человек ищет работу или готов к ней приступить.
Согласно Федеральному Закону (ФЗ) «О занятости населения РФ» (ст. 3) [2] безработными признаются трудоспособные граждане старше 15 лет, которые не имеют работы и заработка, зарегистрированы в органах службы занятости в целях поиска подходящей работы, ищут работу и готовы приступить к ней.
В отличие от методологии МОТ, Федеральный Закон позволяет признать человека безработным только после регистрации в службе занятости («зарегистрированная безработица»).
Экономически активное население (ЭАН) (Рабочая сила) – это лица, обеспечивающие предложение рабочей силы. В количественном отношении ЭАН равно сумме занятых и безработных. В ЭАН входит население, которое ведёт себя активно на рынке труда.
С 2017 года в практику статистики вводится показатель «потенциальная рабочая сила», который включает лиц, частично удовлетворяющих критериям безработных, но формально не относящимся к ним: 1) искали работу, но не были готовы приступить к ней; 2) не искали работу, однако хотели работать и были готовы приступить к работе.
Экономически неактивное население (ЭНН) (Лица, не входящие в состав рабочей силы) – это часть трудоспособного населения и лиц старших возрастов, которые в рассматриваемый период не работали по найму, не имели занятия, приносящего доход, и не были заняты поиском работы:
— учащиеся и студенты очной формы обучения;
— лица, занятые ведением домашнего хозяйства, уходом за детьми, больными и т.д.;
— лица, у которых нет необходимости работать;
— отчаявшиеся найти работу и т.д.
Рынок труда характеризуется следующими статистическими показателями.
Уровень занятости (Уз) – соотношение численности занятого населения (Зан) с той или иной численностью населения. Он может быть вычислен как на определённую дату, так и в среднем за период. Уровень занятости рассчитывается в процентах (%) и определяется в нескольких вариантах:
а) в расчёте на общую численность трудовых ресурсов:

б) в расчёте на трудоспособное население 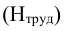 :
:

в) в расчёте на экономически активное население:

Уровень безработицы (Уб) показывает процент безработного населения в общей численности экономически активного населения. В то же время надо различать уровень безработицы по методологии МОТ и по методологии ФЗ «О занятости населения в Российской Федерации»:
А) по методологии МОТ:

Б) по методологии ФЗ «О занятости населения в Российской Федерации» рассчитывается уровень зарегистрированной безработицы (Уб’):

Б’ — численность безработных, зарегистрированных в государственных учреждениях службы занятости.
По своей величине уровень безработицы (МОТ) больше, чем уровень зарегистрированной безработицы, так как числитель его формулы больше числителя в формуле Уб’.
Уровень занятости (в расчёте на экономически активное население) и уровень безработицы взаимодополняют друг друга до 100 %.
Уровень экономической активности населения (Уэан) – это удельный вес (доля) численности экономически активного населения в общей численности населения (Н):

Он также может быть вычислен как на определённую дату, так и в среднем за период.
Коэффициент напряжённости на рынке труда 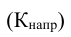 характеризует численность незанятых граждан, зарегистрированных в государственных учреждениях службы занятости населения, в расчёте на одну заявленную вакансию:
характеризует численность незанятых граждан, зарегистрированных в государственных учреждениях службы занятости населения, в расчёте на одну заявленную вакансию:

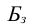 – численность безработных, обратившихся в службу занятости;
– численность безработных, обратившихся в службу занятости;
В – число вакантных должностей и свободных рабочих мест.
Этот коэффициент показывает, какое число не занятых трудовой деятельностью лиц, состоящих на учёте в службе занятости, приходится на одно свободное рабочее место.
Продолжительность безработицы, или Среднее время поиска работы безработными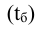 характеризует длительность поиска работы лицами, имеющими статус безработного на конец рассматриваемого периода, а также теми безработными, которые были в этом периоде трудоустроены. Это отрезок времени (измеряемый в месяцах) от момента начала поиска работы до момента трудоустройства. Если безработный ещё не нашёл работу, то срок поиска рассчитывается до начала данного периода.
характеризует длительность поиска работы лицами, имеющими статус безработного на конец рассматриваемого периода, а также теми безработными, которые были в этом периоде трудоустроены. Это отрезок времени (измеряемый в месяцах) от момента начала поиска работы до момента трудоустройства. Если безработный ещё не нашёл работу, то срок поиска рассчитывается до начала данного периода.
Безработица продолжительностью 6 – 12 месяцев называется застойной, а 12 и более месяцев – хронической. Соответственно, рассчитывается показатель «Удельный вес безработных, ищущих работу 12 месяцев и более» (соотношение хронических безработных и всей численности безработных).
Задача с решением №2.4
Результаты выборочного обследования о численности населения региона в среднем за период, тыс. чел.:
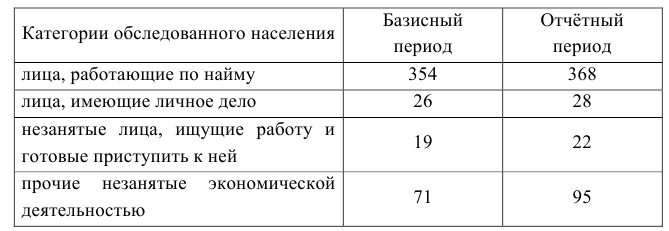
Вычислить:
1) в каждом периоде – численность занятых, безработных, экономически активного населения, уровень занятости (в расчёте на экономически активное население) и безработицы (по методологии МОТ);
2) абсолютные приросты и темпы прироста численности экономически активного населения и безработных.
Решение
1) БАЗИСНЫЙ ГОД
Численность занятых:
Зан = 354+26= 380 тыс. чел.;
Численность безработных: Б = 19 тыс. чел. (так как только эти лица соответствовали всем критериям безработного по методологии МОТ);
Численность экономически активного населения:
ЭАН = Зан + Б = 380+19 = 399 тыс. чел.
Уровень занятости (Уз):
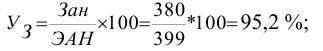
Уровень безработицы (Уб) по методологии МОТ:
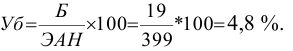
ОТЧЁТНЫЙ ГОД
Численность занятых:
Зан = 268+28= 396 тыс.чел.;
Численность безработных:
41 Б = 22тыс. чел.;
Численность экономически активного населения:
ЭАН = Зан + Б = 396+22 = 418 тыс.чел.
Уровень занятости (Уз):
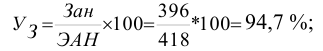
Уровень безработицы (Уб) по методологии МОТ:
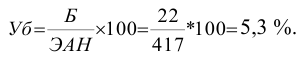
2) Абсолютные приросты и темпы прироста экономически активного населения и безработных (см. тему «Ряды динамики» в курсе «Теории статистики»).
Абсолютный прирост (Δ) — это разность уровней ряда динамики (в абсолютных единицах измерения). Темп прироста (Тп) показывает процентное изменение уровней ряда динамики. Он представляет собой величину, полученную соотношением абсолютного прироста и уровня базисного периода 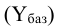 .
.
Абсолютный прирост численности экономически активного населения:
Δ = 417 – 399 = 18 тыс. чел.
Темп прироста численности экономически активного населения:
4,5 %.
Вывод: численность ЭАН в отчётном периоде возросла на 18 тыс. чел., то есть на 4,5 %.
Абсолютный прирост численности безработных:
Δ = 22 – 19 = 3 тыс. чел.
Темп прироста численности безработных:
15,8 %.
Вывод: численность безработных в отчётном периоде возросла на 3 тыс. чел., то есть на 15,8 %.
Статистика национального богатства, понятие и состав национального богатства
Национальное богатство (НБ) — это совокупность накопленных материальных и нематериальных активов (благ), которыми располагает общество в данный момент времени, создающих необходимые условия производства товаров, оказания услуг и обеспечения жизни людей.
Экономические активы — это находящиеся в собственности объекты, владельцы и пользователи которых могут извлекать экономические выгоды в результате их хранения или использования. Все экономические активы, включаемые в состав НБ, по рекомендации ООН подразделяются на две основные группы: нефинансовые и финансовые активы.
В свою очередь, в группе нефинансовых активов выделяют произведённые и непроизведённые активы, материальные и нематериальные активы.
Произведённые активы созданы в результате производственной деятельности; непроизведённые активы не являются результатом производственной деятельности.
Материальные активы имеют натурально-вещественную форму, соответственно, нематериальные активы её не имеют.
Финансовые активы представляют собой средства осуществления финансовых расчетов между институциональными единицами, связанными финансовыми обязательствами и финансовыми требованиями.
По источникам происхождения в составе национального богатства выделяют две основные части: природные ресурсы и национальное имущество.
Природные ресурсы (природные богатства) составляют первую важнейшую группу ресурсов, куда включаются учтенные и вовлеченные в экономический оборот как невозобновляемые природные ресурсы (земля, полезные ископаемые), так и возобновляемые природные ресурсы (вода, воздух, растительные и животные ресурсы).
Вторую важнейшую группу ресурсов составляет национальное имущество — совокупность накопленных материальных благ, созданных в ходе трудовой деятельности людей. Сюда относят материальные, нематериальные, финансовые, нефинансовые активы регионов, отраслей, секторов экономики, а также юридических и физических лиц. В отдельную группу выделяют потребительские товары длительного пользования, прямые иностранные инвестиции и золотой запас. В состав национального имущества включается и личное имущество граждан.
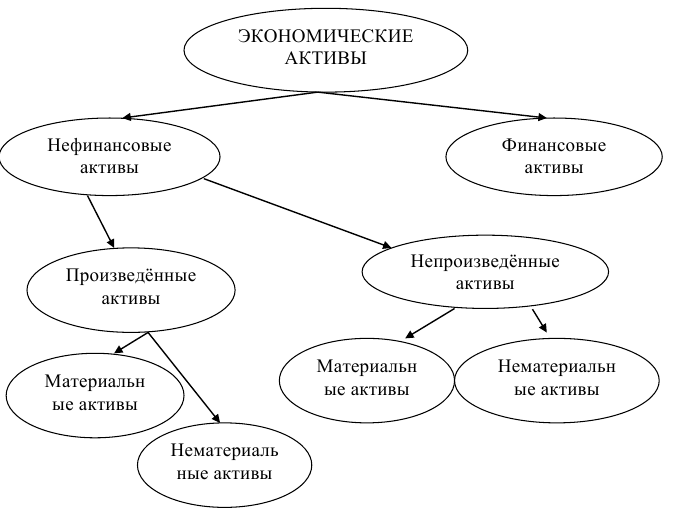
Рис. 3.1. Состав национального богатства
Рассмотрим отдельные элементы национального богатства.
Материальные произведённые нефинансовые активы включают в себя:
— основные фонды (более подробно будут рассмотрены в п. 3.2);
— запасы материальных оборотных средств (более подробно будут рассмотрены в п. 3.3);
— ценности (дорогостоящие предметы длительного пользования, которые приобретаются в расчёте на увеличение их реальной стоимости
— драгоценные металлы и камни, произведения искусства, антиквариат и т.д.).
Нематериальные произведённые нефинансовые активы включают в себя:
— компьютерное программное обеспечение;
— затраты на геологоразведочные работы;
— оригинальные литературные и художественные произведения (в том числе концерты, спектакли) и т. д.
Материальные непроизведённые нефинансовые активы включают в себя природные ресурсы (невыращиваемые биоресурсы). Они делятся на следующие группы: земельные ресурсы; водные ресурсы; лесные ресурсы; запасы полезных ископаемых и т.д. Важно понимать, что не все богатства природы можно отнести к национальному богатству. Как уже отмечалось выше, критерием является наличие права собственности. Исходя из этого, в состав НБ нельзя включить атмосферный воздух, нейтральные воды Мирового океана, естественные космические объекты (планеты и т.д.).
Нематериальные непроизведённые нефинансовые активы включают в себя:
— торговые марки и товарные знаки;
— авторские права;
— патенты;
— гудвилл (деловая репутация) и т.д.
Финансовые активы включают в себя:
— наличные деньги;
— депозиты (денежные средства, размещенные в банках на хранение);
— ценные бумаги (кроме акций);
— акции и прочие виды акционерного капитала;
— займы;
— страховые технические резервы (формируются страховыми организациями в ходе проведения страховых операций как обязательные накопительные суммы, выполняющие функцию финансовых гарантий);
— дебиторская и кредиторская задолженности (торговые кредиты, авансы в счет оплаты незавершенных работ и др.);
— специальные права заимствования (международные резервные и платежные средства, которые используются для безналичных международных расчетов как форма мировых денег);
— монетарное золото (золотой запас страны, хранящийся в государственных денежно-кредитных учреждениях).
Объём НБ предполагает его стоимостную оценку, однако полную стоимость НБ страны крайне сложно достоверно рассчитать, так как по многим элементам НБ нет проработанной методики их денежной оценки (например, по оценке стоимости водных и лесных ресурсов, гудвиллу и т.д.).
Статистика основных фондов
Основные фонды (основные средства) – это активы, которые длительное время (более одного года) многократно используются в экономике в неизменной натурально-вещественной форме, постепенно перенося свою стоимость на вновь создаваемые продукты или услуги в виде амортизационных отчислений [5].
Рассмотрим классификации основных фондов.
1) По видам (здания, сооружения, машины и оборудование, транспортные средства, производственный и хозяйственный инвентарь, многолетние насаждения, продуктивный и рабочий скот, передаточные устройства и т.д.);
2) По назначению:
— производственные (обеспечивающие производственный процесс);
— непроизводственные (объекты культурно-бытового назначения).
3) По степени участия в производственном процессе (классифицируются только основные производственные фонды):
— активные (непосредственное участие в производстве – станки, инструмент);
— пассивные (косвенное участие в производстве – здания, сооружения).
4) Другие классификации (по степени износа, по формам собственности, по возрасту и т.д.).
Так как основные фонды функционируют длительное время, их стоимость подвержена изменению. Исходя из этого, различают несколько видов их стоимостной оценки.
Полная первоначальная стоимость (ПС) – это стоимость основных фондов в фактических ценах на момент ввода их в эксплуатацию, включая не только цену конкретного объекта, но и затраты на его доставку и установку.
Первоначальная стоимость за вычетом износа (остаточная первоначальная стоимость, ОС) — это стоимость основных фондов за вычетом накопленного за время их функционирования износа (И) в виде амортизационных отчислений:
ОС = ПС – И. (3.1)
Полная восстановительная стоимость (ПВС) — стоимость их воспроизводства в современных ценовых условиях. Она учитывает те же самые затраты, что и первоначальная стоимость, но в современных ценах.
Восстановительная стоимость с учётом износа (остаточная восстановительная стоимость, ОВС) — стоимость, характеризующая фактическую степень изношенности объекта в новых условиях воспроизводства:
ОВС = ПВС – И. (3.2)
Восстановительная стоимость рассчитывается после проведения переоценки основных фондов.
Таким образом, полная стоимость больше остаточной стоимости на величину износа.
Для более полного отражения состояния и движения основных фондов используют балансы основных фондов. Они бывают двух видов: по полной стоимости и по остаточной стоимости – и представляют собой таблицы с информацией об изменении стоимости основных фондов за период. Сокращённые формы обоих балансов приводятся на рис. 3.2 и 3.3.

Используя введённые условные обозначения, выразим балансовое равенство:
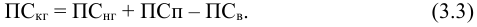
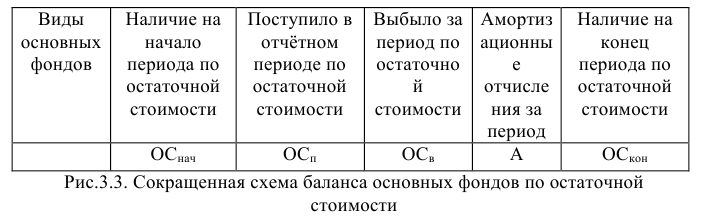
Балансовое равенство будет иметь следующий вид:
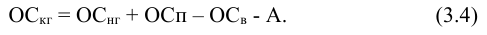
Сумма ежегодных амортизационных отчислений (А) включается в себестоимость изготовленной продукции и определяется по формуле:

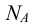 – норма амортизации (%);
– норма амортизации (%); 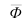 — среднегодовая полная первоначальная (восстановительная) стоимость основных фондов.
— среднегодовая полная первоначальная (восстановительная) стоимость основных фондов.
Задача с решением №3.1
Имеются следующие данные по производственному объединению за год, млн. руб.:
Основные фонды по полной стоимости на начало года 7000.
Сумма износа основных фондов на начало года 2400.
Введено в действие новых основных фондов за год 1100.
Приобретено у других предприятий основных фондов (по полной стоимости) 2300, их износ 600.
Выбыло основных фондов в течение года по полной стоимости 800.
Остаточная стоимость выбывших основных фондов 80.
Годовая сумма амортизационных отчислений 715.
Построить балансы основных фондов.
Решение
Баланс по полной стоимости
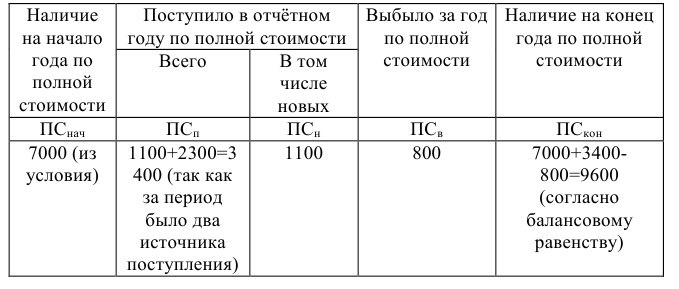
Баланс по остаточной стоимости
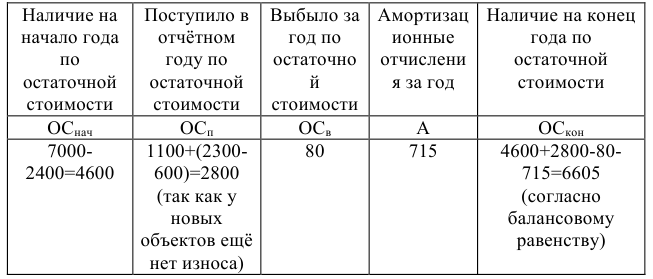
Баланс по полной стоимости
Балансы дают необходимую информацию для анализа основных фондов, который проводится по трём направлениям:
1) анализ состояния основных фондов;
2) анализ движения основных фондов;
3) анализ эффективности использования основных фондов.
По каждому направлению анализа вычисляется своя система показателей (коэффициентов).
К показателям состояния основных фондов относятся коэффициент годности и коэффициент (степень) износа. Они рассчитываются на начало и на конец периода и взаимно дополняют друг друга до 100 %:

Коэффициент годности 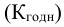 рассчитывается как соотношение основных фондов по остаточной (ОС) и полной стоимости (ПС) — на начало и на конец периода:
рассчитывается как соотношение основных фондов по остаточной (ОС) и полной стоимости (ПС) — на начало и на конец периода:

Он показывает, какую часть своей полной стоимости основные фонды сохранили на определённый момент времени.
Коэффициент износа 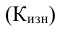 рассчитывается как соотношение суммы износа (И) и полной стоимости основных фондов (ПС) — на начало и на конец периода:
рассчитывается как соотношение суммы износа (И) и полной стоимости основных фондов (ПС) — на начало и на конец периода:
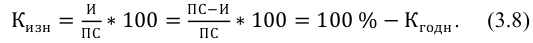
Он показывает, какую часть своей полной стоимости основные фонды уже утратили в результате их использования.
После расчётов делается вывод об изменении состояния основных фондов в конце периода по сравнению с началом.
Здесь возможны 3 ситуации:
1) улучшение состояния (рост коэффициента годности, снижение коэффициента износа);
2) ухудшение состояния (снижение коэффициента годности, рост коэффициента износа);
3) стабильное состояние (оба коэффициента не изменились).
Задача с решением №3.1 (продолжение)
Рассчитать показатели состояния основных фондов.
Решение
Коэффициент годности 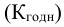 на начало года:
на начало года:
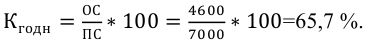
Коэффициент износа 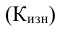 на начало года:
на начало года:
Коэффициент годности  на конец года:
на конец года:
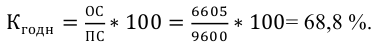
Коэффициент износа 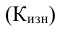 на конец года:
на конец года:
ВЫВОД: Состояние основных фондов к концу года улучшилось (так как коэффициент годности возрос, а коэффициент износа снизился).
К показателям движения основных фондов относятся: коэффициент поступления, коэффициент обновления и коэффициент выбытия. Они рассчитываются только по полной стоимости.
Коэффициент поступления  представляет собой отношение поступивших в данном периоде основных фондов (по полной стоимости) к их полной стоимости на конец года:
представляет собой отношение поступивших в данном периоде основных фондов (по полной стоимости) к их полной стоимости на конец года:

Он показывает долю поступивших объектов (%) в общей стоимости на конец периода.
Коэффициент обновления 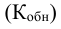 представляет собой отношение вновь введённых в действие в данном периоде основных фондов (по полной стоимости) к полной стоимости на конец года:
представляет собой отношение вновь введённых в действие в данном периоде основных фондов (по полной стоимости) к полной стоимости на конец года:

Он показывает долю новых объектов (%) в общей стоимости на конец периода. Если введены только новые основные фонды, то коэффициенты поступления и обновления равны друг другу.
Коэффициент выбытия 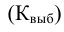 равен отношению полной стоимости выбывших в данном периоде основных фондов к полной стоимости на начало года:
равен отношению полной стоимости выбывших в данном периоде основных фондов к полной стоимости на начало года:

Он показывает долю выбывших объектов (%) в общей стоимости на начало периода.
Задача с решением №3.1 (продолжение)
Рассчитать показатели движения основных фондов.
Решение
Коэффициент поступления 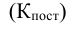 :
:
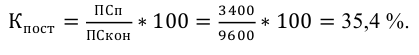
Коэффициент обновления 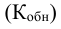 :
:
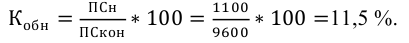
Коэффициент выбытия 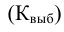 :
:
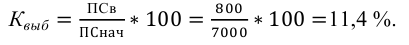
К показателям эффективности использования основных фондов относятся: фондоотдача, фондоёмкость и фондовооружённость.
Фондоотдача 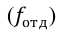 – прямой показатель, характеризующий эффективность использования основных фондов. Его можно рассчитать соотношением стоимости продукции (Q) и среднегодовой стоимости ОФ
– прямой показатель, характеризующий эффективность использования основных фондов. Его можно рассчитать соотношением стоимости продукции (Q) и среднегодовой стоимости ОФ 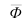 :
:

Уровень фондоотдачи показывает, сколько рублей продукции приходится на каждый рубль, вложенный в основные фонды. Рост данного показателя свидетельствует о повышении эффективности использования основных фондов.
Дополнительным показателем выступает фондоотдача активной части основных фондов 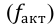 . В этом случае в знаменателе будет использоваться среднегодовая стоимость машин, оборудования, инструмента
. В этом случае в знаменателе будет использоваться среднегодовая стоимость машин, оборудования, инструмента 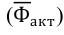 :
:

Между двумя показателями существует взаимосвязь: общую фондоотдачу получают как произведение отдачи активных фондов на их долю в общей стоимости основных фондов 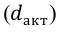 :
:

Фондоёмкость 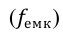 – показатель, обратный фондоотдаче. Уровень фондоёмкости можно определить по формуле:
– показатель, обратный фондоотдаче. Уровень фондоёмкости можно определить по формуле:

Уровень фондоёмкости характеризует размер основных фондов, затраченных предприятием для производства 1 руб. продукции. Предприятие должно стремиться к снижению данного показателя.
Фондовооружённость 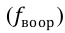 представляет собой соотношение средней стоимости основных фондов и средней численности работников
представляет собой соотношение средней стоимости основных фондов и средней численности работников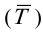 :
:

В знаменателе можно рассматривать как среднесписочную численность персонала в целом, так и численность только одной категории работников.
Результат показывает, сколько рублей основных фондов приходится на одного среднесписочного работника предприятия.
Рост или снижение данного показателя нельзя интерпретировать однозначно. Например, повышение фондовооружённости может происходить как по причине покупки дорогого современного оборудования, так и по причине сокращения персонала. Выводы можно делать только на основании ознакомления с ситуацией на конкретном предприятии.
Задача с решением №3.1 (окончание)
Дополним условие задачи: объём произведённой продукции за год 33200 млн. руб., средняя численность работников 1580 чел.
Рассчитать показатели эффективности использования основных фондов.
Решение
Сделаем предварительный расчёт – вычислим среднюю полную стоимость основных фондов за год:
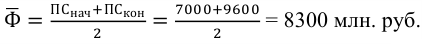
Далее рассчитаем требуемые показатели.
Фондоотдача 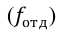 :
:
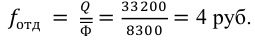
ВЫВОД: каждый рубль, вложенный в основные фонды, принёс 4 руб. продукции.
Фондоёмкость 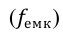 :
:
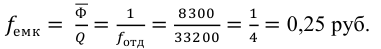
ВЫВОД: для производства 1 руб. продукции затрачено 0,25 руб. (25 коп.) основных фондов.
Фондовооружённость 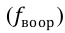 :
:
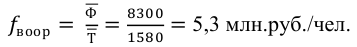
ВЫВОД: на одного работника в среднем приходится основных фондов на сумму 5,3 млн. руб.
Статистика оборотных фондов
Оборотные фонды (оборотные средства) — это наиболее мобильная и постоянно возобновляемая часть национального богатства.
В их состав входят: денежные средства, средства в расчётах, материальные оборотные средства, расходы будущих периодов и т.д.
В производственной деятельности предприятий особую роль играют материальные оборотные средства (МОС). Их основные признаки:
— участвуют в одном производственном цикле (однократно);
— сразу и полностью переносят свою стоимость на вновь созданный продукт или услугу;
— видоизменяют свою натурально-вещественную форму в процессе производства.
Состав МОС:
— производственные запасы (запасы у предприятия-производителя для обеспечения процесса производства
— сырьё, материалы и т.д.);
— незавершённое производство (продукция, производство которой начато, но не завершено к концу отчётного периода);
— готовая продукция (запасы у предприятия-производителя для реализации на сторону);
— товары для перепродажи (запасы на складах торговых организаций);
— животные на выращивании (молодняк) и на откорме;
— государственные материальные резервы (запасы, создаваемые государством на случай чрезвычайных ситуаций – вода, продовольствие, топливо и т.д.).
Показатель размера оборотных средств характеризует их состояние на определённый момент времени. Однако для проведения ряда экономических расчетов нужны, как правило, средние показатели за период времени (месяц, квартал, год). Вычисляют средний остаток оборотных средств 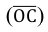 , а формула зависит от исходных данных:
, а формула зависит от исходных данных:
а) по данным об остатке оборотных средств на начало 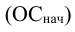 и конец периода
и конец периода 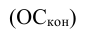 определяется по формуле средней арифметической простой:
определяется по формуле средней арифметической простой:
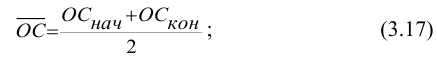
б) по данным на определённые даты через равные промежутки времени между ними по формуле средней хронологической простой:
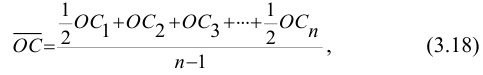
n – число уровней (дат); 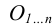 – остаток оборотных средств на определённую дату.
– остаток оборотных средств на определённую дату.
Если же дан моментный ряд динамики с неравными промежутками между датами, то расчёт ведётся по формуле средней арифметической взвешенной (см. тему «Ряды динамики» в курсе «Теория статистики») [1, c. 18-23].
Задача с решением №3.2
Данные по предприятию об остатках оборотных средств (тыс. руб.):
на 1 января – 300, на 1 февраля – 290, на 1 марта – 350, на 1 апреля – 400.
Рассчитать средний остаток оборотных средств за первый квартал.
Решение
Первый квартал – это период времени с 1 января по 1 апреля. Дан моментный ряд динамики с равными промежутками между датами. Расчёт ведётся по формуле средней хронологической:
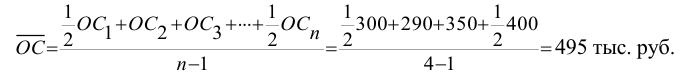
Исходя из их названия, оборотные средства должны оборачиваться, то есть совершать обороты. Схематично оборот оборотных средств производственного предприятия представлен на рисунке 3.4.
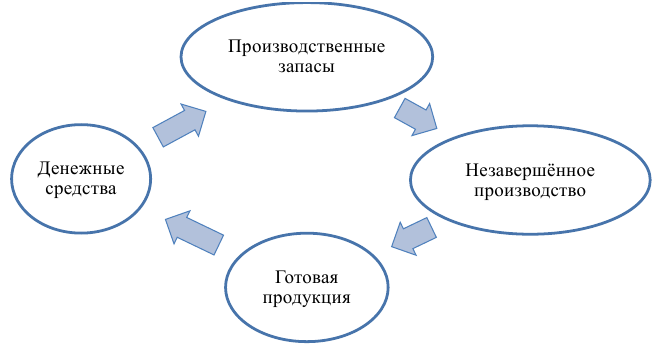
Рис. 3.4. Схема оборота оборотных средств производственного предприятия
В других отраслях экономики схема может видоизменяться; например, у торгового предприятия оборот происходит по схеме «денежные средства – товары для перепродажи – денежные средства».
Важной задачей статистики в управлении предприятием является изучение оборачиваемости оборотных средств. Для этого вычисляются 2 вида показателей:
1) обобщающие (их можно рассчитать в целом по совокупности оборотных фондов предприятия);
2) частные (рассчитываются по отдельным видам оборотных фондов).
К обобщающим показателям оборачиваемости относятся следующие:
1) Коэффициент оборачиваемости 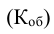 – характеристика скорости оборота:
– характеристика скорости оборота:

Q – объём продукции; 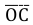 — средний остаток оборотных средств. Показывает число оборотов оборотных средств за период.
— средний остаток оборотных средств. Показывает число оборотов оборотных средств за период.
2) Коэффициент закрепления, или Коэффициент загрузки 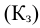 – величина, обратная коэффициенту оборачиваемости:
– величина, обратная коэффициенту оборачиваемости:

Показывает средний размер оборотных средств, приходящихся на 1 руб. продукции.
3) Длительность (продолжительность, время) оборота (t) — соотношение длительности календарного периода 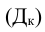 и количества оборотов
и количества оборотов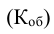 :
:
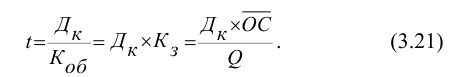
Показывает, за сколько дней в среднем совершается один оборот оборотных средств.
Длительность календарного периода может быть взята как по фактическому числу дней в периоде (май – 31 день, 2015 год – 365 дней и т.д.), так и по так называемому коммерческому (финансовому) календарю (любой месяц – 30 дней, квартал – 90, год – 360).
Задача с решением №3.3
Данные по предприятию за апрель (тыс. руб.):
остатки оборотных средств на 1 апреля – 1700, на 1 мая – 1500; стоимость реализованной продукции 8000.
Рассчитать показатели оборачиваемости оборотных средств за апрель.
Решение
Сделаем предварительный расчёт – вычислим средний остаток оборотных средств в апреле. Остатки оборотных средств даны на начало 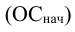 и конец периода
и конец периода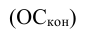 , применяем среднюю арифметическую простую формулу:
, применяем среднюю арифметическую простую формулу:
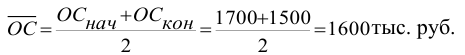
Коэффициент оборачиваемости 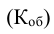 :
:
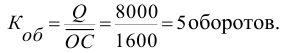
ВЫВОД: оборотные средства в апреле совершили 5 оборотов. Коэффициент закрепления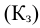 :
:
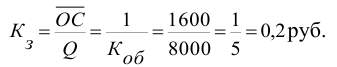
ВЫВОД: для получения 1 руб. продукции было затрачено 0,2 руб. (20 коп.) оборотных средств.
3) Длительность оборота (t):
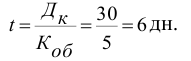
ВЫВОД: средняя продолжительность одного оборота 6 дней.
Изменение этих трёх показателей во времени даёт информацию об изменении эффективности использования оборотных средств. Так как они взаимосвязаны арифметически, то можно выделить 2 ситуации.
1) Снижение коэффициента оборачиваемости, рост коэффициента закрепления и длительности оборота. Такая ситуация называется замедлением оборачиваемости и приводит к тому, что в каждый оборот вовлекается большее количество оборотных средств, то есть каждый оборот становится более затратным. Такое дополнительное привлечение оборотных средств называется мобилизацией оборотных средств.
2) Рост коэффициента оборачиваемости, снижение коэффициента закрепления и длительности оборота. Такая ситуация называется ускорением оборачиваемости и приводит к тому, что каждый оборот требует меньшее количество вовлечённых оборотных средств, то есть становится более экономным. Такое высвобождение оборотных средств из оборота (точнее говоря, их экономия) называется иммобилизацией оборотных средств.
Сумма средств, высвобожденных или дополнительно вовлечённых в оборот в результате изменения скорости оборачиваемости оборотных средств (±Э) рассчитывается по формуле:
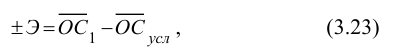
где 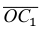 — остаток оборотных средств отчётного периода;
— остаток оборотных средств отчётного периода; 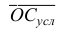 — это сумма оборотных средств, которая потребовалась бы для реализации объёма продукции на уровне отчётного периода при сохранении скорости оборота базисного периода.
— это сумма оборотных средств, которая потребовалась бы для реализации объёма продукции на уровне отчётного периода при сохранении скорости оборота базисного периода.
Эту формулу можно адаптировать под каждый из известных нам показателей оборачиваемости:
а) 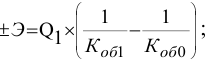
б) 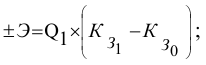
в) 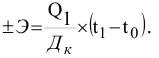 .
.
Подстрочный индекс «0» говорит о том, что показатель представляет базисный период, а «1» — отчётный период.
Если в результате расчётов полученный результат является отрицательным числом, это свидетельствует об иммобилизации (экономии) оборотных средств из-за ускорения оборачиваемости; если получено положительное число – это мобилизация оборотных средств из-за замедления оборачиваемости.
Задача с решением №3.4
Данные по предприятию:
Рассчитать сумма средств, высвобожденных или дополнительно вовлечённых в результате изменения скорости оборачиваемости оборотных средств.
Решение
Исходя из имеющихся данных, выберем следующую формулу:
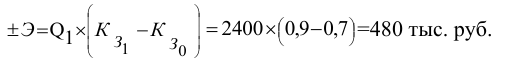
ВЫВОД: произошло замедление оборачиваемости оборотных средств; дополнительно вовлечено в оборот 480 тыс. руб. (мобилизация).
К частным показателям оборачиваемости относятся следующие.
1) Материалоотдача 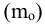 – определяется как отношение объема продукции (Q) к затратам материальных ресурсов на ее производство:
– определяется как отношение объема продукции (Q) к затратам материальных ресурсов на ее производство:

где МЗ – материальные затраты (сырьё, материалы, топливо, энергия и т.д.).
Материалоотдача показывает, сколько рублей продукции принёс каждый рубль материальных затрат.
2) Материалоёмкость 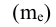 –величина, обратная материалоотдаче:
–величина, обратная материалоотдаче:

Материалоёмкость показывает стоимость материальных затрат для производства одного рубля продукции.
3) Удельный расход материала (M) — средний расход конкретного вида сырья, материалов, топлива или энергии на единицу произведенной годной продукции:

где q– физический объём продукции.
В данной формуле сумма всех затраченных материалов (топлива и т.д.) в натуральном выражении (∑ М) делится на натуральное (физическое) количество произведённой продукции (q). Этот показатель должен соответствовать утверждённым нормам, стандартам или техническим условиям для данного вида продукции.
Система частных показателей не ограничивается рассмотренными коэффициентами. В анализе деятельности предприятия могут использоваться такие показатели, как энергоёмкость, коэффициент оборачиваемости товарных запасов, обеспеченность производства запасами и т.д.
Статистика результатов экономической деятельности, понятие результатов экономической деятельности
Результатами экономической деятельности являются продукты (товары) и услуги.
Продукты – результаты труда, которые имеют материальновещественную форму.
Услуги — результаты труда, которые не воплощаются в материальной форме. Принципиальные отличия услуг от продуктов:
а) на услуги не распространяется право собственности (в Гражданском кодексе РФ услуга считается обязательством);
б) момент производства и потребления услуги совпадают;
в) услугу нельзя хранить, оставить в залог, завещать и т.д. (то есть выполнить те действия, которые возможны с продуктом).
Услуги делятся:
— на материальные и нематериальные;
— на индивидуальные и коллективные.
Материальные услуги удовлетворяют материально-бытовые потребности и связаны с изготовлением, восстановлением (ремонтом), перемещением материальных объектов. Сюда относятся коммунальные, транспортные, бытовые услуги.
Нематериальные услуги связаны с удовлетворением социальнокультурных и духовных потребностей (медицинские, туристические, образовательные услуги).
Индивидуальные услуги носят адресный платный характер: у них есть конкретный заказчик и тариф (ремонт обуви, фотоуслуги, платное образование, проезд в транспорте, кабельное телевидение).
Коллективные услуги (общественные блага) предполагают формально бесплатный характер, а в качестве потребителя выступает всё общество. Примерами являются услуги государственного управления, обеспечения обороны, охраны окружающей среды и т.д.
Снс: сущность и исходные категории
Система национальных счетов (СНС) – система взаимосвязанных показателей и таблиц, комплексно характеризующих состояние экономики страны.
Она была создана в 1950-е годы по заказу ООН и в настоящее время применяется более чем в 150 странах мира с рыночной экономикой (в том числе в России с 1992 г.). Её создание было вызвано потребностями органов государственного управления в информации, необходимой для регулирования экономики, а также для координации потоков экономической информации, которые международные организации получают из разных стран. Поэтому СНС базируется на общих методологических принципах расчёта показателей, хотя допускаются некоторые национальные особенности.
В настоящее время происходит переход от стандарта СНС 1993 года к стандарту 2008 г.
Исходные категории СНС: экономическая территория, институциональная единица, резидент, внутренняя экономика, национальная экономика.
Экономическая территория страны состоит из трёх частей:
1) территория, административно управляемая правительством данной страны, в пределах которой граждане, товары и капиталы могут свободно перемещаться;
2) воздушное пространство, территориальные воды данной страны и континентальный шельф в нейтральных водах, на котором данная страна имеет исключительное право на добычу топлива, сырья и т.д.;
3) территории в других странах (территориальные анклавы), используемые правительством данной страны для дипломатических, военных, научных или других целей (например, посольства).
Из определения следует, что, во-первых, экономическая и административная территории страны пусть незначительно, но не совпадают; во-вторых, территориальные анклавы зарубежных государств в данной стране не включаются в её общую экономическую территорию.
Институциональная единица — хозяйствующие единицы, которые могут от своего имени владеть активами, принимать обязательства, осуществлять экономическую деятельность и операции с другими единицами (юридические лица и домашние хозяйства).
Резидент – институциональная единица, имеющая центр экономических интересов на экономической территории данной страны 1 год и более.
Некоторые категории людей остаются резидентами своих стран, хотя длительное время находятся на территории других стран: дипломатические работники, студенты, лица на отдыхе и лечении и т.д.
Понятие «резидент» не совпадает с понятием гражданства, подданства, национальности.
Резиденты других стран, вступающие в экономические отношения с резидентами данной страны, относятся к экономическому сектору «остальной мир» («нерезиденты»).
Внутренняя экономика охватывает деятельность на территории данной страны как резидентов, так и нерезидентов. Главный показатель внутренней экономики – ВВП (валовой внутренний продукт).
Национальная экономика охватывает деятельность только резидентов данной страны, независимо от их местонахождения. Главный показатель национальной экономики – ВНД (валовой национальный доход). До 1993 г. он носил название «валовой национальный продукт» (ВНП).
Важным методологическим аспектом СНС является концепция границ экономического производства. Она определяет те сферы экономики, в которых создаётся ВВП. В СНС допускается, что в создании ВВП участвуют все виды экономической деятельности (в том числе теневые*), за исключением нижеследующих:
— деятельность, направленная против личности и имущества (грабеж, воровство, терроризм), так как в данном случае один из контрагентов не имеет свободы выбора, а сама экономическая операция не является равноценной для каждой из сторон;
— деятельность, результаты которой не являются её целью (загрязнение окружающей среды, образование мусора и т.д.), так как они являются побочными продуктами производственной деятельности;
— домашние услуги, оказываемые домашними хозяйствами для собственного жилья (приготовление пищи, уборка, ремонт и т.д.), так как крайне сложно вести их статистический учёт и оценивать их в стоимостных единицах.
*(расчёты показателей теневой экономики ведутся на основании косвенной информации, применения балансовых и других специфических методов и экспертных оценок)
Основные макроэкономические показатели
К основным показателям результатов экономической деятельности на макроуровне относятся валовой внутренний продукт (ВВП) и валовой национальный доход (ВНД).
Валовой внутренний продукт (Gross Domestic Product, GDP) — показатель, характеризующий конечный результат производственной деятельности экономических единиц. Он отражает стоимость всех продуктов и услуг, созданных на территории данной страны в течение определённого срока, за вычетом промежуточного потребления.
ВВП имеет 3 метода расчёта, которые в общих чертах соответствуют стадиям воспроизводственного процесса.
Первый метод – производственный. Он позволяет охарактеризовать структуру ВВП с точки зрения результатов деятельности отраслей (секторов) экономики и оценить их вклад в производство. Именно производство является начальной стадией в схеме воспроизводственного процесса, так как на этом этапе создаются продукты и услуги, которые в дальнейшем будут обмениваться и потребляться.
Формула ВВП производственным методом (в рыночных ценах):

где: ВДС – сумма валовой добавленной стоимости (ВДС) по отраслям (секторам) экономики;
ЧНП — чистые налоги на продукты.
Валовая добавленная стоимость (ВДС) определятся по формуле:

где: ВВ — валовой выпуск;
ПП – промежуточное потребление.
Валовой выпуск (Выпуск) – это стоимость всех произведённых за период материальных благ и оказанных услуг. Оценивается в текущих, т.е. рыночных ценах, действующих на момент производства товаров и оказания услуг.
Валовой выпуск (и, соответственно, валовую добавленную стоимость) чаще всего оценивают в основных ценах. Основная цена включает субсидии на продукты и не включает налоги на продукты.
Промежуточное потребление – это стоимость потреблённых в процессе производства товаров и услуг (за исключением потребления основного капитала), которые трансформируются или полностью потребляются в процессе производства в отчётном периоде.
В состав промежуточного потребления входят:
— материальные затраты (затраты сырья, материалов, топлива, энергии и т. п.);
— оплата нематериальных услуг (юридические, страховые, финансовые и т.д.);
— командировочные расходы (оплата проезда и услуг гостиниц).
Чистые налоги на продукты (ЧНП) рассчитываются по формуле:

где: НП – налоги на продукты (НДС, акцизы);
СП – субсидии на продукты.
Распределительный метод ВВП (по источникам дохода) характеризует сумму первичных доходов, распределённых между участниками производства (производителями товаров и услуг). Главными участниками производства являются: предприниматели, наёмные работники, предприятия (организации). Каждый из них получает свой вид доходов:
— оплату труда наёмных работников (ОТНР);
— валовую прибыль экономики (ВПЭ);
— валовые смешанные доходы (ВСД).
Однако в рамках выполнения своих социальных функций государство должно обеспечивать доходами (трансфертами) ту часть населения, которая не участвовала в производстве (инвалидов, пенсионеров, детей, безработных). Для этого участники производства облагаются соответствующими налогами, и рассчитывается показатель ЧНПИ – чистые налоги на производство и импорт:
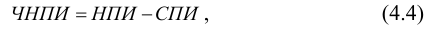
где: НПИ — налоги на производство и импорт;
СПИ — субсидии на производство и импорт.
Формула ВВП распределительным методом:
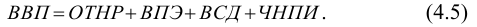
Валовая прибыль экономики представляет собой ту часть добавленной стоимости, которая остаётся у производителя после вычета расходов, связанных с оплатой труда наёмных работников и чистых налогов на производство и импорт.
Валовые смешанные доходы – это доходы, в которых сложно или невозможно отделить доходы от предпринимательской деятельности, от собственности и от оплаты труда (например, доходы фермеров).
Метод конечного использования ВВП (по расходам) характеризует сумму расходов институциональных единиц на приобретение предназначенных для конечного использования товаров и услуг в ценах потребления и чистого экспорта товаров и услуг.
Формула ВВП методом конечного использования:

где: КП — конечное потребление;
ВН – валовое накопление;
ЧЭ – чистый экспорт.
Конечное потребление складывается из расходов на конечное потребление:
— домашних хозяйств;
— государственных учреждений;
— некоммерческих организаций, обслуживающих домашние хозяйства.
Валовое накопление – это вложение средств хозяйственной единицей для создания в будущем дохода в результате их использования в производстве. Оно включает в себя чистое приобретение (то есть за вычетом выбытия) объектов основного капитала, материальных оборотных средств и ценностей.
Чистый экспорт (экспортно-импортное сальдо) есть разница между экспортом (Э) и импортом (И):

Его величина может быть отрицательной в случае превышения величины импорта над величиной экспорта.
Теоретически все три метода ВВП должны дать одинаковый результат. Однако на практике между ними есть так называемое «статистическое расхождение», вызванное различными причинами: использованием различных источников информации, наличием теневой экономики, недостоверностью информации и т.д. Такие расхождения обычно не превышают 1-2 %.
Задача с решением №4.1
Имеются следующие данные по стране (тыс. усл. ед.):

Исчислить ВВП всеми методами.
Решение
ВВП производственным методом:
Сделаем предварительные расчёты – рассчитаем валовую добавленную стоимость (ВДС) и чистые налоги на продукты (ЧНП). Валовая добавленная стоимость:
ВДС = ВВ — ПП = 14800-9340=5460 тыс. усл. ед.;
Чистые налоги на продукты (ЧНП) рассчитываются по формуле:
ЧНП = НП — СП = 920-180=740 тыс. усл. ед.
Таким образом, ВВП будет равен:
ВВП = ВДС + ЧНП= 5460+740=6200 тыс. усл. ед.
ВВП распределительным методом:
Сделаем предварительный расчёт – рассчитаем чистые налоги на производство и импорт (ЧНПИ).
ЧНПИ = НПИ — СПИ = 230-60=170 тыс. усл. ед.
Таким образом, ВВП будет равен:
ВВП = ОТНР + ВПЭ + ВСД + ЧНПИ =2250+3780+170=6200 тыс. усл. ед.
ВВП методом конечного использования:
Сделаем предварительный расчёт – рассчитаем чистый экспорт:
ЧЭ = Э — И =2780-2830=-50 тыс. усл. ед.
Таким образом, ВВП будет равен:
ВВП = КП + ВН + ЧЭ =4110+2140+(-50)=6200 тыс. усл. ед.
Валовой национальный доход (Gross National Income, GNI) — сумма первичных доходов (в рыночных ценах), полученных резидентами данной страны в связи с их участием в производстве ВВП своей страны и ВВП других стран.
К первичным доходам относятся доходы, прямо или косвенно связанные с производством продуктов или услуг: оплата труда, прибыль, налоги на производство, предпринимательский доход, доходы от собственности (проценты, дивиденды, рента и т.п.).
Валовой национальный доход определяется по формуле:

где ΔД — сальдо первичных доходов, полученных от «остального мира» и выплаченных «остальному миру»:

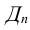 – первичные доходы, полученные от «остального мира»;
– первичные доходы, полученные от «остального мира»; 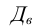 – первичные доходы, выплаченных «остальному миру».
– первичные доходы, выплаченных «остальному миру».
Например, если резиденты России получили за рубежом доходов меньше, чем резиденты других стран получили доходов в России, то сальдо ΔД будет отрицательным, а величина ВВП РФ будет меньше величины ВНД РФ. На региональном уровне в Российской Федерации вычисляют показатель «валовой региональный продукт» (ВРП) — обобщающий показатель экономической деятельности региона, характеризующий процесс производства товаров и услуг для конечного использования.
ВРП по своей сути является аналогом ВВП, рассчитанным на региональном уровне. Каждый регион представляет собой самостоятельную внутреннюю экономику (см. тему 4.2). В то же время сумма валовых региональных продуктов по всем субъектам Федерации не совпадает с объёмом

ВВП больше суммарного ВРП на величину добавленной стоимости по коллективным услугам (государственное управление, оборона и т.д.), которые оказываются всему обществу в целом.
Многие макроэкономические показатели в СНС рассчитываются в двух вариантах:
1) валовые;
2) чистые.
Они отличаются между собой на величину потребления основного капитала (ПОК):
Чистый показатель = Валовой показатель – ПОК.
Потребление основного капитала представляет собой уменьшение стоимости основного капитала в течение отчётного периода в результате его морального и физического износа.
Оно включает:
— сумму амортизации основных фондов за год;
— недоамортизированную стоимость выбывших основных фондов.
Таким образом, можно рассчитать следующие макроэкономические показатели:
— чистый внутренний продукт (ЧВП):

— чистый национальный доход (ЧНД):
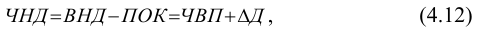
— чистый региональный продукт (ЧРП):

и ряд других показателей.
Задача с решением №4.2
Имеются следующие данные по стране (тыс. усл. ед.):
Валовая добавленная стоимость в основных ценах в сфере производства товаров 3050, а в сфере услуг 2360.
Потребление основного капитала в обеих сферах 1680.
Чистые налоги на продукты 450.
Сальдо доходов от экономической деятельности, полученных от «остального мира» и выплаченных «остальному миру» 170.
Рассчитать:
1) валовой и чистый внутренний продукт;
2) валовой и чистый национальный доход.
Решение
1) Исходя из исходных данных, мы рассчитаем ВВП производственным методом:
ВВП = ВДС + ЧНП= (3050+2360) + 450=5860 тыс. усл. ед.
Чистый внутренний продукт (ЧВП):
ЧВП = ВВП — ПОК = 5860-1680= 4180 тыс. усл. ед.
2) Валовой национальный доход:
ВНД = ВВП + ΔД = 5860+170= 6030 тыс. усл. ед.
Чистый национальный доход (ЧНД):
ЧНД = ВНД — ПОК = ЧВП + ΔД =6030-1680=4180+170=4350 тыс. усл. ед.
Статистика труда, понятие, состав и показатели численности персонала предприятия
Персонал предприятия – это совокупность физических лиц, которые состоят с предприятием в отношениях найма.
Персонал в зависимости от выполняемых работниками функций распределяется по категориям:
— руководители – работники, выполняющие управленческие функции;
— специалисты – работники, выполняющие технические и технологические функции (например, инженерно-технические работники);
— служащие – работники, выполняющие кадровые, учётные, аналитические и иные функции, хозяйственное обслуживание производства;
— рабочие – лица, непосредственно занятые в процессе создания материальных ценностей, оказанием услуг, а также ремонтом, перемещением грузов и т. п.;
— другие категории (младший обслуживающий персонал, охрана, ученики на производстве) [6].
Показатели численности персонала предприятия представлены в таблице 5.1.

Списочная численность – это работники, заключившие договор найма на срок не менее одного дня. Формальным основанием включения в списки (и исключения из списков) служит соответствующий приказ. Исходя из этого, списочная численность в выходной день равна списочной численности в последний рабочий день, так как в выходные дни делопроизводство на предприятии не ведётся.
В списочном составе предприятия не учитываются внешние совместители, так как они должны быть учтены по месту основной работы.
Явочная численность – это работники, явившиеся на работу. Их учёт ведётся только по рабочим дням.
Фактическая численность (Численность фактически работавших) – это работники, фактически приступившие к работе. Они также учитываются только по рабочим дням.
Нормальной считается ситуация, когда явочная и фактическая численности совпадают. Однако расхождения между ними возможны.
Такая ситуация происходит в случае целодневного простоя по объективным причинам:

где: 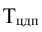 – численность работников, находившихся в целодневных простоях (по объективным причинам).
– численность работников, находившихся в целодневных простоях (по объективным причинам).
Целодневный простой (по объективным причинам) – ситуация, когда работник явился на работу, но по независящим от него причинам к ней не приступил в течение дня (отсутствие материалов, электроэнергии и т.д.). Так как вины работника здесь нет, то работодатель должен оплатить ему этот простой.
Показатели средней численности персонала рассчитываются теми же методами, что и средняя численность населения или трудовых ресурсов (см. темы 1 и 2).
Однако, учитывая тот факт, что предприятие обычно располагает ежедневными данными о количестве сотрудников, применяются нижеследующие формулы.
Среднесписочная численность 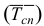 :
:

где: 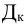 — длительность календарного периода.
— длительность календарного периода.
Результат показывает, сколько человек в среднем состояли в списках каждый календарный день.
Среднеявочная численность 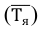 :
:

где: 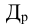 — длительность рабочего периода.
— длительность рабочего периода.
Результат показывает, сколько человек в среднем являлись на работу каждый рабочий день.
Среднефактическая численность 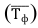 :
:

Результат показывает, сколько человек в среднем приступали к работе каждый рабочий день.
Коэффициент использования среднесписочной численности 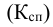 определяется отношением средней фактической численности к среднесписочной численности:
определяется отношением средней фактической численности к среднесписочной численности:

Аналогично рассчитывается коэффициент использования среднеявочной численности 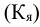 :
:

Задача с решением №5.1
По организации имеются следующие данные о численности работающих за неделю, чел.:
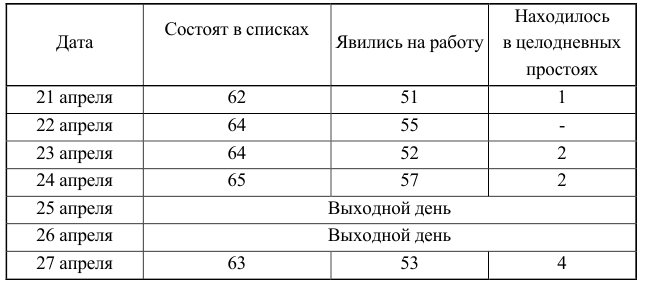
Рассчитать:
1)среднюю численность персонала за неделю;
2)коэффициенты использования среднесписочной и среднеявочной численности за неделю.
Решение
1) Среднесписочная численность 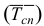 :
:
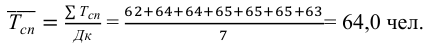
Среднеявочная численность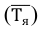 :
:
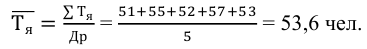
Для вычисления среднефактической численности сделаем предварительный расчёт – рассчитаем фактическую численность за каждый рабочий день, применив формулу:

где: 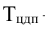 – численность работников, находившихся в целодневных простоях (по объективным причинам):
– численность работников, находившихся в целодневных простоях (по объективным причинам):
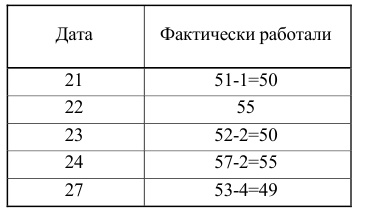
Среднефактическая численность 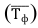 :
:
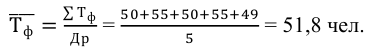
2) Коэффициент использования среднесписочной численности 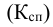 :
:
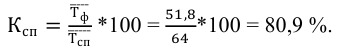
Вывод: из общего списочного состава фактически приступали к работе в среднем 80,9 % работников.
Коэффициент использования среднеявочной численности 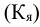 :
:
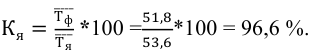
Вывод: из общего числа явившихся фактически приступали к работе в среднем 96,6 % работников.
Рассмотрим статистические особенности расчёта среднесписочной численности:
1) в среднесписочной численности не учитываются работники, которые находятся в списках, но фактически длительное время не работают на данном предприятии и не получают там заработную плату (женщины в отпуске по беременности и родам; лица в отпуске по уходу за ребёнком; работники, обучающиеся в образовательных учреждениях и находившиеся в дополнительном отпуске без сохранения заработной платы);
2) если предприятие работало неполный календарный период (например, закрылось в середине отчётного периода), расчёт средней списочной численности производится так же, то есть путём деления на полный календарный период. Данное правило не распространяется на среднеявочную и среднефактическую численность.
Задача с решением №5.2
Данные по предприятию о численности работников, чел.:
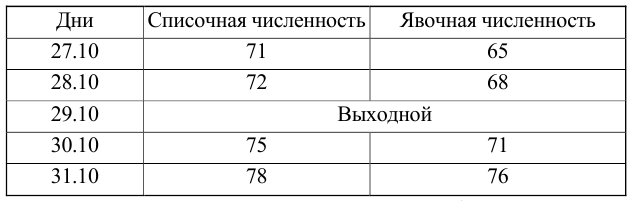
Примечание: предприятие открылось 27 октября.
Рассчитать среднесписочную и среднеявочная численность работников за октябрь.
Решение
Среднесписочная численность 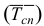 :
:
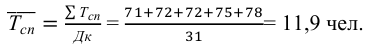
Среднеявочная численность 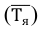 :
:
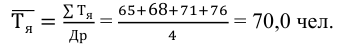
Показатели движения персонала
Движение персонала – это изменение численности персонала предприятия (как в целом, так и по отдельным структурным элементам).
В статистике различают:
1) внутреннее движение (перевод работника в другую категорию, в другой отдел и т.д.);
2) внешнее движение (приём и увольнение).
На общую среднесписочную численность оказывает влияние только внешнее движение персонала.
Выделяют две группы показателей движения персонала.
К первой группе относятся абсолютные показатели (единица измерения — чел.):
— оборот по приёму (ОП) – число принятых на работу за период;
— оборот по увольнению (ОУ) – число уволенных с работы за период;
— общий оборот (ОО) = ОП + ОУ.
Оборот по увольнению делится на два вида:
1) необходимый оборот по увольнению 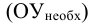 – включает в себя уволенных по причинам естественного, государственного, производственного характера: призыв в армию, выход на пенсию, поступление в учебное заведение на дневную форму обучения, окончание срока действия контракта, сокращение штатов, смерть, переход на инвалидность;
– включает в себя уволенных по причинам естественного, государственного, производственного характера: призыв в армию, выход на пенсию, поступление в учебное заведение на дневную форму обучения, окончание срока действия контракта, сокращение штатов, смерть, переход на инвалидность;
2) излишний оборот по увольнению 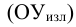 – включает в себя уволенных по субъективным причинам: по собственному жеванию, за прогулы и иные нарушения дисциплины, по приговору суда.
– включает в себя уволенных по субъективным причинам: по собственному жеванию, за прогулы и иные нарушения дисциплины, по приговору суда.
Излишний оборот называется также текучестью кадров. Высокий уровень текучести кадров – отрицательное явление для предприятия, так как это говорит о неудовлетворительной организации производства, вызывает экономические, психологические, кадровые трудности.
Вторая группа – относительные показатели (коэффициенты). Они измеряются в процентах (%). Эти показатели можно применять для характеристики интенсивности движения кадров нескольких предприятий с разной среднесписочной численностью.
Коэффициент оборота по приёму 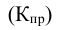 рассчитывается как отношение числа принятых на работу (ОП) к среднесписочной численности работников за отчётный период
рассчитывается как отношение числа принятых на работу (ОП) к среднесписочной численности работников за отчётный период 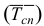 :
:

Коэффициент оборота по увольнению 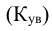 рассчитывается как отношение общего числа уволенных (ОУ) к среднесписочной численности работников за отчётный период
рассчитывается как отношение общего числа уволенных (ОУ) к среднесписочной численности работников за отчётный период 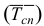 :
:

Коэффициент текучести кадров 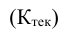 рассчитывается как отношение излишнего оборота по увольнению (ИОУ) к среднесписочной численности работников за отчётный период
рассчитывается как отношение излишнего оборота по увольнению (ИОУ) к среднесписочной численности работников за отчётный период 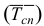 :
:

Коэффициент постоянства кадров 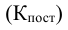 рассчитывается как отношение численности работников, проработавших на предприятии весь период
рассчитывается как отношение численности работников, проработавших на предприятии весь период 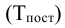 к среднесписочной численности работников за период
к среднесписочной численности работников за период 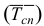 :
:

Числитель можно рассчитать как разность между списочной численностью на начало периода 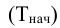 и числом уволенных за период (ОУ):
и числом уволенных за период (ОУ):

Задача с решением №5.3
Динамика численности персонала предприятия (чел.):
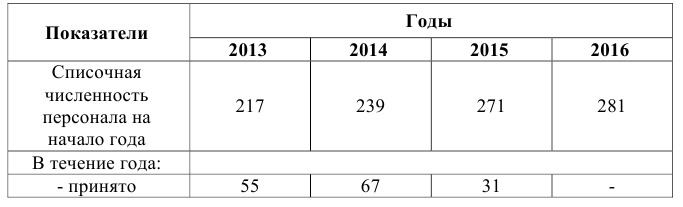

Найти в каждом году (2013, 2014, 2015) относительные показатели движения персонала.
Решение
Сделаем предварительный расчёт – рассчитаем среднесписочную численность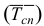 . Так как нам известны только данные о списочном составе на начало каждого года, расчёт производится по средней арифметической простой формуле:
. Так как нам известны только данные о списочном составе на начало каждого года, расчёт производится по средней арифметической простой формуле:

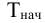 – списочная численность персонала на начало периода;
– списочная численность персонала на начало периода;  — списочная численность персонала на конец периода.
— списочная численность персонала на конец периода.
2013 год: 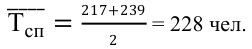
2014 год: 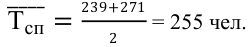
2015 год: 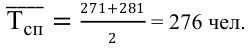
Коэффициент оборота по приёму 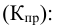

2013 год: 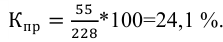
2014 год: 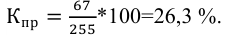
2015 год: 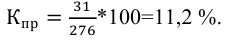
Коэффициент оборота по увольнению 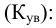

2013 год: 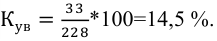
2014 год: 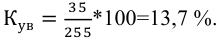
2015 год: 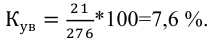
Коэффициент текучести кадров 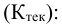

В данном случае к текучести кадров можно отнести уволенных по собственному желанию.
2013 год: 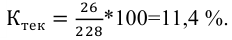
2014 год: 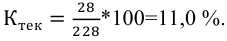
2015 год: 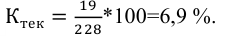
Таким образом, несмотря на нестабильность числа уволенных по собственному желанию по годам, коэффициент текучести кадров неуклонно стремится к снижению, что свидетельствует об улучшении ситуации в системе управления персоналом.
Коэффициент постоянства кадров 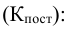

2013 год: 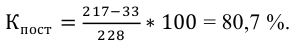
2014 год: 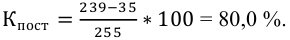
2015 год: 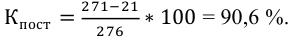
Таким образом, рост коэффициента в 2015 году говорит о стабилизации трудового коллектива предприятия.
Статистика рабочего времени
Рабочее время – это часть календарного времени, затрачиваемого на производство продукции или выполнение работ определённого вида. Оно учитывается как в стандартных единицах (часы, дни и т.д.), так и в специфических единицах: «человеко-час» (чел-ч) и «человекодень» (чел-дн). Человеко-часом отработанного или неотработанного времени считается один час пребывания работника на предприятии, а человеко-днем – один день пребывания работника на предприятии.
2 основные задачи статистического анализа рабочего времени:
1) анализ ресурсов рабочего времени;
2) анализ использования рабочего времени.
Показатели ресурсов рабочего времени обычно измеряются в человеко-днях. К ним относятся фонды рабочего времени.
Календарный фонд (КФ) — всё рабочее время предприятия за период. Он рассчитывается двумя способами: как сумма списочной численности работников за все календарные дни периода; как сумма явок (Я) и неявок (Н) на работу:
КФ = Я + Н. (5.18)
Табельный фонд (ТФ):

где: 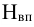 – неявки по выходным и праздничным (нерабочим) дням.
– неявки по выходным и праздничным (нерабочим) дням.
Максимально возможный фонд (МВФ):
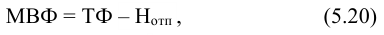
где: 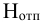 – неявки по очередным отпускам.
– неявки по очередным отпускам.
Максимально возможный фонд характеризует время, которое работники предприятия должны отработать в соответствии с трудовым законодательством, так как положенное им по закону неотработанное время уже вычтено из общего календарного фонда. Соответственно, все три рассмотренных фонда (календарный, табельный и максимально возможный) можно запланировать.
В связи с тем, что существуют внеплановые неявки (по болезни, прогулам, внеочередным отпускам и т.д.), возникает необходимость рассчитывать следующие показатели:
— явочный фонд (ЯФ) = Явки (Я);
— фактический фонд (ФФ) = Фактически отработанное время, т.е. явки минус целодневные простои (ЦДП) по объективным причинам:
ФФ = Я – ЦДП. (5.21)
Соответственно, явочный фонд можно вычислить как сумму фактического фонда и целодневных простоев:
ЯФ = ФФ + ЦДП. (5.22)
Коэффициенты использования фондов рабочего времени характеризуют удельный вес фактически отработанного времени в 83 календарном, табельном или максимально возможном фонде рабочего времени. Чем ближе эти показатели к 100 %, тем полнее используется рабочее время.
Например, коэффициент использования максимально возможного фонда 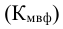 определяется отношением фактического и максимально возможного фондов рабочего времени:
определяется отношением фактического и максимально возможного фондов рабочего времени:

Фонды рабочего времени можно использовать для расчёта средней численности персонала. В этом случае формулы будут иметь следующий вид:
— среднесписочная численность 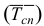 :
:

— среднеявочная численность 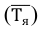 :
:

— среднефактическая численность 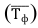 :
:

Задача с решением №5.4
Данные по предприятию за квартал (63 рабочих дня), чел-дн:
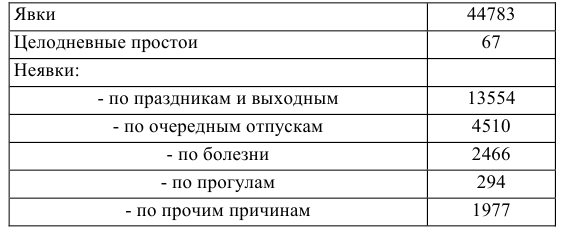
Рассчитать за квартал:
1) фонды рабочего времени;
2) среднюю численность персонала.
Решение
1) Календарный фонд (КФ):
КФ = Я + Н = 44783+13554+ 4510 + 2466 + 294 + 1977 = 67584 чел-дн.
Табельный фонд (ТФ):
ТФ = КФ – Нвп = 67584 – 13554 = 54030 чел-дн.
где: 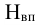 – неявки по выходным и праздничным (нерабочим) дням.
– неявки по выходным и праздничным (нерабочим) дням.
Максимально возможный фонд (МВФ):
МВФ = ТФ – Нотп = 54030 – 4510 = 49520 чел-дн.
Явочный фонд (ЯФ) = Явки (Я) = 44783 чел-дн.
Фактический фонд (ФФ):
ФФ = Я – ЦДП = 44783 – 67 = 44716 чел-дн.
2) Среднесписочная численность 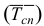 :
:
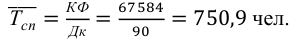
Примечание: календарная длительность квартала возьмём 90 дней.
Среднеявочная численность 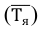 :
:
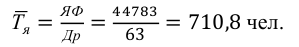
Среднефактическая численность 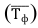 :
:
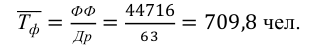
Анализ использования рабочего времени проводится на основе расчёта следующих показателей.
Коэффициент использования установленной продолжительности рабочего дня 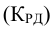 определяется отношением средней фактической продолжительности рабочего дня
определяется отношением средней фактической продолжительности рабочего дня 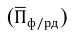 к средней установленной продолжительности рабочего дня
к средней установленной продолжительности рабочего дня 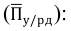

Результат показывает, на сколько процентов в среднем используется рабочий день и сколько процентов занимают внутридневные потери рабочего времени.
Коэффициент использования установленной продолжительности рабочего периода определяется отношением средней фактической продолжительности рабочего периода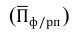 к средней установленной продолжительности рабочего периода
к средней установленной продолжительности рабочего периода 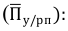 :
:

Результат показывает, на сколько процентов в среднем используется рабочий период (неделя, месяц, квартал, полугодие, год) и сколько процентов занимают целодневные потери рабочего времени.
Интегральный коэффициент использования установленной продолжительности рабочего времени 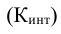 – это произведение двух предыдущих коэффициентов:
– это произведение двух предыдущих коэффициентов:

Результат показывает, на сколько процентов в среднем используется рабочее время и сколько процентов занимают его внутридневные и целодневные потери.
Для расчёта этих показателей необходимо вычислить ряд других, которые встречаются в их формулах.
Средняя фактическая продолжительность рабочего дня 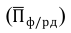 измеряется в часах и рассчитывается соотношением фактически отработанных человеко-часов
измеряется в часах и рассчитывается соотношением фактически отработанных человеко-часов 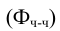 и человеко-дней
и человеко-дней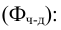

Средняя установленная продолжительность рабочего дня 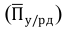 определяется как средняя арифметическая из установленной продолжительности рабочего дня отдельных групп работников, взвешенная по числу работников, имеющих данную продолжительность рабочего дня.
определяется как средняя арифметическая из установленной продолжительности рабочего дня отдельных групп работников, взвешенная по числу работников, имеющих данную продолжительность рабочего дня.
Средняя фактическая продолжительность рабочего периода 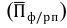 измеряется в днях и рассчитывается делением фактически отработанных человеко-дней
измеряется в днях и рассчитывается делением фактически отработанных человеко-дней 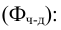 на среднесписочную численность работников
на среднесписочную численность работников 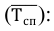

Средняя установленная продолжительности рабочего периода 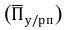 приравнивается к числу рабочих дней в периоде
приравнивается к числу рабочих дней в периоде 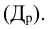
Задача с решением №5.5
Данные по предприятию за апрель:
средняя списочная численность рабочих составляет 500 человек, в том числе работников с продолжительностью рабочего дня 6 часов – 50 человек, с продолжительностью рабочего дня 7 часов – 40 человек. Остальные рабочие имели установленную продолжительность рабочего дня 8 часов. Рабочие предприятия отработали за период 10500 человеко-дней и 79800 человеко-часов. В отчётном месяце было 22 рабочих дня.
Рассчитать показатели использования рабочего времени.
Решение
Сделаем предварительные расчёты:
Средняя фактическая продолжительность рабочего дня 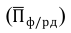 :
:
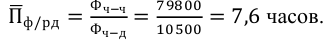
Средняя установленная продолжительность рабочего дня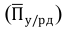 вычисляется по формуле средней арифметической взвешенной (см. тему «Относительные величины» в курсе «Теории статистики»):
вычисляется по формуле средней арифметической взвешенной (см. тему «Относительные величины» в курсе «Теории статистики»):
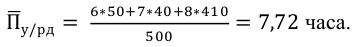
Средняя фактическая продолжительность рабочего периода 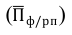 :
:
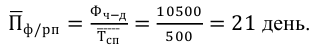
Рассчитаем показатели использования рабочего времени.
Коэффициент использования установленной продолжительности рабочего дня 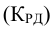 :
:
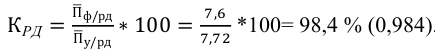
Вывод: рабочий день используется на 98,4 %, т.е. внутридневные потери времени составляют 1,6 % (100 % — 98,4%).
Коэффициент использования установленной продолжительности рабочего периода 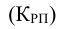 :
:
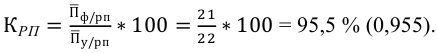
Вывод: рабочий период используется на 95,5 %, т.е. целодневные потери времени составляют 4,5 % (100 % — 95,5%).
Интегральный коэффициент использования установленной продолжительности рабочего времени  :
:
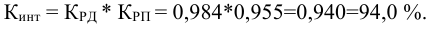
Вывод: в целом рабочее время используется на 94 %, т.е. потери времени составляют 6 % (100 % — 94%).
Таким образом, табельный фонд времени недоиспользован на 6%, в том числе за счет сокращения продолжительности рабочего дня на 1,6% и за счет недоиспользования рабочего периода на 4,5%, т. е. каждым рабочим в отчетном периоде в среднем отработано меньше на один день (22 – 21) и ежедневно на 0,12 часа (7,72 – 7,6).
Статистика производительности труда
Производительность труда — это эффективность труда, то есть его способность производить то или иное количество благ в расчёте на единицу затрат труда.
Уровень производительности труда характеризуется двумя показателями:
1) выработка (прямой показатель);
2) трудоёмкость (обратный показатель).
Выработка (w) рассчитывается соотношением объёма продукции (Q) и затрат труда (T):

Выработка показывает, сколько продукции произведено в среднем за 1 единицу трудовых затрат. В экономике считается положительным явлением рост данного показателя.
Трудоёмкость (t) рассчитывается обратным соотношением:

Трудоёмкость показывает, сколько затрат труда потребовалось в среднем для производства 1 единицы продукции. Предприятие должно стремиться к снижению данного индикатора.
Объём продукции может быть выражен как натуральными, так и стоимостными единицами. Исходя из этого, различают натуральную и стоимостную выработку.
В зависимости от того, чем измеряются затраты труда (затратами рабочей силы или рабочего времени), различают следующие виды показателей производительности труда, выраженных средней выработкой.
Средняя часовая выработка 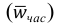 представляет собой соотношение объёма продукции (Q) и фактически отработанных человеко-часов
представляет собой соотношение объёма продукции (Q) и фактически отработанных человеко-часов 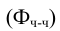 :
:

Результат показывает, сколько продукции в среднем произвёл один рабочий за 1 час.
Средняя дневная выработка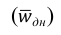 представляет собой соотношение объёма продукции (Q) и фактически отработанных человеко-дней
представляет собой соотношение объёма продукции (Q) и фактически отработанных человеко-дней 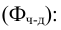

Результат показывает, сколько продукции в среднем произвёл один рабочий за 1 день.
Средняя выработка одного рабочего за период 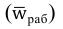 представляет собой соотношение объёма продукции (Q) и среднесписочной численности рабочих
представляет собой соотношение объёма продукции (Q) и среднесписочной численности рабочих 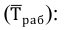

Результат показывает, сколько продукции в среднем произвёл один рабочий за период (месяц, квартал и т.п.).
Средняя выработка одного работника персонала за период 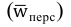 представляет собой соотношение объёма продукции (Q) и среднесписочной численности персонала
представляет собой соотношение объёма продукции (Q) и среднесписочной численности персонала 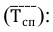

Результат показывает, сколько продукции в среднем произвёл один работник персонала за период (месяц, квартал и т.п.).
Между данными показателями существует следующая взаимосвязь:
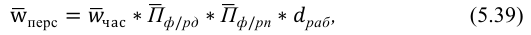
где 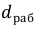 — доля рабочих в среднесписочной численности персонала (рассчитывается как относительная величина структуры – см. тему «Относительные величины» в курсе «Теории статистики»).
— доля рабочих в среднесписочной численности персонала (рассчитывается как относительная величина структуры – см. тему «Относительные величины» в курсе «Теории статистики»).
Для анализа динамики производительности труда применяется индексный метод. Применение того или иного индекса обусловлено как масштабом исследования, так и спецификой анализируемого показателя (см. тему «Индексы» в курсе «Теории статистики»).
Для измерения динамики производительности труда по одной изучаемой единице (например, одному виду продукции) используют индивидуальный индекс, причём он может рассчитываться как по выработке, так и по трудоёмкости.
Индивидуальный индекс производительности труда (по выработке):

где «0» и «1» обозначают, соответственно, базисный и отчётный периоды.
Индивидуальный индекс производительности труда (по трудоёмкости) является обратным предыдущему индексу:

Для измерения динамики производительности труда по совокупности объектов применяют систему общих индексов – индексы переменного состава, постоянного состава и структурных сдвигов. Так как производительность труда характеризуется разными показателями и имеет разные измерители, то используют 3 метода анализа её динамики:
1) натуральный метод (анализируется динамика средней натуральной выработки);
2) стоимостной метод (анализируется динамика средней стоимостной выработки, выраженной в сопоставимых ценах);
3) трудовой метод (анализируется динамика средней трудоемкости).
Рассмотрим натуральный метод анализа.
На динамику средней выработки влияют два фактора:
1. изменение производительности труда по отдельным предприятиям (рабочим, бригадам и т.д.);
2. изменение структуры производства (изменение доли предприятий с той или иной производительностью труда).
Для анализа динамики используется система трёх индексов — переменного, постоянного состава и структурных сдвигов.
Индекс переменного состава 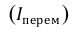 показывает общее изменение производительности труда в отчётном периоде
показывает общее изменение производительности труда в отчётном периоде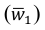 по сравнению с базисным
по сравнению с базисным 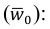

Индекс постоянного (фиксированного) состава 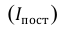 характеризует влияние первого фактора на динамику средней выработки:
характеризует влияние первого фактора на динамику средней выработки:

где 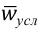 — средняя условная выработка.
— средняя условная выработка.
Индекс структурных сдвигов 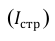 характеризует влияние второго фактора:
характеризует влияние второго фактора:

Все три индекса взаимосвязаны — индекс переменного состава равен произведению двух других индексов:

Задача с решением №5.6
Данные по совокупности предприятий: средняя выработка базисного периода 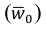 620 шт./чел., средняя выработка отчётного периода
620 шт./чел., средняя выработка отчётного периода 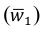 600 шт./чел., средняя условная выработка
600 шт./чел., средняя условная выработка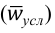 630 шт./чел.
630 шт./чел.
Рассчитать индексы производительности труда натуральным методом.
Решение
Индекс переменного состава 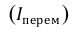 :
:
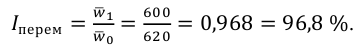
Средняя выработка снизилась на 3,2 %.
Индекс постоянного (фиксированного) состава 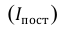 :
:
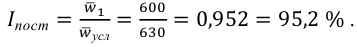
За счёт изменения производительности труда по отдельным предприятиям средняя выработка снизилась на 4,8 %.
Индекс структурных сдвигов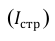 :
:
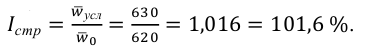
За счёт изменения структуры производства средняя выработка возросла на 1,6 %. Так как данный индекс больше 1, можно сделать вывод, что возросла доля предприятий с более высокой производительностью труда.
Соответственно, индекс структурных сдвигов, по величине меньше 1, свидетельствует о возрастании доли предприятий с более низкой производительностью труда.
Статистика оплаты труда
Оплата труда (заработная плата) – это материальное и натуральное вознаграждение наёмным работникам в соответствии с количеством и качеством их труда, а также с уровнем их квалификации.
Различают две основные формы оплаты труда: сдельную и повременную. При сдельной форме заработок зависит от количества произведённой продукции и сдельной расценки (размера оплаты за единицу продукции), а при повременной – от количества затраченного времени и тарифной ставки (размера оплаты за единицу продукции). В рамках этих форм различают системы (модификации) оплаты труда: сдельно-премиальную и повременно-премиальную (премии за качественную работу), сдельно-прогрессивную (дифференцированная шкала сдельных расценок), аккордную (оплата за весь комплекс работ) и т.д. К повременной форме относят также «должностной оклад» — фиксированный размер оплаты труда административно-управленческого персонала за исполнение трудовых обязанностей определённой сложности за календарный месяц.
Фонд оплаты труда (ФОТ) включает в себя сумму начисленной заработной платы всех работников предприятия. Это интервальный показатель, и он рассчитывается обычно за месяц или за год.
В состав фонда оплаты труда (ФОТ) входят следующие элементы:
1. оплата за отработанное время (зарплата, начисленная в соответствии с тарифными ставками, должностными окладами, сдельными расценками, в процентах от прибыли и т.д.);
2. стимулирующие надбавки и доплаты (за учёную степень, за длительный стаж на данном предприятии, за допуск к государственной тайне и т.д.);
3. компенсационные выплаты, связанные с режимом работы и условиями труда (за работу во вредных или опасных условиях, оплата работы в выходные и праздничные дни, за работу в пустынных, безводных местностях и в высокогорных районах и т.д.);
4. единовременные поощрительные выплаты;
5. регулярные выплаты на питание, жильё, топливо;
6. оплата за неотработанное время (оплата ежегодных и дополнительных отпусков, оплата простоев не по вине работника и т.д.).
Уровень заработной платы характеризуется средней заработной платой одного работника.
Средняя заработная плата 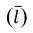 рассчитывается как частное от деления фонда заработной платы (L) на среднесписочную численность работников
рассчитывается как частное от деления фонда заработной платы (L) на среднесписочную численность работников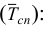

Динамика средней заработной платы изучается с помощью системы индексов.
По отдельным единицам наблюдения (одному участку, предприятию и т.д.) применяют индивидуальный индекс заработной платы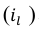 , представляющий собой соотношение уровня заработной платы отчётного
, представляющий собой соотношение уровня заработной платы отчётного 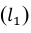 и базисного
и базисного 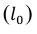 периодов:
периодов:

На динамику средней заработной платы влияют два фактора:
1. изменение уровня заработной платы по отдельным предприятиям (рабочим, бригадам и т.д.);
2. изменение структуры работников (изменение доли работников с той или иной заработной платой).
2. стимулирующие надбавки и доплаты (за учёную степень, за длительный стаж на данном предприятии, за допуск к государственной тайне и т.д.);
3. компенсационные выплаты, связанные с режимом работы и условиями труда (за работу во вредных или опасных условиях, оплата работы в выходные и праздничные дни, за работу в пустынных, безводных местностях и в высокогорных районах и т.д.);
4. единовременные поощрительные выплаты;
5. регулярные выплаты на питание, жильё, топливо;
6. оплата за неотработанное время (оплата ежегодных и дополнительных отпусков, оплата простоев не по вине работника и т.д.).
Уровень заработной платы характеризуется средней заработной платой одного работника.
Средняя заработная плата 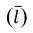 рассчитывается как частное от деления фонда заработной платы (L) на среднесписочную численность работников
рассчитывается как частное от деления фонда заработной платы (L) на среднесписочную численность работников 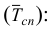

Динамика средней заработной платы изучается с помощью системы индексов.
По отдельным единицам наблюдения (одному участку, предприятию и т.д.) применяют индивидуальный индекс заработной платы 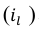 , представляющий собой соотношение уровня заработной платы отчётного
, представляющий собой соотношение уровня заработной платы отчётного 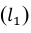 и базисного
и базисного 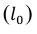 периодов:
периодов:

На динамику средней заработной платы влияют два фактора:
1. изменение уровня заработной платы по отдельным предприятиям (рабочим, бригадам и т.д.);
2. изменение структуры работников (изменение доли работников с той или иной заработной платой).
Для анализа динамики используется система трёх индексов — переменного, постоянного состава и структурных сдвигов (см. тему «Индексы» в курсе «Теории статистики») [1, c. 24-34].
Индекс переменного состава 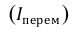 показывает общее изменение средней заработной платы в отчётном периоде
показывает общее изменение средней заработной платы в отчётном периоде 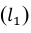 по сравнению с базисным
по сравнению с базисным 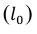 :
:

Индекс постоянного (фиксированного) состава 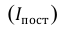 характеризует влияние первого фактора:
характеризует влияние первого фактора:

где 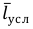 — средняя условная зарплата.
— средняя условная зарплата.
Индекс структурных сдвигов 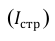 характеризует влияние второго фактора:
характеризует влияние второго фактора:

Все три индекса взаимосвязаны — индекс переменного состава равен произведению двух других индексов:

Задача с решением №5.7
Имеются следующие данные по двум предприятиям о заработной плате работников:
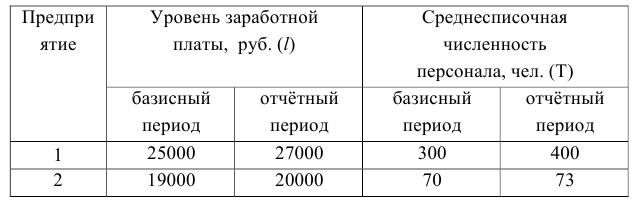
Определите индексы заработной платы:
1) индивидуальные;
2) по двум участкам вместе (переменного, постоянного состава и структурных сдвигов). Проверить взаимосвязь индексов.
Решение
1) индивидуальный индекс заработной платы 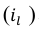 рассчитывается по каждому предприятию в отдельности:
рассчитывается по каждому предприятию в отдельности:
— по предприятию 1:
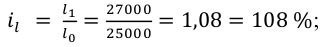
— по предприятию 2:
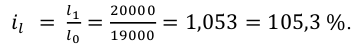
Вывод: уровень заработной платы на предприятии 1 возрос на 8 %, а на предприятии 2 возрос на 5,3 %.
2) сделаем предварительные расчёты – рассчитаем среднюю зарплату по совокупности предприятий:

Индекс переменного состава 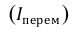 :
:
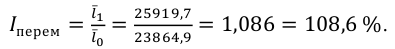
Средняя заработная плата возросла на 8,6 %.
Индекс постоянного (фиксированного) состава 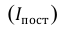 :
:
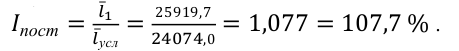
За счёт изменения уровня заработной платы по отдельным предприятиям средняя заработная плата возросла на 7,7 %.
Индекс структурных сдвигов 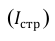 :
:
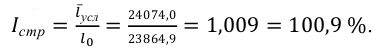
За счёт изменения структуры работников средняя заработная плата возросла на 0,9 %. Так как данный индекс больше 1, можно сделать вывод, что возросла доля предприятий с более высокой заработной платой.
Соответственно, индекс структурных сдвигов, по величине меньше 1, свидетельствует о возрастании доли предприятий с более низкой заработной платой.
Взаимосвязь индексов:
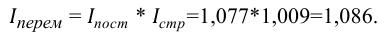
Статистика уровня жизни, понятие уровня жизни
Уровень жизни – это комплексная социально-экономическая категория, включающая в себя различные стороны жизнедеятельности населения.
Современная наука рассматривает категорию «уровень жизни» как сочетание трёх компонентов:
1) благосостояние населения;
2) накопление человеческого капитала;
3) уровень человеческого развития.
Благосостояние населения можно рассматривать с двух сторон – как абсолютное и относительное.
Абсолютное благосостояние характеризуется размером полученных доходов (заработной платы, пенсий, пособий и других), потреблением благ, услуг и продуктов питания, наличием жилья и предметов длительного пользования (телефонов, бытовой техники, автомобилей). Относительное благосостояние предполагает сравнение абсолютных показателей со средними, с нормативными или с показателями прошлых периодов. Например, размер дохода, наличия тех или иных благ, потребления продуктов питания может сравниваться со стандартами данной социальной группы, с физиологическим минимумом, со среднедушевыми показателями данного региона или Российской Федерации в целом.
Накопление человеческого капитала характеризует экономическую сторону воспроизводства рабочей силы. Оно тесно связано с экономическим определением капитала как совокупности активов, приносящих (в данный момент или в перспективе) определённые экономические выгоды. В этом компоненте уровня жизни можно выделить макро- и микроуровень.
На макроуровне предполагается расчёт таких показателей, как «доля расходов государственного бюджета на образование, здравоохранение, культуру и т.д.», в том числе в процентах к ВВП.
На микроуровне накопление человеческого капитала учитывает затраты работодателя и самого человека на повышение образовательного, профессионального, культурного уровня, сохранение и приумножение здоровья. Эти затраты рассматриваются с точки зрения сохранения работоспособности индивида, его конкурентоспособности на рынке труда, что в конечном итоге отражается на его уровне жизни.
Уровень человеческого развития характеризует не столько материальные, сколько духовные, гражданские, правовые и прочие нематериальные аспекты жизнедеятельности людей. Одним из ключевых понятий в оценке уровня человеческого развития является «качество жизни», которое учитывает экологические, демографические, криминогенные, природно-климатические и другие условия жизни. Термин «качество жизни» имеет вполне определённые количественные характеристики, например, уровень преступности, продолжительность жизни, объём выбросов вредных веществ в атмосферу и т.д., которые можно использовать в анализе уровня жизни населения.
Ещё одним аспектом уровня человеческого развития выступает «интеграция человека в общество», которая учитывает наличие демократических прав и свобод, отсутствие дискриминации по различным признакам (расовым, национальным, гендерным и т.д.), наличие доступа к общественным благам. В этом аспекте человек рассматривается не просто как член общества, а как гражданин, обладающий полным комплексом прав и обязанностей.
В статистической практике выделяют следующие виды уровня жизни:
— достаток (пользование благами и услугами, которые обеспечивают всестороннее развитие человека);
— нормальный уровень (потребление благ и услуг по научно обоснованным нормам, которые достаточны для полноценного восстановления физических и интеллектуальных сил человека);
— бедность (потребление благ и услуг на уровне возможности сохранения работоспособности человека);
— нищета (минимальное потребление благ и услуг на уровне биологического выживания человека).
Система показателей уровня жизни
Учитывая сложность и многоплановость понятия «уровень жизни», для его измерения не существует единого показателя, а используется система статистических показателей.
Первый блок – это обобщающие показатели. Они комплексно характеризуют уровень жизни населения, ориентируясь на основные макроэкономические индикаторы. С их помощью международные организации проводят межстрановые сопоставления. К ним относятся:
1) ВВП (или национальный доход) на душу населения (руб./чел) – соотношение величины ВВП и среднегодовой численности населения;
2) индекс стоимости жизни 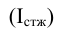 — соотношение величин прожиточного минимума (ПМ) двух периодов:
— соотношение величин прожиточного минимума (ПМ) двух периодов:

где «0» — базисный период, «1» — отчётный период;
3) индекс развития человеческого потенциала ИРЧП (с 2013 года «Индекс человеческого развития» ИЧР — «Human Development Index») — это комбинированный показатель, разработанный ООН. Он включает в себя три компонента.
1) Индекс ожидаемой продолжительности жизни: здоровье и долголетие, измеряемые показателем средней ожидаемой продолжительности жизни при рождении.
2) Индекс образования: доступ к образованию, измеряемый средней ожидаемой продолжительностью обучения детей школьного возраста и средней продолжительностью обучения взрослого населения.
3) Индекс валового национального дохода: достойный уровень жизни, измеряемый величиной валового национального дохода (ВНД) на душу населения в долларах США по паритету покупательной способности (ППС).
Эти три измерения стандартизируются в виде числовых значений от 0 до 1, среднее геометрическое которых представляет собой совокупный показатель ИЧР в диапазоне от 0 до 1.
Второй блок – показатели доходов населения. Это базовая группа, так как именно величина доходов обуславливает уровень потребления и обеспеченности благами (услугами), формирует образ и уклад жизни. Так, рост доходов способствует расширению структуры расходов, в которой доля продуктов питания будет неуклонно уменьшаться за счёт включения таких статей, как приобретение одежды, предметов роскоши, затраты на отдых, культурные мероприятия и т.д.
Доходы структурируются по группам: «Оплата труда», «Доходы от предпринимательской деятельности», «Социальные выплаты», «Доходы от собственности», «Другие доходы».
В СНС существует следующая трактовка понятия «доход», которая базируется на общей концепции английского экономиста Дж. Хикса.
Доход – это максимальная сумма денег, которую субъект может потратить за период, не становясь при этом беднее (то есть, не принимая на себя финансовых обязательств и не уменьшая своего накопленного богатства).
Из данного определения следует, что доходом не считается, например, получение кредита в банке.
Доходы классифицируются по следующим признакам:
— с учётом инфляции (номинальные, реальные);
— по стадии воспроизводства (первичные, располагаемые).
Первичные доходы (ПД) – это доходы, получаемые в результате первичного распределения добавленной стоимости (оплата труда, предпринимательские доходы, доходы от собственности).
Располагаемые доходы (РД) включают в себя первичные доходы и сальдо текущих трансфертов (ΔТТ):
РД = ПД + ΔТТ. (6.2)
Трансфертом называется безвозмездный платёж (то есть поток денег, товаров и услуг, который не вызывает встречный поток денег, товаров и услуг). Сальдо рассчитывается как разность полученных трансфертов (например, пенсий, стипендий, пособий) и выплаченных трансфертов (например, налогов). Его величина может быть отрицательной.
Номинальные доходы (НД) – это первичные и располагаемые доходы, которые рассчитываются в ценах текущего периода.
Реальные доходы (РеалД) – это номинальные доходы, скорректированные на изменение цен, то есть рассчитанные в сопоставимых (постоянных) ценах:
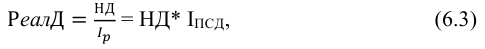
где 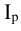 – индекс потребительских цен;
– индекс потребительских цен; 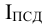 – индекс покупательной способности денег (величина, обратная индексу цен).
– индекс покупательной способности денег (величина, обратная индексу цен).
Сопоставляя реальные доходы отчётного периода с номинальными доходами базисного периода, можно сделать вывод об изменении физического объёма потребления благ населением.
Например, если величина данного индекса больше 1, значит, в натуральном выражении потребление благ возросло по сравнению с базисным периодом.
Расчёт реальных доходов имеет смысл только в динамике. Любой доход, полученный за год, является номинальным. Реальным он станет только после корректировки на индекс цен и сравнения с доходом прошлого периода.
Задача с решением №6.1
Данные по области на душу населения в текущих ценах (руб.):
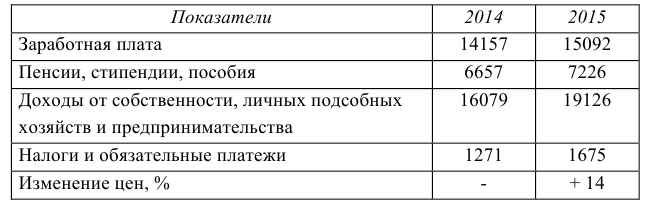
Рассчитать:
1) номинальные располагаемые доходы населения в каждом году;
2) индекс номинальных располагаемых доходов населения;
3) реальные располагаемые доходы населения в 2015 году.
Решение
1) Номинальные располагаемые доходы населения в 2014 году:
14157+6657+16079-1271=35622 руб.
Номинальные располагаемые доходы населения в 2015 году:
15092+7226+19126-1675=39769 руб.
2) Индекс номинальных располагаемых доходов населения:
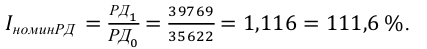
Вывод: номинальные располагаемые доходы населения в 2015 году возросли на 11,6 % (по сравнению с 2014 годом).
3) Реальные располагаемые доходы населения в 2015 году:
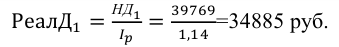
Вывод: реальные располагаемые доходы населения в 2015 году снизились по сравнению с номинальными доходами 2014 года, значит, физический объём потребления благ населением области сократился.
Блок показателей доходов населения дополняется показателями дифференциации доходов. Наибольшее распространение имеют следующие:
1) децильный коэффициент дифференциации доходов – отношение совокупного дохода 10% богатейшего населения к совокупному доходу 10 % беднейшего населения;
2) коэффициент фондов, с помощью которого измеряют различие между суммарными (средними) значениями доходов 10% наиболее обеспеченной и 10% наименее обеспеченной части населения;
3) коэффициент Джини – показатель отклонения фактических доходов населения от абсолютного равенства в распределении доходов. Чем выше его значение, тем выше степень неравенства.
Третий блок – показатели расходов населения. В практической деятельности имеет значение не столько абсолютная величина расходов, сколько их структура, то есть направления затрат. Росстат выделяет следующие градации расходов: «Покупка товаров и оплата услуг», «Обязательные платежи и разнообразные взносы», «Сбережения во вкладах и ценных бумагах», «Расходы на покупку недвижимости», «Приобретение иностранной валюты» и другие расходы.
Четвёртый блок – показатели потребления продуктов питания и обеспеченности благами. В основе расчётов лежит набор из 10 групп продуктов питания продовольственной корзины (см. п. 13.3). Рассчитываются показатели:
— уровень потребления мяса и мясопродуктов (кг на 1 человека в год); — уровень потребления молока и молочных продуктов (кг на 1 человека в год);
— уровень потребления картофеля (кг на 1 человека в год) и т.д.
В качестве наиболее важных благ для населения Росстат рассматривает жильё, автомобили, потребительские товары длительного пользования (телевизоры, персональные компьютеры, стиральные машины и т.д.). Обеспеченность этими благами вычисляется соотношением их общего объёма и численности населения (или домашних хозяйств).
Рассчитываются показатели:
— число собственных легковых автомобилей (штук на 1000 человек населения);
— общая площадь жилых помещений, приходящаяся в среднем на одного жителя (м2 /чел.);
— число телевизоров (штук на 100 домохозяйств) и т.д.
Обобщающую оценку изменения потребления благ дают следующие показатели.
Индивидуальный индекс физического объёма потребления благ 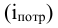 характеризует динамику объёма потребления отдельных видов товаров и услуг:
характеризует динамику объёма потребления отдельных видов товаров и услуг:

где 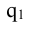 и
и 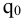 , соответственно, физический объём потребления товара (услуги) в отчётном и базисном периодах.
, соответственно, физический объём потребления товара (услуги) в отчётном и базисном периодах.
Общий индекс физического объёма потребления благ 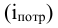 характеризует динамику объёма потребления по совокупности товаров и услуг в сопоставимых ценах:
характеризует динамику объёма потребления по совокупности товаров и услуг в сопоставимых ценах:

где 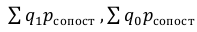 стоимость потреблённых товаров и услуг, соответственно, в отчётном и базисном периодах в сопоставимых ценах.
стоимость потреблённых товаров и услуг, соответственно, в отчётном и базисном периодах в сопоставимых ценах.
Индивидуальный индекс уровня потребления благ 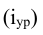 характеризует динамику среднедушевого потребления отдельных видов товаров и услуг:
характеризует динамику среднедушевого потребления отдельных видов товаров и услуг:

где 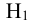 и
и 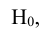 , соответственно, среднегодовая численность населения в отчётном и базисном периодах.
, соответственно, среднегодовая численность населения в отчётном и базисном периодах.
Общий индекс уровня потребления благ 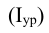 характеризует динамику среднедушевого потребления по совокупности товаров и услуг в сопоставимых ценах:
характеризует динамику среднедушевого потребления по совокупности товаров и услуг в сопоставимых ценах:
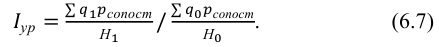
Задача с решением №6.2
Данные по региону:
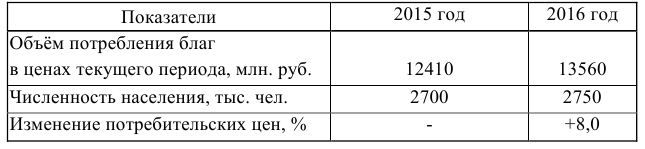
Определите:
1) общий индекс физического объема потребления товаров и услуг;
2) общий индекс уровня потребления товаров и услуг.
Решение
1) сделаем предварительный расчёт – переведём объём потребления благ 2016 года в сопоставимые цены, то есть в данном случае в цены базисного, 2015 года (аналогично задаче 13.1):
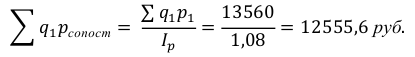
Таким образом, объём потребления благ 2015 года можно обозначить как 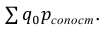
Общий индекс физического объёма потребления благ 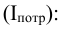
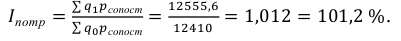
Вывод: физический объём потребления благ в отчётном периоде повысился на 1,2 % (по сравнению с базисным периодом).
2) Общий индекс уровня потребления благ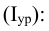
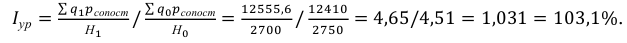
Вывод: уровень потребления благ в отчётном периоде повысился на 3,1 % (по сравнению с базисным периодом).
Таким образом, за счёт роста численности населения региона потребление благ в расчёте на одного человека возросло больше, чем в целом по населению.
В системе показателей уровня жизни можно выделить ещё ряд блоков (демографические, социальные, экологические и другие показатели), однако они традиционно рассматриваются как косвенные по отношению к характеристике уровня жизни населения.
Прожиточный минимум
Прожиточный минимум представляет собой стоимостную оценку потребительской корзины, а также включает в себя обязательные платежи и сборы [3].
Он состоит из потребительской корзины и обязательных платежей и сборов.
Величина прожиточного минимума — это стоимостная оценка потребительской корзины, включающей минимальные наборы продуктов питания, непродовольственных товаров и услуг, необходимых для сохранения здоровья человека и обеспечения его жизнедеятельности, а также обязательные платежи и сборы (в этот пункт включается НДФЛ – налог на доходы физических лиц).
Потребительская корзина в субъектах Российской Федерации устанавливается законодательными органами субъектов Федерации. Её размер – это эталон для мониторинга уровня бедности и решения макроэкономических задач.
Так, прожиточный минимум в целом по Российской Федерации предназначается для решения следующих управленческих задач на государственном уровне:
— оценка уровня жизни населения страны при разработке и реализации социальной политики и федеральных социальных программ;
— обоснование устанавливаемых на федеральном уровне минимального размера оплаты труда, а также для определения устанавливаемых на федеральном уровне размеров стипендий, пособий и других социальных выплат;
-формирование федерального бюджета. Прожиточный минимум в субъектах Российской Федерации предназначается для решения следующих управленческих задач на региональном уровне:
— оценка уровня жизни населения соответствующего субъекта Российской Федерации при разработке и реализации региональных социальных программ;
— оказание необходимой государственной социальной помощи малоимущим гражданам;
— формирование бюджетов субъектов Российской Федерации.
Величина прожиточного минимума на душу населения в целом по Российской Федерации и в субъектах Федерации определяется ежеквартально на основании потребительской корзины и данных об уровне потребительских цен на продукты питания, непродовольственные товары и услуги и расходов по обязательным платежам и сборам. Кроме того, она дифференцирована по возрасту – прожиточный минимум устанавливается не только в среднем на душу населения, но и отдельно для трудоспособного населения, для пенсионеров и для детей.
Величина прожиточного минимума используется в следующих статистических показателях.
Доля населения с доходами ниже прожиточного минимума 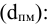
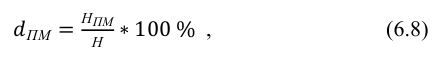
где 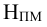 – численность населения с доходами ниже прожиточного минимума (чел.), Н – общая численность населения (чел.).
– численность населения с доходами ниже прожиточного минимума (чел.), Н – общая численность населения (чел.).
Соотношение среднедушевых денежных доходов с величиной прожиточного минимума 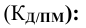
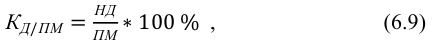
где НД – среднедушевые номинальные доходы населения (руб.), ПМ – величина прожиточного минимума (руб.).
Аналогичным образом с величиной прожиточного минимума сопоставляются среднемесячная начисленная заработная плата и средний размер назначенных пенсий.
Задача с решением №6.3
Величина прожиточного минимума в регионе в базисном периоде составляла 8500 руб., из них 60 % приходилось на приобретение продуктов питания, 8 % — на оплату услуг, 6 % — на оплату налогов. В отчётном периоде цены на продовольственные товары возросли на 12 %, на непродовольственные товары — на 15 %, на услуги – на 10 %. Величина налогов и сборов осталась на уровне базисного периода.
Рассчитать:
1) стоимость каждого элемента прожиточного минимума в базисном периоде;
2) величину прожиточного минимума в отчётном периоде;
3) индекс стоимости жизни.
Решение
1) стоимость каждого элемента прожиточного минимума в базисном периоде.
Приобретение продуктов питания
60 % * 8500 = 0,60 * 8500 = 5100 руб.;
оплата услуг
8 % * 8500 = 0,08 * 8500 = 680 руб.;
обязательные платежи и сборы
6 % * 8500 = 0,06 * 8500 = 510 руб.;
приобретение непродовольственных товаров
8500 – 5100 – 680 – 510 = 2210 руб.
2) величина прожиточного минимума в отчётном периоде 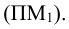 Сделаем предварительные расчёты – рассчитаем стоимость каждого элемента прожиточного минимума в отчётном периоде. Известно, что по трём элементам произошёл рост цен, значит, их стоимость повысилась:
Сделаем предварительные расчёты – рассчитаем стоимость каждого элемента прожиточного минимума в отчётном периоде. Известно, что по трём элементам произошёл рост цен, значит, их стоимость повысилась:
Приобретение продуктов питания:
5100 руб. + 12 % = 5100 * 1,12 = 5712 руб.;
оплата услуг:
680 руб. + 10 % = 680 * 1,10 = 748 руб.;
обязательные платежи и сборы – стоимость не изменилась (510 руб.);
приобретение непродовольственных товаров:
2210 руб. + 15 % = 2210 * 1,15 = 2541,5 руб.
Итого:
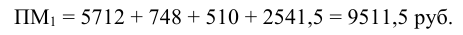
3) индекс стоимости жизни 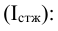
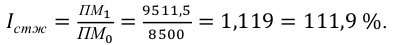
Вывод: стоимость жизни в отчётном периоде повысилась на 11,9 % (по сравнению с базисным периодом).
C 1 января 2013 года в потребительскую корзину России включены следующие продукты и услуги:
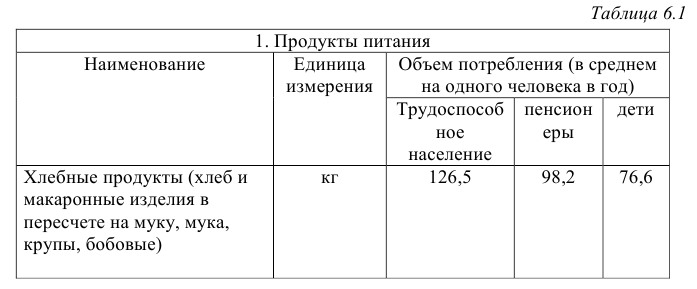
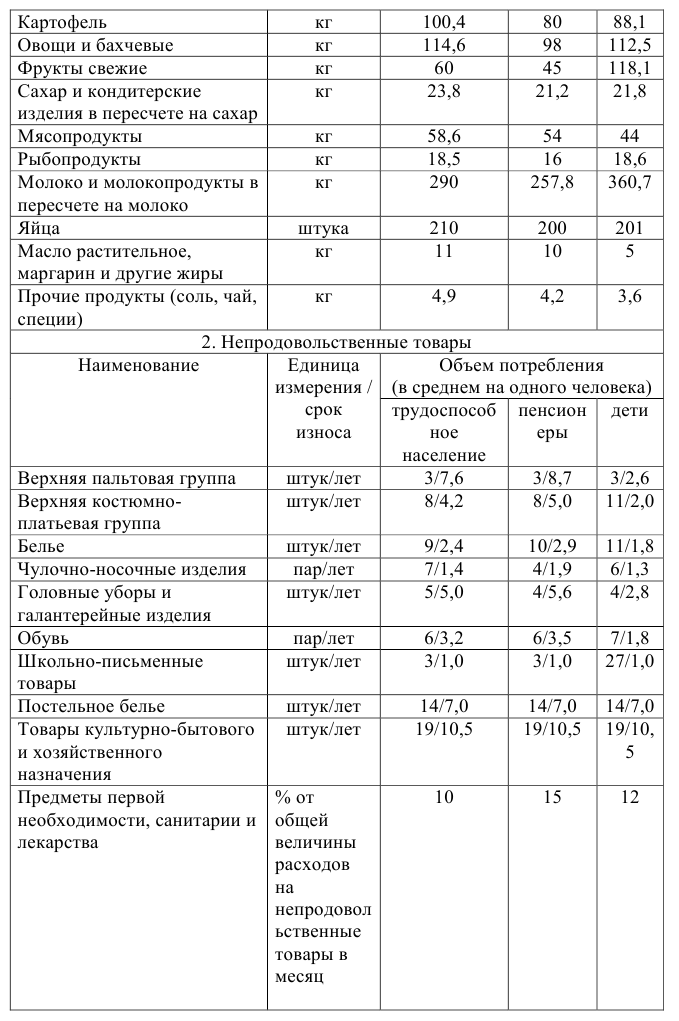
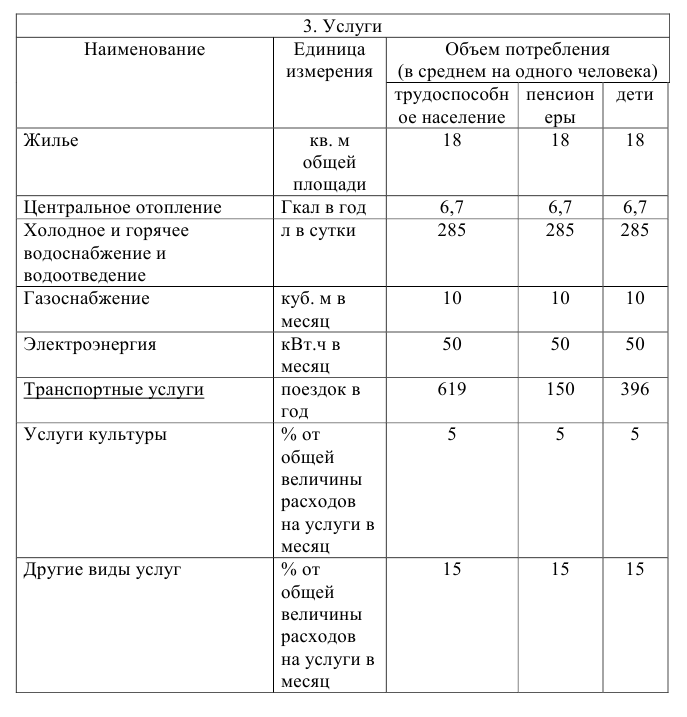

Содержание курса лекций “Статистика”
Выборочное наблюдение как источник статистической информации в изучении социально-экономических явлений и процессов

Статистическая методология исследования массовых явлений различает, как известно, два способа наблюдения в зависимости от полноты охвата объекта: сплошное и несплошное. Разновидностью несплошного наблюдения является выборочное, которое в условиях рыночных отношений в России находит все более широкое применение. Переход статистики РФ на международные стандарты системы национального счетоводства требует более широкого применения выборки для получения и анализа показателей СНС не только в промышленности, но и в других секторах экономики.
Под выборочным наблюдением понимается несплошное наблюдение, при котором статистическому обследованию (наблюдению) подвергаются единицы изучаемой совокупности, отобранные случайным способом. Выборочное наблюдение ставит перед собой задачу ‑ по обследуемой части дать характеристику всей совокупности единиц при условии соблюдения всех правил и принципов проведения статистического наблюдения и научно организованной работы по отбору единиц.
К выборочному наблюдению статистика прибегает по различным причинам. На современном этапе появилось множество субъектов хозяйственной деятельности, которые характерны для рыночной экономики. Речь идет об акционерных обществах, малых и совместных предприятиях, фермерских хозяйствах и т.д. Сплошное обследование этих статистических совокупностей, состоящих из десятков и сотен тысяч единиц, потребовало бы огромных материальных, финансовых и иных затрат. Использование же выборочного обследования позволяет значительно сэкономить силы и средства, что имеет немаловажное значение.
Наряду с экономией ресурсов одной из причин превращения выборочного наблюдения в важнейший источник статистической информации является возможность значительно ускорить получение необходимых данных. Ведь при обследовании, скажем, 10% единиц совокупности будет затрачено гораздо меньше времени, а результаты могут быть представлены быстрее, и будут более актуальными. Фактор времени важен для статистического исследования особенно в условиях изменяющейся социально-экономической ситуации.
Реализация выборочного метода базируется на понятиях генеральной и выборочной совокупностей.
Генеральной совокупностью называется вся исходная изучаемая статистическая совокупность, из которой на основе отбора единиц или групп единиц формируется совокупность выборочная. Поэтому генеральную совокупность также называют основой выборки.
Отбор единиц в выборочную совокупность может быть повторным или бесповторным.
При повторном отборе попавшая в выборку единица подвергается обследованию, т.е. регистрации значений ее признаков, возвращается в генеральную совокупность и наравне с другими единицами участвует в дальнейшей процедуре отбора. Таким образом, некоторые единицы могут попадать в выборку дважды, трижды или даже большее число раз. И при изучении выборочной совокупности они будут рассматриваться как отдельные независимые наблюдения.
Отметим, что число единиц генеральной совокупности, участвующих в отборе, при таком подходе остается постоянным. Поэтому вероятность попадания в выборку для всех единиц совокупности на протяжении всего процесса отбора также не меняется.
На практике методология повторного отбора обычно используется в тех случаях, когда объем генеральной совокупности не известен и теоретически возможно повторение единиц с уже встречавшимися значениями всех регистрируемых признаков.
Например, при проведении маркетинговых исследований мы не можем сколько-нибудь точно оценить, какое число потребителей предпочитают стиральный порошок конкретной торговой марки, сколько покупателей предпочитают делать покупки именно в данном супермаркете и т.д. Поэтому возможно повторение совершенно идентичных единиц как по причине практически неограниченных объемов совокупности, так и вследствие возможной повторной регистрации. Предположим, при проведении обследования один и тот же покупатель может дважды прийти в магазин и дважды подвергнуться обследованию.
При выборочном контроле качества продукции объем генеральной совокупности также часто не определен, так как процесс производства может осуществляться постоянно, каждый день дополняя генеральную совокупность новыми единицами-изделиями. Поэтому в выборочную совокупность могут попасть два и более изделий с абсолютно одинаковыми характеристиками. Следовательно, и в этом случае при обработке результатов выборки необходимо ориентироваться на методологию, используемую при повторном отборе.
При бесповоротном отборе попавшая в выборку единица подвергается обследованию и в дальнейшей процедуре отбора не участвует. Такой отбор целесообразен и практически возможен в тех случаях, когда объем генеральной совокупности четко определен. Получаемые при этом результаты, как правило, являются более точными по сравнению с результатами, основанными на повторной выборке.
Как уже отмечалось выше, выборочное наблюдение всегда связано с определенными ошибками получаемых характеристик. Эти ошибки называются ошибками репрезентативности (представительности).
Ошибки репрезентативности обусловлены тем обстоятельством, что выборочная совокупность не может по всем параметрам в точности воспроизвести совокупность генеральную. Получаемые расхождения или ошибки репрезентативности позволяют заключить, в какой степени попавшие в выборку единицы могут представлять всю генеральную совокупность. При этом следует различать систематические и случайные ошибки репрезентативности.
Систематические ошибки репрезентативности связаны с нарушением принципов формирования выборочной совокупности. Например, вследствие каких-либо причин, связанных с организацией отбора, в выборку попали единицы, характеризующиеся несколько большими или, наоборот, несколько меньшими по сравнению с другими единицами значениями наблюдаемых признаков. В этом случае и рассчитанные выборочные характеристики будут завышенными или заниженными.
Случайные ошибки репрезентативности обусловлены действием случайных факторов, не содержащих каких-либо элементов системности в направлении воздействия на рассчитываемые выборочные характеристики. Но даже при строгом соблюдении всех принципов формирования выборочной совокупности выборочные и генеральные характеристики будут несколько различаться. Получаемые случайные ошибки могут быть статистически оценены и учтены при распространении результатов выборочного наблюдения на всю генеральную совокупность. Оценка ошибок выборочного наблюдения основана на теоремах теории вероятностей.
При дальнейшем рассмотрении теории и методов выборочного наблюдения используются следующие общепринятые условные обозначения:
N ‑ объем (число единиц) генеральной совокупности;
n ‑ объем (число единиц) выборочной совокупности;
![]()
‑ генеральная средняя, т.е. среднее значение изучаемого признака по генеральной совокупности (средняя прибыль, средняя величина активов, средняя численность работников предприятия и т.п.);
![]()
‑ выборочная средняя,
т.е. среднее значение изучаемого признака по выборочной совокупности;
М ‑ численность единиц генеральной совокупности, обладающих определенным вариантом или вариантами изучаемого признака (численность городского населения, численность сельского населения, количество бракованных изделий, число нерентабельных предприятий и т.п.);
р ‑ генеральная доля, т.е. доля единиц, обладающих определенным вариантом или вариантами изучаемого признака, во всей генеральной совокупности (доля городского населения в общей численности населения, доля бракованной продукции в общем выпуске, доля нерентабельных предприятий в общей численности предприятий и т.п.); определяетcя как
m ‑ численность единиц выборочной совокупности, обладающих определенным вариантом или вариантами изучаемого признака;
w ‑ выборочная доля, т.е. доля единиц, обладающих определенным вариантом или вариантами изучаемого признака, в выборочной совокупности,
определяется как ;
![]()
‑ средняя ошибка выборки;
![]()
‑ предельная ошибка выборки;
![]()
‑ коэффициент доверия, определяемый в зависимости от уровня вероятности.
Ошибка выборки или отклонение выборочной средней от средней генеральной находится в прямой зависимости от дисперсии изучаемого признака в генеральной совокупности, и в обратной зависимости ‑ от объема выборки.
Таким образом среднюю ошибку выборки можно представить как

(10.1)
При проведении выборочного наблюдения дисперсия изучаемого признака в генеральной совокупности, как правило, не известна. В то же время, между генеральной дисперсией и средней из всех возможных выборочных дисперсий существует следующее соотношение:

(10.2)
В связи с тем, что на практике в большинстве случаев из генеральной совокупности в определенный момент времени производится только одна выборка, дисперсия изучаемого признака по этой выборке и используется при расчете ошибки.
Учитывая, что при достаточно большом объеме выборки отношение  близко к 1, формула средней ошибки повторной выборки принимает следующий вид:
близко к 1, формула средней ошибки повторной выборки принимает следующий вид:

(10.3)
Где ‑ ![]() дисперсия изучаемого признака по выборочной совокупности.
дисперсия изучаемого признака по выборочной совокупности.
При определении возможных границ значений характеристик генеральной совокупности рассчитывается предельная ошибка выборки, которая зависит от величины ее средней ошибки и уровня вероятности, с которым гарантируется, что генеральная средняя не выйдет за указанные границы.
Согласно теореме А.М. Ляпунова, вероятность той или иной величины предельной ошибки, при достаточно большом объеме выборочной совокупности, подчиняется нормальному закону распределения и может быть определена на основе интеграла Лапласа.
Значения интеграла Лапласа при различных величинах t табулированы и представлены в статистических справочниках.
При обобщении результатов выборочного наблюдения наиболее часто используются следующие уровни вероятности и соответствующие им значения t:
Таблица 10.1 ‑ !!!Некоторые значения t
| Вероятность, рi. | 0,683 | 0,866 | 0,954 | 0,988 | 0,997 | 0,999 |
| Значение t | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 |
Например, если при расчете предельной ошибки выборки мы используем значение t=2, то с вероятностью 0,954 можно утверждать, что расхождение между выборочной средней и генеральной средней не превысит двукратной величины средней ошибки выборки.
Теоретической основой для определения границ генеральной доли, т.е. доли единиц, обладающих тем или иным вариантом признака, является теорема Вернули. Согласно данной теореме вероятность получения сколь угодно малого расхождения между выборочной долей и генеральной долей при достаточно большом объеме выборки будет стремиться к единице. С учетом того, что вероятность расхождения между выборочной и генеральной долями подчиняется нормальному закону распределения, эта вероятность также определяется по функции F(t) при заданном значении t.
Процесс подготовки и проведения выборочного наблюдения включает ряд последовательных этапов:
- Определение цели обследования.
- Установление границ генеральной совокупности.
- Составление программы наблюдения и программы разработки данных
- Определение вида выборки, процента отбора и метода отбора
- Отбор и регистрация наблюдаемых признаков у отобранных единиц.
- Насчет выборочных характеристик и их ошибок.
- Распространение полученных результатов на генеральную совокупность.
В зависимости от состава и структуры генеральной совокупности выбирается вид выборки или способ отбора.
К наиболее распространенным на практике видам относятся:
- собственно-случайная (простая случайная) выборка;
- механическая (систематическая) выборка;
- типическая (стратифицированная, расслоенная) выборка;
- серийная (гнездовая) выборка.
Отбор единиц из генеральной совокупности может быть комбинированным, многоступенчатым и многофазным.
Комбинированный отбор предполагает объединение нескольких видов выборки. Так, например, можно комбинировать типическую и серийную, серийную и собственно-случайную выборки. Ошибка такой выборки определяется ступенчатостью отбора.
Многоступенчатым называется отбор, при котором из генеральной совокупности сначала извлекаются укрупненные группы, потом ‑ более мелкие и так до тех пор, пока не будут отобраны те единицы, которые подвергаются обследованию.
Многофазная выборка, в отличие от многоступенчатой, предполагает сохранение одной и той же единицы отбора на всех этапах его проведения; при этом отобранные на каждой стадии единицы подвергаются обследованию, каждый раз – по более расширенной программе.
Собственно-случайная (простая случайная) выборка заключается в отборе единиц из генеральной совокупности наугад или наудачу без каких-либо элементов системности.
Однако прежде чем производить собственно-случайный отбор, необходимо убедиться, что все без исключения единицы генеральной совокупности имеют абсолютно равные шансы попадания в выборку, в списках или перечне отсутствуют пропуски, игнорирования отдельных единиц и т.п. Следует также установить четкие границы генеральной совокупности таким образом, чтобы включение или не включение в нее отдельных единиц не вызывало сомнений. Так, например, при обследовании студентов необходимо указать, будут ли приниматься во внимание лица, находящиеся в академическом отпуске, студенты негосударственных вузов, военных училищ и т.п.; при обследовании торговых предприятий важно определиться, включит ли генеральная совокупность торговые павильоны, коммерческие палатки и прочие подобные объекты.
Технически собственно-случайный отбор проводят методом жеребьевки или по таблице случайных чисел.
Расчет ошибок позволяет решить одну из главных проблем организации выборочного наблюдения – оценить репрезентативность (представительность) выборочной совокупности.
Различают среднюю и предельную ошибки выборки. Эти два вида связаны следующим соотношением:

(10.4)
Величина средней ошибки выборки рассчитывается дифференцированно в зависимости от способа отбора и процедуры выборки.
Так, при собственно-случайном повторном отборе средняя ошибка определяется по формуле:

(10.5)
а при расчете средней ошибки собственно-случайной бесповторной выборки:

(10.6)
Расчет средней и предельной ошибок выборки позволяет определить возможные пределы, в которых будут находиться характеристики генеральной совокупности.
Например, для выборочной средней такие пределы устанавливаются на основе следующих соотношений:

(10.7)
где ![]() и
и ![]() ‑ генеральная и выборочная средняя соответственно;
‑ генеральная и выборочная средняя соответственно;
![]() ‑ предельная ошибка выборочной средней.
‑ предельная ошибка выборочной средней.
Пример.
При проверке веса импортируемого груза на таможне методом случайной повторной выборки было отобрано 200 изделий. В результате был установлен средний вес изделия 30 г. при среднем квадратическом отклонении 4 г. С вероятностью 0,997 определите пределы, в которых находится средний вес изделия в генеральной совокупности.
Решение. Рассчитаем сначала предельную ошибку выборки. Так как при р = 0,997, t = 3, она равна:
Определим пределы генеральной средней:
 или
или

Вывод: Следовательно, с вероятностью 0,997 можно утверждать, что средний вес изделий в генеральной совокупности находится в пределах от 29,16 г. до 30,84 г.
Пример 2.
В городе проживает 250 тыс. семей. Для определения среднего числа детей в семье была организована 2%-ная случайная бесповторная выборка семей. По ее результатам было получено следующее распределение семей по числу детей:
Таблица 10.2 ‑ Распределение семей по числу детей в городе N
| Число детей в семье | 0 | 1 | 2 | 3 | 4 | 5 |
| Количество
семей |
1000 | 2000 | 1200 | 400 | 200 | 200 |
С вероятностью 0,954 определите пределы, в которых будет находиться среднее число детей в генеральной совокупности.
Решение. В начале на основе имеющегося распределения семей определим выборочные среднюю и дисперсию:
Таблица 10.3 ‑ Вспомогательная таблица для расчета среднего числа детей
|
Число детей в семье, х; |
Количество семей, f | ||||
|
0 1 2 3 4 5 |
1000 2000 1200 400 200 200 |
0
2000 2400 1200 800 1000 |
-1,5
-0,5 0,5 1,5 2,5 3,5 |
2,25
0,25 0,25 2,25 6,25 12,25 |
2250 500 300 900 1250 2450 |
|
Итого |
5000 | 7400 | – | – | 7650 |


Вычислим теперь предельную ошибку выборки (с учетом того, что при р = 0,954 t = 2).

Следовательно, пределы генеральной средней:

Таким образом, с вероятностью 0,954 можно утверждать, что среднее число детей в семьях города практически не отличается от 1,5, т.е. в среднем на каждые две семьи приходится три ребенка.
Наряду с определением ошибок выборки и пределов для генеральной средней эти же показатели могут быть определены для доли признака.
В этом случае особенности расчета связаны с определением дисперсии доли, которая вычисляется так:

(10.8)
где ![]() ‑ доля единиц, обладающих данным признаком в выборочной совокупности, определяемая как отношение количества соответствующих единиц к объему выборки.
‑ доля единиц, обладающих данным признаком в выборочной совокупности, определяемая как отношение количества соответствующих единиц к объему выборки.
Тогда, например, при собственно-случайном повторном отборе для определения предельной ошибки выборки используется следующая формула:

(10.9)
Соответственно, при бесповторном отборе:

(10.10)
Пределы доли признака в генеральной совокупности p выглядят следующим образом:

(10.11)
Рассмотрим пример.
С целью определения средней фактической продолжительности рабочего дня в государственном учреждении с численностью служащих 480 человек, в январе 2009 г. было проведена 25%-ная случайная бесповторная выборка. По результатам наблюдения оказалось, что у 10% обследованных потери времени достигали более 45 мин. в день. С вероятностью 0,683 установите пределы, в которых находится генеральная доля служащих с потерями рабочего времени более 45 мин. в день.
Решение. Определим объем выборочной совокупности:
n= 480 х 0,25 = 120 чел.
Выборочная доля w равна по условию 10%.
Учитывая, что при р = 0,683 t=1, вычислим предельную ошибку выборочной доли:

Пределы доли признака в генеральной совокупности:

Таким образом, с вероятностью 0,683 можно утверждать, что доля работников учреждения с потерями рабочего времени более 45 мин. в день находится в пределах от 7,6% до 12,4%.
Мы рассмотрели определение границ генеральной средней и генеральной доли по результатам уже проведенного выборочного наблюдения, при известном объеме выборки или проценте отбора. На этапе же проектирования выборочного наблюдения именно объем выборочной совокупности и требует определения.
Для определения необходимого объема собственно-случайной повторной выборки применяют следующую формулу:

(10.12)
Полученный на основе использования данной формулы результат всегда округляется в большую сторону. Например, если мы получили, что необходимый объем выборки составляет 493,1 единицы, то обследовав 493 единицы мы не достигнем требуемой точности. Поэтому, для достижения желаемого результата обследованием должны быть охвачены 494 единицы.
С другой стороны, рассчитанное значение необходимого объема выборки свободно может быть увеличено в большую сторону на несколько единиц. Если мы располагаем необходимыми ресурсами, если по причинам организационного порядка (компактность расположения единиц, фиксированная нагрузка на каждого регистратора и т.п.) мы вполне можем охватить больший объем, то включение в выборочную совокупность 500 или, например, 550 единиц только уменьшит значения полученных случайной и предельной ошибок.
При определении необходимого объема выборки для определения границ генеральной доли задача оценки вариации решается значительно проще. Если дисперсия изучаемого альтернативного признака неизвестна, то можно использовать ее максимальное возможное значение:

Например, предприятию связи с вероятностью 0,954 необходимо определить удельный вес телефонный разговоров продолжительностью менее 1 минуты с предельной ошибкой 2%. Сколько разговоров нужно обследовать в порядке собственно-случайного повторного отбора для решения этой задачи?
Для получения ответа на поставленный вопрос воспользуемся формулой (10.12) и будем ориентироваться на максимальную возможную дисперсию доли телефонных разговоров такой продолжительности. Расчет приводит к следующему результату:

Таким образом, обследованием должны быть охвачены не менее 2500 разговоров на предмет их продолжительности.
Необходимый объем собственно-случайной бесповторной выборки может быть определен по следующей формуле:

(10.13)
Укажем на одну особенность формулы (10.13). При проведении вычислений объем генеральной совокупности должен быть выражен только в единицах, а не в тысячах или в миллионах единиц.
Например, подставив в данную формулу общую численность населения региона, выраженную в тысячах человек, мы не получим правильное значение необходимой численности выборки, также выраженное в тысячах человек, как это иногда бывает в других расчетах. Результат вычислений будет неверен.
Механическая выборка может быть применена в тех случаях, когда генеральная совокупность каким-либо образом упорядочена, т.е. имеется определенная последовательность в расположении единиц (табельные номера работников, списки избирателей, телефонные номера респондентов, номера домов и квартир и т.п.). Для проведения отбора желательно, чтобы все единицы также имели порядковые номера от 1 до N.
Для проведения механической выборки устанавливается пропорция отбора, которая определяется соотнесением объемов выборочной и генеральной совокупностей.
Так, если из совокупности в 500000 единиц предполагается отобрать 10000 единиц, то пропорция отбора составит

Отбор единиц осуществляется в соответствии с установленной пропорцией через равные интервалы.
Например, при пропорции 1:50 (2%-ная выборка) отбирается каждая 50-я единица, при пропорции 1:20 (5%-ная выборка) – каждая 20-я единица и т.д.
Интервал отбора также можно определить как частное от деления 100% на установленный процент отбора.
Так, например при 2%-ном отборе интервал составит 50 (100%:2%), при 4%-ном отборе ‑ 25 (100%:4%). В тех случаях, когда результат деления получается дробным, сформировать выборку механическим способом при строгом соблюдении процента отбора не представляется возможным.
Например, по этой причине нельзя сформировать 3%-ную или 6%-ную выборки.
Генеральную совокупность при механическом отборе можно ранжировать или упорядочить по величине изучаемого или коррелирующего с ним признака, что позволит повысить репрезентативность выборки. Однако в этом случае возрастает опасность систематической ошибки, связанной с занижением значений изучаемого признака (если из каждого интервала регистрируется первое значение) или его завышением (если из каждого интервала регистрируется последнее значение). Поэтому целесообразно из каждого интервала отбирать центральную или одну из двух центральных единиц.
Например, при 5%-ной выборке интервал отбора составит 20 единиц, тогда отбор целесообразно начинать с 10-й или с 11-й единицы. В первом случае в выборку попадут 10, 30, 50, 70 и с таким же интервалом последующие единицы; во втором случае – единицы с номерами 11,31,51,71 и т.д.
При механической выборке также может появиться опасность систематической ошибки, обусловленной случайным совпадением выбранного интервала и циклических закономерностей в расположении единиц генеральной совокупности. Так, при переписи населения 1989 г. в ходе 25%-го выборочного обследования семей имела место опасность попадания в выборку квартир только одного типа (например, только однокомнатных или только трехкомнатных), так как на лестничных площадках многих типовых домов располагаются именно по 4 квартиры. Чтобы избежать систематической ошибки, в каждом новом подъезде счетчик менял начало отбора.
Для определения средней ошибки механической выборки, а также необходимой ее численности, используются соответствующие формулы, применяемые при собственно-случайном бесповторном отборе(10.6 и 10.13). При этом, определив необходимую численность выборки и сопоставив ее с объемом генеральной совокупности, как правило, приходится производить соответствующее округление для получения целочисленного интервала отбора.
Например, в области зарегистрировано 12000 фермерских хозяйств. Определим, сколько из них нужно отобрать в порядке механического отбора для определения средней площади сельхозугодий с ошибкой ± 2 га. (Р=0,997). По результатам ранее проведенного обследования известно, что среднее квадратическое отклонение площади сельхозугодий составляет 8 га. Произведем расчет, воспользовавшись формулой (10.13).

С учетом полученного необходимого объема выборки (143 фермерских хозяйства) определим интервал отбора: 12000:143=83,9.
Определенный таким способом интервал всегда округляется в меньшую сторону, так как при округлении в большую сторону произведенная выборка не достигнет рассчитанного по формуле необходимого объема.
Следовательно, в нашем примере, из общего списка фермерских хозяйств необходимо отобрать для обследования каждое 83-е хозяйство. При этом процент отбора составит 1,2% (100% : 83).
Типический отбор целесообразно использовать в тех случаях, когда все единицы генеральной совокупности объединены в несколько крупных типических групп.. Такие группы также называют стартами или слоями, в связи с чем типический отбор также называют стратифицированным или расслоенным. При обследованиях населения в качестве типических групп могут быть выбраны области, районы, социальные, возрастные или образовательные группы, при обследовании предприятий – отрасли или подотрасли, формы собственности и т.п.
Рассматривать генеральную совокупность в разрезе нескольких крупных групп единиц имеет смысл только в том случае, если средние значения изучаемых признаков по группам существенно различаются. Например, с большой уверенностью можно предположить, что доходы населения крупного города будут в среднем выше доходов населения, проживающего в сельской местности; численность работников промышленного предприятия в среднем будет выше численности работников торгового или сельскохозяйственного предприятия; средний возраст студентов будет значительно меньше среднего возраста занятого населения и, тем более, пенсионеров. В то же время, нет никакого смысла при выделении типических групп ориентироваться на признак, не связанный или очень слабо связанный с изучаемым.
Отбор единиц в выборочную совокупность из каждой типической группы осуществляется собственно-случайным или механическим способом. Поскольку в выборочную совокупность в той или иной пропорции обязательно попадают представители всех групп, типизация генеральной совокупности позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки. В то же время, в выделенных типических группах обследуются далеко не все единицы, а только включенные в выборку. Следовательно, на величине полученной ошибки будет сказываться различие между единицами внутри этих групп, т.е. внутригрупповая вариация. Поэтому, ошибка типической выборки будет определяться величиной не общей дисперсии, а только ее части – средней из внутригрупповых дисперсий.
При типической выборке, пропорциональной объему типических групп, число единиц, подлежащих отбору из каждой группы, определяется следующим образом:

(10.14)
Где Ni – объем i-ой группы. а ni ‑ объем выборки из i-ой группы.
Пример. Предположим, общая численность населения области составляет 1,5 млн. чел., в том числе городское – 900 тыс. чел. и сельское – 600 тыс. чел. Если в ходе выборочного наблюдения планируется обследовать 100 тыс. жителей, то эта численность должна быть поделена пропорционально объему типических групп следующим образом:

Средняя ошибка типической выборки определяется по формулам:

(10.15)
 (10.16)
(10.16)
где ![]() – средняя из внутригрупповых дисперсий.
– средняя из внутригрупповых дисперсий.
При выборке, пропорциональной дифференциации признака, число наблюдений по каждой группе рассчитывается по формуле:

(10.17)
Где ![]() ‑ среднее отклонение признака в i-ой группе.
‑ среднее отклонение признака в i-ой группе.
Cредняя ошибка такого отбора определяется следующим образом:

(10.18)

(10.19)
Отбор, пропорциональный дифференциации признака, дает лучшие результаты, однако на практике его применение затруднено вследствие трудности получения сведений о вариации до проведения выборочного наблюдения.
Таблица 10.4 ‑ Результаты обследования рабочих предприятия
| Цех | Всего рабочих, человек | Обследовано, человек | Число дней временной нетрудоспособности за год | |
| средняя | дисперсия | |||
| I
II III |
1000
1400 800 |
100
140 80 |
18
12 15 |
49
25 16 |
Рассмотрим оба варианта типической выборки на условном примере. Предположим, 10% бесповторный типический отбор рабочих предприятия, пропорциональный размерам цехов, проведенный с целью оценки потерь из-за временной нетрудоспособности, привел к следующим результатам (табл. 10.4)
Рассчитаем среднюю из внутригрупповых дисперсий:

Определим среднюю и предельную ошибки выборки (с вероятностью 0,954):

Рассчитаем выборочную среднюю:

С вероятностью 0,954 можно сделать вывод, что среднее число дней временной нетрудоспособности одного рабочего в целом по предприятию находится в пределах:

Воспользуемся полученными внутригрупповыми дисперсиями для проведения отбора пропорционального дифференциации признака. Определим необходимый объем выборки по каждому цеху:


С учетом полученных значений рассчитаем среднюю ошибку выборки:

В данном случае средняя, а следовательно, и предельная ошибки будут несколько меньше, что отразится и на границах генеральной средней.
Серийный отбор. Данный способ отбора удобен в тех случаях, когда единицы совокупности объединены в небольшие группы или серии. В качестве таких серий могут рассматриваться упаковки с определенным количеством готовой продукции, партии товара, студенческие группы, бригады и другие объединения. Сущность серийной выборки заключается в собственно-случайном или механическом отборе серий, внутри которых производится сплошное обследование единиц.
Поскольку внутри групп (серий) обследуются все без исключения единицы, средняя ошибка серийной выборки (при отборе равновеликих серий) зависит от величины только межгрупповой (межсерийной) дисперсии и определяется по следующим формулам:

(10.20)

(10.21)
Где r ‑ число отобранных серий; R ‑ общее число серий.
Межгрупповую дисперсию вычисляют следующим образом:
 (10.22)
(10.22)
где ![]() ‑ средняя i-й серии;
‑ средняя i-й серии;
![]() ‑ общая средняя по всей выборочной совокупности.
‑ общая средняя по всей выборочной совокупности.
Пример.
В области, состоящей из 20 районов, проводилось выборочное обследование урожайности на основе отбора серий (районов). Выборочные средние по районам составили соответственно 14,5 ц/га; 16 ц/га; 15,5 ц/га; 15 ц/га и 14 ц/га. С вероятностью 0,954 определите пределы урожайности во всей области.
Решение. Рассчитаем общую среднюю:

Межгрупповая (межсерийная) дисперсия равна:

Определим теперь предельную ошибку серийной бесповторной выборки (t = 2 при р = 0,954):

Вывод: Следовательно, урожайность будет с вероятностью 0,954 находиться в пределах:

Определение необходимого объема выборки
При проектировании выборочного наблюдения возникает вопрос о необходимой численности выборки. Эта численность может быть определена на базе допустимой ошибки при выборочном наблюдении, исходя из вероятности, на основе которой можно гарантировать величину устанавливаемой ошибки, и, наконец, на базе способа отбора.
Формулы необходимого объема выборки для различных способов формирования выборочной совокупности могут быть выведены из соответствующих соотношений, используемых при расчете предельных ошибок выборки. Приведем наиболее часто применяемые на практике выражения необходимого объема выборки:
– собственно-случайная и механическая выборка:

(10.23)

(10.24)
– типическая выборка:

(10.25)

(10.26)
– серийная выборка:

(10.27)

(10.28)
При этом в зависимости от целей исследования дисперсии и ошибки выборки могут быть рассчитаны для средней величины или доли признака.
Рассмотрим примеры определения необходимого объема выборки при различных способах формирования выборочной совокупности.
Пример.
В 100 туристических агентствах города предполагается провести обследование среднемесячного количества реализованных путевок методом механического отбора. Какова должна быть численность выборки, чтобы с вероятностью 0,683 ошибка не превышала 3 путевок, если по данным пробного обследования дисперсия составляет 225.
Решение. Рассчитаем необходимый объем выборки:

Пример.
С целью определения доли сотрудников коммерческих банков области в возрасте старше 40 лет предполагается организовать типическую выборку пропорциональную численности сотрудников мужского и женского пола с механическим отбором внутри групп. Общее число сотрудников банков составляет 12 тыс. чел., в том числе 7 тыс. мужчин и 5 тыс. женщин.
На основании предыдущих обследований известно, что средняя из внутригрупповых дисперсий составляет 1600. Определите необходимый объем выборки при вероятности 0,997 и ошибке 5%.
Решение. Рассчитаем общую численность типической выборки:

Вычислим теперь объем отдельных типических групп:

Вывод: Таким образом, необходимый объем выборочной совокупности сотрудников банков составляет 550 чел., в т.ч. 319 мужчин и 231 женщина.
Пример.
В акционерном обществе 200 бригад рабочих. Планируется проведение выборочного обследования с целью определения удельного веса рабочих, имеющих профессиональные заболевания. Известно, что межсерийная дисперсия доли равна 225. С вероятностью 0,954 рассчитайте необходимое количество бригад для обследования рабочих, если ошибка выборки не должна превышать 5%.
Решение. Необходимое количество бригад рассчитаем на основе формулы объема серийной бесповторной выборки:

Содержание курса лекций “Статистика”
Контрольные задания
Самостоятельно проведите выборочное наблюдение и произведите соответствующие расчеты.
1.предмет и метод статистики
Предмет статистической науки- изучение количественной стороны общественных явлений в неразрывной связи с их количественной стороной, в определенных условиях места и времени.
2. метод статистики
Метод статистики – это совокупность специфических приемов и методов, которые применяет статистика для исследования своего предмета.
3.основные категории статистики , как науки
В статистике таких категорий 5:
-статистическая совокупность
-единица совокупности
-признак
-статистический показатель
-система статистических показателей
Статистическая совокупность – это совокупность социально-экономических явлений общественной жизни объединенных качественной основой, но отличающихся друг от друга отдельными признаками, например совокупность предприятий, фирм. Совокупность может быть однородная и не однородная. Совокупность называется однородной если один или несколько существенных признаков являются общими для всех единиц совокупности. Например совокупность предприятий по производству обуви.
Единица совокупности – это первичный элемент статистической совокупности, являющийся носителем признаков подлежащих регистрации.
Признак – это качественная особенность единицы совокупности. По характеру отражения свойств единиц изучаемой совокупности признаки делятся на две основные группы:
-признаки имеющие количественное выражение.(возраст, средний заработок и т.д.)
-признаки не имеющие количественного выражения(профессии).-эти признаки называют атрибутивные.
Статистический показатель – это категория которая отражает количественные характеристики (размеры), соотношения признаков общественных явлений. Статистические показатели могут быть:
-отчетными
-прогнозируемыми
Например уровень производительности труда, численность рабочих, численность населения, объем продаж и т.д.
Системы статистических показателей – это совокупность статистических показателей которая отражает взаимосвязи существующие между явлениями . Для каждой общественно-экономической информации характерна определенная система взаимосвязей общественных явлений
4.статистическое наблюдение. Понятие и задачи.
Статистическое наблюдение- это научно-организованный, планомерный , систематический процесс сбора данных о различных социальных и экономических процессах и явлений.
Таким образом, задачами статического наблюдения являются:
1). Обеспечение полноты информации о изучаемом явлении;
2). Получение достоверной информации;
3). Обеспечение оперативности получения данных (в возможно короткий срок).
5.виды статистического наблюдения
Виды статистического наблюдения классифицируются:
1)-по степени охвата исследуемой совокупности
2)-по времени проведения наблюдения
3)-по источникам сведений
1)*Сплошное обследование охватывают все единицы изучаемой совокупности
* не сплошные наблюдения делятся на :
–выборочное
-наблюдение основного массива
-многографическое
2) -по времени проведения наблюдения:
-непрерывное
-прерывное
3) -по источникам сведений:
-непосредственное
-документальное
-опрос
6.способы статистического наблюдения
-Отчетный (предоставление всеми предприятиями отчетов в определенной форме и в определенный срок).
-Экспедиционный (каждой единице наблюдения посылаются специальные лица (счетчики, регистраторы) , которые в специальных формуляра фиксируют сведения о наблюдаемом явлении. Например: перепись населения.)
-Саморегистрация (специальные работники снабжают опршиваемых бланками и дают инструкции о порядке их заполнения. Например: обследование бюджета семей рабочих и служащих).
-Анкетный (определенному кругу лиц вручаются специальные анкеты. Заполнение этих анкет носит добровольный характер и осуществляется анонимно).
7.объект и единица наблюдения. Программа наблюдения.
Объект и единицы наблюдения:
Программа наблюдения:
Для успешной подготовки и проведения статистического наблюдения составляется организационный план наблюдения. В нем указывается организация , которая осуществляет подготовку и проведение наблюдения , а также несет ответственность за эту работу. Такой организацией, осуществляющей наблюдение в масштабе всей республики Молдова является национальное бюро по статистике. Кроме того в этом плане указывается объект наблюдения и организационная форма проведения наблюдения
8.содержание и задачи сводки.этапы сводки.
Сводка это комплекс последовательных действий по обобщению конкретных единичных данных, образующих совокупность в целях выявления типических черт и закономерностей , присущих изучаемому явлению в целом.
Задача сводки: Охарактеризовать исследуемую совокупность (предмет) с помощью систем статистических показателей , выявить и измерить таким путем его существенные черты и особенности. Эта задача решается на 3 этапах:
1этап-осуществляется систематизация материалов, собранных при наблюдении.
2этап-уточняется предусмотренная планом система показателей, с помощью которых количественно характеризуются свойства и особенности изучаемого предмета.
3этап-проводятся расчеты, затем рассчитанные показатели для наглядности представляются в таблице, графиках. К ним даются (делаются) пояснения (анализ представленных данных).
Чаще всего простые итоговые данные сводки не удовлетворяют исследователя, т.к. дают лишь общее представление об изучаемом объекте. Поэтому далее проводят группировку полученных данных по отдельным признакам.
9.статистические группировки. Виды группировок
Группировка – это разделение множества единиц совокупности на однородные группы по определенным, существенным для них признакам.
В соответствии с основными тремя задачами, решаемыми с использованием группировок, принято выделять три основных видов группировок: типологические, структурные, аналитические.
Типологические группировки обеспечивают разграничение массовых явлений на качественно однородные совокупности. При этом качественно однородными совокупностями считаются такие, все единицы которых подчинены определенному закону развития (качеству объекта). Примерами типологических группировок могут служить расчленение при изучении народного хозяйства – на отрасли при изучении отдельной отрасли (например, связи) – на подотрасли основной деятельности (почтовую связь, телефонную связь и т.д.), при изучении предприятий отдельной подотрасли – на отдельные группы по их размерам.
Группировки, применяемые для изучения структуры массовых явлений, называются структурными. С помощью таких группировок можно изучить состав (структуру) качественно однородной совокупности. Например, состав населения по полу, возрасту, образованию, национальности и другим признакам.
В изменении структуры массового явления отражаются важнейшие закономерности их развития. Сопоставляя изменение структуры явления за различные периоды времени можно выявить взаимосвязи варьирующих признаков.
Группировки, предназначенные для изучения взаимосвязей и зависимостей между явлениями и процессами, называются аналитическими. Многие массовые явления достаточно тесно взаимосвязаны между собой: себестоимость продукции зависит от производительности труда: производительность труда в свою очередь зависит от технического уровня производства и труда, квалификации работников и т.д.
10.группировочные признаки. Определение числа групп и величины интервалов.
Результативные –это зависимые признаки, зависят от других признаков.
Факторные признаки-которые оказывают влияние на другие признаки
После того, как выбран группировочный признак, определяется число групп во всей совокупности и величина интервала в каждой группе. На практике для определения число групп используется графический и аналитический методы( согласно этого метода, число групп определяется по формуле Стержесса)
n=1+3,322 lgN (N- число единиц совокупности)
h=(Xmax-Xmin)/n
Интервалы могут быть открытые и закрытые ( это приминимо только для первой и последней группы.)
Кроме того они могут быть равными(ширина интервала в всех группах одна и та же) и разные(ширина интервалов разная)
11.вторичная группировка
Вторичная группировка – это перегруппировка ранее сгруппированных данных. Необходимость вторичной группировки возникает в следующих случаях:
-когда ранее проведенная группировка не удовлетворяет целям исследования в отношении числа групп.
-для сравнения данных относящихся к различным периодам времени или к разным территориям.
-если первичная группировка была произведена по разным группировочным признакам или по разным интервалам.
Существует два способа проведения вторичной группировки:
-объединение мелких групп в более крупные
-выделение определенной доли единиц совокупности
12.ряды распределения. Виды рядов распределения.
Ряд цифровых показателей представляющей распределение единиц совокупности по одному признаку в определенной последовательности называется рядом распределения.
Ряды распределения, построенные по атрибутивному признаку, называются атрибутивными рядами распределения.
Ряды распределения, построенные по количественному признаку (варьирующему) называются вариационными рядами распределения.
В дискретных вариационных рядах значение вариантов отличается друг от друга на определенную величину. Варианты дискретного ряда выражаются целыми числами. Например, число членов семьи
В интервальных рядах распределения величина признака может принимать любые значения в определенном интервале. Варианты могут быть целыми и дробными.
13.Статистические таблицы. Понятие и значение
Статистическая таблица представляет собой наиболее рациональную форму изложения результатов сводки и группировки статистического материала, который позволяет решить конкретные задачи количественного анализа исследуемого явленияСведенные в таблицу данные приобретают компактность, наглядность и исследователь получает возможность делать на основании этого те или иные выводы.
14. Виды статистических таблиц
1) Если в подлежащем содержится простой перечень каких-либо объектов, то таблица называется простой.
2) Групповые таблицы содержат в подлежащем не простой перечень единиц объекта наблюдения, а их группировку по одному существенному признаку.
3) Комбинационные таблицы – это статистические таблицы, подлежащие которых группы единиц, образованных по одному признаку, подразделяются на подгруппы по одному или нескольким другим признакам.
15. Сущность и задачи средних величин
Средняя величина – это обобщающий количественный показатель, характеризующий типичный уровень совокупности по определенному признаку. Средняя величина является наиболее распространеной формой статистических показателей, используемых в экономических исследованиях.
Основные черты средней величины, как типичной характеристики явления:
1.Средняя величина отражает то общее, что присуще всем единицам исследуемой совокупности.
2. Средняя величина представляет значения оприделенного признака совокупности одним числом, несмотря на количественные различия у отдельных единиц совокупности.
3. Средняя величина абстрагируется от индивидуальных значений признака отдельных единиц совокупности и отражает то общее, что содержится в каждом отдельном единичном.
4. Средние величины тесно связаны с законом больших чисел.
16. Средняя арифметическая. Её свойства
1) средняя арифметическая от постоянной величины равна ей самой
2) произведение средней на сумму частот равно сумме произведения вариантов на их частоты
3) изменение каждого варианта на одно и тоже число и на одну и ту же величину изменяет среднюю на ту же величину
4) изменение каждого из весов (частот) в одно и тоже число раз не меняет величины средней
5) изменение каждого варианта в одно и тоже число раз изменяет среднюю во столько же раз
6) сумма отклонений каждого варианта от их средней равна нулю
7) средняя суммы равна сумме средних величин
Рассмотренные свойства средней арифметической используются для упрощения расчетов связанных с вычислением средней величины.
Метод упрощения вычисления средней арифметической называется методом условных моментов или методом отчета от условного нуля.
Согласно этому методу средняя рассчитывается по следующей формуле.
x0 – значение условного нуля
h – ширина интервала
m1 – условный момент первого порядка
17. Виды средних величин
Виды средних величин:
1) Самый распространенный вид средней величины – это средняя арифметическая.
В общем случае ее расчет сводится к суммированию всех значений варьирующего признака и делению полученной суммы на количество единиц совокупности.
2) Средняя гармоническая применяется в тех случаях, когда известны варианты осередняемого признака (xi) и показатели, представляющие произведение вариантов на частоты или веса средней арифметич.
3) Средняя геометрическая применяется в тех случаях, когда определяемый показатель является не суммой значения признака, а их произведением, т.е. во всех случаях, где варианты связаны между собой не знаком «+», а знаком «*» расчитывают не среднюю арифметическую, а среднюю геометрическую. Средняя гармоническая бывает простая и взвешанная.
4) Средняя квадратичная применяется при осереднении величин, выраженных в виде квадратичной функции
5) Средняя хронологическая применяется для расчета средних величин в моментных рядах, когда значения признака представлены в хронологическом порядке через равные промежутки времени.
18. Структурные средние и их использование в экономических расчётах
В статистическом анализе кроме рассмотренных средних используют величины конкретных вариантов, которые занимают в упорядоченном ряду значений признака определенное положение. Это мода, медиана, квартири, децили, процентили. Эти средние называют структурными средними.
1) Медиана – это вариант расположенный в центре ранжированного ряда. Медиана делит ряд на две равные части, таким образом, что у одной половины единиц совокупности значения варьирующего признака меньше медианы, а у другой – больше.
Рассмотрим расчет медианы в вариационных рядах (дискретный и интервальный).
а) В дискретном вариационном ряду с четном числом вариантов медиана рассчитывается как среднее значение двух вариантов, имеющие порядковые номера n/2 и n/2+1.
В этих рядах с нечетным числом членов медиана рассчитывается по формуле n+1/2
б) В интервальных рядах медиана начинается с определения интервала, в котором находится медиана. Этот интервал называется медианный интервал. Этот интервал характерен тем, что его кумулятивная частота (сумма накопленных частот) равна или превышает полусумму всех частот ряда. После того, как нашли медианный интервал, значение медианы рассчитывается по следующей формуле:
XME – нижняя граница медианного интервала
h – ширина медианного интервала
SME-1 – кумулятивная частота, накопленная до медианного интервала.
2) Мода – это вариант, который чаще всего встречается в данной совокупности. Рассмотрим расчет моды в вариационных рядах:
а) В дискретном вариационом ряду модой является вариант обладающий наибольшей частотой.
б) в интервальном вариационном ряду расчет моды осуществляется в следующем порядке:
1. определяем модальный интервал, т.е. интервал обладающей наибольшей частотой;
2. производим расчет моды по формуле
XM0 – нижняя граница модального интервала , h – ширина модального интервала
fM0 – частота модального интервала , fM0-1 – частота предмодального интервала , fM0+1 – частота послемодального интервала
19 Понятие вариации признаков
Вариация – это такие количественные изменения величины исследуемого признака в пределах статистической совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов.
20 показатели вариации признаков
1) Абсолютные (размах вариации) показатели – R – рассчитывается, как разница R=Xmax-Xmin
Чем меньше значение этого показателя, тем совокупность однороднее. Недостаток этого показателя в том, что он не учитывает изменения значений признака внутри предельных значений вариантов.
Вместе с тем для характеристики вариации признака необходимо знать не только размах предельных значений отклонений но и уметь обобщить отклонения всех значений от какой-либо типичной для изучаемой совокупности величины(средней). Такую характеристику вариаций дает среднее линейное отклонение.
Среднее линейное отклонение представляет собой среднюю арифметическую из абсолютных значений отклонений отдельных вариантов от их средней арифметической.
– это невзвешенное среднее линейное уравнение.
Применяется для вариационного ряда с равными частотами.
– это взвешенное.
Дисперсия – это средний квадрат отклонений вариантов от их средней арифметической.
– это простая дисперсия, которая применяется для в вариационных рядах с равными частотами.
В вариационных рядах с неравными частотами рассчитывают дисперсию взвешенную.
Для интервальных вариационных рядов с равными интервалами дисперсия рассчитывается способом условных моментов.
h – ширина интервала
m1 – условный момент 1-го порядка
m2 – условный момент второго порядка
2) Относительные показатели.
В статистической практике часто возникает необходимость сравнения вариации различных признаков. Например, сравнение вариации возраста рабочих и их квалификации, стажа работы и размера из з/п. Для таких сопоставлений абсолютные показатели вариации нельзя и использовать, тюк нельзя сравнивать вариацию стажа работы, выраженного в годах с вариацией з/п, выраженной в леях. Для таких сравнений используют относительный показатель вариации, который наз-ся коэффициентом вариации.
Коэффициент вариации применяется не только для сравнительной оценки вариации, но и для характеристики однородности совокупности. Если к.в. меньше 30 %, то совокупность является однородной.
21. Абсолютные величины. Их виды
Абсолютные величины характеризуют численность совокуп ности и объем (размер) изучаемого социально-экономического яв ления в определенных границах времени и места. Они имеют ка кую-либо единицу измерения.
Единицы измерения могут быть натуральными, условно-нату ральными, стоимостными (денежные) и трудовыми.
1) Индивидуальные абсолютные величины – это абсолютные величины, характеризующие размеры отдельных единиц совокупности. Пример: количество деталей, изготовленных одним рабочим за смену; число детей в отдельной семье.
2) Суммарные абсолютные величины получают путем суммирования отдельных индивидуальных величин.
22.Относительные показатели. Их виды.
Относительные величины представляют собой обобщающие показатели, выражающие меру количественных соотношений, присущих конкретным явлениям общественной жизни. Относительные величины рассчитываются, как отношение двух чисел, при этом числитель – сравниваемая величина, а знаменатель – база относительного сравнения
Существуют следующие виды относительных величин:
1) Относительная величина динамики (темп роста) – это показатель, характеризующий изменение величины общественных явлений во времени (Тр).
2) Относительная величина планового задания представляет собой отношение планового задания в отчетном периоде к фактическому выполнению в базисном периоде.
3) Относительная величина выполнения плана (%)
4) Относительная величина структуры (ОВС) характеризует долю отдельных частей в общей совокупности.
5) Относительная величина координации характеризует соотношение отдельных частей совокупности, одна из которых выступает, как база сравнения (%). Например, на 100 муж – 107 жен.
6) Относительная величина интенсивности – это показатель, характеризующий меру распространения или развития данного явления в определенной среде.
7) Относительная величина сравнения применяется для сравнения показателей одного предприятия по сравнению с показателями другого.
23. Графический способ изображения статистических данных.
Для графического изображения структуры явлений используют столбиковые диаграммы, полосовые и секторные.
Столбиковые явл-ся наиболее простым видом диаграмм и применяется для изображения динамики. Динамика изображается в виде столбиков одинаковой ширины, но разной высоты в зависимости от числовых значений изображаемой величины. К столбиковым диаграммам относятся и гистограммы распространения.
Полосовые диаграммы бывают двух видов:
1. Структурно-абсолютные (служат только для сопоставления абсолютных величин структуры).
2. Структурно-относительные (для сопоставления относительных величин структуры).
Секторные диаграммы.
Часто состав, структура того или иного явления изображается с помощью кругов, разделенных на секторы, площадь которых пропорциональны долям частям явления. Круг прим-ся за 100 % и разбивается на сектора.
Размещение явлений по территориям изображаются графически с помощью картограмм и картодиаграмм.
Картограммы – это схематическая географическая карта, на которой штриховкой различной густоты, точками или окраской определенной степени насыщенности показывается сравнительная интенсивность какого-либо показателя в пределах каждой единицы нанесенного на карту территориального деления. Картограммы делятся на фоновые и точечные.
Картодиаграмма – сочетание диаграмм с географической картой. В качестве изобразительных знаков в картодиаграммах используются диаграммные фигуры (столбики, квадраты, круги, фигуры, полосы), которые размещаются на контуре географической карты. Картодиаграммы дают возможность географически отразить более сложные статистико-географические построения, чем картограммы.
24. Ряды динамики и их виды
Ряды статистических величин, характеризующие изменения явлений во времени называются динамическими рядами. Ряды динамики состоят из двух элементов:
1. Уровень ряда- это показатель,числовые значения которого составляют динамический ряд. 2. Время-это моменты, периоды времени, к которым относятся уровни ряда.
Для проведения анализа динамических рядов их подразделяют на моментные и интервальные.
Моментные ряды– это ряды статистических величин,характеризующие размеры изучаемого явления на определенные даты,моменты времени. Например,численность населения, среднесписочная численность рабочих(за квартал). Их отличительной чертой является то,что их уровни нельзя суммировать.
Интервальные ряды– это ряды статистических величин,характеризующие размеризучаемого явления за определенный промежуток времени(за месяц, квартал, год ). Их уровни можно суммировать.
По способу выражения динамические ряды делятся на :
1. Ряды абсолютных величин –они отражают изменения абсолютных показателей и являются первичными.
2. Ряды относительных величин – рассчитываются на основе рядов динамики абсолютных величин и являются вторичными.
3. Ряды средних величин – рассчитываются на основе рядов абсолютных величин и являются вторичными.
25. основные показатели используемые для анализа динамических рядов.
Для анализа динамических рядов применяются следующие показатели:
-уровень динамического ряда – y
-абсолютный прирост- ∆y
-темп роста- Tр
-темп прироста Тпр
-абсолютное значение 1% прироста- А1%пр
-среднегодовой темп роста-
-среднегодовой темп прирост –
1.Уровень динамического ряда различают начальный уровень(у0), последний уровень(yn) и средний уровень ряда(). Средний уровень ряда определяется по формуле средней арифметической простой:
Уровень который сравнивают называется текущий и обозначатся- yi
Уровень с которым производится сравнение называется начальным( базисным) и обозначается –y0
Расчет показателей производится базисным и цепным методами.
Базисный метод -сравнивают каждый уровень динамического ряда с одним и тем же уровнем принятым за базу сравнения.
Цепной метод – сравнивают каждый уровень ряда с предыдущем уровнем.
2.Абсолютный пророст определяется как разница между текущим уровнем и предыдущем(цепной метод) уровнем или как разница между текущим уровнем и начальным(базисный метод).
Цепной метод: ∆y= yi–yi-1
Базисный метод: ∆y= yi–y0
yi-1-предыдущий уровень
yi– текущий уровень
y0 – начальный уровень.
Средний абсолютный прирост определяется по формуле:
3.Темп роста рассчитывается как отношение текущего уровня к предыдущему (цепной метод) методу или как отношение текущего уровня к начальному(базисный метод):
Цепной метод:
Базисный метод:
4.Темп прироста рассчитывает по формуле:
Цепной метод:
Базисный метод:
5.Абсолютное значение 1% процента прироста:
Цепной метод:
Базисный метод:
6.7.Среднегодовые темпы роста и прироста, расчет среднегодового темпа роста можно проводить по двум формулам, все зависит от данных:
1)когда имеются абсолютные данные динамического ряда, расчет среднего темпа роста проводится по формуле:
2)когда абсолютные данные динамического ряда отсутствуют , а имеются относительные показатели (цепные коэффициента роста) то расчет среднего темпа роста проводится по формуле:
Tр- коэффициент роста
n- число цепных коэффициентов роста
А среднегодовой темп прироста рассчитывается:
___ __
Тпр = Тр – 1
___ __
Тпр = Тр – 100 ( если в %)
26.способы обпработки ряда динамики
–способ укрупнения интервалов
Сущность первого способа заключается в следующем: данные характеризующие динамику изучаемого явления укрупняются т.е. получаем показатель характеризующую динамику за более длительный период времени.
–способ скользящей средней
Сущность второго способа заключается в том что по конкретным уровням ряда рассчитываются сглаженные скользящие средние. Скользящие средние получают из подвижных сумм путем последовательного сдвига на один период суммируемых показателей. Затем подвижные суммы делят на число уровней получая таким образом скользящие средние. Проведем сглаживание данных об объеме произведенной продукции при помощи трехмесячной скользящей средней. …………………
(истори умалчивает)
-метод аналитического выравнивания
Сущность третьего метода состоит в замене эмпирического ряда динамики теоретическим рядом с плавно изменяющимися уровнями согласно уравнению примой или кривой линии.
Первым этапом аналитического выравнивания является обоснованный выбор типа линии т.е. по данным строим график. Уравнение прямой имеет следующий вид:
yt = a0 +a1ti прямой
yt – выравненные уровни
a0 и а1 – параметры
ti– номера месяцев, номер года и т.д.
После выбора типа линии которая отражает тенденцию развития рассматриваемого показателя рассчитывает значения параметров по эмпирическим уровням, те что даны. Вычисления производят по методу наименьших квадратов. Этот метод дает систему двух уравнений на основании которых можно рассчитать параметры:
В рядах динамики техники расчета параметров уровля( а0,а1) упрощается. Для этого показателям времени (t) придают также значения чтобы в сумме они были равны нулю: ∑ti=0
Для этого нумеруют отрезки времени, чтобы до серидины они имели “-“, после “+”( для четного ряда.
27 понятия и значения индексов
Индексы- это относительные показатели , которые характеризуют соотношение уровней социально-экономических явлений во времени по сравнению с планом и в пространстве.
Во всех случаях сопоставляются с собой размеры одноименных показателей имеющих одинаковое экономическое содержание. Т.о. индекс… Продолжение »
