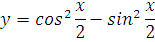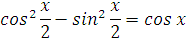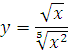Содержание
- Что такое производная?
- Таблица производных.
- Термины и обозначения.
- Таблица производных.
- Производная фукнции, заданной неявно: руководство, примеры
- Как найти производную функции, заданной неявно
- Решаем задачи вместе
- Решить задачи самостоятельно, а затем посмотреть решения
Что такое производная?
Таблица производных.
Производная — одно из главных понятий высшей математики. В этом уроке мы познакомимся с этим понятием. Именно познакомимся, без строгих математических формулировок и доказательств.
Это знакомство позволит:
— понимать суть несложных заданий с производной;
— успешно решать эти самые несложные задания;
— подготовиться к более серьёзным урокам по производной.
Сначала — приятный сюрприз.)
Строгое определение производной основано на теории пределов и штука достаточно сложная. Это огорчает. Но практическое применение производной, как правило, не требует таких обширных и глубоких знаний!
Для успешного выполнения большинства заданий в школе и ВУЗе достаточно знать всего несколько терминов — чтобы понять задание, и всего несколько правил — чтобы его решить. И всё. Это радует.
Приступим к знакомству?)
Термины и обозначения.
В элементарной математике много всяких математических операций. Сложение, вычитание умножение, возведение в степень, логарифмирование и т.д. Если к этим операциям добавить ещё одну, элементарная математика становится высшей. Эта новая операция называется дифференцирование. Определение и смысл этой операции будут рассмотрены в отдельных уроках.
Здесь же важно понять, что дифференцирование — это просто математическая операция над функцией. Берём любую функцию и, по определённым правилам, преобразовываем её. В результате получится новая функция. Вот эта новая функция и называется: производная.
Дифференцирование — действие над функцией.
Производная — результат этого действия.
Так же, как, например, сумма — результат сложения. Или частное — результат деления.
Зная термины, можно, как минимум, понимать задания.) Формулировки бывают такие: найти производную функции; взять производную; продифференцировать функцию; вычислить производную и т.п. Это всё одно и то же. Разумеется, бывают и более сложные задания, где нахождение производной (дифференцирование) будет всего лишь одним из шагов решения задания.
Обозначается производная с помощью штришка вверху справа над функцией. Вот так: y’ или f'(x) или S'(t) и так далее.
Читается игрек штрих, эф штрих от икс, эс штрих от тэ, ну вы поняли. )
Штрих также может обозначать производную конкретной функции, например: (2х+3)’, (x 3 )’, (sinx)’ и т.д. Часто производная обозначается с помощью дифференциалов, но такое обозначение в этом уроке мы рассматривать не будем.
Предположим, что понимать задания мы научились. Осталось всего ничего — научиться их решать.) Напомню ещё раз: нахождение производной — это преобразование функции по определённым правилам. Этих правил, на удивление, совсем немного.
Чтобы найти производную функции, надо знать всего три вещи. Три кита, на которых стоит всё дифференцирование. Вот они эти три кита:
1. Таблица производных (формулы дифференцирования).
3. Производная сложной функции.
Начнём по порядку. В этом уроке рассмотрим таблицу производных.
Таблица производных.
В мире — бесконечное множество функций. Среди этого множества есть функции, которые наиболее важны для практического применения. Эти функции сидят во всех законах природы. Из этих функций, как из кирпичиков, можно сконструировать все остальные. Этот класс функций называется элементарные функции. Именно эти функции и изучаются в школе — линейная, квадратичная, гипербола и т.п.
Дифференцирование функций «с нуля», т.е. исходя из определения производной и теории пределов — штука достаточно трудоёмкая. А математики — тоже люди, да-да!) Вот и упростили себе (и нам) жизнь. Они вычислили производные элементарных функций до нас. Получилась таблица производных, где всё уже готово.)
Вот она, эта табличка для самых популярных функций. Слева — элементарная функция, справа — её производная.
| Функция y |
Производная функции y y’ |
|
| 1 | C (постоянная величина) | C’ = 0 |
| 2 | x | x’ = 1 |
| 3 | x n (n — любое число) | (x n )’ = nx n-1 |
| x 2 (n = 2) | (x 2 )’ = 2x | |
 |
 |
|
 |
 |
|
| 4 | sin x | (sin x)’ = cosx |
| cos x | (cos x)’ = — sin x | |
| tg x |  |
|
| ctg x |  |
|
| 5 | arcsin x |  |
| arccos x |  |
|
| arctg x |  |
|
| arcctg x |  |
|
| 4 | a x |  |
| e x |  |
|
| 5 | loga x |  |
| ln x (a = e) |  |
Рекомендую обратить внимание на третью группу функций в этой таблице производных. Производная степенной функции — одна из самых употребительных формул, если только не самая употребительная! Намёк понятен?) Да, таблицу производных желательно знать наизусть. Кстати, это не так трудно, как может показаться. Попробуйте решать побольше примеров, таблица сама и запомнится!)
Найти табличное значение производной, как вы понимаете, задание не самое трудное. Поэтому очень часто в подобных заданиях встречаются дополнительные фишки. Либо в формулировке задания, либо в исходной функции, которой в таблице — вроде и нету.
Рассмотрим несколько примеров:
1. Найти производную функции y = x 3
Такой функции в таблице нет. Но есть производная степенной функции в общем виде (третья группа). В нашем случае n=3. Вот и подставляем тройку вместо n и аккуратно записываем результат:
(x 3 )‘ = 3·x 3-1 = 3x 2
Ответ: y’ = 3x 2
2. Найти значение производной функции y = sinx в точке х = 0.
Это задание означает, что надо сначала найти производную от синуса, а затем подставить значение х = 0 в эту самую производную. Именно в таком порядке! А то, бывает, сразу подставляют ноль в исходную функцию. Нас же просят найти не значение исходной функции, а значение её производной. Производная, напомню — это уже новая функция.
По табличке находим синус и соответствующую производную:
Подставляем ноль в производную:
Это и будет ответ.
3. Продифференцировать функцию:
Что, внушает? ) Такой функции в таблице производных и близко нет.
Напомню, что продифференцировать функцию — это просто найти производную этой функции. Если забыть элементарную тригонометрию, искать производную нашей функции достаточно хлопотно. Таблица не помогает.
Но если увидеть, что наша функция — это косинус двойного угла, то всё сразу налаживается!
Да-да! Запомните, что преобразование исходной функции до дифференцирования вполне допускается! И, случается, здорово облегчает жизнь. По формуле косинуса двойного угла:
Т.е. наша хитрая функция есть не что иное, как y = cosx. А это — табличная функция. Сразу получаем:
Пример для продвинутых выпускников и студентов:
4. Найти производную функции:
Такой функции в таблице производных нет, разумеется. Но если вспомнить элементарную математику, действия со степенями. То вполне можно упростить эту функцию. Вот так:
А икс в степени одна десятая — это уже табличная функция! Третья группа, n=1/10. Прямо по формуле и записываем:
Вот и всё. Это будет ответ.
Надеюсь, что с первым китом дифференцирования — таблицей производных — всё ясно. Осталось разобраться с двумя оставшимися китами. В следующем уроке освоим правила дифференцирования.
Источник
Производная фукнции, заданной неявно: руководство, примеры
Как найти производную функции, заданной неявно
Будем учиться находить производные функций, заданных неявно. Что значит неявно? Сравним с обычной функцией. Обычная функция задана уравнением вида y=f(x) , где игрек, то есть функция, задан некоторым выражением, в котором присутствует икс. Таким образом, из переменных в левой части — только игрек, в правой — только икс. Если же функция задана неявно, то в левой части различные слагаемые с игреком «смешаны» с различными слагаемыми с иксом (или переменной, обозначенной другой буквой). Примеры функций, заданных неявно:





При этом и икс, и игрек могут быть в различных степенях, а в одном слагаемом могут быть и игрек, и икс.
Если функция задана неявно, то как получить игрек, то есть явную функцию? Просто: выразить игрек через другую переменную, то есть получить в левой части только игрек. А если нужно найти производную функции, заданной неявно, то есть получить в левой части только игрек со штрихом? Нужно сначала найти производные обеих частей уравнения, то есть продифференцировать их. А затем выразить производную игрека через производные других переменных.
Теперь приведенный выше «скелет» решения обрастет «мясом», то есть необходимыми подробностями. Те слагаемые, в которых присутствует только икс, обратятся в обычную производную функции от икса. А слагаемые, в которых присутствуют и икс, и игрек, нужно дифференцировать, пользуясь правилом дифференцирования сложной функции, то есть учитывать, что игрек — это функция от икса. Если совсем просто, то в полученной производной слагаемого с иксом должно получиться: производная функции от игрека, умноженная на производную от игрека. Например, производная слагаемого 



Решаем задачи вместе
Пример 1. Найти производную функции, заданной неявно:

Решение. Дифференцируем обе части уравнения по иксу, считая, что игрек — функция от икса:

Отсюда получаем производную, которая требуется в задании:

Решение производной функции, заданной неявно, можно проверить на онлайн калькуляторе.
y = f(x) . Так, например, заданные неявно функции

не выражаются через элементарные функции, то есть эти уравнения нельзя разрешить относительно игрека. Поэтому и существует правило дифференцирования функции, заданной неявно, которое мы уже изучили и далее будем последовательно применять в других примерах.
Пример 2. Найти производную функции, заданной неявно:

Решение. Дифференцируем обе части уравнения по иксу:

Выражаем игрек штрих и — на выходе — производная функции, заданной неявно:

Пример 3. Найти производную функции, заданной неявно:

Решение. Дифференцируем обе части уравнения по иксу:

Выражаем и получаем производную:

Решение производной функции, заданной неявно, можно проверить на онлайн калькуляторе.
Пример 4. Найти производную функции, заданной неявно:

Решение. Дифференцируем обе части уравнения по иксу:

Выражаем и получаем производную:

Пример 5. Найти производную функции, заданной неявно:

Решение. Переносим слагаемые в правой части уравнение в левую часть и справа оставляем ноль. Дифференцируем обе части уравнения по иксу:
Путь к ответу и в конец сам ответ:
Решить задачи самостоятельно, а затем посмотреть решения
Пример 6. Найти производную функции, заданной неявно:
Пример 7. Найти производную функции, заданной неявно:
Пример 8. Найти производную функции, заданной неявно:
Источник
- Теория, и в конце – разбор из ЕГЭ
Я уже однажды писал о функции здесь (>>), и о том, что зря мы этого слова боимся. А теперь давайте поговорим о “производной”, которая полностью называется “производная функции”. Снова функция! И снова все проще, чем кажется 🙂
Производная – значит “выводимая” по определенному закону. Но сделать из одной функции другую можно многими разными способами. Однако “производной”, о которой мы говорим, называют то, что выводится единственным способом. И чтобы понять, в чем тут суть, нужно обратиться к истории математического анализа.
С развитием математики функции усложнялись, постоянно исследовать их графически было уже не так просто, а при этом было большое желание, используя формулу, узнать не только то, каково значение функции в любой точке, но также и то каково ее поведение! Плюс узнать в целом общую форму ее графика.
Это была мечта!
То есть вам дается формула любой функции, а вы по ней в два счета вычисляете и ее значение в точке “икс”, и то, растет она или убывает, и то, насколько быстро она растет или убывает, и то, где она меняет рост на убывание, и где пересечет ось “ОХ” и так далее!
Здорово же?
Вот для этих целей “сканирования” функций и придумали то, что мы называем “производной”. Давайте посмотрим на Рис 1. Здесь дан график некоторой функции f(x). Попробуем грубо определить его поведение при росте “х” недалеко от заданной точки “а”. Можно определять и при убывании, идея будет такой же. В самой точке “а” функция принимает значение f(a).
При смещении вправо на “дельта-икс”, значение аргумента (икса) становится равным х1. Точки на функции, соответствующие х=а и х=х1 – это “А” и “В”. У них будут соответствующие “игрековые” координаты f(a) и f(x1).
Если мы соединим точки А и В, то получим очень грубую иллюстрацию роста функции между этими точками. Мы как бы “спрямили” график. По графику и по “спрямленному отрезку” АВ видно, что между этими точками функция возрастает. Это также видно по оси ОУ – ведь f(x1) > f(a).
Пока, наверное, все слишком банально, очевидно и не интересно. Но сейчас все начнется. 🙂
Самое главное – ведь розовый отрезок АВ – это не истинное поведение функции, а ОЧЕНЬ ГРУБОЕ. Что же делать, чтобы используя “дельта-икс” оценить поведение функции более точно?
Правильно! Приблизить точку В к точке А. Ну, поскольку В уже занята, давайте отметим точку С, и пусть ее “иксовая” координата будет х2. Вот что получится:
Красный отрезок АС гораздо ближе описывает поведение функции. Он как бы больше “прижат” к самой функции. И мы понимаем, что функция возрастает от а до х2 гораздо быстрее, чем мы оценили промежутком от а до х1.
А какой же, все-таки, величиной оценивать этот рост? Ну, мы рисуем отрезки, а воз-то и ныне там! Ничего мы толком не прояснили, как аналитически оценивать поведение функции.
И тут мы возвращаемся к ТРЕУГОЛЬНИКАМ! Ведь в них мы можем определить через углы, как ведет себя одна сторона относительно другой стороны. Давайте на красном отрезке построим прямоугольный треугольник следующим образом:
То есть горизонтальный катет треугольника будет “дельта-икс2”, а вертикальный – “дельта-игрек2”. Но, зная катеты, мы можем найти тангенс угла “альфа”. А тангенс угла – очень хороший показатель поведения функции. То есть, если тангенс положительный, то функция растет. Если он равен, например, 1, то отрезок АС наклонен под углом в 45 градусов к горизонтали.
Отлично! То есть мы можем приблизительно оценивать поведение функции по тангенсам угла наклона отрезка между заданной точкой и чуть смещенной.
Но ведь это все равно не истинное значение, показывающее рост функции, верно? Чтобы найти истинное, нам нужно бесконечно приближать вторую точку к точке А. Вот примерно так это будет выглядеть:
Тогда уменьшая “дельта-икс” в воображении до нуля, мы получим уже не отрезок, соединяющий две точки графика, а касательную к нему!
Значит, нам нужен именно тангенс угла наклона касательной к оси ОХ, это и будет показатель роста или убывания функции в исследуемой точке (то есть при заданном “икс”).
На Рис. 3 мы используем запись через так называемые “пределы”, здесь lim (сокращенно от “limit”) и является математическим выражением для предела некоторого выражения.
Но ведь на ноль делить нельзя! А мы говорили, что “дельта-икс” должен быть практически нулем.
На самом деле “в пределе” мы как бы не доходим до истинного нуля “дельта-икс”, но бесконечно к нему приближаемся. А сама дробь с “дельта-игрек” в числителе и “дельта-икс” в знаменателе будет иметь конкретное значение при таком “предельном приближении”. Она-то и даст нам тангенс угла наклона.
Но все равно, наверное, не очень понятно, правда?
Мы пока не будем больше “закапываться” в глубины математического анализа. Но когда все это дело исследовали ученые, оказалось, что для любой функции (ну, почти для любой) можно найти другую вторую функцию, которая ВСЕГДА будет показывать именно тангенс угла наклона касательной первой функции к оси ОХ! Эту-то вторую функцию и назвали производной от первой, или просто ПРОИЗВОДНОЙ. Давайте посмотрим на несколько примеров. Производную функцию мы записываем со “штрихом” и читаем “игрек-штрих” или “эф штрих от икс”.
То есть у большинства функций есть соответствующая производная! У некоторых функций производные искать сложнее, у некоторых проще.
И тогда, если, например, мы хотим определить наклон параболы “у=х^2” в точке х=3, мы просто подставляем “тройку” в уравнение производной и получаем 2*3=6. Это и есть производная, или тангенс угла наклона.
Давайте разберем пример из ЕГЭ.
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Чтобы найти производную, нужно найти просто тангенс угла наклона касательной к оси ОХ. А для этого давайте просто достроим треугольник на зеленой линии (нам даже для подсказки выделены 2 жирных зеленых точки). Вот что получится:
Вот и всё!
Очень хочется, чтобы вы проще и легче воспринимали производные, да и в целом темы последних классов школы. Надеюсь, дверь в этот мир нам сегодня немного удалось приоткрыть. 🙂
На этом давайте пока завершим. Тема производной на самом деле шире, и понимаю, что рассказал пока не все.
- Скажите, все ли здесь достаточно понятно мы разобрали?
- Какие еще вопросы остались?
- Какие задачи о производной хотите разобрать?
Делитесь мыслями и предложениями в комментариях! Каждое мнение очень важно.
Спасибо за внимание и до встречи в новых заметках и статьях!
Производная фукнции, заданной неявно: руководство, примеры
Как найти производную функции, заданной неявно
Будем учиться находить производные функций, заданных неявно. Что значит неявно? Сравним с обычной функцией. Обычная функция задана уравнением вида y=f(x) , где игрек, то есть функция, задан некоторым выражением, в котором присутствует икс. Таким образом, из переменных в левой части — только игрек, в правой — только икс. Если же функция задана неявно, то в левой части различные слагаемые с игреком «смешаны» с различными слагаемыми с иксом (или переменной, обозначенной другой буквой). Примеры функций, заданных неявно:





При этом и икс, и игрек могут быть в различных степенях, а в одном слагаемом могут быть и игрек, и икс.
Если функция задана неявно, то как получить игрек, то есть явную функцию? Просто: выразить игрек через другую переменную, то есть получить в левой части только игрек. А если нужно найти производную функции, заданной неявно, то есть получить в левой части только игрек со штрихом? Нужно сначала найти производные обеих частей уравнения, то есть продифференцировать их. А затем выразить производную игрека через производные других переменных.
Теперь приведенный выше «скелет» решения обрастет «мясом», то есть необходимыми подробностями. Те слагаемые, в которых присутствует только икс, обратятся в обычную производную функции от икса. А слагаемые, в которых присутствуют и икс, и игрек, нужно дифференцировать, пользуясь правилом дифференцирования сложной функции, то есть учитывать, что игрек — это функция от икса. Если совсем просто, то в полученной производной слагаемого с иксом должно получиться: производная функции от игрека, умноженная на производную от игрека. Например, производная слагаемого 



Решаем задачи вместе
Пример 1. Найти производную функции, заданной неявно:

Решение. Дифференцируем обе части уравнения по иксу, считая, что игрек — функция от икса:

Отсюда получаем производную, которая требуется в задании:

Решение производной функции, заданной неявно, можно проверить на онлайн калькуляторе.
y = f(x) . Так, например, заданные неявно функции

не выражаются через элементарные функции, то есть эти уравнения нельзя разрешить относительно игрека. Поэтому и существует правило дифференцирования функции, заданной неявно, которое мы уже изучили и далее будем последовательно применять в других примерах.
Пример 2. Найти производную функции, заданной неявно:

Решение. Дифференцируем обе части уравнения по иксу:

Выражаем игрек штрих и — на выходе — производная функции, заданной неявно:

Пример 3. Найти производную функции, заданной неявно:

Решение. Дифференцируем обе части уравнения по иксу:

Выражаем и получаем производную:

Решение производной функции, заданной неявно, можно проверить на онлайн калькуляторе.
Пример 4. Найти производную функции, заданной неявно:

Решение. Дифференцируем обе части уравнения по иксу:

Выражаем и получаем производную:

Пример 5. Найти производную функции, заданной неявно:

Решение. Переносим слагаемые в правой части уравнение в левую часть и справа оставляем ноль. Дифференцируем обе части уравнения по иксу:
Путь к ответу и в конец сам ответ:
Решить задачи самостоятельно, а затем посмотреть решения
Пример 6. Найти производную функции, заданной неявно:
Пример 7. Найти производную функции, заданной неявно:
Пример 8. Найти производную функции, заданной неявно:
Примеры решения дифференциальных уравнений с ответами
Простое объяснение принципов решения дифференциальных уравнений и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Алгоритм решения дифференциальных уравнений
Дифференциальные уравнения не так сильно отличаются от привычных уравнений, где необходимо найти переменную x , как кажется на первый взгляд. Всё различие лишь в том, что в дифференциальных уравнениях мы ищем не переменную, а функцию у(х) , с помощью которой можно обратить уравнение в равенство.
Дифференциальное уравнение – это уравнение, содержащее саму функцию (y=y(x)), производные функции или дифференциалы (y′, y″) и независимые переменные (наиболее распространённая – х). Обыкновенным дифференциальным уравнением называют уравнение, в котором содержится неизвестная функция под знаком производной или под знаком дифференциала.
Чтобы решить ДУ, необходимо найти множество всех функций, которые удовлетворяют данному уравнению. Это множество в большинстве случаев выглядит следующим образом:y=f(x; С), где С – произвольная постоянная.
Проверить решённое ДУ можно, подставив найденную функцию в изначальное уравнение и убедившись, что уравнение обращается в тождество (равенство).
Примеры решения дифференциальных уравнений
Задание
Решить дифференциальное уравнение xy’=y.
Решение
В первую очередь, необходимо переписать уравнение в другой вид. Пользуясь
переписываем дифференциальное уравнение, получаем
Дальше смотрим, насколько реально разделить переменные, то есть путем обычных манипуляций (перенос слагаемых из части в часть, вынесение за скобки и пр.) получить выражение, где «иксы» с одной стороны, а «игреки» с другой. В данном уравнении разделить переменные вполне реально, и после переноса множителей по правилу пропорции получаем
Далее интегрируем полученное уравнение:
В данном случае интегралы берём из таблицы:
После того, как взяты интегралы, дифференциальное уравнение считается решённым. Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения.
– это общий интеграл. Также для удобства и красоты, его можно переписать в другом виде: y=Cx, где С=Const
Ответ
Задание
Найти частное решение дифференциального уравнения
Решение
Действуем по тому же алгоритму, что и в предыдущем решении.
Переписываем производную в нужном виде, разделяем переменные и интегрируем полученное уравнение:
Получили общий интеграл.Далее, воспользуемся свойством степеней, выразим у в «общем» виде и перепишем функцию:
Если – это константа, то
0]» title=»Rendered by QuickLaTeX.com» />
– тоже некоторая константа, заменим её буквой С:
– убираем модуль и теперь константа может принимать и положительные, и отрицательные значения.
Получаем общее решение:
Ответ
Задание
Решить дифференциальное уравнение
Решение
В первую очередь необходимо переписать производную в необходимом виде:
Второй шаг – разделение переменных и перенос со сменой знака второго слагаемого в правую часть:
После разделения переменных, интегрируем уравнение, как в примерах выше.
Чтобы решить интегралы из левой части, применим метод подведения функции под знак дифференциала:
В ответе мы получили одни логарифмы и константу, их тоже определяем под логарифм.
Далее упрощаем общий интеграл:
Приводим полученный общий интеграл к виду: F(x,y)=C:
Чтобы ответ смотрелся красивее, обе части необходимо возвести в квадрат.
Ответ
Задание
Найти частное решение дифференциального уравнения
удовлетворяющее начальному условию y(0)=ln2.
Решение
Первый шаг – нахождение общего решения. То, что в исходном уравнении уже находятся готовые дифференциалы dy и dx значительно упрощает нам решение.
Начинаем разделять переменные и интегрировать уравнение:
Мы получили общий интеграл и следующий шаг – выразить общее решение. Для этого необходимо прологарифмировать обе части. Знак модуля не ставим, т.к. обе части уравнения положительные.
Получаем общее решение:
Далее необходимо найти частное решение, которое соответствует заданному начальному условию y(0)=ln2.
В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:
Подставляем найденное значение константы C=1 в общее решение.
Ответ
Задание
Решить дифференциальное уравнение
Решение
При внимательном разборе данного уравнения видно, что можно разделить переменные, что и делаем, после интегрируем:
В данном случае константу C считается не обязательным определять под логарифм.
Ответ
Задание
Найти частное решение дифференциального уравнения
удовлетворяющее начальному условию y(1)=e. Выполнить проверку.
Решение
Как и в предыдущих примерах первым шагом будет нахождение общего решения. Для этого начинаем разделять переменные:
Общий интеграл получен, осталось упростить его. Упаковываем логарифмы и избавляемся от них:
можно выразить функцию в явном виде.
Осталось найти частное решение, удовлетворяющее начальному условию y(1)=e.
Подставляем найденное значение константы C=1 в общее решение.
Ответ
Проверка
Необходимо проверить, выполняется ли начальное условие:
Из равенства выше видно, что начальное условие y(1)=e выполнено.
Далее проводим следующую проверку: удовлетворяет ли вообще частное решение
дифференциальному уравнению. Для этого находим производную:
Подставим полученное частное решение
и найденную производную в исходное уравнение
Получено верное равенство, значит, решение найдено правильно.
Задание
Найти общий интеграл уравнения
Решение
Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:
Ответ
Задание
Найти частное решение ДУ.
Решение
Данное ДУ допускает разделение переменных. Разделяем переменные:
Найдем частное решение (частный интеграл), соответствующий заданному начальному условию
Подставляем в общее решение
Ответ
Задание
Решить дифференциальное уравнение
Решение
Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:
Левую часть интегрируем по частям:
В интеграле правой части проведем замену:
(здесь дробь раскладывается методом неопределенных коэффициентов)
Ответ
Задание
Решить дифференциальное уравнение
Решение
Данное уравнение допускает разделение переменных.
Разделяем переменные и интегрируем:
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)
Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5
Ввод распознает различные синонимы функций, как asin , arsin , arcsin
Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)
Список математических функций и констант :
• ln(x) — натуральный логарифм
• sh(x) — гиперболический синус
• ch(x) — гиперболический косинус
• th(x) — гиперболический тангенс
• cth(x) — гиперболический котангенс
• sch(x) — гиперболический секанс
• csch(x) — гиперболический косеканс
• arsh(x) — обратный гиперболический синус
• arch(x) — обратный гиперболический косинус
• arth(x) — обратный гиперболический тангенс
• arcth(x) — обратный гиперболический котангенс
• arsch(x) — обратный гиперболический секанс
• arcsch(x) — обратный гиперболический косеканс
источники:
http://nauchniestati.ru/spravka/primery-resheniya-differenczialnyh-uravnenij-s-otvetami/
http://mathdf.com/dif/ru/
13
Курс лекций
по
медицинской и биологической физике
ЛЕКЦИЯ
№1
ПРОИЗВОДНАЯ
И ДИФФЕРЕНЦИАЛ ФУНКЦИИ.
ЧАСТНЫЕ
ПРОИЗВОДНЫЕ.
1. Понятие
производной, ее механический и
геометрический смысл.
а)Приращение
аргумента и функции.
Пусть
дана функция y=f(х), где х – значение
аргумента из области определения
функции. Если выбрать два значения
аргумента хо и х из
определенного интервала области
определения функции, то разность между
двумя значениями аргумента называется
приращением аргумента:
х – хо=∆х.
Значение аргумента x можно определить
через x0 и его приращение:
х = хо+ ∆х.
Разность
между двумя значениями функции называется
приращением функции: ∆y =∆f =
f(хо+∆х) – f(хо).
П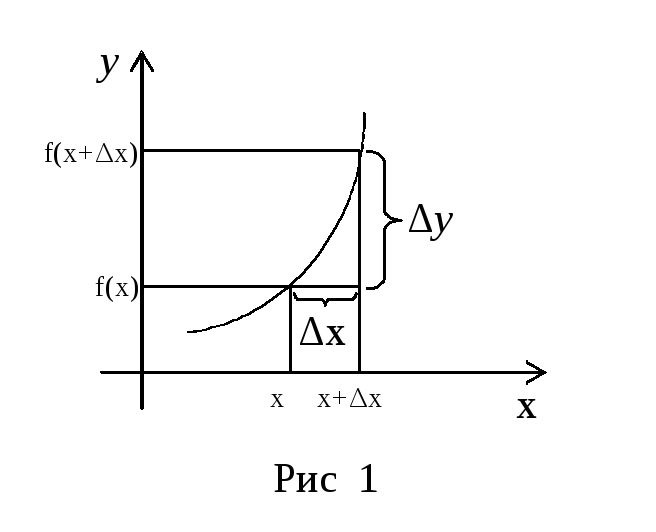
аргумента и функции можно представить
графически (рис.1). Приращение аргумента
и приращение функции может быть как
положительным, так и отрицательным. Как
следует из рис.1 геометрически приращение
аргумента ∆х изображается приращением
абсциссы, а приращение функции ∆у –
приращением ординаты. Вычисление
приращения функции следует проводить
в следующем порядке:
-
даем аргументу
приращение ∆х и получаем значение –
x+Δx;
2) находим значение
функции для значения аргумента (х+∆х)
– f(х+∆х);
3) находим приращение
функции ∆f=f(х + ∆х) – f(х).
Пример: Определить
приращение функции y=х2, если
аргумент изменился от хо=1 до х=3.
Для точки хозначение функции
f(хо)=х²о; для точки (хо+∆х)
значение функции f(хо+∆х) = (хо+∆х)2
= х²о+2хо∆х+∆х2,
откуда ∆f = f(хо+∆х)–f(хо) =
(хо+∆х)2–х²о=
х²о+2хо∆х+∆х2–х²о= 2хо∆х+∆х2; ∆f = 2хо∆х+∆х2;
∆х = 3–1 = 2; ∆f =2·1·2+4 = 8.
б) Задачи, приводящие
к понятию производной. Определение
производной, ее физический смысл.
Понятие приращения
аргумента и функции необходимы для
введения понятия производной, которое
исторически возникло исходя из
необходимости определения скорости
тех или иных процессов.
Рассмотрим, каким
образом можно определить скорость
прямолинейного движения. Пусть тело
движется прямолинейно по закону: ∆Ѕ=
·∆t. Для равномерного
движения:= ∆Ѕ/∆t.
Для
переменного движения значение ∆Ѕ/∆t
определяет значениеср.,
т.е.ср. =∆Ѕ/∆t.
Но средняя скорость не дает возможности
отразить особенности движения тела и
дать представление об истинной скорости
в момент времени t. При уменьшении
промежутка времени, т.е. при ∆t→0 средняя
скорость стремится к своему пределу
– мгновенной скорости:
мгн.=
ср.=
∆Ѕ/∆t.
Таким же образом
определяется и мгновенная скорость
химической реакции:
мгн.=
ср.=
∆х/∆t,
где х – количество
вещества, образовавшееся при химической
реакции за время t. Подобные задачи по
определению скорости различных процессов
привели к введению в математике понятия
производной функции.
Пусть
дана непрерывная функция f(х), определенная
на интервале ]а,в[ и ее приращение
∆f=f(х+∆х)–f(х). Отношениеявляется функцией ∆х и выражает среднюю
скорость изменения функции.
Предел
отношения
,
когда ∆х→0, при условии, что этот
предел существует, называется производной
функции:
y’x=.
Производная обозначается:
– (игрек штрих по икс);f‘(х)
– (эф штрих по икс);
y’
– (игрек штрих); dy/dх – (дэ игрек по
дэ икс);
–
(игрек с точкой).
Исходя
из определения производной, можно
сказать, что мгновенная скорость
прямолинейного движения есть производная
от пути по времени:
мгн.=
S’t =
f‘(t).
Таким
образом, можно сделать вывод, что
производная функции по аргументу х есть
мгновенная скорость изменения функции
f(х):
у’x=f‘(х)=мгн.
В этом и заключается
физический смысл производной. Процесс
нахождения производной называется
дифференцированием, поэтому выражение
«продифференцировать функцию» равносильно
выражению «найти производную функции».
в) Геометрический
смысл производной.
П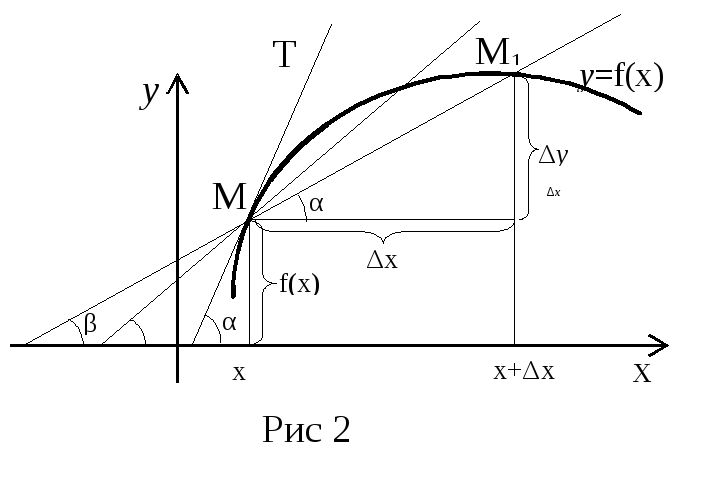
функции у = f(х) имеет простой
геометрический смысл, связанный с
понятием касательной к кривой линии в
некоторой точкеM. При
этом, касательную, т.е. прямую линию
аналитически выражают в виде у = кх = tg· х, где
– угол наклона касательной (прямой)
к оси Х. Представим непрерывную кривую
как функцию у= f(х), возьмем на кривой
точкуMи близкую к ней
точку М1 и приведем через них
секущую. Ее угловой коэффициент ксек=tg
β =.
Если приближать точку М1к M, то
приращение аргумента ∆х будет
стремиться к нулю, а секущая при β=α
займет положение касательной. Из рис.2
следует:tgα =
tgβ
=
=у’x.
Но tgα равен угловому коэффициенту
касательной к графику функции:
к = tgα =
=у’x
= f‘(х). Итак, угловой коэффициент
касательной к графику функции в данной
точке равен значению ее производной в
точке касания. В этом и состоит
геометрический смысл производной.
г) Общее правило
нахождения производной.
Исходя
из определения производной, процесс
дифференцирования функции можно
представить следующим образом:
-
выбрав некоторое
значение аргумента х, дают ему приращениех
и находят приращенное значение функции
в точке (х + ∆х), равное
f(х+∆х) = f(х)+∆f;
-
находят приращение
функции: ∆f= f(х + ∆х) –
f(х); -
составляют отношение
приращения функции к приращению
аргумента:
;
-
находят предел
отношения
при ∆x→0, если этот предел существует:
=f'(х).
Пример: f(х)=х2;
f‘(х)=?.
-
f(х +∆х) = (х+∆х)2;
-
∆f= f(х+∆х)-f(х) = (х+∆х)2-х2=
х2+2х∆х+∆х2-х2 = 2х
∆х+∆х2; -
=
=
2х+х;
-
f‘(х) =
=
(2х+∆х)
=
2х+
∆х
= 2х; -
f‘(х) = 2х.
Однако, как видно даже
из этого простого примера, применение
указанной последовательности при взятии
производных – процесс трудоемкий и
сложный. Поэтому для различных функций
вводятся общие формулы дифференцирования,
которые представлены в виде таблицы
«Основных формул дифференцирования
функций».
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #