Егэ как найти наибольшее наименьшие значение функции – Сайт, где вы сможете решить свои вопросы

Всего: 660 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Найдите наименьшее значение функции y= левая круглая скобка x минус 8 правая круглая скобка e в степени левая круглая скобка x минус 7 правая круглая скобка на отрезке левая квадратная скобка 6;8 правая квадратная скобка .

Найдите наибольшее значение функции y=12 косинус x плюс 6 корень из: начало аргумента: 3 конец аргумента умножить на x минус 2 корень из: начало аргумента: 3 конец аргумента Пи плюс 6 на отрезке левая квадратная скобка 0; дробь: числитель: Пи , знаменатель: 2 конец дроби правая квадратная скобка .

Найдите наименьшее значение функции y=5 косинус x минус 6x плюс 4 на отрезке левая квадратная скобка минус дробь: числитель: 3 Пи , знаменатель: 2 конец дроби ;0 правая квадратная скобка .

Найдите наибольшее значение функции y=15x минус 3 синус x плюс 5 на отрезке левая квадратная скобка минус дробь: числитель: Пи , знаменатель: 2 конец дроби ;0 правая квадратная скобка .

Найдите наименьшее значение функции y=9 косинус x плюс 14x плюс 7 на отрезке левая квадратная скобка 0; дробь: числитель: 3 Пи , знаменатель: 2 конец дроби правая квадратная скобка .

Найдите наименьшее значение функции y=7 синус x минус 8x плюс 9 на отрезке левая квадратная скобка минус дробь: числитель: 3 Пи , знаменатель: 2 конец дроби ;0 правая квадратная скобка .

Найдите наибольшее значение функции y=10 синус x минус дробь: числитель: 36, знаменатель: Пи конец дроби x плюс 7 на отрезке левая квадратная скобка минус дробь: числитель: 5 Пи , знаменатель: 6 конец дроби ;0 правая квадратная скобка .

Найдите наибольшее значение функции y=2 косинус x минус дробь: числитель: 18, знаменатель: Пи конец дроби x плюс 4 на отрезке левая квадратная скобка минус дробь: числитель: 2 Пи , знаменатель: 3 конец дроби ;0 правая квадратная скобка .

Найдите наименьшее значение функции y=5 синус x плюс дробь: числитель: 24, знаменатель: Пи конец дроби x плюс 6 на отрезке левая квадратная скобка минус дробь: числитель: 5 Пи , знаменатель: 6 конец дроби ;0 правая квадратная скобка .

Найдите наименьшее значение функции y=3 синус x плюс дробь: числитель: 30, знаменатель: Пи конец дроби x плюс 3 на отрезке левая квадратная скобка минус дробь: числитель: 5 Пи , знаменатель: 6 конец дроби ;0 правая квадратная скобка .

Найдите наибольшее значение функции y=3 тангенс x минус 3x плюс 5 на отрезке левая квадратная скобка минус дробь: числитель: Пи , знаменатель: 4 конец дроби ;0 правая квадратная скобка .

Найдите наибольшее значение функции y=12 тангенс x минус 12x плюс 3 Пи минус 5 на отрезке левая квадратная скобка минус дробь: числитель: Пи , знаменатель: 4 конец дроби ; дробь: числитель: Пи , знаменатель: 4 конец дроби правая квадратная скобка .

Найдите точку минимума функции y= левая круглая скобка x плюс 16 правая круглая скобка e в степени левая круглая скобка x минус 16 правая круглая скобка .

Найдите точку минимума функции y= левая круглая скобка x плюс 11 правая круглая скобка e в степени левая круглая скобка x минус 11 правая круглая скобка .

Найдите точку максимума функции y= левая круглая скобка 9 минус x правая круглая скобка e в степени левая круглая скобка x плюс 9 правая круглая скобка .

Найдите точку минимума функции y= левая круглая скобка 3 минус x правая круглая скобка e в степени левая круглая скобка 3 минус x правая круглая скобка .

Найдите точку максимума функции y= левая круглая скобка x плюс 16 правая круглая скобка e в степени левая круглая скобка 16 минус x правая круглая скобка .

Найдите наименьшее значение функции y=3x минус натуральный логарифм левая круглая скобка x плюс 3 правая круглая скобка в кубе на отрезке [−2,5; 0].

Найдите наибольшее значение функции y= натуральный логарифм левая круглая скобка x плюс 5 правая круглая скобка в степени левая круглая скобка 5 правая круглая скобка минус 5x на отрезке [−4,5; 0].

Найдите наименьшее значение функции y=4x минус 4 натуральный логарифм левая круглая скобка x плюс 7 правая круглая скобка плюс 6 на отрезке левая квадратная скобка минус 6,5;0 правая квадратная скобка .

Всего: 660 1–20 | 21–40 | 41–60 | 61–80 …

Источник

Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.

Вот какие типы задач могут встретиться в этом задании:

Нахождение точек максимума и минимума функций

Исследование сложных функций

Нахождение наибольших и наименьших значений функций на отрезке

Нахождение точек максимума и минимума функций

1. Найдите точку максимума функции $displaystyle y=-{{x^2+289}over{x}}.$

Найдем производную функции.

Приравняем производную к нулю. Получим:

$x^2=289Leftrightarrow left[ begin{array}{c} x=17, hfill \ x=-17. end{array} right.$

Исследуем знаки производной.

В точке $x = 17$ производная $y$ меняет знак с «плюса» на «минус». Значит, $x= 17$ — точка максимума функции $y(x).$

Ответ: 17.

2. Найдите точку минимума функции $y=2x^2-5x+lnx-3.$

Найдем производную функции.

$y{$

Приравняем производную к нулю.

$4x-5+{{1}over{x}}=0Leftrightarrow 4x^2-5x+1=0Leftrightarrow left[ begin{array}{c} x=1, \ x={{1}over{4}}. end{array} right.$

Определим знаки производной.

В точке $x = 1$ производная $y$ меняет знак с «минуса» на «плюс». Значит, $x= 1$ — точка минимума функции $y(x).$

Ответ: 1.

Исследование сложных функций

3. Найдите точку максимума функции $y=2^{5-8x-x^2}.$

Перед нами сложная функция $y=2^{5-8x-x^2}.$ Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.

Так как функция $y=2^t$ монотонно возрастает, точка максимума функции $y=2^{5-8x-x^2}$ будет при том же $x_0$ , что и точка максимума функции $tleft(xright)=5-8x-x^2.$ А ее найти легко.

$t^{$

$t^{$ при $x=-4$ . В точке $x = -4$ производная ${{ t}}^{{$ меняет знак с «плюса» на «минус». Значит, $x= - 4$ — точка максимума функции ${ t}left({ x}right)$ .

Заметим, что точку максимума функции $tleft(xright)=5-8x-x^2$ можно найти и без производной.

Графиком функции $tleft(xright)$ является парабола ветвями вниз, и наибольшее значение $tleft(xright)$ достигается в вершине параболы, то есть при $x=-frac{8}{2}=-4.$

Ответ: – 4.

4. Найдите абсциссу точки максимума функции $y=sqrt{4-4x-x^2}.$

Напомним, что абсцисса — это координата по $X.$

Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.

Так как функция $y=sqrt{z}$ монотонно возрастает, точка максимума функции $y=sqrt{4-4x-x^2}$ является и точкой максимума функции $tleft(xright)=4-4x-x^2.$

Это вершина квадратичной параболы $tleft(xright)=4-4x-x^2;x_0=frac{-4}{2}=-2.$

Нахождение наибольших и наименьших значений функций на отрезке

5. Найдите наибольшее значение функции $y=x^3+2x^2-4x+4$ на отрезке $[-2;0].$

Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.

Будем искать точку максимума функции $y=x^3+2x^2-4x+4$ с помощью производной. Найдем производную и приравняем ее к нулю.

$y$

${3x}^2+4x-4=0;$

$D=64;x=frac{-4pm 8}{6};x_1=frac{2}{3},x_2=-2.$

Найдем знаки производной.

В точке $x = - 2$ производная равна нулю и меняет знак с “+” на “-“. Значит, x = – 2 — точка максимума функции $y(x)$ . Поскольку при $xin [-2;0]$ функция $y(x)$ убывает, $y_{max}left(xright)=yleft(-2right)=12.$ В этой задаче значение функции на концах отрезка искать не нужно.

Ответ: 12.

6. Найдите наименьшее значение функции $y={4x}^2-10x+2lnx-5$ на отрезке $[0,3;3].$

Найдем производную функции $y={4x}^2-10x+2lnx-5$ и приравняем ее к нулю.

$y$ при $x_1=1,x_2=frac{1}{4}.$

Найдем знаки производной.

Точка $x_1=1$ — точка минимума функции $yleft(xright)$ . Точка $x_2=frac{1}{4}$ не лежит на отрезке $[0,3;1].$ Поэтому

и Значит, наименьшее значение функции на отрезке $left[0,3;1right]$ достигается при $x=1.$ Найдем это значение.

$y_{min}left(xright)=yleft(1right)=4-10-5=-11.$

Ответ: -11.

7. Найдите наименьшее значение функции $y=9x-{ln left(9xright)}+3$ на отрезке $left[frac{1}{18};frac{5}{18}right].$

Иногда перед тем, как взять производную, формулу функции полезно упростить.

$y=9x-{ln left(9xright)}+3=9x-{ln 9-{ln x}}+3.$

Мы применили формулу для логарифма произведения. $y$ при $x=frac{1}{9}.$

Если то Если , то

Значит, $x=frac{1}{9}$ — точка минимума функции $y(x)$ . В этой точке и достигается наименьшее значение функции на отрезке $left[frac{1}{18};frac{5}{18}right].$

$y_{min}left(xright)=yleft(frac{1}{2}right)=1+3=4.$

Ответ: 4.

8. Найдите наибольшее значение функции $y(x)=14x-7tgx-3,5pi +11$ на отрезке $left[-frac{pi }{3};frac{pi }{3}right].$

Найдем производную функции $y(x)=14x-7tgx-3,5pi +11.$ $y$

Приравняем производную к нулю: $14-frac{7}{{cos}^2x}=0.$

${cos}^2x=frac{1}{2}.$

${cos}^2x=pm frac{1}{sqrt{2}}=pm frac{sqrt{2}}{2}$ . Поскольку $xin left[-frac{pi }{3};frac{pi }{3}right], y$ если $x=pm frac{pi }{4}.$

Найдем знаки производной на отрезке $left[-frac{pi }{3};frac{pi }{3}right].$

При $x=frac{pi }{4}$ знак производной меняется с «плюса» на «минус». Значит, $x=frac{pi }{4}$ — точка максимума функции $y(x).$

Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при $x=-frac{pi }{3}$ и $x =frac{pi }{4}.$

$yleft(frac{pi }{4}right)=-7+11=4;$

Мы нашли, что $y_{max}left(xright)=yleft(frac{pi }{4}right)=-7+11=4.$

Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при $-frac{pi }{3}$ не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.

Ответ: 4.

9. Найдите наименьшее значение функции $y=e^{2x}-{8e}^x+9$ на отрезке [0;2].

Снова сложная функция. Запишем полезные формулы:

${{(e}^{-x})}^{$

${left(e^{cx}right)}^{$

${(e}^{x+a})$

Найдем производную функции $y=e^{2x}-{8e}^x+9.$

$y$

$y$ если $e^x=4.$ Тогда $x=ln4.$

При $x=ln4$ знак производной меняется с «минуса» на «плюс». Значит, $x=ln4$ — точка минимума функции $y(x).$ $yleft(ln4right)=4^2-8cdot 4+9=16-32+9=-7.$

Ответ: -7.

10. Найдите наибольшее значение функции $y=12cosx+6sqrt{3}x-2sqrt{3}pi +6$ на отрезке $left[0;frac{pi }{2}.right]$

Как всегда, возьмем производную функции и приравняем ее к нулю.

$y$

$y$ $12sinx=6sqrt{3};$

$sinx=frac{sqrt{3}}{2}.$

По условию, $xin left[0;frac{pi }{2}right]$ . На этом отрезке условие $sinx=frac{sqrt{3}}{2}$ выполняется только для $x=frac{pi }{3}.$ Найдем знаки производной слева и справа от точки $x=frac{pi }{3}.$

В точке $x_0=frac{pi }{3}$ производная функции меняет знак с «плюса» на «минус». Значит, точка $x_0=frac{pi }{3}$ — точка максимума функции $y(x)$ . Других точек экстремума на отрезке $left[0;frac{pi }{2}right]$ функция не имеет, и наибольшее значение функции ${ y=12cosx+6}sqrt{{ 3}}{ }{ x}{ -}{ 2}sqrt{{ 3}}{ }pi { +6}$ на отрезке $left[{ 0};frac{pi }{{ 2}}right]$ достигается при ${ x=}frac{pi }{{ 3}}.$

$y_{max}left(xright)=yleft(frac{pi }{3}right)=12.$

Ответ: 12.

11.Найдите наименьшее значение функции $y=16x-6sinx+6$ на отрезке $left[0;frac{pi }{2}right].$

Найдем производную функции и приравняем ее к нулю. — нет решений.

Что это значит? Производная функции $y=16x-6sinx+6$ не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.

Поскольку $cosxle 1$ , получим, что для всех $x$ , и функция $yleft(xright)=16x-6sinx+6$ монотонно возрастает при $xin left[0;frac{pi }{2}right].$

Значит, наименьшее свое значение функция принимает в левом конце отрезка $left[{ 0};frac{pi }{{ 2}}right]$ , то есть при $x=0.$

$y_{min}left(xright)=yleft(0right)=6.$

Ответ: 6

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 11 Профильного ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение ординаты на рассматриваемом интервале.

Чтобы найти наибольшее или наименьшее значение функции необходимо:

Найти производную функции $f'(х)$
Найти стационарные точки, решив уравнение $f'(х)=0$
Проверить, какие стационарные точки входят в заданный отрезок.
Вычислить значение функции на концах отрезка и в стационарных точках из п.3
Выбрать из полученных результатов наибольшее или наименьшее значение.

Чтобы найти точки максимума или минимума необходимо:

Найти производную функции $f'(х)$
Найти стационарные точки, решив уравнение $f'(х)=0$
Разложить производную функции на множители.
Начертить координатную прямую, расставить на ней стационарные точки и определить знаки производной в полученных интервалах, пользуясь записью п.3.
Найти точки максимума или минимума по правилу: если в точке производная меняет знак с плюса на минус, то это будет точка максимума (если с минуса на плюс, то это будет точка минимума). На практике удобно использовать изображение стрелок на промежутках: на промежутке, где производная положительна, стрелка рисуется вверх и наоборот.

Таблица производных некоторых элементарных функций:

Функция	Производная
$c$	$0$
$x$	$1$
$x^n, n∈N$	$nx^{n-1}, n∈N$
${1}/{x}$	$-{1}/{x^2}$
${1}/x{^n}, n∈N$	$-{n}/{x^{n+1}}, n∈N$
$√^n{x}, n∈N$	${1}/{n√^n{x^{n-1}}, n∈N$
$sinx$	$cosx$
$cosx$	$-sinx$
$tgx$	${1}/{cos^2x}$
$ctgx$	$-{1}/{sin^2x}$
$cos^2x$	$-sin2x$
$sin^2x$	$sin2x$
$e^x$	$e^x$
$a^x$	$a^xlna$
$lnx$	${1}/{x}$
$log_{a}x$	${1}/{xlna}$

Основные правила дифференцирования

1. Производная суммы и разности равна производной каждого слагаемого

$(f(x) ± g(x))′= f′(x)± g′(x)$

Пример:

Найти производную функции $f(x) = 3x^5 – cosx + {1}/{x}$

Производная суммы и разности равна производной каждого слагаемого

$f′(x)=(3x^5)′–(cosx)′+({1}/{x})’=15x^4+sinx-{1}/{x^2}$

2. Производная произведения.

$(f(x)∙g(x))′=f′(x)∙g(x)+f(x)∙g(x)′$

Пример:

Найти производную $f(x)=4x∙cosx$

$f′(x)=(4x)′∙cosx+4x∙(cosx)′=4∙cosx-4x∙sinx$

3. Производная частного

$({f(x)}/{g(x)})’={f^'(x)∙g(x)-f(x)∙g(x)’}/{g^2(x)}$

Пример:

Найти производную $f(x)={5x^5}/{e^x}$

$f'(x)={(5x^5)’∙e^x-5x^5∙(e^x)’}/{(e^x)^2}={25x^4∙e^x-5x^5∙e^x}/{(e^x)^2}$

4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции

$f(g(x))′=f′(g(x))∙g′(x)$

Пример:

$f(x)= cos(5x)$

$f′(x)=cos′(5x)∙(5x)′= – sin(5x)∙5= -5sin(5x)$

Пример:

Найдите точку минимума функции $y=2x-ln⁡(x+11)+4$

Решение:

1. Найдем ОДЗ функции: $х+11>0; х>-11$

2. Найдем производную функции $y’=2-{1}/{x+11}={2x+22-1}/{x+11}={2x+21}/{x+11}$

3. Найдем стационарные точки, приравняв производную к нулю

${2x+21}/{x+11}=0$

Дробь равна нулю если числитель равен нулю, а знаменатель не равен нулю

$2x+21=0; x≠-11$

$2х=-21$

$х=-10,5$

4. Начертим координатную прямую, расставим на ней стационарные точки и определим знаки производной в полученных интервалах. Для этого подставим в производную любое число из крайней правой области, например, нуль.

$y'(0)={2∙0+21}/{0+11}={21}/{11}>0$

5. В точке минимума производная меняет знак с минуса на плюс, следовательно, точка $-10,5$ – это точка минимума.

Ответ: $-10,5$

Пример:

Найдите наибольшее значение функции $y=6x^5-90x^3-5$ на отрезке $[-5;1]$

Решение:

1. Найдем производную функции $y′=30x^4-270x^2$

2. Приравняем производную к нулю и найдем стационарные точки

$30x^4-270x^2=0$

Вынесем общий множитель $30x^2$ за скобки

$30x^2(x^2-9)=0$

$30x^2(х-3)(х+3)=0$

Приравняем каждый множитель к нулю

$x^2=0 ; х-3=0; х+3=0$

$х=0;х=3;х=-3$

3. Выберем стационарные точки, которые принадлежат заданному отрезку $[-5;1]$

Нам подходят стационарные точки $х=0$ и $х=-3$

4. Вычислим значение функции на концах отрезка и в стационарных точках из п.3

$y(-5)= 6∙(-5)^5-90∙(-5)^3-5=6∙(-3125)+90∙125-5= -18750+11250-5=-7505$

$y(-3)= 6∙(-3)^5-90∙(-3)^3-5=-1458+2430-5=967$

$y(0)= -5$

$y(1)= 6∙1^5-90∙1^3-5=6-90-5= -89$

Наибольшее значение равно $967$

Ответ: $967$

Источник

Лайфхаки ЕГЭ. Наибольшее (наименьшее) значение функции на отрезке.

Автор: Новицкая Марина Викторовна

Название учреждения: КГБОУ «Бийский лицей–интернат Алтайского края»

Тема занятия: «Наибольшее(наименьшее) значение функции на отрезке»

Область применения разработки: школы, лицеи, гимназии на уровне среднего общего образования, в классах естественно–

научного и гуманитарного профиля

Возрастная группа обучающихся: 11 класс (16-17 лет)

При подготовке к сдаче ЕГЭ профильного уровня в ходе решения заданий на нахождение наибольшего и наименьшего

значения функции, точек максимума и минимума функции (Задание №12) у учащихся возникают сложности и сомнения о

правильности выполнения задания.

Проанализировав задания №12 профильного ЕГЭ предлагаю Вам лайфхаки, позволяющие более ускоренно решить задачи

на нахождение наибольшего и наименьшего значения функции, точек максимума и минимума некоторых функций без

использования производной.

Задание 12 . Найти наибольшее (наименьшее) значение функции на отрезке.

ОТВЕТ: «красивое число», т.е. без радикалов, числа π, буквы е и т.д

Источник

12. Исследование функций с помощью производной

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Поиск наибольшего/наименьшего значения у сложных функций

(blacktriangleright) Для того, чтобы найти наибольшее/наименьшее значение функции на отрезке ([a,b]), необходимо схематично изобразить график функции на этом отрезке.
В задачах из данной подтемы это можно сделать с помощью производной: найти промежутки возрастания ((f’>0)) и убывания ((f'<0)) функции, критические точки (где (f’=0) или (f’) не существует).

(blacktriangleright) Не стоит забывать, что наибольшее/наименьшее значение функция может принимать не только во внутренних точках отрезка ([a,b]), а также на его концах.

(blacktriangleright) Наибольшее/наименьшее значение функции — это значение координаты (y=f(x)).

(blacktriangleright) Производная сложной функции (f(t(x))) ищется по правилу: [{Large{f'(x)=f'(t)cdot t'(x)}}]
[begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{1} & c & 0\&&\
textbf{2} & x^a & acdot x^{a-1}\&&\
textbf{3} & ln x & dfrac1x\&&\
textbf{4} & log_ax & dfrac1{xcdot ln a}\&&\
textbf{5} & e^x & e^x\&&\
textbf{6} & a^x & a^xcdot ln a\&&\
textbf{7} & sin x & cos x\&&\
textbf{8} & cos x & -sin x\[1ex]
hline
end{array} quad quad quad quad
begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{9} & mathrm{tg}, x & dfrac1{cos^2 x}\&&\
textbf{10} & mathrm{ctg}, x & -,dfrac1{sin^2 x}\&&\
textbf{11} & arcsin x & dfrac1{sqrt{1-x^2}}\&&\
textbf{12} & arccos x & -,dfrac1{sqrt{1-x^2}}\&&\
textbf{13} & mathrm{arctg}, x & dfrac1{1+x^2}\&&\
textbf{14} & mathrm{arcctg}, x & -,dfrac1{1+x^2}\[0.5ex]
hline
end{array}]

Задание
1

#2357

Уровень задания: Равен ЕГЭ

Найдите наименьшее значение функции (y = e^{x^2 – 4}) на отрезке ([-10; -2]).

ОДЗ: (x) – произвольный.

1) [y’ = 2xcdot e^{x^2 – 4}]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [2xcdot e^{x^2 – 4} = 0qquadLeftrightarrowqquad x = 0,.] Таким образом, (y’ = 0) при (x = 0). Производная существует при любом (x).

2) Найдём промежутки знакопостоянства (y’):

3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([-10; -2]):

4) Эскиз графика на отрезке ([-10; -2]):

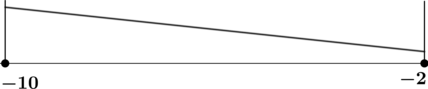
Таким образом, наименьшего на ([-10; -2]) значения функция достигает в (x = -2).

[y(-2) = e^{4 – 4} = 1,.] Итого: (1) – наименьшее значение функции (y) на ([-10; -2]).

Ответ: 1

Задание
2

#2355

Уровень задания: Равен ЕГЭ

Найдите наибольшее значение функции (y = sqrt{2}cdotsqrt{x^2 + 1}) на отрезке ([-1; 1]).

ОДЗ: (x) – произвольный.

1) [y’ = sqrt{2}cdotdfrac{2x}{2sqrt{x^2 + 1}} = sqrt{2}cdotdfrac{x}{sqrt{x^2 + 1}}]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [sqrt{2}cdotdfrac{x}{sqrt{x^2 + 1}} = 0qquadLeftrightarrowqquad x = 0,.] Производная существует при любом (x).

2) Найдём промежутки знакопостоянства (y’):

3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([-1; 1]):

4) Эскиз графика на отрезке ([-1; 1]):

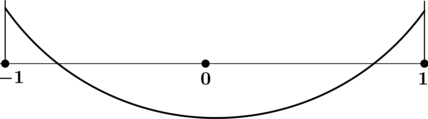
Таким образом, наибольшего на ([-1; 1]) значения функция достигает в (x = -1) или в (x = 1). Сравним значения функции в этих точках.

[y(-1) = sqrt{2}cdotsqrt{1 + 1} = sqrt{2}cdotsqrt{2} = 2qquad y(1) = sqrt{2}cdotsqrt{1 + 1} = sqrt{2}cdotsqrt{2} = 2,.] Итого: (2) – наибольшее значение функции (y) на ([-1; 1]).

Ответ: 2

Задание
3

#2356

Уровень задания: Равен ЕГЭ

Найдите наименьшее значение функции (y = cos 2x) на отрезке ([0; pi]).

ОДЗ: (x) – произвольный.

1) [y’ = -2cdot sin 2x]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [-2cdot sin 2x = 0qquadLeftrightarrowqquad 2x = pi n, ninmathbb{Z}qquadLeftrightarrowqquad x = dfrac{pi n}{2}, ninmathbb{Z},.] Производная существует при любом (x).

2) Найдём промежутки знакопостоянства (y’):

(здесь бесконечное число промежутков, в которых чередуются знаки производной).

3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([0; pi]):

4) Эскиз графика на отрезке ([0; pi]):

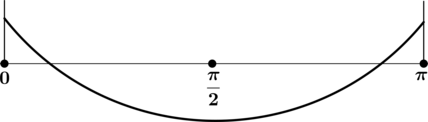
Таким образом, наименьшего на ([0; pi]) значения функция достигает в (x = dfrac{pi}{2}).

[yleft(dfrac{pi}{2}right) = cos pi = -1,.] Итого: (-1) – наименьшее значение функции (y) на ([0; pi]).

Ответ: -1

Задание
4

#915

Уровень задания: Равен ЕГЭ

Найдите наибольшее значение функции

(y = -log_{17}(2x^2 – 2sqrt{2}x + 2)).

ОДЗ: (2x^2 – 2sqrt{2}x + 2 > 0). Решим на ОДЗ:

1) Обозначим (2x^2-2sqrt{2}x+2=t(x)), тогда (y(t)=-log_{17}t).

[y’ = y’_tcdot t’_x = (-log_{17}t)’cdot(2x^2-2sqrt{2}x+2)’ = -dfrac{1}{ln 17}cdotdfrac{1}{t}cdot(4x-2sqrt{2}) = -dfrac{1}{ln 17}~cdot~dfrac{4x-2sqrt{2}}{2x^2-2sqrt{2}x+2}.]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [-dfrac{1}{ln 17}cdotdfrac{4x-2sqrt{2}}{2x^2-2sqrt{2}x+2} = 0qquadLeftrightarrowqquad 4x-2sqrt{2} = 0] – на ОДЗ, откуда находим корень (x = dfrac{sqrt{2}}{2}). Производная функции (y) не существует при (2x^2-2sqrt{2}x+2 = 0), но у данного уравнения отрицательный дискриминант, следовательно, у него нет решений. Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства (y’):

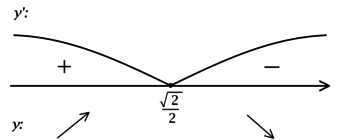
3) Эскиз графика:

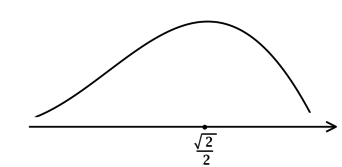
Таким образом, наибольшее значение функция достигает в (x = dfrac{sqrt{2}}{2}):

(yleft(dfrac{sqrt{2}}{2}right) = -log_{17}1 = 0),

Итого: (0) – наибольшее значение функции (y).

Ответ: 0

Задание
5

#2344

Уровень задания: Равен ЕГЭ

Найдите наименьшее значение функции

(y = log_{3}(x^2 + 8x + 19)).

ОДЗ: (x^2 + 8x + 19 > 0). Решим на ОДЗ:

1) Обозначим (x^2 + 8x + 19=t(x)), тогда (y(t)=log_{3}t).

[y’ = y’_tcdot t’_x = (log_{3}t)’cdot(x^2 + 8x + 19)’ = dfrac{1}{ln 3}cdotdfrac{1}{t}cdot(2x+8) = dfrac{1}{ln 3}~cdot~dfrac{2x+8}{x^2 + 8x + 19}.]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{1}{ln 3}cdotdfrac{2x+8}{x^2 + 8x + 19} = 0qquadLeftrightarrowqquad 2x+8 = 0] – на ОДЗ, откуда находим корень (x = -4). Производная функции (y) не существует при (x^2 + 8x + 19 = 0), но у данного уравнения отрицательный дискриминант, следовательно, у него нет решений. Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства (y’):

3) Эскиз графика:

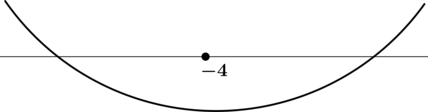
Таким образом, (x = -4) – точка минимума функции (y) и наименьшее значение достигается в ней:

(y(-4) = log_{3}3 = 1).

Итого: (1) – наименьшее значение функции (y).

Ответ: 1

Задание
6

#917

Уровень задания: Сложнее ЕГЭ

Найдите наибольшее значение функции

(y = -e^{(x^2 – 12x + 36 + 2ln 2)}).

1) Обозначим (x^2 – 12x + 36 + 2ln 2=t(x)), тогда (y(t)=-e^{t}).

[y’ = y’_tcdot t’_x = (-e^{t})’cdot(x^2 – 12x + 36 + 2ln 2)’ = -e^{t}cdot(2x-12) = -e^{x^2 – 12x + 36 + 2ln 2}cdot(2x-12).]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [-e^{x^2 – 12x + 36 + 2ln 2}cdot(2x-12) = 0qquadLeftrightarrowqquad 2x-12 = 0] (так как (e^{x^2 – 12x + 36 + 2ln 2} = e^{t}), но (e^{t} > 0) при любом (t)), откуда находим корень (x = 6). Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства (y’):

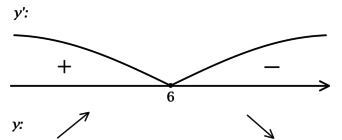
3) Эскиз графика:

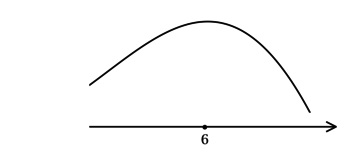
Таким образом, (x = 6) – точка максимума функции (y) и наибольшее значение достигается в ней:

(y(6) = -e^{(2ln 2)}=-e^{ln 4} = -4).

Итого: (-4) – наибольшее значение функции (y).

Ответ: -4

Задание
7

#918

Уровень задания: Сложнее ЕГЭ

Найдите наибольшее значение функции

(y = e^{cos x + sin x – sqrt{2}}).

1) Обозначим (cos x + sin x – sqrt{2}=t(x)), тогда (y(t)=e^{t}). [y’ = y’_tcdot t’_x = (e^{t})’cdot(cos x + sin x – sqrt{2})’ = e^{t}cdot(-sin x + cos x) = e^{cos x + sin x – sqrt{2}}cdot(-sin x + cos x).]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [e^{cos x + sin x – sqrt{2}}cdot(-sin x + cos x) = 0qquadLeftrightarrowqquad -sin x + cos x = 0] (так как (e^{cos x + sin x – sqrt{2}} = e^{t}), но (e^{t} > 0) при любом (t)), что равносильно (mathrm{tg}, x = 1) при (cos x neq 0), откуда находим корни (x = dfrac{pi}{4} + pi k, k in -mathbb{Z}). Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства (y’): (их бесконечно много, но они чередуются)

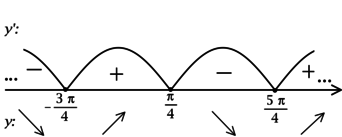
3) Эскиз графика:

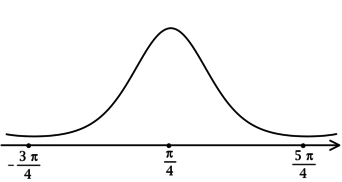
Таким образом, (x = dfrac{pi}{4} + 2pi k, k in mathbb{Z}) – точки локальных максимумов функции (y) и наибольшее значение достигается в одной из них:

(yleft(dfrac{pi}{4} + 2pi kright) = e^{cosleft(frac{pi}{4} + 2pi kright) + sinleft(frac{pi}{4} + 2pi kright) – sqrt{2}} = e^{frac{sqrt{2}}{2} + frac{sqrt{2}}{2} – sqrt{2}} = e^{0} = 1).

Итого: (1) – наибольшее значение функции (y).

Ответ: 1