Эксцентрическая аномалия как найти

Эксцентрическая аномалия как найти

From Wikipedia, the free encyclopedia

In orbital mechanics, the eccentric anomaly is an angular parameter that defines the position of a body that is moving along an elliptic Kepler orbit. The eccentric anomaly is one of three angular parameters (“anomalies”) that define a position along an orbit, the other two being the true anomaly and the mean anomaly.

Graphical representation[edit]

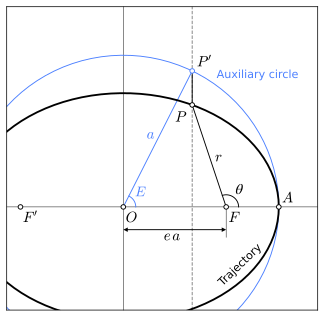
The eccentric anomaly of point P is the angle E. The center of the ellipse is point O, and the focus is point F.

Consider the ellipse with equation given by:

frac{x^2}{a^2} + frac{y^2}{b^2} = 1,

where a is the semi-major axis and b is the semi-minor axis.

For a point on the ellipse, P = P(x, y), representing the position of an orbiting body in an elliptical orbit, the eccentric anomaly is the angle E in the figure. The eccentric anomaly E is one of the angles of a right triangle with one vertex at the center of the ellipse, its adjacent side lying on the major axis, having hypotenuse a (equal to the semi-major axis of the ellipse), and opposite side (perpendicular to the major axis and touching the point P′ on the auxiliary circle of radius a) that passes through the point P. The eccentric anomaly is measured in the same direction as the true anomaly, shown in the figure as theta . The eccentric anomaly E in terms of these coordinates is given by:[1]

cos E = frac{x}{a} ,

and

sin E = frac{y}{b}

The second equation is established using the relationship

{displaystyle left({frac {y}{b}}right)^{2}=1-cos ^{2}E=sin ^{2}E},

which implies that sin E = ±y/b. The equation sin E = −y/b is immediately able to be ruled out since it traverses the ellipse in the wrong direction. It can also be noted that the second equation can be viewed as coming from a similar triangle with its opposite side having the same length y as the distance from P to the major axis, and its hypotenuse b equal to the semi-minor axis of the ellipse.

Formulas[edit]

Radius and eccentric anomaly[edit]

The eccentricity e is defined as:

e={sqrt {1-left({frac {b}{a}}right)^{2}}} .

From Pythagoras’s theorem applied to the triangle with r (a distance FP) as hypotenuse:

{displaystyle {begin{aligned}r^{2}&=b^{2}sin ^{2}E+(ae-acos E)^{2}\&=a^{2}left(1-e^{2}right)left(1-cos ^{2}Eright)+a^{2}left(e^{2}-2ecos E+cos ^{2}Eright)\&=a^{2}-2a^{2}ecos E+a^{2}e^{2}cos ^{2}E\&=a^{2}left(1-ecos Eright)^{2}\end{aligned}}}

Thus, the radius (distance from the focus to point P) is related to the eccentric anomaly by the formula

{displaystyle r=aleft(1-ecos {E}right) .}

With this result the eccentric anomaly can be determined from the true anomaly as shown next.

From the true anomaly[edit]

The true anomaly is the angle labeled theta in the figure, located at the focus of the ellipse. It is sometimes represented by f or v. The true anomaly and the eccentric anomaly are related as follows.[2]

Using the formula for r above, the sine and cosine of E are found in terms of f :

{displaystyle {begin{aligned}cos E&={frac {,x,}{a}}={frac {,ae+rcos f,}{a}}=e+(1-ecos E)cos f\Rightarrow cos E&={frac {,e+cos f,}{1+ecos f}}\sin E&={sqrt {,1-cos ^{2}E;}}={frac {,{sqrt {,1-e^{2};}},sin f,}{1+ecos f}}~.end{aligned}}}

Hence,

{displaystyle tan E={frac {,sin E,}{cos E}}={frac {,{sqrt {,1-e^{2};}},sin f,}{e+cos f}}~.}

Angle E is therefore the adjacent angle of a right triangle with hypotenuse {displaystyle ;1+ecos f;,} adjacent side {displaystyle ;e+cos f;,} and opposite side {displaystyle ;{sqrt {,1-e^{2};}},sin f;.}

Also,

{displaystyle tan {frac {,f,}{2}}={sqrt {{frac {,1+e,}{1-e}},}},tan {frac {,E,}{2}}}

Substituting cos E as found above into the expression for r, the radial distance from the focal point to the point P, can be found in terms of the true anomaly as well:[2]

{displaystyle r={frac {aleft(,1-e^{2},right)}{,1+ecos f,}}={frac {p}{,1+ecos f,}},}

where

{displaystyle ,pequiv aleft(,1-e^{2},right)}

is called “the semi-latus rectum” in classical geometry.

From the mean anomaly[edit]

The eccentric anomaly E is related to the mean anomaly M by Kepler’s equation:[3]

{displaystyle M=E-esin E}

This equation does not have a closed-form solution for E given M. It is usually solved by numerical methods, e.g. the Newton–Raphson method. It may be expressed in a Fourier series as

{displaystyle E=M+2sum _{n=1}^{infty }{frac {J_{n}(ne)}{n}}sin(nM)}

where {displaystyle J_{n}(x)} is the Bessel function of the first kind.

See also[edit]

  • Eccentricity vector
  • Orbital eccentricity

Notes and references[edit]

  1. ^
    George Albert Wentworth (1914). “The ellipse §126”. Elements of analytic geometry (2nd ed.). Ginn & Co. p. 141.
  2. ^ a b Tsui, James Bao-yen (2000). Fundamentals of Global Positioning System receivers: A software approach (3rd ed.). John Wiley & Sons. p. 48. ISBN 0-471-38154-3.
  3. ^ Michel Capderou (2005). “Definition of the mean anomaly, Eq. 1.68”. Satellites: orbits and missions. Springer. p. 21. ISBN 2-287-21317-1.

Sources[edit]

  • Murray, Carl D.; & Dermott, Stanley F. (1999); Solar System Dynamics, Cambridge University Press, Cambridge, GB
  • Plummer, Henry C. K. (1960); An Introductory Treatise on Dynamical Astronomy, Dover Publications, New York, NY (Reprint of the 1918 Cambridge University Press edition)
Источник

Макеты страниц

В этом разделе будут рассмотрены средняя, эксцентрическая и истинная аномалии и связи между ними для случая эллиптической орбиты.

Радиус-вектор за период Т поворачивается на радиан, поэтому для средней угловой скорости (среднего движения) справедлива формула

Соотношение

можно переписать в виде

Рис. 4.6.

Если — момент прохождения через перигелий, то радиус-вектор, вращающийся вокруг S со средней угловой скоростью , за время опишет угол

    (4.49)

Введенная таким образом величина М называется средней аномалией.

Построим на как на диаметре окружность (рис. 4.6) и проведем через точку Р на эллипсе линию, перпендикулярную большой оси АА, до пересечения с окружностью в точке Q. Угол обычно обозначаемый Е, называется эксцентрической аномалией и связан с истинной аномалией

Имеем

но

следовательно,

Кроме того, в силу свойств эллипса имеет место соотношение

    (4.51)

В результате получаем

или

Возводя в квадрат (4.50) и (4.52) и складывая, находим

    (4.53)

Имеем

откуда

Используя (4.50) и (4.53), получаем

и аналогично

Разделив (4.55) на (4.56), окончательно находим

Эксцентрическая аномалия Е и средняя аномалия М связаны между собой важным уравнением, называемым уравнением Кеплера. Выведем его.

Из второго закона Кеплера имеем

или

или, используя (4.47),

С другой стороны, имеем

Если разделить площадь RPA на узкие полосы, параллельные малой оси, и воспользоваться свойством (4.51), то можно показать, что

.

Тогда, воспользовавшись (4.50) и (4.52), получаем

Если сравнить (4.58) и (4.59), то видно, что имеет место связь

Это и есть уравнение Кеплера. Следует отметить, что здесь и и М измеряются в радианах.

Источник

В орбитальной механике эксцентрическая аномалия является угловым параметром, который определяет положение тела, которое движется по эллиптической орбите Кеплера. Эксцентрическая аномалия – это один из трех угловых параметров («аномалий»), которые определяют положение на орбите, два других – это истинная аномалия и средняя аномалия.

Содержание

  • 1 Графическое представление
  • 2 Формулы
    • 2.1 Радиус и эксцентрическая аномалия
    • 2.2 От истинной аномалии
    • 2.3 От средней аномалии
  • 3 См. Также
  • 4 Примечания и ссылки
  • 5 Источники

Графическое представление

Эксцентрическая аномалия точки P – это угол E. Центр эллипса – точка C, а фокус – точка F.

Рассмотрим эллипс с уравнением:

x 2 a 2 + y 2 b 2 = 1, { displaystyle { frac {x ^ {2}} {a ^ {2}}} + { frac {y ^ {2}} {b ^ {2}}} = 1,} frac {x ^ 2} {a ^ 2} + frac {y ^ 2} {b ^ 2} = 1,

где a – большая полуось, а b – малая полуось.

Для точки на эллипсе P = P (x, y), представляющей положение вращающегося тела на эллиптической орбите, эксцентрическая аномалия – это угол E на рисунке. Эксцентрическая аномалия E – это один из углов прямоугольного треугольника с одной вершиной в центре эллипса, прилегающей к нему стороной, лежащей на большой оси, имеющей гипотенузу a (равную большой полуоси эллипса) и противоположную сторона (перпендикулярная большой оси и касающаяся точки P ‘на вспомогательной окружности радиуса a), которая проходит через точку P. Эксцентрическая аномалия измеряется в том же направлении, что и истинная аномалия, показанная на рисунке как f. Эксцентрическая аномалия E в терминах этих координат определяется выражением:

cos ⁡ E = xa, { displaystyle cos E = { frac {x} {a}},} cos E = гидроразрыва {x} {a},

и

sin ⁡ E = yb { displaystyle sin E = { frac {y} {b}}} sin E = frac {y} {b}

Второе уравнение устанавливается с использованием соотношения

(yb) 2 = 1 – cos 2 ⁡ E = sin 2 ⁡ E { displaystyle left ({ frac {y} {b}} right) ^ {2} = 1- cos ^ {2} E = sin ^ {2} E}{ displaystyle left ({ frac {y } {b}} right) ^ {2} = 1- cos ^ {2} E = sin ^ {2} E} ,

, что означает, что грех E = ± y / b. Уравнение sin E = −y / b может быть немедленно исключено, поскольку оно пересекает эллипс в неправильном направлении. Также можно отметить, что второе уравнение можно рассматривать как исходящее из аналогичного треугольника, у которого противоположная сторона имеет ту же длину y, что и расстояние от P до большой оси, а его гипотенуза b равна малой полуоси эллипс.

Формулы

Радиус и эксцентричная аномалия

эксцентриситет e определяется как:

e = 1 – (b a) 2. { displaystyle e = { sqrt {1- left ({ frac {b} {a}} right) ^ {2}}} .}e = { sqrt {1- left ({ frac {b} {a}} right) ^ {2}}} .

Из теоремы Пифагора применительно к треугольник с r (расстояние FP) в качестве гипотенузы:

r 2 = b 2 sin 2 ⁡ E + (ae – a cos ⁡ E) 2 = a 2 (1 – e 2) (1 – cos 2 ⁡ E) + a 2 (e 2 – 2 e cos ⁡ E + cos 2 ⁡ E) = a 2 – 2 a 2 e cos ⁡ E + a 2 e 2 cos 2 ⁡ E = a 2 (1 – e cos ⁡ E) 2 { displaystyle { begin {align} r ^ {2} = b ^ {2} sin ^ {2} E + (ae-a cos E) ^ {2} \ = a ^ {2} left (1-e ^ {2} right) left (1- cos ^ {2} E right) + a ^ {2} left (e ^ {2} -2e cos E + cos ^ {2} E right) \ = a ^ {2} -2a ^ {2} e cos E + a ^ {2} e ^ {2} cos ^ {2} E \ = a ^ {2} left (1-e cos E right) ^ {2} \ end {align}}}{ displaystyle { begin {align} r ^ {2} = b ^ {2} sin ^ {2} E + ( ae-a cos E) ^ {2} \ = a ^ {2} left (1-e ^ {2} right) left (1- cos ^ {2} E right) + a ^ {2} left (e ^ {2} -2e cos E + cos ^ {2} E right) \ = a ^ {2} -2a ^ {2} e cos E + a ^ { 2} e ^ {2} c os ^ {2} E \ = a ^ {2} left (1-e cos E right) ^ {2} \ конец {выровнено}}}

Таким образом, радиус (расстояние от фокуса до точки P) связан с эксцентрической аномалией по формуле

r = a (1 – e cos ⁡ E). { displaystyle r = a left (1-e cos {E} right) .}{ displaystyle r = a left (1-e cos {E} right) .}

С этим результатом эксцентрическая аномалия может быть определена по истинной аномалии, как показано ниже.

От истинной аномалии

Истинная аномалия – это угол, обозначенный буквой f на рисунке, расположенный в фокусе эллипса. В приведенных ниже расчетах он обозначается как θ. Истинная аномалия и эксцентрическая аномалия связаны следующим образом.

Используя приведенную выше формулу для r, синус и косинус E находятся в единицах θ:

cos ⁡ E = xa = ae + r cos ⁡ θ a = e + (1 – e cos ⁡ E) cos ⁡ θ ⇒ cos ⁡ E = e + cos ⁡ θ 1 + e cos ⁡ θ sin ⁡ E = 1 – cos 2 ⁡ E = 1 – e 2 sin ⁡ θ 1 + е соз ⁡ θ. { displaystyle { begin {align} cos E = { frac {x} {a}} = { frac {ae + r cos theta} {a}} = e + (1-e cos E) cos theta \ Rightarrow cos E = { frac {e + cos theta} {1 + e cos theta}} \ sin E = { sqrt {1- cos ^ {2} E}} = { frac {{ sqrt {1-e ^ {2}}} , sin theta} {1 + e cos theta}} . End {align}}}{ displaystyle { begin {align} cos E = { frac {x} {a}} = { frac {ae + r cos theta} {a}} = e + ( 1-e cos E) cos theta \ Rightarrow cos E = { frac {e + cos theta} {1 + e cos theta}} \ sin E = { sqrt {1 - cos ^ {2} E}} = { frac {{ sqrt {1-e ^ {2}}} , sin theta} {1 + e cos theta}} . end { выровнено}}}

Следовательно,

tan ⁡ E = sin ⁡ E cos ⁡ E = 1 – e 2 sin ⁡ θ e + cos ⁡ θ. { displaystyle tan E = { frac { sin E} { cos E}} = { frac {{ sqrt {1-e ^ {2}}} sin theta} {e + cos theta }} .}{ displaystyle tan E = { frac { sin E} { cos E}} = { frac {{ sqrt {1-e ^ {2}}} sin theta} {e + cos theta }} .}

Следовательно, угол E – это угол, прилегающий к прямоугольному треугольнику с гипотенузой 1 + e cos θ, смежной стороной e + cos θ и противоположной стороной √1 – e sin θ.

Кроме того,

tan ⁡ θ 2 = 1 + e 1 – e tan ⁡ E 2 { displaystyle tan { frac { theta} {2}} = { sqrt { frac { 1 + e} {1-e}}} tan { frac {E} {2}}}{ displaystyle tan { frac { theta} {2}} = { sqrt { frac {1 + e} {1-e}}} tan { frac {E} {2}}}

Подставляя cos E, как найдено выше, в выражение для r, радиального расстояния от фокальной точки до точки P, также можно найти в терминах истинной аномалии:

r = a (1 – e 2) 1 + e cos ⁡ θ. { displaystyle r = { frac {a left (1-e ^ {2} right)} {1 + e cos theta}} .}{ displaystyle r = { frac {a left (1-e ^ {2} right)} {1 + e cos theta}} . }

Из средней аномалии

Эксцентрическая аномалия E связана со средней аномалией M с помощью уравнения Кеплера :

M = E – e sin ⁡ E { displaystyle M = Ee sin E}{ displaystyle M = Ee sin E}

Это уравнение не иметь решения в замкнутой форме для E с данным M. Обычно это решается численными методами, например метод Ньютона – Рафсона.

См. также

  • Вектор эксцентриситета
  • Орбитальный эксцентриситет

Примечания и ссылки

  1. ^Джордж Альберт Вентворт (1914). «Эллипс §126». Элементы аналитической геометрии (2-е изд.). Ginn Co. стр. 141.
  2. ^ Джеймс Бао-янь Цуй (2000). Основы приемников глобальной системы позиционирования: программный подход (3-е изд.). Джон Уайли и сыновья. п. 48. ISBN 0-471-38154-3 .
  3. ^Мишель Капдеру (2005). «Определение средней аномалии, уравнение 1.68». Спутники: орбиты и миссии. Springer. п. 21. ISBN 2-287-21317-1 .

Источники

  • Мюррей, Карл Д.; И Дермотт, Стэнли Ф. (1999); Динамика солнечной системы, Cambridge University Press, Cambridge, GB
  • Пламмер, Генри К. К. (1960); Вводный трактат по динамической астрономии, Dover Publications, Нью-Йорк, штат Нью-Йорк (переиздание издания Cambridge University Press 1918 года)
Источник

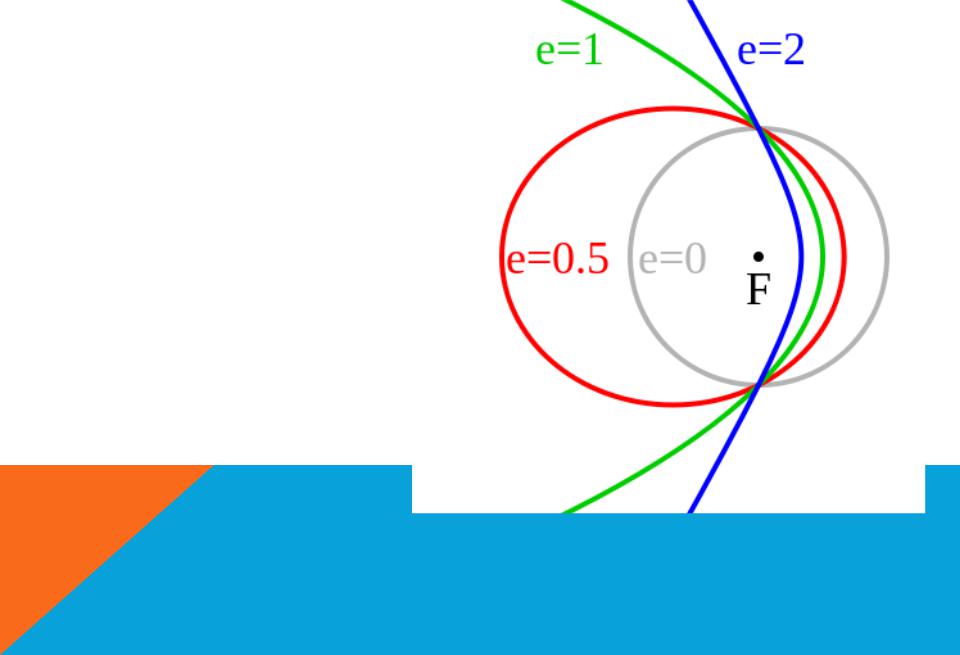
ЭКСЦЕНТРИСИТЕТ МОЖЕТ ПРИНИМАТЬ СЛЕДУЮЩИЕ ЗНАЧЕНИЯ:

Ε= 0 – КРУГОВАЯ ОРБИТА 0 <Ε <1 ЭЛЛИПТИЧЕСКАЯ ОРБИТА

Ε= 1 – ПАРАБОЛИЧЕСКАЯ ТРАЕКТОРИЯ 1 <Ε <∞ – ГИПЕРБОЛИЧЕСКАЯ ТРАЕКТОРИЯ

Ε= ∞ – ЛИНИЯ

(ВЫРОЖДЕННЫЙ СЛУЧАЙ)

Эллиптическая кеплеровская орбита с эксцентриситетом 0,7 (красный эллипс), параболическая (зеленый) и гиперболическая орбита с эксцентриситетом 1,3 (синяя внешняя линия)

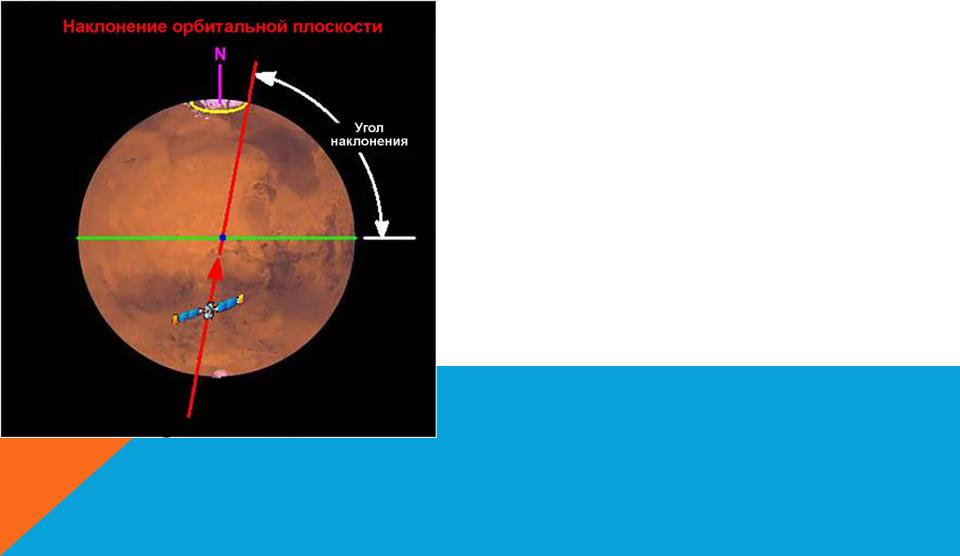
Наклонение (i) – это угловое расстояние от плоскости орбиты до плоскости отсчета (чаще всего экватора или эклиптики), обычно указывается в градусах.

Наклонение орбиты равное 0 ° означает, что тело вращается вокруг планеты в экваториальной плоскости, в том же направлении, в котором вращается и сама планета;

Наклонные орбиты (0º < i < 90º): если наклонение орбиты не более 90°, то движение спутника считается прямым (а сама орбита – прямой), если более 90° – то обратным (обратная орбита);

i = 90 ° – полярная орбита, по которой космический корабль проходит над северным и южным полюсами планеты;

i = 180 ° – обратная экваториальная орбита.

Наклон орбит спутников измеряется по отношению к экваториальной плоскости тела вокруг которого они вращаются, если они расположены достаточно близко. Экваториальная плоскость является плоскостью, перпендикулярной к оси вращения центрального тела.

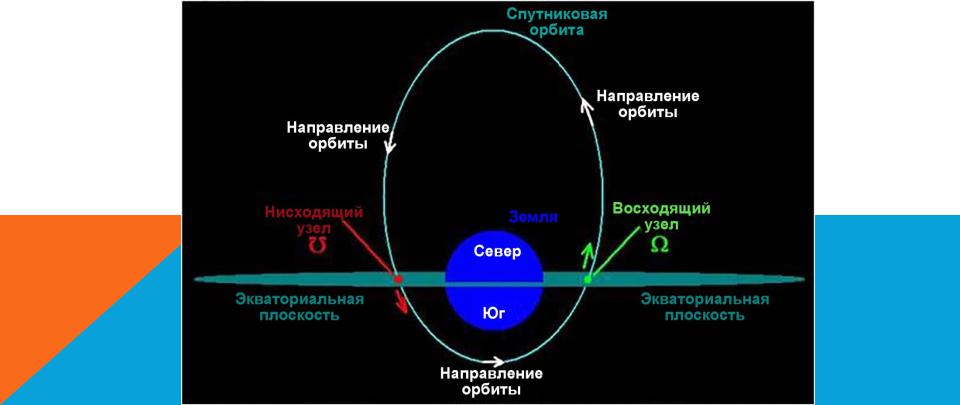
УЗЕЛ ОРБИТЫ

Узел – это одна из двух точек, в которой орбита пересекает плоскость отсчета к которой она склонена.

Поскольку таких точек две, различают восходящий и нисходящий узлы орбиты. Для геоцентрической и гелиоцентрической орбиты, восходящий узел (или Северный Узел) это тот, в котором объект движется по орбите через плоскость отсчета на север, и нисходящий узел (или Южный Узел), в котором он движется на юг.

ВОСХОДЯЩИЕ И НИСХОДЯЩИЕ

ОРБИТЫ

Большинство спутниковых платформ сегодня находится на околополярных орбитах, то есть спутник идѐт на север по одну сторону от Земли, а затем к южному полюсу по второй половине своей орбиты. Они называются восходящими и нисходящими путями соответственно. Если орбита также солнечно-синхронная, то восходящий путь, скорее всего, находится на теневой стороне Земли, а нисходящий — на солнечной. Датчики, записывающие отраженное солнечное излучение, получают изображение поверхности только на нисходящем пути, когда есть солнечное освещение. Активные датчики, которые сами обеспечивают подсветку или пассивные датчики, которые записывают излучаемую Землѐй энергию (например, тепловую),могут также получать изображения поверхности на восходящем пути.

АРГУМЕНТ ПЕРИЦЕНТРА

Аргумент перицентра – это угол между перигеем орбиты (точкой наибольшего сближения с центральной точкой) и восходящим узлом орбиты. Угол измеряется в орбитальной плоскости и в направлении движения. В орбитах тел, движущихся вокруг Солнца (например, планет, астероидов и комет) перицентр и апоцентр обычно называют, соответственно, перигелием́ и афелием́ (апогелием́ ), в орбитах Луны и искусственных спутников Земли — перигей́ и апогей́. Его можно использовать для определения широты точки перицентра. Аргумент перицентра измеряется в градусах от линии восходящего узла на экваториальной плоскости до точки перицентра.

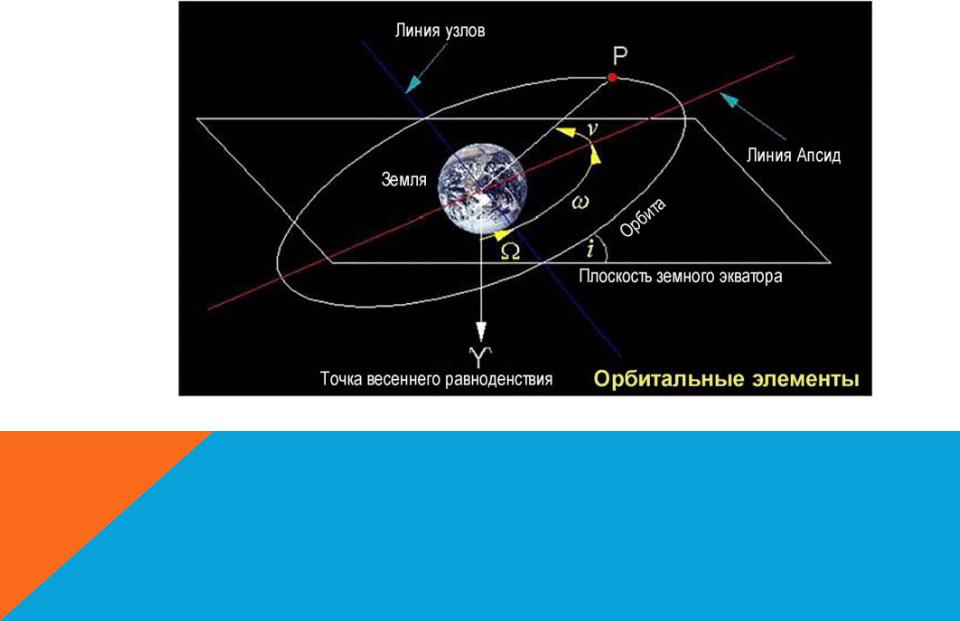
ДОЛГОТА ВОСХОДЯЩЕГО УЗЛА

Определяет угол в базовой плоскости, образуемый между базовым направлением на нулевую точку и направлением на точку восходящего узла орбиты, в которой орбита пересекает базовую плоскость в направлении с юга на север. Для тел, обращающихся вокруг Солнца, базовая плоскость — эклиптика, а нулевая точка — Первая точка Овна (точка весеннего равновесия); угол измеряется от направления на нулевую точку против часовой стрелки.

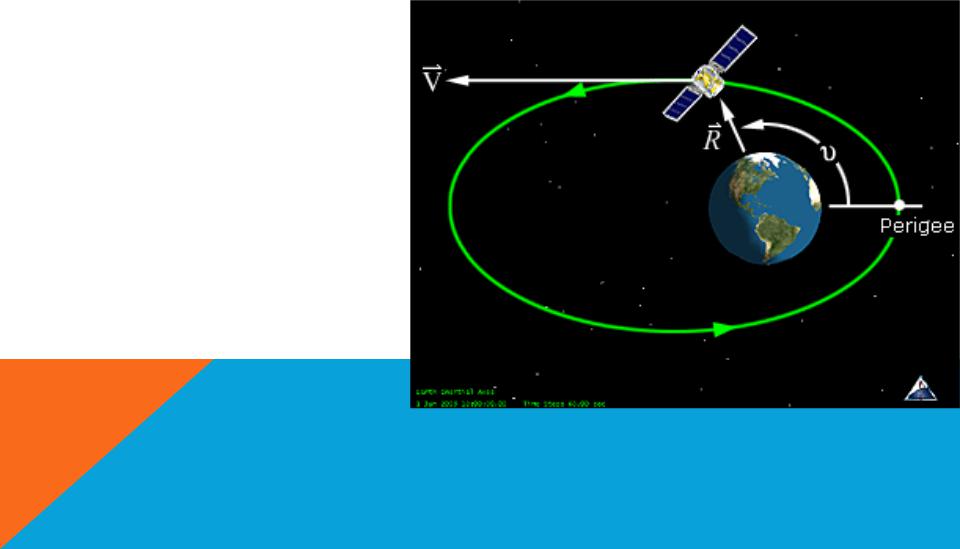
ИСТИННАЯ АНОМАЛИЯ

Термин аномалия (вместо угла), который означает неоднородность, используется астрономами описывающими движение планет. Термин происходит из того факта, что наблюдаемое положение планеты часто демонстрирует маленькие отклонения от прогрозируемого.

Истинная аномалия (ν) – это угловое расстояние от перигея до спутника, если смотреть с Земли. Для круговой орбиты средняя и истинные аномалии совпадают.

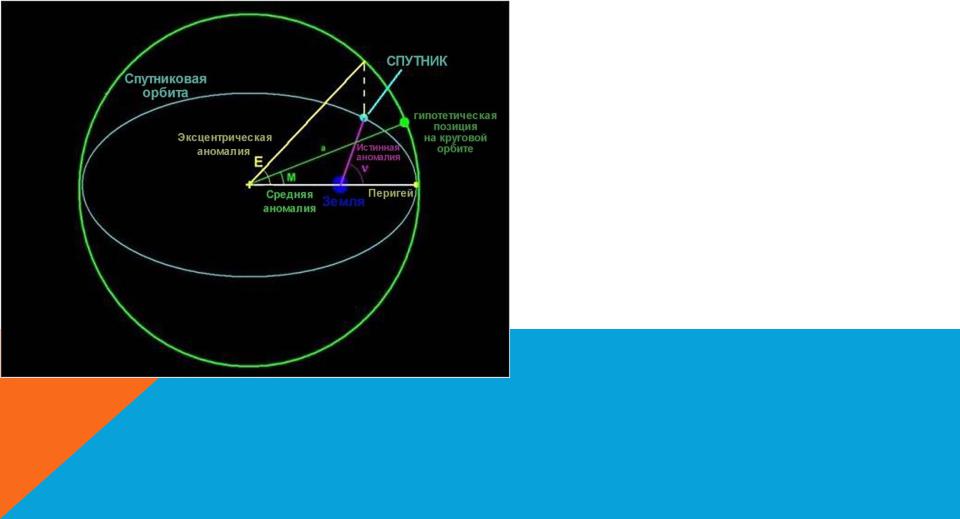
СРЕДНЯЯ АНОМАЛИЯ

Средняя аномалия (M): это параметр, касающиеся местоположения и времени для тела, движущегося по орбите Кеплера. Угол, измеренный с перигее, который огибал бы спутник, если его орбита была идеально круглой. Эта гипотетическая орбита опирается на большую полуось реальной орбиты и ее период. Средняя аномалия указывает местонахождение спутника на орбите в определенное время.

Эксцентрическая аномалия (Е): Угол, измеренный от перигея, основывается на гипотетической позиции на круговой орбите, определяемой линией, перпендикулярной главной оси, проходящей через истинное положение спутника и пересекающейся с круговой орбитой. Средняя аномалия напрямую связана с эксцентрической аномалии через уравнение Кеплера.

Истинная аномалия (N): истинный угол, измеренный от перигея, который спутник проходит по орбите Земли.

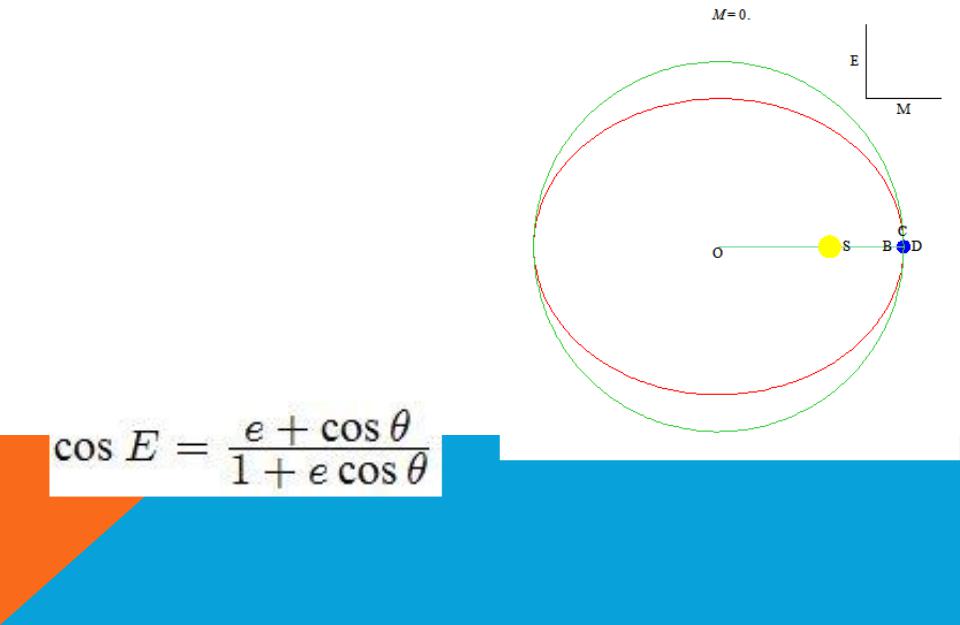
СРЕДНЯЯ АНОМАЛИЯ

Средняя аномалия увеличивается неравномерно от 0 до радиана при движении спутника по орбите. Однако – это не угол. В соответствие со Вторым Законом Кеплера, средняя аномалия пропорциональна площади, охватываемой радиусом-вектором, соединяющим небесное тело и его спутник с момента последнего прохождения перигея.

Средняя аномалия M может быть вычислена из эксцентрической аномалии E и эксцентриситета e через уравнение Кеплера:

M E sin E

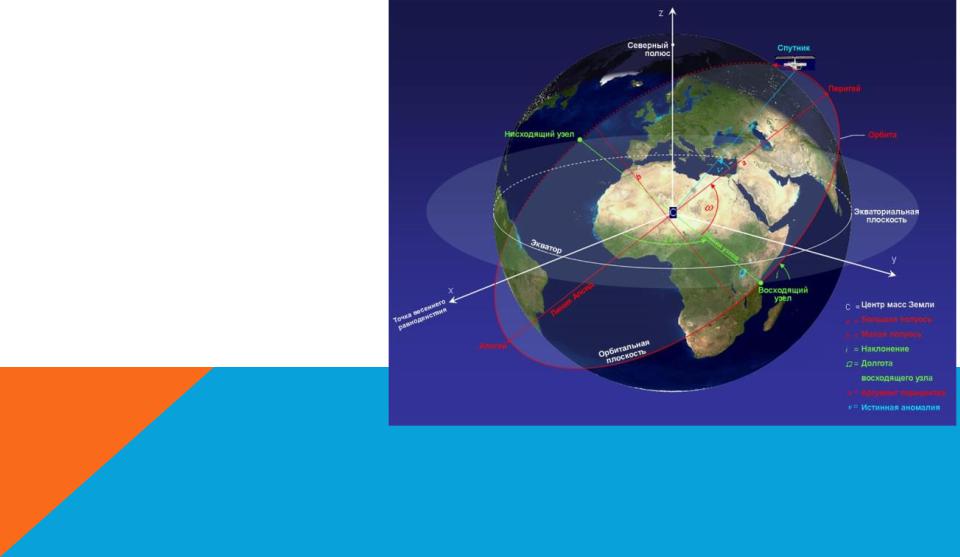
ОРБИТАЛЬНЫЕ ЭЛЕМЕНТЫ

Элементы Кеплера большая полуось (α), эксцентриситет (ε), наклонение (ί),

аргумент перицентра

(ω),

долгота восходящего узла (Ω),

средняя аномалия

(M).

Источник

Орбита́льные элеме́нты, элеме́нты орби́ты небесного тела — набор параметров, задающих размеры и форму орбиты (траектории) небесного тела, расположение орбиты в пространстве и место расположения небесного тела на орбите.

Определение орбит небесных тел является одной из задач небесной механики. Для задания орбиты спутника планеты, астероида или Земли используют так называемые «орбитальные элементы». Орбитальные элементы отвечают за задание базовой системы координат (точки отсчёта, о́си координат), формы и размера орбиты, её ориентации в пространстве и момент времени, в который небесное тело находится в определённой точке орбиты. В основном используются два способа задания орбиты (при наличии системы координат)[1]:

  • при помощи векторов положения и скорости;
  • при помощи орбитальных элементов.

Кеплеровы элементы орбиты[править | править код]

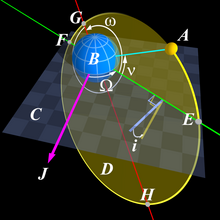
Традиционно в качестве элементов орбиты используют шесть величин, получивших название кеплеровых[2]:

  • большая полуось (a);
  • эксцентриситет орбиты (e);
  • наклонение (i);
  • аргумент перицентра (ω);
  • долгота восходящего узла (☊);
  • средняя аномалия (Mo).

Другие элементы орбиты[править | править код]

Аномалии[править | править код]

Анома́лия (в небесной механике) — угол, используемый для описания движения тела по эллиптической орбите. Термин «аномалия» впервые введён Аделардом Батским при переводе на латынь астрономических таблиц Аль-Хорезми «Зидж» для передачи арабского термина «аль-хеза» («особенность»).

И́стинная анома́лия (на рисунке обозначена nu , так же обозначается T, theta или f) представляет собой угол между радиус-вектором r тела и направлением на перицентр.

Сре́дняя анома́лия (обычно обозначаемая M) для тела, движущегося по невозмущённой орбите, — произведение его среднего движения (средней угловой скорости за один оборот) и интервала времени после прохождения перицентра. Иными словами, средняя аномалия — угловое расстояние от перицентра до воображаемого тела, движущегося с постоянной угловой скоростью, равной среднему движению реального тела, и проходящего через перицентр одновременно с реальным телом.

Эксцентри́ческая анома́лия (обозначаемая E) — параметр, используемый для выражения переменной длины радиус-вектора r.

Зависимость r от E и nu выражается уравнениями

r=a(1-ecdot cos E),
{displaystyle r={frac {a(1-e^{2})}{1+ecdot cos nu }}},

где:

  • a — большая полуось эллиптической орбиты;
  • e — эксцентриситет эллиптической орбиты.

Средняя аномалия и эксцентрическая аномалия связаны между собой через уравнение Кеплера.

Аргумент широты[править | править код]

Аргуме́нт широты́ (обозначаемый u) — угловой параметр, который определяет положение тела, движущегося вдоль кеплеровой орбиты. Это сумма часто используемых истинной аномалии (см. выше) и аргумента перицентра, образующая угол между радиус-вектором тела и линией узлов. Отсчитывается от восходящего узла по направлению движения[3].

{displaystyle u=nu +omega ,}

где:

Аномалистический период обращения[править | править код]

Аномалисти́ческий пери́од обраще́ния — промежуток времени, за который тело, перемещаясь по эллиптической орбите, дважды последовательно проходит через перицентр.

Примечания[править | править код]

  1. ↑ Дубошин Г. Н. Справочное руководство по небесной механике и астродинамике.
  2. ↑ Здесь и далее рассматривается задача двух тел.
  3. ↑ Иллюстрация «Аргумент перигея и аргумент широты» в Большой советской энциклопедии. Дата обращения: 13 января 2012. Архивировано из [bse.sci-lib.com/particle001214.html оригинала] 11 марта 2016 года.

Ссылки[править | править код]

  • Аномалия астрономическая // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.

Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист.

Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым).

Список проблемных ссылок

  • bse.sci-lib.com/particle001214.html
Источник

Добавить комментарий