Эксцесс распределения как найти

Эксцесс распределения как найти

Коэффициент асимметрии. Эксцесс распределения

Краткая теория

При изучении распределений, отличных от нормального,
возникает необходимость количественно оценить это различие. С этой целью вводят
специальные характеристики, в частности асимметрию и эксцесс. Для нормального
распределения эти характеристики равны нулю. Поэтому если для изучаемого
распределения асимметрия и эксцесс имеют небольшие значения, то можно
предположить близость этого распределения к нормальному.
Наоборот, большие значения асимметрии и эксцесса указывают на значительное
отклонение от нормального.

Асимметрией теоретического распределения называют отношение
центрального момента третьего порядка к кубу среднего квадратического
отклонения:

Коэффициент асимметрии характеризует скошенность
распределения по отношению к математическому ожиданию. Асимметрия положительна,
если «длинная часть» кривой распределения расположена справа от математического
ожидания; асимметрия отрицательна, если «длинная часть» кривой расположена слева
от математического ожидания.

На рисунке показаны две кривые распределения: I и II. Кривая I имеет
положительную (правостороннюю) асимметрию

,
а кривая II – отрицательную (левостороннюю)

.

Кроме вышеописанного коэффициента, для характеристики асимметрии
рассчитывают также показатель асимметрии Пирсона:

Коэффициент асимметрии Пирсона характеризует асимметрию только в
центральной части распределения, поэтому более распространенным и более точным
является коэффициент асимметрии, рассчитанный на основе центрального момента третьего
порядка.

Для оценки «крутости», т. е. большего или меньшего подъема кривой
теоретического распределения по сравнению с нормальной кривой, пользуются
характеристикой – эксцессом.

Эксцессом (или коэффициентом эксцесса) случайной величины
называется число:

Число 3 вычитается из отношения

 потому, что для наиболее часто встречающегося
нормального распределения отношение

.

Кривые, более островершинные, чем нормальная,
обладают положительным эксцессом, более плосковершинные – отрицательным
эксцессом.

Примеры решения задач

Задача 1

Для заданного
вариационного ряда вычислить коэффициенты асимметрии и эксцесса.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Составим расчетную
таблицу

Средняя:

Найдем моду – варианту, которой соответствует наибольшая частота.

Дисперсия:

Среднее квадратическое
отклонение:

Коэффициент асимметрии Пирсона:

Коэффициент асимметрии можно найти по формуле:

Центральный момент
3-го порядка:

Получаем:

Эксцесс можно найти по формуле:

Центральный момент
4-го порядка:

Получаем:

Задача 2

Для заданного
вариационного ряда (см. условие задачи 1) вычислить коэффициенты асимметрии и
эксцесса методом произведений, используя условные моменты.

Решение

Составим расчетную таблицу

Перейдем к условным вариантам

В качестве ложного нуля возьмем
3-ю варианту

0

Условные варианты вычислим по
формуле:

где

4
(разность между соседними вариантами)

Условный момент 1-го порядка:

Средняя:

Условный момент 2-го порядка:

Дисперсия:

Среднее квадратическое
отклонение:

Коэффициент асимметрии можно найти
по формуле:

Условный момент 3-го порядка:

Центральный момент 3-го порядка:

Получаем:

Эксцесс можно найти по формуле:

Условный момент 4-го порядка:

Центральный момент 4-го порядка:

Получаем:

Источник

58. Коэффициенты асимметрии и эксцесса.

Центральные
моменты распределения

Для дальнейшего изучения характера
вариации используются средние значения
разных степеней отклонений отдельных
величин признака от его средней
арифметической величины. Эти показатели
получили название центральных
моментов распределения порядка,
соответствующего степени, в которую
возводятся отклонения,
или просто моментов.

Показатели формы распределения

  • Асимметрия – Коэффициент
    асимметрии

    характеризует асимметричность
    («скошенность») распределения признака
    в совокупности

  • Эксцесс – Показатель эксцесса


    представляет собой отклонение вершины
    эмпирического распределения вверх или
    вниз («крутость») от вершины кривой
    нормального распределения

Асимметрия распределения

  • При
    =0
    распределение считается нормальным.

  • При

    > 0 правосторонняя асимметрия.

  • При
    <0
    левосторонняя асимметрия.

  • Если асимметрия более 0,5, то независимо
    от знака она считается значительной

  • Если асимметрия меньше 0,25, то она
    считается незначительной

Асимметрия
распределения рассчитанная по формулам
К.Пирсона:

является
приблизительной

Расчет
асимметрии распределения при помощи
нормированного момента третьего
порядка дает наиболее точный результат

т.е.

– нормированный
момент третьего порядка

Показатель Пирсона зависит от степени
асимметричности в средней части ряда
распределения, а показатель асимметрии,
основанный на моменте третьего порядка,
– от крайних значений признака.

Оценка существенности асимметрии

Для оценки существенности асимметрии
вычисляют показатель средней квадратической
ошибки коэффициента асимметрии

Если отношение

имеет значение больше 2, то это
свидетельствует о существенном характере
асимметрии

Эксцесс распределения

Показатель эксцесса

представляет собой отклонение вершины
эмпирического распределения вверх или
вниз («крутость») от вершины кривой
нормального распределения, НО! График
распределения может выглядеть сколь
угодно крутым в зависимости от силы
вариации признака: чем слабее вариация,
тем круче кривая распределения при
данном масштабе. Не говоря уже о том,
что, изменяя масштабы по оси абсцисс и
по оси ординат, любое распределение
можно искусствен но сделать «крутым»
и «пологим». Чтобы показать, в чем состоит
эксцесс распределения, и правильно его
интерпретировать, нужно сравнить ряды
с одинаковой силой вариации (одной и
той же величиной σ) и разными показателями
эксцесса. Чтобы не смешать эксцесс с
асимметрией, все сравниваемые ряды
должны быть симметричными. Такое
сравнение изображено на рис.

Поскольку эксцесс нормального
распределения равен 3, показатель
эксцесса вычисляется по формуле

или

где

– нормированный момент четвертого
порядка

  • При
    >0
    – высоковершинный эксцесс распределения

  • При
    <0
    – низковершинный эксцесс распределение

  • При

    =0 – нормальное распределение

Оценка существенности эксцесса

Для оценки существенности эксцесса
вычисляют показатель его средней
квадратической ошибки

Если отношение

имеет значение больше 3, то это
свидетельствует о существенном характере
эксцесса

Источник

Может ли эксцесс быть отрицательным?

  • Редакция Кодкампа

17 авг. 2022 г.
читать 2 мин

В статистике эксцесс используется для описания формы распределения вероятностей.

В частности, он сообщает нам, в какой степени значения данных группируются в хвостах или пиках распределения.

Эксцесс распределения может быть отрицательным, равным нулю или положительным.

Нулевой эксцесс

Если эксцесс распределения равен 0, то он равен нормальному распределению, которое имеет следующую колоколообразную форму:

Пример эксцесса при нормальном распределении

Положительный эксцесс

Если распределение имеет положительный эксцесс, говорят, что оно лептокуртическое , что означает, что оно имеет более острый пик и более тяжелые хвосты по сравнению с нормальным распределением.

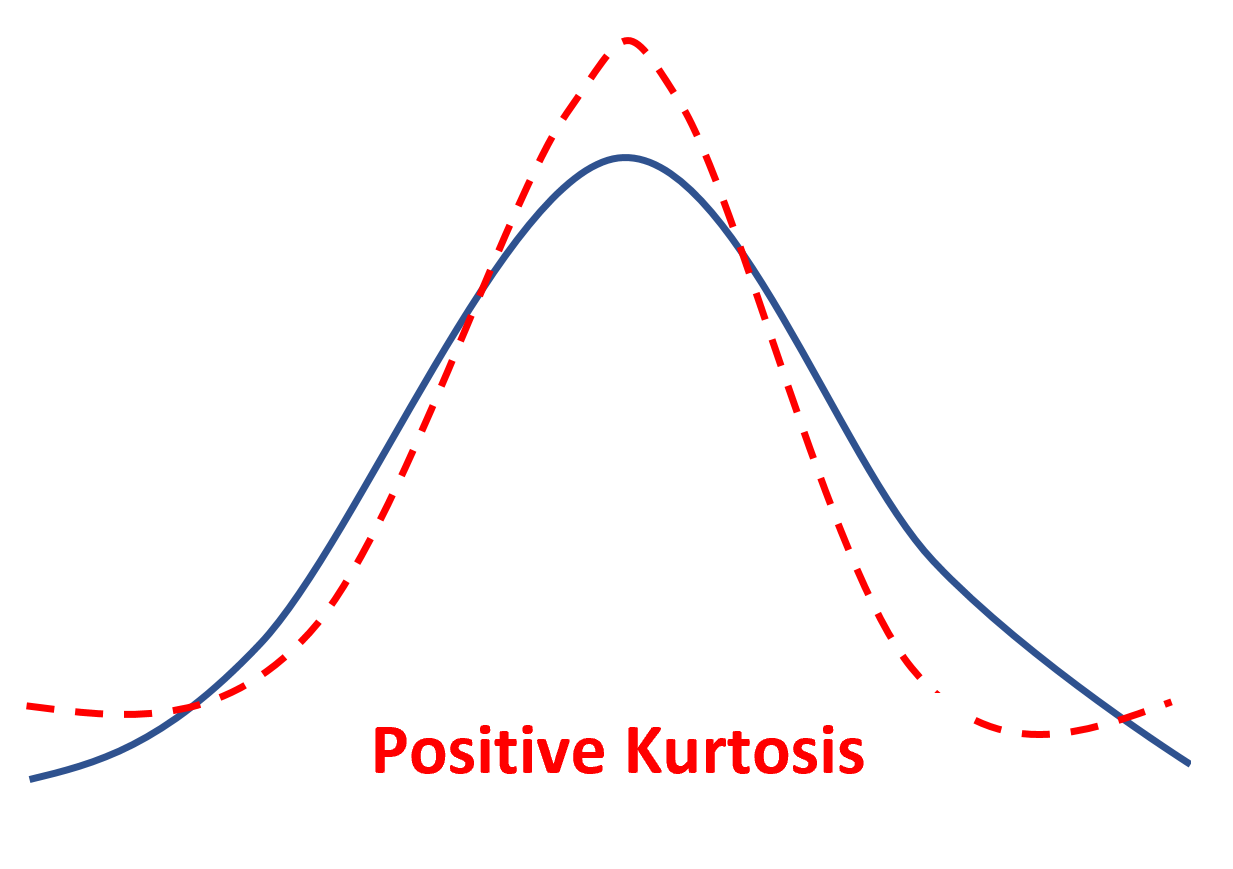
Это просто означает, что меньше значений данных находится рядом со средним значением, а больше значений данных находится на хвостах.

Наиболее известным распределением с положительным эксцессом является t-распределение, которое имеет более острый пик и более тяжелые хвосты по сравнению с нормальным распределением.

Отрицательный эксцесс

Если распределение имеет отрицательный эксцесс, говорят, что оно платикуртическое , что означает, что у него более плоский пик и более тонкие хвосты по сравнению с нормальным распределением.

Пример отрицательного эксцесса

Это просто означает, что больше значений данных находится рядом со средним значением и меньше значений данных находится на хвостах.

Одним крайним примером распределения с отрицательным эксцессом является равномерное распределение , которое вообще не имеет пика и является полностью плоским распределением.

Когда использовать эксцесс на практике

На практике мы часто измеряем эксцесс распределения на исследовательской фазе анализа, когда просто пытаемся лучше понять данные.

Таким образом, если мы видим, что эксцесс положительный, то мы знаем, что работаем с распределением, в котором меньше значений данных расположены ближе к центру и больше значений данных разбросаны вдоль хвостов.

И наоборот, если мы видим, что эксцесс отрицательный, то мы знаем, что работаем с распределением, в котором больше значений данных расположено ближе к центру и меньше значений данных в хвостах.

Дополнительные ресурсы

Чтобы найти асимметрию и эксцесс для данного распределения, вы можете ввести необработанные значения данных в этот Калькулятор асимметрии и эксцесса, который сообщит вам как асимметрию, так и эксцесс для распределения.

Одним из самых популярных статистических тестов, который используется для определения того, имеет ли конкретное распределение асимметрию и эксцесс, соответствующие нормальному распределению, является тест Харке-Бера .

У Академии Хана также есть отличная серия видео , в которой рассказывается, как классифицировать формы распределений.

Источник

В прикладных задачах, например в математической ста­тистике, при теоретическом изучении Эмпирических распре­делений, отличающихся от нормального распределения, воз­никает необходимость количественных оценок этих различий. Для этой цели введены специальные безразмерные характеристики.

Определение 6. Асимметрией теоретического распределения называется отношение центрального момента третьего поряд­ка к кубу среднего квадратического отклонения:

Определение 7. Эксцессом теоретического распределения на­зывается величина, определяемая равенством

Где μ4 — центральный момент четвертого порядка.

Для нормального распределения As = Еk = 0. При отклоне­нии от нормального распределения асимметрия положительна, если “длинная” и более пологая часть кривой распределения расположена справа от точки на оси абсцисс, соответствую­щей моде; если эта часть кривой расположена слева от моды, то асимметрия отрицательна (рис. 18.7, А, б).

Эксцесс характеризует “крутизну” подъема кривой распре­деления по сравнению с нормальной кривой: если эксцесс поло­жителен, то кривая имеет более высокую и острую вершину; в случае отрицательного эксцесса сравниваемая кривая имеет более низкую и пологую вершину (рис. 18.7, В).

Следует иметь в виду, что при использовании указанных характеристик сравнения опорными являются предположения об одинаковых величинах математического ожидания и дис­персии для нормального и теоретического распределений.

Пример 5. Пусть дискретная случайная величина Х задана законом следующего распределения:

Найти асимметрию и эксцесс теоретического распределения.

Решение. Найдем сначала математическое ожидание слу­чайной величины:

Затем вычисляем начальные и центральные моменты 2, 3 и 4-го порядков и среднее квадратическое отклонение (см. фор­мулы (18.27)-(18.31)):

Теперь по формулам (18.45) и (18.46) находим искомые вели­чины:

В данном случае “длинная” часть кривой распределения рас­положена справа от моды, причем сама кривая является не­сколько более островершинной, чем нормальная кривая с теми же величинами математического ожидания и дисперсии.

< Предыдущая   Следующая >
Источник

В предыдущей теме мы обсуждали, как определить, отличается ли распределение доходности от нормального распределения из-за асимметрии.

Еще одна причина, из-за которой распределение может отличаться от нормального распределения, заключается в том, что большее количество доходов может быть сконцентрировано близко к среднему значению (более пиковое распределение) и большее количество доходов может сильнее отклоняется от среднего (у распределения более толстые хвосты).

По сравнению с нормальным распределением, такое распределение имеет большую долю незначительных отклонений от среднего дохода (больше мелких неожиданностей) и большую долю экстремально больших отклонений от среднего дохода (больше больших неожиданностей). Большинство инвесторов воспринимают большую вероятность очень больших отклонений от среднего как повышенный риск.

Эксцесс или крутизна распределения (англ. ‘kurtosis’) – это статистическая мера, которая сигнализирует нам, что распределение более или менее пиковое, по сравнению с нормальным распределением.

  • Распределение с более острой вершиной, чем обычно, называется островершинным или лептокуртическим (англ. ‘leptokurtic’, от греческого слова lepto – узкий).
  • Распределение, более сглаженное, чем обычно, называется плосковершинным или платикуртическим  (англ. ‘platykurtic’, от греческого слова platy – широкий);
  • Распределение, идентичное нормальному распределению отношении крутизны вершины, называют распределением с нормальным эксцессом или мезокуртическим (англ. ‘mesokurtic’, от греческого слова meso – средний).

Описанная нами ситуация с более частыми экстремально большими наблюдениями  – это островершинное наблюдение.

График, представленный ниже, иллюстрирует островершинное распределение. Оно имеет более острую вершину и более толстые хвосты, чем нормальное распределение.

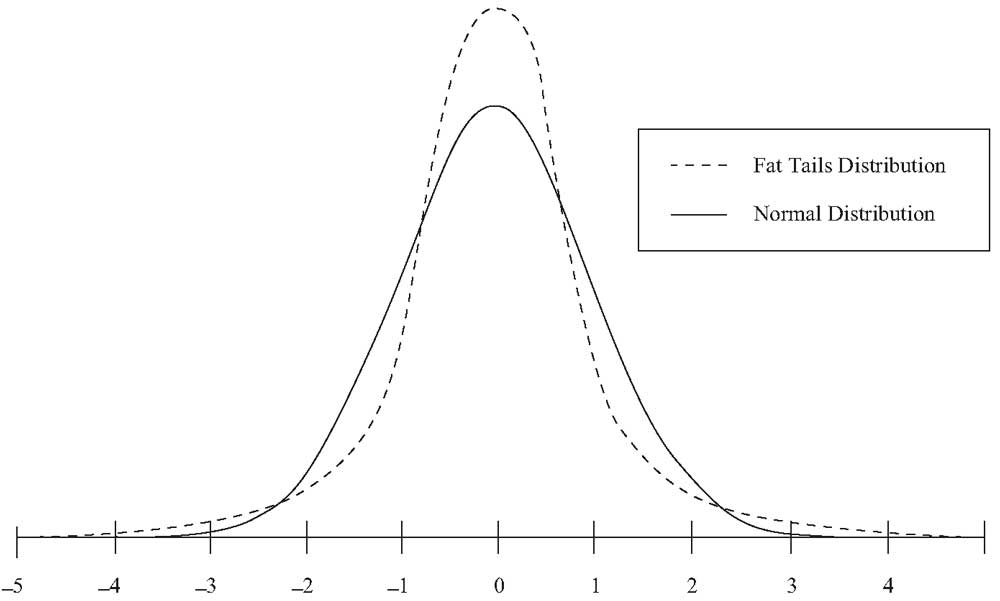Рисунок 8. Островершинное распределение с толстыми хвостами. Рисунок 8. Островершинное распределение с толстыми хвостами.

Расчет коэффициента эксцесса включает в себя определение среднего отклонения от среднего, возведенного в четвертую степень, а затем деление результата на стандартное отклонение, возведенное в четвертую степень.

Эта мера не привязана к шкале. Значение эксцесса всегда положительно, потому что отклонения возведены в четвертую степень.

Для всех нормальных распределений эксцесс равен 3. Многие статистические программные пакеты рассчитывают избыточный эксцесс, как эксцесс минус 3.

Избыточный эксцесс (англ. ‘excess kurtosis’), таким образом, характеризует эксцесс относительно нормального распределения:

  • Распределение с нормальным эксцессом имеет эксцесс равный 0. 
  • Островершинное распределение имеет избыточный эксцесс больше 0.
  • Плосковершинное распределение имеет избыточный эксцесс меньше 0.

Распределение доходности с положительным избыточным эксцессом (островершинное распределение доходности) – имеет больше экстремально больших отклонений от среднего значения, чем нормальное распределение.

Формула избыточного эксцесса выборки.

Ниже приведена формула для расчета выборочного избыточного эксцесса (англ. ‘sample excess kurtosis’):

(Формула 18)

( dst
K_E = left( {n(n+1) over (n-1)(n-2)(n-3)} {dsum_{i=1}^n (X_i – overline X)^4 over s^4} right) – {3(n-1)^2 over (n-2)(n-3)} )

где

  • ( n ) – размер выборки, а
  • (s) – стандартное отклонение выборки.

В Формуле 18 выборочный эксцесс – первый член. Обратите внимание, что когда n становится большим, Формула 18 приблизительна равна:

( begin{aligned} {n^2 over n^3} {sum (X – overline X)^4 over s^4} – {3n^2 over n^2} = {1 over n} {sum (X – overline X)^4 over s^4} – 3 end{aligned} )

Для выборки из 100 наблюдений или больше, при нормальном распределении, избыточный эксцесс выборки равный 1.0 или больше будет считаться необычно большим.

Было обнаружено, что большинство рядов доходности акций являются островершинными. Если обратное распределение имеет положительный избыточный эксцесс (лептокуртоз) и мы используем статистические модели, которые не учитывают более толстые хвосты, мы будем недооценивать вероятность очень плохих или очень хороших результатов.

Например, доходность S&P 500 за 19 октября 1987 года составляла 20 стандартных отклонений от средней дневной доходности. Такой результат возможен при нормальном распределении, но его вероятность почти равна 0.

Если ежедневные ставки доходности взяты из нормального распределения, то

  • доходность в 4 стандартных отклонения или более ожидается раз в 50 лет;
  • доходность в 5 стандартных отклонений или более ожидается каждые 7000 лет.

Доходность за октябрь 1987 года, скорее всего, была получена из распределения с более толстыми хвостами, чем у нормального распределения.

Если посмотреть на Таблицу 27, приведенную ранее, то в месячной доходности индекса S&P 500 наблюдается очень большой избыточный эксцесс, приблизительно 9.4. Это чрезвычайно толстый хвост по сравнению с нормальным распределением. В отличие от месячной доходности, ряд годовой доходности почти не имеет избыточного эксцесса.

Результаты по избыточному эксцессу согласуются с результатами исследований, согласно которым нормальное распределение является лучшим приближением для доходности акций США с годовым периодом владения, чем для доходности с более короткими (например, месячным) периодами владения.

Следующий пример иллюстрирует расчет избыточного эксцесса выборки для одного из двух взаимных фондов, рассмотренных ранее.

Пример расчета выборочного избыточного эксцесса доходности.

Сделав вывод о том, что годовая доходность фонда T. Rowe Price Equity Income была отрицательно ассиметрична в течение периода 2003-2012 гг., что мы можем сказать об эксцессе распределения доходности фонда?

В Таблице 28 (повторно) приводятся годовые доходы фонда.

Таблица 28. Годовая доходность T. Rowe Price Equity Income, 2003-2012 гг. (повторно)

Год

Доходность (%)

2003

25.78

2004

15.05

2005

4.26

2006

19.14

2007

3.30

2008

-35.75

2009

25.62

2010

15.15

2011

-0.72

2012

17.25

Используя информацию из Таблицы 28, сделайте следующее:

  1. Рассчитайте избыточный эксцесс PRFDX с точностью до двух десятичных знаков.
  2. Охарактеризуйте форму распределения доходности PRFDX на основе вашего ответа на часть 1 как лептокуртическую, мезокуртическую или платикуртическую.

Решение для части 1:

Чтобы вычислить избыточный эксцесс, мы находим сумму отклонений от среднего значения, возведенных в четвертую степень, делим ее на стандартное отклонение, возведенное в четвертую степень, и затем умножаем полученный результат на ( n (n + 1) / [(n – 1 ) (n – 2) (n – 3)]). Этот расчет определяет эксцесс.

Избыточный эксцесс – это эксцесс минус ( 3 (n – 1)^2 / [(n – 2) (n – 3)] ).

В Tаблице 30 приведены соответствующие расчеты.

Таблица 30. Расчет эксцесса для PRFDX.

Год

(R_t)

( R_t – overline R )

( (R_t – overline R)^4 )

2003

25.78

16.87

80,995.395

2004

15.05

6.14

1,421.260

2005

4.26

-4.65

467.533

2006

19.14

10.23

10,952.229

2007

3.30

-5.61

990.493

2008

-35.75

-44.66

3,978,092.479

2009

25.62

16.71

77,966.098

2010

15.15

6.24

1,516.137

2011

-0.72

-9.63

8,600.133

2012

17.25

8.34

4,837.981

n =

10

R =

8.91%

Сумма =

4,165,839.738

s =

18.12%

s4 =

107,803.478

Сумма/s4 =

38.643

n(n + 1)/[(n – 1)(n – 2)(n -3)] =

0.2183

Эксцесс =

8.434

3(n – 1)2/[(n – 2)(n -3)] =

4.34

Избыточный эксцесс =

4.09

Источник: performance.morningstar.com.

Используя Формулу 18, делаем расчет:

( dst K_E = {110 over (9)(8)(7)} {4,165,839.738 over 18.12^4} – {3(9)^2 over (8)(7)} = 4.09 )

Решение для части 2:

Распределение годовой доходности PRFDX, по-видимому, является островершинным, исходя из положительного избыточного эксцесса выборки. Довольно большой избыточный эксцесс 4.09 указывает на то, что распределение годовой доходности PRFDX имеет толстые хвосты относительно нормального распределения.

С отрицательной асимметрией и положительным избыточным эксцессом, похоже, что годовая доходность PRFDX не распределялась нормально в течение периода.

Источник

Добавить комментарий