Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.
Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) производная
равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).
Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).


Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
– Производная положительна там, где функция возрастает.
– Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).
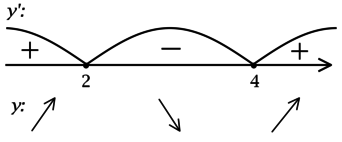
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после – производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.
(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.
(- 9): функция возрастает, а потом убывает – максимум.
(-7): минимум.
(3): максимум.
Все вышесказанное можно обобщить следующими выводами:
– Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
– Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
- Найдите производную функции (f'(x)).
- Найдите корни уравнения (f'(x)=0).
- Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
- Определите знак производной в каждом промежутке (методом интервалов).
- Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
- Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
– если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
– если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
– если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:
(15x^4-60x^2=0) (|:15)
(x^4-4x^2=0)
(x^2 (x^2-4)=0)
(x=0) (x^2-4=0)
(x=±2)
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
Теперь очевидно, что точкой максимума является (-2).
Ответ. (-2).
Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов
Скачать статью
Производная положительна только тогда, когда функция возрастает. То есть, нам необходимо найти точки, в которых функция растет. Смотрим на график нашей функции: функция растет на промежутках: от (x=-7) до (x=0) и от (x = 6) до (x=12).
Так как по условию нам нужны только ЦЕЛЫЕ точки, в которых производная положительна, то это будут: (x=—6); (x=-5), (x=-4), (x=-3), (x=-2), (x=-1), (x=7), (x=8), (x=9), (x=10), (x=11). Всего точек получилось (11). Я отметил их зеленым цветом.
Обратите внимание, что точки (x=-7), (x=0), (x=6), (x=12) мы не считаем, так как в этих точках у нас будут минимумы и максимумы функции, а в них производная равна нулю, то есть не положительна.
Ответ: (11.)
Пример 2
На рисунке 6 изображен график функции, определенной на промежутке ((-10;12)). Найдите количество точек, в которых производная функции равна нулю.
12. Исследование функций с помощью производной
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Поиск точек экстремума у элементарных функций
(blacktriangleright) Простейшие элементарные функции (ПЭФ) и их производные: [begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{1} & c & 0\&&\
textbf{2} & x^a & acdot x^{a-1}\&&\
textbf{3} & ln x & dfrac1x\&&\
textbf{4} & log_ax & dfrac1{xcdot ln a}\&&\
textbf{5} & e^x & e^x\&&\
textbf{6} & a^x & a^xcdot ln a\&&\
textbf{7} & sin x & cos x\&&\
textbf{8} & cos x & -sin x\[1ex]
hline
end{array} quad quad quad quad
begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{9} & mathrm{tg}, x & dfrac1{cos^2 x}\&&\
textbf{10} & mathrm{ctg}, x & -,dfrac1{sin^2 x}\&&\
textbf{11} & arcsin x & dfrac1{sqrt{1-x^2}}\&&\
textbf{12} & arccos x & -,dfrac1{sqrt{1-x^2}}\&&\
textbf{13} & mathrm{arctg}, x & dfrac1{1+x^2}\&&\
textbf{14} & mathrm{arcctg}, x & -,dfrac1{1+x^2}\[0.5ex]
hline
end{array}]
(blacktriangleright) Элементарные функции (ЭФ) — любые линейные комбинации простейших элементарных функций (то есть их сумма, разность, умножение на число).
Пример: (f(x)=4cos x +dfrac{x^3}2)
(blacktriangleright) Основные формулы поиска производной ((f=f(x), g=g(x)) – функции):
1. Умножение функции на число: [(ccdot f)’=ccdot f’]
2. Сумма или разность двух функций: [(fpm g)’=f’pm
g’]
(blacktriangleright) Хитрости, упрощающие поиск производной:
I. Т.к. (sqrt[n]{x^m}=x^{frac mn}), то производную этой функции можно искать по формуле (2).
Частный случай: (sqrt x =x^{frac12}): [(sqrt x)’=dfrac1{2sqrt x}]
II. Т.к. (dfrac1{x^a}=x^{-a}), то производную этой функции можно также искать по формуле (2): [left(dfrac1{x^a}right)’=-dfrac a{x^{a+1}}]
(blacktriangleright) Для того, чтобы найти точки экстремума, необходимо схематично изобразить график функции.
В задачах из данной подтемы это можно сделать с помощью производной: найти промежутки возрастания ((f’>0)) и убывания ((f'<0)) функции, критические точки (где (f’=0) или (f’) не существует).
Задание
1
#2390
Уровень задания: Легче ЕГЭ
Найдите точку максимума функции (y = -x^2).
ОДЗ: (x) – произвольный.
1) [y’ = -2x]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [-2x = 0qquadLeftrightarrowqquad x = 0,.] Производная существует при любом (x).
2) Найдём промежутки знакопостоянства (y’):

3) Эскиз графика:

Таким образом, (x = 0) – точка максимума функции (y).
Ответ: 0
Задание
2
#2391
Уровень задания: Легче ЕГЭ
Найдите точку минимума функции (y = x^2 + 2x + 2) на отрезке ([-2; 2]).
ОДЗ: (x) – произвольный.
1) [y’ = 2x + 2]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [2x + 2 = 0qquadLeftrightarrowqquad x = -1,.] Производная существует при любом (x).
2) Найдём промежутки знакопостоянства (y’):
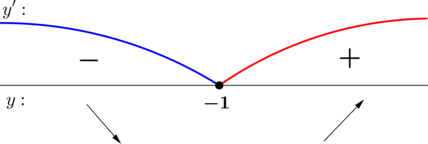
3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([-2; 2]):

4) Эскиз графика на отрезке ([-2; 2]):
Таким образом, (x = -1) – точка минимума функции (y) на ([-2; 2]).
Ответ: -1
Задание
3
#2392
Уровень задания: Легче ЕГЭ
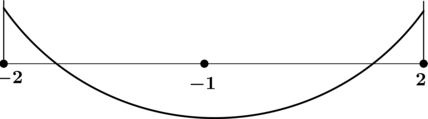
Найдите точку минимума функции (y = 3x^2 – 6x + pi) на отрезке ([-3; 3]).
ОДЗ: (x) – произвольный.
1) [y’ = 6x – 6]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [6x – 6 = 0qquadLeftrightarrowqquad x = 1,.] Производная существует при любом (x).
2) Найдём промежутки знакопостоянства (y’):

3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([-3; 3]):

4) Эскиз графика на отрезке ([-3; 3]):
Таким образом, (x = 1) – точка минимума функции (y) на ([-3; 3]).
Ответ: 1
Задание
4
#2691
Уровень задания: Равен ЕГЭ
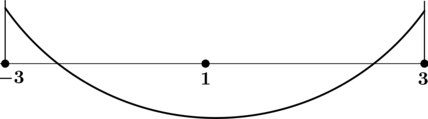
Найдите точку локального минимума функции (y = x^3 – 3x).
ОДЗ: (x) – произвольный.
1) [y’ = 3x^2 – 3]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [3x^2 – 3 = 0qquadLeftrightarrowqquad x = pm 1,.] Производная существует при любом (x).
2) Найдём промежутки знакопостоянства (y’):

3) Эскиз графика (y):
Таким образом, (x = 1) – точка локального минимума функции (y).
Ответ: 1
Задание
5
#2710
Уровень задания: Равен ЕГЭ
Найдите точку локального максимума функции
(y = x^3 – 15x^2 + 48x + e).
1) (y’ = 3x^2 – 30x + 48 = 3(x^2 – 10x + 16)).
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует):
[3(x^2 – 10x + 16) = 0qquadLeftrightarrowqquad x^2 – 10x + 16 = 0,] откуда находим (x_1 = 2, x_2 = 8). Таким образом, [y’ = 3(x – 2)(x – 8).] Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
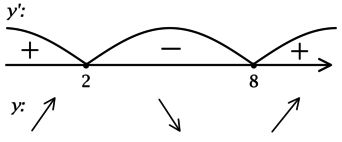
3) Эскиз графика (y):
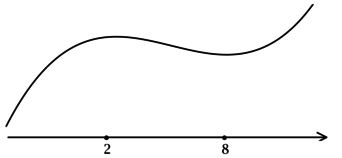
Таким образом, (x = 2) – точка локального максимума функции (y).
Ответ: 2
Задание
6
#869
Уровень задания: Равен ЕГЭ
Найдите точку локального максимума функции (y = dfrac{1}{3}x^3 – 8x^2 + 55x + 11).
1) (y’ = x^2 – 16x + 55).
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует):
(x^2 – 16x + 55 = 0), откуда находим корни (x_1 = 5, x_2 = 11). Таким образом, [y’ = (x-5)(x-11).] Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
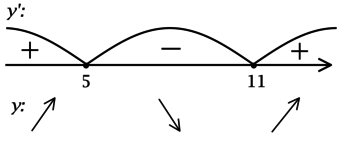
3) Эскиз графика (y):
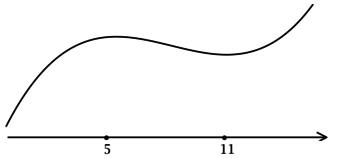
Таким образом, (x = 5) – точка локального максимума функции (y).
Ответ: 5
Задание
7
#868
Уровень задания: Равен ЕГЭ
Найдите точку локального минимума функции (y = dfrac{1}{3}x^3 – 3x^2 + 8x + 2).
1) (y’ = x^2 – 6x + 8).
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует):
(x^2 – 6x + 8 = 0), откуда находим корни (x_1 = 2, x_2 = 4). Таким образом, [y’ = (x-2)(x-4).] Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
3) Эскиз графика (y):
Таким образом, (x = 4) – точка локального минимума функции (y).
Ответ: 4
Задачи, при выполнении которых требуется найти точки экстремума у элементарных функций, в ЕГЭ по математике включаются каждый год. Уметь справляться с ними должны школьники, сдающие как базовый уровень экзамена, так и профильный. Научившись безошибочно находить максимум и минимум элементарной функции в задачах ЕГЭ, выпускники смогут выполнить задание и получить конкурентные баллы.
Восполнить пробелы в знаниях и лучше усвоить информацию вам поможет образовательный проект «Школково». Чтобы учащимся было легче справляться с задачами ЕГЭ, в которых необходимо найти минимум и максимум элементарной функции, мы предлагаем прежде всего повторить определения и основные правила. Эту информацию мы разместили в разделе «Теоретическая справка». Здесь собран материал, подготовленный нашими специалистами для выпускников средних школ.
Чтобы закрепить усвоенную информацию и научиться справляться с задачами в ЕГЭ, выполните упражнения, в которых требуется найти точки экстремума у элементарных функций. Богатая подборка задач представлена в разделе «Каталог». Задания здесь регулярно обновляются и дополняются. Выполнить упражнения на нахождение точек экстремума у элементарных функций, которые встречаются в ЕГЭ, можно в режиме онлайн, находясь в Москве или любом другом городе России.

УСТАЛ? Просто отдохни
Рассмотрим примеры заданий из №7 ЕГЭ, в которых нужно найти точки экстремума на графике производной.
Точка xo, в которой существует производная f'(xo), является точкой экстремума функции f(x), если производная в этой точке равна нулю и при переходе через xo производная меняет свой знак.
Отсюда следует, что в точках экстремума функции график производной должен не просто касаться оси Ox, он должен её пересекать.
№1
На рисунке изображён график производной функции f(x), определённой на интервале (-6;7). Найти точку экстремума функции f(x) на отрезке [-2;5].
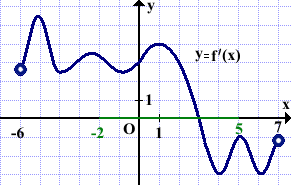
Решение:
На рисунке изображён график производной (а не график функции)!
В точках экстремума функции производная f'(x) равна нулю и меняет знак.
Выделяем отрезок [-2;5]. Точка, в которой производная равна нулю и меняет знак — это точка с абсциссой 3.
Значит x=3 — точка экстремума функции y=f(x).
Ответ: 3.
№2
На рисунке изображён график производной функции f(x), определённой на интервале (-9;5). Найти количество точек экстремума функции f(x) на отрезке [6-;4].
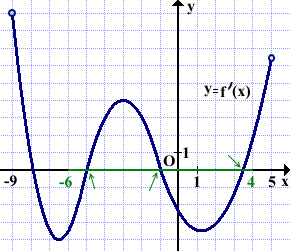
Решение:
Выделяем отрезок [-6;4].
На этом отрезке график производной пересекает ось абсцисс в трёх точках.
Следовательно, на отрезке [-6;4] функция f(x) имеет три точки экстремума.
Ответ: 3.
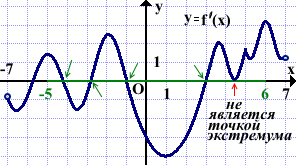
№3
На рисунке изображён график производной функции f(x), определённой на интервале (-7;7). Найти количество точек экстремума функции f(x) на отрезке [-5;6].
Решение:
Выделяем отрезок [-5;6].
На этом отрезке график производной пересекает ось абсцисс в четырёх точках. Значит, функция f(x) имеет на отрезке [-5;6] четыре точки экстремума.
Точка, в которой производная равна нулю, но знак не меняет (график производной коснулся оси Ox, но не пересёк её), не является точкой экстремума.
Ответ: 4.
Важно внимательно читать условие, чтобы не перепутать нахождение точек экстремума по графику производной с заданием на нахождение точек экстремума по графику функции!
Значения функции и точки максимума и минимума
 Наибольшее значение функции
Наибольшее значение функции
Наменьшее значение функции
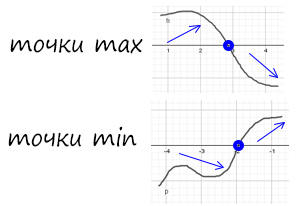
Точки max
Точки min
Как говорил крестный отец: «Ничего личного». Только производные!
Статью Как посчитать производные? надеюсь, ты изучил, без этого дальше будет проблематично.
12 задание по статистике считается достаточно трудным, а все потому, что ребята не прочитали эту статью (joke). В большинстве случаев виной всему невнимательность.
12 задание бывает двух видов:
- Найти точку максимума / минимума (просят найти значения «x»).
- Найти наибольшее / наименьшее значение функции (просят найти значения «y»).
Как же действовать в этих случаях?
Найти точку максимума / минимума
- Взять производную от предложенной функции.
- Приравнять ее к нулю.
- Найденный или найденные «х» и будут являться точками минимума или максимума.
- Определить с помощью метода интервалов знаки и выбрать, какая точка нужна в задании.
Задания с ЕГЭ:
Найдите точку максимума функции
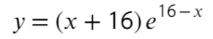
- Берем производную:
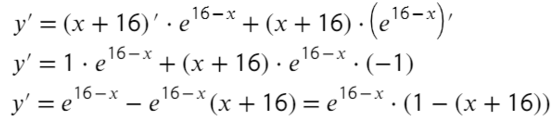
- Приравняем ее к нулю:
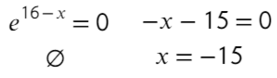
- Получили одно значение икса, для нахождения знаков подставим −20 слева от корня и 0 справа от корня в преобразованную производную (последняя строчка с преобразованием):
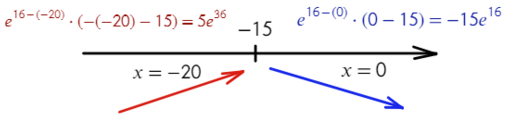
Все верно, сначала функция возрастает, затем убывает — это точка максимума!
Ответ: −15
Найдите точку минимума функции
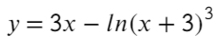
- Преобразуем и возьмем производную:
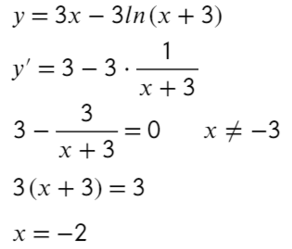
- Получается один корень «−2», однако не стоит забывать о «−3», она тоже будет влиять на изменение знака.
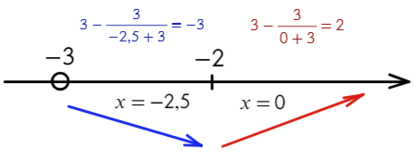
- Отлично! Сначала функция убывает, затем возрасает — это точка минимума!
Ответ: −2
Найти наибольшее / наименьшее значение функции
- Взять производную от предложенной функции.
- Приравнять ее к нулю.
- Найденный «х» и будет являться точкой минимума или максимума.
- Определить с помощью метода интервала знаки и выбрать, какая точка нужна в задании.
- В таких заданиях всегда задается промежуток: иксы, найденные в пункте 3, должны входить в данный промежуток.
- Подставить в первоначальное уравнение полученную точку максимума или минимума, получаем наибольшее или наименьшее значение функции.
Задания с ЕГЭ:
Найдите наибольшее значение функции на отрезке [−4; −1]
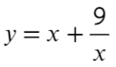
- Преобразуем и возьмем производную:
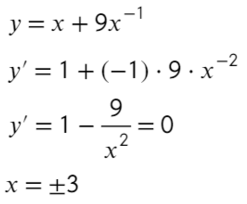
- «3» не вдходит в промежуток [−4; −1]. Значит, остается проверить «−3» — это точка максимума?
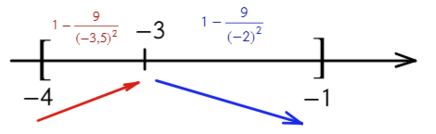
- Подходит, сначала функция возрастает, затем убывает — это точка максимума, и в ней будет наибольшее значение функции. Остается только подставить в первоначальную функцию:
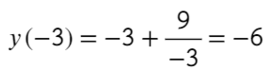
Ответ: −6
Найдите наибольшее значение функции на отрезке [0; 1,5π]
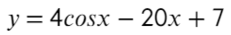
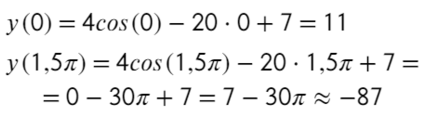
- Наибольшее значение функции равно «11» при точке максимума (на этом отрезке) «0».
Ответ: 11
Выводы:
- 70% ошибок заключается в том, что ребята не запоминают, что в ответ на наибольшее/наименьшее значение функции нужно написать «y», а на точку максимума/минимума написать «х».
- Нет решения у производной при нахождении значений функции? Не беда, подставляй крайние точки промежутка!
- Ответ всегда может быть записан в виде числа или десятичной дроби. Нет? Тогда перерешивай пример.
- В большинстве заданий будет получаться одна точка и наша лень проверять максимум или минимум будет оправдана. Получили одну точку — можно смело писать в ответ.
- А вот с поиском значения функции так поступать не стоит! Проверяйте, что это нужная точка, иначе крайние значения промежутка могут оказаться больше или меньше.
Будь в курсе новых статеек, видео и легкого математического юмора.
