
|
© БГЭУ Лекция № 13-14 |
Исследование функций с помощью производных проф. Дымков М. П. 127 |
||||||||||||||||||||||||||||||||||
В экономических исследованиях часто используется понятие эластичности функциии.
Определение. Эластичностью функции Ex (y) называется предел отношения относительного приращения функции y = f (x) к относительному приращению аргумента х при ∆x → 0 :
|
∆y |
||||||||
|
Ex (y) = lim |
y |
= |
x |
lim |
∆y |
= |
x |
y′. |
|
∆x |
∆x |
|||||||
|
∆x→0 |
y ∆x→0 |
y |
x
Если эластичность функции представить в виде
∆y 100%
Ex (y) = ∆limx→0 ∆yx 100% , x
то легко увидеть, что эластичность функции показывает приближенно, на сколько процентов изменится функция y = f (x) при изменении независимой
переменной х на 1%.
Пользуясь понятием дифференциала, эластичность можно представить иначе:
|
dy |
|||||||||||
|
Ex (y) = |
x |
dy |
= |
y |
= d(ln y) . |
||||||
|
dx |
|||||||||||
|
y dx |
d(ln x) |
||||||||||
|
x |
|||||||||||
|
Геометрическая интерпретация |
|||||||||||
Эластичность функции y = f (x) можно найти из графика этой функции. |
|||||||||||
|
По определению эластичности Ex (y) = |
x |
y′ |
= |
x |
tgα , где |
α – угол наклона |
|||||
|
y |
y |
касательной к функции y = f (x) в точке
Из треугольника ACD :
CDAC = ACy0 = sin(π −α) = sinα .
Из треугольника BCL:
BCLC = BCx0 = cos(π −α) = −cosα
|
Откуда, |
|||||||
|
BC |
x0 |
x0 |
|||||
|
−cosα |
′ |
||||||
|
AC = y0 |
= − y |
||||||
|
f (x0 ) = −Ex (y) |
|||||||
|
0 |
|||||||
|
sinα |
|||||||
С(x0, y0 ) (рис. 20).
|
y |
|
|
В |
y = f ( x ) |
|
L |
C( x0 , y0 ) |
Рис. 20.

© БГЭУ Лекция № 13-14 Исследование функций с помощью производных проф. Дымков М. П. 128
т.е. эластичность убывающей функции равна отношению расстояний по касательной от точки С с координатами (x0, y0 ) до ее пересечения с осями
ординат и абсцисс, взятому со знаком минус. Таким образом, если аккуратно построить график функции y = f (x) и провести касательную к кривой в
исследуемой точке С(x0, y0 ), можно приблизительно определить величину эластичности функции в этой точке.
Свойства эластичности функции
Пусть функция y = f (x) имеет конечную или бесконечную производную на промежутке. Вспомним, что производная есть отношение дифференциалов
|
y′ = |
dy |
||||||||||||||||
|
dx . |
|||||||||||||||||
|
1. Эластичность есть безразмерная величина |
Ex (y) = Eax (by) . |
||||||||||||||||
|
◄Доказательство очевидно: Eax (by) = ax |
d(by) |
= |
x |
dy = |
x |
y′.► |
|||||||||||
|
by d(ax) |
y dx |
y |
|||||||||||||||
|
2. Эластичности взаимно обратных функций есть взаимно обратные |
|||||||||||||||||
|
величины |
|||||||||||||||||
|
Ex (y) = |
1 |
. |
|||||||||||||||
|
Ey (x) |
|||||||||||||||||
|
◄ Ex (y) = |
x |
dy = |
1 |
= |
1 |
.► |
|||||||||||
|
y dx |
|||||||||||||||||
|
y dx |
Ey (x) |
||||||||||||||||
|
x dy |
|||||||||||||||||
|
3. Эластичность произведения функций u = u(x) |
и v = v(x) равна сумме их |
||||||||||||||||
|
эластичностей Ex (uv) = Ex (u) + Ex (v). |
◄При доказательстве свойства воспользуемся
|
дифференциала d(uv) = v du +u dv . Тогда |
||||||||||||
|
Ex (uv) = |
x |
d(uv) |
= |
x vdu +udv |
= |
x |
du |
+ |
x |
dv |
||
|
uv |
dx |
|||||||||||
|
uv dx |
u dx |
v dx |
||||||||||
|
4. Эластичность отношения функций |
u = u(x) и |
|||||||||||
|
их эластичностей |
||||||||||||
|
u |
||||||||||||
|
Ex |
= Ex (u) − Ex (v) . |
|||||||||||
|
v |
следующим свойством
=Ex (u) + Ex (v) .►
v = v(x) равна разности
|
◄Доказательство аналогично: |
|||||||||||||||||||||
|
u |
|||||||||||||||||||||
|
u |
x |
d |
x vdu −udv |
x du |
x dv |
||||||||||||||||
|
E |
x |
( |
) = |
v |
= |
= |
− |
= E |
x |
(u) − E |
x |
(v) .► |
|||||||||
|
v |
u |
dx |
u v2dx |
u dx |
v dx |
||||||||||||||||
|
v |
v |

© БГЭУ Лекция № 13-14 Исследование функций с помощью производных проф. Дымков М. П. 129
5. Эластичность суммы функций u = u(x) и v = v(x) равна сумме их эластичностей, взятых с соответствующими весами:
Ex (u + v) = u u+ v Ex (u) + u +v v Ex (v) .
|
◄Доказательство |
||||||||||||||||
|
Ex (u + v) = |
x d(u + v) |
= |
x du u |
+ |
x dv v |
= |
||||||||||
|
u + v dx |
u + v dx u |
u + v dx v |
||||||||||||||
|
► |
||||||||||||||||
|
u |
x |
du |
+ |
v |
x |
dv |
= |
u |
Ex (u) + |
v |
Ex (v) |
|||||
|
u + v |
u + v |
u + v |
u + v |
|||||||||||||
|
u dx |
v dx |
Эластичность элементарных функций
Вычислим эластичности некоторых функций.
|
1. |
Степенная функция y = xα . Ее эластичность: |
|||||||||||||||
|
α |
x d(xα ) |
x αxα−1dx |
||||||||||||||
|
Ex (x ) = |
= |
=α . |
||||||||||||||
|
α |
dx |
α |
dx |
|||||||||||||
|
x |
x |
|||||||||||||||
|
2. |
Показательная функция |
y = ax . |
||||||||||||||
|
Ex (ax ) = |
x |
d(ax ) |
= |
x |
ax ln a dx = xln a . |
|||||||||||
|
ax |
dx |
ax |
dx |
|||||||||||||
|
3. |
Логарифмическая функция y = ln x . |
|||||||||||||||
|
Ex (ln x) = |
x |
d(ln x) |
= |
1 |
. |
|||||||||||
|
ln x |
dx |
ln x |
||||||||||||||
|
4. |
Линейная функция y = ax +b . |
|||||||||||||||
|
Ex (ax +b) = |
x d(ax +b) |
= |
ax |
. |
||||||||||||
|
ax +b |
dx |
ax +b |
||||||||||||||
Функция в зависимости от величины своей эластичности может быть
|
совершенно эластичная |
Ex (y) |
= +∞ |
||||||||||
|
эластичная |
1< |
Ex (y) |
< +∞ |
|||||||||
|
неэластичная |
0 < |
Ex (y) |
<1 |
|||||||||
|
совершенно неэластичная |
Ex (y) = 0 |
Эластичность функций применяется, например, при анализе спроса и потребления, в процессе анализа проектных рисков в ходе исследования изменений критериев оценки проектной эффективности в зависимости от изменений факторов риска.

|
© БГЭУ Лекция № 13-14 |
Исследование функций с помощью производных проф. Дымков М. П. 130 |
Так, эластичность спроса Q по цене P EP (Q) = QP dQdP
показывает величину относительного изменения спроса на какой-либо товар при изменении цены этого товара. Она характеризует «чувствительность» потребителей к изменению цен на продукцию.
Вопросы для повторения
1.Сформулировать и доказать теорему о производной монотонной функции.
2.Сформулировать определение локального максимума и минимума функции.
3.Сформулировать и доказать теорему о необходимом условии экстремума.
4.Сформулировать и доказать теорему о первом достаточном условии экстремума.
5.Сформулировать и доказать теорему о втором достаточном условии экстремума.
6.Привести схему исследования функции на экстремум.
7.Сформулировать определение наибольшего и наименьшего значения функции.
8.Сформулировать определение выпуклости функции.
9.Сформулировать и доказать теорему об условиях направленности выпуклости функции вверх или вниз.
10.Дать определение точки перегиба и сформулировать необходимое и достаточное условия существования точки перегиба.
11.Привести определения вертикальной, горизонтальной и наклонной асимптот графика функции.
12.Привести схему полного исследования функции с целью построения ее графика.
13.Сформулировать определение эластичности функции, дать геометрическую интерпретацию.
14.Перечислить и доказать свойства эластичности функции.

Лекция № 15 Комплексные числа проф. Дымков М. П. 131
«КОМПЛЕКСНЫЕ ЧИСЛА»
« Число в математике, как и время в физике, известно каждому, но непонятно лишь специалистам».
Из истории чисел. Понятие числа складывалось в математике постепенно с развитием общества, а также под давлением как практики, так и внутренних потребностей самой математической науки. Можно не останавливаться на подробностях числовых множеств N Z Q (натуральных, целых, рацио-
нальных чисел) – их появление и становление имеет очевидную практическую востребованность. (! Заметим лишь, что введение отрицательных чисел можно интерпретировать как необходимость решения уравнения x + n = 0,n N , а потребность рациональных чисел – для решения уравнений mx + n = 0, m,n N .)
Переход (Q → R ) от рациональных чисел к действительным вызван
скорее внутренней логикой развития математики, чем практическими потребностями. В частности, к необходимости введения действительных чисел привело известное математическое открытие, вытекающее из теоремы Пифагора и состоящее в том, что диагональ единичного квадрата несоизмерима с
|
его сторонами (т.е. не может быть измерена – или по-другому, нет такого |
||||
|
рационального числа вида |
p |
, обозначающее длину диагонали – или, что нет |
||
|
r |
||||
|
такой «единицы», что, разбив ее на q |
||||
|
«кусочков» 1 |
и, взяв потом р та- |
|||
|
q |
|
p |
1 |
, полученной «линейкой» измерим длину диагонали). |
||
|
ких «кусочков» |
||||
|
q |
! Заметим, что для чисто практических целей рациональных чисел вполне хватает, так как с их помощью можно с любой наперед заданной точ-
|
ностью произвести измерение любой величины. |
1 |
|||||
|
Алгебраическая запись факта «несоизмеримости» диаго- |
||||||
|
нали ведет к необходимости решить уравнение |
x2 = 2 . Это 1 |
2 |
||||
|
уравнение во множестве рациональных чисел Q не имеет ре- |
||||||
|
шения. Тогда «решили» ввести новый «символ» |
(его назвали иррацио- |
|||||
|
2 |
||||||
|
нальным), которого нет во множестве Q, т.е. он является «внешним» для Q |
||||||
|
(не принадлежащим Q) и расширить множество |
Q , вводя новые «числа» |

|
Лекция № 15 |
Комплексные числа |
проф. Дымков М. П. 132 |
||
|
вида r1 + r2 |
, где r1, r2 Q пробегают все Q. Эти числа (и пределы по- |
|||
|
2 |
следовательностей из таких чисел) относят к действительным (вещественным) числам. Эти числа как бы заполняют промежутки между рациональными числами. Этот факт очень важен для математики, так как действительные числа представляют собой ту непрерывную среду, в которой помещены рациональные числа, и где становится совершенно ясным, что для чисел характерно не только наличие действий сложения (! имеется трудность, например, сложения чисел с непериодическими дробями – как сложить бесконечные «хвосты» – в арифметике оперируют лишь с конечными числами), умноже-
ния, деления, но также неарифметическая операция предельного перехода.
Конечно же, та «непрерывная» среда, куда «затолкали» (обманули, вклеили, и т.п.) рациональные числа, содержит много тайн. Например, если сравнивать «количество» элементов этих множеств (как говорят еще, сравнивать мощности этих множеств), то оказывается, что множество действительных чисел R, «больше» (мощнее), чем другие множества N, Q, чисел (хотя
их тоже бесконечно много). Среди парадоксов бесконечных множеств, например, следующее: все множество и его часть (подмножество) имеют одинаковое «количество» элементов –{10,11,12,….} N .
Про множество N натуральных чисел говорят, что оно счетно. Можно доказать, что Z и Q в некотором смысле эквиваленты множеству N, т.е. имеют одну и ту же мощность (т.е. являются счетными). Множество же R не является счетным, оно «больше». Про множество R говорят, что оно имеет
мощность континуума.
! Интересно заметить, что множество R и его подмножество – например, интервал (0,1) ) – имеют одну и ту же мощность континуума.
Для сравнения мощностей находят так называемые кардинальные числа. Тогда факт, что R больше Q записывается card(R) > card(Q) .
Далее, множество иррациональных чисел тоже сложно устроено. Есть иррациональные алгебраические числа, т.е. это такие иррациональные числа,
которые являются корнем некоторого алгебраического многочлена (т.е. многочлена некоторой конечной степени с целыми коэффициентами). Множество алгебраических иррациональных чисел счетно. Остальные иррациональные числа, т.е. числа, которые не являются алгебраическими, называют трансцендентными числами. Так как множество R имеет мощность континуума, а все перечисленные его подмножества ( N,Q, множество алгебраи-
ческих чисел) имеют меньшую мощность (счетные), то следовательно множество иррациональных трансцендентных чисел самое большое из них и
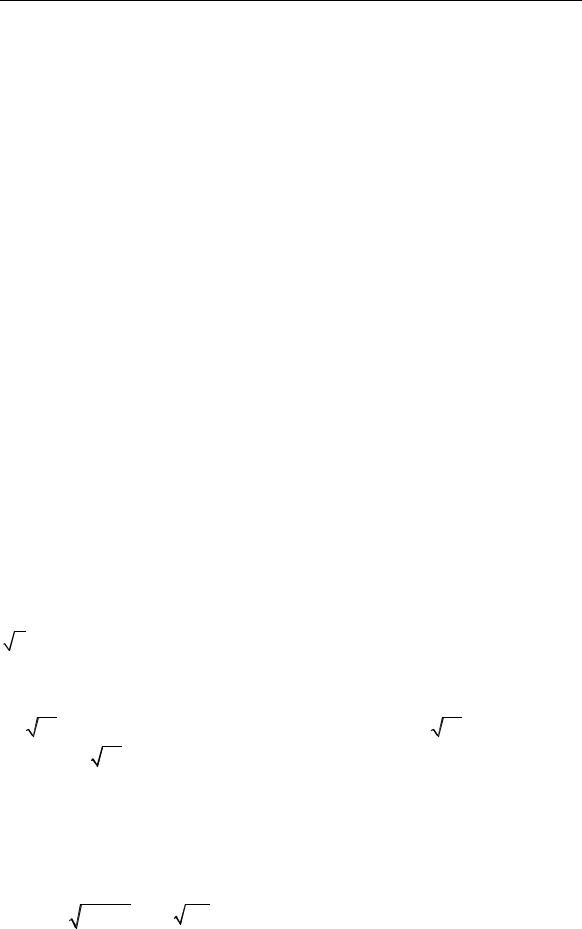
Лекция № 15 Комплексные числа проф. Дымков М. П. 133
имеет мощность континуума. Но, парадокс! Указать конкретно (предъявить) эти числа весьма непросто. (Чисел много больше, чем в N, а «показать» эти числа трудно!). Точнее, трудно доказать, что именно предъявленное число трансцендентно.
Примеры трансцендентности чисел. Совсем недавно доказали, что знаменитые числа «е» , «π »(Линдеман. 1882 г) являются трансцендентными (Напомним, что число «π »можно интерпретировать как отношение длины окружности к ее диаметру. Тогда с учетом трансцендентности числа «π » можно понять невозможность решения старинной задачи о квадратуре кру-
га). Числа вида αβ , где α алгебраическое, а β – иррациональное число, также является числом трансцендентным (Гельфонд, 1934).
! Любопытна так называемая « 7-ая проблема Гильберта»: Есть ли множества промежуточной мощности между «счетным» и « континуумом»? Была гипотеза, что нет таких множеств. В 1968 году Коэн (США) доказал неразрешимость этой проблемы, т.е. она не может быть не доказана, ни опровергнута (примерно ситуация как с «5-м пастулатом» Евклида).
Если теперь вернуться к 1-ой фразе в начале лекции, то должно быть ясно слушателям, что, действительно, числа (как математический объект) вещь далеко не тривиальная.
Перейдем теперь к очередному расширению, теперь уже расширению множества действительных чисел R →C .
Подобно тому, как в ситуации, когда алгебраическое уравнение x2 = 2 не имело решения во множестве рациональных чисел Q, и тогда для «исправления» этой ситуации был введен «внешний» (относительно Q) символ
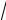
|
i = |
−1 |
и решение уравнения записать в виде x = ± |
−1 |
или |
x = ±i . Здесь |
||
|
символ i = |
или i2 = −1 (введен, по-видимому, Эйлером) |
обозначает но- |
|||||
|
−1 |
вое, «недействительное», число.
Нет такого действительного числа, квадрат которого равен «– 1»! Его называют «мнимой единицей». С помощью этого символа можно сделать
|
расширение |
R →C так, что любое квадратное уравнение будет иметь ре- |
||||||
|
шение |
в |
новом |
множестве C . Например, x2 − 2x + 4 = 0 имеет |
||||
|
x1,2 =1± |
=1± |
. Уже древние индусы знали, что не все квадрат- |
|||||
|
3 (−1) |
3 i |
ные уравнения решаются. Но они, и арабские математики, которые много за-

|
Лекция № 15 |
Комплексные числа |
проф. Дымков М. П. 134 |
|
нимались теорией уравнений, относились к этому спокойно – не все же на свете имеет решение!
Конечно, только возможность извлекать корень квадратный из отрицательного числа недостаточна, чтобы заводить в математике новые числа.
Впервые, по-видимому, мнимые величины появилось в трудах Кардано (1545), который искал выражения в радикалах для решений уравнений 3- ей и 4-ой степеней. (Заметим, что Абель доказал, что, вообще говоря, решения уравнений выше 4-ой степени не выражаются в радикалах.) Он счел их бесполезными и непригодными к употреблению. Действительно, недоверие к этим числам отразилось даже в названии «мнимое». Это недоверие усугублялось тем, что некритическое перенесение формул обычной алгебры на мни-
|
мые числа порождало неприятные |
парадоксы. Например, i = |
, |
i2 = −1, но |
|||||
|
−1 |
||||||||
|
по |
правилам |
действия |
с |
квадратными |
корнями |
получим |
−1 = i2 = 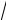

чисел нет понятия арифметического корня). Многие математики того времени изгоняли их, не признавали природы их, казалась им неясной, загадочной и даже мистической. Например, Ньютон не включал мнимые величины в понятие числа, Лейбниц ─ тоже, и ему принадлежит высокопарная фраза «Мнимые числа – это убежище божественного духа, почти что амфибия (гибрид) бытия и небытия».
Пользу мнимых величин впервые оценил Бомбелли (1572 г.). Он для записи решений кубических уравнений, которые имеют три действительных корня, использовал мнимые величины. Кроме того, дал описание основных операций над числами новой породы.
Термин «Комплексные числа» ввел Карно, но полное «гражданство» комплексным числам дал Гаусс. На протяжении 200 лет шли споры о природе комплексных чисел и само название «мнимые» числа отражало их нелегальный характер. Только на рубеже 18 – 19 веков Гаусс придал им полные гражданские права, дал им геометрическую интерпретацию, доказал основную теорему алгебры (любой многочлен имеет хотя бы один корень – действительный или комплексный). Комплексным числам предстоял долгий путь, прежде чем они стали ценнейшим математическим инструментом для решения важных прикладных задач в механике (упругость каркасов кораблей), физике (профили крыльев самолетов), гидродинамике ( обтекание препятствий).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Эластичность функции
- Определение и свойства эластичности функций
- Свойства эластичности функции
- Эластичность спроса относительно цены
- Эластичность предложения относительно цены
Эластичность функции
В экономических исследованиях приросты тех или иных показателей, характеризующих экономические процессы, чаще всего выражают в процентах к базовым значениям. Поэтому и изменение величин, которые связаны с ними функциональной зависимостью, также выражают в процентах. Для этого используют понятие эластичности функции, которое выражается через производную функции.
Определение и свойства эластичности функций
Пусть задана функция y = f (x). Если аргумент x получил приращение Δx и при этом функция y получила приращение Δy, то 

Определение. Предел отношения относительного приращения функции к относительному приращению аргумента при условии, что приращение аргумента стремится к нулю, если существует, называется эластичностью функции.
Обозначают эластичность функции y = f (x) относительно переменной x Ex(y). То есть,
Итак, если в точке x функция имеет производную, то эластичность определяется формулой 
Эластичность выражает приближенный процент приращения функции, который соответствует 1 % приращения аргумента.
Пример. Найти эластичность функции y = x2 – 4 x +7 и вычислить ее при x = 1, x = 2, x = 5.
Решение.
Итак, если x вырастет на 1 % с 1 до 1,01, то y снизится на 0,5 %. Если x вырастет на 1 % с 2 до 2,02, то значение переменной y практически не изменится. Если x вырастет на 1 % с 5 до 5,05, то y вырастет на 2,5 %.
Свойства эластичности функции
ТЕОРЕМА 1. Эластичность произведения двух функций равна сумме эластичности сомножителей:
Ex (U ⋅ V) = Ex (U) + Ex (V).
Доказательство. По определению эластичности
ТЕОРЕМА 2. Эластичность частного двух функций равна разности показателей эластичности делимого и делителя:
Доказательство. По определению эластичности
Эластичность спроса относительно цены
В анализе и прогнозах ценовой политики применяется понятие эластичности спроса и предложения.
Пусть p цена одного изделия, а Q — количество изделий, произведенных и проданных через некоторое время, что определяет спрос. Величина Q зависит от цены, т. е. Q является функцией от p: Q = f (p).
Пусть приращение цены Δp вызывает приращение ΔQ. тогда относительные приращения цены и спроса будут соответственно 
Отношение 
Эластичностью спроса относительно цены называется предел отношения относительного приращения спроса к относительному приращению цены при условии, что приращение цены стремится к нулю.
Эластичность спроса относительно цены приближенно определяет, как меняется спрос на данное изделие, если его цена возрастает на 1 %.
Так, например, если рост цены на 5 % вызывает падение спроса на 8 %, то эластичность будет
Если эластичность спроса η = –0,5, то 10 % роста стоимости товара вызывает падение спроса на (–0,5) 10% = –5%.
Определение. Если процент изменения спроса больше процента изменения цены (η < 1), то спрос называют эластичным, если процент изменения спроса меньше процента изменения цены (-1 < η < 0), то спрос называют не эластичным, а если процент изменения спроса равен проценту изменения цены (η = 1), то спрос называют нейтральным.
Пример. Установлено, что количество произведенных и проданных изделий Q по цене p определяется по формуле Q = 10000 – 500p (0 < p < 20). Определить, при какой цене спрос эластичный, нейтральный, не эластичный.
Решение. Эластичность спроса относительно цены
Спрос будет эластичным, если η < –1, 

Спрос нейтральный при цене p = 10 (руб.). Спрос будет не эластичный, когда -1 < η < 0.
Итак, спрос не эластичный при цене меньшей 10 руб. за изделие.
Пример 2. Установить связь между доходом предприятия и эластичностью спроса от цены.
Решение. Доход определяется как произведение стоимости каждого изделия на количество произведенных и проданных изделий Q : D (Q) = p⋅ Q.
Найдем маржинальный доход, учитывая, что Q есть функция от p.
Если η ≤ –1, то 1 + η < 0, а 
Если –1 < η < 0, то 1 + η > 0, а
То есть функция D (Q) дохода растет с ростом цены p, когда спрос не эластичный.
Эластичность предложения относительно цены
Понятие эластичности можно применять и к другим функциям экономического содержания.
Рассмотрим понятие эластичности предложения S в зависимости от цены товара p. Под предложением понимают количество некоторого товара, который предлагается на продажу за единицу времени. Как правило, предложение какого-либо товара является возрастающей функцией цены. Но бывают случаи, когда предложение повышается со снижением цены. Величина S является функцией от цены товара. То есть, S = S (p).
Пусть Δp — приращение цены, а ΔS — соответствующее приращение предложения. Тогда относительные приращения цены и предложения будут соответственно 

Эластичностью предложения относительно цены называется предел отношения относительного приращения предложения к относительному приращению цены при условии, что приращение цены стремится к нулю.
Эластичность предложения относительно цены приближенно определяет процент приращения предложения на 1 % приращения цены.
Пример 3. Функция предложения некоторого товара 
Решение.
Если p = 2, то
Следовательно, при цене p = 2 увеличение ее на 1 % вызовет увеличение предложения на 0,2 %.
Лекции:
- Разностные уравнения
- Случайная вероятность
- Эквивалентные бесконечно малые функции. Сравнение бесконечно больших функций
- Решение определённых интегралов
- Параллельные прямые
- Экстремум функции многих переменных
- Пределы в математике
- Дифференциал функции
- Объемы подобных фигур
- Алгебра логики
Эта страница — подборка. Общая информация о подборках: http://iloveeconomics.ru/blogs/id3/1081.
Общая идея всех эластичностей:
$text{эластичность функции}approxfrac{text{процентное изменение функции}}{text{процентное изменение аргумента}}$
Точечная эластичность дифференцируемой функции
Пусть f — некоторая дифференцируемая1 функция одной переменной, определённая на множестве неотрицательных чисел и принимающая неотрицательные значения.
Рассмотрим некоторую точку $x>0$, такую что $f(x)>0$.
Точечная эластичность функции f в точке x обозначается $Ef(x)$ и по определению равна следующей величине: $f'(x)frac{x}{f(x)} $
Ту же самую величину можно записать по-другому: $$Ef(x)=mathop{lim }limits_{Delta xto 0} frac{frac{Delta f}{f(x)} }{frac{Delta x}{x} },$$
где $Delta f=f(x+Delta x)-f(x)$
(Константы x и f(x) выносятся за знак предела, и таким образом из второй формулы получаем первую).
Если в данной точке x такой предел существует, значит, при небольших $Delta x$ мы можем записать: $Ef(x)approx frac{Delta f/f}{Delta x/x} $. То есть эластичность функции в некоторой точке x приближённо показывает отношение процентного изменения функции к процентному изменению аргумента при небольших значениях $Delta x$ (подробнее о процентных изменениях можно почитать в главе 3 «Про размерности и проценты».
Упражнения:
-
Эластичность линейной функции
- График эластичности линейного спроса
- График эластичности линейного предложения
- Когда линейный спрос эластичен?
- Геометрический смысл эластичности
- Сравнение эластичностей линейных спросов при заданной цене
- Эластичности произведения и частного
- Эластичность и возрастание функции
- Эластичность спроса и возрастание выручки
- График спроса и возрастание выручки
- Эластичность и возрастание среднего значения
- Когда AC возрастает
- Как определить эластичность по графику
- Эластичности суммы и разности
- Эластичности рыночного и индивидуальных спросов
- Эластичность функции Q(P)=AP^b
- (*) Все функции с постоянной эластичностью
Эластичности произведения и частного функций и их применения
Эластичность суммы
Прочее
Другие виды эластичности
Рассматривается функция Q(P).
- Эластичность перехода линейной функции
- Эластичность перехода и дуговая эластичность
- Выручка и зоопарк эластичностей
- Связь выручки, точечной и дуговой эластичностей
- (*) Постоянная дуговая эластичность. Advanced
Эластичность перехода из точки $P_{1} $ в точку $P_{2} $:
[E=frac{Delta Q/Q_{1} }{Delta P/P_{1} } =frac{Q_{2} -Q_{1} }{P_{2} -P_{1} } frac{P_{1} }{Q_{1} } ]
Т.е. эластичность перехода из точки $P_1$ в точку $P_2$ буквально равна величине $frac{text{процентное изменение функции}}{text{процентное изменение аргумента}} $.
Термин «эластичность перехода» не является распространённым. В школьных учебниках и задачниках эту величину часто называют тем же термином «точечная эластичность», как и ту, что определяется через производную.
Дуговая эластичность:
[E=frac{Delta Q/(Q_{1} +Q_{2} )}{Delta P/(P_{1} +P_{2} )} =frac{Q_{2} -Q_{1} }{P_{2} -P_{1} } frac{P_{1} +P_{2} }{Q_{1} +Q_{2} } ]
Точечная эластичность функции нескольких переменных
Если функция f зависит от нескольких переменных, то нужно указывать, по какой переменной мы считаем эластичность. Например, если функция спроса на некоторый товар зависит от цены этого товара и от дохода покупателя, т.е. $Q_{d} =f(P,I)$, то мы можем посчитать две эластичности: эластичность спроса по цене и эластичность спроса по доходу. Отличие только в том, что в определении используется частная производная (что это такое — см. ниже):
Эластичность спроса по цене:$E_{P} f(P,I)=f_{P}^{‘} (P,I)frac{P}{f(P,I)} $, где $f_{P}^{‘} (P,I)$ — (частная) производная функции f по цене.
Эластичность спроса по доходу:$E_{I} f(P,I)=f_{I}^{‘} (P,I)frac{I}{f(P,I)} $, где $f_{I}^{‘} (P,I)$ — (частная) производная функции f по доходу.
Что такое частная производная
Пусть задана функция $f$ нескольких переменных (обозначим их число буквой n). Набор из n чисел $x_{1} ,x_{2} ,…,x_{n} $ определяет значение функции: $f(x_{1} ,x_{2} ,…,x_{n} )$. Если позволить меняться только одной переменной (например, первой), а все остальные переменные зафиксировать на некотором уровне (например, $x_{2} =8,x_{3} =0.5,…$), то фактически получится функция одной переменной. Производная этой получившейся функции — это и есть то, что называется частной производной функции $f$ по данной переменной (в нашем примере — по первой переменной). Интерпретация: если нарисовать график функции f в зависимости от этой переменной (при фиксированных значениях остальных переменных), то угловой коэффициент касательной к этому графику в некоторой точке $x_{1} $ равен частной производной функции f «в точке» $x_{1} ,x_{2} ,…,x_{n} $. Естественно, если мы поменяем значения какой-либо из фиксированных переменных (например, вместо $x_{2} =8$ поставим $x_{2} =8.5$), то весь этот график может изменить свою форму, в частности, может поменяться наклон в тех или иных точках $x_{1} $. Таким образом, частная производная функции f по первой переменной зависит не только от значения первой переменной, но и от значений остальных переменных. Это отражается и в обозначении: например, если спрос задаётся формулой $Q_{d} =f(P,I)$, то частная производная функции спроса по доходу обозначается $f_{I}^{‘} (P,I)$.
1 Дифференцируемая — имеющая производную. Подробнее: глава 2 «Функции».
Лекция 4. Эластичность и ее свойства.
Эластичности элементарных функций
Изучение различных экономических вопросов, таких, как определение динамики спроса населения на данный товар при изменении его цены или при изменении доходов населения, исследование диапазона взаимозаменяемости ресурсов производства, определение эффективности тех или иных затрат, прогнозирование изменения прибыли предприятия или фирмы под воздействием различных факторов и решение многих других проблем, приводит к необходимости выяснения на сколько процентов изменится одна величина, если другая увеличилась на 1%.
Характеристика, дающая ответ на поставленный вопрос, называется эластичностью соответствующей функции.
Приступим к построению этого показателя. Пусть аргумент 



Приращения 

Величина 

Отношение 


Рекомендуемые материалы
Это отношение будет характеризовать поведение функции 




Отношение 

Определение. Предел отношения относительного приращения функции 





Если функция 

и формула (4) принимает вид
или

Из (3) следует, что эластичность 


Формулу (5) можно переписать в виде
Это означает, что для функции выпуска 
Пример 17.
Эластичность данной функции вычисляется по формуле
При 




Пример 18. 
Здесь
При 



Свойства эластичности
1. Эластичность – безразмерная величина, значение которой не зависит от того, в каких единицах измерены величины у и х. 

2. Эластичности взаимно обратных функций – взаимно обратные величины:

Например, эластичность величины спроса по цене обратна эластичности цены по величине спроса
3. Эластичность произведения двух функций u(x) и v(x), зависящих от одного и того же аргумента х, равна сумме эластичностей:
4. Эластичность частного двух функций u(x) и v(x), зависящих от одного и того же аргумента х, равна разности эластичностей
5. Эластичность суммы двух функций u(x) и v(x) может быть найдена по формуле:
Например, эластичность величины спроса по цене обратна эластичности цены по величине спроса
3. Эластичность произведения двух функций u(x) и v(x), зависящих от одного и того же аргумента х, равна сумме эластичностей:
4. Эластичность частного двух функций u(x) и v(x), зависящих от одного и того же аргумента х, равна разности эластичностей
5. Эластичность суммы двух функций u(x) и v(x) может быть найдена по формуле:
Эластичности элементарных функций
1. Эластичность степенной функции у=хa постоянна и равна показателю степени a: Ех(хa) = a.
2. Эластичность показательной функции у=ах пропорциональна х:
3. Эластичность линейной функции 
Если график линейной функции имеет отрицательный наклон (а<0), то эластичность функции меняется от нуля к точке ym пересечения графиком оси у до минус бесконечности (-¥) в точке пересечения оси х, проходя через значение (-1) в средней точке.
Таким образом, хотя прямая имеет постоянный наклон, её эластичность зависит не только от наклона, но и от того, в какой точке х мы её находим (рис.10). Функция с бесконечной эластичностью во всех точках называется совершенно эластичной, с нулевой эластичностью во всех точках – совершенно неэластичной.
 |
Задания для самостоятельной работы
1. Используя свойства эластичности, найдите 
а) 


г) 


Лекция 5. Виды эластичностей в экономике
Рассмотрим основные виды эластичностей.
1.Эластичность спроса по цене (прямая)
показывающая относительное изменение (выраженное в процентах) величины спроса на какое-либо благо при изменении цены этого блага на один процент и характеризующая чувствительность потребителей к изменению цен на продукцию. Если ценовая эластичность спроса по абсолютной
 |
величине больше единицы, то спрос называют эластичным (совершенно эластичным при бесконечно большой величине эластичного спроса). Если ценовая эластичность спроса по абсолютной величине меньше единицы, то спрос называют неэластичным (совершенно неэластичным при нулевой эластичности спроса).
И, наконец, если ценовая эластичность спроса по абсолютной величине равна единице, то говорят о спросе с единичной эластичностью.
2.Эластичность спроса по доходу
характеризующая относительное изменение (в процентах) величины спроса на какое-либо благо при изменении дохода потребителей этого блага на один процент. Положительная эластичность спроса по доходу характеризует нормальные (качественные) товары, а отрицательная величина – малоценные (некачественные) товары
Так, высокий положительный коэффициент спроса по доходу в отрасли указывает, что её вклад в экономический рост больше, чем доля в структуре экономики, и она имеет шансы на расширение и процветание в будущем. Наоборот, если коэффициент эластичности спроса на продукцию отрасли по доходу имеет небольшое положительное или отрицательное значение, то её может ожидать застой и перспектива сокращения производства.
3. Перекрестная эластичность спроса по цене
характеризующая относительное изменение (в процентах) величины спроса на одно благо при изменении цены на другое благо (замещающее или дополняющее его в потреблении) на один процент. Положительный знак перекрестной эластичности спроса по цене свидетельствует о замещаемости благ, а отрицательный – о дополняемости.
4.Ценовая эластичность ресурсов
характеризующая относительное изменение (в процентах) величины спроса на какой-нибудь ресурс (например, труд) при изменении цены этого ресурса (соответственно, заработной платы) на один процент.
5.Эластичность замещения одного ресурса другим
характеризующая необходимое изменение (в процентах) величины одного ресурса (например, капитала) при изменении количества другого ресурса (например, труда) на один процент с тем, чтобы выпуск при этом не изменился.
Рассмотрим подробнее эластичность спроса относительно цены. Изучается зависимость спроса 

Предположим, что цены на аналогичные товары, доходы потребителей и структура их потребностей – постоянные величины. Тогда зависимость спроса от цены можно описать с помощью функции

Во многих экономических исследованиях необходимо установить не величину спроса при каждом конкретном уровне цены, а характер изменения спроса при определенном изменении цены. В этом случае находят эластичность спроса относительно цены. В наших обозначениях
Эластичность спроса относительно цены определяет, на сколько процентов изменится спрос на товар, если цена на него увеличится на 1%. Так как в большинстве случаев спрос является убывающей функцией цены и

то, чтобы избежать отрицательных чисел, в этих случаях при изучении эластичности принимают
Знак «-» показывает, что спрос уменьшается при увеличении цены.
Пример 19. Если функция спроса линейная:

то
При 




Пример 20. Для 


Действительно,

Если спрос обратно пропорционален цене, то при любой цене увеличение ее на 1% влечет за собой уменьшение спроса также на 1 %.
Определение. Говорят, что спрос эластичен, если повышению цены на 1% соответствует снижение спроса более чем на 1%, т.е. 


В примере 19 спрос нейтрален при 



Другими словами, спрос на товар эластичен, если небольшое изменение цены товара вызывает значительные изменения величины спроса на него. В обратной ситуации, когда изменение цены ведет к сравнительно небольшому изменению величины спроса, последний является неэластичным. Примерами товаров с эластичным спросом могут служить, например, яблоки, помидоры, персики и т.п. При росте цен на них покупательский спрос может переключиться на другие виды овощей и фруктов. При определенном уровне цен покупатели могут полностью отказаться, например, от употребления фруктов или заменить их соками и другими консервами. В то же время спрос на товары первой необходимости (лекарства, обувь, электричество, газ, телефон), на вещи, цена которых малоощутима для семейного бюджета (карандаш, зубная паста, крем для обуви) и труднозаменяемые товары (электрические лампочки, хлеб, бензин) является неэластичным.
Исследуем динамику выручки при различных видах спроса.
Общие расходы населения на данный товар (выручка от его продажи) при цене 

Предельная выручка равна

или

а) Если спрос эластичен, т.е. 
и с повышением цены выручка от продажи снижается.
б) При нейтральном спросе (

и выручка практически не зависит от цены.
В этом случае 


Следовательно, в случае нейтрального взноса его размер пропорционален цене (см. пример 20).
в) При неэластичном спросе (

Из сказанного видно, что знание эластичности спроса на данный товар позволяет прогнозировать направление изменения суммы выручки под влиянием роста или снижения цены. Очевидно, каждой фирме выгодно, чтобы спрос на ее продукцию был как можно более эластичным, ибо в такой ситуации существует возможность назначать сравнительно высокие цены.
Значит, фирма должна прилагать все усилия к поддержанию спроса на ее товар на достаточно высоком уровне. Достижению этой цели способствуют хорошее качество продукции, четко организованное обслуживание потребителей, высокое качество рекламы
Пример 21. Известно, что эластичность спроса на товар составляет 0.4. Определим, как изменится доход от реализации товара, если цену на него увеличить на 5%.
При эластичности 







Выручка от реализации товара по цене 

Эластичность предложения определяется аналогично эластичности спроса:

Для дифференцируемой функции 

или

В отличии от формулы (5), выражающей эластичность спроса, в (7) и (8) отсутствует знак «-». Это связано с тем, что с ростом рыночной цены на товар предложение этого товара обычно растет. Каждому предпринимателю выгодно реализовать свою продукцию по более высокой цене. Поэтому 

Равенство (8) означает, что эластичность предложения равна отношению предельного предложения к среднему.
Предложение также может быть эластичным и неэластичным.
Определение. Предложение называется эластичным, если 


Например, фирма решила пригласить на работу дополнительное количество разнорабочих и квалифицированных наладчиков для скорейшего ввода в строй новой автоматической линии. Чтобы увеличить предложение услуг, руководство фирмы объявило об увеличении заработной платы на 1000 рублей в месяц. Если в городе много безработных, студентов, малооплачиваемых трудящихся, то такая надбавка к семейному бюджету может оказаться для них существенной, и предложение услуг в качестве разнорабочего будет эластичным по цене. Однако едва ли много квалифицированных, а следовательно и высокооплачиваемых наладчиков согласиться сменить место работы из-за такой прибавки к зарплате. Транспортные расходы, моральный ущерб, необходимость хотя бы частичной переквалификации для работы с новым для них оборудованием не окупятся дополнительной суммой в 1000 рублей. Здесь предложение услуг едва ли окажется эластичным по цене.
Пример 22. Пусть зависимость предложения 


а) 

б) 
в) 
Зависимость между спросом на товар и его ценой (а значит, и вид соответствующей кривой) в значительной степени определятся полезностью товара. На вид функции предложения в первую очередь оказывают влияние издержки производства.
Определение. Цена, при которой величина спроса равняется величине предложения, называется равновесной (или ценой равновесия).
В точке М величина спроса равна величине предложения, 
Пример 23. 



отсюда
или


Следовательно, цена равновесия 
Задания для самостоятельной работы
1. Спрос 

2. Найдите цену, при которой спрос совпадает с предложением (цену равновесия). Рассчитайте эластичность спроса при этой цене. Постройте графики спроса и предложения.
3. Формула
выражает зависимость спроса от цены. Определите, при каких значениях 
4. Функция спроса имеет вид 

5. Определите, на сколько процентов приблизительно изменится выручка от реализации товара. Если эластичность спроса равна 

а) 
б) 
в) 
Лекция 6. Многофакторные производственные функции, эластичности
Определение. Функция 



Если (9) выражает зависимость объема выпускаемой данным предприятием продукции от затрат ресурсов 

где 
Не нарушая общности рассуждений, в дальнейшем будем рассматривать лишь функции двух независимых переменных.
При моделировании экономики страны в качестве основных ресурсов используют затраты труда L и объём производственных фондов К. Национальный доход Y выступает в роли результата деятельности экономики:
Y=F(K,L).
В математических моделях функционирования отдельного предприятия, цеха, участка и т.д. Y обозначает объем выпускаемой данным экономическим объектом продукции.
Формальные свойства производственных функций
Производственная функция f(x1, x2) определена при х1≥0, х2≥0. ПФ должна удовлетворять ряду (для каждой конкретной ПФ – своему) свойств:
1. 

2. 
3. 

4. 
Свойство 1 означает, что без ресурсов нет выпуска, что при отсутствии хотя бы одного из ресурсов нет выпуска.
Свойство 2 означает, что с ростом затрат хотя бы одного ресурса объем выпуска растет, и что с ростом затрат одного ресурса при неизменном количестве другого ресурса объем выпуска растет.
Свойство 3 означает что с ростом затрат одного (i-го) ресурса при неизменном количестве другого ресурса величина прироста выпуска на каждую дополнительную единицу i-го ресурса не растет (закон убывающей эффективности), при росте одного ресурса предельная эффективность другого ресурса возрастает. Если выполнены условия 3, то график Г ПФ есть поверхность, расположенная в неотрицательном ортанте 
Свойство 4 означает, что ПФ является однородной функцией (ОФ) степени p>0. При p>1 с ростом масштаба производства в t раз (число t>1), т.е. с переходом от вектора х к вектору tx, объем выпуска возрастает в tp (>t) раз, т.е. имеет рост эффективности производства от роста масштаба производства. При p<1 имеем падание эффективности производства от роста масштаба производства. При p=1 имеем постоянную эффективность производства при росте его масштаба (или имеем независимость удельного выпуска от масштаба производства – в английской терминологии constant returns to scale).
Для ПФКД 
Для ЛПФ 


Множество (линия) lq уровня 

Различные наборы 



Функция Кобба-Дугласа, функция с постоянными пропорциями
Функция Кобба-Дугласа имеет вид:

При 

К такому же выводу приходим и при 
Если K и L увеличить в λ раз, то в такое же количество раз возрастает и Y.
Действительно,

Эта функция находит широкое применение в моделях долгосрочного прогнозирования.
Функцию с постоянными пропорциями
выбирают тогда, когда один из ресурсов производства резко дефицитен, а второй избыточен.
Убедимся в том, что в этой функции реализуются предположения о свойствах производственных функций.
1. Если 

и

2. Предположим, что 

и

К такому же результату придем, если 

Предельные (маржинальные) и средние значения
производственной функции
Пусть 
называется средней производительностью i-го ресурса (фактора производства) (СПФ) или средним выпуском по i-му ресурсу (фактору производства). Символика: 
Напомним, что в случае двухфакторной ПФКД 




Пусть 
называется предельной (маржинальной) производительностью i-го ресурса (фактора производства) (ППФ) или предельным выпуском по i-му ресурсу (фактору производства). Символика: 
Обозначим символами 






Следовательно, ППФ (приближенно) показывает, на сколько единиц увеличится объем выпуска у, если объем затрат 




Пример 24. 1). Для ПФКД 




Решение задачи. Имеем:






Для ПФ 

(т.е. предельная производительность i-го ресурса не больше средней производительности этого ресурса) обычно выполняются.
2). Для ЛПФ 
Решение задачи. Имеем:






Пусть 




Сумма 
Поскольку при малом приращении 
(крайнее правое выражение есть отношение двух относительных величин 





Пример 25. 1). Выписать в явном виде для ПФКД выражения для Е1, Е2 и Ех.
Решение задачи. Имеем:



2). Для ЛПФ 
Решение задачи. Имеем:



Пусть 


при постоянной у.
Обратим внимание на то, что i – номер заменяемого ресурса, j – номер замещающего ресурса. Используется также термин: предельная технологическая норма замены (замещения) i-ого ресурса (фактора производства) j-м ресурсом (фактором производства). Приведем более краткий (но не менее точный) термин: (предельная) норма замены (замещения) ресурсов.
Пусть выпуск у является постоянным (т.е. все наборы затрачиваемых ресурсов расположены на одной изокванте), тогда первый полный дифференциал dy ПФ 
(здесь dx1, dx2 – дифференциалы переменных x1, x2), откуда, выражая первый дифференциал dxj, получим (

откуда, поделив на dxi, получим

На основании (10), (11) и (12) имеем:

Отметим, что строгий вывод формулы (13) опирается в действительности на теорему о неявной функции, формулировка которой в настоящем пособии не приводится.
Непосредственно проверяется, что для двухфакторной ПФ справедливо равенство

Задания для самостоятельной работы
Задача 1. Найдите значения функций при заданных значениях независимых переменных:
а) 
б) 
в) 
г) 
Задача 2. Определите, как изменится значение функции
если 
а) К увеличить на 3 единицы;
б) L уменьшить на 1 единицу;
в) К увеличить в 2 раза при неизменном значении другой переменной;
А если затраты обоих ресурсов одновременно
г) уменьшить в 4 раза;
д) увеличить в 3 раза;
е) увеличить на 3 единицы?
Вместе с этой лекцией читают “1 Цели, задачи и содержание ГЗК”.
Задача 3. Процесс производства описывается с помощью степенной функции выпуска

а) как следует изменить затраты К, чтобы компенсировать уменьшение L на 50% (Уровень выпуска при этом сохраняется)
б) на сколько процентов уменьшатся затраты К при увеличении L на 25%?
в) как изменится выпуск, если затраты обоих ресурсов увеличить в 2 раза (уменьшить в 3 раза)?
г) во сколько раз надо увеличить затраты L, чтобы компенсировать уменьшение К в 4 раза?
Спрос и предложение
Сегодня практически любой развитой стране мира свойственна рыночная экономика, при которой вмешательство государства минимально или вовсе отсутствует. Цены на товары, их ассортимент, объемы производства и продажи — все это складывается стихийно в результате работы рыночных механизмов, важнейшие из которых это закон спроса и предложения. Поэтому рассмотрим хотя бы сжато основные понятия экономической теории в этой области: спрос и предложение, их эластичность, кривая спроса и кривая предложения, а также факторы их определяющие, рыночное равновесие.
Спрос: понятие, функция, график
Очень часто приходится слышать (видеть), что такие понятия как спрос и величина спроса смешивают, считая их синонимами. Это неправильно — спрос и его величина (объем) совершенно разные понятия! Рассмотрим их по отдельности.
Спрос (англ. «Demand») — платежеспособная потребность покупателей в определенном товаре при определенном уровне цен на него.
Величина спроса (объем спроса) — количество товаров, которое покупатели желают и могут приобрести по данной цене.
Итак, спрос — это потребность покупателей в некотором товаре, обеспеченная их платежеспособностью (то есть у них есть деньги, чтобы удовлетворить свою потребность). А величина спроса — конкретное количество товаров, которое покупатели хотят и могут (у них есть на это деньги) купить.
Пример: Даша хочет яблок и у нее есть деньги на их покупку — это спрос. Даша идет в магазин и покупает 3 яблока, потому что она хочет купить именно 3 яблока и у нее достаточно денег на эту покупку — это величина (объем) спроса.
Различают следующие виды спроса:
- индивидуальный спрос — отдельного конкретного покупателя;
- общий (совокупный) спрос — всех покупателей имеющихся на рынке.
Спрос, зависимость между его величиной и ценой (а также другими факторами) можно выразить математически, в виде функции спроса и кривой спроса (графическая интерпретация).
Функция спроса — закон зависимости величины спроса от различных факторов оказывающих на него влияние.
Кривая спроса — графическое выражение зависимости величины спроса на некоторый товар от цены на него.
В простейшем случае функция спроса представляет собой зависимость его величины от одного ценового фактора:
где: QD — величина спроса на данный товар;
P — цена на данный товар.
Графическое выражение этой функции (кривая спроса) — прямая линия с отрицательным углом наклона. Описывает такую кривую спроса обычное линейное уравнение:
где: QD — величина спроса на данный товар;
P — цена на данный товар;
a — коэффициент задающий смещение начала линии по оси абсцисс (X);
b — коэффициент задающий угол наклона линии (отрицательное число).
Но, в реальности, конечно все намного сложнее и на величину спроса влияет не только цена, но и многие неценовые факторы. В этом случае функция спроса приобретает следующий вид:
где: QD — величина спроса на данный товар;
PX — цена на данный товар;
P1..Pn — цена на другие взаимосвязанные товары (заменители, дополнители);
I — доход покупателей;
E — ожидания покупателей относительно роста цен в будущем;
N — количество возможных покупателей в данном регионе;
T — вкусы и предпочтения покупателей (привычки, следование моде, традициям и пр.);
Графически такую кривую спроса можно представить в виде дуги, но это опять же упрощение — в реальности график спроса может иметь любую самую причудливую форму.
Таким образом, факторы влияющие на спрос:
- Ценовой фактор спроса — цена на данный товар;
- Неценовые факторы спроса:
- наличие взаимосвязанных товаров (заменителей, дополнителей);
- уровень доходов покупателей (их платежеспособность);
- количество покупателей в данном регионе;
- вкусы и предпочтения покупателей;
- ожидания покупателей (относительно роста цен, будущих потребностей и пр.);
- иные факторы.
Закон спроса
Для понимания рыночных механизмов очень важно знать базовые законы рынка, к числу которых относится закон спроса и предложения.
Закон спроса — при росте цены на товар, спрос на него снижается, при прочих неизменных факторах, и наоборот.
Математически закон спроса означает наличие между величиной спроса и ценой обратной зависимости.
С обывательской точки зрения закон спроса полностью логичен — чем ниже цена на товар, тем привлекательнее его покупка и тем большее количество единиц товара будет куплено.
Но, как это ни странно, бывают парадоксальные ситуации, при которых закон спроса дает сбой и действует в обратную сторону. Это проявляется в том, что величина спроса растет по мере роста цены! Примерами могут служить эффект Веблена или товары Гиффена.
Закон спроса имеет теоретическое обоснование. В его основе лежат следующие механизмы:
1. Эффект дохода — стремление покупателя приобрести большее количество данного товара при снижении цены на него, при этом не уменьшая объема потребления других товаров.
2. Эффект замещения — готовность покупателя при снижении цены на данный товар отдать предпочтение именно ему, отказавшись от других более дорогостоящих товаров.
3. Закон убывающей предельной полезности — по мере потребления данного товара каждая его дополнительная единица будет приносить все меньшее удовлетворение (продукт «приедается»). Поэтому потребитель будет готов продолжать покупать данный товар только при снижении его цены.
Таким образом, изменение цены (ценового фактора) приводит к изменению величины спроса. Графически это выражается в перемещении по кривой спроса.
Воздействие иных (неценовых) факторов приводит к сдвигу кривой спроса — изменению спроса. При росте спроса график смещается вправо и вверх, при снижении спроса — влево и вниз. Рост называется — расширение спроса, снижение — сужение спроса.
Эластичность спроса
При росте цены на товар, величина спроса на него уменьшается. При снижении цены — увеличивается. Но это происходит по-разному: в одних случаях незначительное колебание уровня цен может вызвать резкий рост (падение) спроса, в других изменение цены в очень широких пределах практически никак не повлияет на спрос. Степень такой зависимости, чувствительности величины спроса к изменению цены или других факторов называется эластичностью спроса.
Эластичность спроса — степень изменения величины спроса при изменении цены (или другого фактора) в ответ на изменение цены или другого фактора.
Числовой показатель, отражающий степень подобного изменения — коэффициент эластичности спроса.
Соответственно, эластичность спроса по цене показывает насколько изменится объем спроса при изменении цены на 1%.
Дуговая эластичность спроса по цене — применяется, когда нужно вычислить примерную эластичность спроса между двумя точками на дуговой кривой спроса. Чем более выпуклой будет дуга спроса, тем выше будет погрешность определения эластичности.
где: EP D — эластичность спроса по цене;
P1 — первоначальная цена на товар;
Q1 — первоначальная величина спроса на товар;
P2 — новая цена;
Q2 — новая величина спроса;
ΔP — приращение цены;
ΔQ — приращение величины спроса;
Pср. — средняя цены;
Qср. — средняя величина спроса.
Точечная эластичность спроса по цене — применяется тогда, когда задана функция спроса и есть значения исходной величины спроса и уровня цены. Характеризует относительное изменение величины спроса при бесконечно малом изменении цены.
где: dQ — дифференциал величины спроса;
dP — дифференциал цены;
P1, Q1 — значение цены и величины спроса в анализируемой точке.
Эластичность спроса можно рассчитать не только по цене, но например, по доходу покупателей, а также по другим факторам. Существует и перекрестная эластичность спроса. Но мы не будем здесь настолько глубоко рассматривать эту тему, ей будет посвящена отдельная статья.
В зависимости от абсолютного значения коэффициента эластичности различают следующие виды спроса (виды эластичности спроса):
- Совершенно неэластичный спрос или абсолютная неэластичность (|E| = 0). При изменении цены величина спроса практически не меняется. Близкими примерами могут служить товары первой необходимости (хлеб, соль, лекарства). Но в реальности нет товаров с совершенно неэластичным спросом на них;
- Неэластичный спрос (0 ГРАФИК
Предложение: понятие, функция, график
Теперь поговорим о другом рыночном явлении, без которого невозможен спрос, его неразлучном спутнике и противоборствующей силе — предложении. Здесь также следует различать само предложение и его величину (объем).
Предложение (англ. «Supply») — способность и готовность продавцов продать товар по данной цене.
Величина предложения (объем предложения) — количество товаров, которое продавцы желают и могут продать по данной цене.
Различают следующие виды предложения:
- индивидуальное предложение — конкретного отдельного продавца;
- общее (совокупное) предложение — всех продавцов присутствующих на рынке.
Функция предложения — закон зависимости величины предложения от различных факторов оказывающих на него влияние.
Кривая предложения — графическое выражение зависимости величины предложения на некоторый товар от цены на него.
Упрощенно функция предложения представляет собой зависимость его величины от цены (ценового фактора):
где: QS — величина предложения на данный товар;
P — цена на данный товар.
Кривая предложения в этом случае — прямая линия с положительным углом наклона. Описывает эту кривую предложения следующее линейное уравнение:
где: QS — величина предложения на данный товар;
P — цена на данный товар;
c — коэффициент задающий смещение начала линии по оси абсцисс (X);
d — коэффициент задающий угол наклона линии.
Функция предложения, в ее более сложной форме учитывающей влияние и неценовых факторов, представлена ниже:
где: QS — величина предложения;
PX — цена данного товара;
P1..Pn — цены других взаимосвязанных товаров (заменителей, дополнителей);
R — наличие и характер производственных ресурсов;
K — применяемые технологии;
C — налоги и дотации;
X — природно-климатические условия;
В этом случае кривая предложения будет иметь форму дуги (хотя это опять же упрощение).
Таким образом, факторы влияющие на предложение:
- Ценовой фактор — цена на данный товар;
- Неценовые факторы:
- наличие товаров-дополнителей и товаров-заменителей;
- уровень развития технологий;
- количество и доступность необходимых ресурсов;
- природные условия;
- ожидания продавцов (производителей): социальные, политические, инфляционные;
- налоги и дотации;
- тип рынка и его емкость;
- прочие факторы.
Закон предложения
Закон предложения — при росте цены на товар, предложение на него увеличивается, при прочих неизменных факторах, и наоборот.
Математически закон предложения означает, что между величиной предложения и ценой существует прямая зависимость.
Закон предложения, также как и закон спроса, очень логичен. Естественно, что любой продавец (производитель) стремится подать свой товар по более высокой цене. Если уровень цен на рынке повышается — продавцам выгодно продавать больше, если снижается — нет.
Изменение цены на товар приводит к изменению величины предложения. На графике это проявляется движением по кривой предложения.
Изменение неценовых факторов приводит к сдвигу кривой предложения (изменению самого предложения). Расширение предложения — сдвиг кривой предложения вправо и вниз. Сужение предложения — сдвиг влево и вверх.
Эластичность предложения
Предложении, как и спрос, может находиться в различной степени зависимости от изменения цены и других факторов. В этом случае говорят об эластичности предложения.
Эластичность предложения — степень изменения величины предложения (количества предлагаемых товаров) в ответ на изменение цены или другого фактора.
Числовой показатель, отражающий степень такого изменения — коэффициент эластичности предложения.
Соответственно, эластичность предложения по цене показывает насколько изменится величина предложения при изменении цены на 1%.
Формулы для расчета дуговой и точечной эластичности предложения по цене (Eps) полностью аналогичны формулам для спроса.
Виды эластичности предложения по цене:
- абсолютно неэластичное предложение (|E| = 0). Изменение цены совершенно не влияет на величину предложения. Это возможно в краткосрочном периоде;
- неэластичное предложение (0 Рыночное равновесие графически выражается пересечением графиков спроса (D) и предложения (S) в одной точке. Этой точке рыночного равновесия соответствуют: PE — равновесная цена, и QE — равновесный объем.
Есть разные теории и подходы объясняющие как именно устанавливается рыночное равновесие. Самые известные — подход Л. Вальраса и А. Маршалла. Но это, также как паутинообразная модель равновесия рынка продавца и рынка покупателя — тема для отдельной статьи.
Если очень кратко и упрощенно, то механизм рыночного равновесия можно объяснить следующим образом. В точке равновесия все (и покупатели, и продавцы) довольны. Если одна из сторон получает преимущество (отклонение рынка от точки равновесия в ту или другую сторону), другая сторона будет недовольна и первой из сторон придется пойти на уступки.
Например: цена выше равновесной. Продавцам выгодно продавать товар по более высокой цене и предложение повышается, возникает избыток товаров. А покупатели будут недовольны ростом цены на товар. Вдобавок конкуренция высокая, предложение избыточно и продавцам, чтобы реализовать товар придется снизить цену, пока она не придет к равновесному значению. При этом снизится и объем предложения до равновесного объема.
Или другой пример: объем предлагаемых на рынке товаров меньше равновесного объема. То есть на рынке дефицит товаров. В таких условиях покупатели готовы заплатить большую цену за товар, чем та по которой он продается в данный момент. Это побудит продавцов увеличивать объемы предложения с одновременным повышением цены. В итоге цена и объем спроса/предложения придут к равновесному значению.
По сути это была иллюстрация к теориям рыночного равновесия Вальраса и Маршалла, но как уже говорилось, более подробно рассмотрим их в другой статье.
- Галяутдинов Р. Р. Обзорные лекции для подготовки к госэкзаменам по специальности “Экономика и управление на предприятии”. 2012.
© Копирование любых материалов статьи допустимо только при указании прямой индексируемой ссылки на источник: Галяутдинов Р.Р.
Закон спроса и предложения
О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Что такое спрос
Спрос в экономике — это желание купить товар или услугу. Спрос — один из ключевых факторов рыночного ценообразования.
Изобразим понятие спроса на графике, где P — цена, а Q — объем спроса.
Величина спроса — это объем (количество) товара или услуги определенного вида, который покупатели готовы приобрести в течение определенного периода при определенном уровне цены на этот товар.
Цена спроса — максимальная цена, по которой покупатель готов приобрести товар или услугу.
Платежеспособный спрос — это возможность приобрести товар покупателями.
Спрос может изменяться под воздействием одного или нескольких факторов. Рассмотрим ценовые и неценовые факторы спроса.
Факторы, влияющие на спрос:
полезность и необходимость товара;
ожидания изменения цены;
уровень доходов населения;
наличие товара на рынке;
предложение альтернативных товаров и их цены;
Спрос может изменяться: увеличиваться или уменьшаться. Графически изменение спроса можно показать через изменение положения кривой спроса.
Увеличение спроса можно показать, переместив кривую вправо, дальше от осей координат. Это выглядит так:
Движение кривой влево, ближе к осям координат, означает уменьшение спроса. Вот так:
Теперь покажем изменение величины спроса на графике.
Изменение величины спроса графически отображается не сдвигом всей кривой, а движением по кривой спроса (D), то есть перемещением, например, из точки D1 в D2. Можно заметить закономерность: чем дороже товары или услуги, тем меньше желающих их приобрести.
Например, если цена Р1 высокая, значит, количество товаров, которые купили по такой цене — Q1, небольшое. При этом по невысокой цене Р2 количество покупок Q2 значительно выше.
Что такое предложение
Предложение — это желание продать товары, которые произвели и представили на продажу в конкретный отрезок времени. Объем предложения при этом зависит от объема производства.
Предложение товара будет расти, если у него высокая маржинальность, то есть производитель получает большой доход от каждой единицы проданной продукции. Например, себестоимость товара составляет 120 рублей, а продают его за 1000 рублей.
Цена предложения — это минимальная цена продавцов.
Перечислим факторы, которые влияют на величину предложения:
ожидания по будущей цене и потребности товара;
цены на аналогичные товары;
Рассмотрим график изменения величины предложения.
Изменение величины предложения выражается в движении кривой предложения (S) из позиции точки S1 к S2 при неизменности факторов предложения. В этом случае мы учитываем ценовой фактор, а другие рассматриваем как неизменные. Можно заметить закономерность: чем дороже товары или услуги, тем больше желающих по такой цене их продать.
Поможем закрепить новый материал на курсах по обществознанию в онлайн-школе Skysmart.
Что такое закон спроса и предложения
Закон спроса и предложения отражает взаимозависимость между количеством товаров и услуг и объемом спроса и предложения на них.
Закон спроса
Повышение цен может привести к снижению величины спроса, а снижение цен — к ее увеличению.
Закон предложения
Чем выше цена товара, тем больше величина его предложения. Чем ниже цена товара, тем меньше величина его предложения
Спрос определяется платежеспособной потребностью покупателей, а предложение — совокупностью товаров, которые предлагают продавцы или производители.
Рынок — это огромная система, участников которой называют покупателями и продавцами. На рынке все заинтересованы в обмене товаров и услуг. Есть разные рынки, при этом принципы закона работают одинаково: чем больше спрос, тем выше цены. Но со временем предложение становится больше, что может привести к снижению цены.
Функции спроса и предложения:
пропорциональное развитие производства;
рыночное регулирование цен;
отражение общественных отношений;
Что значит эластичность спроса и эластичность предложения
Эластичность спроса — это показатель, который выражает колебания спроса, которые возникают от изменения цен на товары или услуги. При этом важный факт — чем эластичнее спрос, тем выше цена, которая может быть установлена на товар.
Виды эластичности спроса:
Эластичный спрос — если при изменении цены спрос на товар сильно меняется, такой спрос на товар считается эластичным.
Неэластичный спрос — если при изменении цены спрос на товар значительно не меняется, то спрос называют неэластичным.
Абсолютно эластичный спрос — когда есть только одна цена, при которой потребители будут покупать товар. Изменение цены может привести к нулевому или неограниченному спросу.
Абсолютно неэластичный спрос — вне зависимости от изменения цены спрос остается на прежнем уровне.
Эластичность предложения — это показатель, который воспроизводит изменения совокупного предложения с ростом цен. Эластичность предложения отражает чувствительность предложения товаров на изменения их цен.
Виды эластичности предложения:
Неэластичное предложение — предложение существенно не меняется при изменении цены. Например, рынок рыбы. Так как товар портится, его нужно продать. К концу срока годности уже не важно, по какой цене.
Эластичное предложение — при изменении цены предложение существенно изменяется. Свойственно товарам длительного хранения.
Абсолютно неэластичное предложение — как бы ни менялась цена, предложение будет постоянно на одном уровне.
Абсолютно эластичное предложение — существует только одна цена, по которой товар будет предлагаться на рынке. Любое изменение цены приводит к полному отказу от производства либо к неограниченному увеличению предложения.
Эластичность спроса и предложения показывает, насколько изменится цена при изменении предложения.
Формула эластичности
E = [(Q 1 – Q 2 )/[1/2 × (Q 1 + Q 2 )] ] / [ (P 2 – P 1 )/[1/2 × (P 1 + P 2 )] ]
Q1 — спрос в начале;
Q2 — спрос в следующий момент времени;
P1 — цена в начале;
P2 — цена в следующий момент времени.
Например, цена изделия равна 50, спрос — 300. При росте цены до 54 спрос сокращается до 270. Тогда эластичность спроса рассчитывается так:
E = ((270 – 300) / 285) / ((54 – 50) / 52) = -0,1052 / 0,07692 = -1,367
Что такое рыночное равновесие спроса и предложения
Есть теория, при которой свободные рыночные отношения могут уравновесить спрос и предложение без сильного вмешательства государства и прочих факторов. Именно это явление называют рыночным равновесием.
Рыночное равновесие — это момент, когда спрос равен предложению.
Равновесная цена — цена, которая соответствует точке рыночного равновесия.
Типы рыночного равновесия:
- Мгновенное — когда возрастает спрос, при этом производители не могут увеличить предложение. Тогда равновесие устанавливается через повышение цены до момента установления рыночного равновесия.
- Краткосрочное — когда при повышении спроса предложение повышается через дополнительную загрузку производственных мощностей.
- Долгосрочное — когда происходит расширение производственных мощностей или создаются новые предприятия по производству товара.
Большая часть экономик в мире работают при соблюдении принципов свободного рыночного регулирования, то есть без вмешательства государства.
Рыночная экономика — это механизм взаимодействия товарооборотов между собой, который основан на частной собственности, товарно-денежных отношениях, свободе выбора и конкуренции.
Вместе с тем, достигнуть рыночное равновесие можно за счет слишком высокой цены. Например, некоторые отрасли экономики могут испытать сильный спад, кризис, а другие перепроизводство. Поэтому государство предпринимает меры, чтобы сгладить переходные процессы для равновесия спроса и предложения.
Какие действия может предпринять государство для проблемных отраслей:
Снизить налог на прибыль.
Уменьшить ставки по кредиту.
Ввести льготы, субсидии.
Графически пересечение кривых спроса и предложения можно отметить точкой А, которая и будет точкой равновесия. Это компромисс между желаниями и возможностями потребителя и производителя.
Это значит, что товар или услуга реализовывается по равновесной цене, то есть цене, по которой покупатель готов купить, а продавец готов продать товар или оказать услугу.
Эластичность функции
Содержание:
Эластичность функции
В экономических исследованиях приросты тех или иных показателей, характеризующих экономические процессы, чаще всего выражают в процентах к базовым значениям. Поэтому и изменение величин, которые связаны с ними функциональной зависимостью, также выражают в процентах. Для этого используют понятие эластичности функции, которое выражается через производную функции.
Определение и свойства эластичности функций
Пусть задана функция y = f (x). Если аргумент x получил приращение Δx и при этом функция y получила приращение Δy, то 

Определение. Предел отношения относительного приращения функции к относительному приращению аргумента при условии, что приращение аргумента стремится к нулю, если существует, называется эластичностью функции.
Обозначают эластичность функции y = f (x) относительно переменной x Ex(y). То есть,
Итак, если в точке x функция имеет производную, то эластичность определяется формулой 
Эластичность выражает приближенный процент приращения функции, который соответствует 1 % приращения аргумента.
Пример. Найти эластичность функции y = x 2 – 4 x +7 и вычислить ее при x = 1, x = 2, x = 5.
Решение. 
Итак, если x вырастет на 1 % с 1 до 1,01, то y снизится на 0,5 %. Если x вырастет на 1 % с 2 до 2,02, то значение переменной y практически не изменится. Если x вырастет на 1 % с 5 до 5,05, то y вырастет на 2,5 %.
Свойства эластичности функции
ТЕОРЕМА 1. Эластичность произведения двух функций равна сумме эластичности сомножителей:
Ex (U ⋅ V) = Ex (U) + Ex (V).
Доказательство. По определению эластичности
ТЕОРЕМА 2. Эластичность частного двух функций равна разности показателей эластичности делимого и делителя:
Доказательство. По определению эластичности
Эластичность спроса относительно цены
В анализе и прогнозах ценовой политики применяется понятие эластичности спроса и предложения.
Пусть p цена одного изделия, а Q — количество изделий, произведенных и проданных через некоторое время, что определяет спрос. Величина Q зависит от цены, т. е. Q является функцией от p: Q = f (p).
Пусть приращение цены Δp вызывает приращение ΔQ. тогда относительные приращения цены и спроса будут соответственно 

Отношение 
Эластичностью спроса относительно цены называется предел отношения относительного приращения спроса к относительному приращению цены при условии, что приращение цены стремится к нулю.
Эластичность спроса относительно цены приближенно определяет, как меняется спрос на данное изделие, если его цена возрастает на 1 %.
Так, например, если рост цены на 5 % вызывает падение спроса на 8 %, то эластичность будет 
Если эластичность спроса η = –0,5, то 10 % роста стоимости товара вызывает падение спроса на (–0,5) 10% = –5%.
Определение. Если процент изменения спроса больше процента изменения цены (η 0, имеем 

То есть функция D (Q) дохода растет с ростом цены p, когда спрос не эластичный.
Эластичность предложения относительно цены
Понятие эластичности можно применять и к другим функциям экономического содержания.
Рассмотрим понятие эластичности предложения S в зависимости от цены товара p. Под предложением понимают количество некоторого товара, который предлагается на продажу за единицу времени. Как правило, предложение какого-либо товара является возрастающей функцией цены. Но бывают случаи, когда предложение повышается со снижением цены. Величина S является функцией от цены товара. То есть, S = S (p).
Пусть Δp — приращение цены, а ΔS — соответствующее приращение предложения. Тогда относительные приращения цены и предложения будут соответственно 

Эластичностью предложения относительно цены называется предел отношения относительного приращения предложения к относительному приращению цены при условии, что приращение цены стремится к нулю.
Эластичность предложения относительно цены приближенно определяет процент приращения предложения на 1 % приращения цены.
Пример 3. Функция предложения некоторого товара 
Решение. 
Если p = 2, то 
Следовательно, при цене p = 2 увеличение ее на 1 % вызовет увеличение предложения на 0,2 %.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
[spoiler title=”источники:”]
http://skysmart.ru/articles/obshestvoznanie/zakon-sprosa-i-predlojeniya
http://natalibrilenova.ru/elastichnost-funktsii/
[/spoiler]




























































