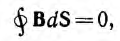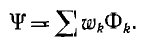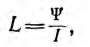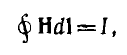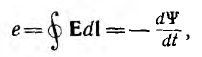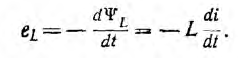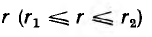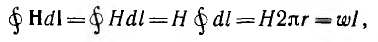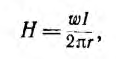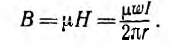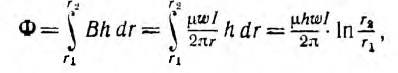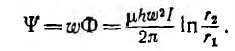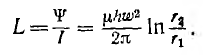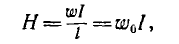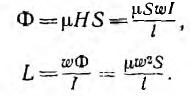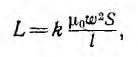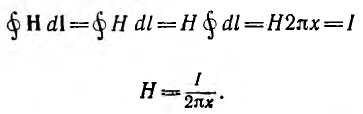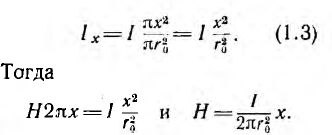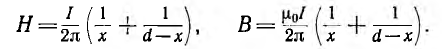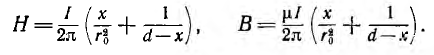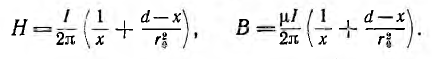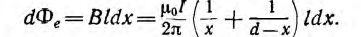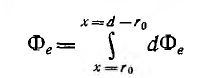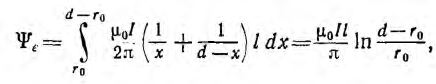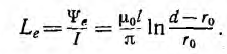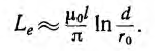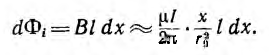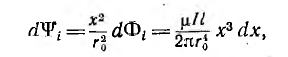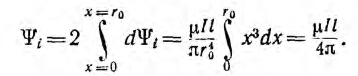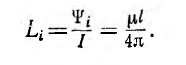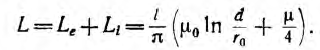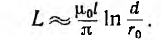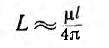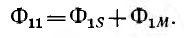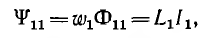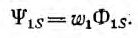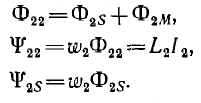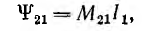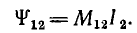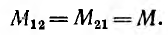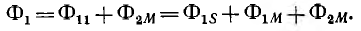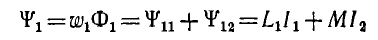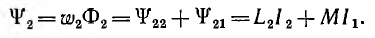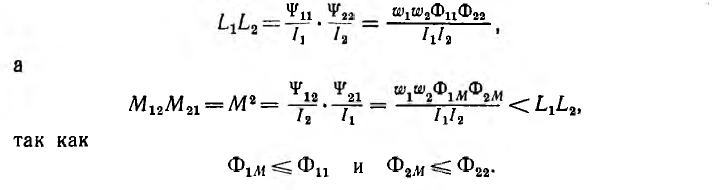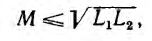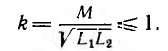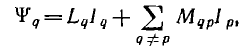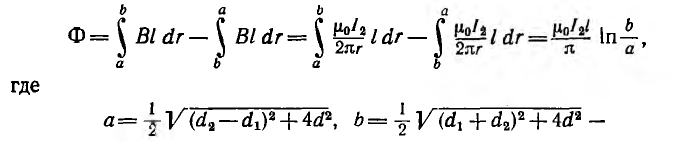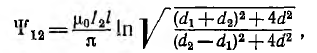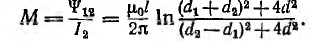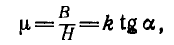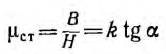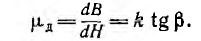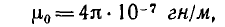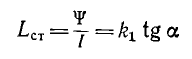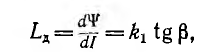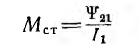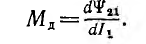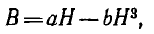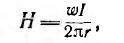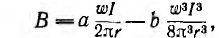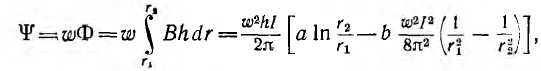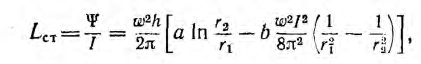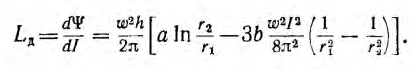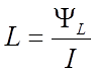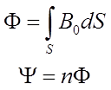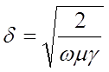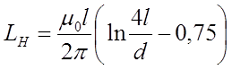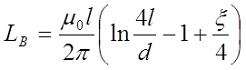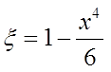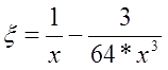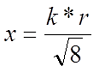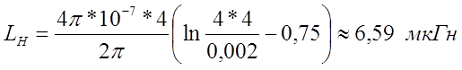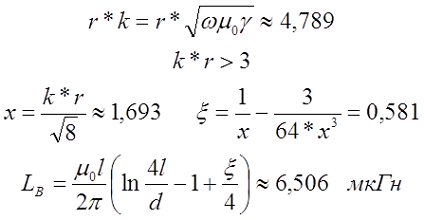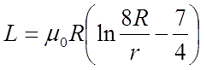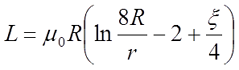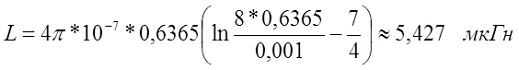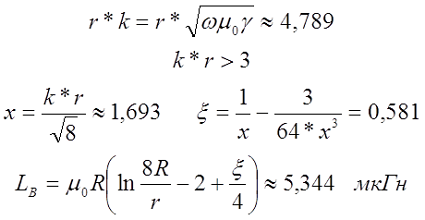Электротехника как найти индуктивность

Электротехника как найти индуктивность

Индуктивность
L
Размерность L2MT−2I−2
Единицы измерения
СИ Гн
СГС см−1·с2
Классическая электродинамика
VFPt Solenoid correct2.svg
Электричество · Магнетизм

Электростатика

Закон Кулона
Теорема Гаусса
Электрический дипольный момент
Электрический заряд
Электрическая индукция
Электрическое поле
Электростатический потенциал

Магнитостатика

Закон Био — Савара — Лапласа
Закон Ампера
Магнитный момент
Магнитное поле
Магнитный поток
Магнитная индукция

Электродинамика

Векторный потенциал
Диполь
Потенциалы Лиенара — Вихерта
Сила Лоренца
Ток смещения
Униполярная индукция
Уравнения Максвелла
Электрический ток
Электродвижущая сила
Электромагнитная индукция
Электромагнитное излучение
Электромагнитное поле

Электрическая цепь

Закон Ома
Законы Кирхгофа
Индуктивность
Радиоволновод
Резонатор
Электрическая ёмкость
Электрическая проводимость
Электрическое сопротивление
Электрический импеданс

Ковариантная формулировка

Тензор электромагнитного поля
Тензор энергии-импульса
4-потенциал
4-ток

См. также: Портал:Физика

Индуктивность микрополосковой линии является распределённой и характеризуется значением индуктивности на единицу длины.

Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током I, текущим в каком-либо замкнутом контуре, и полным магнитным потоком Psi , называемым также потокосцеплением, создаваемым этим током через поверхность[1], краем которой является данный контур[2][3][4]:

displaystyle Psi = LI.

Зависит от формы проводников с током и магнитной проницаемости среды. Обозначается буквой L, в СИ измеряется в генри.

Словом «индуктивность» также называют сосредоточенный элемент электрической цепи, в котором накапливается магнитная энергия.

Определение. Некоторые формулы[править | править код]

Индуктивность определяется как отношение {displaystyle L=Psi /I} магнитного потока Psi , пронизывающего контур, к току в контуре I. Обычно {displaystyle L=,} const(I), кроме тех случаев, когда магнитная проницаемость среды зависит от поля.

Величина L используется при характеризации свойства проводника противодействовать появлению, прекращению и всякому изменению в нём тока. Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении I[4]:

{displaystyle {mathcal {E}}_{i}=-{frac {dPsi }{dt}}=-L{frac {dI}{dt}}}.

Как следует из этой формулы, индуктивность численно равна ЭДС самоиндукции (в вольтах), возникающей в контуре при изменении силы тока на 1 А за 1 с. Вышеуказанное свойство, по сути, является электрической инерцией (её мерой служит ЭДС), подобной инерции тел в механике.

При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого током[4]:

W={frac {LI^{2}}{2}}.

Это соотношение может быть удобным для вычисления L в ситуациях, когда адекватно указать замкнутый контур непросто (особенно если неприменимо квазистационарное приближение), скажем, при рассмотрении индуктивности прямого длинного провода.

Создание индуктивности[править | править код]

Практически участки цепи со значительной индуктивностью выполняют в виде катушек индуктивности[4]. Элементами малой индуктивности (применяемыми для больших рабочих частот) могут быть одиночные (в том числе и неполные) витки или даже прямые проводники; при высоких рабочих частотах необходимо учитывать индуктивность всех проводников[5].

Для имитации индуктивности, то есть ЭДС на элементе, пропорциональной и противоположной по знаку скорости изменения тока через этот элемент, в электронике используются[6] и устройства, не основанные на электромагнитной индукции (см. Гиратор); такому элементу можно приписать определённую эффективную индуктивность, используемую в расчётах полностью (хотя вообще говоря с определёнными ограничивающими условиями) аналогично тому, как используется обычная индуктивность.

Обозначение и единицы измерения[править | править код]

В системе единиц СИ индуктивность выражается в генри[7][8], сокращённо «Гн». Контур обладает индуктивностью в один генри, если при изменении тока на один ампер в секунду на выводах контура будет возникать напряжение в один вольт.

В вариантах системы СГС — системе СГСМ и в гауссовой системе индуктивность измеряется в сантиметрах (1 Гн = 109 см; 1 см = 1 нГн)[4]; для сантиметров в качестве единиц индуктивности применяется также название абгенри. В системе СГСЭ единицу измерения индуктивности либо оставляют безымянной, либо иногда называют статгенри (1 статгенри ≈ 8,987552⋅1011 генри: коэффициент перевода численно равен 10−9 от квадрата скорости света, выраженной в см/с).

Символ L, используемый для обозначения индуктивности, был принят в честь Эмилия Христиановича Ленца[9][10]. Единица измерения индуктивности названа в честь Джозефа Генри[11]. Сам термин индуктивность был предложен Оливером Хевисайдом в феврале 1886 года[12].

Теоретическое обоснование[править | править код]

Если в проводящем контуре течёт ток, то ток создаёт магнитное поле[4].

Будем вести рассмотрение в квазистатическом приближении, подразумевая, что переменные электрические поля достаточно слабы либо меняются достаточно медленно, чтобы можно было пренебречь порождаемыми ими магнитными полями.

Ток считаем одинаковым по всей длине контура (пренебрегая ёмкостью проводника, которая позволяет накапливать заряды в разных его участках, что вызвало бы неодинаковость тока вдоль проводника и заметно усложнило бы картину).

По закону Био — Савара — Лапласа, величина вектора магнитной индукции, создаваемой некоторым элементарным (в смысле геометрической малости участка проводника, рассматриваемого как элементарный источник магнитного поля) током в каждой точке пространства, пропорциональна этому току. Суммируя поля, создаваемые каждым элементарным участком, приходим к тому, что и магнитное поле (вектор магнитной индукции), создаваемое всем проводником, также пропорционально порождающему току.

Рассуждение выше верно для вакуума. В случае присутствия магнитной среды[13] (магнетика) с заметной (или даже большой) магнитной восприимчивостью, вектор магнитной индукции (который и входит в выражение для магнитного потока) будет заметно (или даже во много раз) отличаться от того, каким бы он был в отсутствие магнетика (в вакууме). Мы ограничимся здесь линейным приближением, тогда вектор магнитной индукции, хотя, возможно, возросший (или уменьшившийся) в заметное количество раз по сравнению с отсутствием магнетика при том же контуре с током, тем не менее остаётся пропорциональным порождающему его току.

Тогда магнитный поток, то есть поток поля вектора магнитной индукции:

{displaystyle Psi =int limits _{S}mathbf {B} cdot mathbf {dS} }

через любую конкретную фиксированную поверхность S (в частности и через интересующую нас поверхность, краем которой является наш контур с током) будет пропорционален току, так как пропорционально току B всюду под интегралом.

Заметим, что поверхность, краем которой является контур, может быть достаточно сложна, если сложен сам контур. Уже для контура в виде просто многовитковой катушки такая поверхность оказывается достаточно сложной. На практике это приводит к использованию некоторых упрощающих представлений, позволяющих легче представить такую поверхность и приближённо рассчитать поток через неё (а также в связи с этим вводятся некоторые дополнительные специальные понятия, подробно описанные в отдельном параграфе ниже). Однако здесь, при чисто теоретическом рассмотрении нет необходимости во введении каких-то дополнительных упрощающих представлений, достаточно просто заметить, что как бы ни был сложен контур, в данном параграфе мы имеем в виду «полный поток» — то есть поток через всю сложную (как бы многолистковую) поверхность, натянутую на все витки катушки (если речь идет о катушке), то есть о том, что называется потокосцеплением. Но поскольку нам здесь не надо конкретно рассчитывать его, а нужно только знать, что он пропорционален току, нам не слишком интересен конкретный вид поверхности, поток через которую нас интересует (ведь свойство пропорциональности току сохраняется для любой).

Итак, мы обосновали:

{displaystyle Psi }~ I,

этого достаточно, чтобы утверждать, введя обозначение L для коэффициента пропорциональности, что

{displaystyle Psi =LI.}

В заключение теоретического обоснования покажем, что рассуждение корректно в том смысле, что магнитный поток не зависит от конкретной формы поверхности, натянутой на контур. (Действительно, даже на самый простой контур может быть натянута — в том смысле, что контур должен быть её краем — не единственная поверхность, а разные, например, начав с двух совпадающих поверхностей, затем одну поверхность можно немного прогнуть, и она перестанет совпадать со второй). Поэтому надо показать, что магнитный поток одинаков для любых поверхностей, натянутых на один и тот же контур.

Но это действительно так: возьмём две такие поверхности. Вместе они будут составлять одну замкнутую поверхность. А мы знаем (из закона Гаусса для магнитного поля), что магнитный поток через любую замкнутую поверхность равен нулю. Это (с учетом знаков) означает, что поток через одну поверхность и другую поверхность — равны. Что доказывает корректность определения.

Свойства индуктивности[править | править код]

Индуктивность в ряде важных случаев[править | править код]

Виток, цилиндрическая катушка[править | править код]

Величина магнитного потока, пронизывающего одновитковый контур, связана с величиной тока в нём следующим образом[4]:

{displaystyle displaystyle Phi =L_{1}I}

где L_{1} — индуктивность витка.

В случае катушки, состоящей из N витков, предыдущее выражение модифицируется к виду:

displaystyle Psi = LI

где Psi =sumlimits_{i=1}^{N}{Phi _{i}} — сумма магнитных потоков через все витки (это полный поток, называемый в электротехнике потокосцеплением, именно он фигурирует в качестве магнитного потока в общем определении индуктивности и в теоретическом обосновании выше), а L — индуктивность многовитковой катушки. Psi называют потокосцеплением или полным магнитным потоком[17]. Коэффициент пропорциональности L иначе называется коэффициентом самоиндукции катушки[4].

Если принять, что потоки, пронизывающие каждый из витков, одинаковы (что часто соответствует реальности, в хорошем приближении), то {displaystyle Psi =Ncdot Phi }. При этом, что существенно, поток Phi через конкретный виток отличается от того, каким он был бы в «одновитковой» ситуации, ибо присутствие N витков приводит к N-кратному росту магнитного поля B, а значит, и потока через конкретный виток (как если бы в N раз возрос ток в самом витке). В результате {displaystyle Psi =Ncdot (NL_{1}I)}, откуда

{displaystyle L=L_{1}N^{2}}.

Чуть иными словами, магнитный поток через каждый виток увеличивается в N раз — так как его создают теперь N единичных витков, и потокосцепление ещё в N раз, поскольку это поток через N единичных витков.

На практике магнитные поля в центре и на краях катушки всё-таки не совсем одинаковы, поэтому используются более сложные формулы.

Соленоид[править | править код]

Катушка в форме соленоида (конечной длины).

Соленоид — катушка, длина которой намного больше, чем её диаметр (также в дальнейших выкладках подразумевается, что толщина обмотки намного меньше, чем диаметр катушки). При этих условиях и без использования магнитного сердечника плотность магнитного потока (или магнитная индукция) B, которая выражается в системе СИ в тесла [Тл], внутри катушки вдали от её концов (приближённо) равна

{displaystyle displaystyle B=mu _{0}Ni/l}

или

{displaystyle displaystyle B=mu _{0}ni,}

где mu_0 — магнитная постоянная, N — число витков, i — ток в амперах [А], l — длина катушки в метрах [м] и n — плотность намотки витков в [м-1]. Пренебрегая краевыми эффектами на концах соленоида, получим[18], что потокосцепление через катушку равно плотности потока B [Тл], умноженному на площадь поперечного сечения S [м2] и число витков N:

{displaystyle displaystyle Psi =mu _{0}N^{2}iS/l=mu _{0}n^{2}iV,}

где {displaystyle V=Sl} — объём катушки. Отсюда следует формула для индуктивности соленоида (без сердечника):

{displaystyle displaystyle L=mu _{0}N^{2}S/l=mu _{0}n^{2}V.}

Если катушка внутри полностью заполнена магнитным сердечником, то индуктивность отличается на множитель mu  — относительную магнитную проницаемость[19] сердечника:

{displaystyle displaystyle L=mu _{0}mu N^{2}S/l=mu _{0}mu n^{2}V.}

В случае, когда {displaystyle mu gg 1}, под S можно понимать площадь сечения сердечника [м2] и пользоваться данной формулой даже при толстой намотке, если только полная площадь сечения катушки не превосходит площади сечения сердечника во много раз.

Тороидальная катушка[править | править код]

Для тороидальной катушки, намотанной на сердечнике из материала с большой магнитной проницаемостью, можно приближённо пользоваться формулой для бесконечного прямого соленоида (см. выше):

L = N^2 cdot frac{mu_0mu S}{2 pi r},,

где 2 pi r — оценка длины соленоида (r — средний радиус тора).
Лучшее приближение дает формула

L = N^2 cdot frac{mu_0mu h}{2 pi} cdot ln frac{R}{r},,

где предполагается сердечник прямоугольного сечения с наружным радиусом R и внутренним радиусом r, высотой h.

Длинный прямой проводник[править | править код]

Для длинного прямого (или квазилинейного) провода кругового сечения индуктивность выражается приближённой формулой[20]:

L = frac{mu_0}{2pi} l Big( mu_e mathrm{ln}frac{l}{r} + frac{1}{4}mu_i Big),

где mu_0 — магнитная постоянная, mu_e — относительная магнитная проницаемость внешней среды (которой заполнено пространство (для вакуума mu_e = 1), mu _{i} — относительная магнитная проницаемость материала проводника, l — длина провода, {displaystyle rll l} — радиус его сечения.

Таблица индуктивностей[править | править код]

Символ mu _{0} обозначает магнитную постоянную (4π⋅10−7 Гн/м). В высокочастотном случае ток течёт в поверхности проводников (скин-эффект) и в зависимости от вида проводников иногда нужно различать индуктивность высокой и низкой частоты. Для этого служит постоянная Y: Y = 0, когда ток равномерно распределён по поверхности провода (скин-эффект), Y = 1⁄4, когда ток равномерно распределён по поперечному сечению провода. В случае скин-эффекта нужно учитывать, что при маленьких расстояниях между проводниками в поверхностях текут дополнительные вихревые токи (эффект экранирования), и выражения, содержащие Y, становятся неточными.

Коэффициенты самоиндукции некоторых замкнутых контуров

Вид Индуктивность Комментарий
соленоид
с тонкой обмоткой[21] 		{displaystyle {frac {mu _{0}r^{2}N^{2}}{3l}}left[-8w+3{frac {sqrt {1+m}}{m}}left(Kleft({sqrt {frac {m}{1+m}}}right)-left(1-mright)Eleft({sqrt {frac {m}{1+m}}}right)right)right]}

{displaystyle ={frac {mu _{0}r^{2}N^{2}pi }{l}}left(1-{frac {8w}{3pi }}+{frac {w^{2}}{2}}-{frac {w^{4}}{4}}+{frac {5w^{6}}{16}}-{frac {35w^{8}}{64}}+...right)} для {displaystyle wll 1}
{displaystyle =mu _{0}rN^{2}left[left(1+{frac {1}{32w^{2}}}+Oleft({frac {1}{w^{4}}}right)right)log(8w)-1/2+{frac {1}{128w^{2}}}+Oleft({frac {1}{w^{4}}}right)right]} для {displaystyle wgg 1}

N: Число витков
r: Радиус
l: Длина
w = r/l
m = 4w2
E,K: Эллиптический интеграл
Коаксиальный кабель,
высокая частота 		{displaystyle {frac {mu _{0}l}{2pi }}log left({frac {a_{1}}{a}}right)} a1: Радиус
a: Радиус
l: Длина
единичный
круглый виток[20][22] 		{displaystyle mu _{0}rcdot left(log left({frac {8r}{a}}right)-2+Y+Oleft(a^{2}/r^{2}right)right)} r: Радиус витка
a: Радиус проволоки
прямоугольник[20][23][24] {displaystyle {frac {mu _{0}}{pi }}left(blog left({frac {2b}{a}}right)+dlog left({frac {2d}{a}}right)-left(b+dright)left(2-Yright)+2{sqrt {b^{2}+d^{2}}}right)}

;; -frac {mu_0}{pi}left(bcdotoperatorname{arsinh}left(frac {b}{d}right)+dcdotoperatorname{arsinh}left(frac {d}{b}right) + Oleft(aright)right)

b, d: Длины краёв
d >> a, b >> a
a: Радиус проволоки
Две параллельные
проволоки 		{displaystyle {frac {mu _{0}l}{pi }}left(log left({frac {d}{a}}right)+Yright)} a: Радиус проволоки
d: Расстояние, d ≥ 2a
l: Длина пары
Две параллельные
проволоки, высокая
частота 		{displaystyle {frac {mu _{0}l}{pi }}operatorname {arcosh} left({frac {d}{2a}}right)={frac {mu _{0}l}{pi }}log left({frac {d}{2a}}+{sqrt {{frac {d^{2}}{4a^{2}}}-1}}right)} a: Радиус проволоки
d: Расстояние, d ≥ 2a
l: Длина пары
Проволока параллельна
идеально проводящей
стене 		{displaystyle {frac {mu _{0}l}{2pi }}left(log left({frac {2d}{a}}right)+Yright)} a: Радиус проволоки
d: Расстояние, d ≥ a
l: Длина
Проволока параллельна
стене,
высокая частота 		{displaystyle {frac {mu _{0}l}{2pi }}operatorname {arcosh} left({frac {d}{a}}right)={frac {mu _{0}l}{2pi }}log left({frac {d}{a}}+{sqrt {{frac {d^{2}}{a^{2}}}-1}}right)} a: Радиус проволоки
d: Расстояние, d ≥ a
l: Длина

См. также[править | править код]

  • Взаимоиндукция
  • Соленоид
  • Катушка индуктивности
  • Индуктивный датчик

Примечания[править | править код]

  1. ↑ Если контур многовитковый (катушка) или вообще сложной формы, поверхность, краем которой он будет являться, может иметь достаточно сложную форму. Это никак не сказывается на большей части общих утверждений, однако для упрощения конкретного понимания ситуации и количественных оценок в случае катушки обычно приближенно рассматривают эту поверхность как совокупность («стопку») отдельных листков, каждый из которых привязан к отдельному единичному витку, а общий поток через такую поверхность рассматривается приближенно как сумма потоков через все такие листки.
  2. ↑ Касаткин А. С. Основы электротехники. М.:Высшая школа, 1986.
  3. ↑ Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. М.:Высшая школа, 1978.
  4. ↑ 1 2 3 4 5 6 7 8 Индуктивность — статья из Большой советской энциклопедии. 
  5. ↑ Правда, этот случай в принципе выходит за рамки квазистационарного приближения, позволяющего рассматривать элементы схемы как независимые, то есть понятие индуктивности отдельного элемента цепи начинает терять четкий смысл; однако оно во всяком случае может быть использовано хотя бы для оценочного расчета.
  6. ↑ Прежде всего использование таких устройств, не основанных на электромагнитной индукции, обусловлено такими причинами, как необходимость или желательность иметь меньший размер элемента, чем это возможно для катушки индуктивности; например — в микросхемах, а также для элементов очень большой индуктивности.
  7. ↑ Генри (единица индуктивности) — статья из Большой советской энциклопедии. 
  8. ↑ Индуктивность // Казахстан. Национальная энциклопедия. — Алматы: Қазақ энциклопедиясы, 2005. — Т. II. — ISBN 9965-9746-3-2. (CC BY-SA 3.0)
  9. ↑ Glenn Elert. The Physics Hypertextbook: Inductance (1998–2008). Архивировано 19 ноября 2012 года.
  10. ↑ Michael W. Davidson. Molecular Expressions: Electricity and Magnetism Introduction: Inductance (1995–2008). Архивировано 19 ноября 2012 года.
  11. ↑ Генри Джозеф — статья из Большой советской энциклопедии. 
  12. ↑ Heaviside, O. Electrician. Feb. 12, 1886, p. 271. См. репринт Архивная копия от 16 февраля 2022 на Wayback Machine.
  13. ↑ Присутствие магнетика особенно важно для катушек с ферромагнитным сердечником и т. п.
  14. ↑ Здесь имеется в виду настоящая индуктивность; в электронике можно создать искусственно элементы (не основанные на явлении самоиндукции), зависимость ЭДС в которых от производной тока будет такой же, как в катушке индуктивности, но с коэффициентом противоположного знака — такие элементы можно условно назвать (по их поведению в электрической цепи) элементами с отрицательной индуктивностью, однако они не имеют отношения к предмету данной статьи.
  15. ↑ Если считать структуру токов (точно или приближенно) фиксированной, то есть если токи не перераспределяются по объёму проводника в процессе их возбуждения.
  16. ↑ См., напр. в книге: О. И. Клюшников, А. В. Степанов. Теоретические основы электротехники Архивная копия от 10 марта 2022 на Wayback Machine, РГППУ, Екатеринбург, 2010 — стр. 9.
  17. ↑ Потокосцепление — статья из Большой советской энциклопедии. 
  18. ↑ * Сивухин Д. В. Общий курс физики. — М.. — Т. III. Электричество.
  19. ↑ Как и в других случаях, присутствие магнетика, особенно если это ферромагнетик, для какового всегда имеет место гистерезис, приводит к более или менее существенной нелинейности (особенно большой для магнитожестких материалов сердечника); поэтому формулу для индуктивности, подразумевающей именно линейное приближение, следует считать приближенной, а в общем случае в качестве магнитной проницаемости в формулу входит некоторая эффективная величина, зависящая от величины тока в катушке.
  20. ↑ 1 2 3 Физическая энциклопедия, Главный редактор А. М. Прохоров. Индуктивность // Физический энциклопедический словарь. — Советская энциклопедия. — М., 1983.
  21. ↑ Lorenz, L. Über die Fortpflanzung der Elektrizität // Annalen der Physik. — 1876. — Т. VII. — С. 161—193. (The expression given is the inductance of a cylinder with a current around its surface)..
  22. ↑ Elliott, R. S. Electromagnetics. — New York: Institute of Electrical and Electronics Engineers, 1993. Замечание: Постоянная −3/2 неправильна.
  23. ↑ Rosa, E.B. The Self and Mutual Inductances of Linear Conductors (англ.) // Bulletin of the Bureau of Standards : journal. — 1908. — Vol. 4, no. 2. — P. 301—344.
  24. ↑ Moscow Power Engineering Institute: Mathcad Calculation Server. Дата обращения: 16 апреля 2012. Архивировано 17 февраля 2020 года.
Источник

Содержание:

Индуктивность и ее расчет:

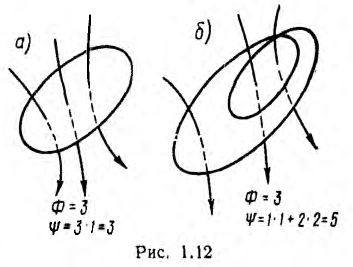
Основным соотношением для магнитного поля является принцип непрерывности магнитного потока: Индуктивность и ее расчет

Индуктивность и ее расчет

На рис. 1.12, а и б проиллюстрировано различие между потоком и
потокосцеплением, причем число линий в условном масштабе равно
величине потока.

Индуктивность и ее расчет

Индукция измеряется в тесла (тл), магнитный поток и потокосцепление — в веберах (вб).
Индуктивность уединенного контура, равная отношению потокосцепления к току:

Индуктивность и ее расчет

пропорциональна магнитной проницаемости среды, в которой он находится, и определяется конфигурацией контура. Единицей индуктивности является генри (гн).
Для расчета индуктивности контура необходимо предварительно рассчитать его магнитное поле по основному соотношению — закону полного тока:

Индуктивность и ее расчет

устанавливающему связь между напряженностью магнитного поля 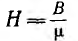Индуктивность и ее расчети полным током I — алгебраической суммой токов, сцепляющихся с путем интегрирования. При этом положительное направление тока I связано с направлением dI обхода правилом правого винта.
Напряженность магнитного поля измеряется в а/м, магнитная проницаемость — в гн/м.
Если потокосцепление контура изменяется во времени, то в контуре появляется э. д. с. индукции е, величина и направление которой определяется законом электромагнитной индукции:

Индуктивность и ее расчет

где Е — вектор напряженности наведенного в контуре электрического поля.
Таким образом, закон электромагнитной индукции связывает между собой изменение магнитного поля с возникающим электрическим полем.
Максвеллом было постулировано обобщение этого закона, заключающееся в том, что электрическое поле возникает при изменении магнитного поля в любой среде, а не только в проводящем контуре.

Закон электромагнитной индукции, открытый Фарадеем в 1831 г., был дополнен Ленцем в 1832— 1834 гг. Им было установлено общее правило: з. д. с. индукции всегда стремится создать ток, направленный так, чтобы препятствовать изменению потока, сцепляющегося с контуром.
При изменении тока в контуре изменяется потокосцепление ψL созданное этим током, и в контуре наводится э. д. с. самоиндукции

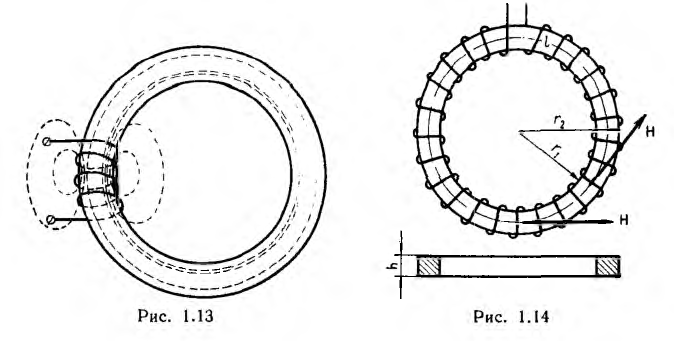
Индуктивность и ее расчет

Индуктивность тороида и соленоида

Если на кольцевой сердечник — тороид, выполненный из материала проницаемостью µ > µ0, нанести обмотку не по всей его длине (рис. 1.13), то только часть потока проходит по сердечнику, остальная часть — поток рассеяния — замыкается в воздухе. Тороид же, содержащий витки, плотно и равномерно распределенные по всей длине сердечника (рис. 1.14), замечателен тем, что практически весь магнитный поток сосредоточивается в сердечнике, т. е. потока рассеяния нет. Линии вектора напряженности поля представляют собой окружности, сцепляющиеся со всеми витками. Ввиду симметрии напряженность поля в каждой точке окружности по величине постоянна; по направлению она совпадает с касательной к окружности.

Индуктивность и ее расчет

Тороиды широко применяются в трансформаторах, магнитных усилителях и электроизмерительных приборах.

Пусть тороид имеет прямоугольное сечение высотой Н, с радиусами г1 и г2, магнитная проницаемость материала µ.

По закону полного тока для окружности с радиусом Индуктивность и ее расчет

Индуктивность и ее расчет

откуда

Индуктивность и ее расчет

т. е. напряженность поля убывает по мере приближения к наружному краю тороида. Это в равной мере относится и к индукции

Индуктивность и ее расчет

Поток в сердечнике тороида

Индуктивность и ее расчет

а потокосцепление

Индуктивность и ее расчет

Отсюда индуктивность тороида

Индуктивность и ее расчет

Если расчет вести для средней линии I и приближенно считать поле в тороиде распределенным равномерно, то напряженность

Индуктивность и ее расчет

где w0 — число витков на единицу длины, а магнитный поток и индуктивность, соответственно,

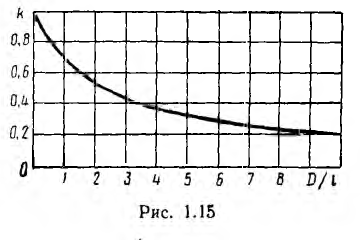
Индуктивность и ее расчет

Обычно в реальных тороидах отношение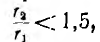Индуктивность и ее расчет что приводит при этих приближенных формулах к погрешности, не превышающей 1,2 %. Последняя формула для индуктивности может быть применена и к длинному соленоиду, рассматриваемому как часть тороида бесконечно большого радиуса. Для соленоида конечной длины µ=µ0

Индуктивность и ее расчет

где k < 1 — коэффициент, учитывающий, что в таком соленоиде не весь поток пронизывает все витки.

Индуктивность и ее расчет

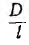
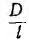
Как показывает точный расчет, этот коэффициент зависит от отношения диаметра D катушки к ее длине I (рис. 1.15). При Индуктивность и ее расчет = 0,1 коэффициент k — 0,96, поэтому при Индуктивность и ее расчет < 0 ,1 приближенно принимают k = 1.

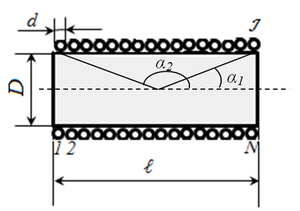
Индуктивность двухпроводной линии

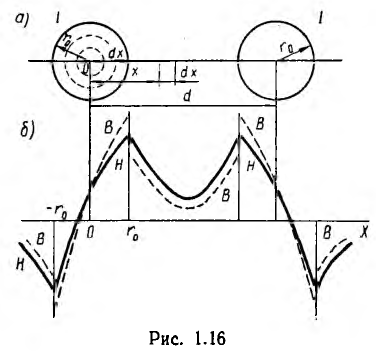
Двухпроводная линия (рис. 1.16, а) состоит из двух параллельных проводов одинакового радиуса г0, имеющих большую длину I по сравнению с расстоянием d между ними. Магнитная проницаемость материала проводов (г, окружающей среды — µ0. Токи I в прямом и обратном проводах отличаются лишь направлением; начало координат взято в центре сечения левого провода.

Для отдельного провода ввиду его осевой симметрии, при пренебрежении искажением поля у его концов, применение закона полного тока к окружности радиуса 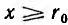Индуктивность и ее расчет дает:

Индуктивность и ее расчет

При интегрировании по окружности, лежащей внутри отдельного провода 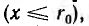Индуктивность и ее расчет охватывается лишь часть LХ всего тока, протекающая внутри круга радиуса х, равная при равномерном распределении тока по сечению

Индуктивность и ее расчет

В воздухе между проводами на линии, соединяющей центры их сечений 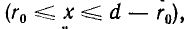Индуктивность и ее расчет направления полей, создаваемых обоими токами согласно правилу правого винта, совпадают и напряженности поля и индукции складываются:

Индуктивность и ее расчет

Эти же формулы справедливы и для 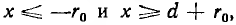Индуктивность и ее расчет т. е. снаружи линии, но здесь они дают разность полей.

Индуктивность и ее расчет

Внутри левого провода линии напряженность поля и индукция от обоих проводов будут:

Индуктивность и ее расчет

Внутри правого провода 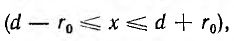Индуктивность и ее расчетсоответственно,

Индуктивность и ее расчет

На рис. 1.16, б представлено распределение напряженности поля и индукции вдоль оси х для магнитной проницаемости материала проводов µ > µ0. Посередине между проводами поле минимально, но в нуль не обращается. Поле также не равно нулю на осях проводов.

На внутренней стороне проводов напряженность поля и индукция больше, чем на внешней. В отличие от напряженности поля индукция имеет разрыв у поверхности проводов. Для вычисления индуктивности линии необходимо найти потокосцепление. Элементарный поток, проходящий через площадку Idx в воздухе между проводами,

Индуктивность и ее расчет

Весь поток между проводами – внешний поток

Индуктивность и ее расчет

одновременно является внешним потокосцеплением, так как сцепляется с контуром один раз. Поэтому

Индуктивность и ее расчет

а соответствующая ему внешняя индуктивность

Индуктивность и ее расчет

Для большинства линий расстояние d между проводами значительно превышает радиус r0 проводов. В этом случае

Индуктивность и ее расчет

Для определения внутренней индуктивности, соответствующей внутреннему потоку, при d > r0 поле внутри провода линии может вычисляться как поле уединенного провода, так как поле, создаваемое вторым проводом внутри первого, по сравнению с полем первого, пренебрежимо мало. Тогда элементарный поток внутри провода

Индуктивность и ее расчет

Так как поток dФi охватывает не весь ток, а только его часть [см. формулу (1.3)], элементарное потокосцепление

Индуктивность и ее расчет

Весь поток между проводами — внешний поток

Индуктивность и ее расчет

Соответственно, внутренняя индуктивность

Индуктивность и ее расчет

Суммарная индуктивность линии

Индуктивность и ее расчет

При медных или алюминиевых проводах (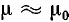Индуктивность и ее расчет) в большинстве случаев вторым членом можно пренебречь по сравнению с первым и тогда

Индуктивность и ее расчет

Для стальных проводов (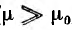Индуктивность и ее расчет) основной частью потока является
внутренний поток и индуктивность

Индуктивность и ее расчет

практически не будет зависеть от расстояния между проводами.

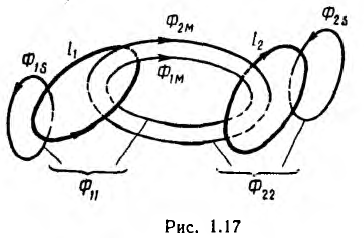
Взаимоиндуктивность и ее расчет

Для двух контуров, имеющих w1 и w2 витков с токами I1 и I2 (рис. 1.17), поток первого контура, определяемый током этого контура, — поток самоиндукции Ф1l—может быть разложен на поток рассеяния Ф1s, пронизывающий только этот контур, и поток взаимоиндукции Ф1m, пронизывающий также и второй контур:

Индуктивность и ее расчет

Индуктивность и ее расчет

Потокосцепление, соответствующее потоку Ф11 (при условии, что этот поток пронизывает все витки первого контура, равно

Индуктивность и ее расчет

а потокосцепление рассеяния

Индуктивность и ее расчет

Аналогично для второго контура

Индуктивность и ее расчет

Потокосцепление второго контура, определяемое током первого,

Индуктивность и ее расчет

а потокосцепление первого контура, определяемое током второго,

Индуктивность и ее расчет

Можно показать, что

Индуктивность и ее расчет

Величина M называется взаимоиндуктивностью и определяется конфигурацией контуров, их взаимным расположением и магнитной проницаемостью среды. Взаимоиндуктивность также измеряется в генри (гн).
Суммарный поток, пронизывающий первый контур,

Индуктивность и ее расчет

Суммарное потокосцепление первого контура

Индуктивность и ее расчет

и соответственно для второго контура

Индуктивность и ее расчет

В этих алгебраических суммах первый член всегда положителен, а знак перед вторым членом определяется направлением токов в контурах; положительный знак соответствует случаю совпадения направлений потоков Ф1м и Ф2м (см. рис. 1.17).
Из изложенного видно, что

Индуктивность и ее расчет

Таким образом, взаимоиндуктивность и индуктивности всегда удовлетворяют неравенству

Индуктивность и ее расчет

а используемый в технических расчетах коэффициент связи двух контуров

Индуктивность и ее расчет

Аналогично, в системе многих контуров потокосцепление контура определяется токами всех контуров:

Индуктивность и ее расчет

где Lq — индуктивность q-то контура, Мqp = Мрq — взаимоиндуктивность q- и р-го контуров. Общий прием расчета взаимоиндуктивности контуров заключается
в нахождении потокосцепления, пронизывающего контур q, но созданного током р-го контура, и делении его на этот ток.

Взаимоиндуктивность двух параллельных двухпроводных линий

Пусть две параллельные двухпроводные линии расположены симметрично так, как это было показано на рис. 1.4. При условии d> г0 внутренним потоком в проводах по сравнению с внешним можно пренебречь.
Магнитный поток, пронизывающий первую линию и созданный током I2 второй, может быть найден как сумма потоков, создаваемых каждым из проводов второй линии в отдельности.
Тогда магнитный поток, пронизывающий первую линию,

Индуктивность и ее расчет

расстояния от провода линии 1 до проводов линии 2 .

Магнитный поток Ф одновременно является потокосцеплением 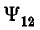Индуктивность и ее расчет первой линии, так как сцепляется с ней один раз; поэтому

Индуктивность и ее расчет

а взаимоиндуктивность

Индуктивность и ее расчет

Для уменьшения коэффициента связи между линиями связи l и передачи 2 применяют транспозицию линии связи, заключающуюся в перекрещивании проводов линии связи через равные расстояния; тогда суммарное потокосцепление 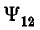Индуктивность и ее расчет будет равно нулю.

Линейные и нелинейные катушки индуктивности

У линейных материалов магнитная проницаемость µ, не зависит от напряженности поля и характеристика 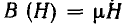Индуктивность и ее расчет для них изображается прямой линией (рис. 1.18, а). Магнитная проницаемость пропорциональна тангенсу угла а наклона этой прямой:

Индуктивность и ее расчет

где k — масштабный коэффициент.

К нелинейным материалам относятся ферромагнетик и — железо, никель, кобальт и гадолиний. Важное значение в электротехнике имеют первые три элемента, главным образом в виде сплавов. У нелинейных материалов магнитная проницаемость очень велика 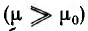Индуктивность и ее расчет и зависит от напряженности поля.

Подобно нелинейным диэлектрикам по кривой первоначальногo намагничивания В (Н) (рис. 1.18, б) могут быть определены статическая магнитная проницаемость

Индуктивность и ее расчет

и дифференциальная, а при быстрых изменениях поля — динамическая магнитная проницаемость

Индуктивность и ее расчет

На рис. 1.18, б эти проницаемости представлены в функции напряженности поля. Максимальные значения магнитной проницаемости в очень чистом железе и в некоторых сплавах, например в пермаллое (сплав железа и-никеля с различными присадками), в сотни тысяч раз превышают магнитную постоянную равную

Индуктивность и ее расчет

магнитной проницаемости вакуума.

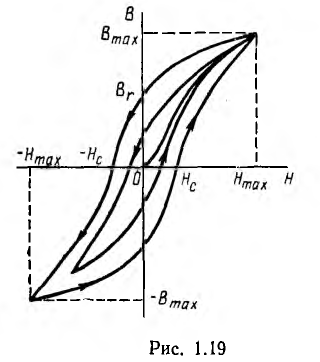
Индуктивность и ее расчет

В переменных магнитных полях в ферромагнетиках имеет место явление магнитного гистерезиса (рис. 1.19), заключающееся в несовпадении кривой В (Н) при возрастании напряженности поля с кривой при убывании поля.

Кривая, соединяющая вершины петель гистерезиса, называется основной кривой намагничивания и практически совпадает с кривой первоначального намагничивания, Ферромагнитные свойства зависят от температуры и проявляются лишь в определенном ее интервале.

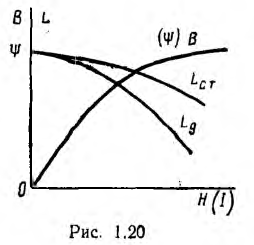
Для расчета индуктивности основной является зависимость потокосцепления ψ от тока I, называемая веберамперной характеристикой.

В зависимости от материала сердечника тороиды по виду своей веберамперной характеристики будут также линейными или нелинейными. В качестве примера рассматривается нелинейный тороид.

Для тороида 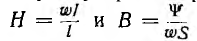Индуктивность и ее расчет и веберамперные характеристики ψ (I) в соответствующем масштабе совпадают с кривыми В (H); поэтому прямая и кривые на рис. 1.18 а и б соответствуют также веберамперным характеристикам при величинах, указанных в скобках.

Индуктивность и ее расчет

Для нелинейных тороидов вводятся понятия статической индуктивности

Индуктивность и ее расчет

и дифференциальной, а также динамической индуктивности

Индуктивность и ее расчет

являющихся функциями тока (см. рис. 1.18, б); для линейных тороидов эти индуктивности совпадают.

Аналогично индуктивностям в нелинейных системах контуров вводятся статическая взаимоиндуктивность

Индуктивность и ее расчет

и дифференциальная, взаимоиндуктивность, а также динамическая

Индуктивность и ее расчет

Индуктивность нелинейного тороида

Расчет нелинейного тороида может быть произведен, если задана зависимость В (H) или µ(H). Так как эти зависимости теоретически не выводятся, то для приближенного решения подбирают по кривой В(H) аппроксимирующую функцию.

Индуктивность и ее расчет

Пусть аппроксимирующая функция для характеристики В (H) (рис. 1.20)
материала сердечника тороида будет

Индуктивность и ее расчет

где а и b — постоянные.

Так как для тороида с ферромагнитным однородным cердечником напряженность поля по-прежнему определяется формулой 

Индуктивность и ее расчет

то индукция будет равна

Индуктивность и ее расчет

а потокосцепление

Индуктивность и ее расчет

откуда статическая индуктивность

Индуктивность и ее расчет

а дифференциальная индуктивность

Индуктивность и ее расчет

Кривые зависимости этих индуктивностей от тока представлены
на рис. 1.20.

  • Энергия в электрических цепях
  • Линейные электрические цепи
  • Нелинейные электрические цепи
  • Магнитные цепи и их расчёт
  • Электрическая ёмкость и ее расчет
  • Линейные н нелинейные диэлектрики и конденсаторы
  • Сопротивление и его расчет
  • Линейные и нелинейные резисторы
Источник

Индуктивность – это элемент цепи, где происходит накопление энергии от магнитного поля. Так происходит запас поля или его преобразование в иные виды энергий. Самым идеальным примером служит катушка индуктивности. В ней происходит запасание поля и его дальнейшее преобразование в энергию других видов, в том числе и тепловую. Способность накапливать магнитное поле и является индуктивностью. Индуктивность напрямую связана с электромагнитной индукцией, статья о которой, также есть на нашем сайте. В данной статье будет описано данное физическое явление, как оно происходит, а также как используется на практике, в чем измеряется и как можно рассчитать физические характеристики.

Что такое индуктивность???

Индуктивность в цепи переменного тока

Прохождение электрического тока по проводнику или катушке сопровождается появлением магнитного поля. Рассмотрим электрическую цепь переменного тока, в которую включена катушка индуктивности, имеющая небольшое количество витков проволоки сравнительно большого сечения, активное сопротивление которой можно считать практически равным нулю. Под действием э. д. с. генератора в цепи протекает переменный ток, возбуждающий переменный магнитный поток. Этот поток пересекает «собственные» витки катушки и в ней возникает электродвижущая сила самоиндукции

Электродвижущая сила самоиндукции, согласно правилу Ленца, всегда противодействует причине, вызывающей ее. Так как э. д. с. самоиндукции всегда противодействует изменениям переменного тока, вызываемым э. д. с. генератора, то она препятствует прохождению переменного тока. При расчетах это учитывается по индуктивному сопротивлению, которое обозначается XL и измеряется в омах.

Измерение катушки индуктивности мультиметром
Измерение катушки индуктивности мультиметром

Таким образом, индуктивное сопротивление катушки XL, зависит от величины э. д. с. самоиндукции, а следовательно, оно, как и э. д. с. самоиндукции, зависит от скорости изменения тока в катушке (от частоты ω) и от индуктивности катушки L

XL = ωL,

  • где XL— индуктивное сопротивление, ом;
  • ω — угловая частота переменного тока, рад/сек;
  • L— индуктивность катушки, гн.

Так как угловая частота переменного тока ω = 2πf, то индуктивное сопротивление

XL = 2πf L,    (59)

где f — частота переменного тока, гц.

Индуктивностью называется идеализированный элемент электрической цепи, в котором происходит запасание энергии магнитного поля. Запасания энергии электрического поля или преобразования электрической энергии в другие виды энергии в ней не происходит.

Пример. Катушка, обладающая индуктивностью L = 0,5 гн, присоединена к источнику переменного тока, частота которого f = 50 гц. Определить:
1) индуктивное сопротивление катушки при частоте f = 50 гц;
2) индуктивное сопротивление этой катушки переменному току, частота которого f = 800 гц.
Решение. Индуктивное сопротивление переменному току при f = 50 гц

XL = 2πf L = 2 · 3,14 · 50 · 0,5 = 157 ом.

При частоте тока f = 800 гц

XL = 2πf L = 2 · 3,14 · 800 · 0,5 = 2512 ом.

Индуктивность сварочной дуги
Индуктивность сварочной дуги

Приведенный пример показывает, что индуктивное сопротивление катушки повышается с увеличением частоты переменного тока, протекающего по ней. По мере уменьшения частоты тока индуктивное сопротивление убывает. Для постоянного тока, когда ток в катушке не изменяется и магнитный поток не пересекает ее витки, э. д. с. самоиндукции не возникает, индуктивное сопротивление катушки XL равно нуло. Катушка индуктивности для постоянного тока представляет собой лишь сопротивление

Выясним, как изменяется з. д. с. самоиндукции, когда по катушке индуктивности протекает переменный ток. Известно, что при неизменной индуктивности катушки э. д. с. самоиндукции зависит от скорости изменения силы тока и она всегда направлена навстречу причине, вызвавшей ее.

В первую четверть периода сила тока возрастает от нулевого до максимального значения. Электродвижущая сила самоиндукции ес, согласно правилу Ленца, препятствует увеличению тока в цепи. Поэтому на графике (пунктирной линией) показано, что ес в это время имеет отрицательное значение. Во вторую четверть периода сила тока в катушке убывает до нуля. В это время э. д. с. самоиндукции изменяет свое направление и увеличивается, препятствуя убыванию силы тока. В третью четверть периода ток изменяет свое направление и постепенно увеличивается до максимального значения; э. д. с. самоиндукции имеет положительное значение и далее, когда сила тока убывает, э. д. с. самоиндукции опять меняет свое направление и вновь препятствует уменьшению силы тока в цепи.

Индуктивность
Индуктивность

Из сказанного следует, что ток в цепи и э. д. с. самоиндукции не совпадают по фазе. Ток опережает э. д. с. самоиндукции по фазе на четверть периода или на угол φ = 90°. Необходимо также иметь в виду, что в цепи с индуктивностью, не содержащей г, в каждый момент времени электродвижущая сила самоиндукции направлена навстречу напряжению генератора U. В связи с этим напряжение и э. д. с. самоиндукции ес также сдвинуты по фазе друг относительно друга на 180°.

Из изложенного следует, что в цепи переменного тока, содержащей только индуктивность, ток отстает от напряжения, вырабатываемого генератором, на угол φ = 90° (на четверть периода) и опережает э. д. с. самоиндукции на 90°. Можно также сказать, что в индуктивной цепи напряжение опережает по фазе ток на 90°. Построим векторную диаграмму тока и напряжения для цепи переменного тока с индуктивным сопротивлением. Для этого отложим вектор тока I по горизонтали в выбранном нами масштабе.

Чтобы на векторной диаграмме показать, что напряжение опережает по фазе ток на угол φ = 90°, откладываем вектор напряжения U вверх под углом 90°. Закон Ома для цепи с индуктивностью можно выразить так:

Следует подчеркнуть, что имеется существенное отличие между индуктивным и активным сопротивлением переменному току. Когда к генератору переменного тока подключена активная нагрузка, то энергия безвозвратно потребляется активным сопротивлением.

Если же к источнику переменного тока присоединено индуктивное сопротивление r = 0, то его энергия, пока сила тока возрастает, расходуется на возбуждение магнитного поля. Изменение этого поля вызывает возникновение э. д. с. самоиндукции. При уменьшении силы тока энергия, запасенная в магнитном поле, вследствие возникающей при этом э. д. с. самоиндукции возвращается обратно генератору.

  • В первую четверть периода сила тока в цепи с индуктивностью возрастает и энергия источника тока накапливается в магнитном поле. В это время э. д. с. самоиндукции направлена против напряжения.
  • Когда сила тока достигнет максимального значения и начинает во второй четверти периода убывать, то э. д. с. самоиндукции, изменив свое направление, стремится поддержать ток в цепи. Под действием э. д. с. самоиндукции энергия магнитного поля возвращается к источнику энергии — генератору. Генератор в это время работает в режиме двигателя, преобразуя электрическую энергию в механическую.
  • В третью четверть периода сила тока в цепи под действием э. д. с. генератора увеличивается, и при этом ток протекает в противоположном направлении. В это время энергия генератора вновь накапливается в магнитном поле индуктивности.
  • В четвертую четверть периода сила тока в цепи убывает, а накопленная в магнитном поле энергия при воздействии э. д. с. самоиндукции вновь возвращается генератору.

Таким образом, в первую и третью четверть каждого периода генератор переменного тока расходует свою энергию в цепи с индуктивностью на создание магнитного поля, а во вторую и четвертую четверть каждого периода энергия, запасенная в магнитном поле катушки в результате возникающей э. д. с. самоиндукции, возвращается обратно генератору.

Из этого следует, что индуктивная нагрузка в отличие от активной в среднем не потребляет энергию, которую вырабатывает генератор, а в цепи с индуктивностью происходит «перекачивание» энергии от генератора в индуктивную нагрузку и обратно, т. е. возникают колебания энергии. Из сказанного следует, что индуктивное сопротивление является реактивным. В цепи, содержащей реактивное сопротивление, происходят колебания энергии от генератора к нагрузке и обратно.

Индуктивность и емкость в цепи переменного тока

Изменения силы тока, напряжения и э. д. с. в цепи переменного тока происходят с одинаковой частотой, но фазы этих изменений, вообще говоря, различны. Поэтому если начальную фазу силы тока условно принять за нуль, то начальные фазы напряжения и э. д. с. соответственно будут иметь некоторые значения ϕ и ψ. При таком условии мгновенные значения силы тока, напряжения и э. д. с. будут выражаться следующими формулами:

i = Iм sin ωt

u = Uм sin (ϕ + ωt),

e = Ɛm sin (ψ + ωt).

Сопротивление цепи, которое обусловливает безвозвратные потери электрической энергии на тепловое действие тока, называют активным. Это сопротивление для тока низкой частоты можно считать равным сопротивлению R этого же проводника постоянному току и находить по формуле:

R=(pl/S)(1 + at).

В цепи переменного тока, имеющей только активное сопротивление, например в лампах накаливания, нагревательных приборах и т. п., сдвиг фаз между напряжением и током равен нулю, т. е. ϕ=0. Это означает, что ток и напряжение в такой цепи изменяются в одинаковых фазах, а электрическая энергия полностью расходуется на тепловое действие тока.

График и схема подключения
График и схема подключения

Включение в цепь переменного тока катушки с индуктивностью L проявляется как увеличение сопротивления цепи. Объясняется это тем, что при переменном токе в катушке все время действует э. д. с. самоиндукции, ослабляющая ток. Сопротивление XL, которое обусловливается явлением самоиндукции, называют индуктивным сопротивлением. Так как э. д. с. самоиндукции тем больше, чем больше индуктивность цепи и чем быстрее изменяется ток, то индуктивное сопротивление прямо пропорционально индуктивности цепи L и круговой частоте переменного тока ω:

ХL = ωL.

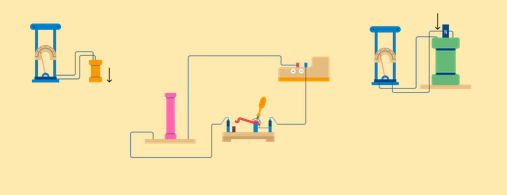
Влияние индуктивного сопротивления на силу тока в цепи наглядно иллюстрируется опытом, изображенным на рис. 26.6. При опускании ферромагнитного сердечника в катушку лампа гаснет, а при его удалении вновь загорается. Это объясняется тем, что индуктивность катушки сильно возрастает при введении в нее сердечника. Следует отметить, что напряжение на индуктивном сопротивлении опережает по фазе ток.

Постоянный ток не проходит через конденсатор, так как между его обкладками находится диэлектрик. Если конденсатор включить в цепь постоянного тока, то после зарядки конденсатора ток в цепи прекратится.

Катушки индуктивности
Катушки индуктивности

Пусть конденсатор включен в цепь переменного тока. Заряд конденсатора (q=CU) вследствие изменения напряжения непрерывно изменяется, поэтому в цепи течет переменный ток. Сила тока будет тем больше, чем больше емкость конденсатора и чем чаще происходит его перезарядка, т. е. чем больше частота переменного тока. Сопротивление, обусловленное наличием электроемкости в цепи переменного тока, называют емкостным сопротивлением Хс. Оно обратно пропорционально емкости С и круговой частоте ω;

Хс = 1/ωС

Из сравнения формул (26.11) и (26.12) видно, что катушки индуктивности представляют собой очень большое сопротивление для тока высокой частоты и небольшое для тока низкой частоты, а конденсаторы — наоборот. Напряжение на емкостном сопротивлении Ха отстает по фазе от тока. Индуктивное XL и емкостное Хс сопротивления называют реактивными. В теории переменного тока доказывается, что при последовательном включении индуктивного и емкостного сопротивлений общее реактивное сопротивление равно их разности:

X = XL—XC

и имеет индуктивный характер при XL > Хс и емкостный характер при XL < Xc.

В заключение заметим, что средняя активная мощность переменного тока, показывающая, сколько энергии за единицу времени передается электрическим током данному участку цепи, определяется формулой:

P = IU cos ϕ.

Мощность, затрачиваемая только на тепловое действие тока, выражается формулой:

Р = I2R

Для увеличения активной мощности переменного тока нужно повышать cos ϕ. (Объясните, почему наибольшее значение cos ϕ имеет при XL=XC.)

Индуктивность
Индуктивность

Более близким к идеализированному элементу — индуктивности — является реальный элемент электронной цепи — индуктивная катушка. В отличие от индуктивности в индуктивной катушке имеют место также запасание энергии электронного поля и преобразование электронной энергии в другие виды энергии, а именно в термическую. Количественно способность реального и идеализированного частей электронной цепи припасать энергию магнитного поля характеризуется параметром, именуемым индуктивностью.

Таким макаром термин «индуктивность» применяется как заглавие идеализированного элемента электронной цепи, как заглавие параметра, количественно характеризующего характеристики этого элемента, и как заглавие основного параметра индуктивной катушки.

Связь меж напряжением и током в индуктивной катушке определяется законом электрической индукции, из которого следует, что при изменении магнитного потока, пронизывающего индуктивную катушку, в ней наводится электродвижущая сила е, пропорциональная скорости конфигурации потокосцепления катушки ψ и направленная таким макаром, чтоб вызываемый ею ток стремился воспрепятствовать изменению магнитного потока:

e = — dψ / dt

В системе единиц СИ магнитный поток и потокосцепление выражают в веберах (Вб).

Магнитный поток Ф, пронизывающий любой из витков катушки, в общем случае может содержать две составляющие: магнитный поток самоиндукции Фси и магнитный поток наружных полей Фвп: Ф — Фси + Фвп.

1-ая составляющая представляет собой магнитный поток, вызванный протекающим по катушке током, 2-ая — определяется магнитными полями, существование которых не связано с током катушки — магнитным полем Земли, магнитными полями других катушек и неизменных магнитов. Если 2-ая составляющая магнитного потока вызвана магнитным полем другой катушки, то ее именуют магнитным потоком взаимоиндукции.

Потокосцепление катушки ψ, так же как и магнитный поток Ф, может быть представлено в виде суммы 2-ух составляющих: потокосцепления самоиндукции ψси, и потокосцепления наружных полей ψвп

ψ= ψси + ψвп

Наведенная в индуктивной катушке ЭДС е, в свою очередь, может быть представлена в виде суммы ЭДС самоиндукции, которая вызвана конфигурацией магнитного потока самоиндукции, и ЭДС, вызванной конфигурацией магнитного потока наружных по отношению к катушке полей:

e = eси + eвп,

тут еси — ЭДС самоиндукции, евп — ЭДС наружных полей.

Если магнитные потоки наружных по отношению к индуктивной катушке полей равны нулю и катушку пронизывает только поток самоиндукции, то в катушке наводится только ЭДС самоиндукции.

Друзья, не забывайте подписываться на обновления блога, ведь чем больше читателей подписано на обновления, тем больше я понимаю что  делаю что-то важное и полезное и это чертовски мотивирует на новые статьи и материалы.

Источник

Индуктивность контура — теоретические основы

Индуктивностью называется идеализированный элемент, приближающийся по своим свойствам к индуктивной катушке, в котором накапливается энергия магнитного поля.

Условное обозначение индуктивности и положительные направления тока, ЭДС самоиндукции и напряжения:

условное обозначение индуктивности
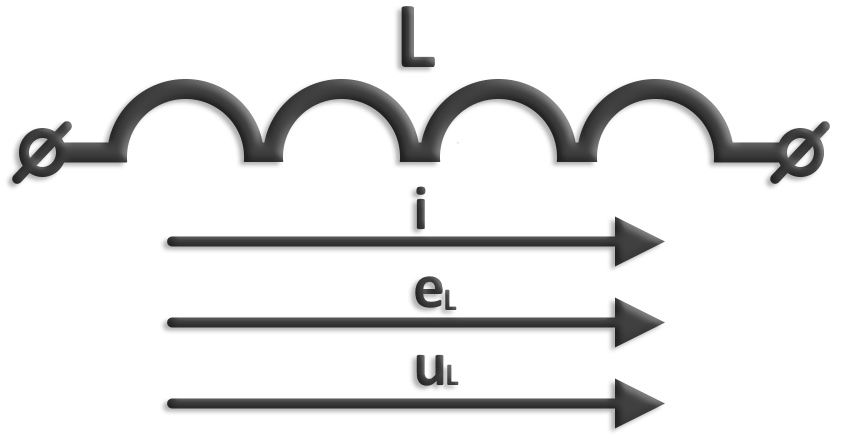
Если по проводнику пропустить ток, то вокруг него создается магнитный поток Φ. Суммарный магнитный поток (поток сцепления) катушки индуктивности равен Ψ= w×Φ, где Φ — магнитный поток, создаваемый одним витком; w — число витков.

По определению собственная индуктивность (или просто индуктивность) равна коэффициенту пропорциональности между потокосцеплением и током
катушки L=Ψ/i.

Индуктивность измеряется в генри 1 Гн = 1 Вб / 1 А. Символ L, используемый для обозначения индуктивности, был принят в честь Эмилия Христиановича Ленца (Heinrich Friedrich Emil Lenz). Единица измерения индуктивности названа в честь Джозефа Генри(Joseph Henry). Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года.

Поток сцепления катушки индуктивности равен Ψ=L×i.

В соответствии с законом электромагнитной индукции при изменении магнитного потока в катушке наводится ЭДС самоиндукции eL=-dΨ/dt. Знак «-» ставится потому, что ЭДС имеет такое направление, что образуемый ею ток своим магнитным полем препятствует изменению магнитного потока, вызывающего данную ЭДС.

Напряжение на индуктивности уравновешивает ЭДС и может быть записано в
виде uL=-eL=dΨ/dt=L×di/dt.

Мгновенная мощность, поступающая в катушку индуктивности равна p=uL×i=L×i×di/dt.

Энергия, запасаемая в катушке индуктивности равна wM=∫(0^t)ptd=∫(0^t)L×i×dt×di/dt=(L×i²)/2.

Взаимная индуктивность характеризует свойство одного элемента с током i1 создавать магнитное поле, частично сцепляющиеся с витками w2 другого элемента.

Коэффициент взаимной индуктивности определяется по формуле M=Ψ12/i2=Ψ21/i1, где Ψ12 — поток сцепления первого контура, вызванный током второго контура (аналогично Ψ21). Измеряется в Гн.

Электрическая цепь и индуктивность контура

Индуктивность характеризует электромагнитные свойства электроцепей. В более узком понятии, это элемент или участок цепи, обладающий большой величиной самоиндукции.

Таким элементом может считаться один, несколько или даже часть витка проводника, на высоких частотах также прямой отрезок провода любой длины.

Электромагнитная индукция

Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции открыл Майкл Фарадей в ходе серии опытов.

Опыт раз. На одну непроводящую основу намотали две катушки таким образом, что витки одной катушки были расположены между витками второй. Витки первой катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.

При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.

Опыт два. Первую катушку подключили к источнику тока, а вторую — к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки фиксировался ток.

Опыт три. Катушку замкнули на гальванометр, а магнит передвигали относительно катушки.

Опыт с катушкой и магнитом

Вот что показали эти опыты:

    1. Индукционный ток возникает только при изменении линий магнитной индукции.
    1. Направление тока различается при увеличении числа линий и при их уменьшении.
  1. Сила индукционного тока зависит от скорости изменения магнитного потока. При этом как само поле может изменяться, так и контур может перемещаться в неоднородном магнитном поле.

Почему возникает индукционный ток?

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна электродвижущей силе (ЭДС).

Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Самоиндукция и измерение индуктивности

Индуктивность проводника

При изменении тока, который протекает в замкнутом электрическом контуре, меняется создаваемый им магнитный поток. Вследствие этого наводится ЭДС, которая называется ЭДС самоиндукции.

Напряжение ЭДС определяется формулой расчета индукции:

Ꜫ=-L∙di/dt.

То есть ЭДС прямо пропорциональна величине скорости изменения тока с некоторым коэффициентом L, который и называется «индуктивность».

Как найти индуктивность контура

Формула, которая является простейшей для нахождения величины, следующая:

  • L = F : I,

где F – магнитный поток, I – ток в контуре.

Через индуктивность можно выразить ЭДС самоиндукции:

  • Ei = -L х dI : dt.

Из формулы напрашивается вывод о численном равенстве индукции с ЭДС, которое возникает в контуре при изменении силы тока на один амперметр за одну секунду.

Переменная индуктивность дает возможность найти и энергию магнитного поля:

  • W = L I2 : 2.

Необходимые формулы для расчетов

Чтобы найти индуктивность соленоида, формула применяется следующая:

  • L= µ0n2V,

где µ0 показывает магнитную проницаемость вакуума, n – это число витков, V – объем соленоида.

Также провести расчет индуктивности соленоида можно и с помощью еще одной формулы:

  • L = µ0N2S : l,

где S – это площадь поперечного сечения, а l – длина соленоида.

Чтобы найти индуктивность соленоида, формула применяется любая, которая подходит по решению к данной задаче.

Обозначение и единицы измерения

Сопротивление тока: формула

В честь Ленца, единица измерения индуктивности получила обозначение символом «L». Выражается в Генри, сокращенно Гн (в англоязычной литературе Н), в честь известного американского физика.

Индуктивность контура
Джозеф Генри

Если при изменении тока в один ампер за каждую секунду ЭДС самоиндукции составляет 1 вольт, то индуктивность цепи будет измеряться в 1 генри.

Как может обозначаться индуктивность в других системах:

  • В системе СГС, СГСМ – в сантиметрах. Для отличия от единицы длины обозначается абгенри;
  • В системе СГСЭ – в статгенри.

Свойства

Имеет следующие свойства:

  • Зависит от количества витков контура, его геометрических размеров и магнитных свойств сердечника;
  • Не может быть отрицательной;
  • Исходя из определения, скорость изменения тока в контуре, ограничена значением его индуктивности;
  • При увеличении частоты тока реактивное сопротивление катушки увеличивается;
  • Обладает свойством запасать энергию – при отключении тока запасенная энергия стремится компенсировать падение тока.

Индуктивность и конденсатор

Токоведущие элементы устройства способны создавать его собственную индуктивность. Это такие конструктивные части, как кладки, соединительные шины, токоотводы, выводы и предохранители. Можно создать дополнительную индуктивность конденсатора путем присоединения шин. Режим работы электрической цепи зависит от индуктивности, емкости и активного сопротивления. Формула расчета индуктивности, которая возникает при приближении к резонансной частоте, следующая:

  • Ce = C : (1 – 4Π2f2LC),

где Ce определяет эффективную емкость конденсатора, C показывает действительную емкость, f – это частота, L – индуктивность.

Значение индуктивности всегда должно учитываться при работе с силовыми конденсаторами. Для импульсных конденсаторов наиболее важна величина собственной индуктивности. Их разряд приходится на индуктивный контур и имеет два вида – апериодический и колебательный.

Индуктивность в конденсаторе находится в зависимости от схемы соединения элементов в нем. Например, при параллельном соединении секций и шин эта величина равна сумме индуктивностей пакета главных шин и выводов. Чтобы найти такого рода индуктивность, формула следующая:

  • Lk = Lp + Lm + Lb,

где Lk показывает индуктивность устройства, Lp –пакета, Lm – главных шин, а Lb – индуктивность выводов.

Если при параллельном соединении ток шины меняется по ее длине, то тогда эквивалентная индуктивность определяется так:

  • Lk = Lc : n + µ0 l х d : (3b) + Lb,

где l – длина шин, b – ее ширина, а d – расстояние между шинами.

индуктивность тока
Чтобы снизить индуктивность устройства, необходимо токоведущие части конденсатора расположить так, чтобы взаимно компенсировались их магнитные поля. Иными словами, токоведущие части с одинаковым движением тока нужно удалять друг от друга как можно дальше, а с противоположным направлением сближать. При совмещении токоотводов с уменьшением толщины диэлектрика можно снизить индуктивность секции. Этого можно достигнуть еще путем деления одной секции с большим объемом на несколько с более мелкой емкостью.

“Катушка ниток”

Катушка индуктивности представляет собой намотанную изолированную медную проволоку на твердое основание. Что касается изоляции, то выбор материала широк – это и лак, и проводная изоляция, и ткань. Величина магнитного потока зависит от площади цилиндра. Если увеличить ток в катушке, то магнитное поле будет становиться все больше и наоборот.

индуктивность соленоида формула

Если подать электрический ток на катушку, то в ней возникнет напряжение, противоположное напряжению тока, но оно внезапно исчезает. Такого рода напряжение называется электродвижущей силой самоиндукции. В момент включения напряжения на катушку сила тока меняет свое значение от 0 до некоего числа. Напряжение в этот момент тоже меняет значение, согласно закону Ома:

  • I = U : R,

где I характеризует силу тока, U – показывает напряжение, R – сопротивление катушки.

Еще одной особенной чертой катушки является следующий факт: если разомкнуть цепь “катушка – источник тока”, то ЭДС добавится к напряжению. Ток тоже вначале вырастет, а потом пойдет на спад. Отсюда вытекает первый закон коммутации, в котором говорится, что сила тока в катушке индуктивности мгновенно не меняется.

Катушку можно разделить на два вида:

  1. С магнитным наконечником. В роли материала сердца выступают ферриты и железо. Сердечники служат для повышения индуктивности.
  2. С немагнитным. Используются в случаях, когда индуктивность не больше пяти миллиГенри.

Устройства различаются и по внешнему виду, и внутреннему строению. В зависимости от таких параметров находится индуктивность катушки. Формула в каждом случае разная. Например, для однослойной катушки индуктивность будет равна:

  • L = 10µ0ΠN2R2 : 9R + 10l.

А вот уже для многослойной другая формула:

  • L= µ0N2R2 :2Π(6R + 9l + 10w).

Основные выводы, связанные с работой катушек:

  1. На цилиндрическом феррите самая большая индуктивность возникает в середине.
  2. Для получения максимальной индуктивности необходимо близко наматывать витки на катушку.
  3. Индуктивность тем меньше, чем меньше количество витков.
  4. В тороидальном сердечнике расстояние между витками не играет роли катушки.
  5. Значение индуктивности зависит от “витков в квадрате”.
  6. Если последовательно соединить индуктивности, то их общее значение равно сумме индуктивностей.
  7. При параллельном соединении нужно следить, чтобы индуктивности были разнесены на плате. В противном случае их показания будут неправильными за счет взаимного влияния магнитных полей.

Применение катушек индуктивности

Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.

Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.

Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют трансформатор, являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.

По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.

Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.

Общие сведения

Для того чтобы понять, от чего зависит индуктивность катушки, необходимо подробно изучить всю информацию об этой физической величине. Первым делом следует рассмотреть принятое международное обозначение параметра, его назначение, характеристики и единицы измерения.

Само понятие индуктивности было предложено известным английским физиком Оливером Хевисайдом, который занимался её изучением. Этот учёный подарил миру и другие известные термины — электропроводимость, магнитная проницаемость и сопротивление, а также ЭДС (электродвижущая сила).

Знаменитый физик— Эмилий Ленц
Первая буква фамилии другого знаменитого физика — Эмилия Ленца — была взята в качестве обозначения индуктивности в формулах и при проведении расчётов. В наше время символ L продолжает использоваться при упоминании этого параметра.

Выдающийся американский физик Джозеф Генри первым обнаружил явление индуктивности. В его честь физики назвали единицу измерения в международной СИ, которая чаще всего используется в расчётах. В других системах (гауссова и СГС) индуктивность измеряют в сантиметрах. Для упрощения вычислений было принято соотношение, в котором 1 см равняется 1 наногенри. Очень редко используемая система СГСЭ оставляет коэффициент самоиндукции без каких-либо единиц измерения или использует величину статгенри. Она зависит от нескольких параметров и приблизительно равняется 89875520000 генри.

Среди основных свойств индуктивности выделяются:

  1. Величина параметра никогда не может быть меньше нуля.
  2. Показатель зависит только от магнитных свойств сердечника катушки, а также от геометрических размеров контура.

Способы расчёта

Существует несколько основных способов определить индуктивность катушки. Все формулы, которые будут использоваться в расчётах, легко можно найти в справочной литературе или интернете. Весь процесс вычисления довольно простой и не составит труда для людей, имеющих элементарные математические и физические знания.

Через силу тока

Этот расчёт считается самым простым способом определения индуктивности катушки. Формула через силу тока вытекает из самого термина. Какова индуктивность катушки — можно определить по формуле: L=Ф/I, где:

  • L — индуктивность контура (в генри);
  • Ф — величина магнитного потока, измеряемого в веберах;
  • I — сила тока в катушке (в амперах).

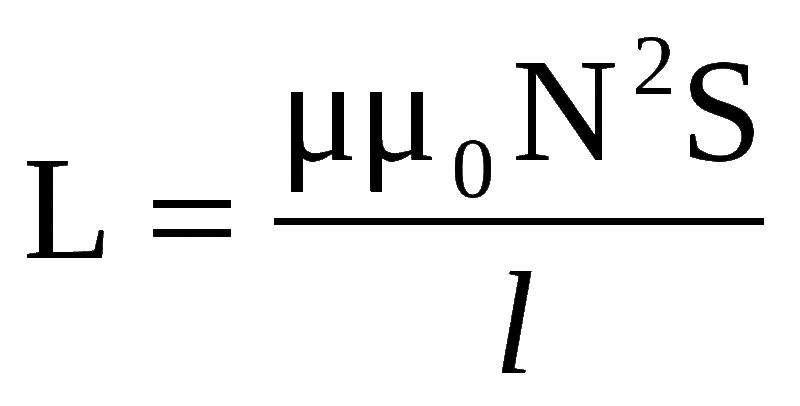
Формула индуктивности катушки

Такая формула подходит только для одновиткового контура. Если катушка состоит из нескольких витков, то вместо величины магнитного потока используется полный поток (суммарное значение). Когда же через все витки проходит одинаковый магнитный поток, то для определения суммарного значения достаточно умножить величину одного из них на общее количество.

Соленоид конечной длины

Соленоид представляет собой тонкую длинную катушку, где толщина обмотки значительно меньше диаметра. В этом случае расчёты ведутся по той же формуле, что и через силу тока, только величина магнитного потока будет определяться следующим образом: Ф=µ0NS/l, где:

  • Соленоид конечной длины
    µ0 — магнитная проницаемость среды, определяющаяся по справочным таблицам (для воздуха, который принимается по умолчанию в большинстве расчётов, она равна 0,00000126 генри/метр);
  • N — количество витков в катушке;
  • S — площадь поперечного сечения витка, измеряемая в квадратных метрах;
  • l — длина соленоида в метрах.

Коэффициент самоиндукции соленоида можно рассчитать и исходя из способа определения энергии магнитного потока поля. Это более простой вариант, но он требует наличия некоторых величин. Формула для нахождения индуктивности — L=2W/I 2 , где:

  • W — энергия магнитного потока, измеряемая в джоулях;
  • I — сила тока в амперах.

Катушка с тороидальным сердечником

большинстве случаев тороидальная катушка наматывается на сердечник, изготовленный из материала, обладающего большой магнитной проницаемостью. В этом случае для расчётов индуктивности можно использовать формулу для прямого соленоида бесконечной длины. Она имеет такой вид: L=N µ0 µS/2 πr, где:

  • N — число витков катушки;
  • µ — относительная магнитная проницаемость;
  • µ0 — магнитная постоянная;
  • S — площадь сечения сердечника;
  • π — математическая постоянная, равная 3,14;
  • r — средний радиус тора.

Катушка с тороидальным сердечником

Длинный проводник

Большинство таких квазилинейных проводников имеет круглое сечение. В этом случае величина коэффициента самоиндукции будет определяться по стандартной формуле для приближённых расчётов: L= µ0l (µelnl/r+ µi/4)/2 π. Здесь используются следующие обозначения:

  • Вычисления по формуле
    l — длина проводника в метрах;
  • r — радиус сечения провода, измеряемый в метрах;
  • µ0 — магнитная постоянная;
  • µi — относительная магнитная проницаемость, характерная для материала, из которого изготовлен проводник;
  • µe — относительная магнитная проницаемость внешней среды (чаще всего принимается значение для вакуума, которое равняется 1);
  • π — число Пи;
  • ln — обозначение логарифма.

Графический вывод формулы

Существует возможность получить записанную формулу, используя графический метод. Для этого отобразим на графике зависимость магнитного потока Φ(I) от тока I (рис. 1.21.2). Полное количество выделившейся теплоты, которое равно изначальному запасу энергии магнитного поля, определится как площадь получившегося на рис. 1.21.2 треугольника:

Рисунок 1.21.2. Вычисление энергии магнитного поля.

В итоге формула энергии Wм магнитного поля катушки с индуктивностью L, создаваемого током I, будет записана в виде формулы:

Wм=ΦI2=LI22=Φ22L

Используем выражение, которое мы получили, для энергии катушки к длинному соленоиду с магнитным сердечником. Применяя указанные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, получим запись:

Wм=μ0·μ·n2·I22V=B22μ0·μV

В этой формуле V является объемом соленоида. Полученное выражение демонстрирует нам, что магнитная энергия имеет локализацию не в витках катушки, по которым проходит ток, а распределена по всему объему, в котором возникло магнитное поле.

Определение 4

Объёмная плотность магнитной энергии – это физическая величина, которая равна энергии магнитного поля в единице объема: Wм=B22μ·μ.

В свое время Максвелл продемонстрировал, что указанная формула (в нашем случае выведенная для длинного соленоида) верна для любых магнитных полей.

Об индуктивности простыми словами

Индуктивностью является физическая величина, которая была введена с целью оценки способности электрического проводника противодействовать току. Т.е. индуктивность, или как ее еще называют – коэффициент самоиндукции, показывает зависимость Ɛ от свойств проводника и от магнитной проницаемости среды, в которой он находится. Единицей измерения величины является генри (Гн).

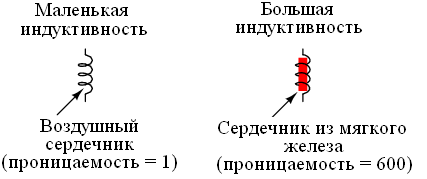
Если рассмотреть величину на примере катушки индуктивности, то можно понять, что ее показатели будут изменяться в зависимости от числа витков катушки, а также ее размеров и формы. Чем больше количество витков, тем больше индуктивность. Данная величина также будет увеличена, если внутрь катушки будет помещен сердечник, так как изменится относительная магнитная проницаемость среды, в которой находится проводник. Данную зависимость можно увидеть на схеме.

Индуктивность

Если посмотреть на формулу зависимости ЭДС от индуктивности, то можно понять, что чем больше будет величина, тем заметнее будет электродвижущая сила, что говорит о их прямой пропорциональности. Следуя из этого, можно сделать вывод, что индуктивность выступает неким «хранилищем» энергии, которое открывается в момент изменения тока.

Ɛ=- L(dI/dt), где:

  • Ɛ – ЭДС самоиндукции;
  • L-индуктивность;
  • I – сила тока;
  • t – время.

При этом L равно магнитному полю (Ф) деленному на силу тока (I).

Польза и вред

Такое явление, как самоиндукция, большинство людей наблюдают ежедневно, даже не осознавая этого. Так, например, принцип работы люминесцентных трубчатых ламп основан именно на явлении самоиндукции. Также данное явление можно наблюдать в цепи зажигания транспортных средств, работающих на бензине. Это возможно благодаря наличию катушки индуктивности и прерывателя. Так, в момент, когда через катушку проходит ток, прерыватель разрывает цепь питания катушки, в результате чего и образуется ЭДС, которая далее приводит к тому, что импульс более 10 кВ поступает на свечи зажигания.

Явление самоиндукции также приносит пользу, убирая лишнюю пульсацию, частоты или различные шумы в музыкальных колонках или другой аудиотехнике. Именно на ней основано работа различных «шумовых» фильтров.

Однако самоиндукция способна приносить не только пользу, но и заметный вред. Особенно часто она вредит различным выключателям, рубильникам, розеткам и другим устройствам, размыкающим электрическую цепь. Ее негативное воздействие на электроприборы можно заметить невооруженным глазом: искра в розетке в момент вытаскивания вилки, работающего фена и есть проявление сопротивления изменению силы тока.

Именно поэтому лампочки чаще всего перегорают именно в момент выключения света, а не наоборот. Это связано с тем, что сопротивление приводит к выгоранию контактов и накоплению цепей с токами в различных электроприборах, что в свою очередь представляет собой довольно серьезную техническую проблему.

Индуктивность и самоиндукция – незнакомые многим термины, с которыми люди встречаются ежедневно. И если первый термин является физической величиной, обозначающей способность проводника препятствовать изменению напряжения, то второй объясняет появление ЭДС индукции в том же проводнике.

Предыдущая

РазноеЧто такое фазное и линейное напряжение?

Следующая

РазноеБлуждающие токи и способы борьбы с ними

Источник

Всем доброго времени суток! В прошлой статье я рассказывал о таком явлении как электромагнитная индукция и ЭДС возникающая при самоиндукции и взаимной индукции. Устройства, в основе которых лежат данные явления и процессы, называются индуктивными элементами (катушки колебательных контуров, трансформаторы, дроссели, реакторы). В качестве одного из основных параметров данных элементов выступает индуктивность L(также имеет название коэффициента самоиндукции). О том, как рассчитать данный параметр пойдёт речь в данной статье.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Методы расчёта индуктивностей

Индуктивностью (обозначается L) или коэффициентом самоиндукции называется коэффициент пропорциональности между потокосцеплением (обозначается Ψ­L) и электрическим током, который возбуждает данное потокосцепление.

В простых случаях индуктивность можно рассчитать, применяя формулы для вычисления магнитной индукции B0 (закон Био-Савара-Лапласа), магнитного потока Φ и потокосцепления Ψ­L

где S – площадь поверхности ограниченная контуром, который создает магнитную индукцию;

n – количество контуров с током, которые пронизывает магнитный поток.

Однако это в идеальном случае, в реальности говоря о токе I, который протекает по проводнику, необходимо отметить, что его распределение по сечению проводника не всегда равномерно, вследствие возникновения скин-эффекта при переменном токе. В результате этого эффекта плотность электрического тока распределяется неравномерно, происходит её уменьшение от внешнего слоя проводника к его центру. Уменьшение плотности тока также происходит неравномерно и зависит от частоты переменного тока. Для оценки скин-эффекта ввели понятие толщины скин-слоя ∆, которая показывает, на каком расстоянии от поверхности проводника плотность тока падает в е = 2,718 раз. Толщину скин-слоя можно вычислить по выражению

где δ – глубина проникновения переменного тока или толщина скин-слоя;

μ – магнитная проницаемость вещества;

γ – удельная электрическая проводимость материала проводника;

ω – круговая частота переменного тока, ω = 2πf.

Поэтому непосредственный способ вычисления индуктивности практически не применяется.

На практике применяется выражения для индуктивности, выведенные с некоторыми допущениями, погрешности вычисления индуктивности по этим выражениями составляет порядка нескольких процентов.

Так как индуктивные элементы довольно разнообразны, их можно разделить на три группы:

индуктивные элементы без сердечников;

индуктивные элементы с замкнутыми сердечниками;

индуктивные элементы с сердечниками, имеющие воздушный зазор.

Самые простые по конструкции являются индуктивные элементы без сердечников, поэтому рассмотрим их в первую очередь. Простейшим из таких элементов является прямой провод.

Индуктивность прямолинейного провода круглого сечения

При расчёте индуктивности необходимо разделять индуктивность на постоянном токе и индуктивность на высокой частоте. Под высокой частотой следует понимать такую частоту, на которой толщина скин-слоя меньше размеров поперечного сечения провода. В случае если толщина скин-слоя больше поперечных размеров провода, то можно вести расчёт для постоянного тока.

Индуктивность прямого провода
Определение индуктивности прямого провода. l – это длина проводника, d = 2r – диаметр проводника.

В случае постоянного тока или тока низкой частоты индуктивность составит

где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;

l – длина провода, м;

d – диаметр провода, м.

Как я уже говорил, на величину индуктивности влияет частота переменного тока, поэтому в случае необходимости рассчитать индуктивность на любой частоте применяется следующее выражение

где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода. Данный коэффициент зависит от величины k*r, где

d = 2r – диаметр поперечного сечения провода, м.

где ω – угловая частота переменного тока, ω = 2πf;

μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;

γ – удельная проводимость вещества проводника.

Тогда если k*r < 3, то

если k*r > 3, то

где

Пример. Необходимо рассчитать индуктивность прямолинейного провода круглого сечения из меди (γ = 5,81*107 См/м) диаметром d = 2 мм и длиной l = 4 м, при постоянном токе и токе частотой f = 50 кГц.

На постоянном токе

На частоте 50 кГц

Online калькулятор индуктивности прямолинейного проводника

Индуктивность кругового кольца круглого сечения

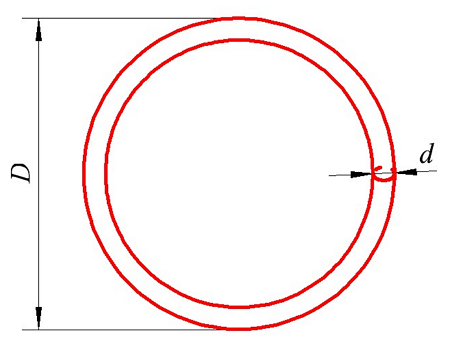
Теперь рассмотрим, какова будет индуктивность если провод свернуть в кольцо. Такой индуктивный элемент будет иметь вид

Индуктивность кольца (витка) из провода
Определение индуктивности кругового витка. D – диаметр кольца (витка), d – диаметр провода, из которого сделано кольцо (виток).

При этом его индуктивность можно вычислить по следующему выражению

для  постоянного тока

где R – радиус витка, м, R = D/2;

r – радиус провода, м, r = d/2;

μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м.

Так же как и для проводника существует выражение для индуктивности кругового витка на любой частоте

где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода. Определяется также как и для прямого проводника.

Пример. В качестве примера рассчитаем индуктивность такого же провода, как и в первом примере, только свёрнутом в кольцо. В этом случае диаметр провода d = 2 мм, а диаметр кольца D = l/π = 4/3,142 ≈ 1,273 м, провод выполнен из меди (γ = 5,81*107 См/м).

Для постоянного тока индуктивность составит

На частоте 50 кГц

Online калькулятор индуктивности кольца кругового сечения

В следующей части я продолжу рассмотрение расчётов индуктивности для различных индуктивных элементов.

Источник

Добавить комментарий