Сергей ответил не точно. Все зависит от того как ваши диэлектрики находятся относительно плат конденсатора. Параллельно или перпендикулярно?
Если диэл. параллельно, то последовательная цепь конденсаторов.
Если же диэл. перпендикулярно, то параллельная цепь конденсаторов.
Источник: Студент-электротехник… 🙂
Илья Н.Мастер (1276)
9 лет назад
Плохо себе представляю перпендикулярно расположенный диэлектрик в плоском конденсаторе, да и не проходили мы этого на первом курсе техникума.
Petr Germann
Профи
(844)
“поставьте” конденсатор так, чтобы платы были ориентированы не сверху вниз, а слева на право. Затем мысленно налейте в конденсатор воду и масло. Вода будет снизу, масло сверху. Разделительная полоса будет перпендикулярно к платам
В случае заполнения конденсатора диэлектриком, напряженность электрического поля в каждой точке между сферами уменьшается в в раз. Докажем, что и разность потенциалов так же уменьшается в е раз. Для этого разобьем отрезок радиуса АВ на малые отрезки, такие, что поле на протяжении каждого из них можно считать практически однородным и воспользуемся связью между напряженностью и разностью потенциалов:
где $frac>< epsilon>$ — напряженность электрического поля на участке $Delta d_, E_$ — напряженность в отсутствие диэлектрика. Суммируя (4) по всем $Delta d_$, находим:
Подставляя (5) в определение электроемкости (1), Получаем:
Другой способ вычисления разности потенциалов между сферами при наличии диэлектрика основан на применении результата задачи 1535 с учетом того, что наличие на внешней сфере заряда — $q^< prime>$ дает одинаковую добавку как к потенциалу внешней сферы, так и внутренней. Таким образом, разность потенциалов, вычисленную с учетом 1535, следует подставить в определение (1).
Источник
Емкость плоского и других конденсаторов
Екатерина Владимировна Мосина
Эксперт по предмету «Физика»
С нами работают 108 689 преподавателей из 185 областей знаний. Мы публикуем только качественные материалы
Что такое конденсатор
Напомним, что конденсатором называется совокупность двух любых проводников, (обкладок) заряды которых одинаковы по величине и противоположны по знаку.
Конфигурация конденсатора такова, что поле, которое создается зарядами, локализовано между обкладками. В общем случае электроемкость конденсатора равна:
где $<varphi >_1-<varphi >_2=U$ — разность потенциалов обкладок, которую называют напряжением и обозначают $U$. Емкость по определению считается положительной величиной. Она зависит только от геометрии обкладок конденсатора их взаиморасположения и диэлектрика. Форму обкладок и их расположение подбирают так, чтобы внешние поля минимально влияли на внутреннее поле конденсатора. Силовые линии поля конденсатора начинались на проводнике с положительным зарядом и заканчивались на проводнике с отрицательным зарядом. Конденсатор может быть проводником, который помещен в полость, окруженную замкнутой оболочкой.
В соответствии с конфигураций конденсаторов можно выделить три большие группы: плоские, сферические и цилиндрические (по форме обкладок). Вычисление емкости конденсатора сводится к определению $напряжения$ конденсатора при известном заряде на его обкладках.
Плоский конденсатор
Плоский конденсатор (рис.1) — это две разноименно заряженные пластины, разделенные тонким слоем диэлектрика. Формула для расчета емкости такого конденсатора представляет собой выражение:
где $S$ — площадь обкладки, $d$ — расстояние между обкладками, $varepsilon $ — диэлектрическая проницаемость вещества. Чем меньше $d$, тем больше совпадает расчётная емкость конденсатора (2), с реальной емкостью.
Электроемкость плоского конденсатора, заполненного N слоями диэлектрика, толщина слоя с номером i равна $d_i$, диэлектрическая проницаемость этого слоя $<varepsilon >_i$ вычисляется по формуле:
Сферический конденсатор
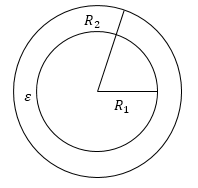
В том случае, если внутренний проводник шар или сфера, внешняя замкнутая оболочка — концентрическая ему сфера, то конденсатор является сферическим. Сферический конденсатор (рис.2) состоит из двух концентрических проводящих сферических поверхностей с пространством между обкладками, заполненным диэлектриком. Емкость его можно рассчитать по формуле:
где $R_1< и R>_2$ — радиусы обкладок.
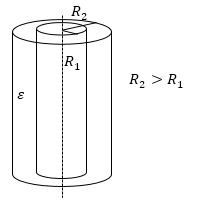
Цилиндрический конденсатор
Емкость цилиндрического конденсатора равна:
где $l$ — высота цилиндров, $R_1$ и $R_2$ — радиусы обкладок. Этот вид конденсаторов представляет собой две коаксиальных (соосных) проводящих цилиндрических поверхности (рис.3).
Еще одной, но не маловажной характеристикой всех конденсаторов является пробивное напряжение ($U_$)— это напряжение, при котором происходит электрический разряд через слой диэлектрика. $U_$ зависит от толщины слоя и свойств диэлектрика, конфигурации конденсатора.
Помимо одиночных конденсаторов применяют их соединения. Для того чтобы увеличить емкость используют параллельное соединение конденсаторов (соединение одноименными обкладками). В этом случае результирующая емкость такого соединения может быть найдена как сумма$< С>_i$ где $С_i$ — емкость конденсатора с номером i:
Если конденсаторы соединить последовательно (обкладками с разными знаками заряда), то суммарная емкость соединения будет всегда меньше, чем минимальная емкость любого конденсатора, который входит в систему. В этом случаем для того чтобы рассчитать результирующую емкость складывают величины, обратные к емкостям отдельных конденсаторов:
Задание: Вычислите электроемкость плоского конденсатора, если площадь обкладок его равна 1см2, расстояние между обкладками равно 1 мм. Пространство между обкладками вакуумировано.
Формула для расчета емкости, данного в задаче конденсатора имеет вид:
Ответ: С $approx $0,9 пФ.
Задание: Какова напряженность электростатического поля сферического конденсатора на расстоянии x=1 см=$<10>^<-2>м$ от поверхности внутренней обкладки, если внутренний радиус обкладки конденсатора $R_1=$1 см$<=10>^<-2>м$, внешний $R_2=$ 3 см=$<3cdot 10>^<-2>м$. Напряжение на обкладках равно $<10>^3В$.
Напряженность поля, которое создается проводящей заряженной сферой, вычисляется в соответствии с формулой:
где $q$ — заряд внутренней сферы (обкладки конденсатора), $r=R_1+x$ —расстояние от центра сферы.
Заряд сферы найдем из определения емкости конденсатора (С):
Емкость сферического конденсатора определяется как:
где $R_1< и R>_2$ — радиусы обкладок конденсатора.
Подставим выражения (2.2) и (2.3) в (2.1), получим искомую напряженность:
Так как все данные в задаче уже переведены в систему СИ, проведем вычисления:
Источник
Чертов / Глава 3.Электростатика / 17.Емкость.Конденсаторы / Емкость
§ 17. ЭЛEКTPИЧECКAЯ EMКOCTЬ. КOHДEHCATOPЫ
Электрическая емкость уединенного проводника или конденсатора
где ΔQ — заряд, сообщенный проводнику (конденсатору); Δφ — изменение потенциала, вызванное этим зарядом.
Электрическая емкость уединенной проводящей сферы радиусом R, находящейся в бесконечной среде с диэлектрической проницаемостью ε,
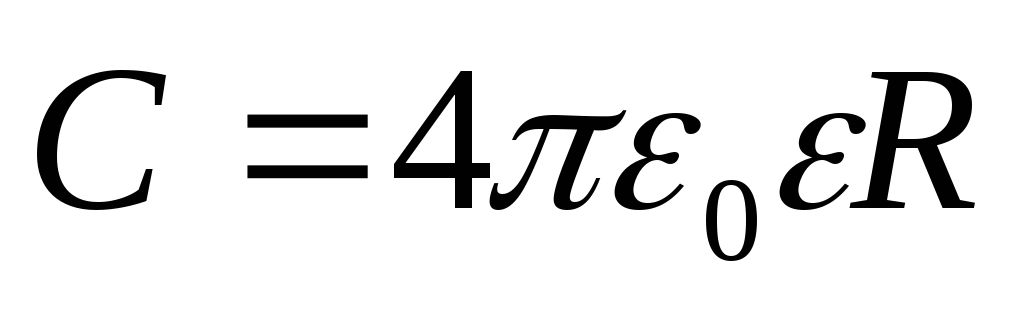
Если сфера полая и заполнена диэлектриком, то электроемкость ее от этого не изменяется.
Электрическая емкость плоского конденсатора
,
где S — площадь пластин (каждой пластины); d — расстояние между ними; ε — диэлектрическая проницаемость диэлектрика, заполняющего пространство между пластинами.
Электрическая емкость плоского конденсатора, заполненного п слоями диэлектриком толщиной di каждый с диэлектрическими проницаемостями ε, (слоистый конденсатор),
Электрическая емкость сферического конденсатора (две концентрические сферы радиусами R1 и R2, пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью ε)
Электрическая емкость цилиндрического конденсатора (два коаксиальных цилиндра длиной l и радиусами R1 и R2, пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью ε)
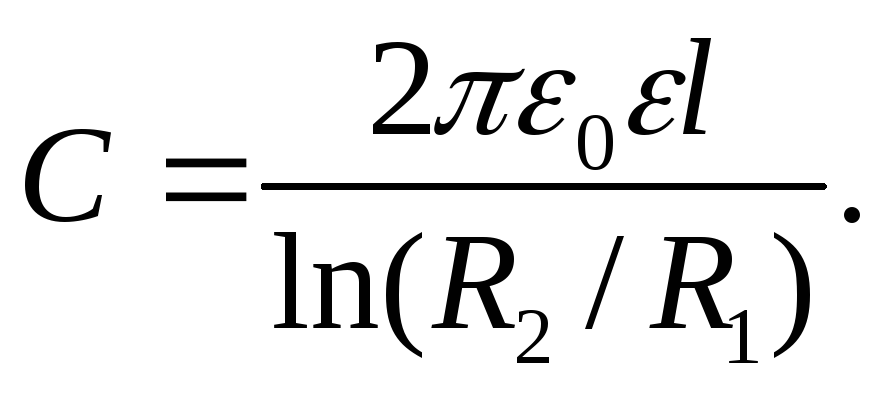
Электрическая емкость С последовательно соединенных конденсаторов:
в общем случае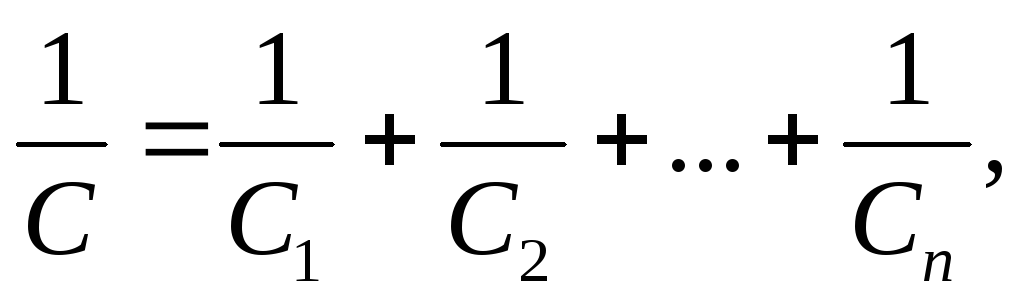 
где п — число конденсаторов;
в случае двух конденсаторов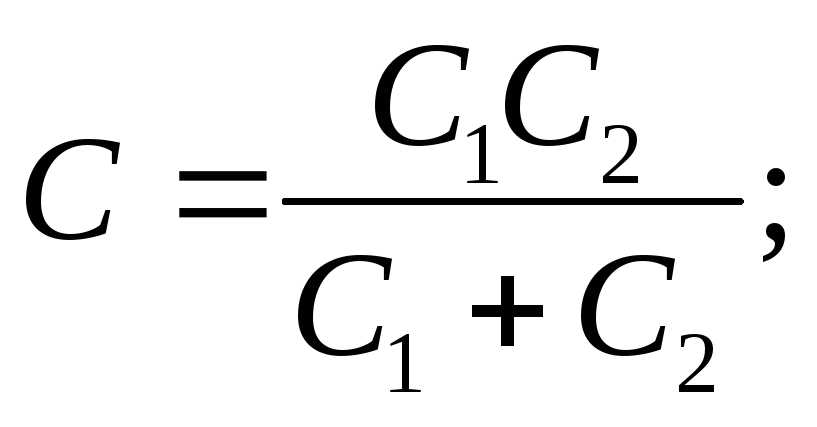 
в случае п одинаковых конденсаторов с электроемкостью С1 каждый
Электрическая емкость параллельно соединенных конденсаторов:
в случае п одинаковых конденсаторов с электроемкостью С1 каждый C=nC1.
Примеры решения задач
Пример 1. Определить электрическую емкость С плоского конденсатора с двумя слоями диэлектриков: фарфора толщиной d1=2 мм и эбонита толщиной d2= 1,5 мм, если площадь S пластин равна 100 см 2 .
Р е ш е н и е. Емкость конденсатора, по определению, C=Q/U , где Q — заряд на пластинах конденсатора; U — разность потенциалов пластин. Заменив в этом равенстве общую разность потенциалов U конденсатора суммой U1+U2 напряжений на слоях диэлектриков, получим
Приняв во внимание, что Q=σS, U1= Е1di=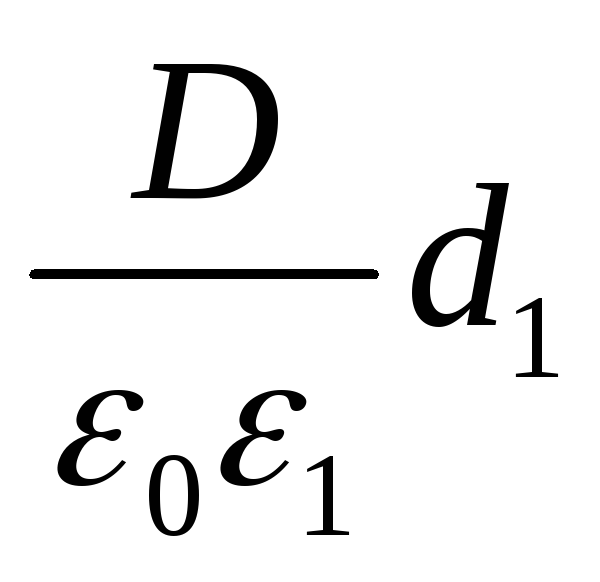
и U2=E2d2=
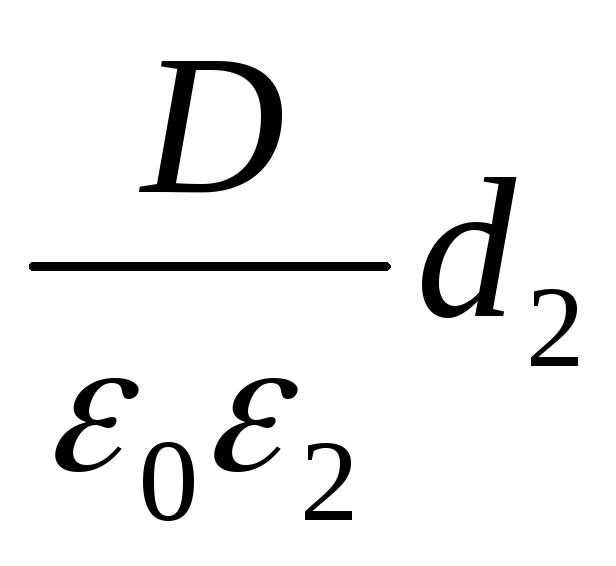, равенство (1) можно переписать в виде
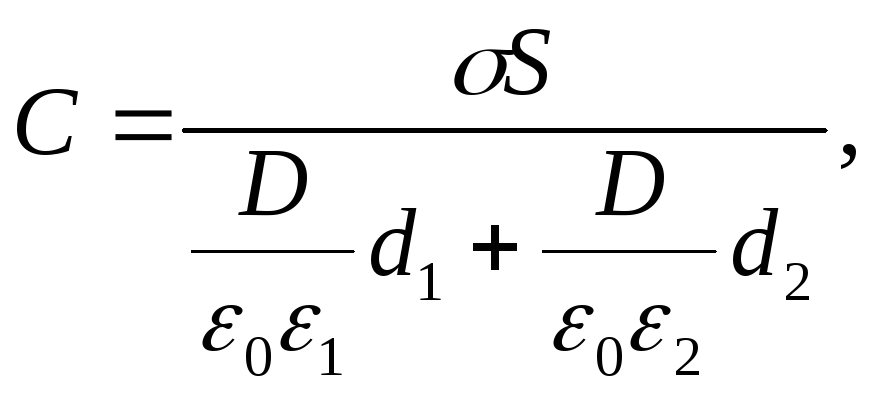(2)
где σ — поверхностная плотность заряда на пластинах; Е1 и Е2 — напряженности поля в первом и втором слоях диэлектрика соответственно; D — электрическое смещение поля в диэлектриках.
Умножив числитель и знаменатель равенства (2) на ε и учтя, что D=σ, окончательно получим
Пример 2. Два плоских конденсатора одинаковой электроемкости С1=С2=С соединены в батарею последовательно и подключены источнику тока с электродвижущей силой ε. Как изменится разность потенциалов U1 на пластинах первого конденсатора, если пространство между пластинами второго конденсатора, не отключая источника тока, заполнить диэлектриком с диэлектрической проницаемостью ε =7?
Р е ш е н и е. До заполнения второго конденсатора диэлектриком разность потенциалов на пластинах обоих конденсаторов была одинакова: U1=U2=ε/2. После заполнения электроемкость второго конденсатора возросла в ε раз:
Электроемкость С первого не изменилась, т. е. C1‘=C.
Так как источник тока не отключался, то общая разность потенциалов на батарее конденсаторов осталась прежней, она лишь перераспределилась между конденсаторами. На первом конденсаторе
где Q — заряд на пластинах конденсатора. Поскольку при последовательном соединении конденсаторов заряд на каждой пластине и на всей батареи одинаков, то
где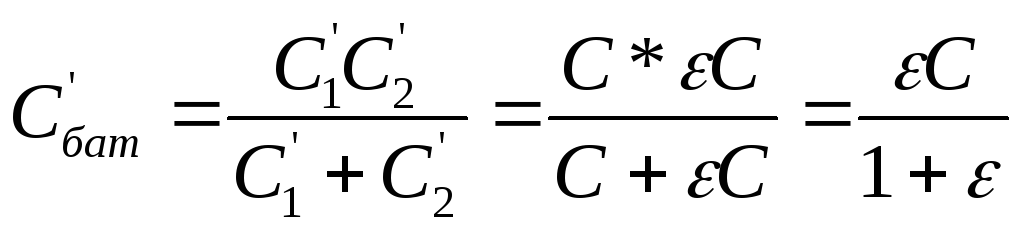 
. Таким образом,
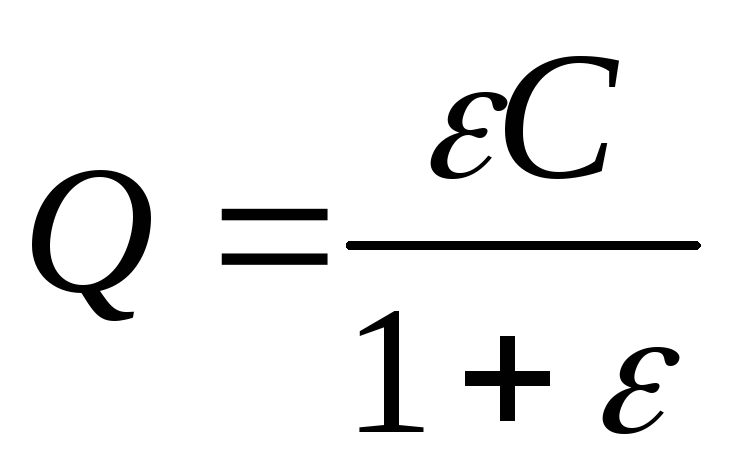ε.
Подставив это выражение заряда в формулу (1), найдем
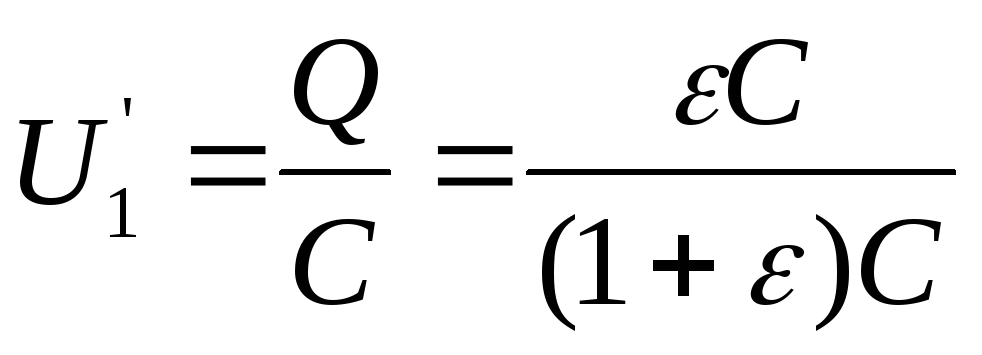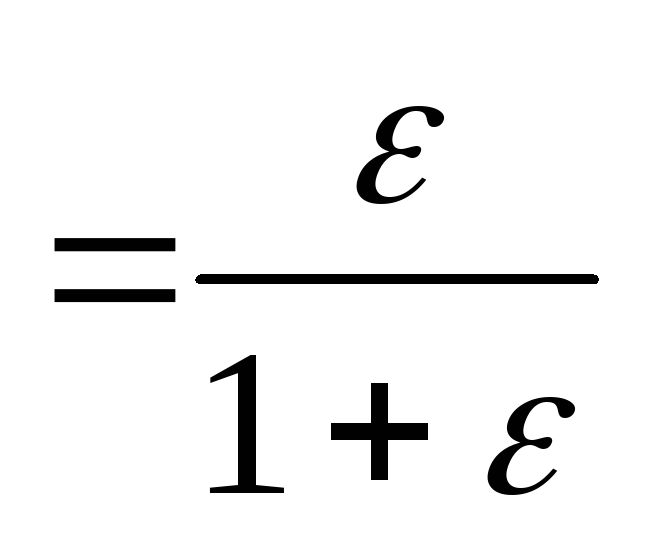ε
ε.
Чтобы найти, как изменилась разность потенциалов на пластинах первого конденсатора, вычислим отношение:
После подстановки значения ε получим
Следовательно, разность потенциалов на пластинах первого конденсатора после заполнения второго конденсатора диэлектриком возросла в 1,75 раза.
Электрическая емкость проводящей сферы
17.1. Найти электроемкость С уединенного металлического шара радиусом R=1 см.
17.2. Определить электроемкость С металлической сферы радиусом R=2 см, погруженной в воду.
17.3. Определить электроемкость С Земли, принимая ее за шар радиусом R=6400 км.
17.4. Два металлических шара радиусами R1=2 см и R2=6 см соединены проводником, емкостью которого можно пренебречь. Шарам сообщен заряд Q= 1 нКл. Найти поверхностную плотность σ зарядов на шарах.
17.5. Шар радиусом R1=6 см заряжен до потенциала φ1=300 В, а шар радиусом R2=4 см — до потенциала φ2=500 В. Определить потенциал φ шаров после того, как их соединили металлическим проводником. Емкостью соединительного проводника пренебречь.
Электрическая емкость плоского конденсатора
17.6. Определить электроемкость С плоского слюдяного конденсатора, площадь S Пластин которого равна 100 см2, а расстояние между ними равно 0,1 мм.
17.7. Между пластинами плоского конденсатора, заряженного до разности потенциалов U =600 В, находятся два слоя диэлектриков: стекла толщиной d1=7 мм и эбонита толщиной d2=3 мм. Площадь S каждой пластины конденсатора равна 200 см 2 . Найти: 1) электроемкость С конденсатора; 2) смещение D, напряженность Е поля и падение потенциала Δφ в каждом слое.
17.8. Расстояние d между пластинами плоского конденсатора равно 1,33 мм площадь S пластин равна 20 см 2 . В пространстве между пластинами конденсатора находятся два слоя диэлектриков: слюды толщиной d1=0,7 мм и эбонита толщиной d2=0,3 мм. Определить электроемкость с конденсатора.
17.9. На пластинах плоского конденсатора равномерно распределен заряд с поверхностной плотностью σ =0,2 мкКл/м 2 . Расстояние d между пластинами равно 1 мм. На сколько изменится разность потенциалов на его обкладках при увеличении расстояния d между пластинами до 3 мм?
17.10. В плоский конденсатор вдвинули плитку парафина толщиной d= 1 см, которая вплотную прилегает к его пластинам. На сколько нужно увеличить расстояние между пластинами, чтобы получить прежнюю емкость?
17.11. Электроемкость с плоского конденсатора равна 1,5 мкФ . Расстояние d между пластинами равно 5 мм. Какова будет электроемкость С конденсатора, если на нижнюю пластину положить лист эбонита толщиной d1=3 мм?
17.12. Между пластинами плоского конденсатора находится плотно прилегающая стеклянная пластинка. Конденсатор заряжен до разности потенциалов U1 = 100 В. Какова будет разность потенциалов U 2, если вытащить стеклянную пластинку из конденсатора?
Электрическая емкость сферического конденсатора
17.13. Две концентрические металлические сферы радиусами Rl=2 см и R2=2,1 см образуют сферический конденсатор. Определить его электроемкость С, если пространство между сферами заполнено парафином.
17.14. Конденсатор состоит из двух концентрических сфер. Радиус Rl внутренней сферы равен 10 см, внешней R2=10,2 см, Промежуток между сферами заполнен парафином. Внутренней сфере сообщен заряд Q=5 мкКл. Определить разность потенциалов U между сферами.
17.15. К воздушному конденсатору, заряженному до разности потенциалов U =600 в и отключенному от источника напряжения, присоединили параллельно второй незаряженный конденсатор таких же размеров и формы, но с диэлектриком (фарфор). Определить диэлектрическую проницаемость ε фарфора, если после присоединения второго конденсатора разность потенциалов уменьшилась до U1=100 В.
17.16. Два конденсатора электроемкостями С1=3 мкФ и С2=6 мкФ соединены между собой и присоединены к батарее с ЭДС. ε=120 В. Определить заряды Q1 и Q2 конденсаторов и разности
потенциалов U1 и U2 между их обкладками, если конденсаторы соединены: 1) параллельно; 2) последовательно.
17.11. Конденсатор электроемкостью С1=0,2 мкФ был заряжен, до разности потенциалов U1=320 В. После того как его соединили параллельно со вторым конденсатором, заряженным до разности потенциалов U2=450 В, напряжение U на нем изменилось до 400 В. Вычислить емкость С2 второго конденсатора.
17.18. Конденсатор электроемкостью С1=0,6 мкФ был заряжен до разности потенциалов U1=300 В и соединен со вторым конденсатором электроемкостью С2=0,4 мкФ, заряженным до разности потенциалов U1=150 В. Найти заряд ΔQ, перетекший с пластин первого конденсатора на второй.
17.19. Три одинаковых плоских конденсатора соединены последовательно. Электроемкость С такой батареи конденсаторов равна 89 пФ. Площадь S каждой пластины равна 100 см 2 . Диэлектрик -стекло. Какова толщина d стекла?
17.20. Конденсаторы соединены так, как это показано на pис. 17.1. Электроемкости конденсаторов: C1=0,2 мкФ, C2= 0,1 мкФ, C3=0,3 мкФ, С4=0,4 мкФ. Определить электроемкость С батареи конденсаторов.
17.21. Конденсаторы электроемкостями C1=0,2 мкФ, С2=0,6 мкФ, С3=0,3 мкФ, С4=0,5 мкФ соединены так, как это указано на рис. 17.2. Разность потенциалов U между точками А и В равна 320 В. Определить разность потенциалов U1и заряд Q1на пластинах каждого конденсатора (i=l, 2, ,3, 4).
17.22. Конденсаторы электроемкостями С1=10 нФ, С2 =40 нФ,. С3=2 нФ и С4=30 нФ соединены так, как это показано на рис. 17.3. Определить электроемкость с соединения конденсаторов.
17.23. Конденсаторы электроемкостями С1=2 мкФ, С2 = 2 мкФ,. С3=3 мкФ и С4=1 мкФ соединены так, как это показано на рис. 17.4.
Р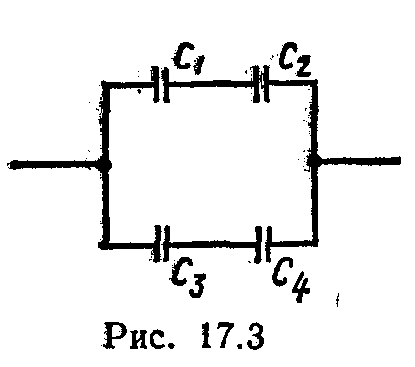
азность потенциалов на обкладках четвертого конденсатора U4 =100 В. Найти заряды и разности потенциалов на обкладках каждого конденсатора, а также общий заряд и разность потенциалов батареи конденсаторов.
17.24. Определить электроемкость схемы, представленной на рис. 17.5, где С1=1 пФ, С2 =2 пФ,. С3=2 пФ и С4=4 пФ
17.25. Пять различных конденсаторов соединены согласно схеме, приведенной на рис. 17.6. Определить электроемкость С4, при которой электроемкость всего соединения не зависит от величины электроемкости С5. Принять С1=8 пФ, С2 =12 пФ,. С3=6 пФ.
Источник
Найти электроемкость плоского конденсатора, имеющего два диэлектрика равной толщины (d = 2 мм) из слюды (Е1 = 6) и парафина (Е2 = 2) , заполнящих весь объем между обкладками.
Площадь обкладки конденсатора S = 200 см2.
На этой странице сайта вы найдете ответы на вопрос Найти электроемкость плоского конденсатора, имеющего два диэлектрика равной толщины (d = 2 мм) из слюды (Е1 = 6) и парафина (Е2 = 2) , заполнящих весь объем между обкладками?,
относящийся к категории Физика. Сложность вопроса соответствует базовым
знаниям учеников 10 – 11 классов. Для получения дополнительной информации
найдите другие вопросы, относящимися к данной тематике, с помощью поисковой
системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и
задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям.
Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы
помогут найти нужную информацию.
1 способ.
Такой конденсатор (рис. 1) можно представить в виде двух последовательно соединенных конденсаторов С1 и С2 с расстояниями между обкладками d1 и d2 и площадью обкладок S (рис. 2). Электроемкости этих конденсаторов равны
[ C_{1} = frac{ varepsilon_{0} cdot varepsilon_{1} cdot S}{d_{1}}, ; ;
C_{2} = frac{ varepsilon_{0} cdot varepsilon_{2} cdot S}{d_{2}}. ]
Тогда емкость батареи С, состоящей их двух последовательно соединенных конденсаторов, можно найти следующим образом:
[ frac{1}{C} = frac{1}{C_{1}} + frac{1}{C_{2}} =
frac{d_{1}}{varepsilon_{0} cdot varepsilon_{1} cdot S} +
frac{d_{2}}{varepsilon_{0} cdot varepsilon_{2} cdot S} =
frac{d_{1} cdot varepsilon_{2} + d_{2} cdot varepsilon_{1}}
{varepsilon_{0} cdot varepsilon_{1} cdot varepsilon_{2} cdot S}, ]
[ C = frac{varepsilon_{0} cdot varepsilon_{1} cdot varepsilon_{2} cdot S}
{d_{1} cdot varepsilon_{2} + d_{2} cdot varepsilon_{1}}. ]
Зная общее напряжение и общую электроемкость можно найти общий заряд системы
[ q = C cdot U = frac{varepsilon_{0} cdot varepsilon_{1} cdot varepsilon_{2} cdot S cdot U}{d_{1} cdot varepsilon_{2} + d_{2} cdot varepsilon_{1}}.
]
Так как конденсаторы соединены последовательно, то q1 = q2 = q. Тогда
[ U_{1} = frac{q_{1}}{C_{1}} = frac{varepsilon_{0} cdot varepsilon_{1} cdot varepsilon_{2} cdot S cdot U}{d_{1} cdot varepsilon_{2} + d_{2} cdot varepsilon_{1}} cdot frac{d_{1}}{varepsilon_{0} cdot varepsilon_{1} cdot S} = frac{varepsilon_{2} cdot d_{1} cdot U}{d_{1} cdot varepsilon_{2} + d_{2} cdot varepsilon_{1}}. ]
Напряженность электрического поля внутри первого диэлектрика (конденсатора)
[ E_{1} = frac{U_{1}}{d_{1}} = frac{varepsilon_{2} cdot U}{d_{1} cdot varepsilon_{2} + d_{2} cdot varepsilon_{1}}.
]
Аналогично находим напряженность внутри второго диэлектрика
[ E_{2} = frac{q_{2}}{C_{2}} cdot frac{1}{d_{2}} =
frac{varepsilon_{1} cdot U}{d_{1} cdot varepsilon_{2} + d_{2} cdot varepsilon_{1}}. ]
Если удалить первый диэлектрик, то изменится (уменьшится в ε1 раз) электроемкость конденсатора C1 (рис. 3). Так как система отключена от батареи, то при изменении электроемкости одного конденсатора общий заряд остается прежним.
Электроемкость второго конденсатора C2 не изменяется, поэтому при неизменном заряде, не изменяются напряжение и, следовательно, напряженность во втором диэлектрике.
Таким образом, изменение напряженности электрического поля во втором диэлектрике равно нулю.
2 способ см. здесь.
Конденсатор – радиоэлектронный прибор, способный накапливать и отдавать заряд. Как правило, на его корпусе дается информация о его емкости, но иногда требуется самому рассчитать этот номинал.
Конденсаторами могут выступать и проводники, они также обладают определенной емкостью. Для расчета существует несколько формул емкости конденсатора, их и рассмотрим.
В чем измеряется емкость конденсатора
Что такое заряд еще проходят в школе, когда эбонитовую палочку натирают о шерстяную ткань и подносят к маленьким кусочкам бумаги.
Под действием электромагнитных сил бумага прилипает к палочке. Подобный заряд накапливается в конденсаторе. Но для начала познакомимся с самим конденсатором.
Простейшим конденсатором являются две металлические пластины, разделенные диэлектриком. От качества диэлектрика зависит, как долго энергия заряженного конденсатора может сохраняться.
На этих пластинах, они еще называются обкладками, накапливается разноименный заряд. Как это происходит?
Электрический заряд, а в случае с металлами это электроны, способен перемещаться под действием электродвижущей силы (э. д. с.).
Подключая металлические пластинки к источнику тока, мы получаем замкнутую цепь, но разделенную диэлектриком. Электростатическое поле проходит этот диэлектрик, замыкая цепь, а электроны, дойдя до препятствия, останавливаются и скапливаются.
Полная статья на блоге “Электрик в доме”:
Получается, на одной обкладке наблюдается избыток электронов, и эта пластина имеет отрицательный знак, а на другой пластине электронов недостает настолько же, знак на этой обкладке, конечно же, будет положительным.
Вот теперь нужна для определения емкости конденсатора формула, определяющая, какой заряд способен разместится на конкретном конденсаторе.
В качестве единицы измерения в международной системе (СИ) емкость определяется в Фарадах.
Много это или мало – емкость в 1Ф? Чтобы конденсатор обладал емкостью в 1Ф, он должен содержать в себе заряд в 1К (кулон) и при этом напряжение между обкладками должно равняться 1 вольту.
Интересно. Что такое заряд в 1 кулон? Если два предмета, каждый из которых имеет заряд в один кулон разместить в вакууме на расстоянии один метр, то сила притяжения между ними будет равна силе притяжения землей тела массой в один миллион тонн.
Как и любая буквальная емкость один и тот же конденсатор может вмещать разное количество заряда.
Рассмотрим пример.
- В трехлитровую банку входит три литра воздуха. Его хватит для дыхания, допустим, на 3 минуты. Но если воздух закачать под каким-то давлением, то емкость так и останется три литра, однако дышать можно будет дольше. Так устроен акваланг для ныряльщиков. Получается, количество воздуха в банке зависит от давления, которое в ней создается. Точно так же есть некая зависимость между различными силами, влияющими на емкость.
Формула емкости плоского конденсатора
Прежде чем узнать, по какой формуле вычисляется емкость плоского конденсатора, рассмотрим формулу для одиночного проводника. Она имеет вид:
- где Q – заряд,
- φ – потенциал.
Как видно емкость конденсатора, формула которого здесь приведена, будет тем больше, чем больший заряд способен накапливаться на нем при незначительном потенциале. Чтобы легче это было понять, рассмотрим получившие широкое распространение плоские конденсаторы разных размеров.
Для получения качественного конденсатора важны любые мелочи:
- ровная поверхность каждой обкладки;
- обе пластинки по всей площади должны располагаться на одинаковом расстоянии;
- размеры обкладок должны быть строго идентичными;
- от качества диэлектрика, расположенного между пластинками, будет зависеть ток утечки;
- емкость напрямую зависит от расстояния между обкладками, чем оно меньше, тем больше емкость.
Теперь обратимся к плоскому конденсатору. Формула определения емкости конденсатора несколько отличается от приведенной выше:
- где S – площадь одной обкладки,
- εr – диэлектрическая проницаемость диэлектрика,
- ε0 – электрическая постоянная,
- d – расстояние между обкладками.
Электрическая постоянная выражается числом 8,854187817×10-12.
Внимание! Эта формула справедлива только тогда, когда расстояние между пластинами намного меньше их площади.
Попробуем разобраться с каждой переменной подробнее. Площадь измеряется в м2, точнее, приводится к этой величине. А вот проницаемость диэлектрика может обозначаться по-разному.
В России это εr (также означает относительная проницаемость), в англоязычной литературе встречается εa (также означает абсолютная проницаемость), а то может и вовсе использоваться без индекса, просто ε. О том, что здесь используется диэлектрическая проницаемость диэлектрика можно понять из контекста.
Дальше идет ε0. Это уже вычисленное значение, измеряемое в Ф/м. Последняя переменная – d. Измеренное расстояние также приводится к метру. Емкость конденсатора, формула которого сейчас рассматривается, показывает сильную зависимость от расстояния обкладок. Поэтому стараются это расстояние по возможности сокращать. Почему этот показатель так важен?
Идеальными условиями для получения наибольшей емкости – это отсутствие промежутка между обкладками, чего, конечно, добиться невозможно. Чем ближе находятся разноименные заряды, тем сильнее сила притяжения, но здесь возникает компромисс.
При уменьшении толщины диэлектрика, а именно он разделяет разноименные заряды, возникает вероятность его пробоя из-за разности потенциалов на обкладках. С другой стороны, как уже говорилось, при увеличении напряжения увеличивается количество зарядов. Вот и приходится выбирать между емкостью и рабочим напряжением конденсатора.
Есть другая формула для плоского переменного конденсатора:
Здесь диэлектрическая проницаемость обозначена буквой ε, π = 22/7 ≈ 3,142857142857143, d – толщина диэлектрика. Формула предназначена для конденсатора, состоящего из нескольких пластин.
Допустимая толщина диэлектрика d также зависит от εr, чем выше коэффициент, тем тоньше можно использовать диэлектрик, тем большую емкость будет иметь конденсатор. Это был самый сложный материал, дальше будет легче.
Формула емкости цилиндрического конденсатора
Теперь поговорим о том, как найти емкость конденсатора цилиндрической формы. К ним относятся конденсаторы, состоящие из двух металлических цилиндров, вставленных один в другой.
Для разделения между ними расположен диэлектрик. Формула емкости конденсатора выглядит следующим образом:
Здесь видим несколько новых переменных:
- l – высота цилиндра;
- R1 и R2 – радиус первого и второго (внешнего) цилиндров;
- ln – это не переменная, а математический символ натурального логарифма. На некоторых калькуляторах он имеется.
Всегда нужно помнить, что все величины должны приводиться к единой системе, в приведенной ниже таблице указаны международные системы единиц (СИ).
Из нее видно, что все расстояния нужно приводить к метру.
Еще стоит обращать внимание на качество диэлектрика. Если толщина диэлектрика влияет только на емкость конденсатора, то его качество затрагивает сохранность энергии. Другими словами, конденсатор с качественным диэлектриком будет иметь меньший саморазряд.
Определить качество можно по числу, стоящему возле вещества, чем оно больше, тем лучше качество. Сравнение производится по вакууму, значение которого равно единице.
Формула емкости сферического конденсатора
Последнее что осталось разобрать – формулу определения емкости конденсатора, состоящего из двух сфер. Причем одна сфера находится внутри другой. Формула имеет следующий вид:
Из приведенных переменных здесь все знакомо. Стоит обратить внимание лишь на сам конденсатор.
Кроме своей необычной формы у него есть свои особенности: внутри малой сферы никакого заряда нет, он образуется на внешней части малой сферы и внутренней части большого шара. Также заряд отсутствует и на внешней стороне внешней сферы.
Так же как и все другие конденсаторы, сферы разделены диэлектриком. Толщина и качество диэлектрика оказывают такое же влияние на емкость, как в случае с другими конденсаторами.
После того как были рассмотрены формулы, стоит испробовать их на практике. Рассмотрим, как найти емкость конденсатора каждого вида.
Примеры решения задач
Начнем с плоского конденсатора. Формула для этого вида:
Допустим, у нас есть следующие значения:
- в качестве диэлектрика возьмем слюду толщиной 0,02 мм, ε = 6;
- конденсатор квадратный со сторонами в 7 мм.
Определяем площадь пластин: 7×7 = 49 мм2.
Приводим к единой системе: 4,9×10-5 = 0,000049 м2. Толщина диэлектрика 0,02×10-5 = 0,00002 м. Электрическая постоянная 8,854187817×10-12.
Подставляем в формулу и высчитываем числитель: 6×8,854187817×10-12 ×4,9×10-5, сокращаем и решаем 6×49×8,854187817×10-17 = 2,603131218198×10-14.
Делим на толщину диэлектрика: 2,603131218198×10 / 2×10 = 1301,565609099×10 = 1,301565609099×10. Шесть нулей – это тысячи или приставка «микро», получается округлено 1,3 мкФ.
Возможно, при вычислении была допущена ошибка, но это не экзамен по математике. Важно понять сам метод вычисления.
Формула для цилиндрического конденсатора:
Выбираем значения:
- l = 1 см;
- R1 = 0,25 мм;
- R2 = 0,26 мм;
- ε = 2.
Подгоняем под единую систему: l – 1 см = 1×10-2 = 0,01 м; R1 – 0,25 мм = 0,0025 м; R2 – 0,26 мм = 0,0026 м.
Подставляем значения в числитель: 2×3,142857142857143×8,854187817×10-12×2×0,01 1,11×10-12. Находим знаменатель: 0,26:0,25 = 1,04.
Находим натуральный логарифм, он равен примерно 0,39. Числитель делим на знаменатель: 1,11×10-12/0,39 = 2,85×10-12.
Число с 12 нулями это приставка «пико», получаем 2,85 пФ.
Формула для сферического конденсатора:
Выбираем значения:
- ε= 4;
- r1= 5 см;
- r2= 5,01 см.
Снова все подгоняем: 5 см = 0,05 м; 5,01 см = 0,0501 м. Заполняем числитель. 4×3,142857142857143×4×8,854187817×10-12×0,05×0,0501 1,11×10-12 Вычисляем знаменатель: 0,0501 – 0,05 = 0,01. Производим деление: 1,11×10-12×0,01 = 1,11×10-10. Снова получили пикофарады, а именно 1,11 пФ.
Интересные статьи на канале:
Статья заинтересовала? Лайк, подписка, комментарий!
Друзья ПОДПИСЫВАЙТЕСЬ Дзен на канал, а также заходите на блог https://electricvdome.ru 👍!
#конденсатор #емкость #формула
