Энергия активации как найти в химии

Эне́ргия актива́ции в химии — эмпирически определяемый параметр, характеризующий показательную зависимость константы скорости реакции от температуры^[1]. Выражается в джоулях на моль. Термин введён Сванте Августом Аррениусом в 1889. Типичное обозначение энергии активации:

Энергия активации в физике — минимальное количество энергии, которое должны получить электроны донорной примеси, для того чтобы попасть в зону проводимости.

В химической модели, известной как теория активных соударений (ТАС), есть три условия, необходимых для того, чтобы произошла реакция:

• Молекулы должны столкнуться. Это важное условие, однако его не достаточно, так как при столкновении не обязательно произойдёт реакция.
• Молекулы должны обладать необходимой энергией (энергией активации). В процессе химической реакции взаимодействующие молекулы должны пройти через промежуточное состояние, которое может обладать большей энергией. То есть, молекулы должны преодолеть энергетический барьер; если этого не произойдёт, реакция не происходит.
• Молекулы должны быть правильно ориентированы относительно друг друга.

При низкой (для определённой реакции) температуре большинство молекул обладают энергией меньшей, чем энергия активации, и неспособны преодолеть энергетический барьер. Однако в веществе всегда найдутся отдельные молекулы, энергия которых значительно выше средней. Даже при низких температурах большинство реакций продолжают идти. Увеличение температуры позволяет увеличить долю молекул, обладающих достаточной энергией, чтобы преодолеть энергетический барьер. Таким образом повышается скорость реакции.

Для большинства реакций кДж/моль.

Математическое описание[править | править код]

Уравнение Аррениуса устанавливает связь между энергией активации и скоростью протекания реакции:

,

где k — константа скорости реакции,

 — предэкспоненциальный множитель (фактор частоты) для реакции,

 — универсальная газовая постоянная,

 — температура в кельвинах.

С повышением температуры растёт вероятность преодоления энергетического барьера.

Для количественного описания температурных эффектов в химической кинетике для приближённых вычислений кроме уравнения Аррениуса используют правило Вант-Гоффа: повышение температуры на 10 К увеличивает для большинства реакций скорость в 2—4 раза (для биохимических реакций 7—9 раз). Математически это означает, что скорость реакции зависит от температуры как показательная функция:

,

где  — температурный коэффициент скорости (его значение лежит в интервале от 2 до 4, для биохимических реакций до 9),

 — скорости реакции при температурах .

Правило Вант-Гоффа является весьма приближённым и применимо только в очень ограниченном интервале температур: от 10 до 400 °С, а также при энергии активации от 60 до 120 кДж/моль. Правило Вант-Гоффа дает неверные результаты для крупных молекул, например, белков и полимеров.

Переходное состояние[править | править код]

Переходное состояние — состояние системы, при котором уравновешены разрушенные и созданные связи. В переходном состоянии система находится в течение небольшого (10⁻¹⁵ с) времени. Энергия, которую необходимо затратить, чтобы привести систему в переходное состояние, называется энергией активации. В многоступенчатых реакциях, которые включают в себя несколько переходных состояний, энергия активации соответствует наибольшему значению энергии. После преодоления переходного состояния молекулы вновь разлетаются с разрушением старых связей и образованием новых или с преобразованием исходных связей. Оба варианта возможны, так как происходят с высвобождением энергии (это хорошо видно на рисунке, поскольку оба положения лежат энергетически ниже энергии активации). Существуют вещества, способные уменьшить энергию активации для данной реакции. Такие вещества называют катализаторами. В биологических реакциях в качестве катализаторов выступают ферменты.

Утверждение о том, что катализатор снижает энергию активации, строго говоря, не корректно, так как реакция в присутствии катализатора не идентична исходной реакции^[2]. Это совершенно иная реакция, имеющая более низкий активационный барьер.

См. также[править | править код]

• Скорость химической реакции
• Квантовое туннелирование
• Катализаторы

Примечания[править | править код]

Ссылки[править | править код]

• Activation Energy (англ.)
• Основы биохимии. Физическая химия.

Лекция
по теме «Зависимость
скорости химической реакции

от
температуры»

Учебные
вопросы

1. Уравнение
   Аррениуса

2. Энергия
   активации

3. Распределение
   молекул по энергиям

4. Энтропия
   активации. Стерический фактор

5. Решение
   уравнения Аррениуса

1.
Уравнение Аррениуса

В
большинстве случаев, скорость химической
реакции увеличивается при повышении
температуры.
При этом возрастает константа скорости
реакции.

Зависимость
константы скорости реакции от температуры
выражается уравнением Аррениуса:

,

(1)

где
k
– константа скорости реакции;

A
– константа, называемая предэкспоненциальным
множителем;

– основание натурального логарифма;

Е_a
– энергия
активации,
Дж/моль;

Т
– температура, К;

R
– газовая постоянная, 8,31 Дж/мольК.

2. Энергия
активации

Для
того чтобы произошла реакция, необходимо
преодолеть отталкивание электронных
оболочек молекул и разорвать или ослабить
связи между атомами. На это надо затратить
определенную энергию.

Избыточная
энергия (по сравнению со средней энергией
при данной температуре), которой должны
обладать молекулы, для протекания
реакции, называется энергией активации.

Молекулы,
обладающие такой энергией, называются
активными
молекулами.

В
ходе реакции вещества переходят в
неустойчивое промежуточное состояние,
характеризующееся большим запасом
энергии. Именно для его образования
необходима энергия активации (рис. 1,
2).

Переходным
состоянием системы (или активированным
комплексом) называется состояние системы
реагирующих веществ, соответствующее
максимальной энергии на пути реакции.

Энергия
активации – это количество дополнительной
энергии, необходимой для перехода
системы из исходного состояния в
состояние активированного комплекса.

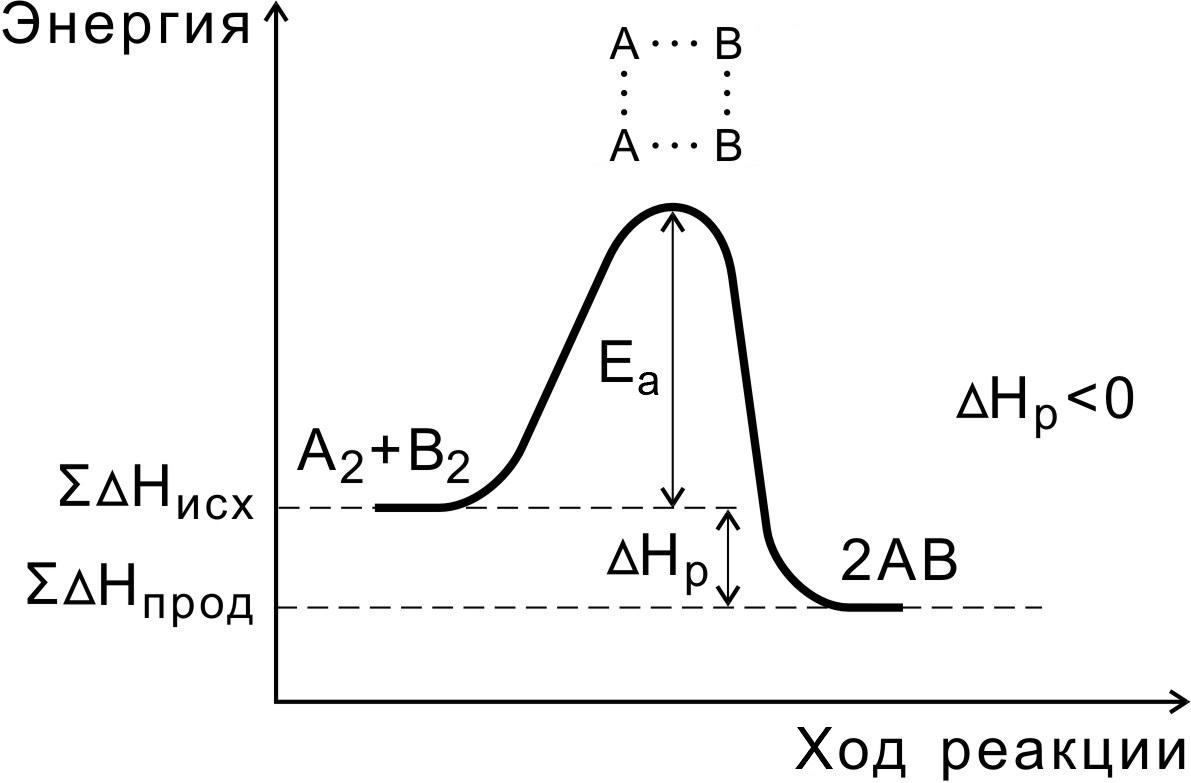
Рис. 1. Энергетическая
диаграмма экзотермической
реакции

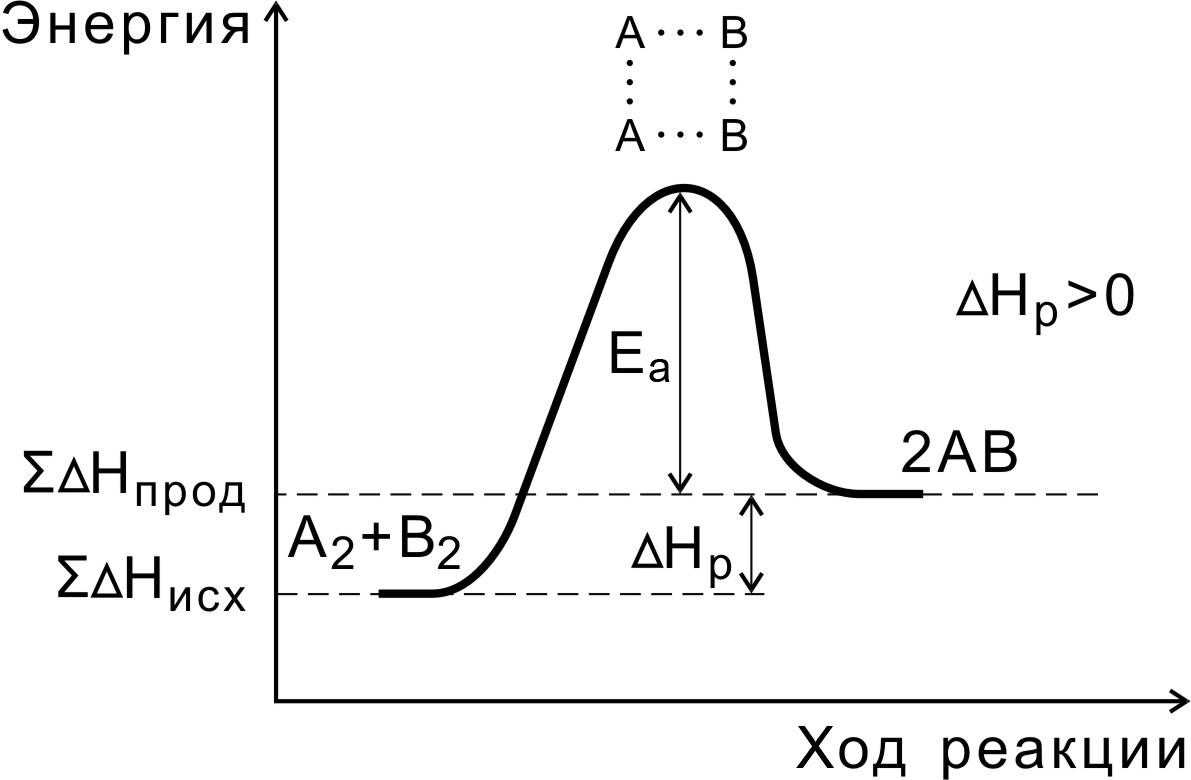
Рис. 2. Энергетическая
диаграмма эндотермической реакции

Число
частиц, входящих в активированный
комплекс, определяет молекулярность
данной стадии реакции.

В
переходном состоянии старые химические
связи ослаблены, но окончательно не
разорваны, а новые связи начали
образовываться, но еще не сформировались.
Неустойчивый активированный комплекс
(т.к. обладает избытком энергии) существует
очень короткое время. Он распадается с
образованием исходных веществ или
продуктов реакции.

Переходное
состояние возникает в ходе как прямой,
так и обратной реакции (рис. 3). Энергетически
оно отличается от исходных веществ на
величину энергии активации прямой
реакции, а от конечных – на энергию
активации обратной реакции. Разность
энергий активации прямой и обратной
реакций равна изменению внутренней
энергии (тепловому эффекту) реакции:

 

Н_р
= Е_а
– Е_а

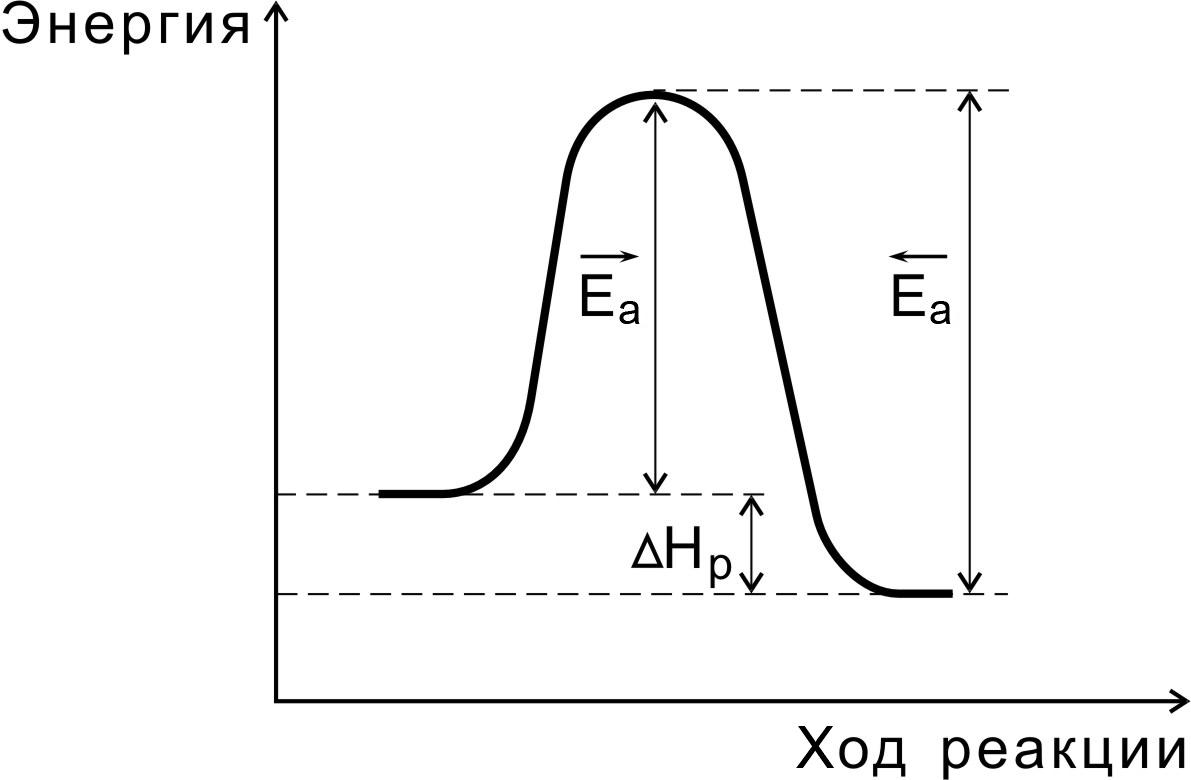
Рис.3. Соотношение между
энергиями активации прямой

и обратной реакций и
теплового эффекта

1. Распределение
   молекул по энергиям

Скорость
реакции зависит от числа молекул,
обладающих энергией, достаточной для
образования активированного комплекса.
На рис. 4 показано распределение молекул
идеального газа по кинетической энергии
согласно статистическому закону
Максвелла-Больцмана при двух разных
температурах. Доля молекул с энергией,
превышающей энергию активации Еа
(доля активных молекул), с повышением
температуры резко возрастает (площадь
заштрихованной области).

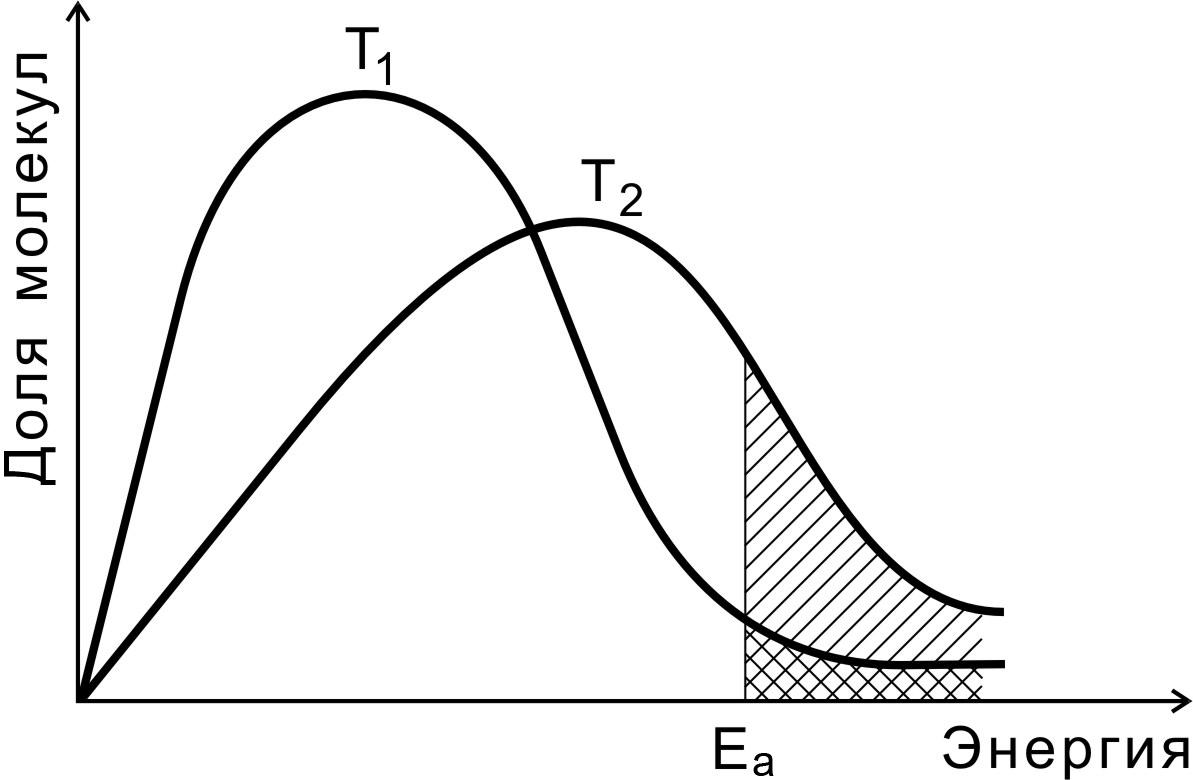
Рис. 4. Распределение
молекул по энергиям

при двух разных
температурах

Чем
выше температура, тем больше в системе
активных молекул, тем выше скорость
реакции.

1. Энтропия
   активации. Стерический фактор

Кроме
энергии активации важным условием
осуществления химической реакции
является ориентация молекул в момент
столкновения. Большую роль играют
размеры и форма молекул, место расположения
реакционно-способных атомов или групп
атомов в молекуле.

Например,
в реакции

А₂
+ B₂


2AB

ориентация
(а) реагирующих частиц при столкновении
будет более благоприятна, чем ориентация
(б) (рис. 5).

Рис.5. Благоприятная
(а) и неблагоприятная (б) ориентация

молекул при столкновении

Вероятность
необходимой для взаимодействия ориентации
молекул при столкновении

где,
n_взаим
– число способов ориентации, приводящих
к взаимодействию;

n_общ
–
общее число возможных способов
ориентации.

Энтропия
активации для 1 моля по уравнению
Больцмана

.

Вероятность
необходимой ориентации

.

Чем
больше вероятность необходимой для
реакции ориентации, т.е. чем больше
значение энтропии активации, и чем
меньше значение энергии активации, тем
выше скорость реакции и, соответственно,
константа скорости:

,
(2)

где
Z
– коэффициент пропорциональности.

Для
бимолекулярных реакций Z
– это число столкновений частиц в
единице объема за единицу времени (1с,
1 см³).

Уравнение
(2) называют основным уравнением химической
кинетики. Энергия активации и энтропия
активации являются теми факторами,
посредством которых сказывается влияние
природы реагирующих веществ на скорость
реакции.

Множитель

называется стерическим фактором (или
стерическим множителем, или фактором
вероятности).

Стерический
фактор (
)
и
частота столкновений (Z)
учитываются в уравнении Аррениуса (1)
через предэкспоненциальный множитель
(А).

5.
Решение уравнения Аррениуса

Энергию
активации можно рассчитать по
экспериментальным данным графическим
или аналитическим способами, используя
уравнение
Аррениуса

^,

представив
его в логарифмическом виде

(3)

Графический
способ

По
экспериментальным значениям константы
скорости реакции при различных
температурах строят график зависимости
lnk
= f
()
(рис. 6).

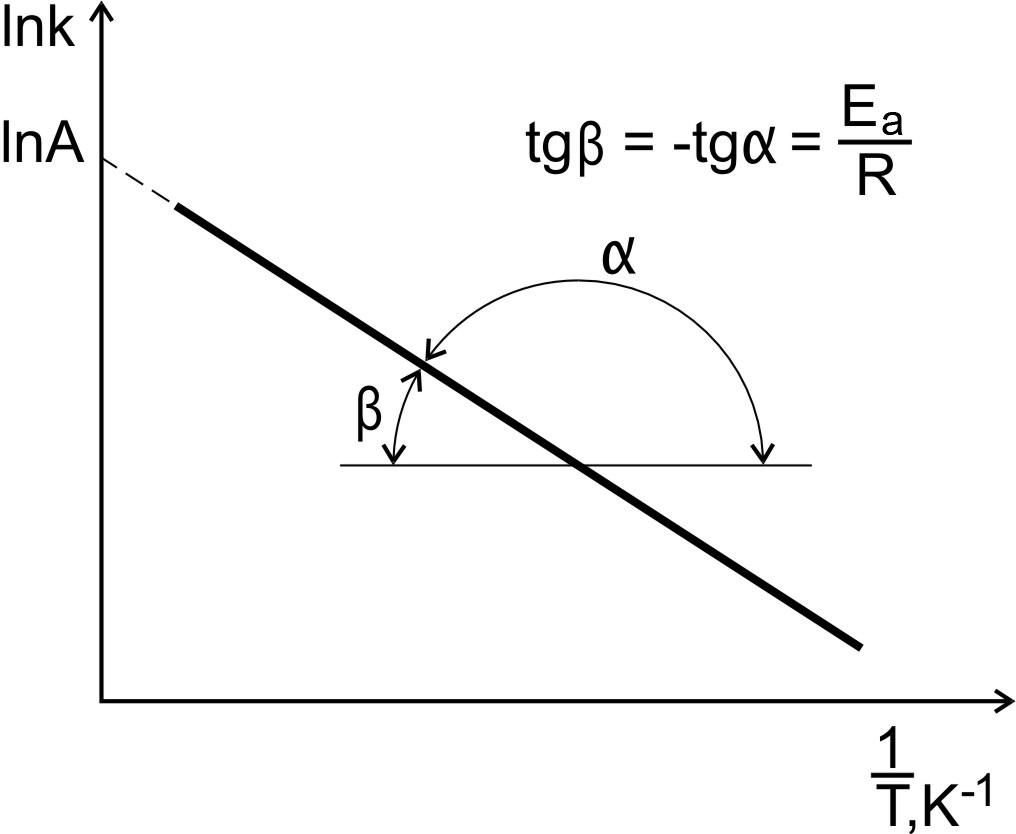
Рис. 6. Зависимость
константы скорости реакции

от температуры.

По
тангенсу угла наклона прямой к оси
абсцисс вычисляют энергию активации

,

Отрезок,
отсекаемый прямой на оси ординат при

(),
численно равен ln
А.

Аналитический
способ

Если
предположить, что для выбранной реакции
величины А
и Е_а
постоянны в небольших пределах температур
от Т₁
до
Т₂,
то уравнение Аррениуса (3) можно применить
для двух различных температур (Т₂
Т₁;
k
(Т₂)
= k₂;
k
(Т₁)
= k₁):

В
результате вычитания первого уравнения
из второго получим

,

следовательно,

.

Под
символом логарифма находится отношение
констант скоростей реакции при двух
температурах, поэтому константы можно
заменить любыми пропорциональными им
величинами при тех же температурах.
Например, вместо констант скоростей
можно подставить скорости реакции, если
исходные концентрации реагирующих
веществ при измерении скоростей в обоих
опытах были одинаковы, и скорость
изменилась только под влиянием изменения
температуры. Тогда получим следующие
выражения:

;

.

Литература

1. Глинка
   Н.Л. Общая химия. – М.: Интеграл-Пресс,
   2006. Гл.VI.

§6.2.

1. Коровин
   Н.В. Общая химия. – М.: Высш. шк., 2007. Гл.
   VII,
   §
   7.1-7.2.

2. Глинка
   Н.Л. Задачи и упражнения по общей химии.-
   М: Интеграл-Пресс, 2006, гл.V,
   §
   5.2.

9

Соседние файлы в папке Кинетика_лекции

• #
• #
• #
• #

If you buy through links on our site, we may earn a commission.

Энергия активации – это количество энергии, которое необходимо подать для протекания химической реакции. В приведенном ниже примере задачи показано, как определить энергию активации реакции по константам скорости реакции при различных температурах.

Проблема энергии активации

Наблюдалась реакция второго порядка. Константа скорости реакции при трех градусах Цельсия составила 8,9 x 10 ^-3 л/моль и 7,1 x 10 ^-2 л/моль при 35 градусах. Цельсия. Какова энергия активации этой реакции?

Решение

Энергию активации можно определить с помощью уравнения:
ln (k ₂ /k ₁ ) = E _a /R x (1/T ₁ – 1/T ₂ )
, где
E _a = энергия активации реакция в Дж/моль
R = постоянная идеального газа = 8,3145 Дж/К · моль
T ₁ и T ₂ = абсолютные температуры (в Кельвинах)
k ₁ и k ₂ = константы скорости реакции при T ₁ и T ₂

Шаг 1: преобразование температуры из градусов Цельсия до Кельвина
T = градусы Цельсия + 273,15
T ₁ = 3 + 273,15
T ₁ = 276,15 К
T ₂ = 35 + 273,15
T ₂ = 308,15 Кельвина

Шаг 2 – Найдите E _a
ln (k ₂ /k ₁ ) = E _a /R x (1/T ₁ – 1/T ₂ )
ln (7,1 x 10 ^-2 /8,9 x 10 ^-3 ) = E _a /8,3145 Дж/К · моль x (1/276,15 K – 1/308,15 K)
ln (7,98) = E _a / 8,3145 Дж/К · моль x 3,76 x 10 ^-4 K ^-1
2,077 = E _a (4,52 x 10 ^-5 моль/Дж)
E _a = 4,59 x 10 ⁴ Дж/моль
или в кДж/моль (разделить на 1000)
E _a = 45,9 кДж/моль

Ответ: Энергия активации этой реакции составляет 4,59 x 10 ⁴ Дж/моль или 45,9 кДж/моль.

Как использовать график для определения энергии активации

Другой способ вычислить энергию активации реакции – построить график ln k ( константа скорости) в зависимости от 1/T (величина, обратная температуре в Кельвинах). График будет образовывать прямую линию, выраженную уравнением:

m = – E _a /R

где m – наклон линии, Ea – энергия активации, а R – постоянная идеального газа, равная 8,314 Дж/моль-К. Если вы измеряли температуру в градусах Цельсия или Фаренгейта, не забудьте преобразовать их в градусы Кельвина, прежде чем рассчитывать 1/T и строить график..

Если бы вы построили график зависимости энергии реакции от координаты реакции, разница между энергией реагентов и продуктов была бы ΔH , в то время как избыточная энергия (часть кривой выше, чем у продуктов) будет энергией активации.

Имейте в виду, в то время как скорость большинства реакций увеличивается В зависимости от температуры в некоторых случаях скорость реакции уменьшается с увеличением температуры. Эти реакции имеют отрицательную энергию активации. Итак, хотя вы должны ожидать, что энергия активации будет положительным числом, имейте в виду, что она также может быть отрицательной.

Кто обнаружил энергию активации?

Шведский ученый Сванте Аррениус предложил термин «энергия активации» в 1880 году для определения минимальной энергии, необходимой для набора химических реагентов для взаимодействия и образования продуктов. На диаграмме энергия активации изображена как высота энергетического барьера между двумя точками минимума потенциальной энергии. Точки минимума – это энергии стабильных реагентов и продуктов.

Даже экзотермические реакции, такие как горение свечи, требуют ввода энергии. В случае возгорания горящая спичка или сильный жар запускают реакцию. Оттуда тепло, выделяющееся в результате реакции, обеспечивает энергию, чтобы сделать ее самоподдерживающейся.

Энергия активации

Для эффективного соударения молекул (частиц), приводящего к химической реакции, требуется определенная энергия.

Минимальное количество энергии, необходимое для прохождения реакции называют энергией активации.

Эта энергия требуется для достижения системой переходного состояния и образования активированного (переходного) комплекса, который превращается в продукты реакции уже самопроизвольно (примечаниеТермины “переходное состояние” и “переходный комплекс” часто используют как взаимозаменяемые, хотя переходное состояние – это уровень энергии на пути реакции, а переходный комплекс – группировка атомов, находящаяся в переходном состоянии.).

Изменение энергии реагирующей системы можно показать на примере элементарной реакции А + В АВ:

Энергия активации Е_а равна разности энергий переходного (Е_ПС) и исходного (Е_исх) состояний:

Е_а = Е_ПС – Е_исх.

Величина Е_а служит важной характеристикой любой реакции. Она зависит от природы реагирующих веществ и наличия катализатора, влияющего на энергию переходного состояния, но не зависит от температуры.

Энергия активации определяет скорость реакции: чем меньше значение Е_а, тем выше скорость реакции. Эта зависимость выражается уравнением Аррениуса, которое связывает константу скорости реакции Константа скорости реакции (k) – коэффициент пропорциональности, численно равный скорости реакции, когда произведение молярных концентраций реагентов равно 1. Константа скорости реакции зависит от температуры, от природы реагирующих веществ, но не зависит от их концентрации. с энергией активации и температурой. Уравнение Аррениуса более точно, чем правило Вант-ГоффаПравило Вант-Гоффа: “При повышении температуры на 10°С скорость реакции увеличивается в 2-4 раза”.
Это правило является приближенным и применимо лишь для ориентировочной оценки влияния температуры на скорость реакций, протекающих при температурах, близких к комнатной (энергия активации таких реакций 50-150 кДж/моль). отражает зависимость скорости (константы скорости) реакции от температуры.

В сложной реакции отдельные стадии отличаются скоростью и, соответственно, величиной E_а. Энергия, необходимая для прохождения всего процесса, определяется самой медленной – лимитирующей – стадией.

Лимитирующая стадия – элементарная стадия сложной реакции, которая имеет наиболее высокую энергию активации и протекает намного медленнее остальных, ограничивая общую скорость процесса.

Для примера рассмотрим изменение энергии в ходе двухстадийной реакции:

В данном случае стадия 1 является лимитирующей, так как имеет более высокую энергию переходного состояния ПС₁. Следовательно, для осуществления двухстадийной реакции в целом требуется энергия Е_а, активирующая стадию 1.