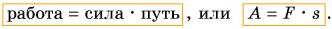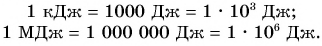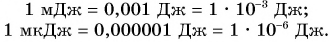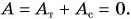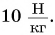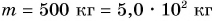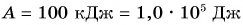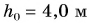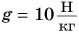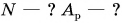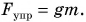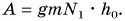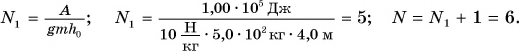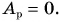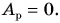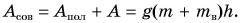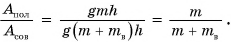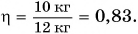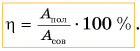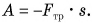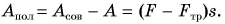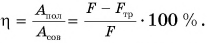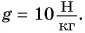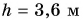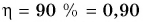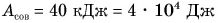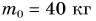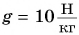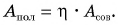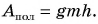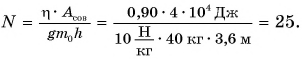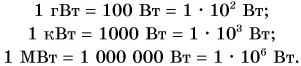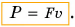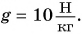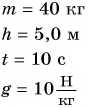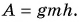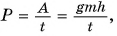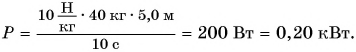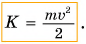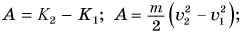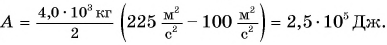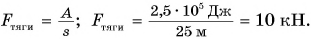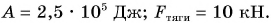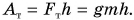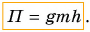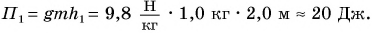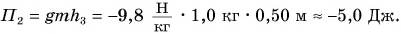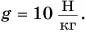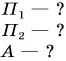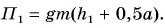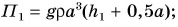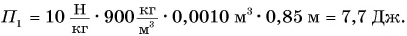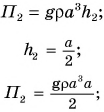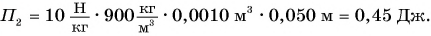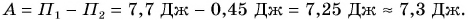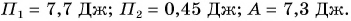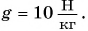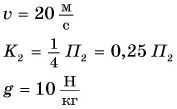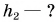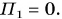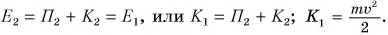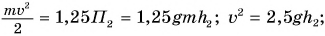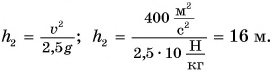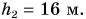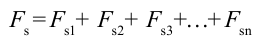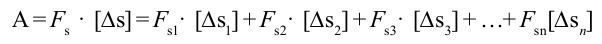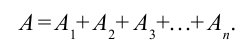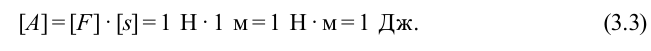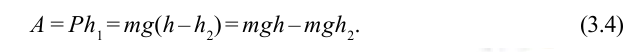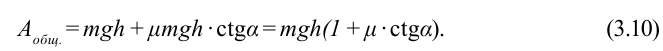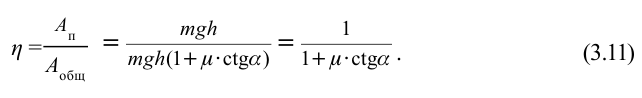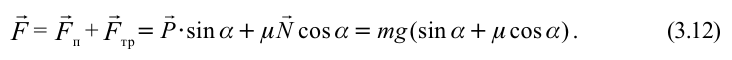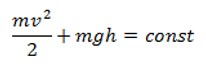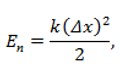| Энергия | |
|---|---|
 , ,  |
|
| Размерность |
 |
| Единицы измерения | |
| СИ | Дж |
| СГС | эрг |
Солнце является источником энергии для большей части жизни на Земле. Оно получает свою энергию главным образом от ядерного синтеза в его ядре, превращая массу в энергию, когда протоны объединяются в гелий. Эта энергия переносится на поверхность Солнца, а затем высвобождается в космос в основном в форме лучистой (световой) энергии.
Эне́ргия (др.-греч. ἐνέργεια — деятельность, действие, сила, мощь) — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой силы перехода движения материи из одних форм в другие для приведения её в состояние покоя. Введение понятия энергии удобно тем, что в случае, если физическая система является замкнутой, то её энергия сохраняется в этой системе на протяжении времени, в течение которого система будет являться замкнутой. Это утверждение носит название закона сохранения энергии.
С фундаментальной точки зрения энергия представляет собой один из трёх (наравне с импульсом и моментом импульса) аддитивных интегралов движения (то есть сохраняющихся во времени величин), связанный, согласно теореме Нётер, с однородностью времени, то есть независимостью законов, описывающих движение, от времени.
Слово «энергия» введено Аристотелем в трактате «Физика», однако там оно обозначало деятельность человека.
Используемые обозначения[править | править код]
Обычно энергия обозначается символом Е — от лат. energīa (действие, деятельность, мощь).
Для обозначения количества теплоты (величины энергии, переданной теплообменом) обычно используется символ Q — от англ. quantity of heat (количество теплоты).
Для обозначения работы, как количества переданной энергии, обычно используется символ A — от нем. arbeit (работа, труд) или символ W— от англ. work (работа, труд).
Для обозначения мощности, как количества изменения энергии за единицу времени, используют символ W.
Для обозначения внутренней энергии тела обычно используется символ U (происхождение символа подлежит уточнению).
История термина[править | править код]
Термин «энергия» происходит от греческого слова ἐνέργεια, которое впервые появилось в работах Аристотеля и обозначало действие или действительность (то есть действительное осуществление действия в противоположность его возможности). Это слово, в свою очередь, произошло от греческого ἔργον («эргон») — «работа». Праиндоевропейский корень werg обозначал работу или деятельность (ср. англ. work, нем. Werk) и в виде οργ/ουργ присутствует в таких греческих словах, как оргия или теургия и т. п.
Томас Юнг первым использовал понятие «энергия» в современном смысле слова
Прибор Джоуля для измерения механического эквивалента тепла. Нисходящий груз, прикреплённый к струне, вызывает вращение погружённого в воду весла.
Лейбниц в своих трактатах 1686 и 1695 годов ввёл понятие «живой силы» (vis viva), которую он определил как произведение массы объекта и квадрата его скорости (в современной терминологии — кинетическая энергия, только удвоенная). Кроме того, Лейбниц верил в сохранение общей «живой силы». Для объяснения уменьшения скорости тел из-за трения, он предположил, что утраченная часть «живой силы» переходит к атомам.
Маркиза Эмили дю Шатле в книге «Учебник физики» (фр. Institutions de Physique, 1740), объединила идею Лейбница с практическими наблюдениями Виллема Гравезанда.
В 1807 году Томас Юнг первым использовал термин «энергия» в современном смысле этого слова взамен понятия «живая сила»[1]. Гаспар-Гюстав Кориолис раскрыл связь между работой и кинетической энергией в 1829 году. Уильям Томсон (будущий лорд Кельвин) впервые использовал термин «кинетическая энергия» не позже 1851 года, а в 1853 году Уильям Ренкин впервые ввёл понятие «потенциальная энергия».
Несколько лет велись споры, является ли энергия субстанцией (теплород) или только физической величиной.
Развитие паровых двигателей требовало от инженеров разработать понятия и формулы, которые позволили бы им описать механический и термический КПД своих систем. Физики (Сади Карно, Джеймс Джоуль, Эмиль Клапейрон и Герман Гельмгольц), математики — все развивали идею, что способность совершать определённые действия, называемая работой, была как-то связана с энергией системы. В 1850-х годах, профессор натурфилософии из Глазго Уильям Томсон и инженер Уильям Ренкин начали работу по замене устаревшего языка механики с такими понятиями как «кинетическая и фактическая (actual) энергии»[1]. Уильям Томсон соединил знания об энергии в законы термодинамики, что способствовало стремительному развитию химии. Рудольф Клаузиус, Джозайя Гиббс и Вальтер Нернст объяснили многие химические процессы, используя законы термодинамики. Развитие термодинамики было продолжено Клаузиусом, который ввёл и математически сформулировал понятие энтропии, и Джозефом Стефаном, который ввёл закон излучения абсолютно чёрного тела. В 1853 году Уильям Ренкин ввёл понятие «потенциальная энергия»[1]. В 1881 году Уильям Томсон заявил перед слушателями[2]:
Само слово энергия, хотя и было впервые употреблено в современном смысле доктором Томасом Юнгом приблизительно в начале этого века, только сейчас входит в употребление практически после того, как теория, которая дала определение энергии, … развилась от просто формулы математической динамики до принципа, пронизывающего всю природу и направляющего исследователя в области науки.
The very name energy, though first used in its present sense by Dr Thomas Young about the beginning of this century, has only come into use practically after the doctrine which defines it had … been raised from mere formula of mathematical dynamics to the position it now holds of a principle pervading all nature and guiding the investigator in the field of science.
В течение следующих тридцати лет эта новая наука имела несколько названий, например, «динамическая теория тепла» (англ. dynamical theory of heat) и «энергетика» (англ. energetics). В 1920-х годах общепринятым стало название «термодинамика» — наука о преобразовании энергии.
Особенности преобразования тепла и работы были показаны в первых двух законах термодинамики. Наука об энергии разделилась на множество различных областей, таких как биологическая термодинамика и термоэкономика (англ. thermoeconomics). Параллельно развивались связанные понятия, такие как энтропия, мера потери полезной энергии, мощность, поток энергии за единицу времени, и так далее. В последние два века использование слова энергия в ненаучном смысле широко распространилось в популярной литературе.
В 1918 году было доказано, что закон сохранения энергии есть математическое следствие трансляционной симметрии времени, величины сопряжённой энергии. То есть энергия сохраняется потому, что законы физики не изменяются с течением времени (см. Теорема Нётер, изотропия пространства).
В 1961 году выдающийся преподаватель физики и нобелевский лауреат, Ричард Фейнман в лекциях так выразился о концепции энергии[3]:
Существует факт, или, если угодно, закон, управляющий всеми явлениями природы, всем, что было известно до сих пор. Исключений из этого закона не существует; насколько мы знаем, он абсолютно точен. Название его — сохранение энергии. Он утверждает, что существует определённая величина, называемая энергией, которая не меняется ни при каких превращениях, происходящих в природе. Само это утверждение весьма и весьма отвлечённо. Это по существу математический принцип, утверждающий, что существует некоторая численная величина, которая не изменяется ни при каких обстоятельствах. Это отнюдь не описание механизма явления или чего-то конкретного, просто-напросто отмечается то странное обстоятельство, что можно подсчитать какое-то число и затем спокойно следить, как природа будет выкидывать любые свои трюки, а потом опять подсчитать это число — и оно останется прежним.
There is a fact, or if you wish, a law, governing natural phenomena that are known to date. There is no known exception to this law—it is exact so far we know. The law is called conservation of energy; it states that there is a certain quantity, which we call energy that does not change in manifold changes which nature undergoes. That is a most abstract idea, because it is a mathematical principle; it says that there is a numerical quantity, which does not change when something happens. It is not a description of a mechanism, or anything concrete; it is just a strange fact that we can calculate some number, and when we finish watching nature go through her tricks and calculate the number again, it is the same.
Виды энергии[править | править код]
| Виды энергии: | ||
|---|---|---|
| Механическая | Потенциальная Кинетическая |
|
| ‹♦› | Внутренняя | |
| Электромагнитная | Электрическая Магнитная |
|
| Химическая | ||
| Ядерная | ||
 |
Гравитационная | |
 |
Вакуума | |
| Гипотетические: | ||
 |
Тёмная | |
| См. также: Закон сохранения энергии |
Механика различает потенциальную энергию (или, в более общем случае, энергию взаимодействия тел или их частей между собой или с внешними полями) и кинетическую энергию (энергия движения). Их сумма называется полной механической энергией.
Энергией обладают все виды полей. По этому признаку различают: электромагнитную (разделяемую иногда на электрическую и магнитную энергии), гравитационную (тяготения) и атомную (ядерную) энергии (также может быть разделена на энергию слабого и сильного взаимодействий).
Термодинамика рассматривает внутреннюю энергию и иные термодинамические потенциалы.
В химии рассматриваются такие величины, как энергия связи, химическое сродство, имеющие размерность энергии, отнесённой к количеству вещества. См. также: химический потенциал.
Энергия взрыва иногда измеряется в тротиловом эквиваленте.
Кинетическая[править | править код]
Кинетическая энергия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения. Единица измерения в СИ — джоуль. Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением.
Потенциальная[править | править код]
Потенциальная энергия 
Термин «потенциальная энергия» был введён в XIX веке шотландским инженером и физиком Уильямом Ренкином. Единицей измерения энергии в СИ является джоуль. Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии.
Электромагнитная[править | править код]
Гравитационная[править | править код]
Гравитационная энергия — потенциальная энергия системы тел (частиц), обусловленная их взаимным тяготением. Гравитационно-связанная система — система, в которой гравитационная энергия больше суммы всех остальных видов энергий (помимо энергии покоя). Общепринята шкала, согласно которой для любой системы тел, находящихся на конечных расстояниях, гравитационная энергия отрицательна, а для бесконечно удалённых, то есть для гравитационно не взаимодействующих тел, гравитационная энергия равна нулю. Полная энергия системы, равная сумме гравитационной и кинетической энергии постоянна, для изолированной системы гравитационная энергия является энергией связи. Системы с положительной полной энергией не могут быть стационарными.
Ядерная[править | править код]
Ядерная энергия (атомная энергия) — это энергия, содержащаяся в атомных ядрах и выделяемая при ядерных реакциях.
Энергия связи — энергия, которая требуется, чтобы разделить ядро на отдельные нуклоны, называется энергией связи. Энергия связи, приходящаяся на один нуклон, неодинакова для разных химических элементов и, даже, изотопов одного и того же химического элемента.
Внутренняя[править | править код]
Внутренняя энергия тела (обозначается как E или U) — это сумма энергий молекулярных взаимодействий и тепловых движений молекул. Внутреннюю энергию тела нельзя измерить напрямую. Внутренняя энергия является однозначной функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между её значениями в конечном и начальном состояниях, независимо от пути, по которому совершался переход.
Химический потенциал[править | править код]
Химический потенциал 
Энергия взрыва[править | править код]
Основная статья: Взрыв
Взрыв — физический или/и химический быстропротекающий процесс с выделением значительной энергии в небольшом объёме за короткий промежуток времени, приводящий к ударным, вибрационным и тепловым воздействиям на окружающую среду и высокоскоростному расширению газов.
При химическом взрыве, кроме газов, могут образовываться и твёрдые высокодисперсные частицы, взвесь которых называют продуктами взрыва. Энергию взрыва иногда измеряют в тротиловом эквиваленте — мере энерговыделения высокоэнергетических событий, выраженной в количестве тринитротолуола (ТНТ), выделяющем при взрыве равное количество энергии.
Энергия вакуума[править | править код]
Энергия вакуума — энергия, равномерно распределённая в вакууме и, предположительно, вызывающая отталкивание между любыми материальными объектами во Вселенной с силой, прямо пропорциональной их массе и расстоянию между ними. Обладает крайне низкой плотностью.
Осмотическая энергия[править | править код]
Осмотическая энергия — работа, которую надо произвести, чтобы повысить концентрацию молекул или ионов в растворе.
Энергия и работа[править | править код]
Энергия является мерой способности физической системы совершить работу. Например, изменение полной механической энергии тела численно равно величине механической работы, совершённой над телом. Поэтому количественно энергия и работа выражаются в одних единицах.
В специальной теории относительности[править | править код]
Энергия и масса[править | править код]
Согласно специальной теории относительности между массой и энергией существует связь, выражаемая знаменитой формулой Эйнштейна:
- где
— энергия системы;
— её масса;
— скорость света в вакууме.
Несмотря на то, что исторически предпринимались попытки трактовать это выражение как полную эквивалентность понятия энергии и массы, что, в частности, привело к появлению такого понятия как релятивистская масса, в современной физике принято сужать смысл этого уравнения, понимая под массой массу тела в состоянии покоя (так называемая масса покоя), а под энергией — только внутреннюю энергию, заключённую в системе.
Энергия тела, согласно законам классической механики, зависит от системы отсчёта, то есть неодинакова для разных наблюдателей. Если тело движется со скоростью 


Эта зависимость энергии от системы отсчёта сохраняется также в теории относительности. Для определения преобразований, происходящих с энергией при переходе от одной инерциальной системы отсчёта к другой используется сложная математическая конструкция — тензор энергии-импульса.
Зависимость энергии тела от скорости рассматривается уже не так, как в ньютоновской физике, а согласно вышеназванной формуле Эйнштейна:
- где
— инвариантная масса. В системе отсчёта, связанной с телом, его скорость равна нулю, а энергия, которую называют энергией покоя, выражается формулой:
Это минимальная энергия, которую может иметь тело, обладающее массой. Значение формулы Эйнштейна также в том, что до неё энергия определялась с точностью до произвольной постоянной, а формула Эйнштейна указывает абсолютное значение этой постоянной.
Энергия и импульс[править | править код]
Специальная теория относительности рассматривает энергию как компоненту 4-импульса (4-вектора энергии-импульса), в который наравне с энергией входят три пространственные компоненты импульса. Таким образом энергия и импульс оказываются связанными и оказывают взаимное влияние друг на друга при переходе из одной системы отсчёта в другую.
В квантовой механике[править | править код]
В квантовой механике энергия 



[6][7] Это уравнение является математическим выражением принципа корпускулярно-волнового дуализма волн и частиц для случая энергии.[8] В квантовой механике энергия двойственна времени. В частности, в силу фундаментальных причин принципиально невозможно измерить абсолютно точно энергию системы в каком-либо процессе, время протекания которого конечно. При проведении серии измерений одного и того же процесса значения измеренной энергии будут флуктуировать, однако среднее значение всегда определяется законом сохранения энергии. Это приводит к тому, что иногда говорят, что в квантовой механике сохраняется средняя энергия.
В общей теории относительности[править | править код]
В общей теории относительности время не является однородным, поэтому возникают определённые проблемы при попытке введения понятия энергии. В частности, оказывается невозможным определить энергию гравитационного поля как тензор относительно общих преобразований координат.
Энергия и энтропия[править | править код]
Внутренняя энергия (или энергия хаотического движения молекул) является самым «деградированным» видом энергии — она не может превращаться в другие виды энергии без потерь (см.: энтропия).
Физическая размерность и соотношение между единицами измерения[править | править код]
В системе физических величин LMT энергия имеет размерность 
| Единица | Эквивалент | |||
|---|---|---|---|---|
| в Дж | в эрг | в межд. кал | в эВ | |
| 1 Дж | 1 | 107 | 0,238846 | 0,624146⋅1019 |
| 1 эрг | 10−7 | 1 | 2,38846⋅10−8 | 0,624146⋅1012 |
| 1 межд. Дж[9] | 1,00020 | 1,00020⋅107 | 0,238891 | 0,624332⋅1019 |
| 1 кгс·м | 9,80665 | 9,80665⋅107 | 2,34227 | 6,12078⋅1019 |
| 1 кВт·ч | 3,60000⋅106 | 3,60000⋅1013 | 8,5985⋅105 | 2,24693⋅1025 |
| 1 л·атм | 101,3278 | 1,013278⋅109 | 24,2017 | 63,24333⋅1019 |
| 1 межд. кал (calIT) | 4,1868 | 4,1868⋅107 | 1 | 2,58287⋅1019 |
| 1 термохим. кал (калТХ) | 4,18400 | 4,18400⋅107 | 0,99933 | 2,58143⋅1019 |
| 1 электронвольт (эВ) | 1,60219⋅10−19 | 1,60219⋅10−12 | 3,92677⋅10−20 | 1 |
Источники энергии[править | править код]
Турбогенератор преобразует энергию пара под давлением в электрическую энергию
Условно источники энергии можно поделить на два типа: невозобновляемые и постоянные. К первым относятся газ, нефть, уголь, уран и т. д. Технология получения и преобразования энергии из этих источников отработана, но, как правило, неэкологична, и многие из них истощаются. К постоянным источникам можно отнести энергию солнца, энергию, получаемую на ГЭС и т. д.
| Вид ресурса | Запасы, Дж |
| Термоядерная энергия | 3,6·1026 |
| Ядерная энергия | 2·1024 |
| Химическая энергия нефти и газа | 2·1023 |
| Внутреннее тепло Земли | 5·1020 |
| Вид ресурса | Запасы, Дж |
| Солнечная энергия | 2·1024 |
| Энергия морских приливов | 2,5·1023 |
| Энергия ветра | 6·1021 |
| Энергия рек | 6,5·1019 |
Потребление энергии[править | править код]
Существует довольно много форм энергии, большинство из которых[11] так или иначе используются в энергетике и различных современных технологиях.
Темпы энергопотребления растут во всем мире, поэтому на современном этапе развития цивилизации наиболее актуальна проблема энергоэффективности и энергосбережения.
См. также[править | править код]
- Тензор энергии-импульса
- Эквивалентность массы и энергии
- Тёмная энергия
- Количество теплоты
Примечания[править | править код]
- ↑ 1 2 3 Смит, Кросби. The science of energy: a cultural history of energy physics in Victorian Britain. — The University of Chicago Press, 1998. — ISBN 0-226-76421-4.
- ↑ Томсон, Уильям. Об источниках энергии, доступных человеку для совершения механических эффектов = On the sources of energy available to man for the production of mechanical effect. — BAAS Rep, 1881. С. 513
- ↑ Richard Feynman. The Feynman Lectures on Physics. — США: Addison Wesley, 1964. — Vol. 1. — ISBN 0-201-02115-3.
- ↑ Фейнман, Ричард. Фейнмановские лекции по физике = The Feynman Lectures on Physics. — Т. 1.
- ↑ Ландау, Л. Д., Лифшиц, Е. М. Теоретическая физика. — 5-е изд. — М.: Физматлит, 2004. — Т. I. Механика. — 224 с. — ISBN 5-9221-0055-6.
- ↑ Паули, 1947, с. 11.
- ↑ Широков, 1972, с. 18.
- ↑ Широков, 1972, с. 19.
- ↑ Джоуль (единица энергии и работы) — статья из Большой советской энциклопедии. Г. Д. Бурдун.
- ↑ 1 2 Алексеев, 1978, с. 134.
- ↑ http://profbeckman.narod.ru/InformLekc.files/Inf03.pdf
Литература[править | править код]
- Добиаш А. А. Энергия // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Паули В. Общие принципы волновой механики. — М.: Гостехтеориздат, 1947. — 332 с.
- Широков Ю. М., Юдин Н. П. Ядерная физика. — М.: Наука, 1972. — 670 с.
- Пономарёв Л. И. Под знаком кванта. — М.: Наука, 1989. — 368 с. — ISBN 5-02-014049-X.
- Алексеев Г. Н. Энергия и энтропия. — М.: Знание, 1978. — 192 с.
Ссылки[править | править код]
- Энергия в Физической энциклопедии
Энергия – важнейшее понятие и термин в механике. Что такое энергия, и что она значит? Существует множество определений, и вот одно из них.
Что такое энергия?
Энергия в физике – это способность тела совершать работу.
Кинетическая энергия
Что такое кинетическая энергия?
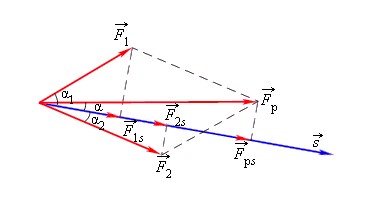
Рассмотрим тело, которое двигалось под действием каких-то сил, изменило свою скорость с v1→ до v2→. В этом случае силы, действующие на тело, совершили определенную работу A.
Работа всех сил, действующих на тело, равна работе равнодействующей силы.
Fр→=F1→+F2→
A=F1·s·cosα1+F2·s·cosα2=Fрcosα.
Как находить связь между изменением скорости тела и работой, совершенной действующими на тело силами. Для простоты будем считать, что на тело действует одна сила F→, направленная вдоль прямой линии. Под действием этой силы тело движется равноускоренно и прямолинейно. В этом случае векторы F→, v→, a→, s→ совпадают по направлению и их можно рассматривать как алгебраические величины.
Работа силы F→ равна A=Fs. Перемещение тела выражается формулой s=v22-v122a. Отсюда:
A=Fs=F·v22-v122a=ma·v22-v122a
A=mv22-mv122=mv222-mv122.
Если вычислять, то работа, совершенная силой, пропорционально изменению квадрата скорости тела.
Кинетическая энергия тела равна половине произведения массы тела на квадрат его скорости. Вот как выглядит формула кинетической энергии:
EK=mv22.
Кинетическая энергия – это энергия движения тела. При нулевой скорости она равна нулю.
Теорема о кинетической энергии
Вновь будем работать с рассмотренным примером и сформулируем теорему о кинетической энергии тела.
Работа приложенной к телу силы равна изменению кинетической энергии тела. Данное утверждение справедливо и тогда, когда тело движется под действием изменяющейся по модулю и направлению силы.
A=EK2-EK1.
Таким образом, кинетическая энергия тела массы m, движущегося со скоростью v→, будет измеряться (при измерении) и равна работе, которую сила должна совершить, чтобы разогнать тело до этой скорости.
A=mv22=EK.
Чтобы остановить тело, нужно совершить работу
A=-mv22=-EK
Потенциальная энергия
Что будет означать или обозначать кинетическая энергия?
Кинетическая энергия – это энергия движения. Наряду с кинетической энергией есть еще такой вид энергии как потенциальная энергия, то есть энергия взаимодействия тел, которая будет вычисляться и зависеть от их положения. Кинетическая и потенциальная энергии рассматриваются параллельно.
Формула потенциальной энергии:
E пот = m * g * h
Например, тело поднято над поверхностью земли. Чем выше оно поднято, тем больше будет потенциал-я энергия. Когда тело движется и падает вниз под действием силы тяжести (притяжения), эта сила совершает работу. Причем работа силы тяжести определяется только вертикальным перемещением тела и не зависит от траектории.
Вообще о потенциально энергии можно говорить только в контексте тех сил, работа которых не зависит от формы траектории тела. Такие силы называются консервативными.
Примеры консервативных сил: сила тяжести, сила упругости.
Когда тело движется вертикально вверх, сила тяжести совершает отрицательную работу.
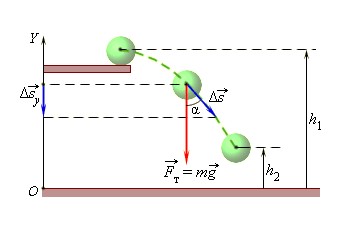
Рассмотрим вычисление на примере, когда шар переместился из точки с высотой h1 в точку с высотой h2.
При этом сила тяжести совершила работу, равную
A=-mg(h2-h1)=-(mgh2-mgh1).
Эта работа равна изменению величины mgh, взятому с противоположным знаком.
Величина ЕП=mgh – потенциальна энергия в поле силы тяжести. На нулевом уровне (на земле) потенциальную энергию тела можно не рассчитывать: она равна нулю.
Потенциальная энергия – часть полной механической энергии системы, с нахождением в поле консервативных сил. Потенциальная энергия зависит от положения точек, составляющих систему. Механическая энергия – это сумма потенциальной и кинетической энергий, которые есть в компонентах механической системы.
Можно говорить о потенциальной энергии в поле силы тяжести, потенциальной энергии сжатой пружины (пружинной энергии) и т.д.
Работа силы тяжести равна изменению потенциальной энергии, взятому с противоположным знаком.
A=-(EП2-EП1).
Ясно, что потенциальная энергия зависит от выбора нулевого уровня (начала координат оси OY). Подчеркнем, что физический смысл имеет изменение потенциальной энергии при перемещении тел друг относительно друга. При любом выборе нулевого уровня изменение потенциальной энергии будет одинаковым.
При расчете движения тел в поле гравитации Земли, но на значительных расстояниях от нее, во внимание нужно принимать закон всемирного тяготения (зависимость силы тяготения от расстояния до цента Земли). Приведем формулу, выражающую зависимость потенциальной энергии тела.
EП=-GmMr.
Здесь G – гравитационная постоянная, M – масса Земли.
Потенциальная энергия пружины
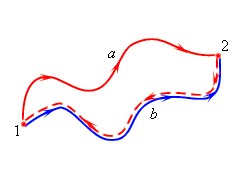
Представим, что в первом случае мы взяли пружину и удлинили ее на величину x. Во втором случае мы сначала удлинили пружину на 2x, а затем уменьшили на x. В обоих случаях пружина оказалась растянута на x, но это было сделано разными способами.
При этом работа силы упругости при изменении длины пружины на x в обоих случаях была одинакова и равна
Aупр=-A=-kx22.
Величина Eупр=kx22 называется потенциальной энергией сжатой пружины. Она равна работе силы упругости при переходе из данного состояния тела в состояние с нулевой деформацией.
Если перед вами часто поднимается вопрос определения и характеристики энергии, как явления, вам стоит подумать о сохранении описанной выше информации.
Содержание:
Работа, мощность и энергия:
Мы часто слышим от друзей: «Я сегодня выполнил большую работу: выучил наизусть стихотворение и решил пять задач по математике». Но с точки зрения физики никакой работы не совершено, даже если выучить наизусть целую поэму. Что же такое работа в физике?
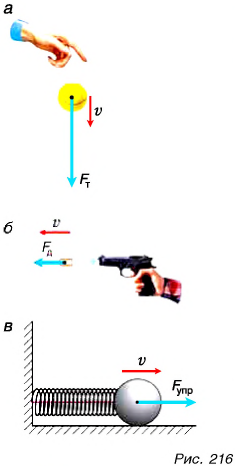
В физике работа оценивает то, что вызвала сила, действуя на движущееся тело. Покажем это на примерах. Рассмотрите внимательно рисунок 216. Что общего в результатах действия силы тяжести на мяч (рис. 216, а), силы давления газа на пулю в пистолете (рис. 216, б) и силы упругости сжатой пружины на шарик (рис. 216, в) после пережигания нити? Все перечисленные силы вызывают разгон тел (мяча, пули, шарика), т. е. увеличение скорости движения.
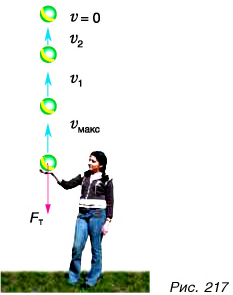
Л может ли сила, действующая на движущееся тело, уменьшать его скорость? Подбросьте мяч и наблюдайте за его движением вверх (рис. 217). Теперь сила тяжести уменьшает скорость его движения. Во всех случаях, когда сила изменяет скорость движения (увеличивает или уменьшает), говорят, что сила совершает механическую работу.
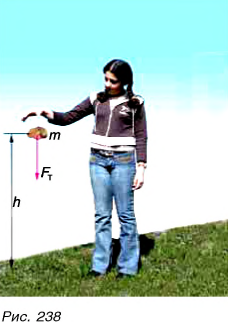
Механическая работа является физической величиной. Ее значение можно рассчитать. Рассмотрим самый простой случай: направление силы совпадает с направлением движения. Например, идет разгон спортивных саней (рис. 218). Изменение скорости саней, а значит, и работа по их разгону зависят от значения действующей силы (силы спортсменов, разгоняющих сани) и от пройденного санями пути. Чем больше сила и путь, тем большая совершается работа. Этот вывод справедлив для всех движущихся под действием силы тел.
Таким образом, механическая работа — физическая величина, пропорциональная действующей на тело силе и пройденному пути.
Обозначим работу буквой А. Тогда, если направление силы совпадает с направлением движения тела,
Единицей работы в СИ является 1 джоуль (1 Дж). Названа она в честь известного английского физика Дж. П. Джоуля. Один джоуль — это работа, совершаемая силой 1 Н на пути 1 м.
1 джоуль = 1 ньютон • 1 метр.
Для измерения большой работы используют кратные джоулю единицы:
В случае малой работы применяются дольные единицы:
Из формулы работы следует, что если есть силы, но нет движения, то нет и работы. Например, сила тяжести, действующая на лежащий на столе мяч (рис. 219, а), работы не совершает, а в случае падающего мяча (рис. 219, б) — совершает.
Сила не всегда увеличивает скорость движения тела. Так, при движении мяча вверх (см. рис. 217) сила тяжести замедляет его движение. Аналогично при скольжении шайбы по льду сила трения уменьшает скорость движения шайбы. Работу силы (тяжести, трения) в подобных случаях считают отрицательной.
Но положительная и отрицательная работы могут совершаться одновременно и даже быть равными по абсолютной величине. В этом случае скорость движения постоянна. Например, электропоезд на данном участке пути движется равномерно. Это значит, что равнодействующая сил (тяги двигателя и сопротивления движению) равна нулю. По и сила тяги, и сила сопротивления совершают работу. Только работа силы тяги 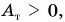
Главные выводы:
- Механическая работа характеризует результат действия силы на движущееся тело и пропорциональна действующей на тело силе и пройденному телом пути.
- Силы, ускоряющие движение тела; совершают положительную работу.
- Силы, замедляющие движение тела, совершают отрицательную работу.
- Единица работы в СИ — 1 джоуль (1 Дж).
Пример решения задачи:
Подъемный кран равномерно поднимает с земли бетонную плиту массой m = 500 кг на один из этажей строящегося дома. Сила упругости троса при этом совершает работу А = 100 кДж. Определите, на какой этаж была поднята плита, если высота одного этажа 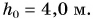
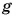
Дано:
Решение:
При равномерном подъеме сила упругости троса равна силе тяжести, действующей на плиту:
Работа силы упругости 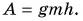
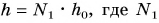
Отсюда
Так как движение плиты равномерное, то равнодействующая сил, приложенных к ней, 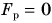
Ответ: плита поднята на 6-й этаж; работа равнодействующей сил
Полезная и совершённая работа
Оценивая работу машины, механизма и др., говорят об их коэффициенте полезного действия (КПД). Но что такое КПД? Что означают слова «полезного действия»? А что такое неполезное действие?
Рассмотрим ситуацию: идет уборка картофеля на поле. Фермер поднимает картофель в ведре в кузов автомашины (рис. 221), выгружает, а ведро опускает на землю. Механическую работу совершает мускульная сила фермера, поднявшего ведро массой, например, 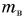
Цель фермера — погрузить в кузов картофель. Исходя из этого, полезной работой является работа по подъему картофеля: 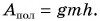
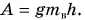
Какую долю составляет полезная работа от совершенной?
Обозначим отношение 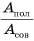
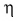
КПД, как правило, выражают в процентах.
Таким образом, КПД (эффективность работы) в данном случае равен 83 %.
Рассмотрим еще один пример. Дети разгоняют санки, действуя силой F в направлении их движения (рис. 222). Совершенная (полная) работа здесь 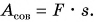
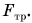
Полезной же работой была
Тогда доля полезной работы (КПД)
Физическая величина, равная отношению полезной работы к совершенной (полной), называется коэффициентом полезного действия.
А могут ли механизм, машина, человек работать так, чтобы КПД = 100 %, т. е. чтобы вся совершенная работа была полезной?
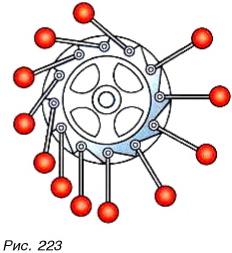
Ученые неоднократно пытались создать такую машину (рис. 223), но все попытки оказались безуспешными. (Самостоятельно познакомьтесь в Интернете или справочной литературе с информацией о вечном двигателе.) В работе любой машины, механизма всегда есть неполезная работа, идущая на преодоление трения, сопротивления. А значит, КПД всегда меньше 100 %. А вот сделать неполезную работу минимальной означает повысить КПД.
Главные выводы:
- Совершенная (т. е. полная) механическая работа всегда больше полезной.
- КПД показывает, какую долю составляет полезная работа от всей совершенной.
- Чем больше полезная работа, тем выше КПД.
- КПД всегда меньше 100 %.
Пример решения задачи:
При подъеме картофеля из хранилища глубиной h = 3,6 м подъемным устройством с КПД 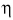
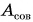
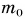
Дано:
Решение:
Зная совершенную работу и КПД, можно найти полезную работу по подъему мешков картофеля:
Полезная работа – это работа подъемного устройства по преодолению силы тяжести, действующей на картофель:
Масса 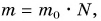
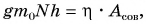
Ответ: N = 25 мешков.
Мощность и единицы мощности
Приобретая автомобиль (рис. 226), газонокосилку, микроволновую печь (рис. 227) и др., человек интересуется их мощностью. Именно мощность является паспортной характеристикой машин и механизмов. Что же такое мощность? Почему так важно ее знать?
Рассмотрим пример. Человек лопатой копает яму для погреба в течение нескольких дней. Такую же яму экскаватор (рис. 228) выкопает за несколько минут. Работа выполняется одинаковая. Одинаковая масса грунта поднимается на одну и ту же высоту. Но быстрота совершения работы человеком и экскаватором разная. За единицу времени экскаватор выполняет во много раз большую работу, чем человек. Для описания быстроты совершения работы вводится мощность.
Физическая величина, равная отношению работы к промежутку времени, за который эта работа совершена, называется мощностью. Обозначается мощность буквой Р.
За единицу мощности в СИ принимается мощность, при которой действующая на тело сила за время t = 1 с совершает работу А = 1 Дж. Эта единица мощности называется ватт (Вт) в честь английского изобретателя Дж. Уатта. Для измерения больших мощностей используют кратные единицы: гектоватт (гВт), киловатт (кВт), мегаватт (МВт). Обратите внимание:
Для малых мощностей употребляются дольные единицы — милливатт (мВт), микроватт (мкВт):
В быту часто необдуманно единицу мощности киловатт принимают за единицу работы. Но работа 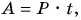
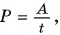
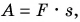
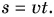
Мощность пропорциональна силе, совершающей работу, и скорости движения. Тогда при постоянной мощности чем меньше скорость, тем больше сила. Вот почему водитель, трогаясь с места или поднимаясь в гору (рис. 229), когда требуется большая сила, едет на малой скорости. Тем самым он увеличивает силу тяги двигателя автомобиля.
Главные выводы
- Мощность — физическая величина, характеризующая быстроту совершения работы.
- Единицей мощности в СИ является 1 ватт.
- Одинаковую мощность можно получить либо при большой скорости и небольшой силе, либо при малой скорости и большой силе.
Для любознательных
В автомобилестроении по традиции используют старинную единицу мощности — лошадиную силу (л. с.). С помощью рисунка сформулируйте самостоятельно определение мощности в 1 лошадиную силу.
Запишем связь 1 л. с. и ватта: 1 л. с. = 736 Вт.
В этих внесистемных единицах мощность первого белорусского трактора МТЗ-2 (1953 г.) была равна 37 л. с. Освоенный в 2010 г. трактор «Беларус-3023» имеет двигатель мощностью 300 л. с. Переведите эти знамения мощности в единицы СИ самостоятельно и сравните их.
Пример решения задачи:
На уроке физкультуры мальчик массой m = 40 кг поднялся по канату на высоту h = 5,0 м за промежуток времени t = 10 с. Определите среднюю мощность, развиваемую мальчиком при подъеме. Коэффициент
Дано:
Решение:
При подъеме по канату работа мускульной силы рук идет на преодоление силы тяжести.
Тогда
Ответ: P = 0, 20 кВт.
Кинетическая энергия
Энергия — одно из наиболее важных и сложных понятий. Причем не только в физике, но и в других науках. А что же такое кинетическая энергия?
Рассмотрим два примера. Шайба, попадая в сетку ворот (рис. 230), прогибает ее. Молот для забивания свай (рис. 231), падая на сваю, загоняет ее в землю на некоторую глубину. Чтобы сильнее прогнуть сетку или глубже забить сваю, шайба и молот должны иметь большую скорость. И шайба, и молот совершили работу. При этом скорость их движения изменилась (уменьшилась до нуля). Совершенные ими работы были разными, даже если предположить, что скорости движения были одинаковыми. Но массы молота и шайбы не равны.
Если тело способно совершить работу, то оно обладает энергией. В физике энергию движущегося тела называют кинетической (от греч. kinetikos — приводящий в движение). Кинетическая энергия обозначается буквой К (или 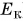
Большая кинетическая энергия движущихся тел — камня, автомобиля, железнодорожного состава (рис. 232), метеорита и др. — означает, во-первых, что при разгоне их до данной скорости разгоняющей силой была совершена большая работа и, во-вторых, при их остановке тормозящей силой будет совершена такая же большая работа.
Из примеров следует, что кинетическая энергия зависит от массы тела и скорости его движения. Какой является эта зависимость?
Опыты показывают, что кинетическая энергия прямо пропорциональна массе тела и квадрату скорости его движения:
Увеличение скорости движения тела, например в 4 раза, приводит к возрастанию кинети- Обратите внимание! ческой энергии в 16 раз. Об этом должны всегда помнить водители и пешеходы.
Главные выводы:
- Кинетическая энергия выражает способность движущихся тел совершать работу.
- Кинетическая энергия, как и работа, измеряется в джоулях.
- Кинетическая энергия тела зависит от его массы и скорости.
- Изменить (увеличить или уменьшить) кинетическую энергию тела можно только путем совершения работы (положительной или отрицательной).
Пример решения задачи:
Скорость движения груженого автомобиля массой m = 4,0 т увеличилась от 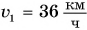
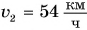
Дано:
Решение:
Чтобы увеличить кинетическую энергию от 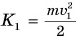
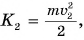
Но работа 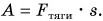
Ответ:
Потенциальная энергия
При разгоне любого тела (санок, автомобиля и др.) у него возникает способность совершить механическую работу — у движущегося тела появляется кинетическая энергия. А если тело неподвижно? Обладает ли оно способностью совершить работу?
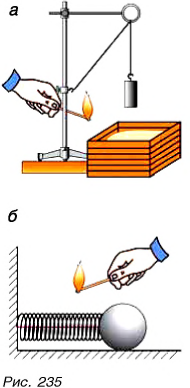
Проведем два опыта. В первом поднимем и укрепим на нити над ящиком с песком гирю (рис. 235, а). Во втором между упором и шариком поместим предварительно сжатую и связанную ниткой пружину (рис. 235, б). Оба тела (гиря и пружина) неподвижны 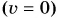
Важно понимать, что потенциальная энергия не появляется сама по себе. В этих опытах гиря была поднята над столом, пружина была сжата какой-то силой. Значит, чтобы тело запасло потенциальную энергию, необходимо совершить работу. Чем сильнее будет сжата пружина, чем выше будет поднято тело, тем больше у них будет запас потенциальной энергии. Тела, представленные на рисунке 236, уже обладают потенциальной энергией. У трамплина она вызвана прогибом (деформацией) доски, у мышеловки — закручиванием пружины, у лука — изменением расположения древка и тетивы. Из этих и других примеров следует, что потенциальная энергия — это энергия, обусловленная взаимным расположением взаимодействующих тел или частей тела (гири и Земли, стрелы и тетивы, звеньев пружины). Обозначается потенциальная энергия буквой П (или 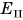
Именно благодаря потенциальной энергии сжатой (закрученной) пружины работают механические часы, реле времени микроволновых печей, стиральных машин, движутся некоторые детские игрушки. Потенциальная энергия поднятой с помощью плотины воды заставляет работать гидроэлектростанции (рис. 237).
Главные выводы:
- Неподвижные взаимодействующие тела (система тел) могут обладать способностью совершать механическую работу, а значит, потенциальной энергией.
- Значение потенциальной энергии зависит от взаимного расположения взаимодействующих тел (частей тела).
- Потенциальная энергия изменяется только при совершении работы.
Расчет потенциальной энергии
Кинетическая энергия тела, зависящая от его массы и скорости, выражается формулой 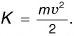
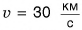
Рассмотрим отдельно два случая: потенциальную энергию притяжения поднятого над поверхностью Земли тела и потенциальную энергию деформированного тела.
В первом случае формулу для расчета потенциальной энергии легко вывести. Если тело массой m поднято относительно поверхности Земли на высоту h (рис. 238), то при его падении сила тяжести 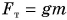
Это и есть потенциальная энергия поднятого тела:
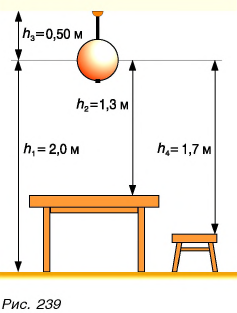
Значение потенциальной энергии относительно. Так, относительно пола потенциальная энергия светильника (рис. 239) массой m = 1,0 кг, центр тяжести которого расположен на высоте 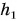
Относительно потолка 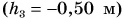
Поэтому, приводя значение потенциальной энергии, необходимо указывать уровень, относительно которого она задана, — нулевой уровень потенциальной энергии (это может быть, к примеру, поверхность пола, потолка, стола и т. д.).
Гораздо сложнее дело обстоит с расчетом потенциальной энергии деформированного тела. Мы можем растянуть или сжать пружину, изогнуть или закрутить ее (рис. 240). Потенциальная энергия у пружины будет в каждом из этих случаев. И чем больше упругая деформация, тем больше потенциальная энергия пружины. В данном примере расчет потенциальной энергии придется вести по различным формулам. Более детально с этим вы будете знакомиться в 9-м классе.
Главные выводы:
- Потенциальная энергия притяжения тела к Земле зависит от массы тела и высоты его подъема над нулевым уровнем энергии.
- Значение потенциальной энергии тела зависит от выбора нулевого уровня энергии.
- Потенциальная энергия деформированного тела зависит от величины деформации.
Пример решения задачи:
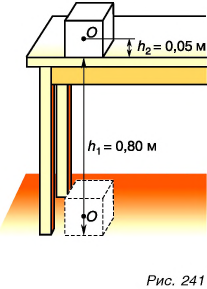
Парафиновый однородный кубик с длиной ребра а = 10 см лежит на столе на высоте 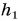
Дано:
Решение:
Потенциальная энергия кубика относительно поверхности пола (рис. 241) определяется положением его центра (точки O):
Масса кубика 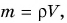
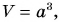
Потенциальная энергия кубика относительно поверхности стола:
Работа по подъему кубика на высоту 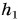
Ответ:
Закон сохранения механической энергии
Кинетическая и потенциальная энергии — это два вида механической энергии. Связаны ли они друг с другом? И если да, то в чем выражается эта связь?
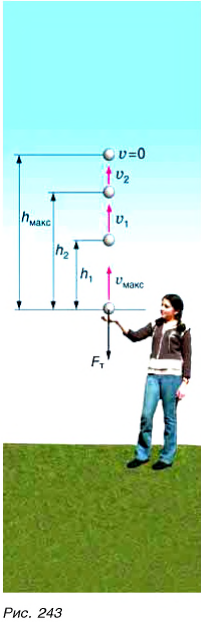
Проследим за движением брошенного вверх металлического шарика (рис. 243). В нижней точке траектории сила действия руки на шарик сообщает ему кинетическую энергию. Шарик движется вверх. Скорость его движения, а значит, и кинетическая энергия уменьшаются. Но исчезает ли кинетическая энергия бесследно? Поднимаясь выше, шарик приобретает все большую потенциальную энергию (вспомните: 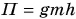
Если сопротивление воздуха мало (и им можно пренебречь), брошенный вверх шарик возвращается назад практически с такой же, как в момент бросания, скоростью и кинетической энергией.
А каким будет значение механической энергии шарика в промежуточных точках? Например, на высоте 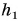
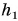
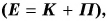
Если силами трения или сопротивления движению нельзя пренебречь, этот закон не выполняется. Заменим в опыте металлический шарик на пенопластовый брусок такой же массы (рис. 244). Мы увидим, что даже при большей, чем у металлического шарика, начальной скорости он не поднимется на такую же высоту и вернется назад с заметно меньшей скоростью. Убывает кинетическая энергия движущейся по горизонтальной поверхности льда шайбы, но потенциальная энергия взамен не появляется. За счет кинетической энергии шайбы совершается работа против сил трения.
В заключение заметим, что явление превращения энергии из одного вида в другой человек научился использовать в практических целях. Энергия падающей воды приводит в действие водяные мельницы и гидроэлектростанции. В Республике Беларусь успешно реализуется государственная программа использования энергии рек. Важная роль в ней отводится таким рекам, как Неман и Западная Двина. Па Немане работает Гродненская ГЭС мощностью 17 МВт. Установленная мощность Витебской ГЭС на Западной Двине — 40 МВт.
Кинетическую энергию ветра человек с давних времен начал использовать с помощью паруса (рис. 245), затем стал применять в ветряных мельницах. В последние годы в нашей стране начато сооружение ветроэлектростанций (рис. 246). Они уникальны тем, что не оказывают вредного воздействия на окружающую среду. Во многих странах успешно используют энергию приливов и отливов вод морей и океанов. Там созданы приливные электростанции.
Главные выводы:
- Кинетическая и потенциальная энергии взаимо-превращаемы.
- При отсутствии сил трения и сопротивления движению полная механическая энергия тела (системы тел) сохраняется.
- Закон сохранения механической энергии не выполняется, если силами трения (сопротивления) нельзя пренебречь.
- Заказать решение задач по физике
Пример решения задачи:
Камень бросили вертикально вверх со скоростью 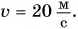
Дано:
Решение:
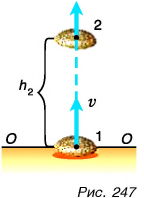
За нулевой уровень потенциальной энергии примем уровень O – O, проходящий через точку бросания камня (рис. 247). Значит,
Полная механическая энергия камня в точке бросания 1:
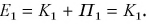
Полная механическая энергия камня в точке 2:
По условию 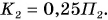
Ответ:
Энергия и работа
Энергия – эта количественная мера различных форм движения и взаимодействия (по гречески слово «энергия» означает действие). Энергия в зависимости от вида движения в природе проявляется по-разному. Например, механическая, тепловая, электромагнитная, ядерная энергия и другие. В результате взаимодействия энергия одного вида превращается в энергию другого вида. Однако во всех этих процессах энергия, переданная от одного тела второму (независимо от ее вида), будет равна энергии, полученной вторым телом от первого.
Как известно из второго закона Ньютона, чтобы изменить механическое движение тела на него должны подействовать другие тела. Иначе говоря, среди этих тел происходит обмен энергиями. Для описания такого обмена энергии в механике введено понятие механическая работа, которую принято обозначать буквой 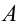
Механическая работа. Величина, равная скалярному произведению силы на перемещение в направлении действия силы, называется механической работой, т.е.
Здесь: 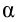
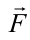
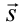
Если учитывать, что 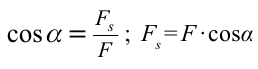
Здесь 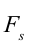
Основываясь на выражении (3.2), можно сделать следующий вывод:
если 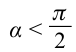
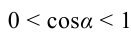
если 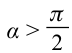
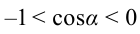
если 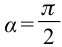
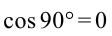
Работа считается аддитивной (аддитив – по-латински означает суммарный) величиной (в физике аддитивность величины означает, что величина, относящаяся к системе в целом, равна сумме величины, относящихся к ее составным частям).
Если на тело действует несколько сил, то будет:
тогда полная работа равна работе, выполненной равнодействующей сил.
или
Единица работы. Единица измерения работы в системе СИ – Джоуль (Дж):
В качестве единицы работы в СИ принята работа выполненная силой 1Н при смещении тела на 1 м.
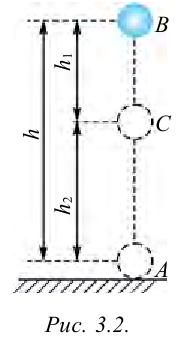
Работа силы тяжести. На поверхности Земли на тело действует сила тяжести со стороны Земли, равная 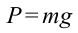
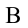
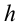
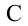
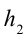
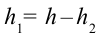
Здесь выполненная силой тяжести работа выражается следующей формулой:
Здесь: 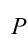
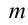
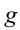
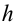
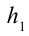
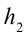
Работа, выполненная силой тяжести, не зависит от формы пути, зависит только от высоты спуска. Поэтому работа, выполненная под действием силы тяжести, зависит не от формы траектории, а от начального и конечного состояний. Такая сила называются потенциальной или консервативной. Поле такой силы называется потенциальным полем.
При движении тела вниз из-за соответствия направления силы тяжести и смещения выполненная работа будет положительной, при движении вверх из-за противоположности направлений работа будет отрицательной. Поэтому в случае, когда тело под воздействием силы тяжести смещено и вернулось обратно, выполненная общая работа равняется нулю.
Полной механической энергией системы называется сумма кинетической и потенциальной энергии системы. Например, полная механическая энергия тела массой 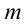
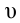
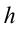
Полная механическая энергия системы остается неизменной с течением времени:
Возможны лишь превращения потенциальной энергии и кинетическую и обратно. Выражение (3.5) представляет собой закон сохранения механической энергии.
Проведенные многочисленные эксперименты, теоретические выводы подтвердили строгое соблюдение закона сохранения энергии.
В природе постоянно происходят превращения одного вида энергии в другой (например, механическая энергия переходит в тепловую энергию). Поэтому этот закон также называют законом сохранения и превращения энергии. Этот закон является основным законом природы и действителен не только для макроскопических, но и микроскопических систем.
Энергия никогда не исчезает, ниоткуда не появляется, она может только преобразовываться из одного вида в другой.
В закрытых системах полная энергия сохраняется.
Например, потенциальная энергия тела, падающего с высоты 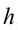
Коэффициент полезного действия. Введена величина, показывающая, какая часть израсходованной энергии машин и двигателей превращается в полезную работу.
Отношение полезной работы к полной работе называется коэффициентом полезного действия (КПД) и обозначается буквой 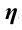
Если полезную работу обозначить 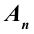
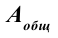
КПД не может быть больше единицы (100%). В машинах и двигателях в результате работы силы трения часть полной энергии расходуется и поэтому КПД всегда меньше единицы.
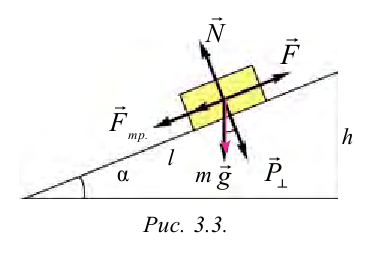
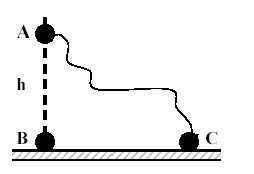
Рассмотрим наклонную плоскость и выполненную работу при подъеме тела вверх. По «золотому правилу» механики, во сколько раз выигрываем в силе, во столько раз проиграем в расстоянии. Но из-за увеличения расстояния смещения не меняется выполненная работа.
Рассмотрим груз с весом 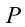
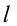
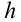
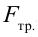
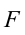
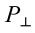
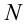
Если не учитывать силу трения, получим уравнение:
Однако с учетом силы трения,
Тогда 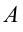
Коэффициент полезного действия:
Сила притяжения, действующая на груз, равна:
- Движение и силы
- Давление в физике
- Строение вещества в физике
- Физическое тело и вещество в физике
- Золотое правило механики
- Потенциальная энергия
- Кинетическая энергия
- Закон сохранения и превращения механической энергии
На чтение 4 мин Просмотров 5.6к. Опубликовано 21 октября, 2020
Энергия — что это в физике, как понять на какую энергию задача, что такое закон сохранения энергии, кинетическая энергия, мощность, потенциальная энергия и формула мощности, формула работы все это мы с вами сейчас изучим. Это базовые понятия физики, которые разберем подробно.
Содержание
- Что такое энергия в физике
- Энергия и работа
- Кинетическая энергия
- Потенциальная энергия
- Закон сохранения энергии
- Закон сохранения механической энергии
- Закон сохранения энергии для математического маятника
- Потенциальная энергия пружины
Что такое энергия в физике
Энергия — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие.
В механике есть два вида энергии: кинетическая энергия и потенциальная энергия. Их сумма называется полной механической энергией.
Энергия и работа
Энергия является мерой способности физической системы совершить работу, поэтому количественно энергия и работа выражаются в одних единицах (джоулях, [Дж]).
Механическая работа численно равна изменению механической энергии. Эту связь работы и энергии мы легко можем почувствовать на себе: например, если провести день очень активно, то к вечеру никаких сил и энергии не останется.
В механике принято считать, что работу по перемещению тела из одного положения в другое совершает сила. Работу силы можно вычислить по формуле:
A=F∙s∙cosα,
где F — сила, совершающая работу, [H];
S — перемещение тела, [м];
α — угол между направлением силы и направлением перемещения.
Если угол α острый, то работа силы положительна, если прямой, то работа равна нулю, если тупой, то работа отрицательна.
Кинетическая энергия
Кинетическая энергия — это энергия движения тела. Кинетическая энергия зависит только от скорости и от массы тела, и определяется формулой:
.
где m — масса тела, [кг],
v — скорость тела, [м/с].
Если тело покоится, его кинетическая энергия равна нулю.
Движущееся тело обладает способностью совершить работу. Например, шар для боулинга способен сбить все 10 кеглей.
Потенциальная энергия
Потенциальная энергия — это энергия взаимодействия тел или частей тела между собой или с внешними полями. Основной физический смысл имеет не само потенциальной энергии, а её изменение. Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Любая физическая система стремится к состоянию с наименьшей потенциальной энергией.
Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его. Такие силы называются консервативными (потенциальными).
Например, работа силы тяжести не зависит от траектории перемещения тела и равна mgh.
Закон сохранения энергии
Энергия замкнутой физической системы сохраняется. Замкнутой называется система, в которой действуют только консервативные силы.
Закон сохранения механической энергии
Общая сумма потенциальной и кинетической энергии тела остается неизменной, если действуют только силы упругости и тяготения, а сила трения отсутствует.
Eкин+Eпот=const
Потенциальная энергия в поле силы тяжести выражается формулой:
Eпот=mgh
где m — масса тела, [кг],
g — ускорение свободного падения, [Н/кг] или [м/c2].
h — высота положения тела над поверхностью, [м].
За нулевое положение тела может быть принято любое удобное нам положение в зависимости от условий, проводимых опыта и измерений. Это может быть поверхность пола, стола, Земли и так далее.
Закон сохранения энергии для математического маятника
Закон сохранения энергии в поле силы тяжести хорошо иллюстрируется движением математического маятника.
В положении 1 и 3 шарик находится в состоянии покоя на высоте h, его кинетическая энергия равна нулю, а потенциальная равна mgh. При переходе из положения 1 в положение 2 высота и потенциальная энергия уменьшаются, но зато скорость и кинетическая энергия увеличиваются, и в положении 2 кинетическая энергия максимальна и равна mv2/2, а потенциальная энергия минимальна и равна нулю.
Таким образом,
Поднятый над землей груз работы не совершает, но может совершить, если начнет падать вниз. Например, потенциальная энергия падающей воды может превратиться в механическую энергию жернова.
Потенциальная энергия пружины
Потенциальная энергия характеризует взаимодействие между собой частей тела и приближённо выражается формулой:
где k — жёсткость деформированного тела, [Н/м],
Δx — смещение от положения равновесия.
Потенциальная энергия пружины равна нулю, когда пружина не растянута.
Сжатая пружина, распрямляясь, может совершить работу, например, поднять вверх небольшой груз.
Внутренняя энергия тела (обозначается как E или U) — это сумма энергий молекулярных взаимодействий и тепловых движений молекул. Внутреннюю энергию тела нельзя измерить напрямую.
Оглавление:
- Основные теоретические сведения
- Механическая работа
- Мощность
- Кинетическая энергия
- Потенциальная энергия
- Коэффициент полезного действия
- Закон сохранения механической энергии
- Некоторые рекомендации к решению задач на работу
- Закон сохранения энергии и динамика вращательного движения
- Неупругие соударения
- Абсолютно упругий удар
- Рекомендации к решению некоторых сложных задач на законы сохранения
Основные теоретические сведения
Механическая работа
К оглавлению…
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы. Работой, совершаемой постоянной силой F, называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла между векторами силы F и перемещения S:
Работа является скалярной величиной. Она может быть как положительна (0° ≤ α < 90°), так и отрицательна (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж). Джоуль равен работе, совершаемой силой в 1 ньютон на перемещении 1 метр в направлении действия силы.
Если же сила изменяется с течением времени, то для нахождения работы строят график зависимости силы от перемещения и находят площадь фигуры под графиком – это и есть работа:
Примером силы, модуль которой зависит от координаты (перемещения), может служить сила упругости пружины, подчиняющаяся закону Гука (Fупр = kx).
Мощность
К оглавлению…
Работа силы, совершаемая в единицу времени, называется мощностью. Мощность P (иногда обозначают буквой N) – физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:
По этой формуле рассчитывается средняя мощность, т.е. мощность обобщенно характеризующая процесс. Итак, работу можно выражать и через мощность: A = Pt (если конечно известна мощность и время совершения работы). Единица мощности называется ватт (Вт) или 1 джоуль за 1 секунду. Если движение равномерное, то:
По этой формуле мы можем рассчитать мгновенную мощность (мощность в данный момент времени), если вместо скорости подставим в формулу значение мгновенной скорости. Как узнать, какую мощность считать? Если в задаче спрашивают мощность в момент времени или в какой-то точке пространства, то считается мгновенная. Если спрашивают про мощность за какой-то промежуток времени или участок пути, то ищите среднюю мощность.
КПД – коэффициент полезного действия, равен отношению полезной работы к затраченной, либо же полезной мощности к затраченной:
Какая работа полезная, а какая затраченная определяется из условия конкретной задачи путем логического рассуждения. К примеру, если подъемный кран совершает работу по подъему груза на некоторую высоту, то полезной будет работа по поднятию груза (так как именно ради нее создан кран), а затраченной – работа, совершенная электродвигателем крана.
Итак, полезная и затраченная мощность не имеют строгого определения, и находятся логическим рассуждением. В каждой задаче мы сами должны определить, что в этой задаче было целью совершения работы (полезная работа или мощность), а что было механизмом или способом совершения всей работы (затраченная мощность или работа).
В общем случае КПД показывает, как эффективно механизм преобразует один вид энергии в другой. Если мощность со временем изменяется, то работу находят как площадь фигуры под графиком зависимости мощности от времени:
Кинетическая энергия
К оглавлению…
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела (энергией движения):
То есть если автомобиль массой 2000 кг движется со скоростью 10 м/с, то он обладает кинетической энергией равной Ек = 100 кДж и способен совершить работу в 100 кДж. Эта энергия может превратиться в тепловую (при торможении автомобиля нагревается резина колес, дорога и тормозные диски) или может быть потрачена на деформацию автомобиля и тела, с которым автомобиль столкнулся (при аварии). При вычислении кинетической энергии не имеет значения куда движется автомобиль, так как энергия, как и работа, величина скалярная.
Тело обладает энергией, если способно совершить работу. Например, движущееся тело обладает кинетической энергией, т.е. энергией движения, и способно совершать работу по деформации тел или придания ускорения телам, с которыми произойдёт столкновение.
Физический смысл кинетической энергии: для того чтобы покоящееся тело массой m стало двигаться со скоростью v необходимо совершить работу равную полученному значению кинетической энергии. Если тело массой m движется со скоростью v, то для его остановки необходимо совершить работу равную его первоначальной кинетической энергии. При торможении кинетическая энергия в основном (кроме случаев соударения, когда энергия идет на деформации) «забирается» силой трения.
Теорема о кинетической энергии: работа равнодействующей силы равна изменению кинетической энергии тела:
Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения. Применять данную теорему удобно в задачах на разгон и торможение тела.
Потенциальная энергия
К оглавлению…
Наряду с кинетической энергией или энергией движения в физике важную роль играет понятие потенциальной энергии или энергии взаимодействия тел.
Потенциальная энергия определяется взаимным положением тел (например, положением тела относительно поверхности Земли). Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения тела и определяется только начальным и конечным положениями (так называемые консервативные силы). Работа таких сил на замкнутой траектории равна нулю. Таким свойством обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.
Потенциальная энергия тела в поле силы тяжести Земли рассчитывается по формуле:
Физический смысл потенциальной энергии тела: потенциальная энергия равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень (h – расстояние от центра тяжести тела до нулевого уровня). Если тело обладает потенциальной энергией, значит оно способно совершить работу при падении этого тела с высоты h до нулевого уровня. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком:
Часто в задачах на энергию приходится находить работу по поднятию (переворачиванию, доставанию из ямы) тела. Во всех этих случаях нужно рассматривать перемещение не самого тела, а только его центра тяжести.
Потенциальная энергия Ep зависит от выбора нулевого уровня, то есть от выбора начала координат оси OY. В каждой задаче нулевой уровень выбирается из соображения удобства. Физический смысл имеет не сама потенциальная энергия, а ее изменение при перемещении тела из одного положения в другое. Это изменение не зависит от выбора нулевого уровня.
Потенциальная энергия растянутой пружины рассчитывается по формуле:
где: k – жесткость пружины. Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, то есть сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Растяжение или сжатие х надо рассчитывать от недеформированного состояния тела.
Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией. Если в начальном состоянии пружина уже была деформирована, а ее удлинение было равно x1, тогда при переходе в новое состояние с удлинением x2 сила упругости совершит работу, равную изменению потенциальной энергии, взятому с противоположным знаком (так как сила упругости всегда направлена против деформации тела):
Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой силами упругости.
Работа силы трения зависит от пройденного пути (такой вид сил, чья работа зависит от траектории и пройденного пути называется: диссипативные силы). Понятие потенциальной энергии для силы трения вводить нельзя.
Коэффициент полезного действия
К оглавлению…
Коэффициент полезного действия (КПД) – характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии. Он определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой (формула уже приведена выше).
КПД можно рассчитывать как через работу, так и через мощность. Полезная и затраченная работа (мощность) всегда определяются путем простых логических рассуждений.
В электрических двигателях КПД – отношение совершаемой (полезной) механической работы к электрической энергии, получаемой от источника. В тепловых двигателях – отношение полезной механической работы к затрачиваемому количеству теплоты. В электрических трансформаторах – отношение электромагнитной энергии, получаемой во вторичной обмотке, к энергии, потребляемой первичной обмоткой.
В силу своей общности понятие КПД позволяет сравнивать и оценивать с единой точки зрения такие различные системы, как атомные реакторы, электрические генераторы и двигатели, теплоэнергетические установки, полупроводниковые приборы, биологические объекты и т.д.
Из–за неизбежных потерь энергии на трение, на нагревание окружающих тел и т.п. КПД всегда меньше единицы. Соответственно этому КПД выражается в долях затрачиваемой энергии, то есть в виде правильной дроби или в процентах, и является безразмерной величиной. КПД характеризует как эффективно работает машина или механизм. КПД тепловых электростанций достигает 35–40%, двигателей внутреннего сгорания с наддувом и предварительным охлаждением – 40–50%, динамомашин и генераторов большой мощности – 95%, трансформаторов – 98%.
Задачу, в которой нужно найти КПД или он известен, надо начать с логического рассуждения – какая работа является полезной, а какая затраченной.
Закон сохранения механической энергии
К оглавлению…
Полной механической энергией называется сумма кинетической энергии (т.е. энергии движения) и потенциальной (т.е. энергии взаимодействия тел силами тяготения и упругости):
Если механическая энергия не переходит в другие формы, например, во внутреннюю (тепловую) энергию, то сумма кинетической и потенциальной энергии остаётся неизменной. Если же механическая энергия переходит в тепловую, то изменение механической энергии равно работе силы трения или потерям энергии, или количеству выделившегося тепла и так далее, другими словами изменение полной механической энергии равно работе внешних сил:
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему (т.е. такую в которой не действует внешних сил, и их работа соответственно равна нолю) и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной:
Это утверждение выражает закон сохранения энергии (ЗСЭ) в механических процессах. Он является следствием законов Ньютона. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой силами упругости и тяготения. Во всех задачах на закон сохранения энергии всегда будет как минимум два состояния системы тел. Закон гласит, что суммарная энергия первого состояния будет равна суммарной энергии второго состояния.
Алгоритм решения задач на закон сохранения энергии:
- Найти точки начального и конечного положения тела.
- Записать какой или какими энергиями обладает тело в данных точках.
- Приравнять начальную и конечную энергию тела.
- Добавить другие необходимые уравнения из предыдущих тем по физике.
- Решить полученное уравнение или систему уравнений математическими методами.
Важно отметить, что закон сохранения механической энергии позволил получить связь между координатами и скоростями тела в двух разных точках траектории без анализа закона движения тела во всех промежуточных точках. Применение закона сохранения механической энергии может в значительной степени упростить решение многих задач.
В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими силами действуют силы трения или силы сопротивления среды. Работа силы трения зависит от длины пути.
Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание). Таким образом энергия в целом (т.е. не только механическая) в любом случае сохраняется.
При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую. Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии.
Одним из следствий закона сохранения и превращения энергии является утверждение о невозможности создания «вечного двигателя» (perpetuum mobile) – машины, которая могла бы неопределенно долго совершать работу, не расходуя при этом энергии.
Разные задачи на работу
К оглавлению…
Если в задаче требуется найти механическую работу, то сначала выберите способ её нахождения:
- Работу можно найти по формуле: A = FS∙cosα. Найдите силу, совершающую работу, и величину перемещения тела под действием этой силы в выбранной системе отсчёта. Обратите внимание, что угол должен быть выбран между векторами силы и перемещения.
- Работу внешней силы можно найти, как разность механической энергии в конечной и начальной ситуациях. Механическая энергия равна сумме кинетической и потенциальной энергий тела.
- Работу по подъёму тела с постоянной скоростью можно найти по формуле: A = mgh, где h – высота, на которую поднимается центр тяжести тела.
- Работу можно найти как произведение мощности на время, т.е. по формуле: A = Pt.
- Работу можно найти, как площадь фигуры под графиком зависимости силы от перемещения или мощности от времени.
Закон сохранения энергии и динамика вращательного движения
К оглавлению…
Задачи этой темы являются достаточно сложными математически, но при знании подхода решаются по совершенно стандартному алгоритму. Во всех задачах Вам придется рассматривать вращение тела в вертикальной плоскости. Решение будет сводиться к следующей последовательности действий:
- Надо определить интересующую Вас точку (ту точку, в которой необходимо определить скорость тела, силу натяжения нити, вес и так далее).
- Записать в этой точке второй закон Ньютона, учитывая, что тело вращается, то есть у него есть центростремительное ускорение.
- Записать закон сохранения механической энергии так, чтобы в нем присутствовала скорость тела в той самой интересной точке, а также характеристики состояния тела в каком-нибудь состоянии про которое что-то известно.
- В зависимости от условия выразить скорость в квадрате из одного уравнения и подставить в другое.
- Провести остальные необходимые математические операции для получения окончательного результата.
При решении задач надо помнить, что:
- Условие прохождения верхней точки при вращении на нити с минимальной скоростью – сила реакции опоры N в верхней точке равна 0. Такое же условие выполняется при прохождении верхней точки мертвой петли.
- При вращении на стержне условие прохождения всей окружности: минимальная скорость в верхней точке равна 0.
- Условие отрыва тела от поверхности сферы – сила реакции опоры в точке отрыва равна нулю.
Неупругие соударения
К оглавлению…
Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда неизвестны действующие силы. Примером такого рода задач является ударное взаимодействие тел.
Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.
С ударным взаимодействием тел нередко приходится иметь дело в обыденной жизни, в технике и в физике (особенно в физике атома и элементарных частиц). В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары.
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.
При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание). Для описания любых ударов Вам нужно записать и закон сохранения импульса, и закон сохранения механической энергии с учетом выделяющейся теплоты (предварительно крайне желательно сделать рисунок).
Абсолютно упругий удар
К оглавлению…
Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел. Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара. При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии. Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя.
Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров. Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения. Центральный удар очень редко реализуется на практике, особенно если речь идет о столкновениях атомов или молекул. При нецентральном упругом соударении скорости частиц (шаров) до и после столкновения не направлены по одной прямой.
Частным случаем нецентрального упругого удара может служить соударения двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров. В этом случае векторы скоростей шаров после упругого соударения всегда направлены перпендикулярно друг к другу.
Законы сохранения. Сложные задачи
К оглавлению…
Несколько тел
В некоторых задачах на закон сохранения энергии тросы с помощью которых перемещаются некие объекты могут иметь массу (т.е. не быть невесомыми, как Вы могли уже привыкнуть). В этом случае работу по перемещению таких тросов (а именно их центров тяжести) также нужно учитывать.
Если два тела, соединённые невесомым стержнем, вращаются в вертикальной плоскости, то:
- выбирают нулевой уровень для расчёта потенциальной энергии, например на уровне оси вращения или на уровне самой нижней точки нахождения одного из грузов и обязательно делают чертёж;
- записывают закон сохранения механической энергии, в котором в левой части записывают сумму кинетической и потенциальной энергии обоих тел в начальной ситуации, а в правой части записывают сумму кинетической и потенциальной энергии обоих тел в конечной ситуации;
- учитывают, что угловые скорости тел одинаковы, тогда линейные скорости тел пропорциональны радиусам вращения;
- при необходимости записывают второй закон Ньютона для каждого из тел в отдельности.
Разрыв снаряда
В случае разрыва снаряда выделяется энергия взрывчатых веществ. Чтобы найти эту энергию надо от суммы механических энергий осколков после взрыва отнять механическую энергию снаряда до взрыва. Также будем использовать закон сохранения импульса, записанный, в виде теоремы косинусов (векторный метод) или в виде проекций на выбранные оси.
Столкновения с тяжёлой плитой
Пусть навстречу тяжёлой плите, которая движется со скоростью v, движется лёгкий шарик массой m со скоростью uн. Так как импульс шарика много меньше импульса плиты, то после удара скорость плиты не изменится, и она будет продолжать движение с той же скоростью и в том же направлении. В результате упругого удара, шарик отлетит от плиты. Здесь важно понять, что не поменяется скорость шарика относительно плиты. В таком случае, для конечной скорости шарика получим:
Таким образом, скорость шарика после удара увеличивается на удвоенную скорость стены. Аналогичное рассуждение для случая, когда до удара шарик и плита двигались в одном направлении, приводит к результату согласно которому скорость шарика уменьшается на удвоенную скорость стены:
Задачи о максимальных и минимальных значениях энергии сталкивающихся шаров
В задачах такого типа главное понять, что потенциальная энергия упругой деформации шаров максимальна, если кинетическая энергия их движения минимальна – это следует из закона сохранения механической энергии. Сумма кинетических энергий шаров минимальна в тот момент, когда скорости шаров будут одинаковы по величине и направлены в одном направлении. В этот момент относительная скорость шаров равна нулю, а деформация и связанная с ней потенциальная энергия максимальна.