Энергия гельмгольца как найти

Эне́ргия Гельмго́льца (или просто свобо́дная эне́ргия) — термодинамический потенциал, убыль которого в квазистатическом изотермическом процессе равна работе, совершённой системой над внешними телами.

Определение[править | править код]

Свободная энергия Гельмгольца для системы с постоянным числом частиц определяется так:

Отсюда дифференциал свободной энергии равен:

• .

Видно, что это выражение является полным дифференциалом относительно независимых переменных и . Поэтому часто свободную энергию Гельмгольца для равновесного состояния выражают как функцию .

Для системы с переменным числом частиц дифференциал свободной энергии Гельмгольца записывается так:

• ,

где — химический потенциал, а — число частиц в системе. При этом свободная энергия Гельмгольца для равновесного состояния записывается как функция .

В соответствии с рекомендациями ИЮПАК энергию Гельмгольца в химической термодинамике можно также обозначать как A^[1].

Свободная энергия Гельмгольца и устойчивость термодинамического равновесия[править | править код]

Можно показать, что в системе с фиксированными температурой и объёмом положение устойчивого равновесия соответствует точке минимума свободной энергии Гельмгольца. Другими словами, в этой точке (для такой системы) никакие изменения макроскопических параметров невозможны.

Свободная энергия Гельмгольца и максимальная работа[править | править код]

Свободная энергия Гельмгольца получила своё название из-за того, что она является мерой работы, которую может совершить термодинамическая система над внешними телами.

Пусть система переходит из состояния в состояние . Поскольку работа не является функцией состояния системы, работа, совершённая системой в данном процессе будет зависеть от пути, по которому этот переход будет осуществляться.

Зададимся целью определить максимальную работу, которую система может совершить в этом случае.

Можно показать, что эта максимальная работа равна убыли свободной энергии Гельмгольца :

• . Здесь индекс ^f означает, что рассматриваемая величина является полной работой системы в данном процессе (см. ниже).

Свободные энергии Гельмгольца и Гиббса[править | править код]

В приложениях «свободной энергией» иногда называют не свободную энергию Гельмгольца, а энергию Гиббса. Это связано с тем, что энергия Гиббса также является мерой максимальной работы, но в данном случае рассматривается только работа над внешними телами, исключая среду:

См. также[править | править код]

• Термодинамические потенциалы
• Энергия Гиббса
• Термодинамическая работа

Примечания[править | править код]

Литература[править | править код]

• Базаров И. П. Термодинамика. (недоступная ссылка) М.: Высшая школа, 1991. 376 с.
• Квасников. И. А. Термодинамика и статистическая физика. Теория равновесных систем, том. 1. М.: Изд-во МГУ, 1991. (2-е изд., испр. и доп. М.: УРСС, 2002. 240 с.)
• Сивухин Д. В. Общий курс физики. — М.: Наука, 1975. — Т. II. Термодинамика и молекулярная физика. — 519 с.
• Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1. — Издание 3-е, доп. — М.: Наука, 1976. — 584 с. — («Теоретическая физика», том V).

Чтобы дать ответ на вопрос о возможности протекания той или иной реакции, о ее направлении и глубине необходимо снова воспользоваться II – законом термодинамики, который может быть сформулирован следующим образом: любой самопроизвольно протекающий процесс, а также и химическая реакция, идет в том направлении, которое сопровождается уменьшением свободной энергии в системе (при постоянных температуре и давлении) или энергии Гельмгольца (при постоянных температуре и объеме).

Свободная энергия или Энергия Гиббса G – это та часть всей энергии системы, которую можно использовать для совершения максимальной работы.

Энергия Гельмгольца A — это та часть внутренней энергии системы, также определяющая работоспособность и может быть применена для совершения максимальной работы.

При протекании химических реакций единовременно совершаются два направления: стремление простых частиц объединиться в более сложные, а также стремление сложных частиц к распаду на более простые.

Они не зависят друг от друга и их величины противоположны, и процесс идет в сторону той реакции, при которой изменение величины больше. Разность между этими величинами определяет свободную энергию реакции (при постоянных температуре и давлении). Ее изменение в реакции определяется разностью сумм энергий Гиббса конечных продуктов реакции и исходных веществ:

ΔG= G_кон – G_исх

При постоянных температуре и давлении изменение энергии Гиббса связано с энтальпией и энтропией следующим выражением:

ΔG = ΔH– TΔS

Здесь изменение энергии Гиббса учитывает одновременно изменение энергетического запаса системы и степень ее беспорядка (самопроизвольность протекания процесса).

Т.к. энергия Гиббса является мерой самопроизвольности протекания процесса, то между знаком ΔG для любой реакции и ее самопроизвольным протеканием (при постоянных температуре и давлении) существуют такие зависимости:

1. Если ΔG отрицательно (ΔG<0), то реакция протекает самопроизвольно в прямом направлении.
2. Если ΔG равно нулю (ΔG=0), то реакция находится в равновесном состоянии.
3. Если ΔG положительно (ΔG>0), то реакция протекать самопроизвольно в прямом направлении не может. Однако обратная реакция идет самопроизвольно.

Энтальпийный и энтропийный факторы и направление процесса

Выясним, как функция свободной энергии зависит от изменений энтропии и энтальпии идущего процесса. Вернемся к выражению, связывающему энергию Гиббса с энтальпией и энтропией:

ΔG= ΔH – TΔS

Без энтропийных факторов все экзотермические реакции (ΔH˂0) должны были быть самопроизвольными. Но энтропийный фактор, который определяется величиной – TΔS, может привести к росту или, наоборот, к падению способности самопроизвольного протекания.

Так, при ΔS>0, член – TΔS вносит отрицательный вклад в общую величину ΔG, следовательно он повышает возможность реакции протекать самопроизвольно.

А при при ΔS<0, член – TΔS напротив уменьшает возможность реакции протекать самопроизвольно.

Если ΔH и – TΔS имеют противоположные знаки, то от их величины зависит будет ли ΔG отрицательным или положительным. В таком случае, необходимо учитывать температурный фактор. Т.о. при высоких температурах роль энропийного фактора становится значительным.

Далее приведена таблица, наглядно показывающая влияние температуры на самопроизвольное протекание реакции.

ΔH	ΔS	ΔG	Протекание реакции
˂0	>0	Всегда ˂0	Реакция самопроизвольна при любых температурах, обратная реакция всегда несамопроизвольна
>0	˂0	Всегда >0	Реакция несамопроизвольна при любых температурах, обратная реакция самопроизвольна
˂0	˂0	При низких температурах ˂0, при высоких температурах >0	Реакция самопроизвольна при низких температурах, обратная реакция становится самопроизвольной при высоких температурах
>0	>0	При низких температурах >0, при высоких температурах ˂0	Реакция несамопроизвольна при низких температурах, но при высоких температурах становится самопроизвольной

Изменение энергии Гиббса. Для удобства принято сравнивать значения ΔG при стандартных условиях – концентрации равны 1 моль/л, парциальное давление газообразных веществ равно 101,3 кПа, температура 298,15 К. Тогда свободную энергию обозначают через ΔG⁰, на основе значений которой можно вычислить изменение энергии Гиббса химической реакции:

ΔG⁰_р-ции = Σ ΔG⁰_прод — Σ ΔG⁰_исх

Величина ΔG⁰_р-ции позволяет определить, будет ли данная реакция, находящаяся в стандартных условиях, протекать самопроизвольно в прямом или обратном направлении. Аналогично теплоте образования, энергии Гиббса образования простых веществ равны нулю.

Энергия Гельмгольца системы с определенной внутренней энергией (U), энтропией (S) при абсолютной температуре (Т) определяется уравнением:

A = U – TS

Изменение энергии Гельмгольца для процессов (при постоянных температуре и объеме) можно определить соотношением:

ΔA= ΔU – TΔS

ΔA — величина, которая не зависит от пути, а зависит только от исходного и конечного состояния системы, т.е. ΔA также, как и другие рассмотренные термодинамические величины, является функцией состояния.

Энергия Гельмгольца подобно энергии Гиббса связана с самопроизвольностью протекания процесса. Если допустить, что система изолирована, а объем и температура постоянны, то самопроизвольно будут протекать только те процессы, при которых А уменьшается.

Таким образом, при ΔA<0 процесс идет самопроизвольно в прямом направлении,

при ΔA>0 – в обратном направлении,

а при ΔA=0 система находится в состоянии равновесия.

Энергию Гельмгольца и энергию Гиббса в стандартных состояниях можно связать с константой равновесия:

ΔG⁰_Т = ΔH⁰_Т – TΔS⁰_Т = —RTlnK,

Где R– универсальная газовая постоянная, K – константа равновесия, Т – абсолютная температура.

Если K>>1, т.е. реакция идет в прямом направлении, то ΔG⁰˂˂0.

Если K<<1, т.е. реакция идет в обратном направлении, то ΔG⁰>>0

Если K=1, то ΔG⁰=0

В случае химической реакции, протекающей в гальваническом элементе при стандартных условиях ΔG⁰ можно связать с ЭДС гальванического элемента следующим соотношением:

ΔG⁰=-nFE⁰, где

nF – количество прошедшего электричества

E⁰ – электродвижущая сила, при условии что все вещества, принимающие участие в реакции, находятся в стандартном состоянии.

При самопроизвольном протекании процесса, его ΔG<0, а ЭДС>0.

Порог реакционной способности веществ для большинства реакций имеет значение ΔG⁰≈41 кДж/моль.

То есть, если ΔG⁰<-41 кДж/моль, то процесс осуществим,

если ΔG⁰>+41 кДж/моль, то процесс неосуществим в любых реальных и стандартных условиях.

In thermodynamics, the Helmholtz free energy (or Helmholtz energy) is a thermodynamic potential that measures the useful work obtainable from a closed thermodynamic system at a constant temperature (isothermal). The change in the Helmholtz energy during a process is equal to the maximum amount of work that the system can perform in a thermodynamic process in which temperature is held constant. At constant temperature, the Helmholtz free energy is minimized at equilibrium.

In contrast, the Gibbs free energy or free enthalpy is most commonly used as a measure of thermodynamic potential (especially in chemistry) when it is convenient for applications that occur at constant pressure. For example, in explosives research Helmholtz free energy is often used, since explosive reactions by their nature induce pressure changes. It is also frequently used to define fundamental equations of state of pure substances.

The concept of free energy was developed by Hermann von Helmholtz, a German physicist, and first presented in 1882 in a lecture called “On the thermodynamics of chemical processes”.^[1] From the German word Arbeit (work), the International Union of Pure and Applied Chemistry (IUPAC) recommends the symbol A and the name Helmholtz energy.^[2] In physics, the symbol F is also used in reference to free energy or Helmholtz function.

Definition[edit]

The Helmholtz free energy is defined as^[3]

where

• F is the Helmholtz free energy (sometimes also called A, particularly in the field of chemistry) (SI: joules, CGS: ergs),
• U is the internal energy of the system (SI: joules, CGS: ergs),
• T is the absolute temperature (kelvins) of the surroundings, modelled as a heat bath,
• S is the entropy of the system (SI: joules per kelvin, CGS: ergs per kelvin).

The Helmholtz energy is the Legendre transformation of the internal energy U, in which temperature replaces entropy as the independent variable.

Formal development[edit]

The first law of thermodynamics in a closed system provides

where is the internal energy, is the energy added as heat, and is the work done on the system. The second law of thermodynamics for a reversible process yields . In case of a reversible change, the work done can be expressed as (ignoring electrical and other non-PV work) and so:

Applying the product rule for differentiation to , it follows

and

The definition of enables to rewrite this as

Because F is a thermodynamic function of state, this relation is also valid for a process (without electrical work or composition change) that is not reversible.

Minimum free energy and maximum work principles[edit]

The laws of thermodynamics are only directly applicable to systems in thermal equilibrium. If we wish to describe phenomena like chemical reactions, then the best we can do is to consider suitably chosen initial and final states in which the system is in (metastable) thermal equilibrium. If the system is kept at fixed volume and is in contact with a heat bath at some constant temperature, then we can reason as follows.

Since the thermodynamical variables of the system are well defined in the initial state and the final state, the internal energy increase , the entropy increase , and the total amount of work that can be extracted, performed by the system, , are well defined quantities. Conservation of energy implies

The volume of the system is kept constant. This means that the volume of the heat bath does not change either, and we can conclude that the heat bath does not perform any work. This implies that the amount of heat that flows into the heat bath is given by

The heat bath remains in thermal equilibrium at temperature T no matter what the system does. Therefore, the entropy change of the heat bath is

The total entropy change is thus given by

Since the system is in thermal equilibrium with the heat bath in the initial and the final states, T is also the temperature of the system in these states. The fact that the system’s temperature does not change allows us to express the numerator as the free energy change of the system:

Since the total change in entropy must always be larger or equal to zero, we obtain the inequality

We see that the total amount of work that can be extracted in an isothermal process is limited by the free-energy decrease, and that increasing the free energy in a reversible process requires work to be done on the system. If no work is extracted from the system, then

and thus for a system kept at constant temperature and volume and not capable of performing electrical or other non-PV work, the total free energy during a spontaneous change can only decrease.

This result seems to contradict the equation dF = −S dT − P dV, as keeping T and V constant seems to imply dF = 0, and hence F = constant. In reality there is no contradiction: In a simple one-component system, to which the validity of the equation dF = −S dT − P dV is restricted, no process can occur at constant T and V, since there is a unique P(T, V) relation, and thus T, V, and P are all fixed. To allow for spontaneous processes at constant T and V, one needs to enlarge the thermodynamical state space of the system. In case of a chemical reaction, one must allow for changes in the numbers N_j of particles of each type j. The differential of the free energy then generalizes to

where the are the numbers of particles of type j and the are the corresponding chemical potentials. This equation is then again valid for both reversible and non-reversible changes. In case of a spontaneous change at constant T and V, the last term will thus be negative.

In case there are other external parameters, the above relation further generalizes to

Here the are the external variables, and the the corresponding generalized forces.

Relation to the canonical partition function[edit]

A system kept at constant volume, temperature, and particle number is described by the canonical ensemble. The probability of finding the system in some energy eigenstate r, for any microstate i, is given by

where

Z is called the partition function of the system. The fact that the system does not have a unique energy means that the various thermodynamical quantities must be defined as expectation values. In the thermodynamical limit of infinite system size, the relative fluctuations in these averages will go to zero.

The average internal energy of the system is the expectation value of the energy and can be expressed in terms of Z as follows:

If the system is in state r, then the generalized force corresponding to an external variable x is given by

The thermal average of this can be written as

Suppose that the system has one external variable . Then changing the system’s temperature parameter by and the external variable by will lead to a change in :

If we write as

we get

This means that the change in the internal energy is given by

In the thermodynamic limit, the fundamental thermodynamic relation should hold:

This then implies that the entropy of the system is given by

where c is some constant. The value of c can be determined by considering the limit T → 0. In this limit the entropy becomes , where is the ground-state degeneracy. The partition function in this limit is , where is the ground-state energy. Thus, we see that and that

Relating free energy to other variables[edit]

Combining the definition of Helmholtz free energy

along with the fundamental thermodynamic relation

one can find expressions for entropy, pressure and chemical potential:^[4]

These three equations, along with the free energy in terms of the partition function,

allow an efficient way of calculating thermodynamic variables of interest given the partition function and are often used in density of state calculations. One can also do Legendre transformations for different systems. For example, for a system with a magnetic field or potential, it is true that

Bogoliubov inequality[edit]

Computing the free energy is an intractable problem for all but the simplest models in statistical physics. A powerful approximation method is mean-field theory, which is a variational method based on the Bogoliubov inequality. This inequality can be formulated as follows.

Suppose we replace the real Hamiltonian of the model by a trial Hamiltonian , which has different interactions and may depend on extra parameters that are not present in the original model. If we choose this trial Hamiltonian such that

where both averages are taken with respect to the canonical distribution defined by the trial Hamiltonian , then the Bogoliubov inequality states

where is the free energy of the original Hamiltonian, and is the free energy of the trial Hamiltonian. We will prove this below.

By including a large number of parameters in the trial Hamiltonian and minimizing the free energy, we can expect to get a close approximation to the exact free energy.

The Bogoliubov inequality is often applied in the following way. If we write the Hamiltonian as

where is some exactly solvable Hamiltonian, then we can apply the above inequality by defining

Here we have defined to be the average of X over the canonical ensemble defined by . Since defined this way differs from by a constant, we have in general

where is still the average over , as specified above. Therefore,

and thus the inequality

holds. The free energy is the free energy of the model defined by plus . This means that

and thus

Proof of the Bogoliubov inequality[edit]

For a classical model we can prove the Bogoliubov inequality as follows. We denote the canonical probability distributions for the Hamiltonian and the trial Hamiltonian by and , respectively. From Gibbs’ inequality we know that:

holds. To see this, consider the difference between the left hand side and the right hand side. We can write this as:

Since

it follows that:

where in the last step we have used that both probability distributions are normalized to 1.

We can write the inequality as:

where the averages are taken with respect to . If we now substitute in here the expressions for the probability distributions:

and

we get:

Since the averages of and are, by assumption, identical we have:

Here we have used that the partition functions are constants with respect to taking averages and that the free energy is proportional to minus the logarithm of the partition function.

We can easily generalize this proof to the case of quantum mechanical models. We denote the eigenstates of by . We denote the diagonal components of the density matrices for the canonical distributions for and in this basis as:

and

where the are the eigenvalues of

We assume again that the averages of H and in the canonical ensemble defined by are the same:

where

The inequality

still holds as both the and the sum to 1. On the l.h.s. we can replace:

On the right-hand side we can use the inequality

where we have introduced the notation

for the expectation value of the operator Y in the state r. See here for a proof. Taking the logarithm of this inequality gives:

This allows us to write:

The fact that the averages of H and are the same then leads to the same conclusion as in the classical case:

Generalized Helmholtz energy[edit]

In the more general case, the mechanical term must be replaced by the product of volume, stress, and an infinitesimal strain:^[5]

where is the stress tensor, and is the strain tensor. In the case of linear elastic materials that obey Hooke’s law, the stress is related to the strain by

where we are now using Einstein notation for the tensors, in which repeated indices in a product are summed. We may integrate the expression for to obtain the Helmholtz energy:

Application to fundamental equations of state[edit]

The Helmholtz free energy function for a pure substance (together with its partial derivatives) can be used to determine all other thermodynamic properties for the substance. See, for example, the equations of state for water, as given by the IAPWS in their IAPWS-95 release.

Application to training auto-encoders[edit]

Hinton and Zemel^[6] “derive an objective function for training auto-encoder based on the minimum description length (MDL) principle”. “The description length of an input vector using a particular code is the sum of the code cost and reconstruction cost. They define this to be the energy of the code. Given an input vector, they define the energy of a code to be the sum of the code cost and the reconstruction cost.” The true expected combined cost is

“which has exactly the form of Helmholtz free energy”.

See also[edit]

• Gibbs free energy and thermodynamic free energy for thermodynamics history overview and discussion of free energy
• Grand potential
• Enthalpy
• Statistical mechanics
• This page details the Helmholtz energy from the point of view of thermal and statistical physics.
• Bennett acceptance ratio for an efficient way to calculate free energy differences and comparison with other methods.

References[edit]

Further reading[edit]

• Atkins’ Physical Chemistry, 7th edition, by Peter Atkins and Julio de Paula, Oxford University Press
• HyperPhysics Helmholtz Free Energy Helmholtz and Gibbs Free Energies

Содержание

• Как рассчитывается свободная энергия Гельмгольца?
• Спонтанные процессы
• Решенные упражнения
• Упражнение 1
• Решение
• Упражнение 2.
• Решение для
• Решение б
• Ссылки

В Свободная энергия Гельмгольца представляет собой термодинамический потенциал, который измеряет полезную работу замкнутой системы в условиях постоянной температуры и объема. Свободная энергия Гельмгольца обозначается какF y определяется как разность внутренней энергии ИЛИ минус произведение температуры Т по энтропии S:

F = U – T⋅S

Поскольку это энергия, она измеряется в Джоулях в Международной системе (СИ), хотя другие соответствующие единицы также могут быть эргами (СГС), калориями или электрон-вольтами (эВ).

Отрицательное изменение энергии Гельмгольца во время процесса приравнивается к максимальной работе, которую система может выполнять в изохорическом процессе, то есть при постоянном объеме. Когда уровень громкости не поддерживается постоянным, часть этой работы может выполняться с окружающей средой.

В этом случае мы имеем в виду работу, в которой объем не меняется, например, электрическую работу: dW = Φdq, где Φ – электрический потенциал, а q – электрический заряд.

Если температура также постоянна, энергия Гельмгольца минимизируется при достижении равновесия. Для всего этого энергия Гельмгольца особенно полезна в процессах с постоянным объемом. В этом случае у вас есть:

– Для самопроизвольного процесса: ΔF <0

– Когда система находится в равновесии: ΔF = 0

– В неспонтанном процессе: ΔF> 0.

Как рассчитывается свободная энергия Гельмгольца?

Как указано в начале, энергия Гельмгольца определяется как «внутренняя энергия U системы за вычетом произведения абсолютной температуры T системы на энтропию S системы»:

F = U – T⋅S

Это функция температуры T и объема V. Шаги, чтобы отобразить это, следующие:

– Исходя из первого закона термодинамики, внутренняя энергия U связана с энтропией S системы и ее объемом V для обратимых процессов следующей дифференциальной зависимостью:

dU = dQ – dW = TdS – PdV

Отсюда следует, что внутренняя энергия U является функцией переменных S Y V, Таким образом:

U = U (S, V)

– Теперь возьмем определение F и получается:

dF = dU – d (TS) = dU – TdS – SdT

– Подставляя туда дифференциальное выражение, полученное для dU на первом шаге, остается:

dF = TdS – PoV – TdS – SdT = -SdT – PoV

– Наконец, делается вывод, что F является функцией температуры T и объема V и может быть выражено как:

F = F (T, V)

Спонтанные процессы

Энергию Гельмгольца можно применять как общий критерий спонтанности в изолированных системах, но сначала удобно уточнить некоторые понятия:

– Асистема закрыта он может обмениваться энергией с окружающей средой, но не может обмениваться материей.

– Вместо изолированная система он не обменивается веществом или энергией с окружающей средой.

– Наконец открытая система обмениваться веществом и энергией с окружающей средой.

В обратимых процессах изменение внутренней энергии рассчитывается следующим образом:

dU = TdS – PdV

Теперь предположим процесс с постоянным объемом (изохорическим), в котором второй член предыдущего выражения не имеет никакого вклада. Также следует помнить, что согласно Неравенство Клаузиуса: 

dS ≥ dQ / T

Такое неравенство относится к изолированной термодинамической системе.

Итак, для процесса (обратимого или нет), в котором объем остается постоянным, верно следующее:

T dS ≥ dU (при фиксированной громкости)

Принимая во внимание, что:

dF = dU – T dS

У нас будет, что в изохорном процессе при постоянной температуре выполняется следующее:dF ≤ 0, как указано в начале.

Таким образом, энергия Гельмгольца F является уменьшающейся величиной в спонтанном процессе, пока это изолированная система. F достигает минимального и стабильного значения при достижении обратимого равновесия.

Решенные упражнения

Упражнение 1

Вычислите изменение свободной энергии Гельмгольца F для 2 моль идеального газа при температуре 300K во время изотермического расширения, которое приводит к увеличению объема системы с начального 20 литров до конечного объема 40 литров.

Решение

Исходя из определения F:

F = U – T S

Тогда конечная вариация F, называемая ΔF, будет:

ΔF = ΔU – T ΔS

Поскольку в заявлении указано, что температура постоянная: ΔT = 0. Итак, в идеальных газах внутренняя энергия зависит только от их абсолютной температуры, но поскольку это изотермический процесс, тогда ΔU = 0 Y ΔF = – Т ΔS. Для идеальных газов изменение энтропии изотермического процесса записывается так:

ΔS = n.R.ln (V₂/ V₁)

Применяя это выражение:

ΔS = 2 моль x 8,314 Дж / (К моль) x ln (40 л / 20 л) = 11,53 Дж / K

Наконец, изменение энергии Гельмгольца:

ΔF = – T ΔS = – 300K x 11,53 Дж / K = -3457,70 Дж.

Упражнение 2.

Внутри цилиндра находится поршень, который делит его на две части, и на каждой стороне поршня расположены п моль одноатомного идеального газа, как показано на рисунке ниже.

Стенки цилиндра хорошо проводят тепло (диатермический) и контактируют с резервуаром с температурой T_или.

Начальный объем каждой из секций цилиндра V_1i и V_2i, а его окончательные объемы – V_1f и V_2f после квазистатического смещения. Поршень перемещается с помощью плунжера, который герметично проходит через две крышки цилиндра.

Просит найти:

а) Изменение внутренней энергии газа и работы, выполняемой системой и

б) Вариация энергии Гельмгольца.

Решение для

Поскольку поршень движется квазистатически, внешняя сила, приложенная к поршню, должна уравновешивать силу из-за разницы давлений в двух секциях цилиндра.

Работа dW в исполнении внешней силы F_доб во время бесконечно малого сдвига dx это:

dW = – F_доб dx = (P₁ – П₂) a dx = P₁ dV₁ + P₂ dV₂

Где использовались отношения dV₁ = – dV₂ = a dx,будучи к область плунжера. С другой стороны, изменение энергии Гельмгольца:

dF = -SdT – PoV

Так как температура в процессе не меняется, то dT = 0 Y dF = – PoV. Применяя это выражение к каждой секции цилиндра, мы получаем:

dW = P₁ dV₁ + P₂ dV₂ = – dF₁ – dF₂

Быть F₁ Y F₂ Энергии Гельмгольца в каждой из камер.

Конечная работа W может быть вычислена из конечного изменения энергии Гельмгольца каждой камеры:

W = -ΔF₁ – ΔF₂

Решение б

Чтобы найти изменение энергии Гельмгольца, используется определение: F = U – T S.Так как в каждой камере есть одноатомный идеальный газ при постоянной температуре Т_или, внутренняя энергия не изменяется (ΔU = 0), так что: ΔF = – Т_или ΔS. В дальнейшем:

ΔS = nR ln (V_F/Увидел)

Это путем замены finally позволяет проделанной работе:

W = -T_или nR ln (В_1f/ V_1i) -To nR ln (V_2f/ V_2i) = -ΔF₁ -ΔF₂

W = – К nR ln [(V_1f⋅ V_1i) / (V_2f.V_2i)] = – ΔF_общее

Быть ΔF_общее полное изменение энергии Гельмгольца.

Ссылки

1. Каштаны E. Упражнения на свободную энергию. Получено с: lidiaconlaquimica.wordpress.com
2. Либретексты. Гельмгольца Энергия. Получено с: chem.libretexts.org
3. Либретексты. Что такое бесплатные энергии. Получено с: chem.libretexts.org
4. Википедия. Энергия Гельмгольца. Получено с: es.wikipedia.com
5. Википедия. Свободная энергия Гельмгольца. Получено с: en.wikipedia.com

Энергия
Гельмгольца (изохорно-изотермический
потенциал) является характеристической
функцией, если независимыми переменными
выбраны объем и температура.
Полный дифференциал энергии Гельмгольца
для простых систем записывается в виде:

, (4.56)

а
в случае обратимых процессов как

. (4.57)

Полагая
V
= const,
из уравнения (4.57) получаем

,

. (4.58)

Функция
А = f (T)
при V = const
является убывающей, а кривая зависимости
энергии Гельмгольца от температуры при
постоянном объеме обращена выпуклостью
вверх (рис. 4.3). Мерой
убыли энергии Гельмгольца при повышении
температуры вещества является энтропия.

Полагая
Т = const,
из уравнения (4.57) получаем

,

. (4.59)

Функция
А = f (V)
при T = const
также является убывающей, но кривая
зависимости энергии Гельмгольца от
объема при постоянной температуре
обращена выпуклостью вниз (рис. 4.3).

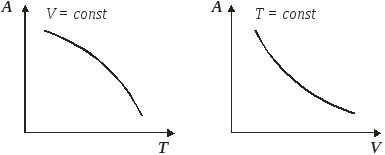
Рис.4.3.
Зависимость энергии Гельмгольца от
температуры и объема.

При
протекании обратимых процессов в сложных
системах, способных выполнять кроме
работы расширения и другие виды работы
(полезную работу), справедливо:

. (4.60)

Если
процесс изотермический (Т
= const),
то

,

,

. (4.61)

Итак,
в обратимом
изотермическом процессе убыль энергии
Гельмгольца равна максимальной (полной)
работе, производимой системой.
В этом заключается основной смысл
введения новой функции А:
через изменение функции состояния в
изотермических условиях можно определить
максимальную работу в обратимом процессе.

Если
обратимый процесс протекает в
изохорно-изотермических
условиях,
то

,

. (4.62)

В
обратимом изохорно-изотермическом
процессе убыль энергии Гельмгольца
равна максимальной полезной работе.

Рассмотрим
систему и окружающую среду, которые
находятся в тепловом равновесии:
Т_сист. = Т_ср..
Пусть в системе протекает процесс, в
результате которого в окружающую среду
переходит количество теплоты δQ_cр..
Тогда общее изменение энтропии dS_общ
(ее называют изменением
энтропии вселенной)
равно:

.

Поскольку
теплота уходит из системы, то
δQ_cр. = –δQ_сист.,
поэтому

.

Но
dS_общ.
положительно для любого самопроизвольного
(необратимого) процесса и равно нулю
при равновесии. Следовательно,

. (4.63)

Значение
неравенства (4.63) состоит в том, что оно
выражает критерий самопроизвольного
изменения только через свойства системы.
Если система теряет теплоту при постоянном
объеме, то

δQ_V = dU,

поэтому
соотношение (4.63) принимает вид:

или
. (4.64)

В
последнем соотношении нижний индекс
опущен, поскольку все величины относятся
к системе. Следует понимать, что dS
– это изменение энтропии системы, а
‑dU/T
– изменение энтропии среды: суммарная
энтропия стремится к максимуму.

Поскольку
в конечном итоге рассматривается
изохорно-изотерми-ческий процесс, то

.

Следовательно,
при протекании процессов в
изохорно-изотермических условиях должно
выполняться неравенство

, (4.65)

где
знак равенства относится к обратимым
процессам, а знак неравенства – к
необратимым.

Далее,
для обратимого изотермического процесса

. (4.66)

Если
в обратимом процессе энтропия системы
увеличивается, то максимальная работа
больше, чем –ΔU,
так как TΔS
положительно. Система не изолирована
и поэтому в нее может поступать теплота,
служащая источником энергии для
производства работы. Если же ΔS
отрицательно, то теплота должна выделяться
из системы, чтобы привести к общему
увеличению энтропии (энтропии вселенной).
Поэтому не все изменение внутренней
энергии может перейти в работу и W_max
< (–ΔU).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #