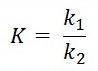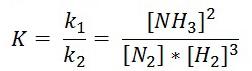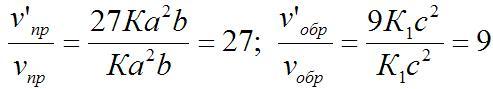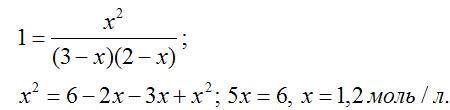Энергия гиббса как найти температуру

Скорость
химической реакции (v) 
характеризуется изменением концентрации
реагирующих веществ (моль/л или
моль/см³) в единицу времени (сек.,
мин., ч.).

Для
гомогенной (однородной) системы
скорость химической реакции измеряется
количеством веществ, вступивших в
реакцию или образовавшихся в результате
реакции за единицу времени в единице
объема системы. Для гетерогенной
системы скорость химической реакции
измеряется количеством веществ,
вступивших в реакцию или образовавшихся
в результате реакции за единицу времени
на единице поверхности раздела фаз.

Факторы,
влияющие на скорость химической
реакции

1)
Природа реагирующих веществ (характер
связи в молекулах реагентов);

2)
Концентрация реагентов;

3)
Температура;

4)
Катализатор;

5)
Давление (для газов);

6)
Излучение (ИК-, УФ-, рентгеновское,
радиоактивное и др.);

7)
Площадь поверхности раздела фаз (для
гетерогенных реакций).

Влияние
концентрации реагирующих веществ
выражается законом действия масс: при
постоянной температуре скорость
химической реакции, протекающей в
однородной среде, пропорциональна
произведению концентраций реагирующих
веществ, возведенных в степени их
стехиометрических коэффициентов.

Например,
для обратимой гомогенной реакции,
выражающейся уравнением  aA  + 
bB  ↔  cC  +  dD, в соответствии
с законом действия масс, можно записать
выражение скорости прямой и обратной
реакций:

где
k₁ и k₂ – константы скоростей
прямой и обратной реакций.

Физический
смысл константы скорости заключается
в том, что она показывает численное
значение скорости химической реакции,
с которой реагируют вещества при их
концентрации (или произведении
концентраций), равной единице. Константа
скорости реакции зависит от природы
реагентов, температуры, наличия
катализатора, но не зависит от
концентрации реагентов.

Химическое
равновесие

Химические
реакции по признаку обратимости
делятся на необратимые и обратимые.
К необратимым реакциям относятся
такие реакции, которые протекают до
тех пор, пока один из реагентов полностью
не израсходуются. Признаками необратимых
реакций, протекающих в растворах,
являются: а) выпадение осадка, б)
образование газа, в) образование
слабого электролита.

Обратимыми
реакциями называются такие реакции,
которые протекают одновременно в двух
взаимно противоположных направлениях.
Для подобных реакций вместо знака
равенства пользуются противоположно
направленными стрелками (↔).

С
течением времени скорость любой
реакции, измеряется по убывающим
концентрациям исходных веществ, будет
уменьшаться, так как по мере взаимодействия
веществ их концентрации уменьшаются
(скорость прямой реакции). Если реакция
является обратимой, то по мере увеличения
концентрации продуктов ее скорость
будет возрастать (скорость обратной
реакции). Как только скорости прямой
и обратной реакций становятся
одинаковыми, в системе устанавливается
химическое равновесие и дальнейшее
изменение концентраций всех веществ,
находящихся в системе, прекращается.

Количественной
характеристикой состояния равновесия
является константа химического
равновесия К, которая определяется
отношением констант скоростей прямой
и обратной реакцией

В
подавляющем большинстве случаев
константы скоростей прямой и обратной
реакций не равны. Константа равновесия
– постоянная при данной температуре
величина и определяет соотношение
между равновесными концентрациями
продуктов реакции и исходных веществ,
возведенных в степени их стехиометрических
коэффициентов.

Например,
для процесса    N₂ + 
3H₂ ↔  2NH₃

Квадратной
скобкой обозначена концентрация
каждого вещества в момент равновесия,
так называемая равновесная
концентрация.

Константа
равновесия зависит от природы
реагирующих веществ и температуры.
Катализатор не влияет на состояние
равновесия. Присутствие катализатора
в системе лишь изменяет время его
достижения. В состоянии равновесия
система может находиться до тех пор,
пока не изменится хотя бы одно из
внешних воздействий: температура,
концентрация одного из реагентов,
давление (для газов). Изменения,
происходящие в равновесной системе
в результате внешних воздействий,
определяются принципом подвижного
равновесия (принцип Ле-Шателье): внешнее
воздействие на систему, находящуюся
в состоянии равновесия, приводит к
смещению этого равновесия в направлении,
при котором эффект произведенного
воздействия ослабляется.

На
смещение равновесия оказывает влияние:

1)
изменение температуры:
эндотермический процесс ускоряется
в большей степени при повышении
температуры и, наоборот, при понижении
температуры ускоряется экзотермический
процесс;

2)
изменение давления
(для реакций, протекающих в газовой
фазе): при повышении давления равновесие
реакции смещается в направлении
образования веществ, занимающих
меньший объем, и, наоборот, понижение
давления способствует процессу,
сопровождающемуся увеличением объема.
Если реакция протекает без изменения
объема, то изменение давления в системе
не оказывает влияние на
химическое равновесие.

3)
изменение концентрации:
увеличение концентрации исходных
веществ приводит к увеличению скорости
прямой реакции, при этом протекающий
в системе процесс завершится, когда
скорости прямой и обратной реакций
станут равны и установится новое
равновесие. Уменьшение концентрации
одного из продуктов реакции (вывод из
системы) приводит к смещению равновесия
в сторону его образования.

 Критерием
принципиальной осуществимости реакций
является неравенство ΔG_p,
T
< 0. Но это неравенство не
является еще полной гарантией
фактического течения процесса в данных
условиях, не является достаточным для
оценки кинетических возможностей
реакции. Так, ΔG^о_298,
H₂O(г) = – 228,59 кДж/моль, а ΔG^о_298,
AlI₃(к) = -313;8 кДж/моль и,
следовательно, при Т = 298 К и р
= 1,013 • 10⁵ Па возможны реакции,
идущие по уравнениям:

Н₂(г)
+ ½О₂(г) = Н₂О (1)

2Аl(к)
+ 3l₂(к) = 2Аll₃(к)
(2)

Однако
эти реакции при стандартных условиях
идут только в присутствии катализатора
(платины для первой и воды для второй).
Катализатор как бы снимает кинетический
“тормоз”, и тогда проявляется
термодинамическая природа вещества,
Скорость химических реакций зависит
от многих факторов, основные из которых
– концентрация (давление) реагентов,
температура и действие катализатора.
Эти же факторы определяют и достижение
равновесия в реагирующей системе.

Пример
1. Во сколько раз изменится скорость
прямой и обратной реакции в системе:

2SO₂(г)
+ O₂(г) = 2SO₃(г)

если
объем газовой смеси уменьшить в три
раза? В какую сторону сместится
равновесие системы?

Решение.
Обозначим концентрации реагирующих
веществ: [SO₂]= a,
[О₂] = b,
[SO₃] = с. Согласно
закону действия масс скорости v
прямой и обратной реакции до
изменения объема:

v_пр
= Ка²b;
v_обр = К₁с².

После
уменьшения объема гомогенной системы
в три раза концентрация каждого из
реагирующих веществ увеличится в три
раза: [SO₂] = 3а,
[О₂] = 3b;
[SO₃] = 3с.
При новых концентрациях скорости v’
прямой и обратной реакции:

v’_пр
= К(3а)²(3b)
= 27Ка²b;
v’_обр
= К₁(3с)² = 9К₁с².

Отсюда:

Следовательно,
скорость прямой реакции увеличилась
в 27 раз, а обратной – только в девять
раз. Равновесие системы сместилось в
сторону образования SO₃.

Пример
2. Вычислите, во сколько раз
увеличится скорость реакции, протекающей
в газовой фазе, при повышении температуры
от 30 до 70^оС, если температурный
коэффициент реакции равен 2.

Решение.
Зависимость скорости химической
реакции от температуры определяется
эмпирическим правилом Вант-Гоффа по
формуле:

Следовательно,
скорость реакции νТ₂
при температуре 70^оС больше
скорости реакции νТ₁
при температуре 30^оС в 16 раз.

Пример
3. Константа равновесия гомогенной
системы:

СО(г)
+ Н₂О(г) = СО₂(г) + Н₂(г)

при
850^оС равна 1. Вычислите концентрации
всех веществ при равновесии, если
исходные концентрации: [СО]_исх
=3 моль/л, [Н₂О]_исх = 2 моль/л.

Решение.
При равновесии скорости прямой и
обратной реакций равны, а отношение
констант этих скоростей постоянно и
называется константой равновесия
данной системы:

v_прК₁
[СО][Н₂О]; v_обр
= К₂[СО₂][Н₂];

В
условии задачи даны исходные
концентрации, тогда как в выражение
К_р входят только равновесные
концентрации всех веществ системы.
Предположим, что к моменту равновесия
концентрации [СО₂]_р = х
моль/л. Согласно уравнению системы
число молей образовавшегося водорода
при этом будет также х моль/л. По
столько же молей (х моль/л) СО и
Н₂О расходуется для образования
по х молей СО₂ и Н₂.
Следовательно, равновесные концентрации
всех четырех веществ:

[СО₂]_р
= [Н₂]_р = х моль/л; [СО]_р
= (3 – х) моль/л;

[Н₂О]_р
= (2 – х) моль/л.

Зная
константу равновесия, находим значение
х, а затем исходные концентрации
всех веществ:

Таким
образом, искомые равновесные
концентрации:

[СО₂]_р
= 1,2 моль/л;

[Н₂]_р=
1,2 моль/л;

[СО]_р
= 3 – 1,2 = 1,8 моль/л;

[Н₂О]_р
= 2 – 1,2 = 0,8 моль/л.

Пример
4. Эндотермическая реакция
разложения пентахлорида фосфора
протекает по уравнению:

PCl₅(г)
= РСl₃(г) + Сl(г);
ΔН = + 92,59 кДж.

Как
надо изменить: а) температуру; б)
давление; в) концентрацию, чтобы
сместить равновесие в сторону прямой
реакции – разложения PCl₅?

Решение.
Смещением или сдвигом химического
равновесия называют изменение
равновесных концентраций реагирующих
веществ в результате изменения одного
из условий реакции. Направление, в
котором сместилось равновесно,
определяется по принципу Ле Шателье:
а) так как реакция разложения PCl₅
эндотермическая (ΔН > 0) то для
смещения равновесия в сторону прямой
реакции нужно повысить температуру;
б) так как в данной системе разложение
РСl₅ ведет к увеличению объема
(из одной молекулы газа образуются
две газообразные молекулы), то для
смещения равновесия в сторону прямой
реакции надо уменьшить давление; в)
смещения равновесия в указанном
направлении можно достигнуть как
увеличением концентрации РСl₅,
так и уменьшением концентрации РСl₃
или Сl₂.

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 сентября 2020 года; проверки требуют 23 правки.

Свобо́дная эне́ргия Ги́ббса (или просто эне́ргия Ги́ббса, или потенциа́л Ги́ббса, или изобарно-изотермический потенциал, или термодинами́ческий потенциа́л в узком смысле) — это величина, изменение которой в ходе химической реакции равно изменению внутренней энергии системы. Энергия Гиббса показывает, какая часть от полной внутренней энергии системы может быть использована для химических превращений или получена в их результате в заданных условиях и позволяет установить принципиальную возможность протекания химической реакции в заданных условиях. Математически это термодинамический потенциал следующего вида:

Энергию Гиббса можно понимать как полную потенциальную химическую энергию системы (кристалла, жидкости и т. д.)

Понятие энергии Гиббса широко используется в термодинамике и химии.

Самопроизвольное протекание изобарно-изотермического процесса определяется двумя факторами: энтальпийным, связанным с уменьшением энтальпии системы (), и энтропийным , обусловленным увеличением беспорядка в системе вследствие роста её энтропии. Разность этих термодинамических факторов является функцией состояния системы, называемой изобарно-изотермическим потенциалом или свободной энергией Гиббса (, кДж)

Определение[править | править код]

Классическим определением энергии Гиббса является выражение

где  — внутренняя энергия,  — давление среды,  — объём,  — абсолютная температура среды,  — энтропия.

Дифференциал энергии Гиббса для системы с постоянным числом частиц, выраженный в собственных переменных — через давление и температуру :

Для системы с переменным числом частиц этот дифференциал записывается так:

Здесь  — химический потенциал, который можно определить как энергию, которую необходимо затратить, чтобы добавить в систему ещё одну частицу.

Связь с термодинамической устойчивостью системы[править | править код]

Покажем, что минимум потенциала Гиббса соответствует устойчивому равновесию термодинамической системы с фиксированными температурой, давлением и числом частиц.

Запишем обобщённое уравнение первого и второго начал термодинамики:

При

Таким образом в системе при постоянных температуре и давлении энергия Гиббса достигает минимального значения.

Применение в химии[править | править код]

Связь с химическим потенциалом[править | править код]

Используя свойства экстенсивности термодинамических потенциалов, математическим следствием которых является соотношение Гиббса-Дюгема, можно показать, что химический потенциал для системы с одним типом частиц есть отношение энергии Гиббса к числу молей вещества n в системе:

Если система состоит из частиц нескольких сортов с числом молей частиц каждого сорта, то соотношения Гиббса-Дюгема приводят к выражению

Химический потенциал применяется при анализе систем с переменным числом частиц, а также при изучении фазовых переходов. Так, исходя из соотношений Гиббса — Дюгема и из условий равенства химических потенциалов находящихся в равновесии друг с другом фаз, можно получить уравнение Клапейрона — Клаузиуса, определяющее линию сосуществования двух фаз в координатах через термодинамические параметры (удельные объёмы) фаз и теплоту перехода между фазами.^[1]

Энергия Гиббса и направление протекания реакции[править | править код]

В химических процессах одновременно действуют два противоположных фактора — энтропийный () и энтальпийный (). Суммарный эффект этих противоположных факторов в процессах, протекающих при постоянном давлении и температуре, определяет изменение энергии Гиббса () согласно
уравнению Гиббса — Гельмгольца :

Из этого выражения следует, что , то есть некоторое количество теплоты расходуется на увеличение энтропии (), эта часть энергии потеряна для совершения полезной работы (рассеивается в окружающую среду в виде тепла), её часто называют связанной энергией. Другая часть теплоты () может быть использована для совершения работы, поэтому энергию Гиббса часто называют также свободной энергией.

Характер изменения энергии Гиббса позволяет судить о принципиальной возможности осуществления процесса.

	процесс может протекать — самопроизвольный процесс,
	система находится в состоянии химического равновесия.
	процесс протекать не может — несамопроизвольный процесс

Иными словами, если энергия Гиббса в исходном состоянии системы больше, чем в конечном, то процесс принципиально может протекать, если наоборот — то не может. Речь идёт исключительно о принципиальной возможности протекания реакции. В реальных же условиях реакция может не начинаться и при соблюдении неравенства (по кинетическим причинам).

Изотерма Вант-Гоффа[править | править код]

Изотерма Вант-Гоффа — соотношение, связывающее изменение свободной энергии Гиббса в ходе химической реакции с её константой равновесия :

где  — равновесная константа (безразмерная величина).

 — коэффициент реакции

Вообще говоря, любая реакция может быть рассмотрена как обратимая (даже если на практике она таковой не является). При этом константа равновесия определяется как

где  — константа скорости прямой реакции,  — константа скорости обратной реакции.

Историческая справка[править | править код]

Энергия Гиббса названа в честь одного из основателей термодинамики, Джозайи Уилларда Гиббса.

Примечания[править | править код]

Литература[править | править код]

• Ахметов Н. С. Актуальные вопросы курса неорганической химии. — М.: Просвещение, 1991. — 495 с. — ISBN 5-09-002630-0.
• Базаров И. П. Термодинамика. — М.: Высшая школа, 1991. — 376 с. — ISBN 5-06-000626-3.
• Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1. — Издание 3-е, доп. — М.: Наука, 1976. — 584 с. — («Теоретическая физика», том V).

См. также[править | править код]

• Термодинамический потенциал
• Свободная энергия Гельмгольца

Здесь вы найдете примеры задач на вычисление таких термодинамических параметров как энтальпия, энтропия, энергия Гиббса. Определение возможности самопроизвольного протекания процесса, а также составление термохимических уравнений.

Задачи к разделу Основы термодинамики с решениями

Задача 1. Рассчитайте стандартную энтальпию и стандартную энтропию химической реакции. Определите в каком направлении при 298 °К  (прямом или обратном) будет протекать реакция. Рассчитайте температуру, при которой равновероятны оба направления реакции.
Fe₂O_{3 (к)} + 3H₂ = 2Fe_(к) + 3H₂O_(г)

Показать решение »

Задача 2. Вычислите энергию Гиббса и определите возможность протекания реакции при температурах 1000 и 3000 К.

	Cr2O3 (т) + 3C (т) = 2Cr (т) + 3CO (г)
ΔH298, кДж/моль	— 1141	0	0	— 110,6
ΔS298, Дж/(моль×К)	81,2	5,7	23,6	197,7

Задача 3. Определите тепловой эффект сгорания жидкого CS₂(ж) до образования газообразных СО₂ и SO_2. Сколько молей CS₂ вступят в реакцию, если выделится 700 кДж тепла?

Задача 4. Вычислите тепловой эффект реакции восстановления оксида железа (II) водородом, исходя из следующих термохимических уравнений:
1. FeO (к) + CO (г) = Fe (к) + CО₂ (г);          ΔH₁ = -18,20 кДж;
2. СO (г) + 1/2O₂ (г) = СO₂ (г)                         ΔН₂ = -283,0 кДж;
3. H₂ (г) + ½ O₂ (г) = H₂O (г)                         ΔН₃ = -241,83 кДж.

Задача 5. Реакция горения бензола выражается термохимическим уравнением:
С₆Н_6(ж) + 7½ О_2(г) = 6СО_2(г) + 3Н₂О_(г) – 3135,6 кДж.
Вычислите теплоту образования жидкого бензола. Определите теплотворную способность жидкого бензола при условии, что стандартные условия совпадают с нормальными.

Задача 6. Реакция окисления этилового спирта выражается уравнением:
С₂Н₅ОН_(ж) + 3,0 О_2(г) = 2СО_2(г) + 3Н₂О_(ж).
Определить теплоту образования С₂Н₅ОН_(ж), зная ΔН х.р. = — 1366,87 кДж. Напишите термохимическое уравнение. Определите мольную теплоту парообразования С₂Н₅ОН_(ж) → С₂Н₅ОН_(г), если известна теплота образования С₂Н₅ОН_(г), равная  –235,31 кДж·моль^-1.

Задача 7. Чем можно объяснить, что при стандартных условиях, невозможна экзотермическая реакция:
СО_{2 (г)}+Н_{2 (г)} ↔ СО _(г)+Н₂О _(ж)?
Рассчитайте ΔG данной реакции. При каких температурах данная реакция становится самопроизвольной?

Задача 8. Рассчитав на основании табличных данных ΔG и ΔS, определите тепловой эффект реакции:
2 NO _(г) + Cl_{2 (г)} ↔  2 NOCl_(г).

Задача 9. С чем  будет более интенсивно взаимодействовать газообразный хлористый водород (в расчете на 1 моль): с алюминием или с оловом? Ответ дайте, рассчитав ΔG⁰ обеих реакций. Продуктами реакций являются твердая соль и газообразный водород.

Задача 10. Не прибегая к вычислениям, определите, какие знаки (>0, <0, ≅0) имеют ΔG, ΔH и ΔS для протекающей в прямом направлении реакции:
4 НBr _(г) +  O_2(г) ↔ 2 H₂O_(г) + 2 Br_2(г)
Как повлияет повышение температуры на направленность химической реакции?

Материалы из методички: Сборник задач по теоретическим основам химии для студентов заочно-дистанционного отделения / Барботина Н.Н., К.К. Власенко, Щербаков В.В. – М.: РХТУ им. Д.И. Менделеева, 2007. -155 с.

Понятие энтропии

Абсолютная энтропия веществ и изменение энтропии в процессах

Стандартная энтропия

Стандартная энтропия образования

Энергия Гиббса

Стандартная энергия Гиббса образования

Энтальпийный, энтропийный фактор и направление процесса

Примеры решения задач

Задачи для самостоятельного решения

Понятие энтропии

Энтропия S – функция состояния системы. Энтропия характеризует меру неупорядоченности (хаотичности) состояния системы. Единицами измерения энтропии являются Дж/(моль·К).

Абсолютная энтропия веществ и изменение энтропии в процессах

При абсолютном нуле температур (Т = 0 К) энтропия идеального кристалла любого чистого простого вещества или соединения равна нулю. Равенство нулю S при 0 К позволяет вычислить абсолютные величины энтропий веществ на основе экспериментальных данных о температурной зависимости теплоемкости.

Изменение энтропии в процессе выражается уравнением:

ΔS = S_(прод.) – S_(исх.)

где S_(прод.) и S_(исх.) – соответственно абсолютные энтропии продуктов реакции и исходных веществ.

На качественном уровне знак S реакции можно оценить по изменению объема системы ΔV в результате процесса. Знак ΔV определяется по изменению количества вещества газообразных реагентов Δn_г. Так, для реакции

CaCO₃(к) = CaO(к) + CO₂(г)

(Δn_г = 1) ΔV > 0, значит, ΔS > 0.

Для реакции:

С(графит) + 2Н₂(г) = СН₄(г)

(Δn_г = -1) ΔV < 0, следовательно и ΔS < 0.

Стандартная энтропия

Величины энтропии принято относить к стандартному состоянию. Чаще всего значения S рассматриваются при Р = 101,325 кПа (1 атм) и температуре Т = 298,15 К (25^оС). Энтропия в этом случае обозначается S^о₂₉₈ и называется стандартной энтропией при Т = 298,15 К. Следует подчеркнуть, что энтропия вещества S (S^о) увеличивается при повышении температуры.

Стандартная энтропия образования

Стандартная энтропия образования ΔS^о_f,298 (или ΔS^о_обр,298) – это изменение энтропии в процессе образования данного вещества (обычно 1 моль), находящегося в стандартном состоянии, из простых веществ, также находящихся в стандартном состоянии.

Энергия Гиббса

Энергия Гиббса G – функция состояния системы. Энергия Гиббса равна:

G = Н – ТS.

Абсолютное значение энергии Гиббса определить невозможно, однако можно вычислить изменение δG в результате протекания процесса.

Критерий самопроизвольного протекания процесса: в системах, находящихся при Р, Т = const, самопроизвольно могут протекать только процессы, сопровождающиеся уменьшением энергии Гиббса (ΔG < 0). При достижении равновесия в системе ΔG = 0.

Стандартная энергия Гиббса образования

Стандартная энергия Гиббса образования δG^о_f,298 (или δG^о_обр,298) – это изменение энергии Гиббса в процессе образования данного вещества (обычно 1 моль), находящегося в стандартном состоянии, из простых веществ, также находящихся в стандартном состоянии, причем простые вещества пристутствуют в наиболее термодинамически устойчивых состояниях при данной температуре.

Для простых веществ, находящихся в термодинамически наиболее устойчивой форме, δG^о_f,298 = 0.

Энтальпийный, энтропийный фактор и направление процесса

Проанализируем уравнение ΔG^о_Т = ΔН^о_Т — ΔТS^о_Т. При низких температурах ТΔS^о_Т мало. Поэтому знак ΔG^о_Т определяется в основном значением ΔН^о_Т (энтальпийный фактор). При высоких температурах ТΔS^о_Т – большая величина, знак Δ G^о_Т определяется и энтропийным фактором. В зависимости от соотношения энтальпийного (ΔН^о_Т) и энтропийного (ТΔS^о_Т) факторов существует четыре варианта процессов.

• • 1. Если ΔН^о_Т < 0, ΔS^о_Т > 0, то ΔG^о_Т < 0 всегда (процесс может протекать самопроизвольно при любой температуре).
    2. Если ΔН^о_Т > 0, ΔS^о_Т < 0, то ΔG^о_Т > 0 всегда (процесс не протекает ни при какой температуре).
    3. Если ΔН^о_Т < 0, ΔS^о_Т < 0, то ΔG^о_Т < 0 при Т < ΔН^о/ΔS^о (процесс идет при низкой температуре за счет энтальпийного фактора).
    4. Если ΔН^о_Т > 0, ΔS^о_Т > 0, то ΔG^о_Т < 0 при Т > ΔН^о/ ΔS^о (процесс идет при высокой температуре за счет энтропийного фактора).

Примеры решения задач

Задача 1. Используя термодинамические справочные данные, вычислить при 298,15 К изменение энтропии в реакции:

4NH_3(г) + 5O_2(г) = 4NО_(г) + 6H₂O_(ж)

Объяснить знак и величину ΔS^о.

Решение. Значения стандартных энтропий исходных веществ и продуктов реакции приведены ниже:

Вещество	NH3(г)	O2(г)	NО(г)	H2O(ж)
Sо298, Дж/(моль·К)	192,66	205,04	210,64	69,95

ΔS^о_х.р.,298 = 4S^о₂₉₈(NО_(г) ) + 6S^о₂₉₈(H₂O_(ж)) — 4S^о₂₉₈(NH_3(г)) — 5S^о₂₉₈(O_2(г)) = 4× 210,64 + 6× 69,95 — 4× 192,66 — 5× 205,04 = — 533,58 Дж/К

В данной реакции ΔV < 0 (Δn_г = — 5), следовательно и ΔS^o_х.р.,298 < 0, что и подтверждено расчетом.

Задача 2. Используя справочные термодинамические данные, рассчитать стандартную энтропию образования NH₄NO_3(к). Отличается ли стандартная энтропия образования NH₄NO_3(к) от стандартной энтропии этого соединения?

Решение. Стандартной энтропии образования NH₄NO₃ отвечает изменение энтропии в процессе:

N_(г) + 2H_2(г) + 3/2O_2(г) = NH₄NO_3(к); δS^о_f,298(NH₄NO_3(к)) = ?

Значения стандартных энтропий исходных веществ и продуктов реакции приведены ниже:

Вещество	N2(г)	H2(г)	O2(г)	NH4NO3(к)
Sо298, Дж/(моль·К)	191,50	130,52	205,04	151,04

ΔS^о_х.р.,298 = ΔS^о_f,298(NH₄NO_3(к)) = S^о₂₉₈(NH₄NO_3(к)) — S^о₂₉₈(N_2(г)) — 2S^о₂₉₈(H_2(г)) – 3/2S^о₂₉₈(O_2(г)) = 151,04–191,50 —— 2× 130,52–3/2× 205,04 = — 609,06 Дж/(моль·К).

Стандартная энтропия образования NH₄NO₃(к), равная — 609,06 Дж/(моль·К), отличается от стандартной энтропии нитрата аммония S^о₂₉₈(NH₄NO_3(к)) = +151,04 Дж/(моль·К) и по величине, и по знаку. Следует помнить, что стандартные энтропии веществ S^о₂₉₈ всегда больше нуля, в то время как величины ΔS⁰_f,298, как правило, знакопеременны.

Задача 3. Изменение энергии Гиббса реакции:

2Н_2(г) + О_2(г) = 2 Н₂О_(ж)

равно δG^о₂₉₈= –474,46 кДж. Не проводя термодинамические расчеты, определить, за счет какого фактора (энтальпийного или энтропийного) протекает эта реакция при 298 К и как будет влиять повышение температуры на протекание этой реакции.

Решение. Поскольку протекание рассматриваемой реакции сопровождается существенным уменьшением объема (из 67,2 л (н.у.) исходных веществ образуется 36 мл жидкой воды), изменение энтропии реакции ΔS^о<0. Поскольку ΔG^о₂₉₈ реакции меньше нуля, то она может протекать при температуре 298 К только за счет энтальпийного фактора. Повышение температуры уменьшает равновесный выход воды, поскольку ТΔS^о<0.

Задача 4. Используя справочные термодинамические данные, определить может ли при 298,15 К самопроизвольно протекать реакция:

С₄Н_10(г) = 2С₂Н_4(г) + Н_2(г)

Если реакция не будет самопроизвольно протекать при 298,15 К, оценить возможность ее протекания при более высоких температурах.

Решение. Значения стандартных энергий Гиббса и энтропий исходных веществ и продуктов реакции приведены ниже:

Вещество	С4Н10(г)	С2Н4(г)	Н2(г)
ΔGоf,298× , кДж/моль	— 17,19	68,14	0
Sо298, Дж/(моль·К)	310,12	219,45	130,52

ΔG^о_х.р.,298 = 2ΔG^о_f,298(С₂Н_4(г)) + ΔG^о_f,298(Н_2(г)) — ΔG^о_f,298(С₄Н_10(г)) = 2× 68,14 + 17,19 = 153,47 кДж.

ΔG^о_х.р.,298 > 0, следовательно, при Т = 298,15 К реакция самопроизвольно протекать не будет.

ΔS^о_х.р.,298 = 2S^о₂₉₈(С₂Н_4(г)) + S^о₂₉₈(Н_2(г)) — S^о₂₉₈(С₄Н_10(г)) = 2× 219,45 + 130,52 – 310,12 = +259,30 Дж/К.

Поскольку ΔS^о_х.р.,298 > 0, то при температуре Т>ΔН^о/ΔS^о величина ΔG^о_х.р.,298 станет величиной отрицательной и процесс сможет протекать самопроизвольно.

Задача 5. Пользуясь справочными данными по ΔG^о_f,298 и S^о₂₉₈, определите ΔH^о₂₉₈ реакции:

N₂O_(г) + 3H_2(г) = N₂H_4(г) + H₂O_(ж)

Решение. Значения стандартных энергий Гиббса и энтропий исходных веществ и продуктов реакции приведены ниже:

Вещество	N2O(г)	H2(г)	N2H4(г)	H2O(ж)
ΔGоf,298, кДж/моль	104,12	0	159,10	-237,23
Sо298, Дж/(моль·К)	219,83	130,52	238,50	69,95

ΔG^о_х.р.,298 = ΔG^о_f,298(N₂H₄(г)) + ΔG^о_f,298(H₂O(ж)) – ΔG^о_f,298(N₂O(г)) – 3ΔG^о_f,298(H₂(г)) = 159,10 + (–237,23) – 104,12 – 0 = –182,25 кДж.

ΔS^о_х.р.,298 = S^о₂₉₈(N₂H₄(г)) + S^о₂₉₈(H₂O(ж)) – S^о₂₉₈(N₂O(г)) — 3S^о₂₉₈(H₂(г)) = 238,50 + 69,95 – 219,83 –3× 130,52 = –302,94 Дж/К.

ΔG^о₂₉₈ = ΔН^о₂₉₈ – ТΔS^о₂₉₈. Подставляя в это уравнение величины ΔН^о₂₉₈ и ТΔS^о₂₉₈, получаем:

ΔН^о₂₉₈ = –182,25× 10³ + 298·(–302,94) = –272526,12 Дж = – 272,53 кДж.

Следует подчеркнуть, что поскольку ΔS^о₂₉₈ выражена в Дж/(моль× К), то при проведении расчетов ΔG⁰₂₉₈ необходимо также выразить в Дж или величину ΔS⁰₂₉₈ представить в кДж/(мольK).

Задачи для самостоятельного решения

1. Используя справочные данные, определите стандартную энтропию образования ΔS^о_f,298 NaHCO_3(к).

2. Выберите процесс, изменение энергии Гиббса которого соответствует стандартной энергии Гиббса образования NO_2(г):

а) NO_(г) + 1/2O_2(г) = NO_2(г);

б) N_2(г) + 2O_2(г) = 2NO_2(г);

в) 1/2N_2(г) + O_2(г) = NO_2(г);

г) N_(г) + O_2(г) = NO_2(г).

3. Используя справочные данные, вычислите при 298,15 К изменение энтропии в реакции:

2NH₄NO_3(к) = 2N_2(г) + 4H₂O_(г) + О_2(г).

Объясните знак и величину  ΔSº реакции.

• .

δSох.р.,298 =1040,84 Дж/К. В данной реакции δV > 0 (D nг = 7), следовательно и δSох.р.,298 > 0, что и подтверждено расчетом.

4. Используя справочные данные, определите принципиальную возможность протекания реакции при 298,15 К:

NiO_(к) + C_{(графит)} = Ni_(к) + CO_(г)

Если реакция не будет самопроизвольно протекать при 298,15 К, оценить возможность ее протекания при более высоких температурах.

ΔGох.р.,298 = 74,45 кДж > 0, следовательно, при Т = 298,15 К реакция самопроизвольно протекать не будет. Поскольку ΔSох.р.,298 = 183,69 Дж/К, то есть больше нуля, то при достаточно высоких температурах ΔGох.р.,298 изменит знак на обратный.

5. Рассчитайте стандартную энергию Гиббса образования ΔG^о_f,298 C₂H₅OH_(ж), используя справочные данные о величинах ΔН^о_f,298 и S^о₂₉₈.

6. Используя справочные данные, определите стандартную энтропию образования ΔS^о_f,298 K₂Cr₂O_7(к).

7. На основе расчетов термодинамических величин покажите, чем эффективнее восстанавливать при 298 К Cr₂O_3(к) до металла — алюминием или магнием:

1) Cr₂O_3(к) + 3Mg_(к) = 3MgO_(к) + 2Cr_(к); ΔG^о₁;
2) Cr₂O_3(к) + 2Al_(к) = Al₂O_3(к) + 2Cr_(к); ΔG^о₂.

ΔGо1=-648,9 кДж; ΔGо2=-523,3 кДж. Таким образом, самопроизвольно протекают два процесса. Так как значение ΔGо1 более отрицательное, то эффективнее при 298 К будет протекать процесс восстановления магнием.

8. Используя справочными данными по величинам S^о₂₉₈, определите возможность самопроизвольного протекания в изолированной системе при 298 К процесса:

KClO_3(к) = KCl_(к) + 3/2O_2(к)

ΔSо298=247,1 Дж/К. ΔSо298 больше 0, следовательно данный процесс будет протекать самопроизвольно в изолированной системе при 298 К.

9. Используя справочные данные, вычислите при 298 К изменение энтропии в процессе:

Н_2(г) + 1/2О_2(г) = Н₂О_(г)

10. На основе справочных данных оценить температуру восстановления WO_3(к) водородом:

WO_3(к) + 3H_2(г) = W_(к) + 3H₂O_(г).

Свободная энергия Гиббса (или просто энергия Гиббса, или потенциал Гиббса, или термодинамический потенциал в узком смысле) — это величина, показывающая изменение энергии в ходе химической реакции и дающая таким образом ответ на вопрос о принципиальной возможности протекания химической реакции; это термодинамический потенциал следующего вида:

G = U + PV – TS

Энергию Гиббса можно понимать как полную химическую энергию системы (кристалла, жидкости и т. д.)

Понятие энергии Гиббса широко используется в термодинамике и химии.

Самопроизвольное протекание изобарно-изотермического процесса определяется двумя факторами: энтальпийным, связанным с уменьшением энтальпии системы (ΔH), и энтропийным T ΔS, обусловленным увеличением беспорядка в системе вследствие роста её энтропии. Разность этих термодинамических факторов является функцией состояния системы, называемой изобарно-изотермическим потенциалом или свободной энергией Гиббса (G, кДж).

1 Основные понятия энергии Гиббса

Классическим определением энергии Гиббса является выражение:

G = U + PV – TS,

где U – внутренняя энергия, P – давление, V – объем, T – абсолютная температура, S – энтропия.

Дифференциал энергии Гиббса для системы с постоянным числом частиц, выраженный в собственных переменных — через давление p и температуру T:

dG = – S dT + VdP.

Для системы с переменным числом частиц этот дифференциал записывается так:

dG = – S dT + V dP + dN.

Здесь – химический потенциал, который можно определить как энергию, которую необходимо затратить, чтобы добавить в систему еще одну частицу.

Правило фаз Гиббса в термодинамике: число равновесно сосуществующих в какой-либо системе фаз не может быть больше числа образующих этих фаз.

Эенергия Гиббса: (изобарно-изотермический потенциал, свободная энтальпия), один из потенциалов термодинамических системы. Обозначается G, определяется разностью между энтальпией H и произведением энтропии S на термодинамическую температуру Т: G = H — T·S. Изотермический равновесный процесс без затраты внешних сил может протекать самопроизвольно только в направлении убывания энергии Гиббса до достижения ее минимума, которому отвечает термодинамическое равновесное состояние системы. Названа по имени Дж. У. Гиббса.

Термодинамические потенциалы , функции объема, давления, температуры, энтропии, числа частиц и других независимых макроскопических параметров, характеризующих состояние термодинамической системы. К потенциалам термодинамическим относятся внутренняя энергия, энтальпия, изохорно-изотермический потенциал (Гельмгольца энергия), изобарно-изотермический потенциал (Гиббса энергия). Зная какие-либо потенциалы термодинамические как функцию полного набора параметров, можно вычислить любые макроскопические характеристики системы и рассчитать происходящие в ней процессы.

Распределение Гиббса: каноническое, распределение вероятностей различных состояний макроскопической системы с постоянным объемом и постоянным числом частиц, находящейся в равновесии с окружающей средой заданной температуры; если система может обмениваться частицами со средой, то распределение Гиббса называется большим каноническим. Для изолированной системы справедливо Гиббса распределение микроканоническое, согласно которому все микросостояния системы с данной энергией равновероятны. Названо по имени открывшего это распределение Дж. У. Гиббса.

2 Значение энергии Гиббса

Самопроизвольность протекания процессов в системах открытого и закрытого типов описывается через специальный критерий, получивший название энергии Гиббса. Он является функцией состояния. Д.У. Гиббс, работая с термодинамическими системами, сумел вывести ее через энтропию и энтальпию. Энергия Гиббса, в частности, позволяет предсказывать направленность протекания самопроизвольных биологических процессов и оценивать их теоретически достижимый КПД.

Если применить выводы Гиббса ко второму термодинамическому закону, то формулировка будет следующей: при постоянных (const) давлении и температуре без внешнего воздействия система может поддерживать самопроизвольное протекание лишь таких процессов, следствием которых является уменьшение уровня энергии Гиббса до значения, которое наступает при достижении ею установившегося минимума. Равновесие любой термодинамической системы означает неизменность указанной энергии (минимум). Поэтому энергия Гиббса представляет собой потенциал (свободную энтальпию) в изобарно-изотермических системах. Поясним, почему указан именно минимум. Дело в том, что это одно из важнейших постулатов равновесия в термодинамике: данное состояние при неизменности температуры и давления означает, что для очередного изменения необходимо увеличить уровень энергии, а такое возможно лишь при смене каких-либо внешних факторов.

Буквенное обозначение – G. Численно равна разности между известной энтальпией и значением произведения температуры на энтропию. То есть энергия Гиббса может быть выражена через следующую формулу:

где S – энтропия системы, t – температура термодинамическая, H – энтальпия.

Энтропия системы в данную формулу включена для того, чтобы учитывать тот факт, что высокая температура приводит к уменьшению упорядоченного состояния системы (беспорядок), а низкая же – наоборот.

Так как и Гиббсова энергия, и энтальпия – одни из функций системы в термодинамике, то посредством изменения G или H можно охарактеризовать протекающие химические превращения. Если приводится уравнение реакции и изменение энергии Гиббса, то его относят к классу термохимических.

Применительно к этой энергии может быть сформулировано Правило Гесса: если давление и температура неизменны, то создание новых веществ из первоначальных (базовых реагентов) приводит к тому, что энергия в системе изменяется, при этом вид происходящих реакций и их количество на результат никак не влияют.

Так как энергия, о которой говорится в представленном докладе, является изменчивой величиной, то для выполнения расчетов было введено понятие «стандартная энергия Гиббса». Эта величина присутствует в любом химическом справочнике, численно равна 298 кДж/моль (обратите внимание, что размерность точно такая же, как для любой другой молярной энергии). Это значение позволяет рассчитать изменение практически для любого химического процесса.

Если в процессе протекания химической реакции на систему оказывается внешнее воздействие (совершается работа), то значение энергии Гиббса увеличивается. Такие реакции относят к эндергоническим. Соответственно, если сама система совершает работу, затрачивая энергию, то речь идет о экзергонических проявлениях.

Понятие Гиббсовой энергии нашло широчайшее применение в современной химии. К примеру, синтез полимеров основан на реакциях присоединения. При их проведении несколько частиц объединяются в одну, при этом значение энтропии уменьшается. Основываясь на формуле Гиббса, можно утверждать, что внешнее воздействие (например, высокотемпературное) может обратить подобную экзотермическую реакцию присоединения, что и подтверждается на практике [2].

3 Методы измерения энергии Гиббса

Существует значительное число способов расчета изобарно- изотермического потенциала. Это объясняется тем, что для расчета Δσot необходимо в соответствии с уравнением (1.6) знать ΔН оt и ΔS оt. Если учесть, что эти величины в свою очередь связаны с температурой уравнением теплоемкости (Ср = f(Т)), то становится понятным, что вычисление Δσot является довольно сложной задачей и требует знания этих величин для каждого компонента, входящего в уравнение реакции. Следует отметить, что для большинства веществ величины Δσot, ΔSot, ΔНot, а также коэффициенты уравнения Ср = а + bТ + с/Т2 обобщены и приведены в таблицах различных справочников [1]. Поскольку в данных справочниках все величины даны в калориях, расчеты выполнены с учетом этих величин. В связи с изложенным рассмотрим расчет Δσo t реакции окисления сернистого ангидрида в серный SО2 + 0.5О2 ↔ SО3 наиболее распространенным методом. В таблице1 приведены исходные термодинамические данные для всех компонентов реакции:

Т а б л и ц а 1 – Термодинамические величины реакции окисления

Компонент реакции ΔНо 298 ккал/моль Δσо 298 Ккал/моль Sо 298 Кал/(моль*град) Ĉр кал /(моль *град 298 – 600

SO2 70,96 71,748 59,30 10,76

O2 0 0 49,03 7,22

SO3 94,45 88,69 61,24 14,84

По значениям стандартных величин ΔНo 298 и So 298

Δσo298 = ΔНo298 – ТΔSo298

Изобарно-изотермический потенциал реакции

Δσo298 = [–94.45 – (–70.96) – 0.298 (61.24 – 0.5 · 49.03 – 59.30] = –16.76 ккал,

что хорошо согласуется с расчетом по закону Гесса:

Δσo298 = –88.69 – (–71.748) = –16.94 ккал

При наличии в справочниках величины средней теплоемкости ΔĈр в исследуемом температурном интервале Δσo 298 определяют

Δσot = ΔНo298 + Δ Ĉр( Т – 298) – Т ΔSo298 – Т ĈрlnТ/298 (1)

Это уравнение неприменимо для расчета Δσo Т в растворах, даже в узком температурном интервале.

Пример 1. Определить Δσ600 для вышеприведенной реакции, если значения Ĉр600 для SО2 О2, SО3 составляют 10.76; 7.22; 18.84 кал/(моль*град). Для решения использовать значение ΔН0 298 и S0 298 из таблицы 1.

Решение.

Δσ600 = [–94.45 –(–70.96) ] +[(18.84 – 0.5 · 7.22 – 10.76) · (600 – 298)] – – 600 (61.24 – 0.5 · 49.03 – 59.30) – 600 · 4.47 ln400/298 = = –23.49 + 1.349 + 13.545 – 1.876 = –10.472 ккал/моль.