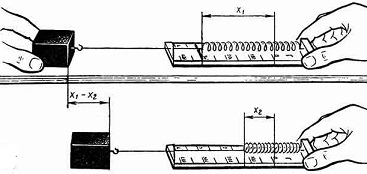
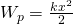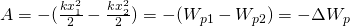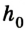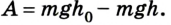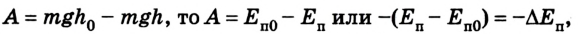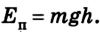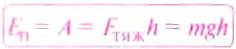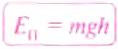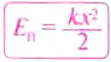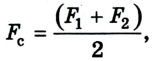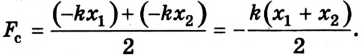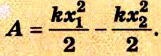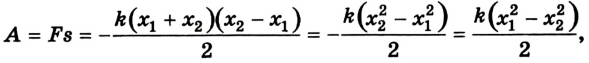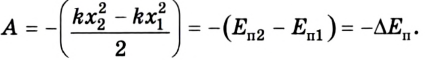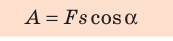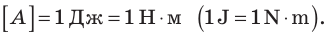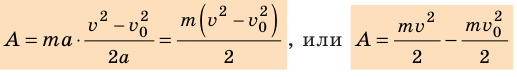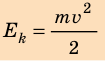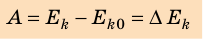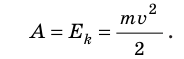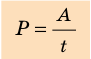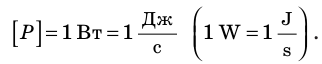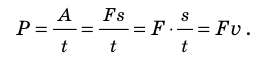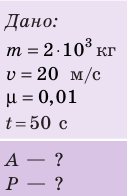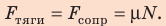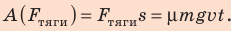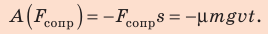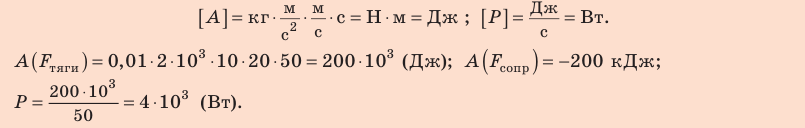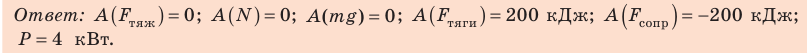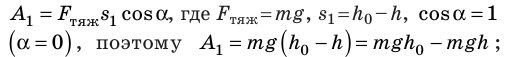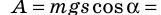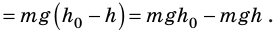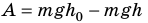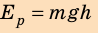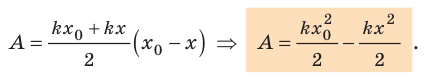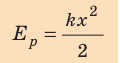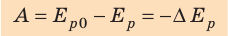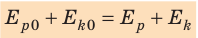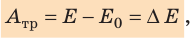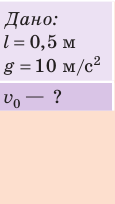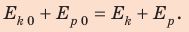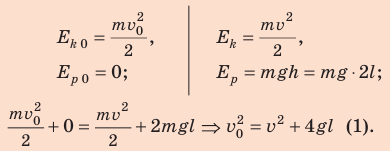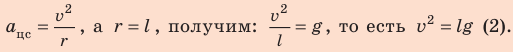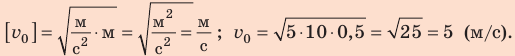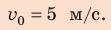Энергия упругости как найти

Упругая потенциальная энергия

Это энергия, запасенная в результате приложения силы для деформации упругого объекта.

Энергия сохраняется до тех пор, пока сила не будет снята, и объект не вернется к своей первоначальной форме, выполняя работу в процессе. Деформация может включать сжатие, растяжение или скручивание объекта.
Многие объекты предназначены специально для хранения упругой потенциальной энергии, например:

спиральная пружина заводных часов;
растянутый лук лучника;
надувной шар, сжатый в тот момент, когда он отскакивает от кирпичной стены.

Объект, предназначенный для хранения потенциальной упругой энергии, обычно имеет высокий предел упругости, однако все упругие объекты имеют предел нагрузки, которую они могут выдержать.

Когда деформация превышает предел упругости, объект больше не вернется к своей первоначальной форме.

Совсем недавно заводные механические часы с пружинами были популярными аксессуарами. В настоящее время мы не склонны использовать их, потому что не существует материалов с достаточно высоким пределом упругости для хранения упругой потенциальной энергии с достаточно высокой плотностью энергии.

Как рассчитать упругую потенциальную энергию для идеальной пружины?

Закон Гука об упругости обсуждает, как величина силы FF в идеальной пружине линейно зависит от длины сжатия или растяжения ΔxΔx.

F=−k⋅ΔxF = – k cdot Δx,

где kk – некоторое положительное число, известное как постоянная пружины.

Сила пружины

Это консервативная сила, а у консервативных сил есть потенциальные энергии, связанные с ними.

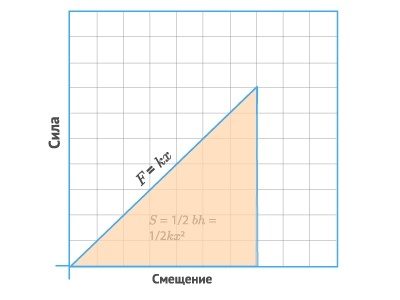
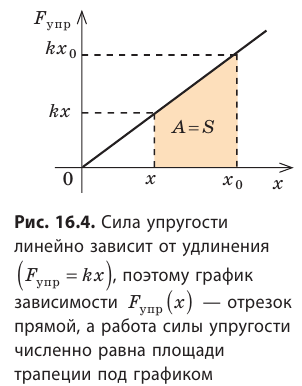
Из определения работы мы знаем, что площадь под графиком силы против смещения дает работу, проделанную силой. На рисунке 1 показан график зависимости силы от смещения для пружины. Поскольку площадь под кривой представляет собой треугольник, и в идеальной пружине энергия не теряется, потенциальная энергия упругости UU можно найти по проделанной работе:

U = 12(△x)⋅k(△x) = 12k(△x)2U;=;frac12(triangle x)cdot k(triangle x);=;frac12k(triangle x)^2

Настоящие упругие материалы

Некоторые упругие материалы, такие как резиновые ленты и гибкие пластмассы, могут функционировать как пружины, но часто имеют гистерезис, это означает, что кривая сила –растяжение следует по другому пути, когда материал деформируется, по сравнению с тем, когда он возвращается к своему равновесному положению.

К счастью, основной метод применения определения работы, который мы использовали для идеальной пружины, также работает для упругих материалов в целом. Упругая потенциальная энергия всегда может быть найдена из области под кривой зависимости силы от растяжения, независимо от формы кривой.

Тест по теме «Упругая потенциальная энергия»

Источник

From Wikipedia, the free encyclopedia

Elastic energy is the mechanical potential energy stored in the configuration of a material or physical system as it is subjected to elastic deformation by work performed upon it. Elastic energy occurs when objects are impermanently compressed, stretched or generally deformed in any manner. Elasticity theory primarily develops formalisms for the mechanics of solid bodies and materials.^[1] (Note however, the work done by a stretched rubber band is not an example of elastic energy. It is an example of entropic elasticity.) The elastic potential energy equation is used in calculations of positions of mechanical equilibrium. The energy is potential as it will be converted into other forms of energy, such as kinetic energy and sound energy, when the object is allowed to return to its original shape (reformation) by its elasticity.

${displaystyle U={frac {1}{2}}k,Delta x^{2}}$

The essence of elasticity is reversibility. Forces applied to an elastic material transfer energy into the material which, upon yielding that energy to its surroundings, can recover its original shape. However, all materials have limits to the degree of distortion they can endure without breaking or irreversibly altering their internal structure. Hence, the characterizations of solid materials include specification, usually in terms of strains, of its elastic limits. Beyond the elastic limit, a material is no longer storing all of the energy from mechanical work performed on it in the form of elastic energy.

Elastic energy of or within a substance is static energy of configuration. It corresponds to energy stored principally by changing the interatomic distances between nuclei. Thermal energy is the randomized distribution of kinetic energy within the material, resulting in statistical fluctuations of the material about the equilibrium configuration. There is some interaction, however. For example, for some solid objects, twisting, bending, and other distortions may generate thermal energy, causing the material’s temperature to rise. Thermal energy in solids is often carried by internal elastic waves, called phonons. Elastic waves that are large on the scale of an isolated object usually produce macroscopic vibrations sufficiently lacking in randomization that their oscillations are merely the repetitive exchange between (elastic) potential energy within the object and the kinetic energy of motion of the object as a whole.

Although elasticity is most commonly associated with the mechanics of solid bodies or materials, even the early literature on classical thermodynamics defines and uses “elasticity of a fluid” in ways compatible with the broad definition provided in the Introduction above.^[2]^{: 107 et seq.}

Solids include complex crystalline materials with sometimes complicated behavior. By contrast, the behavior of compressible fluids, and especially gases, demonstrates the essence of elastic energy with negligible complication. The simple thermodynamic formula: where dU is an infinitesimal change in recoverable internal energy U, P is the uniform pressure (a force per unit area) applied to the material sample of interest, and dV is the infinitesimal change in volume that corresponds to the change in internal energy. The minus sign appears because dV is negative under compression by a positive applied pressure which also increases the internal energy. Upon reversal, the work that is done by a system is the negative of the change in its internal energy corresponding to the positive dV of an increasing volume. In other words, the system loses stored internal energy when doing work on its surroundings. Pressure is stress and volumetric change corresponds to changing the relative spacing of points within the material. The stress-strain-internal energy relationship of the foregoing formula is repeated in formulations for elastic energy of solid materials with complicated crystalline structure.

Elastic potential energy in mechanical systems[edit]

Components of mechanical systems store elastic potential energy if they are deformed when forces are applied to the system. Energy is transferred to an object by work when an external force displaces or deforms the object. The quantity of energy transferred is the vector dot product of the force and the displacement of the object. As forces are applied to the system they are distributed internally to its component parts. While some of the energy transferred can end up stored as the kinetic energy of acquired velocity, the deformation of component objects results in stored elastic energy.

A prototypical elastic component is a coiled spring. The linear elastic performance of a spring is parametrized by a constant of proportionality, called the spring constant. This constant is usually denoted as k (see also Hooke’s Law) and depends on the geometry, cross-sectional area, undeformed length and nature of the material from which the coil is fashioned. Within a certain range of deformation, k remains constant and is defined as the negative ratio of displacement to the magnitude of the restoring force produced by the spring at that displacement.

${displaystyle k=-{frac {F_{r}}{L-L_{o}}}}$

The deformed length, L, can be larger or smaller than L_o, the undeformed length, so to keep k positive, F_r must be given as a vector component of the restoring force whose sign is negative for L>L_o and positive for L< L_o. If the displacement is abbreviated as

${displaystyle L-L_{o}=x,}$

then Hooke’s Law can be written in the usual form

${displaystyle F_{r}=-k,x.}$

Energy absorbed and held in the spring can be derived using Hooke’s Law to compute the restoring force as a measure of the applied force. This requires the assumption, sufficiently correct in most circumstances, that at a given moment, the magnitude of applied force, F_a is equal to the magnitude of the resultant restoring force, but its direction and thus sign is different. In other words, assume that at each point of the displacement F_a = k x, where F_a is the component of applied force along the x direction

${displaystyle mathbf {F} _{a}cdot mathbf {x} =F_{a},x.}$

For each infinitesimal displacement dx, the applied force is simply k x and the product of these is the infinitesimal transfer of energy into the spring dU. The total elastic energy placed into the spring from zero displacement to final length L is thus the integral

${displaystyle U=int _{0}^{L-L_{o}}k,x,dx={tfrac {1}{2}}k(L-L_{o})^{2}}$

For a material of Young’s modulus, Y (same as modulus of elasticity λ), cross sectional area, A₀, initial length, l₀, which is stretched by a length, Delta l :

${displaystyle U_{e}=int {frac {YA_{0}Delta l}{l_{0}}},dleft(Delta lright)={frac {YA_{0}{Delta l}^{2}}{2l_{0}}}}$

where U_e is the elastic potential energy.

The elastic potential energy per unit volume is given by:

${displaystyle {frac {U_{e}}{A_{0}l_{0}}}={frac {Y{Delta l}^{2}}{2l_{0}^{2}}}={frac {1}{2}}Y{varepsilon }^{2}}$

where $varepsilon = frac {Delta l} {l_0}$ is the strain in the material.

In the general case, elastic energy is given by the free energy per unit of volume f as a function of the strain tensor components ε_ij

${displaystyle f(varepsilon _{ij})={frac {1}{2}}lambda varepsilon _{ii}^{2}+mu varepsilon _{ij}^{2}}$

where λ and μ are the Lamé elastic coefficients and we use Einstein summation convention. Noting the thermodynamic connection between stress tensor components and strain tensor components,^[1]

${displaystyle sigma _{ij}=left({frac {partial f}{partial varepsilon _{ij}}}right)_{T},}$

where the subscript T denotes that temperature is held constant, then we find that if Hooke’s law is valid, we can write the elastic energy density as

${displaystyle f={frac {1}{2}}varepsilon _{ij}sigma _{ij}.}$

Continuum systems[edit]

Matter in bulk can be distorted in many different ways: stretching, shearing, bending, twisting, etc. Each kind of distortion contributes to the elastic energy of a deformed material. In orthogonal coordinates, the elastic energy per unit volume due to strain is thus a sum of contributions:

${displaystyle U={frac {1}{2}}C_{ijkl}varepsilon _{ij}varepsilon _{kl},}$

where $C_{ijkl}$ is a 4th rank tensor, called the elastic tensor or stiffness tensor^[3] which is a generalization of the elastic moduli of mechanical systems, and $varepsilon _{ij}$ is the strain tensor (Einstein summation notation has been used to imply summation over repeated indices). The values of $C_{ijkl}$ depend upon the crystal structure of the material: in the general case, due to symmetric nature of sigma and , the elastic tensor consists of 21 independent elastic coefficients.^[4] This number can be further reduced by the symmetry of the material: 9 for an orthorhombic crystal, 5 for an hexagonal structure, and 3 for a cubic symmetry.^[5] Finally, for an isotropic material, there are only two independent parameters, with ${displaystyle C_{ijkl}=lambda delta _{ij}delta _{kl}+mu left(delta _{ik}delta _{jl}+delta _{il}delta _{jk}right)}$ , where lambda and are the Lamé constants, and $delta _{ij}$ is the Kronecker delta.

The strain tensor itself can be defined to reflect distortion in any way that results in invariance under total rotation, but the most common definition with regard to which elastic tensors are usually expressed defines strain as the symmetric part of the gradient of displacement with all nonlinear terms suppressed:

${displaystyle varepsilon _{ij}={frac {1}{2}}left(partial _{i}u_{j}+partial _{j}u_{i}right)}$

where $u_{i}$ is the displacement at a point in the -th direction and $partial _{j}$ is the partial derivative in the -th direction. Note that:

${displaystyle varepsilon _{jj}=partial _{j}u_{j}}$

where no summation is intended. Although full Einstein notation sums over raised and lowered pairs of indices, the values of elastic and strain tensor components are usually expressed with all indices lowered. Thus beware (as here) that in some contexts a repeated index does not imply a sum overvalues of that index ( in this case), but merely a single component of a tensor.

References[edit]

^ ^a ^b Landau, L.D.; Lifshitz, E. M. (1986). Theory of Elasticity (3rd ed.). Oxford, England: Butterworth Heinemann. ISBN 0-7506-2633-X.
^ Maxwell, J.C. (1888). Peter Pesic (ed.). Theory of Heat (9th ed.). Mineola, N.Y.: Dover Publications Inc. ISBN 0-486-41735-2.
^ Dove, Martin T. (2003). Structure and dynamics : an atomic view of materials. Oxford: Oxford University Press. ISBN 0-19-850677-5. OCLC 50022684.
^ Nye, J. F. (1985). Physical properties of crystals : their representation by tensors and matrices (1st published in pbk. with corrections, 1985 ed.). Oxford [Oxfordshire]: Clarendon Press. ISBN 0-19-851165-5. OCLC 11114089.
^ Mouhat, Félix; Coudert, François-Xavier (2014-12-05). “Necessary and sufficient elastic stability conditions in various crystal systems”. Physical Review B. 90 (22): 224104. arXiv:1410.0065. Bibcode:2014PhRvB..90v4104M. doi:10.1103/PhysRevB.90.224104. ISSN 1098-0121. S2CID 54058316.

Sources[edit]

^[1]

^ Eshelby, J.D (November 1975). “The elastic energy-momentum tensor”. Journal of Elasticity. 5 (3–4): 321–335. doi:10.1007/BF00126994. S2CID 121320629.

Источник

1.Консервативная и Диссипативная сила. Потенциальное поле.

Консервативными
силами называются силы, работа которых
не зависит от пути перехода тела или
системы из начального положения в
конечное. Характерное свойство таких
сил – работа на замкнутой траектории
равна нулю:

К
консервативным силам относятся: сила
тяжести, гравитационная сила, сила
упругости и другие силы.

Неконсервативными(диссипативными)
силами называются силы, работа которых
зависит от пути перехода тела или системы
из начального положения в конечное.
Работа этих сил на замкнутой траектории
отлична от нуля. К неконсервативным
силам относятся: сила трения, сила тяги
и другие силы.

Пусть
взаимодействие тел осуществляется
посредством силовых полей (например,
поля упругих сил, поля гравитационных
сил), характеризующихся тем, что работа,
совершаемая действующими силами при
перемещении тела из одного положения
в другое, не зависит от того, по какой
траектории это перемещение произошло,
а зависит только от начального и конечного
положений. Такие поля называются
потенциальными, а силы, действующие
в них, — консервативными

2.Потенциальная энергия упругой силы и работа по растяжению и сжатию пружины.

Энергию
деформированного упругого тела также
называют энергией положения или
потенциальной энергией (ее называют
чаще упругой энергией ), так как она
зависит от взаимного положения частей
тела, например витков пружины. Работа,
которую может совершить растянутая
пружина при перемещении ее конца, зависит
только от начального и конечного
растяжений пружины. Найдем работу,
которую может совершить растянутая
пружина, возвращаясь к нерастянутому
состоянию, т.е. найдем упругую энергию
растянутой пружины.

Пусть,
например, растянутая пружина закреплена
одним концом, а второй конец, перемещаясь,
совершает работу. При нахождении работы
мы должны учитывать, что сила , с которой
действует пружина, не остается постоянной
при изменении растяжения. Мы видели (§
37), что сила упругости пружины
пропорциональна ее растяжению. Если
первоначальное растяжение пружины,
считая от ее нерастянутого состояния,
равнялось l, то первоначальное значение
силы упругости составляло F=kl, где k —
коэффициент пропорциональности, который
называют коэффициентом упругости
пружины. По мере сокращения пружины эта
сила равномерно убывает от значения kl
до нуля.

Значит,
среднее значение силы равно Fср=kl. Можно
показать, что для вычисления работы А
изменяющейся силы упругости нужно это
среднее значение силы умножить на
перемещение точки приложения силы :

A=1/2
kl•l=1/2kl2.

Таким
образом, потенциальная энергия
упругости Еп равна

Eп
= 1/2 kl2. (98.1)

8. Консервативные и диссипативные силы. Потенциальное поле. Потенциальная энергия гравитационной силы. Работа по поднятию тела.

1.Консервативная и Диссипативная сила. Потенциальное поле.

К
консервативным силам относятся: сила
тяжести, гравитационная сила, сила
упругости и другие силы.

2.Потенциальная
энергия гравитационной силы. Работа по
поднятию тела.

Найдем,
чему равна работа А, совершаемая при
подъеме тела весом Р на высоту h. Будем
считать, что поднятие тела происходит
медленно и что силами трения при подъеме
можно пренебречь. Мы уже знаем что
произведенная работа против силы
тяжести не будет зависеть от того, как
мы поднимаем тело : по вертикали (как
гирю в часах), по наклонной плоскости
(как при втаскивании санок в гору) или
еще каким-либо способом. Во всех случаях
эта работа будет равна А = Рh. При
опускании тела на первоначальный
уровень сила тяжести произведет такую
же работу , какая была затрачена на
подъем тела . Значит, поднимая тело ,
мы запасли работу , равную Ph, т. е. поднятое
тело обладает энергией , равной
произведению веса тела на высоту
поднятия .

Эта
энергия не зависит от того, по какому
пути происходил подъем, а определяется
лишь положением тела (высотой, на
которую оно поднято). Поэтому эту энергию
называют энергией положения. Чаще ее
называют потенциальной энергией .

Итак,
потенциальная энергия Еп тела ,
поднятого на некоторую высоту, выражается
формулой

Eп
= Ph. (97.1)

Потенциальная
энергия гравитационного взаимодействия
системы двух материальных точек с
массами m и М, находящихся
на расстоянии r одна от другой, равна :
Ep= G*(M*m)/r

где G –
гравитационная постоянная, а нуль
отсчета потенциальной энергии (Еp = 0)
принят при r = ∞. Потенциальная энергия
гравитационного взаимодействия тела
массой т с Землей, где h – высота тела
над поверхностью Земли, М3 – масса Земли,
R3 – радиус Земли, а нуль отсчета
потенциальной энергии выбран при h = 0.

Ep=
G*(Mз*m*h)/(Rз(Rз+h))

При том же
условии выбора нуля отсчета потенциальная
энергия гравитационного взаимодействия
тела массой т с Землей для малых высот
h равна

Еp = m∙g∙h,
где g=G*Mз/Rз^2–
модуль ускорения свободного падения
вблизи поверхности Земли.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Потенциальная энергия упруго деформированного тела — физическая величина, равная половине произведения жесткости тела на квадрат его деформации.

Потенциальная энергия упруго деформированного тела зависит от взаимного положения частей тела относительно друг друга, например витков пружины. Работа, которую может совершить растянутая пружина при перемещении ее конца, зависит только от начального и конечного растяжений пружины.

Найдем работу, которую может совершить растянутая пружина, возвращаясь к не растянутому состоянию, то есть найдем потенциальную энергию растянутой пружины.

Потенциальная энергия упруго деформированного тела равна работе, которую совершает сила упругости при переходе тела в состояние, в котором деформация равна нулю.

Из этой формулы видно, что, растягивая с одной и той же силой разные пружины, мы сообщим им различный запас потенциальной энергии: чем жестче пружина, то есть чем больше коэффициент упругости, тем меньше потенциальная энергия; и наоборот: чем мягче пружина, тем больше энергия, которую она запасет при данной силе, растянувшей ее. Это можно уяснить себе наглядно, если учесть, что при одинаковых действующих силах растяжение мягкой пружины больше, чем жесткой, а потому больше и произведение силы на путь точки приложения силы.

Обозначения:

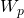
— потенциальная энергия тела

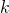
— коэффициент жесткости (или просто жесткость) пружины

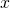
— абсолютная деформация (удлинение или сжатие пружины)

A — работа, которую совершает растянутая пружина

Источник

Содержание:

Потенциальная энергия:

По определению потенциальная энергия – это энергия взаимодействия. Т. е. потенциальную энергию имеют все взаимодействующие тела. Для каждого вида механического взаимодействия можно рассчитать потенциальную энергию, учитывая особенности данного взаимодействия.

Самым распространенным в природе является гравитационное взаимодействие, проявлением которого является сила тяжести. При определенных условиях эта сила может выполнять работу.

Допустим, тело массой т подвешено над полом на высоте

Если нить перерезать, то тело начнет падать под действием силы тяжести.

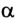
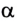
По определению работа А = Fs cos = mgs cos.

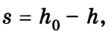
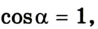
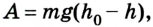
Если учесть, что a то или

Поскольку работа равна изменению энергии, то можно считать, что выражение mgh определяет потенциальную энергию тела в поле силы тяжести Земли на высоте Л. Движение под действием силы тяжести может происходить по разным траекториям. Выясним, будет ли это влиять на значение работы.

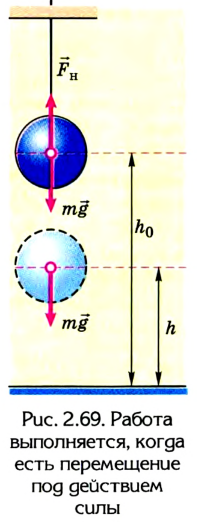
Дадим возможность телу свободно скользить без трения по наклонной плоскости под действием силы тяжести (рис. 2.70).

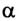
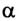
Если учитывать, что А = mgscos, s=AB, то А = mgABcos.

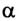
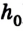
Из треугольника ABC ABcos = ВС и вместе с тем BD = – h.

Тогда работа силы тяжести при скольжении тела без трения по наклонной плоскости будет равна А = mg(h – ).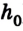

Следовательно, работа силы тяжести по перемещению тела по наклонной плоскости будет такой же, как и при его падении из точки В, расположенной на высоте 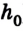, в точку D, находящуюся на высоте Л.

Таким образом, работа силы тяжести определяется положением точек начала и конца движения и не зависит от формы траектории.

В тех случаях, когда работа силы не зависит от формы траектории, а определяется начальным и конечным положением тела, пользуются понятием потенциальной энергии.

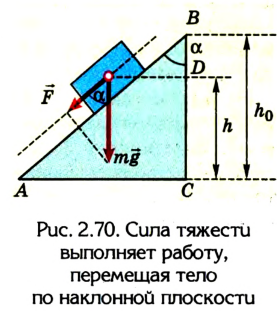
Если записать формулу для работы силы тяжести в виде

т. е. работа определяется изменением величины mgh, которая называется потенциальной энергией тела в поле силы тяжести:

Работа силы тяжести равна изменению потенциальной энергии тела с противоположным знаком. Это означает, что при падении тела, когда сила тяжести выполняет положительную работу, его потенциальная энергия уменьшается. И наоборот, при движении тела вверх, когда сила тяжести выполняет отрицательную работу, его потенциальная энергия увеличивается. Эта особенность характерна для всех случаев, когда работа силы не зависит от формы траектории.

Что такое потенциальная энергия

Потенциальная энергия (от латинского слова потенциал – возможность) – это энергия, которая определяется взаимным положением взаимодействующих тел или частей одного тела.

Поскольку любое тело и Земля притягивают друг друга, т. е. взаимодействуют, то потенциальная энергия тела, поднятого над Землей, будет зависеть от высоты подъёма h. Чем больше высота подъёма тела, тем больше его потенциальная энергия.

Опытами установлено, что потенциальная энергия тела зависит не только от высоты, на которую оно поднято, но и от массы тела. Если тела подняты на одинаковую высоту, то тело, у которого масса больше, будет иметь и ббльшую потенциальную энергию. Во время падения поднятого тела на поверхность Земли сила тяжести выполнила работу, соответствующую изменению потенциальной энергии тела со значения её на высоте И до значения на поверхности Земли. Если для удобства принять, что потенциальная энергия тела на поверхности Земли равна нулю, то потенциальная энергия поднятого тела будет равна выполненной во время падения работе:

Итак, потенциальную энергию тела, поднятого на некоторую высоту, будем определять по формуле:

где Е_п — потенциальная энергия поднятого тела; m — масса тела; 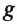= 9,81

h — высота, на которую поднято тело.

Большой запас потенциальной энергии у воды горных или равнинных рек, поднятых плотинами. Падая с высоты вниз, вода выполняет работу: приводит в движение турбины гидроэлектростанций. В Украине на Днепре построено несколько гидроэлектростанций, в которых используют энергию воды для получения электроэнергии. На рисунке 174 изображено сечение такой станции. Вода с более высокого уровня падает вниз и вращает колесо гидротурбины. Вал турбины соединён с генератором электрического тока.

Потенциальной энергией обладает самолёт, летящий высоко в небе; дождевые капли в туче; молот копра при забивании свай. Открывая двери с пружиной, мы растягиваем её, преодолевая силу упругости, т. е. выполняем работу. Вследствие этого пружина приобретает потенциальную энергию. За счёт этой энергии пружина, сокращаясь, выполняет работу – закрывает двери. Потенциальную энергию пружин используют в часах, разнообразных заводных игрушках. В автомобилях, вагонах пружины амортизаторов и буферов, деформируясь, уменьшают толчки.

Потенциальная энергия пружины зависит от её удлинения (изменения длины при сжатии или растяжении) и жёсткости (зависит от конструкции пружины и упругости материала, из которого она изготовлена). Чем больше удлинение (деформация) пружины, и чем больше её жёсткость, тем большую потенциальную энергию она приобретает при деформации. Такая зависимость свойственна любому упруго деформированному телу.

Потенциальную энергию упругодеформированного тела определяют по формуле:

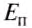
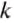
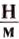
где — потенциальная энергия упруго деформированного тела (пружины); — жёсткость тела (единица жёсткости — 1 — удлинение (деформация) тела (пружины).

Но тела могут обладать энергией не только потому, что они находятся в определённом положении или деформируются, а и потому, что они находятся в движении.

Определение потенциальной энергии

В повседневной жизни можно обнаружить множество различных тел, при перемещении которых может выполняться работа. Так, выпавший из рук шарик начнет падать под действием силы притяжения, которая будет выполнять работу по перемещению шарика.

Сжатая пружина может поднять на определенную высоту груз. В этом случае сила упругости выполняет работу по перемещению груза.

Что такое энергия

Энергия – это физическая величина, показывающая, какая работа может быть выполнена при перемещении тела.

Можно привести еще много разных примеров из природы, из повседневной жизни, из техники, в которых речь идет о телах, находящихся в таком состоянии, что при определенных условиях может выполняться работа при их перемещении. О таких телах говорят, что они обладают энергией. При различных условиях результат выполнения работы может быть разным. Поэтому и энергия может иметь различные значения и может быть рассчитана.

Единицы энергии

Поскольку речь идет о возможности выполнения работы, то энергию целесообразно измерять в таких же единицах, что и работу. Поэтому единицей энергии есть 1 Дж.

Виды механической энергии

В физике выделяют два вида механической энергии: потенциальную и кинетическую. Если тело неподвижно, но па него действует определенная сила, то говорят, что оно обладает потенциальной энергией.

Потенциальной энергией обладает тело, поднятое над поверх-136 ностью Земли, сжатая пружина, сжатый газ, речная вода в водоеме и другие тела.

Как рассчитывают потенциальную энергию

Рассчитывают потенциальную энергию с учетом природы сил, действующих на эти тела. Проще всего рассчитать потенциальную энергию тела, поднятого над поверхностью Земли, поскольку сила, действующая на него, остается практически постоянной на протяжении всего времени его движения под действием этой силы.

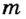
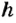
Пусть тело массой находится на высоте над землей. Если оно упадет на поверхность, то будет выполнена работа

Следовательно, о таком теле можно сказать, что оно обладает потенциальной энергией

Потенциальная энергия тела, поднятого над поверхностью Земли, пропорциональна массе тела и его высоте над поверхностью Земли.

При расчете потенциальной энергии важно помнить, что высота 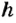является путем, который тело преодолеет в вертикальном направлении. Таким образом, всегда следует указывать, относительно какой поверхности определяется потенциальная энергия. Например, тело массой 2 кг, поднятое над столом на высоту 1,5 м, будет обладать потенциальной энергией, равной примерно 30 Дж, а потенциальная энергия этого тела, рассчитанная для высоты 3 м над полом, будет 60 Дж.

Потенциальная энергия упруго деформированного тела

Расчет работы силы упругости усложняется тем, что в ходе выполнения работы значение силы изменяется. Поскольку изменение силы упругости происходит линейно, то при расчетах работы используют среднее значение силы:

где 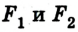– значения силы упругости в начале и в конце процесса.

Учитывая, что 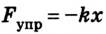(по закону Гука), то

В случае, когда 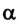= 0, т. е. сила упругости действует вдоль прямой, по которой происходит перемещение, получим выражение для расчета работы силы упругости:

где 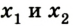– удлинение, характеризующее начальную и конечную деформации соответственно.

Для потенциальной энергии тела в поле силы тяжести можно записать:

Потенциальная энергия упруго деформированного тела зависит от его деформации.

Работа силы упругости равна изменению потенциальной энергии упруго деформированного тела, взятой с противоположным знаком.

Как и в случае работы силы тяжести, работа силы упругости зависит не от формы траектории, а только от начальной и конечной деформации тела.

Механическая работа и кинетическая энергия

Чтобы шли механические часы, их нужно завести — закрутить пружину; раскручиваясь, пружина совершит работу. Поднявшись на вершину горы, лыжник создаст «запас работы» и в результате сможет скатиться вниз; при этом работу совершит сила тяжести. Самый простой способ разбить окно в горящем доме — бросить в окно камень. Если скорость движения камня достаточна, он разобьет окно — совершит работу. О теле или системе тел, которые могут совершить работу, говорят, что они обладают энергией.

Когда сила совершает механическую работу

Основная задача механики — определение механического состояния тела (координат тела и скорости его движения) в любой момент времени. Механическое состояние тела не изменяется само по себе — необходимо взаимодействие, то есть наличие силы. Когда тело перемещается (изменяет свое механическое состояние) под действием силы, говорят, что данная сила совершает механическую работу.

Механическая работа (работа силы) A — физическая величина, характеризующая изменение механического состояния тела и равная произведению модуля силы F, модуля перемещения s и косинуса угла a между вектором силы и вектором перемещения:

Единица работы в СИ — джоуль:

1 Дж равен механической работе, которую совершает сила 1 Н, перемещая тело на 1 м в направлении действия этой силы.

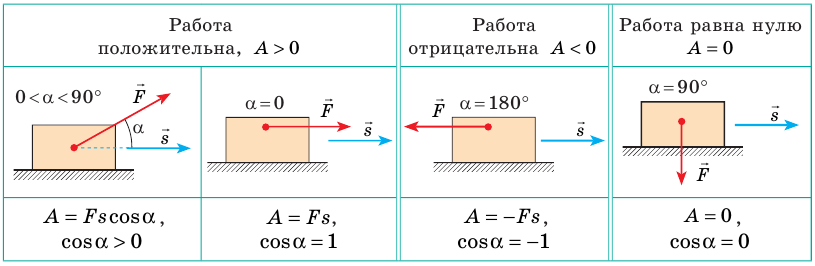
Работа силы — величина скалярная, однако она может быть положительной, отрицательной, равной нулю — в зависимости от того, куда направлена сила относительно направления движения тела (см. таблицу).

Геометрический смысл работы силы

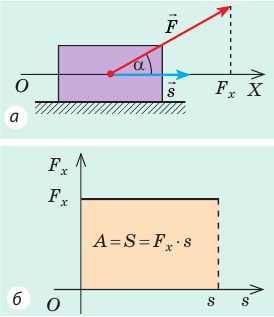
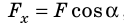
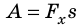
Рассмотрим силу, действующую под некоторым углом α к направлению движения тела. Найдем проекцию этой силы на направление перемещения тела, для чего ось ОХ направим в сторону движения тела (рис. 15.1, а). Из рисунка видим, что , следовательно, .

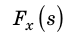
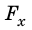
Построим график — зависимости проекции силы от модуля перемещения. Если сила, действующая на тело, постоянна, график этой зависимости представляет собой отрезок прямой, параллельной оси перемещения (рис. 15.1, б). Из рисунка видим, что произведение и s соответствует площади S прямоугольника под графиком.

Рис. 15.1. Если направление оси ОХ совпадает с направлением движения тела, то работа A силы численно равна площади S фигуры под графиком зависимости

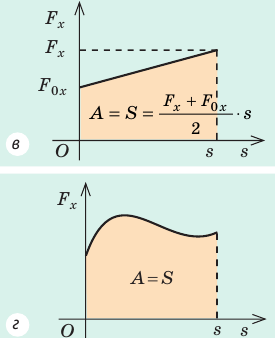
В этом состоит геометрический смысл работы силы: работа силы численно равна площади фигуры под графиком зависимости проекции силы от модуля перемещения. Это утверждение распространяется и на случаи, когда сила переменная (рис. 15.1, в, г).

Когда тело имеет кинетическую энергию

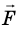
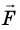
Рассмотрим тело массой m, которое под действием равнодействующей силы увеличивает скорость своего движения от v0 до v. Пусть равнодействующая не изменяется со временем и направлена в сторону движения тела. Определим работу этой силы.

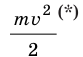
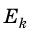
Величину называют кинетической энергией тела .

Кинетическая энергия — физическая величина, которая характеризует механическое состояние движущегося тела и равна половине произведения массы m тела на квадрат скорости v его движения:

Теорема о кинетической энергии: работа равнодействующей всех сил, которые действуют на тело, равна изменению кинетической энергии тела:

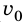
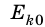
Если в начальный момент времени тело неподвижно ( = 0), то есть= 0, то теорема о кинетической энергии сводится к равенству:

Кинетическая энергия тела, движущегося со скоростью v, равна работе, которую совершает сила, чтобы придать неподвижному телу данную скорость.

Мощность

До сих пор мы говорили о работе силы. Но любая сила характеризует действие определенного тела (или поля). Поэтому работу силы часто называют работой тела (работой поля), со стороны которого действует эта сила. На практике большое значение имеет не только выполненная работа, но и время, за которое эта работа была выполнена. Поэтому для характеристики механизмов, предназначенных для совершения работы, используют понятие мощности.

Мощность P (или N) — физическая величина, характеризующая скорость выполнения работы и равная отношению работы А к интервалу времени t, за который эта работа выполнена:

Единица мощности в СИ — ватт:

(Названа в честь Джеймса Ватта (1736–1819). Как единицу мощности он ввел лошадиную силу, которую иногда используют и сейчас: 1 л. с. = 746 Вт.)

Мощность, которую развивает транспортное средство, удобно определять через силу тяги и скорость движения. Если тело движется равномерно, а направление силы тяги совпадает с направлением перемещения, тяговую мощность двигателя можно вычислить по формуле:

Обратите внимание! Данная формула справедлива для любого движения: мощность, которую развивает двигатель в данный момент времени, равна произведению модуля силы тяги двигателя на модуль его мгновенной скорости: P = Fv (рис. 15.3).

Рис. 15.3. Когда для движения автомобиля требуется большая сила тяги, водитель переходит на меньшую скорость или нажимает на газ, увеличивая таким образом мощность двигателя

Чтобы определить механическую работу и мощность, нужно знать силу, действующую на тело, перемещение тела и время его движения. Поэтому обычно решение задач на определение работы и мощности сводится к решению задач по кинематике и динамике.

Пример №1

Автомобиль массой 2 т движется равномерно со скоростью 20 м/с по горизонтальному участку дороги. Какие силы действуют на автомобиль? Найдите работу каждой силы и тяговую мощность двигателя автомобиля, если коэффициент сопротивления движению равен 0,01, а время движения — 50 с.

Решение:

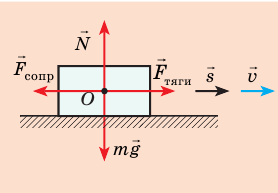
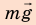
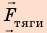
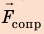
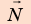
Выполним пояснительный рисунок, на котором укажем силы, действующие на автомобиль: силу тяжести , силу тяги , силу сопротивления движению , силу нормальной реакции опоры. По определению работы: A = Fscosα

Чтобы определить работу каждой силы, нужно найти::

угол между направлением этой силы и направлением перемещения;
модуль силы и модуль перемещения.

1. Автомобиль движется равномерно, поэтому действующие на него силы скомпенсированы: — сила тяжести уравновешена силой нормальной реакции опоры: N = mg; — сила тяги уравновешена силой сопротивления движению:

2. Перемещение автомобиля можно найти по формуле: s = vt .

3. Сила тяжести и сила нормальной реакции опоры перпендикулярны направлению движения автомобиля (α = 90°, cosα = 0). Следовательно, работа этих сил равна нулю. Сила тяги направлена в сторону движения тела: α = 0, cosα = 1, поэтому:

Сила сопротивления противоположна движению: α = 180°, cosα = −1, поэтому:

4. Тяговую мощность двигателя автомобиля определим по формуле 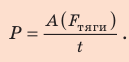Проверим единицы, найдем значения искомых величин:

Выводы:

Потенциальная энергия и закон сохранения механической энергии

Поднятый молот не обладает кинетической энергией, так как его скорость равна нулю. Но если молот отпустить, он совершит работу (расплющит металл). Натянутая тетива лука не имеет кинетической энергии, но, выпрямляясь, она придаст скорость стреле, а значит, совершит работу. И деформированное тело, и тело, поднятое над поверхностью Земли, способны совершить работу, то есть обладают энергией. Что это за энергия и как ее рассчитать?

Когда тело обладает потенциальной энергией

Механическая энергия E — физическая величина, характеризующая способность тела (системы тел) совершить работу.

Единица энергии (как и работы) в СИ — джоуль [E] = 1 Дж (J).

Любое движущееся тело может совершить работу, поскольку оно обладает кинетической энергией, или «живой силой», как ее называли раньше. Есть еще один вид механической энергии — ее называли «мертвая сила». Это — потенциальная энергия (от лат. potentia — сила, возможность), — энергия, которую имеет тело в результате взаимодействия с другими телами.

Потенциальная энергия — энергия, которой обладает тело вследствие взаимодействия с другими телами или вследствие взаимодействия частей тела.

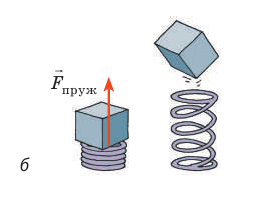
Рис. 16.1. И девочка в результате взаимодействия с Землей (а), и сжатая пружина в результате взаимодействия ее витков (б) обладают потенциальной энергией

Девочка на вершине горки (рис. 16.1, а) обладает потенциальной энергией, поскольку в результате взаимодействия с Землей может начать движение и сила тяжести совершит работу. Но как вычислить эту работу, ведь горка неровная и в течение всего времени движения угол между направлением силы тяжести и направлением перемещения будет изменяться?

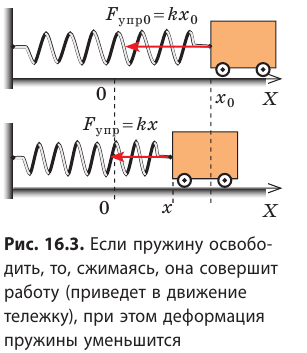
Сжатая пружина (рис. 16.1, б) тоже обладает потенциальной энергией: при распрямлении пружины сила упругости совершит работу — подбросит брусок. Но как вычислить эту работу, ведь во время действия пружины на брусок сила упругости непрерывно уменьшается?

Оказывается, все не так сложно. И сила тяжести, и сила упругости имеют одно «замечательное» свойство — работа этих сил не зависит от формы траектории. Силы, работа которых не зависит от формы траектории, а определяется только начальным и конечным механическими состояниями тела (системы тел), называют потенциальными, или консервативными, силами (от лат. conservare — сохранять, охранять).

Потенциальная энергия поднятого тела

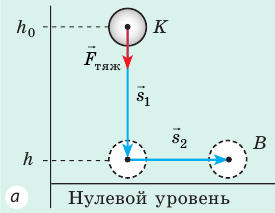
Докажем, что сила тяжести — консервативная сила. Для этого определим работу силы тяжести при движении тела из точки K в точку B по разным траекториям.

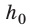
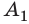
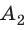
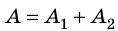
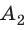
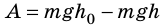
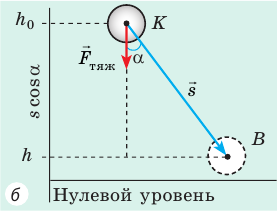
Случай 1. Пусть траектория движения тела — «ступенька» (рис. 16.2, а): сначала тело падает с некоторой высоты до высоты h и сила тяжести совершает работу , затем тело движется горизонтально и сила тяжести совершает работу . Работа — величина аддитивная, поэтому общая работа .

= 0, так как сила тяжести перпендикулярна перемещению тела. Итак: .

Случай 2. Пусть тело перемещается из точки K в точку В, скользя по наклонной плоскости (рис. 16.2, б). В этом случае работа силы тяжести равна:

Рис. 16.2. При перемещении тела с высоты 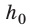до высоты h работа силы тяжести, независимо от траектории движения тела, определяется по формуле:

Тот же результат получим и для случаев перемещения тела по произвольной траектории. Следовательно, работа силы тяжести не зависит от траектории движения тела, то есть сила тяжести — консервативная сила. Величину mgh называют потенциальной энергией поднятого тела:

Потенциальная энергия поднятого тела зависит от высоты, на которой находится тело, то есть зависит от выбора нулевого уровня, — уровня, от которого будет отсчитываться высота. Нулевой уровень выбирают из соображений удобства. Так, находясь в комнате, за нулевой уровень целесообразно взять пол, определяя высоту горы — поверхность Мирового океана.

Обратите внимание! Изменение потенциальной энергии, а следовательно, и работа силы тяжести от выбора нулевого уровня не зависят.

Заказать решение задач по физике

Потенциальная энергия упруго деформированного тела

Пусть имеется упруго деформированное тело — растянутая пружина. Определим работу, которую совершит сила упругости при уменьшении удлинения пружины от 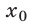до x (рис. 16.3). Воспользуемся для этого геометрическим смыслом механической работы (рис. 16.4):

Таким образом, работа силы упругости определяется только начальным и конечным состояниями пружины, то есть сила упругости — консервативная сила. Величину 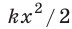называют потенциальной энергией упруго деформированного тела:

Работа силы упругости (как и силы тяжести) равна изменению потенциальной энергии тела, взятому с противоположным знаком:

Данное выражение — математическая запись теоремы о потенциальной энергии: работа всех консервативных сил, действующих на тело, равна изменению потенциальной энергии тела, взятому с противоположным знаком.

Состояние с меньшей потенциальной энергией является энергетически выгодным; любая замкнутая система стремится перейти в такое состояние, в котором ее потенциальная энергия минимальна, — в этом заключается принцип минимума потенциальной энергии. Действительно, камень, выпущенный из руки, никогда не полетит вверх — он будет падать, стремясь достичь состояния с наименьшей потенциальной энергией. Недеформированная пружина никогда не станет сама растягиваться или сжиматься, а деформированная пружина стремится перейти в недеформированное состояние.

Закон сохранения полной механической энергии

Как правило, тело или система тел обладают и потенциальной, и кинетической энергиями. Сумму кинетических и потенциальных энергий тел системы называют полной механической энергией системы тел: 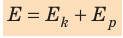(рис. 16.5).

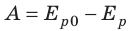
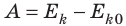
Рассмотрим замкнутую систему тел, взаимодействующих друг с другом только консервативными силами (силами тяготения или силами упругости). По теореме о потенциальной энергии работа A, совершаемая этими силами, равна: . С другой стороны, согласно теореме о кинетической энергии эта же работа равна: . Приравняв правые части равенств, получим закон сохранения и превращения полной механической энергии:

В замкнутой системе тел, взаимодействующих только консервативными силами, полная механическая энергия остается неизменной (сохраняется):

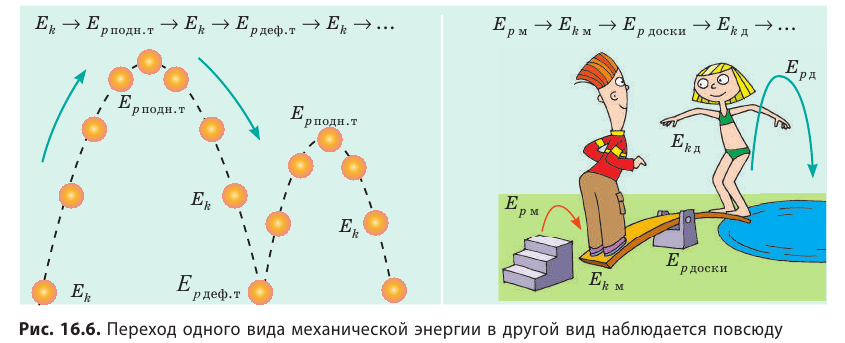
Закон сохранения полной механической энергии предполагает превращение кинетической энергии в потенциальную и наоборот (рис. 16.6). Однако сохраняется ли при этом полная механическая энергия? Наш опыт подсказывает, что нет. И действительно, закон сохранения полной механической энергии справедлив только в случаях, когда в системе отсутствует трение. Однако в природе не существует движений, не сопровождающихся трением. Сила трения всегда направлена против движения тела, поэтому при движении она совершает отрицательную работу, при этом полная механическая энергия системы уменьшается:

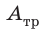
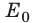
где — работа силы трения; E, — полная механическая энергия системы в конце и в начале наблюдения соответственно.

Потери энергии наблюдаются и в случае неупругого удара. Так что, при наличии трения или при неупругой деформации энергия бесследно исчезает? Казалось бы, да. Однако измерения показывают, что в результате и трения, и неупругого удара температуры взаимодействующих тел увеличиваются, то есть увеличиваются внутренние энергии тел. Значит, кинетическая энергия не исчезает, а переходит во внутреннюю энергию.

Энергия никуда не исчезает и ниоткуда не появляется: она только переходит из одного вида в другой, передается от одного тела к другому.

Алгоритм решения задач с применением закона сохранения механической энергии

Прочитайте условие задачи. Выясните, является ли система замкнутой, можно ли пренебречь действием сил сопротивления. Запишите краткое условие задачи.
Выполните пояснительный рисунок, на котором укажите нулевой уровень, начальное и конечное состояния тела (системы тел).
Запишите закон сохранения механической энергии. Конкретизируйте запись, воспользовавшись данными условия задачи и соответствующими формулами для определения энергии.
Решите полученное уравнение относительно неизвестной величины.
Проверьте единицу, найдите значение искомой величины.
Проанализируйте результат, запишите ответ.

Пример №2

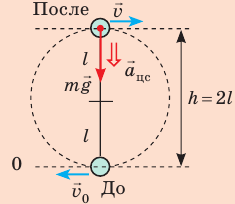
Какую минимальную скорость нужно сообщить шарику, подвешенному на нити длиной 0,5 м, чтобы он смог совершить полный оборот в вертикальной плоскости? Сопротивлением воздуха пренебречь.

Анализ физической проблемы

Сопротивлением воздуха пренебрегаем, поэтому система «шарик — нить — Земля» является замкнутой и можно воспользоваться законом сохранения механической энергии.
За нулевой уровень примем самое низкое положение шарика.
В самой высокой точке траектории шарик имеет некоторую скорость, иначе он не продолжил бы вращаться, а стал бы падать вертикально вниз.
Для определения скорости движения шарика в наивысшей точке траектории воспользуемся определением центростремительного ускорения и вторым законом Ньютона.
Нужно найти минимальную скорость движения шарика в момент толчка, поэтому понятно, что в наивысшей точке траектории нить натянута не будет, то есть сила ее натяжения будет равна нулю.

Решение:

На рисунке отметим положения шарика в самой нижней и самой верхней точках траектории; силы, действующие на шарик в верхней точке; направление ускорения. По закону сохранения механической энергии:

Согласно второму закону Ньютона: .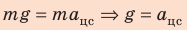

Поскольку

Подставим выражение (2) в выражение (1): 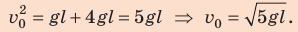Проверим единицу, найдем значение искомой величины:

Ответ:

Выводы:

Кинетическая энергия
Закон сохранения и превращения механической энергии
Работа, мощность и энергия
Движение и силы
Мощность в физике
Взаимодействие тел
Механическая энергия и работа
Золотое правило механики

Источник

Как рассчитать упругую потенциальную энергию для идеальной пружины?

Настоящие упругие материалы

Тест по теме «Упругая потенциальная энергия»

Elastic potential energy in mechanical systems[edit]

Continuum systems[edit]

See also[edit]

References[edit]

Sources[edit]

1.Консервативная и Диссипативная сила. Потенциальное поле.

2.Потенциальная энергия упругой силы и работа по растяжению и сжатию пружины.

8. Консервативные и диссипативные силы. Потенциальное поле. Потенциальная энергия гравитационной силы. Работа по поднятию тела.

1.Консервативная и Диссипативная сила. Потенциальное поле.

Потенциальная энергия упруго деформированного тела — физическая величина, равная половине произведения жесткости тела на квадрат его деформации.

Что такое потенциальная энергия

Определение потенциальной энергии

Что такое энергия

Единицы энергии

Виды механической энергии

Как рассчитывают потенциальную энергию

Потенциальная энергия упруго деформированного тела

Механическая работа и кинетическая энергия

Когда сила совершает механическую работу

Геометрический смысл работы силы

Когда тело имеет кинетическую энергию

Мощность

Пример №1

Потенциальная энергия и закон сохранения механической энергии

Когда тело обладает потенциальной энергией

Потенциальная энергия поднятого тела

Потенциальная энергия упруго деформированного тела

Закон сохранения полной механической энергии

Пример №2

Добавить комментарий Отменить ответ

Как рассчитать упругую потенциальную энергию для идеальной пружины?

Настоящие упругие материалы

Тест по теме «Упругая потенциальная энергия»

Elastic potential energy in mechanical systems[edit]

Continuum systems[edit]

See also[edit]

References[edit]

Sources[edit]

1.Консервативная и Диссипативная сила. Потенциальное поле.

2.Потенциальная энергия упругой силы и работа по растяжению и сжатию пружины.

8. Консервативные и диссипативные силы. Потенциальное поле. Потенциальная энергия гравитационной силы. Работа по поднятию тела.

1.Консервативная и Диссипативная сила. Потенциальное поле.

Потенциальная энергия упруго деформированного тела — физическая величина, равная половине произведения жесткости тела на квадрат его деформации.

Что такое потенциальная энергия

Определение потенциальной энергии

Что такое энергия

Единицы энергии

Виды механической энергии

Как рассчитывают потенциальную энергию

Потенциальная энергия упруго деформированного тела

Механическая работа и кинетическая энергия

Когда сила совершает механическую работу

Геометрический смысл работы силы

Когда тело имеет кинетическую энергию

Мощность

Пример №1

Потенциальная энергия и закон сохранения механической энергии

Когда тело обладает потенциальной энергией

Потенциальная энергия поднятого тела

Потенциальная энергия упруго деформированного тела

Закон сохранения полной механической энергии

Пример №2

Вам также может понравиться

Bloodborne как найти пуповины

Как составить график работы в excel образец заполнения

Как найти анимированный фон для стима

Добавить комментарий Отменить ответ