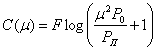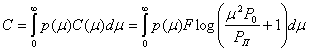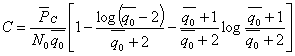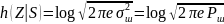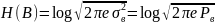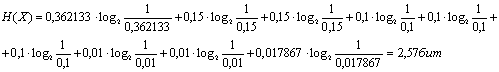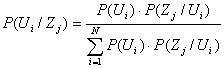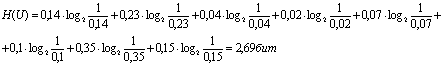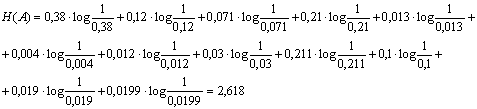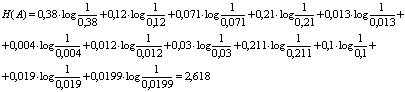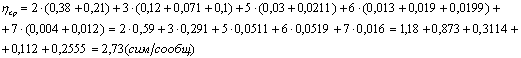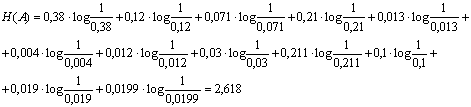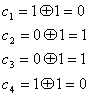6.1. Мера количества информации
6.2. Энтропия источника дискретных сообщений
6.3. Статистические свойства источников сообщений
6.4. Скорость передачи информации и пропускная способность дискретного канала без помех
6.5. Оптимальное статистическое кодирование сообщений
6.6. Скорость передачи информации и пропускная способность дискретных каналов с помехами
6.7. Теорема Шеннона для дискретного канала с помехами
6.8. Энтропия непрерывных сообщений
6.9. Скорость передачи и пропускная способность непрерывного канала. Формула Шеннона
6.10. Пропускная способность каналов с переменными параметрами
6.11. Эффективность систем передачи информации
6.1. Мера количества информации
В теории информации изучаются количественные закономерности передачи, хранения ,и обработки информации.
Назначение любой системы связи — передать в течение заданного времени как можно больше достоверных сведений от одного объекта или корреспондента к другому.
Проблема достоверности при различных способах приема и передачи сообщений рассматривалась в теории помехоустойчивости. Эта теория, как мы убедились, позволяет не только найти достоверность передачи при заданных условиях, но и выяснить, при каких методах передачи и обработки сигналов эта достоверность будет наибольшей.
В теории информации основное внимание уделяется определению средней скорости передачи информации и решению задачи максимизации этой скорости путем применения соответствующего кодирования [13]. Предельные соотношения теория информации позволяют оценить эффективность различных систем связи и установить условия согласования, в информационном отношении источника с каналом и канала с потребителем.
Для исследования этих вопросов с общих позиций необходимо прежде всего установить универсальную количественную меру информации, не зависящую от конкретной физической природы передаваемых сообщений. Когда принимается сообщение о каком-либо событии, то наши знания о нем изменяются. Мы получаем при этом некоторую информацию об этом событии. Сообщение о хорошо известном нам событии, очевидно, никакой информации не несет. Напротив, сообщение о малоизвестном событии содержит много информации. Например, сообщение бюро погоды от 20 июня о том, что в Одессе «завтра выпадет снег» несет больше информации, чем сообщение «завтра ожидается ясная погода». Первое сообщение является неожиданным, оно несет сведения о редком, маловероятном явлении и поэтому содержит много информации. Второе сообщение является весьма вероятным, оно содержит мало нового и поэтому несет мало информации.
Таким образом, количество информации в сообщении о некотором событии существенно зависит от вероятности этого события.
Вероятностный подход и положен в основу определения меры количества информации. Для количественного определения информации, в принципе, можно использовать любую монотонно убывающую функцию вероятности F[P(a)] где Р(а) — вероятность, сообщения а. Простейшей из них является функция F=1/Р(а) которая характеризует меру неожиданности (неопределенности) сообщения. Однако удобнее исчислять количество информации а логарифмических единицах, т. е. определять количество информации в отдельно взятом сообщении как
(6.1)
Так как 0<P(a)l, то J(a) — величина всегда положительная и конечная. При Р(а)=1 количество информации равно нулю, т. е., сообщение об известном событии никакой информации не несет. Логарифмическая мера обладает естественным в данном случае свойством аддитивности, согласно которому количество информации, содержащееся в нескольких независимых сообщениях, равна сумме количества информации в каждом из них. Действительно, так как совместная вероятность п независимых сообщений
, то количество информации а этих сообщениях равно:
, что соответствует интуитивным представлениям об увеличении информации при получении дополнительных сообщений. Основание логарифма k может быть любым. Чаще всего принимают k=2, и тогда количество информации выражается в двоичных единицах:
дв. ед.
Двоичную единицу иногда называют бит. Слово бит произошло от сокращения выражения binary digit (двоичная цифра). В двоичных системах связи для передачи сообщения используется два символа, условно .обозначаемых 0 и 1. В таких системах при независимых и равновероятных символах, когда P(0)=P(1)=1/2, каждый из них несет одну двоичную единицу информации:
Формула (6.1) позволяет вычислять количество информация в. сообщениях, вероятность которых отлична от нуля. Это, в свою очередь, предполагает, что сообщения дискретны, а их число ограничено. В таком случае принято говорить об ансамбле сообщений, который описывается совокупностью возможных сообщений и их вероятностей:
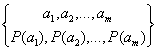
Ансамбль сообщений образует полную группу событий, поэтому всегда .
Если все сообщения равновероятны:, то количество информации в каждом из них определяется величиной
(6.3)
Отсюда следует, что количество информации в сообщении зависит от ансамбля, из которого, оно выбрано. До передачи сообщения имеется неопределенность относительно того, какое из m сообщений ансамбля будет передано после приема сообщения эта неопределенность снимается. Очевидно, чем больше т, тем больше неопределенность и тем большее количество информации содержится в переданном сообщении.
Рассмотрим пример. Пусть ансамбль возможных сообщений представляет собой алфавит, состоящий из m различных букв. Необходимо определить, какое количество информации содержится в передаваемом слове длиной п букв, если вероятности появления букв одинаковы, а сами буквы следуют независимо друг от друга. Количество информации при передаче одной буквы:. Так как все буквы равновероятны, то
и количество информации, содержащееся в любой букве,
. Буквы следуют независимо поэтому количество информации в слове из п букв
К определению информации можно подойти и с другой стороны. Будем рассматривать в качестве сообщения не отдельную букву, а целое слово. Если все буквы равновероятны и следуют независимо, то все слова будут также равновероятны и , где N=mn — число возможных слов. Тогда можно записать
Для двоичного кода ансамбль элементарных сообщений состоит из двух элементов 0 и 1 (m=2). В этом случае сообщение из п элементов несет информацию,
(6.4)
В общем случае при передаче сообщений неопределенность снимается не полностью. Так, в канале с шумами возможны ошибки. По принятому сигналу v только с некоторой вероятностью можно судить о том, что было передано сообщение а. Поэтому после получения сообщения остается некоторая неопределенность, характеризуемая величиной апостериорной вероятности P(a/v), а количество информации, содержащееся в сигнале v, определяется степенью уменьшения неопределенности при его приеме. Если Р(а) — априорная ,вероятность, то количество информации в принятом сигнале v относительно переданного сообщения а, очевидно, будет равно:
(6.5)
Это выражение можно рассматривать также как разность между количеством информации, поступившим от источника сообщений, и тем количеством информации, которое потеряло в канале за счет действия шумов.
6.2. Энтропия источника дискретных сообщений
Энтропия источника независимых сообщений. До сих пор определялось количество информации, содержащееся в отдельных сообщениях. Вместе с тем во многих случаях, когда требуется согласовать канал с источником сообщений, таких сведений оказывается недостаточно. Возникает потребность. в характеристиках, которые, бы позволяли оценивать информационные свойства источника сообщений в целом. Одной из важных характеристик такого рода является среднее количество информации, приходящееся на одно сообщение.
В простейшем случае, когда все сообщения равновероятны, количество информации в каждом из них одинаково и, как было показано выше, определяется выражением (6.3). При этом среднее количество информации равно log т. Следовательно, при равновероятных независимых сообщениях информационные свойства источника зависят только от числа сообщений в ансамбле т.
Однако в реальных условиях сообщения, как правило, имеют разную вероятность. Так, буквы алфавита О, Е, А встречаются в тексте сравнительно часто, а буквы Щ, Ы, Ъ — редко. Поэтому знание числа сообщений т в ансамбле является недостаточным, необходимо иметь сведения о вероятностях каждого сообщения: .
Так как вероятности сообщений неодинаковы, то они несут различное количество информации J(a)=–logP(a
). Менее вероятные сообщения несут большее количество информации и наоборот. Среднее количество информации, приходящееся на одно сообщение источника, определяется как математическое ожидание J(a
):
(6.6)
Величину Н(а) называется энтропией. Этот термин заимствован из термодинамики, где имеется аналогичное по своей форме выражение, характеризующее неопределенность состояния физической системы. В теории информации энтропия Н(а) также характеризует неопределенность ситуации до передачи сообщения, поскольку заранее неизвестно, какое из сообщений ансамбля источника будет передано. Чем больше энтропия, тем сильнее неопределенность и тем большую информацию в среднем несет одно сообщение источника.
В качестве примера вычислим энтропию источника сообщений, который характеризуется ансамблем, состоящим из двух сообщений и
с вероятностями
и
. На основании (6.6) энтропия такого источника будет равна:
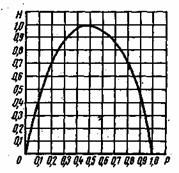
Рис. 6.1. Зависимость энтропии от вероятности р
Зависимость Н(а) от р показана на рис. 6.1. Максимум имеет место при р=1/2, т. е. когда ситуация является наиболее неопределенной. При р=1 или р=0, что соответствует передаче одного из сообщений или
, неопределенность отсутствует. В этих случаях энтропия Н(а) равна нулю.
Среднее количество информации, содержащееся в последовательности из п сообщений, равно:
Отсюда следует, что количество передаваемой информации можно увеличить не только за счет увеличения числа сообщений, но и путем повышения энтропии источника, т. е. информационной емкости его сообщений.
Обобщая полученные выше результаты, сформулируем следующие основные свойства энтропии источника независимых сообщений (6.6):
— энтропия— величина всегда положительная, так как
— при равновероятных сообщениях, когда , энтропия максимальна и равна:
(6.7)
— энтропия равняется нулю лишь в том случае, когда все вероятности Р(a) равны нулю, за исключением одной, величина которой ,равна единице;
— энтропия нескольких независимых источников равна сумме энтропии этих источников .
Энтропия источника зависимых сообщений. Рассмотренные выше источники независимых дискретных сообщений являются простейшим типом источников. В реальных условиях картина значительно усложняется из-за наличия статистических связей между сообщениями. Примерам может быть обычный текст, где появление той или иной буквы зависит от предыдущих буквенных сочетаний. Так, например, после сочетания ЧТ вероятность следования гласных букв О, Е, И больше, чем согласных.
Статистическая связь ожидаемого сообщения с предыдущим сообщением количественно оценивается совместной вероятностью или условной вероятностью
, которая выражает вероятность появления сообщения
при условии, что до этого было передано сообщение а
Количество информации, содержащееся в сообщении
, при условии, что известно предыдущее сообщение а
согласно (6.1) будет равно:
. Среднее количество информации при этом определяется условной энтропией
, которая вычисляется как математическое ожидание информации
по всем возможным сообщениям а
и
. Учитывая соотношение (2.25), .получаем
(6.8)
В тех случаях, когда связь распространяется на три сообщения , условная энтропия источника определяется аналогичным соотношением
(6.9)
В общем случае n зависимых сообщений
(6.10)
Важным свойством условной энтропии источника зависимых сообщений является то, что при неизменном количестве сообщений в ансамбле источника его энтропия уменьшается с увеличением числа сообщений, между которыми существует статистическая взаимосвязь. В соответствии с этим свойством, а также свойством энтропии источника независимых сообщений можно записать неравенства
(6.11)
Таким образом, наличие статистических связей между сообщениями всегда приводит к уменьшению количества информации, приходящегося в среднем на одно сообщение.
Избыточность источника сообщений. Уменьшение энтропии источника с увеличением статистической взаимосвязи (6.11) можно рассматривать как снижение информационной емкости сообщений. Одно и то же сообщение при наличия взаимосвязи содержит в среднем меньше информации, чем при ее отсутствии. Иначе говоря, если источник создает последовательность сообщений, обладающих статистической связью, и характер этой связи известен, то часть сообщений, выдаваемая источником, является избыточной, так как она может быть восстановлена по известным статистическим связям. Появляется возможность передавать сообщения в сокращенном виде без потери информации, содержащейся в них. Например, при передаче телеграммы мы исключаем из текста союзы, предлоги, знаки препинания, так как они легко восстанавливаются, при чтении телеграммы на основании известных правил построения фраз и слов.
Таким образом, любой источник зависимых сообщений, как принято говорить, обладает избыточностью. Количественное определение избыточности может быть получено из следующих соображений. Для того чтобы передать количество информации, источник без избыточности должен выдать в среднем сообщений, а источник с избыточностью
сообщений.
Поскольку и
, то для передачи одного и того же количества информации источник с избыточностью должен использовать большее количество сообщений. Избыточнее количество сообщений равно kn–k0, а избыточность определяется как отношение
(6.12)
Величина избыточности лежит в пределах и согласно (6.11) является неубывающей функцией п. Для русского языка, например,
дв. ед.,
,
,
дв. ед. Отсюда на основании (6.12) для русского языка получаем избыточность порядка 50%.
Коэффициент
(6.13)
называется коэффициентом сжатия. Он показывает, до какой величины можно сжать передаваемые сообщения, если устремить избыточность. Источник, обладающий избыточностью, передает излишнее количество сообщений. Это увеличивает продолжительность передачи и снижает эффективность использования канала связи. Сжатие сообщений можно осуществить посредством соответствующего кодирования. Информацию необходимо передавать такими сообщениями, информационная емкость которых используется наиболее полно. Этому условию удовлетворяют равновероятна и независимые сообщения.
Вместе с тем избыточность источника не всегда является отрицательным свойством. Наличие взаимосвязи между буквами текста дает возможность восстанавливать его при искажении отдельных букв, т. е. использовать избыточность для повышения достоверности передачи информации.
6.3. Статистические свойства источников сообщений
Использование энтропия в качестве усредненной величины, количественно характеризующей информационные свойства источника, выдающего последовательности дискретных сообщений, является целесообразным при условии, что вероятностные соотношения для этих последовательностей сохраняются неизменными. Источник называют стационарным, когда распределение вероятностей сообщений не зависит от их места в последовательности сообщений, создаваемых этим источником, т. е.
(6.14)
где п — любое целое число.
По аналогии со стационарным случайным процессом статистические характеристики последовательности сообщений стационарного источника не зависят от выбора начала отсчета.
Среди стационарных источников сообщений важное место занимают эргодические источники, которые отличаются тем, что с вероятностью, близкой к единице, любая достаточно длинная последовательность сообщений такого источника полностью характеризует его статистические свойства. Важной особенностью эргодических источников является то, что статистическая взаимосвязь между сообщениями всегда распространяется только на конечное число предыдущих сообщений.
Существует стационарные источники, которые могут работать в различных режимах, отличающихся друг от друга своими статистическими характеристиками. В этом случае источник не является эргодическим, так как при работе в одном режиме даже продолжительная последовательность сообщений уже не может в целом характеризовать свойства источника.
Условная энтропия стационарного источника находится как результат усреднения по всем режимам работы
(6.15)
где ) — вероятность и условная энтропия j-го режима работы.
Рассмотрим условную энтропию при заданной последовательности предыдущих сообщений
(6.16)
Здесь символом обозначена последовательность п—1 предыдущих сообщений
, причем индексом а нумеруются все возможные соединения из т сообщений по п—1, т. е. всего
последовательностей
Последовательность можно трактовать как состояние источника, в котором он находится после ее передачи. Подобного рода случайные последовательности (обладающие эргодическими свойствами) известны в математике как дискретные цепи А. А. Маркова.
В марковском эргодическом источнике вероятность передачи того или иного сообщения однозначно определяется состоянием источника. После передачи сообщения источник переходит в новое состояние, которое зависит от предыдущего состояния и переданного сообщения.
Достаточно длинные эргодические последовательности сообщений, с высокой степенью вероятности содержащие все сведения о статистических характеристиках источника, называются типичными. Чем длиннее последовательность, тем больше вероятность того, что она является типичной. В типичных последовательностях частота появления отдельных сообщений или групп сообщений сколь угодно мало отличается от их вероятности. Отсюда вытекает важное свойство типичных последовательностей, состоящее в том, что типичные последовательности одинаковой длины примерно равновероятны. Это легко показать для последовательностей независимых сообщений.
Предположим, что ансамбль сообщений состоит из m сообщений: и нас интересует вероятность того, что в последовательности длиной в п сообщений число сообщений а
равно k
, число сообщений а
равно k
и т. д., am соответствует km, причем
. При независимых сообщениях эта вероятность, очевидно, равна:
(6.17)
где P — вероятность сообщения а
. Так как во всех типичных последовательностях по определению выполняется условие
, то вероятности типичных последовательностей приблизительно одинаковы и равны:
(6.18)
В этом случае количество информация в любой из типичных последовательностей
(6.19).
С другой стороны, величину Jn можно выразить через энтропию. источника Н(а):
(6.20)
Используя выражения (6.19) и (6.20), энтропию источника можно определить как
(6.21)
Для общего случал, в том числе и для зависимы сообщений, ib теории информации доказывается следующая теорема. Все эргодические последовательности, содержащие достаточно большое число сообщений п, могут быть разбиты на две группы:
— типичные последовательности с вероятностями Рп, для которых удовлетворяется неравенство
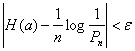
где Н(а) — энтропия источника и ε — сколь угодно малая величина;
— нетипичные последовательности, суммарная вероятность которых δ сколь угодно мала.
Величины ε и δ неограниченно уменьшаются с ростом п, что позволяет всегда выбрать такое значение п, при котором все последовательности источника, за исключением весьма малой их части могут быть отнесены к равновероятным типичным последовательностям.
Важным следствием теоремы является возможность установления зависимости между числом вариантов всевозможных типичных последовательностей Мпи энтропией источника. Для достаточно длинных последовательностей величины ε и δ малы. Тогда на основании (6.22)
(6.23)
Что касается нетипичных последовательностей, то вследствие их малой вероятности при большом п они во многих случаях вообще не учитываются.
6.4. Скорость передачи информации и пропускная способность дискретного канала без помех
Передача информации происходит во времени, поэтому можно ввести понятие скорости передачи как количества информации, передаваемой в среднем за единицу времени. Для эргодических последовательностей сообщений, где допускается усреднение времени, скорость передачи равна:
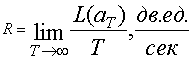
Здесь — количество информация, содержащейся в последовательности сообщений аТ, общая длительность которых равна Т, причём предполагается, что все сообщения, входящие в последовательность аТ, имеют определенную длительность.
Количество информации, создаваемое источником сообщений в среднем за единицу времени, называется производительностью источника . Эту величину удобно выразить через энтропию источника Н(а). Действительно, при
можно считать
и
, где п — число сообщений, а
— средняя длительность одного сообщения. Тогда, подставляя в (6.24) значения J(aT) и Т, получим
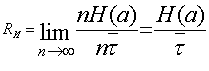
Величина для независимых сообщений может быть вычислена как математическое ожидание
(6.26)
где P()=P(
) — вероятность сообщения
длительностью
. Если длительность всех сообщений одинакова и равна
, выражение (6.25) принимает вид
(6.27)
Отсюда следует, что наибольшей производительностью обладает источник с максимальной энтропией (§ 6.7), т.е.
(6.28)
Выданная источником информация в виде отдельных сообщений поступает в канал связи, где осуществляются кодирование и ряд других преобразований, в результате которых информация переносится уже сигналами и, имеющими другую природу и в общем случае обладающими другими статистическими характеристиками. Для сигналов также может быть найдена скорость передачи информации по каналу связи
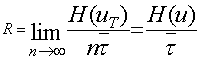
Высокая скорость передачи информации является одним из основных требований, предъявляемых к системам связи. Однако в реальных условиях существует ряд причин, ведущих к ее ограничению. Остановимся на некоторых из них.
В реальном канале число используемых сигналов т всегда конечно, поэтому энтропия в соответствии с (6.7) есть величина ограниченная:
(6.30)
С другой стороны, уменьшение длительности сигналов приводит как известно, к расширению их спектра, что ограничивается полосой пропускания канала. Это в конечном счете ставит предал уменьшению и средней длительности . Таким образом, существуют, по крайней мере, две причины: конечное число сигналов я конечная длительность сигналов, которые не позволяют беспредельно повышать скорость передачи информации по каналу связи.
Максимально возможная скорость передачи информации по каналу связи при фиксированных ограничениях называется пропускной способностью канала:
(6.31)
Пропускная способность канала характеризует его предельные возможности в отношении передачи среднего количества информации за единицу времени. Максимум скорости R в выражение (6.31) ищется по всем возможным ансамблям сигналов и,
Определим пропускную способность канала, в котором существуют два ограничения: число используемых сигналов не должно превышать т,_ а длительность их не может быть меньше т, сек. Так как Н(и) и независимы, то согласно выражению (6.31) следует искать раздельно максимум Н(и) и минимум
. Тогда
(6.32)
Для двоичных сигналов т=2 и пропускная способность
(6.33)
т. е. совпадает со скоростью телеграфирования в бодах. При передаче информации простейшими двоичными сигналами — телеграфными посылками — необходимая полоса пропускания канала зависит от частоты манипуляции FM=1/2T, которая по определению равна частоте первой гармоники спектра сигнала, представляющего собой периодическую последовательность посылок и пауз. Очевидно, минимальная полоса пропускания канала, при которой еще возможна передача сигналов, F=FM. Отсюда максимальная скорость передачи двоичных сигналов по каналу без помех равна: С=V=2FM (предел Найквиста).
Понятие пропускной способности применимо не только ко всему каналу в целом, но и к отдельным, его звеньям. Существенным здесь является то, что пропускная способность С’ какого-либо звена не превышает пропускной способности С” второго звена, если оно расположено внутри первого. Соотношение С’С” обусловлено возможностью появления дополнительных ограничений, накладываемых на участок канала при его расширении, и снижающих пропускную способность.
6.5. Оптимальное статистическое кодирование сообщений
Для дискретных каналов без помех Шенноном была доказана следующая теорема: если производительность источника , где ε — сколь угодно малая величина, то всегда существует способ кодирования, позволяющий передавать по каналу все сообщения источника. Передачу всех сообщений при
осуществить невозможно.
Смысл теоремы сводится к тому, что как бы ни была велика избыточность источника, все его сообщения могут быть переданы по каналу, если. Обратное утверждение теоремы легко доказывается от противного. Допустим,
, но для передачи всех сообщений источника по каналу необходимо, чтобы скорость передачи информации R была не меньше
. Тогда имеем
, что невозможно, так как по определению пропускная способность
.
Для рационального использования пропускной способности канала необходимо применять соответствующие способы кодирования сообщений. Статистическим или оптимальным называется кодирование, при котором наилучшим образом используется пропускная способность канала без помех. При оптимальном кодировании фактическая скорость передачи информации по каналу R приближается к пропускной способности С, что достигается путем согласования источника с каналом. Сообщения источника кодируются таким образом, чтобы они в наибольшей степени соответствовали ограничениям, которые накладываются на сигналы, передаваемые по каналу связи. Поэтому структура оптимального кода зависит как от статистических характеристик источника, так и от особенностей канала.
Рассмотрим основные принципы оптимального кодирования на примере источника независимых сообщений, который необходимо согласовать с двоичным каналом без помех. При этих условиях процесс кодирования заключается в преобразовании сообщений источника в двоичные кодовые комбинации. Поскольку имеет место однозначное соответствие между сообщениями источника и комбинациями кода, то энтропия кодовых комбинаций равна энтропии источника:
(6.34)
а скорость передачи информации в канале определяется на основании (6.29) отношением
(6.35)
Здесь — средняя длительность кодовой комбинации, которая в общем случае неравномерного кода записывается по аналогии с выражением (6.26) как
(6.36)
где — длительность одного элемента кода и,
— число элементов в комбинации, присваиваемой сообщению
.
Подстановка в ф-лу (6.35) выражений (6.6) и (6.36) приводит к соотношению
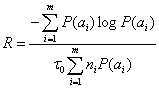
в котором числитель определяется исключительно статистическими свойствами источника, а величина — характеристиками канала. При этом возникает вопрос, можно ли так закодировать сообщения, чтобы скорость передачи R (6.37) достигла своего максимального значения, равного пропускной способности двоичного канала С=1/
. Легко заметить, что это условие выполняется, если
(6.38)
что соответствует минимуму и максимуму R. Очевидно, выбор
<J(
) не имеет смысла, так как в этом случае R>C, что противоречит выше доказанному утверждению теоремы Шеннона.
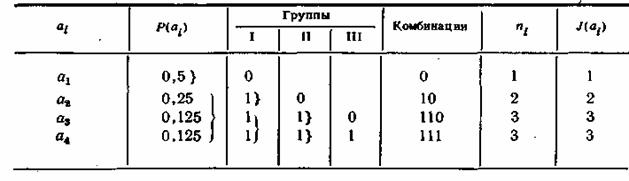
Одним из кодов, удовлетворяющих условию (6.38), является код Шеннона-Фано. Для ознакомления с принципами его построения рассмотрим в качестве примера источник сообщений, вырабатывающий четыре сообщения и
с вероятностями:
;
;
Все сообщения выписываются в кодовую таблицу (табл. 6.1) в порядке убывания их вероятностей. Затем они разделяются на две группы так, чтобы суммы их вероятностей то возможности были одинаковыми. В данном примере в первую группу входит сообщение с вероятностью
и во вторую — сообщения
и
с суммарной вероятностью, также равной 0,5.
Комбинациям, которые соответствуют сообщениям первой группы, притаивается в качестве первого символа кода 0, а комбинациям второй группы -1. Каждая из двух групп опять делится на две группы с применением того же правила присвоения символов 0 и 1.
Таблица 6.1
В идеальном случае после первого деления вероятности каждой группы должны быть равны 0,5, после второго деления— 0,25 и т. д. Процесс деления продолжается до тех пор, пока в группах не останется по одному сообщению.
При заданном распределении вероятностей сообщений код получается неравномерным, его комбинации имеют различное число элементов пi, причем, как нетрудно заметить, такой способ кодирования обеспечивает выполнение условия (6.38) полностью для всех сообщений.
В неравномерных кодах при декодировании возникает трудность в определении границ между комбинациями. Для устранения возможных ошибок обычно применяются специальные разделительные знаки. Так, в коде Морзе между буквами передается разделительный знак в виде паузы длительностью в одно тире. Передача разделительных знаков занимает дополнительное время, что снижает скорость передачи информации.
Важным свойством кода Шеннона—Фано является то, что, несмотря на его неравномерность, здесь не требуются разделительные знаки. Это обусловлено тем, что короткие комбинации не являются началом более длинных комбинаций. Указанное свойство легко проверить на примере любой последовательности:
Таким образом, все элементы закодированного сообщения несут полезную информацию, что при выполнении условия (6.38) позволяет получить максимальную скорость передачи. Она может быть найдена также путем непосредственного вычисления по ф-ле (6.37)’

Для сравнения рассмотрим кодирование тех же четырех сообщений ,
,
, с применением обычного равномерного двоичного кода. Количество комианаций при этом определяется выражением
где n — число элементов в комбинации. Так как m=4, то
, а длительность каждой комбинации 2
. Производя вычисления по аналогии с (6.39), получим
Пропускная способность в этом случае используется только частично. Из выражения (6.38) вытекает основной принцип оптимального кодирования. Он сводится к тому, что наиболее вероятным сообщениям должны присваиваться короткие комбинации, а сообщениям с малой вероятностью — более длинные комбинации.
Возможность оптимального кодирования по методу Шеннона—Фано доказывает, что сформулированная выше теорема справедлива, по крайней мере, для источников независимых сообщений. Теорема Шеннона может быть доказана и для общего случая зависимых сообщений.
Одним из способов оптимального кодирования зависимых сообщений является применение так называемых «скользящих» кодов, основная идея которых состоит в том, что присвоение кодовых комбинаций по правилу Шеннона—Фано производится с учетом условных, а не априорных вероятностей сообщений. Число элементов в кодовой комбинации выбирается как , т. е. текущему сообщению присваивается та или иная комбинация в зависимости от того, какие сообщения ему предшествовали.
Необходимо подчеркнуть, что при оптимальном способе кодирования в сигналах, передающих сообщения источника, совершенно отсутствует какая-либо избыточность. Устранение избыточности приводит к тому, что процесс декодирования становится весьма чувствительным к воздействию помех. Это особенно сильно проявляется при оптимальном кодировании зависимых сообщений. Например, в «скользящих» кодах одна единственная ошибка может вызвать неправильное декодирование всех последующих сигналов. Поэтому оптимальные коды применимы только для каналов, в которых влияние помех незначительно.
Отличительной особенностью рассмотренных ранее каналов без помех является то, что при выполнении условия теоремы Шеннона количество принятой информации на выходе канала всегда равно количеству информации, переданной от источника сообщений. При этом, если на вход канала поступил сигнал , то на выходе возникает сигнал
, вполне однозначно определяющий переданный сигнал
. Количество информация, прошедшее по каналу без помех в случае передачи
и приема
равно количеству информации, содержащейся в сигнале
:
(6.40)
Здесь величина вероятности P() характеризует ту неопределенность в отношении сигнала
, которая существовала до его передачи. После приема
в силу однозначного соответствия между
и
неопределенность полностью устраняется.
Иное положение имеет место в каналах, где присутствуют различного рода помехи. Их воздействие на передаваемый сигнал приводит к разрушению и необратимой потере части информации, поступающей от источника сообщения. Поскольку в канале с помехами принятому сигналу может соответствовать передача одного из нескольких сигналов и, то после приема
остается некоторая неопределенность в отношении переданного сигнала. Здесь соответствие между u и v носит случайный характер, поэтому степень неопределенности характеризуется условной апостериорной вероятностью P(
), причем всегда P(
)<1. Количество информации, необходимое для устранения оставшейся неопределенности
, очевидно, равно той части информации, которая разрушена вследствие действия помех. Тогда в соответствии с ф-лой (6.5) количество принятой информации определяется как разность
(6.41)
Для оценки среднего количества принятой информации при передаче одного сообщения выражение (6.41) необходимо усреднить по всему ансамблю и и v:
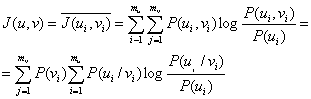
где P() = p(
)p(
) — совместная вероятность переданного и принятого сигналов, ти— количество сигналов и в ансамбле на входе канала и тv — количество сигналов ib ансамбле на выходе канала (в общем случае
).
Величина J(u,v) характеризует в среднем количество информации, которое содержит принятый сигнал v относительно переданного сигнала и, поэтому ее называют также средней взаимной информацией между и и v.
Выражение (6.42) обычно представляют в двух формах. Первая из них
(6.43)
где
— энтропия источника сигналов u и
(6.45)
— условная энтропия или ненадежность.
Соотношение (6.43) показывает, что среднее количество, принятой информации равно среднему количеству переданной информации Н(и) минус среднее количество информации H(u/v), потерянное в канале вследствие воздействия помех.
Вторая форма записи средней взаимной информации, может быть получена, если в (6.42) подставить выражение для условной вероятности в соответствии с ф-лой (2.26). После соответствующих преобразований получаем
(6.46)
Здесь
(6.47)
энтропия выхода канала и
(6.48)
— условная энтропия, равная, как будет показано ниже, энтропии шума. Она определяет бесполезную часть информации, которая содержится в принятых сигналах за счет действия помех.
Понятия скорости передачи информации и пропускной способности, введенные в § 6.7 для каналов без помех, могут быть использованы и в каналах с помехами. В этом случае скорость передачи информации ло каналу определяется как
(6.49)
где и
— соответственно последовательности передаваемых и принимаемых сигналов длительностью Т.
Необходимым условием применимости ф-лы (6.49) является соблюдение свойства эргодичности как для последовательности иT, так и последовательности vT,. Последнее означает, что помехи, действующие в канале, также должны быть эргодическими. По аналогии с (6.29) скорость передачи можно представить с учетом (6.43) и (6.46) в более удобных формах:
(6.50)
Пропускная способность канала с помехами определяется как максимально возможная скорость передачи при заданных ограничениях, накладываемых на передаваемые сигналы:
(6.51)
Для каналов с сигналами одинаковой длительности, равной τ, пропускная способность
(652)
где максимум ищется по всем возможным ансамблям сигналов u.
Рассмотрим двоичный канал с помехами без памяти, по которому передаются дискретные сигналы, выбранные да ансамбля, содержащего два независимых сигнала u1 и u2 с априорными вероятностями p(u1) и p(u2). На выходе канала образуются сигналы v1 и v2 при правильном приеме отражающие соответственно сигналы u1 и u2. В результате действия помех возможны ошибки, которые характеризуются при передаче u1 условной вероятностью P(), при передаче и2— условной вероятностью P(
). Вычислим энтропию сигнала (6.47)
(6.53)
и энтропию шума (6.48)
(6.54)
Будем полагать канал симметричным. Для такого канала вероятности переходов одинаковы: , а полная вероятность ошибки
(6.55)
Отсюда вытекают соотношения:
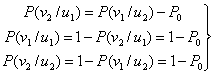
После их подстановки в выражение (6.54) получаем
(6.57)
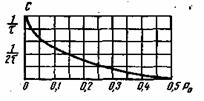
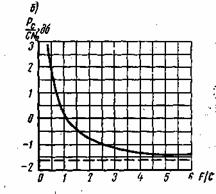
Рис. 6.2. Зависимость пропускной способности двоичного канала от вероятности ошибки Ро
Для того чтобы определить пропускную способность (6.52), необходимо максимизировать J(u,v)=H(v)-H(v/u). При заданной вероятности ошибки, как следует из (6.57), величина H(v/u) .постоянна, а максимум следует искать, изменяя H(v). Энтропия сигнала H(v), выраженная ф-лой (6.53), имеет максимальное значение H0(v)=1 случае равновероятных сигналов, когда P()=P(
)=0,5. Подставляя выражения (6.53) и (6.57) в ф-лу (6.52) получим следующее выражение для пропускной способности двоичного симметричного канала:
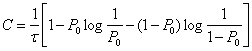
Для многопозиционного симметричного канала при mu=mv=m>2
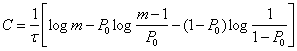
На рис. 6.2 приведена зависимость С от вероятности ошибки для двоичного канала (6.58). Увеличение Р0приводит к снижению пропускной способности, которая становится равной нулю при P0=0,5. В этом случае в соответствии с (6.56) полностью исчезает какая-либо зависимость между передаваемыми и принятыми сигналами: и
. Значение P0=1/2 для бинарного канала является предельным.
6.7. Теорема Шеннона для дискретного канала с помехами
Для дискретных каналов с помехами Шеннон доказал теорему, имеющую фундаментальное значение в теории передачи информации. Эта теорема может быть сформулирована следующим образом.
Если производительность источника, где ε — сколь угодно малая величина, то существует способ кодирования, позволяющий передавать все сообщения источника со сколь угодно малой вероятностью ошибки. При
такая передача невозможна.
Предположим, на вход канала поступают сигналы и, которые вызывают, на его выходе сигналы v. Предварительно будем полагать, что по каналу могут передаваться исключительно типичные последовательности (§6.3), состоящие из п сигналов и:. Соответственно на выходе канала сигналы при достаточно большом п образуют типичные последовательности:
, содержащие типичные последовательности ошибок. Общее число типичных последовательностей и на основании (6.23) равно:
где Н(и) — энтропия сигналов и. Соответственно число типичных последовательностей V определяется как
(6.60)
где H(v) — энтропия сигналов v.
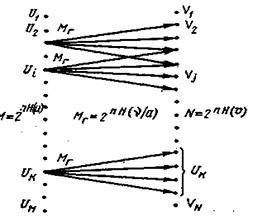
Рис. 6.3. Схема переходов типичных последовательностей сигналов от входа к выходу канала с шумами
Действие помех проявляется в том, что нарушается однозначное соответствие между последовательностями U и V, т. е. при передаче некоторой последовательности Ui возможно появление на выходе канала одной из нескольких последовательностей V. Процесс передачи в этих условиях можно представить так, как показано на рис. 6.3, где стрелками отмечены переходы от типичных последовательностей V к типичным последовательностям V. Так как последовательности ошибок типичные, то и переходы от U к V также являются типичными. Каждой последовательности U соответствует определенная группа типичных переходов, которая характеризует неопределенность, возникающую при передаче U. Количественно указанная неопределенность описывается произведением nH(v/u), где H(v/u) — условная энтропия сигналов при передаче сообщений и (6.48). Тогда в соответствии с (6.23) количество типичных переходов в каждой группе
(6.61)
В общем случае переходы перекрещиваются, т. е. одна и та же последовательность может образоваться в результате передачи одной из нескольких последовательностей U. Для того чтобы иметь возможность с высокой точностью однозначно определить принадлежность принятой последовательности V переданной последовательности U (на рис. 6.3 этому условию удовлетворяет. U
), очевидно, необходимо между грушами последовательностейV установить достаточный интервал. Поэтому из всего набора последовательностей U только часть может использоваться для передачи информации.
Обозначим последовательности, выбранные для переноса информации, через UИ, а их число — буквой МИ. Выясним взаимосвязь МИс вероятностью ошибки при определении принадлежности V, т. е. взаимосвязь с вероятностью ошибки при декодирования принятых сигналов. Вероятности всех типичных переходов от U, к V одинаковы, поэтому полная вероятность ошибки равна вероятности перекрещивания переходов Р. Для вычисления Р
. необходимо знать ансамбль последовательностей UИ. Иными словами, нужно указать конкретный способ кодирования. Решение вопроса об оптимальном выборе последовательностей UИ в общем случае представляет собой чрезвычайно сложную задачу, требующую отдельного рассмотрения. С целью ее упрощения будем полагать, что последовательности UИ выбираются из последовательностей U случайным образом. При этом условии вероятность того, что случайный переход от UИ к V будет перекрещиваться с другими переходами, приближенно равна отношению общего числа переходов ко всему количеству типичных последовательностей V. Следовательно, вероятность ошибки декодирования
(6.62)
Эта оценка вероятности ошибки является грубым приближением, однако она правильно указывает на характер зависимости Род от М и.
При согласовании канала с источником каждой типичной последовательности источника присваивается одна из последовательностей , поэтому их число МИвыбирается равным количеству типичных последовательностей источника. Если энтропия источника равна
, то на основании (6.23) можно записать
(6.63)
Подставляя в (6.62) значения МИ, МГи N из (6.63), (6,61) и (6.60) и логарифмируя, получаем
Разделив это равенство на среднюю длительность сообщений в соответствии с (6.50), будем иметь
где
При максимальной скорости передачи сообщений по каналу и
(6.64)
Из выражения (6.62) следует, что вероятность ошибки декодирования Род может быть сколь угодно малой при неограниченном уменьшении g. Для того чтобы при этих, условиях сохранить достаточно малой величину ε, необходимо увеличивать количество сообщений п в типичных последовательностях. Что касается всех остальных нетипичных последовательностей из п сообщений, которые до сих пор не рассматривались, то их можно закодировать весьма сложными сигналами, обладающими высокой помехоустойчивостью, не заботясь о длительности таких сигналов, поскольку суммарная вероятность нетипичных последовательностей весьма кала и они не вызовут существенного уменьшения скорости передачи информации.
Таким образом, возможность одновременного установления сколь угодно малой вероятности ошибки декодирования Род и малой величины ε доказывает справедливость теоремы Шеннона.
Обратное утверждение теоремы о том, что при RИ>C декодирование со сколь угодно малой ошибкой невозможно, следует из того факта, что в этих условиях MИMГ>N и, следовательно, всегда будут иметь место перекрещивания переходов от U к V, coздающие неопределенность в установлении принадлежности V.
На первый взгляд может показаться, что поскольку вероятность ошибки в канале Р0монотонно уменьшается с увеличением длительности сигналов, то сколь угодно высокая достоверность при декодировании достигается только при неограниченном уменьшении скорости передачи. Теорема Шеннона доказывает, что наличие помех и ошибок в канале само по себе не препятствует передаче сообщений со сколь угодно малой вероятностью ошибок декодирования Род, а лишь ограничивает максимальную скорость передачи информации С. Высокая достоверность декодирования и конечная скорость передачи не исключают друг друга. В этом состоит чрезвычайно важное значение теоремы для теории и техники связи. Вместе с тем следует подчеркнуть, что из теоремы не вытекает конкретный способ наилучшего кодирования.
Применение на практике рассмотренного в теореме Шеннона общего метода, основанного на укрупнении кодируемых последовательностей, сильно усложняет кодирующие и декодирующие устройства и увеличивает задержку сигналов. Поэтому с инженерной точки зрения такой метод не эффективен. Однако теорема не утверждает, что укрупнение кодируемых сообщений является единственным способом. Поэтому в настоящее время продолжаются интенсивные поиски способов кодирования, которые бы позволяли с аппаратурой приемлемой сложности достигать предельных возможностей, указанных теоремой Шеннона.
Для обеспечения высокой достоверности передачи сообщений необходимо применять коды с избыточностью. Если R=C, то в соответствии с (6.50) средняя взаимная информация . В канале без помех она приобретает максимальное значение
. Тогда коэффициент избыточности по аналогии с (6.12) равен:
(6.65)
Иными, словами, теорема утверждает, что для перелагай сообщений со сколь угодно малой вероятностью ошибки декодирования: Род могут быть найдены коды с минимальной избыточностью, равной χ. При передаче бинарных сигналов на основании (6.65), (6.33) и (6.58) минимальная избыточность равна:
(6.66)
6.8. Энтропия непрерывных сообщений
При передаче непрерывных сообщений переданные сигналы s(t) являются функциями времени, принадлежащими некоторому множеству, а принятые сигналы x(t) будут их искаженными вариантами. Все реальные сигналы имеют спектры, основная энергия которых сосредоточена в ограниченной полосе F. Согласно теореме Котельникова такие сигналы определяются своими значениями в точках отсчета, выбираемых через интервалы . В канале на сигнал накладываются помехи, вследствие чего количество различимых уровней сигнала в точках отсчета будет конечным. Следовательно, совокупность значений непрерывного сигнала эквивалентна некоторой дискретной конечной совокупности. Это позволяет нам определить необходимое количество информации и пропускную способность канала при передаче непрерывных сообщений на основании результатов, полученных для дискретных сообщений.
Определим сначала количество информации, которое содержится в одном отсчете сигнала. относительно переданного сигнала
. Это можно сделать на основании соотношения (6.41), если в последнем вероятности выразить через соответствующие плотности вероятности и взять предел при
(6.67)
Среднее количество информации в одном отсчете непрерывного сигнала определяется путем усреднения выражения (6.67) по всем значениям s и x:
(6.68)
где p(s, x) — совместная плотность вероятности, а S и X — области возможных значений s и х.
Выражение (6.68) можно представить как разность
(6.69)
где
(6.70)
Величина H(s) характеризует информационные свойства сигналов и по форме записи аналогична энтропии дискретных сообщений (6.6). Так как в выражение (6.70) входит дифференциальное распределение вероятностей p(s), то H(s) называют дифференциальной энтропией сигнала s. Выражение H(s/x) представляет собой условную дифференциальную энтропию сигнала s:
(6.71) Подобно тому, как это было сделано для дискретного канала, выражение (6.68) можно записать в другой форме
(6.72)
где
(6.73)
— дифференциальная энтропия сигнала х и
(6.74)
— условная дифференциальная энтропия сигнала х, называемая также энтропией шума.
Многие свойства энтропии непрерывного распределения аналогичны свойствам энтропии дискретного распределения. Если непрерывный сигнал s ограничен интервалом то энтропия H(s) максимальна и равна log(
), когда сигнал 5 имеет равномерное распределение
(6.75)
Если ограничено среднеквадратичное значение непрерывного сигнала
то энтропия, максимальная при нормальном распределении,
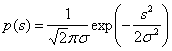
и равна:
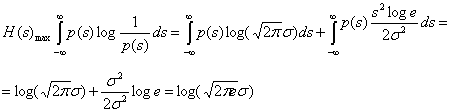
Необходимо отметить, что, в отличие от энтропии дискретных сигналов, величина дифференциальной энтропии зависит от размерности непрерывного сигнала. По этой причине она не является мерой количества информации, хотя и характеризует степень неопределенности, присущую источнику. Только разность дифференциальных энтропии (6.69) или (6.72) количественно определяет среднюю информацию
6.9. Скорость передачи и пропускная способность непрерывного канала. Формула Шеннона
Для того чтобы найти среднее количество информации T(s,x), передаваемое сигналом на интервале Т, необходимо рассмотреть n=2FT отсчетов непрерывного сигнала на входе канала: s1; s2;.., sn и на выходе канала: x1; x2;..;хп. В этом случае по аналогии с выражениями (6.69) и (6.72) можно записать
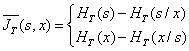
где
s, sbx, х„
Энтропии HT(s) и HT(s/x) описываются аналогичными выражениями, только всюду необходимо поменять местами переменные s и х Скорость передачи информации по непрерывному каналу находится как предел:
(6.79)
Максимальная скорость передачи в непрерывном канале определяет его пропускную способность
(6.80)
где максимум определяется по всем возможным ансамблям входных сигналов s.
Вычислим пропускную способность непрерывного канала, в котором помехой является аддитивный шум. w(t), представляющий собой случайный эргодический процесс с нормальным распределеннием и равномерным спектром. Средние мощности сигнала я шума ограничены величинами Рси Р, а ширина их спектра paвна F.
Согласно выражениям (6,80) и (6.78) имеем
(6.81)
Прежде всего найдем величину НT (x/s). С этой целью рассмотрим энтропию шума для одного отсчета (6.74), которая с учетом соотношения p(s, x)=p(s)p(x/s) может быть представлена в следующем виде:
(6.82)
При заданном значении s сигнал на выходе канала x=s+w полностью определяется аддитивным шумом w. Поэтому
(6.83)
где рш(х—s) — плотность вероятности шума.
Подставляя (6.83) в (6.82) и заменяя переменную х на , т. е. подставляя вместо х сумму s +
, можем записать
Принимая во внимание, что, получим
Следовательно, условная энтропия H(x/s) при аддитивном шуме зависит только от его распределения рш(), что и объясняет термин энтропия шума. Следовательно, на интервале Т
(6.84)
где n=2FT.
Значения шума с равномерным спектром некоррелированы между собой в моменты отсчетов, разделенные интервалом
Отсутствие статистической взаимосвязи между отсчетами шума позволяет представить энтропию суммы п отсчетов шума (6.84) как сумму энтропий отдельных отсчетов, которые вследствие стационарности шума равны между собой. С учетом этих соображений можно записать
Поскольку отсчеты шума статистически независимы, а каждый из них распределен по нормальному закону, то энтропия HT(w) максимальна и в соответствии с (6.77) равна:
(6.85)
где вместо подставлено
.
При данной величине HT(x/s) = HT(w) пропускная способность (6.81) отыскивается путем максимизации НТ(х). Максимум НТ(х), очевидно, имеет место, когда сигнал х так же, как и шум, характеризуется нормальным распределением и равномерным спектром.
Отсюда
(6.86)
Здесь предполагается, что сигнал s и помеха w независимы, поэтому мощность сигнала х равна сумме мощностей. Подставляя (6.85) и (6.86) в (6.81), окончательно получим
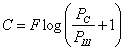
Так как х и w имеют нормальное распределение, то сигнал s=x–w также должен иметь нормальное распределение. Отсюда следует важный вывод: для того чтобы получить максимальную скорость передачи информации, необходимо применять сигналы с нормальным распределением и равномерным спектром.
Формула (6.87), впервые выведенная Шенноном, играет важную роль в теории и технике связи, Она показывает те предельные возможности, к которым следует стремиться при разработке современных систем связи. Так как при равномерном спектре мощность шума определяется произведением Pш=N0F, то ф-лу (6.87J можно записать в другом виде
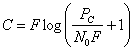
С увеличением F пропускная способность монотонно возрастает стремится, как показано на рис. 6.4а, к величине
(6.89)
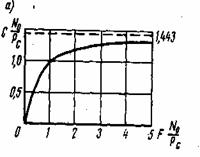
Рис. 6.4. Зависимость пропускной способности С от полосы пропускания F в непрерывном канале
Нa рис. 6.46 зависимость (6.88) изображена в другой нормировке, из которой следует, что при фиксированных значениях пропускной способности С и энергетического спектра шума N существует обратная зависимость между Рси F. Иными словами, допускается уменьшение мощности сигнала за счет расширения его спектра.
Формулу (6.87), выведенную для равномерных спектров сигнала и шума, можно распространить и на случай неравномерных спектров. С этой целью в окрестностях некоторой частоты выберем достаточно узкую полосу, в которой спектры сигнала Gc(f) и шума Gш(f) будут постоянными. Тогда для этой полосы в соответствии с (6.87) /пропускная способность будет равна:
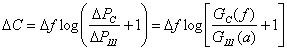
где и
Полная пропускная способность вычисляется как интеграл от (6.90) по всем частотам спектра сигнала
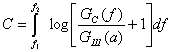
Можно показать, что при заданном спектре шума Gш(f) и ограниченной мощности сигнала максимум С имеет место в случае выполнения условия
(6.92)
т. е. мощность сигнала должна возрастать на тех частотах, где уменьшается мощность шума и наоборот. Можно также поставить вопрос: если выполняется условие (6.92), то при каком спектре шума получается минимальная пропускная способность? Оказывается, что этому условию удовлетворяет равномерный спектр, т. е. спектр белого шума. Таким образом, белый шум, уменьшающий в наибольшей степени пропускную способность, является самым опасным видом помех.
Рассмотрим теперь вопрос о производительности источника непрерывных сообщений и о влиянии на качество их передачи помех, действующих в канале связи. При отсутствии каких-либо ограничений, накладываемых на непрерывные сообщения, количество содержащейся в них информации согласно (6.1) равно бесконечности:
Поэтому источник таких сообщений обладает бесконечной производительностью (6.25). Для того чтобы количество информации и производительность источника приобрели определенный смысл и стали конечными величинами, необходимо рассматривать непрерывное сообщение u(t) с учетам точности его оценки. Последняя, в частности, определяется погрешностью приборов, с помощью которых измеряется или регистрируется непрерывное сообщение. Обычно погрешность количественно оценивается среднеквадратичным отклонением приближенного непрерывного сообщения u*(t) от его точного значения u(t):
Нетрудно понять, что чем меньше , тем большее количество информации в среднем содержится в u*(t) относительно u(t) и тем выше производительность источника.
Количество информации на выходе источника при >0 по аналогии с (6.68) определяется как
(6.93)
Для ограниченной погрешности всегда можно найти такой способ воспроизведения u(t) посредством и* (t), а следовательно, такое распределение р'(и, и*), при котором выражение (6.93) достигает наименьшего значения. Распределение р'(и, и*) является наиболее выгодным, так как оно позволяет при заданной .погрешности воспроизводить u(t), используя минимальное количество информации. Наименьшее значение J(и, и*) при
называется эпсилон-энтропией
(6.94)
Тогда производительность источника непрерывных сообщений
Для непрерывного канала с пропускной способностью С, на вход которого подключается источник, обладающий производительностью , Шенноном была доказана следующая теорема.
Если при заданной погрешности оценки сообщений источника его производительность
<C, то существует способ кодирования, позволяющий передавать все непрерывные сообщения источника с ошибкой в воспроизведении на выходе канала, сколь угодно мало отличающейся от
.
Иначе говоря, дополнительная неточность в воспроизведении сообщения v(t) на выходе канала, обусловленная воздействием помех, может быть сделана весьма незначительной, т. е.
, где
— сколь угодно малая величина.
Скорость передачи информации по каналу в конечном счете определяется скоростью потока информации на выходе приемника
где НТ(и) — энтропия принятого сообщения v(t), HT(w*) — энтропия шума на выходе приемника. Если считать, что сообщение v(t) и помеха w*(t) на выходе приемника имеют нормальное распределение и равномерный спектр, то
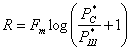
Здесь Fm — ширина спектра частот принимаемого сообщения, обычно равная полосе пропускания приемника по низкой частоте; P* — средняя мощность принятого сообщения v(t); Р
* — средняя мощность шума на выходе приемника.
6.10. Пропускная способность каналов с переменными параметрами
Характеристики системы связи в значительной степени зависят от параметров канала связи, который используется для передачи сообщений. Исследуя пропускную способность каналов, мы предполагали, что их параметры сохраняются постоянными. Однако большинство реальных каналов обладают переменными параметрами. Параметры канала, как правило, изменяются во времени случайным образом. Как уже отмечалось (§ 5.7), случайные изменения коэффициента передачи канала μ вызывают замирания сигнала, что эквивалентно воздействию мультипликативной помехи. Эквивалентная мощность этой помехи согласно (5.76) равна Тогда суммарная мощность помех в канале с переменными параметрами при наличии аддитивной помехи будет равна:
Отсюда следует, что замирания сигнала приводят к увеличению мощности помех, а следовательно, и к снижению пропускной способности канала (6.87) .
Рассмотрим, каким образом вычисляется пропускная способность канала с замираниями при передаче непрерывных сообщений. В этих условиях необходимо найти такое распределение вероятностей сигнала, которое при заданных статистических свойствах коэффициента передачи μ обеспечивало бы максимальную скорость передачи информации.
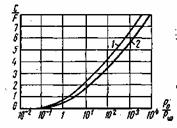
Рис. 6.5. Зависимость пропускной способности от среднего отношения сигнала к помехе для каналов с постоянными параметрами (1) и рэлеевскими замираниями (2)
Решение задачи в общем виде вызывает значительные трудности. Однако в случае медленных замираний, когда скорость замираний намного меньше скорости изменения непрерывного сообщения, можно с достаточной точностью предсказывать по текущим значениям коэффициента его последующие значения. При таком допущении максимум скорости передачи по-прежнему имеет место для сообщений с нормальным распределением, что дает возможность пользоваться ф-лой (6.87). Подставляя в (6.87) мощность принимаемого сигнала
2Р0, где Р0—переданная мощность сигнала, получим пропускную способность при фиксированном
:
Усреднив по всем значениям
, найдем среднее значение пропускной способности канала при медленных замираниях
где p() — плотность вероятности коэффициента передачи.
Во многих каналах изменения коэффициента
подчиняются закону Рэлея (5.77). На рис. 6.5 показаны зависимости C/F от среднего отношения Р
/Р
для канала с постоянными параметрами 1 и канала с рэлеевскими замираниями 2. Из анализа кривых рис. 6.5 следует, что медленные рэлеевеские замирания уменьшают пропускную способность канала не более чем на 17%.
Для вычисления пропускной способности дискретных каналов при быстрых замираниях могут быть использованы выражения для С, полученные при постоянных параметрах (6.58) и (6.59). В эти формулы необходимо подставить вместо вероятности ошибки ее среднюю статистическую величину, найденную путем усреднения по всем значениям коэффициента . Подставляя (5.81) в (6.58), получаем выражение для пропускной способности канала с ортогональными двоичными сигналами ири быстрых рэлеевских замираниях
Здесь – что дает возможность заменить
в (6.58)
отношением
Полученное выражение для С обладает максимумом, который достигается при :
В этом случае наблюдается значительный проигрыш по сравнению с пропускной способностью аналогичного канала без замираний
В многопозиционных системах положение существенно улучшается. Если число позиций , то при рэлеевских замираниях
Это дает проигрыш всего лишь на 27% по сравнению с таким же каналом без замираний. Отсюда следует вывод, что в условиях замираний передача дискретных сообщений более эффективна при использовании многопозиционных кодов.
6.11. Эффективность систем передачи информации
Пропускная способность канала связи С определяет максимальную скорость передачи информации, т. е. является тем пределом, которого можно достичь при идеальном кодировании. Естественно, что в реальных каналах скорость передачи R всегда будет меньше С. Степень отличия R от С зависит от того, насколько рационально выбрана и эффективно используется та или иная система связи. Наиболее общей оценкой эффективности системы связи является коэффициент использования канала
(6.96)
Для дискретных систем связи можно записать, где
и
— эффективность системы кодирования и эффективность системы модуляции. Вводя избыточность сообщения
, и избыточность сигнала
, получим
(6.97)
где — полная избыточность системы.
При передаче непрерывных сообщений согласно выражениям (6.87) и (6.95) имеем
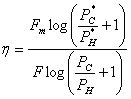
В ряде практических случаев удобными оценками эффективности связи являются коэффициент использования мощности сигнала
(6.99)
где — интенсивность помехи, и коэффициент использования полосы частот канала
(6.100)
Коэффициент является основным показателем эффективности для тех систем, о которых мощность сигнала жестко ограничена (например, для космических систем). В системах проводной связи более важным показателем является коэффициент
.
Согласно выражению (6.97) для коэффициента использования канала эффективность системы связи полностью определяется величиной ее избыточности. Отсюда задача повышения эффективности связи сводится к задаче уменьшения избыточности сообщения и сигнала.
Избыточность сообщения, как мы видели, обусловлена тем, что элементы сообщения не являются равновероятными и между ними имеется статистическая связь. При кодировании можно перераспределить вероятности исходного сообщения так, чтобы распределение вероятностей символов кода приближалось к оптимальному (к равномерному в дискретном случае или к нормальному при передаче непрерывных сообщений). Такое перераспределение позволяет устранить избыточность, зависящую от распределения вероятностей элементов сообщения. Примером подобного кодирования является код ШеннонаФано, рассмотренный в § 6.5
Если перейти от кодирования отдельных символов сообщения к кодированию целых групп символов, то можно устранить взаимосвязь между ними и тем самым еще уменьшить избыточность. Общая идея такого метода кодирования, который называют методом укрупнения, состоит в следующем. Исходное сообщение разбивается на отрезки по k символов в каждом. Такие отрезки мо-гут рассматриваться как укрупненные элементы сообщения. Можно показать, что вероятностные связи между такими укрупненными элементами слабее, чем между элементами исходного сообщения. Очевидно, чем больше k (крупнее отрезки), тем слабее будет связь между ними. Далее укрупненные элементы кодируются с учетом их распределения вероятностей.
Следует заметить, что при укрупнении элементов происходит преобразование, состоящее в переходе к коду с более высоким основанием , где т— первоначальное основание.
Своеобразным примером метода укрупнения сообщений является стенографический текст. Каждый стенографический знак в этом тексте выражает целое слово или даже группу слов.
Что касается сигнала, то его избыточность зависит от способа
модуляции и от вида переносчика. Процесс модуляции обычно сопровождается расширением полосы частот сигнала по сравнению
с полосой частот передаваемого сообщения. Это расширение полосы и является избыточным. Частотная избыточность также увеличивается при переходе от синусоидального переносчика к переносчику импульсному или шумоподобному. С точки зрения повышения эффективности передачи следовало бы выбирать такие способы модуляции, которые имеют малую избыточность. К таким системам, в частности, относится однополосная передача, в которой передаваемые сигналы не содержат частотной избыточности — они являются просто копиями передаваемых сообщений.
Однако, говоря об эффективности системы связи, нельзя забывать о ее помехоустойчивости. Устранение избыточности повышает эффективность передачи, но снижает при этом достоверность (помехоустойчивость) и, наоборот, сохранение или введение избыточности позволяет обеспечить высокую достоверность передачи. Например, при телеграфной передаче текста устранение избыточности приводит к тому, что становится труднее исправлять ошибки в сообщении и в конечном счете снижается помехоустойчивость. При сохранении избыточности в тексте помехоустойчивость будет выше.
При кодировании в ряде случаев избыточность специально вводится с целью повышения достоверности передачи. Примером такого кодирования являются корректирующие коды.
Аналогичная ситуация имеет место и в отношении избыточности сигнала. Частотная избыточность гори различных видах модуляции, используется по-разному. При частотной модуляции, например, мы можем получить больший выигрыш в помехоустойчивости, чем при амплитудной модуляции, а при кодовой импульсной модуляции этот выигрыш еще больше. Частотная избыточность шумового переносчика позволяет снизить влияние замираний и сосредоточенных помех.
Следовательно, при оценке различных систем связи необходимо учитывать, по крайней мере, два показателя: эффективность и помехоустойчивость, совокупность этих двух показателей составляет достаточно полную характеристику системы.
Наиболее совершенной системой считается такая, которая обеспечивает наибольшую эффективность при заданной помехоустойчивости или, наоборот, обеспечивает наибольшую помехоустойчивость при заданной эффективности [2].
Вопросы для повторения
1. Какой критерий используется для количественной оценки информации? Почему применяется логарифмическая мера количества информации?
2. Что называется энтропией и как она определяется для источников независимых и зависимых сообщений?
3. Каковы причины появления избыточности в сообщении?
4. Какие источники сообщения называются стационарными и эргодическими?
5. Что называется пропускной способностью канала? Чему она равна для двоичного канала без помех?
6. Поясните принцип оптимального статистического кодирования.
7. Как определяется скорость передачи и пропускная способность канала с помехами?
8. Какие выводы следуют из теоремы Шеннона для дискретного канала с помехами?
9. Как определяется количество передаваемой информации в непрерывных каналах?
10. Проанализируйте формулу Шеннона для пропускной способности непрерывного канала.
11. Сформулируйте теорему Шеннона для непрерывного канала и поясните ее смысл.
12. Как вычисляется пропускная способность каналов с переменными параметрами?
13. Что называется эффективностью системы связи и как она определяется количественно?
14. Поясните зависимость между помехоустойчивостью и эффективностью связи. Приведите примеры.
Пропускная
способность канала связи – это
максимально возможная скорость передачи
информации по каналу связи.
C
= Vk‧maxI(A,B)
Найдем
пропускную способность дискретного
симметричного n-разрядного канала:
(1)
Найдем
энтропию шума H(B|A):

Так как канал симметричный, то все
сообщения на его входе появляются с
одинаковой вероятностью. Поэтому
P(
)=1/n
При
верной передаче символа i=k:
P(
)
= 1–p
При
ошибочной передаче символа i≠k:
P(
)
= p/(n–1)
Поскольку
на вход канала поступает всего n сообщений,
то количество всех случаев ошибочной
передачи будет n*(n-1).
Подставим
все в формулу энтропии шума и разобьем
двойную сумму на случай правильной и
неправильной передачи:

H(B)=log(N)
Подставить
все в формулу (1)
6.Пропускная способность непрерывного канала связи (вывод формулы).
Найдем пропускную способность непрерывного
канала связи:
(1)
h(Z|S)
соответствует гауссовскому закону:
, потому что дисперсия пропорциональная
плотности шума
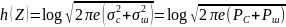
Подставим все в (1):
=
7.Эпсилон-энтропия и эпсилон-производительность (вывод формулы)
Эпсилон-энтропия Hε(B)
это то минимальное количество информации,
которое необходимо передать по каналу
связи чтобы принятый сигнал b*(t) был бы
еще эквивалентен переданному b(t).
(1)
H(B|A)
соответствует гауссовскому закону:
,
где Pε
– это мощность шума воспроизведения
H(B) тоже
подчиняется гауссовскому закону:
,
где Pв – мощность сигнала посылаемого
от кодера в канал связи
Подставим в (1) и сократим:

Эпсилон-производительность
источника непрерывной информации –
это минимальное количество информации,
которое необходимо передать за 1 с, чтобы
принятый сигнал был еще эквивалентен
переданному:
,
где Fв – верхняя частота спектра сообщения
8.Эффективное кодирование. Цель и принцип. Коды Хаффмена и Шеннона-Фано.
Эффективное
кодирование осуществляется с применением
неравномерных кодов, в которых более
короткие кодовые комбинации соответствуют
более вероятным символам сообщения, а
более длинные — менее вероятным символам.
Основными требованиями, предъявляемыми
к эффективному коду, являются: 1)
однозначность декодирования, т. е.
каждому символу кодируемого сообщения
должна соответствовать своя кодовая
комбинация и для всех символов комбинации
должны быть различны; 2) в среднем на
один символ сообщения должно приходиться
минимальное число элементов кодовой
комбинации эффективного кода; 3) ни какая
более короткая комбинация эффективного
кода не должна являться началом другой,
более длинной комбинации.
Цель эффективного кодирования – снижение
первоначальной избыточности источника
и уменьшение тем самым времени передачи
информации. Достигается это за счет
неравной вероятности появления сообщений
источника.
9.Помехоустойчивое кодирование. Цель и принцип. Основные параметры пу кодов.
Помехоустойчивым (корректирующим)
кодированием называется кодирование,
при котором осуществляется обнаружение
либо обнаружение и исправление ошибок
в принятых кодовых комбинациях.
Возможность помехоустойчивого кодирования
осуществляется на основании теоремы,
сформулированной Шенноном.
Основным принципом помехоустойчивого
кодирования является использование
избыточных кодов, причем если для
кодирования сообщения используется
простой код, то в него специально вводят
избыточность. Необходимость избыточности
объясняется тем, что в простых кодах
все кодовые комбинации являются
разрешенными, поэтому при ошибке в любом
из разрядов приведет к появлению другой
разрешенной комбинации, и обнаружить
ошибку будет невозможно. В избыточных
кодах для передачи сообщений используется
лишь часть кодовых комбинаций (разрешенные
комбинации). Прием запрещенной кодовой
комбинации означает ошибку.
Основные понятия и характеристики
помехоустойчивых кодов: 1) q
(кратность ошибки) – количество ложных
импульсов в принятой кодовой комбинации;
2) d(bi, bj) (кодовое расстояние) – расстояние
между двумя кодовыми комбинациями; 3)
dmin (минимальное кодовое расстояние) –
минимальное расстояние среди всех пар
кодовых комбинаций данного кода. Если
dmin = 1, код считается не помехоустойчивым;
4) кратность исправляемой ошибки
qи=(dmin-1)/2
неч и qи=(dmin/2)-1
чет; 5) кратность обнаруживаемой ошибки
qо=dmin-1

Расчет источников сообщений, сигналов и каналов
Введение
сигнал кодирование информационный дискретный
Эффективная организация обмена информации приобретает все
большее значение как условие успешной практической деятельности людей. Объем
информации, необходимой для нормального функционирования современного общества
растет пропорционально квадрату развития промышленного потенциала. Доля рабочей
силы, занятой вопросами обеспечения информации, превышает долю рабочей силы,
занятой непосредственно в производстве. Поэтому, науки, изучающие структуру и
закономерности протекания информационных процессов, к числу которых относится и
теория информации, в такой ситуации становятся исключительно актуальными.
Расчет информационных характеристик дискретных сообщений и
дискретных каналов, а также их согласование являются первоочередными задачами
теории информации. Целью данного курсового проекта является решение подобных
задач.
Курсовой проект включает четыре раздела. Первый раздел –
расчет информационных характеристик источников дискретных сообщений. В процессе
выполнения данного этапа курсового проекта было составлено подробное решение
трех задач: на определение энтропии шума в двоичном симметричном канале без
памяти, на определение производительности источника.
Второй раздел – расчет информационных характеристик дискретного
канала – содержит две задачи. В результате решения первой задачи были найдены
апостериорные вероятности. Вторая задача направлена на определение пропускной
способности канала и скорости передачи информации.
Третий раздел курсового проекта направлен на решение задач в
области эффективного кодирования. В первых двух осуществлялось кодирование
методом Фано, в остальных – методом Хаффмена.
Последний раздел, содержащий две задачи, посвящен
помехоустойчивому кодированию. Первая задача предполагает оценить, возможна ли
безошибочная передача сообщений источника по двоичному симметричному каналу, а
в случае отсутствия такой возможности оценить минимально неизбежные потери
информации в единицу времени. Во второй задаче требуется построить производящую
матрицу линейного двоичного блочного кода, способного исправлять одиночную
ошибку при передаче дискретных сообщений источника.
1. Расчет информационных характеристик источников
дискретных сообщений
Задача №1.26
Распределение вероятностей дискретной случайной величины
имеет вид: p(x1)=0,362133; p(x2)=0,15; p(x3)=0,15; p(x4)=0,1; p(x5)=0,1; p(x6)=0,1; p(x7)=0,01; p(x8)=0,01; p(x9)=0,017867. Определить
число n
значений случайной величины, при которых энтропия Hp(X) равномерного
распределения будет равна энтропии H(X) заданного распределения.
Решение:
Пользуясь формулой Шеннона, найдем энтропию:
Подставляя значения в указанную формулу, получаем:
Равномерное распределение предполагает равные вероятности всех
возможных исходов.
Hp(X)=log2n
Ответ: .
Задача №1.41
Найти энтропию шума в двоичном симметричном канале без памяти, если энтропия источника
на входе канала бит, энтропия ансамбля на выходе канала
бит, ненадежность канала
бит.
Решение:
Энтропия шума в двоичном симметричном канале без памяти
вычисляется по формуле (1.17) лекции:
Таким образом, для того чтобы воспользоваться вышеуказанной
формулой для вычисления энтропии шума в двоичном симметричном канале без памяти
необходимо найти количество переданной информации. Для этого воспользуемся формулой
(1.13) лекции:
Подставив данную формулу в ранее представленную, получим
необходимое выражение для вычисления энтропии шума в двоичном симметричном
канале без памяти:
Подставив в указанное выражение набор заданных параметров получим
соответствующее значение энтропии шума в двоичном симметричном канале без
памяти:
(бит)
Ответ: энтропия шума в двоичном симметричном канале без памяти
составляет бит.
Задача №1.76
Дискретный источник выбирает сообщения из ансамбля . Длительности сообщений соответственно
равны: tu1=0,8c, tu2=0,6c, tu3=0,5c, tu4=0,3c. Определить
производительность источника.
Решение:
Производительность источника определяется как суммарная энтропия
сообщений, переданных за единицу времени:
Пользуясь формулой Шеннона, находим:
бит
Среднее время определим как
Откуда
Подставим в формулу полученные данные и получим производительность
источника:
(бит/с)
Ответ: производительность источника бит/с.
2 Расчет информационных характеристик дискретного канала
Задача №2.3
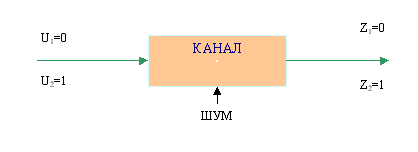
На вход дискретного симметричного канала без памяти поступают
двоичные символы и
с априорными вероятностями p(U1) = 0,15 и p(U2) = 0,85. Переходные вероятности
в таком канале задаются соотношением
, где p – вероятность ошибки, p = 0,1.
Определить все апостериорные вероятности .
Решение:
Ситуация в канале характеризуется схемой, изображенной на рисунке
2.1:
Рисунок 2.1
Так как р – вероятность ошибки, следовательно вероятность
правильного приема – q, причем
Найдем переходные вероятности:
В таком канале каждый кодовый символ может быть принят с ошибочной
вероятностью:
Но не вся информация, передающаяся по каналу может быть ошибочной.
Таким образом, правильно переданная информация описывается следующим
распределением вероятностей:
По формуле Байеса определим апостериорные вероятности:
Используя формулу Байеса, получаем:
Ответ: апостериорные вероятности составляют соответственно ,
,
и
.
Задача №2.51
По каналу связи передаётся сообщение из ансамбля . Средняя длительность передачи одного
элемента сообщения в канале τ = 0,5 мс. Шум в канале отсутствует. Определить
пропускную способность канала и скорость передачи информации.
Решение:
В соответствие с формулой (1.25а) лекции пропускная
способность дискретного канала без шума определяется:
, где М=8,
Подставляя в формулу (1.25а) полученные значения, получаем
Скорость передачи информации определяется по формуле:
, где
, т.к.
=0,
т.к. шум отсутствует. Энтропию найдем по формуле Шеннона:
Подставляя исходные значения в формулу, получаем:
Ответ: ,
3. Согласование дискретного источника с
дискретным каналом без шума. Эффективное кодирование
Задача №3.3
Закодировать двоичным кодом Фано ансамбль сообщений {ai}, заданных таблицей 1.
Таблица 1
|
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
a7 |
a8 |
a9 |
a10 |
a11 |
a12 |
|
0,38 |
0,12 |
0,071 |
0,21 |
0,013 |
0,004 |
0,012 |
0,03 |
0,0211 |
0,1 |
0,019 |
0,0199 |
Закодировать произвольную комбинацию, состоящую из 5 символов
из ансамбля {ai}. Определить потенциальный минимум среднего количества
символов кода, приходящихся на одно сообщение ансамбля {ai} и среднее количество
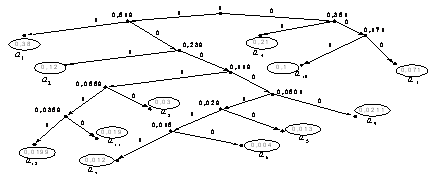
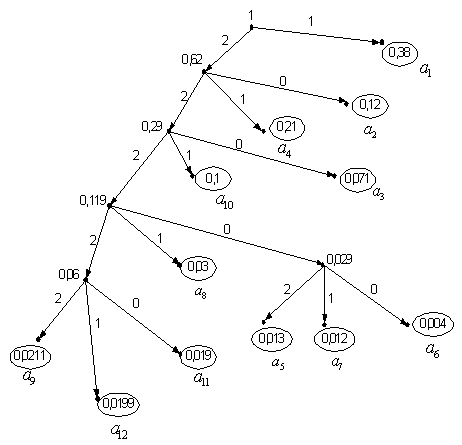
символов, разработанного кода Фано, приходящихся на одно сообщение из {ai}. Рассчитать
эффективность разработанного кода.
Решение:
Для удобства закодирования расположим вероятности появления
сообщений в порядке убывания. Результат представлен в таблице 2.
Таблица 2
|
a1 |
0,38 |
0 |
0,59 |
0 |
00 |
|||||||||
|
a4 |
0,21 |
1 |
01 |
|||||||||||
|
a2 |
0,12 |
1 |
0,41 |
0 |
0,22 |
0 |
100 |
|||||||
|
a10 |
0,1 |
1 |
101 |
|||||||||||
|
a3 |
0,071 |
1 |
0,19 |
0 |
0,101 |
0 |
1100 |
|||||||
|
a8 |
0,03 |
1 |
1101 |
|||||||||||
|
a9 |
0,0211 |
1 |
0,089 |
0 |
0,041 |
0 |
11100 |
|||||||
|
a12 |
0,0199 |
1 |
11101 |
|||||||||||
|
a11 |
0,019 |
1 |
0,048 |
0 |
11110 |
|||||||||
|
a5 |
0,013 |
1 |
0,029 |
0 |
111110 |
|||||||||
|
a7 |
0,012 |
1 |
0 |
1111110 |
||||||||||
|
a6 |
0,004 |
1 |
1111111 |
Выберем из ансамбля сообщений {ai} произвольную комбинацию
из пяти символов и закодируем их полученным кодом Фано:
a4 a6 a8 a10 a12
Потенциальный минимум будем искать по формуле (2.3) лекции
Так как код является двоичным, то основание кода . Отсюда следует:
Тогда потенциальный минимум будет равен энтропии источника:
Найдем энтропию источника, пользуясь теоремой Шеннона:
Подставив в данную формулу заданные значения, получим:
Подставив полученное значение в формулу для вычисления
потенциального минимума, получим:
Рассчитаем среднее количество символов, приходящихся на одно
сообщение, по формуле (2.9) лекции:
m – количество символов в коде.
Количество символов в коде представлено в таблице 3.
Таблица 3
|
Сообщение |
Вероятность |
Количество |
|
a1 |
0,38 |
2 |
|
a2 |
0,12 |
3 |
|
a3 |
0,071 |
4 |
|
a4 |
0,21 |
2 |
|
a5 |
0,013 |
6 |
|
a6 |
0,004 |
7 |
|
a7 |
0,012 |
7 |
|
a8 |
0,03 |
4 |
|
a9 |
0,0211 |
5 |
|
a10 |
0,1 |
3 |
|
a11 |
0,019 |
5 |
|
a12 |
0,0199 |
5 |
Найдем эффективность кода по формуле:
Подставив найденные значения в вышеуказанную формулу, получим:
Ответ: потенциальный минимум , среднее количество символов, приходящихся на одно сообщение,
составляет , эффективность кода равна
.
Задача №3.33
Закодировать троичным кодом Фано ансамбль сообщений, заданных
таблицей 4.
Таблица 4
|
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
a7 |
a8 |
a9 |
a10 |
a11 |
a12 |
|
0,38 |
0,12 |
0,071 |
0,21 |
0,013 |
0,004 |
0,012 |
0,03 |
0,0211 |
0,1 |
0,019 |
0,0199 |
Закодировать произвольную комбинацию, состоящую из 5 символов
из ансамбля {ai}. Определить потенциальный минимум среднего количества
символов кода, приходящихся на одно сообщение ансамбля {ai} и среднее количество
символов, разработанного кода Фано, приходящихся на одно сообщение из {ai}. Рассчитать
эффективность разработанного кода.
Решение:
Для удобства кодирования расположим вероятности появления
сообщений в порядке убывания. Результат представлен в таблице 5.
Таблица 5
|
a1 |
0,38 |
0 |
0 |
|||
|
a4 |
0,21 |
1 |
0 |
10 |
||
|
a2 |
0,12 |
1 |
11 |
|||
|
a10 |
0,1 |
2 |
0 |
20 |
||
|
a3 |
0,071 |
1 |
0 |
210 |
||
|
a8 |
0,03 |
1 |
211 |
|||
|
a9 |
0,0211 |
2 |
0 |
220 |
||
|
a12 |
0,0199 |
1 |
0 |
2210 |
||
|
a11 |
0,019 |
1 |
2211 |
|||
|
a5 |
0,013 |
2 |
0 |
2220 |
||
|
a7 |
0,012 |
1 |
2221 |
|||
|
a6 |
0,004 |
2 |
2222 |
Выберем из ансамбля {ai} произвольную комбинацию
из пяти символов и закодируем их полученным кодом Фано:
a1 a2 a3 a4 a5
Потенциальный минимум будем искать по формуле (2.3) лекции
Так как код является троичным, то основание кода . Отсюда следует:
Найдем энтропию источника, пользуясь теоремой Шеннона:
Подставив в данную формулу заданные значения, получим:
Подставив полученное значение в формулу для вычисления
потенциального минимума, получим:
Рассчитаем среднее количество символов, приходящихся на одно
сообщение, по формуле (2.9) лекции:
где Ps – вероятность появления события;
m – количество символов в коде.
Таблица 6
|
Сообщение |
Вероятность |
Количество |
|
a1 |
0,38 |
1 |
|
a2 |
0,12 |
2 |
|
a3 |
0,071 |
3 |
|
a4 |
0,21 |
2 |
|
a5 |
0,013 |
4 |
|
a6 |
0,004 |
4 |
|
a7 |
0,012 |
4 |
|
a8 |
0,03 |
3 |
|
a9 |
0,0211 |
3 |
|
a10 |
0,1 |
2 |
|
a11 |
0,019 |
4 |
|
a12 |
0,0199 |
4 |
Найдем эффективность кода по формуле:
Подставив найденные значения в вышеуказанную формулу, получим:
Ответ: потенциальный минимум , среднее количество символов, приходящихся на одно сообщение,
составляет , эффективность кода равна
.
Задача №3.63
Закодировать двоичным кодом Хаффмана ансамбль сообщений,
представленных в таблице 7.
Таблица 7
|
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
a7 |
a8 |
a9 |
a10 |
a11 |
a12 |
|
0,38 |
0,12 |
0,071 |
0,21 |
0,013 |
0,004 |
0,012 |
0,03 |
0,0211 |
0,1 |
0,019 |
0,0199 |
Закодировать произвольную комбинацию, состоящую из 5 символов
из ансамбля {ai}. Определить потенциальный минимум среднего количества
символов кода, приходящихся на одно сообщение ансамбля {ai} и среднее количество
символов, разработанного кода Хаффмана, приходящихся на одно сообщение из {ai}. Рассчитать
эффективность разработанного кода.
Решение:
Для удобства закодирования расположим вероятности появления
сообщений в порядке убывания. Две последние вероятности объединим в одну
вспомогательную букву, которой приписывается суммарная вероятность.
Вероятности, не учитывающиеся в объединении, и суммарную вероятность снова
расположим в порядке убывания. Полученный ряд вероятностей записываем в таблицу
и две последние вновь объединяем. Процесс будем повторять до последней
вспомогательной буквы, с вероятностью равной единице. Процесс закодирования
представлен в таблице 8.
Таблица 8
|
a1 |
0,38 |
0,38 |
0,38 |
0,38 |
0,38 |
0,38 |
0,38 |
0,38 |
0,38 |
0,381 |
0,619 |
1 |
|
a4 |
0,21 |
0,21 |
0,21 |
0,21 |
0,21 |
0,21 |
0,21 |
0,21 |
0,239 |
0,38 |
0,381 |
|
|
a2 |
0,12 |
0,12 |
0,12 |
0,12 |
0,12 |
0,12 |
0,12 |
0,171 |
0,21 |
0,239 |
||
|
a10 |
0,1 |
0,1 |
0,1 |
0,1 |
0,1 |
0,1 |
0,119 |
0,12 |
0,171 |
|||
|
a3 |
0,071 |
0,071 |
0,071 |
0,071 |
0,071 |
0,071 |
0,1 |
0,119 |
||||
|
a8 |
0,03 |
0,03 |
0,03 |
0,0389 |
0,0501 |
0,0689 |
0,071 |
|||||
|
a9 |
0,0211 |
0,0211 |
0,029 |
0,03 |
0,0389 |
0,0501 |
||||||
|
a12 |
0,0199 |
0,0199 |
0,0211 |
0,029 |
0,03 |
|||||||
|
a11 |
0,019 |
0,019 |
0,0199 |
0,0211 |
||||||||
|
a5 |
0,013 |
0,016 |
0,019 |
|||||||||
|
a7 |
0,012 |
0,013 |
||||||||||
|
a6 |
0,004 |
Затем строится кодовое дерево, в процессе которого
осуществляется кодирование: верхняя точка дерева равна единице; из нее
направляется две ветви, причем ветви с большей вероятностью приписывается
значение «1», а с меньшей – «0». Такое последовательное ветвление продолжается
до тех пор, пока не добиваются вероятности каждой буквы. Кодовое дерево
представлено на рисунке 3.1.
Затем двигаясь по кодовому дереву сверху вниз, записываем для
каждой буквы соответствующую ей кодовою комбинацию. Результат представлен в
таблице 9.
Таблица 9
|
a1 |
11 |
|
a2 |
101 |
|
a3 |
000 |
|
a4 |
01 |
|
a5 |
100010 |
|
a6 |
1000110 |
|
a7 |
1000111 |
|
a8 |
10010 |
|
a9 |
10000 |
|
a10 |
001 |
|
a11 |
100110 |
|
a12 |
100111 |
Выберем из ансамбля сообщений {ai} произвольную комбинацию
из пяти символов и закодируем их полученным кодом Фано:
a4 a6 a8 a10 a12
Потенциальный минимум будем искать по формуле (2.3) лекции
Так как код является двоичным, то основание кода . Отсюда следует:
Тогда потенциальный минимум будет равен энтропии источника:
Найдем энтропию источника, пользуясь теоремой Шеннона:
Подставив в данную формулу заданные значения, получим:
Подставив полученное значение в формулу для вычисления
потенциального минимума, получим:
Рассчитаем среднее количество символов, приходящихся на одно
сообщение, по формуле (2.9) лекции:
где Ps – вероятность появления события;
m – количество символов в коде.
Количество символов в коде представлено в таблице 10.
Таблица 10
|
Сообщение |
Вероятность |
Количество |
|
a1 |
0,38 |
2 |
|
a2 |
0,12 |
3 |
|
a3 |
0,071 |
3 |
|
a4 |
0,21 |
2 |
|
a5 |
0,013 |
6 |
|
a6 |
0,004 |
7 |
|
a7 |
0,012 |
7 |
|
a8 |
0,03 |
5 |
|
a9 |
0,0211 |
5 |
|
a10 |
0,1 |
3 |
|
a11 |
0,019 |
6 |
|
a12 |
0,0199 |
6 |
Найдем эффективность кода по формуле:
Подставив найденные значения в вышеуказанную формулу, получим:
Ответ: потенциальный минимум , среднее количество символов, приходящихся на одно сообщение,
составляет , эффективность кода равна
.
Задача №3.93
Закодировать троичным кодом Хаффмана ансамбль сообщений,
представленных в таблице 11.
Таблица 11
|
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
a7 |
a8 |
a9 |
a10 |
a11 |
a12 |
|
0,38 |
0,12 |
0,071 |
0,21 |
0,013 |
0,004 |
0,012 |
0,03 |
0,0211 |
0,1 |
0,019 |
0,0199 |
Закодировать произвольную комбинацию, состоящую из 5 символов
из ансамбля {ai}. Определить потенциальный минимум среднего количества
символов кода, приходящихся на одно сообщение ансамбля {ai} и среднее количество
символов, разработанного кода Хаффмана, приходящихся на одно сообщение из {ai}. Рассчитать
эффективность разработанного кода.
Решение:
Для удобства кодирования расположим вероятности появления
сообщений в порядке убывания. Три последние вероятности объединим в одну
вспомогательную букву, которой приписывается суммарная вероятность.
Вероятности, не учитывающиеся в объединении, и суммарную вероятность снова
расположим в порядке убывания. Полученный ряд вероятностей записываем в таблицу
и две последние вновь объединяем. Процесс будем повторять до последней
вспомогательной буквы, с вероятностью равной единице. Процесс закодирования
представлен в таблице 12.
Таблица 12
|
a1 |
0,38 |
0,38 |
0,38 |
0,38 |
0,38 |
0,62 |
1 |
|
a4 |
0,21 |
0,21 |
0,21 |
0,21 |
0,29 |
0,38 |
|
|
a2 |
0,12 |
0,12 |
0,12 |
0,12 |
0,21 |
||
|
a10 |
0,1 |
0,1 |
0,1 |
0,119 |
0,12 |
||
|
a3 |
0,071 |
0,071 |
0,071 |
0,1 |
|||
|
a8 |
0,03 |
0,03 |
0,06 |
0,071 |
|||
|
a9 |
0,0211 |
0,029 |
0,03 |
||||
|
a12 |
0,0199 |
0,0211 |
0,029 |
||||
|
a11 |
0,019 |
0,0199 |
|||||
|
a5 |
0,013 |
0,019 |
|||||
|
a7 |
0,012 |
||||||
|
a6 |
0,004 |
Затем строится кодовое дерево, в процессе которого
осуществляется кодирование: верхняя точка дерева равна единице; из нее
направляется три ветви, причем ветви с большей вероятностью приписывается
значение «2», следующей ветви – «1», а ветви с меньшей вероятностью – «0».
Такое последовательное ветвление продолжается до тех пор, пока не добиваются
вероятности каждой буквы. Кодовое дерево представлено на рисунке 3.2.
Рисунок 3.2
Таблица 13
|
a1 |
1 |
|
a2 |
20 |
|
a3 |
220 |
|
a4 |
21 |
|
a5 |
22202 |
|
a6 |
22200 |
|
a7 |
22201 |
|
a8 |
2221 |
|
a9 |
22222 |
|
a10 |
221 |
|
a11 |
22220 |
|
a12 |
22221 |
Выберем из ансамбля сообщений {ai} произвольную комбинацию
из пяти символов и закодируем их полученным кодом Фано:
a4 a6 a8 a10 a12
Потенциальный минимум будем искать по формуле (2.3) лекции
Так как код является троичным, то основание кода . Отсюда следует:
Найдем энтропию источника, пользуясь теоремой Шеннона:
Подставив в данную формулу заданные значения, получим:
Подставив полученное значение в формулу для вычисления
потенциального минимума, получим:
Рассчитаем среднее количество символов, приходящихся на одно
сообщение, по формуле (2.9) лекции:
где Ps – вероятность появления события;
m – количество символов в коде.
Количество символов в коде представлено в таблице 14.
Таблица 14
|
Сообщение |
Вероятность |
Количество |
|
a1 |
0,38 |
1 |
|
a2 |
0,12 |
2 |
|
a3 |
0,071 |
3 |
|
a4 |
0,21 |
2 |
|
a5 |
0,013 |
5 |
|
a6 |
0,004 |
5 |
|
a7 |
0,012 |
5 |
|
a8 |
0,03 |
4 |
|
a9 |
0,0211 |
5 |
|
a10 |
0,1 |
3 |
|
a11 |
0,019 |
5 |
|
a12 |
0,0199 |
5 |
Найдем эффективность кода по формуле:
Подставив найденные значения в вышеуказанную формулу, получим:
Ответ: потенциальный минимум , среднее количество символов, приходящихся на одно сообщение,
составляет , эффективность кода равна
.
4. Согласование дискретного источника с дискретным каналом без
шума. Помехоустойчивое кодирование
Задача №4.3
Дискретный источник U выдает независимые равновероятные сообщения с
объемом алфавита N=20 со скоростью Vc=3200 сообщений в секунду. Оценить, возможна ли
безошибочная передача сообщений источника по двоичному симметричному каналу,
вероятность ошибки в котором p=0,05, а скорость передачи канальных символов Vk не может превышать Vc более чем в n=3 раз. В случае
отсутствия такой возможности оценить минимально неизбежные потери информации в
единицу времени.
Решение:
В соответствие с теоремой Шеннона безошибочная передача
информации возможна при условии (2.15) лекции:
, где
Подставляя значение N в последнюю
формулу, получим:
Полученное значение энтропии используем для вычисления
производительности источника:
В соответствии с формулой (1.28) лекции пропускная способность
двоичного симметричного канала равна:
, где
По результатам вычисления делаем вывод о том, что условие не выполняется, поэтому безошибочная
передача информации источника невозможна в такой ситуации.
В соответствии со вторым утверждением прямой теоремы минимальная
потеря информации в единицу времени составляет:
Подставляя полученные значения производительности источника и
пропускной способности, получим:
Ответ: Безошибочная передача сообщений источника невозможна, .
Задача №4.33
Построить производящую матрицу G линейного двоичного
блочного кода, способного исправлять одиночную ошибку при передаче дискретных
сообщений источника, представляющих собой последовательность десятичных цифр из
диапазона 0 … M-1 (с объёмом алфавита M = 49). Пользуясь
разработанной матрицей G, сформировать кодовую комбинацию для сообщения i =
56. Построить соответствующую производящей матрице G проверочную
матрицу H и с её помощью сформировать кодовую комбинацию для сообщения i.
По виду синдрома найти и исправить ошибку в принимаемой кодовой комбинации
(дополнительно заданной преподавателем). Определить, является ли разработанный
код кодом Хэмминга.
Решение:
Производящая матрица G линейного двоичного
блочного кода имеет размерность (n; k), где n – общее число разрядов
кода, k – число информационных разрядов кода. Так как код является
двоичным, то
Откуда находим k:
Матрица G линейного
двоичного кода имеет следующий вид:
, где
Ik – единичная матрица, содержащая
информационные символы,
Rk,r – прямоугольная матрица, составленная из проверочных симвлов.
Построим матрицу I, где k=6.
Построим матрицу R: R – матрица размерности (k, n – k), где k – число строк, (n – k) – число столбцов.
Матрицу R будем
строить по определенным правилам:
так как код должен исправлять единичную ошибку, получим,
что исправная способность будет равна единице, т.е.
В одной строке матрицы должно быть не менее единиц. Найдем d как:
2 все строки должны быть разными;
3 число элементов в строке должно быть минимально.
Используя вышеуказанные правила построения, получим матрицу R:
После построения вспомогательных матриц можно построить матрицу G:
Проверочная матрица H
имеет размерность (n–k, k) и
имеет следующий вид:
, где
RT – транспонированная матрица R,
I – единичная матрица.
Пользуясь, разработанной матрицей G, сформируем кодовую комбинацию для сообщения – i (i = 56). Переведем ее из десятичного в двоичный
вид: .
Кодовая комбинация представляет k –
информационных и r – проверочных символов:
Внесем в этот кодовый блок одну ошибку. Пусть в четвертом разряде.
Тогда примем комбинацию.
Найдем на приеме и исправим эту ошибку. Для этого:
а) по принятым информационным найдем проверочные разряды:
б) складываем по модулю 2 полученные разряды и разряды
проверочного блока в принятой комбинации:
в) строим проверочную матрицу и отслеживаем в ней найденную
комбинацию:
Данная комбинация обнаружена в четвертом столбце, следовательно,
ошибочно передан четвертый разряд.
Код является кодом Хемминга, если будут выполняться следующие
условия:
, (10,6)
n=10, k=6, r=4 – разработанный код
Полученная матрица G имеет разрядность (10,6),
которая не удовлетворяет данному условию. Значит, данный код не является кодом
Хемминга.
Заключение
сигнал кодирование информационный дискретный
В процессе выполнения работы были закреплены теоретические
знания в области теории информации. И в то же время были разобраны конкретные
примеры способов кодирования сообщений. В частности был рассмотрен метод
кодирования, способный обнаруживать и исправлять одиночные ошибки передачи.
Таким
образом, все задание на курсовой проект выполнено полностью.
Шум в больших данных. Анализ на основе энтропии информации
Время на прочтение
4 мин
Количество просмотров 6.7K
Попалась задача под названием «Квартет Энскомба (Анскомба)» (англ.версия).
На рисунке 1 представлено табличное распределение 4 случайных функций (взято из Википедии).
Рис. 1. Табличное распределение четырех случайных функций
На рисунке 2 представлены параметры распределения этих случайных функций
Рис. 2. Параметры распределений четырех случайных функций
И их графики на рисунке 3.
Рис. 3. Графики четырех случайных функций
Проблема различения этих функций решается достаточно просто, путем сопоставления моментов высших порядков и их нормированных показателей: коэффициента асимметрии и коэффициента эксцесса. Данные показатели представлены на рисунке 4.
Рис. 4. Показатели моментов третьего и четвертого порядка и коэффициентов асимметрии и эксцесса четырех случайных функций
Как видно из таблицы рисунка 4, комбинация этих показателей для всех функций различна.
Первый вывод, который, напрашивался естественным образом, что информация о взаимном расположении точек сохраняется в параметрах распределения на более высоком уровне, чем дисперсия случайного распределения.
Множество аналитиков пытаются выделить частные уравнения регрессии в больших данных и пока, на сегодняшний день, это методом подбора уравнения с наименьшей остаточной дисперсией. Тут особо добавить не получилось. Но обратил внимание на то, что это все информация, а у информации есть показатель энтропии. И она, энтропия, имеет свои границы от 0, когда информация полностью определена до белого шума. И белый шум, в канале передачи, имеет равномерное распределение.
Когда требуется проанализировать данные, то изначально предполагается, что в них есть связанные данные, которые необходимо формализовать в виде взаимосвязи. А это предполагает, что данные не являются белым шумом. То есть первый этап это подбор уравнения регрессии и определение остаточной дисперсии. Если регрессия подобрана правильно, то остаточная дисперсия будет подчиняться закону нормального распределения. Посмотрим и, на рисунках 5-7, представлены формулы энтропий для равномерно распределенной и нормально распределенной случайной величины.
Рис. 5. Формула дифференциальной энтропии для нормально распределенной величины (Афанасьев В.В. Теория вероятностей в вопросах и задачах. Министерство образования и науки Российской Федерации Ярославский государственный педагогический университет имени К. Д. Ушинского)
Рис. 6. Формула дифференциальной энтропии для нормально распределенной величины (Пугачев В.С. Теория случайных функций и ее применение к задачам автоматического управления. Изд. 2-ое, перераб. и допол. — М.: Физматлит, 1960. — 883 с.)
Рис. 7. Формула дифференциальной энтропии для равномерно распределенной величины (Пугачев В.С. Теория случайных функций и ее применение к задачам автоматического управления. Изд. 2-ое, перераб. и допол. — М.: Физматлит, 1960. — 883 с.)
Далее покажем на примере. Но предварительно возьмем условия что каждая из четырех функций это координата гиперплоскости, то есть одновременно проверим работу модели в многомерном пространстве. Проведем свертку гиперкуба до плоскости. Механизм представим на рисунке 8.
Рис. 8. Исходные данные с механизмом свертки
Рис. 9. Сводная группировка на рисунке.
Рис. 10. Параметры распределений четырех случайных функций и сводной группировки.
Рассмотрим механизм выбора величины интервала разбиения. Первоначальные условия представлены на рисунке 11.
Рис. 11. Первоначальные условия разбиения на интервалы.
Условие 1. Он должен быть с ненулевой вероятностью на области вариации, так как в противном случае, энтропия равна бесконечности. Как для первоначальной выборки, так и для остаточной.
Условие 2. Так как нельзя игнорировать возможность выброса, в новых данных, и т.п., то для крайних интервалов, необходимо установить вероятность по нормальному, либо другому общепринятому теоретическому закону распределения вероятностей, по принципу вероятности хвостов.
Условие 3. Шаг интервала должен обеспечивать минимально необходимое количество интервалов на разбросе остаточной выборки.
Условие 4. Количество интервалов должно быть нечетное.
Условие 5. Количество интервалов должно обеспечивать надежное согласование с теоретическим законом распределения, выбранного для исследования.
Рис. 12. Остаточный ряд распределения
Определим механизм выбора интервалов на рисунке 13.
Рис. 13. Алгоритм выбора интервалов
Основной проблемой, на мой взгляд, было принятие решения о необходимости вводить или не вводить хвостовые интервалы. Если для остаточной дисперсии это выглядело достаточно естественно, то для основного ряда, достаточно натянуто.

Рис. 14. Результаты обработки значений данных при определении информационной энтропии
Выводы. Где этот инструмент можно применить
Сравнивая результирующие показатели таблицы на рисунке 14, видно, что они отреагировали на изменение структуры данных. А это значит, что инструмент имеет чувствительность, и позволяет решать задачи аналогичные задаче «квартета Энскомба».
Без сомнения эти задачи можно решать и с помощью моментов высших порядков. Но по своей сути, информационная энтропия зависит от дисперсии случайной величины, то есть, это сторонняя характеристика дисперсии. А значит, может нам указать интервалы, где использования дисперсионного анализа может привести к конкретному результату.
Числовая характеристика энтропии дает возможность проведение корреляционного анализа с независимыми переменными. Как один из примеров проявления возможной связи, следующий: Допустим на интервале от а до b увеличилась, в существенной степени, шумность ряда данных, сопоставляя значения независимых переменных, обнаружили, что переменная хn вошла в диапазон более 5 ед., после того как она, переменная, снизилась ниже +5, шум снизился. Далее можно сделать дополнительную проверку и, если эта гипотеза подтвердиться, то в дальнейших исследованиях запретить переменной xn повышаться выше +5. Так как в этом случае данные становятся бесполезными.
Предполагаю, что есть и другие варианты использования данного инструмента.
Как использовать
В этом аспекте просматривается естественный механизм «скользящего среднего», предполагаю, что объем выборки полученный по формуле объема выборки из статистического анализа, даст разумный объем области скольжения. По текущему анализу был сделан вывод, что объем выборки следует определять из минимальной доли, которая приходится на с наименьшей вероятностью. В нашем примере, для остаточной дисперсии, минимальная доля эмпирического интервала 0,15909. Это необходимо делать, так как если какой-то интервал, в объеме скольжения окажется пустым, то в этом случае показатель шума окажется запредельным или сработает правило что логарифм 0 равен минус бесконечности. А при правильно выбранном объеме выборки, запредельные значения этого показателя засвидетельствуют об кардинальном изменении структуры информации.
Связь между и
найдем перемножив их.
(8)
Таким образом произведение равно постоянной величине, то есть между
к и
э существует обратная зависимость. При увеличении времени корреляции происходит уменьшение ширины спектральной плотности мощности. Следовательно, медленно протекающий случайный процесс, имеющий большое время корреляции, будет иметь относительно узкую ширину спектральной плотности, а быстродействующий процесс будет иметь малое время корреляции и относительно большое значение ширины спектральной плотности мощности.
Используя графический редактор Еxell построим графики зависимостей и G(f). Они изображены на рис.3. и рис.4.
Определим верхнюю граничную частоту Fв, используя выражение:
(9)
применив обратное преобразование Фурье (7) и табличный интеграл
(10)
подставив значение G(f) получим:

Возьмем тангенс с правой и левой стороны
(11)
Подставив значения получим:
3. РАСЧЕТ ЭНТРОПИИ КВАНТОВАННОГО СИГНАЛА,ЕГО ИЗБЫТОЧНОСТИ И СКОРОСТИ СОЗДАНИЯ ИНФОРМАЦИИ НА ВЫХОДЕ КВАНТУЮЩЕГО УСТРОЙСТВА.
Нам заданы начальные условия:
-
шаг квантования
= 2.5*10-2 ;
-
дисперсия нормального закона распределения 2=3 В;
-
максимальное значение шкалы квантования Xmax=3.2 В;
Энтропия характеризует среднее количество информации, содержащей- ся в сообщении. Энтропия является основной характеристикой источника. Чем она выше, тем труднее передать сообщение по каналу связи. Необходимая затрата энергии на передачу сообщения пропорциональна его энтропии.
Для вычисления энтропии квантованного сигнала применим сле-
дующую формулу:
, (12)
где число n определяется числом уровней квантования :
L=2n+1;
L — число уровней квантования;
P(ai) — вероятность появления уровней квантования ;
Максимальное значение шкалы квантования определяется по формуле :
(13)
Из формулы (13)найдем число уровней квантования :
L=2*3.2/2.5*10-2=256
Вероятность появления уровней квантования сигнала определяется по
формуле:
(14)
где W(xi) плотность распределения выборочных значений определяется
нормальным законом распределения тоесть:
(15)
где xi — значение квантованного сигнала, берется на середине интервала квантования.
— дисперсия
Вычисление энтропии квантованного сигнала осуществляем с помощью ПЭВМ. Произведя необходимые расчеты, получим энтропию квантованного сигнала:
H(A)=7.74 бит/отсчет
Избыточность показывает, какая доля максимально возможной энтропии не используется источником. Избыточность квантованного сигнала:
(16)
где Hmax(A) — величина энтропии если все состояния дискретного источника равновероятны тоесть
(17)
тогда
Hmax(A) = log2256=8 бит/отсчет
Подставив значения H(A) и Hmax(A) в формулу (16) получим:
=8-7.74/8=0.03
Избыточность составляет 3%.
Производительность источника (скорость создания на выходе информа-ции квантующего устройства) представляет собой суммарную энтропию сообщений, переданных за единицу времени и рассчитывается по формуле :
(18)
H’(A)=7,742100073=1549,13 кБит/с
4. ОПРЕДЕЛЕНИЕ ПРОПУСКНОЙ СПОСОБНОСТИ ДИСКРЕТНОГО КАНАЛА СВЯЗИ.
Заданы начальные условия:
-
дискретный канал является симметричным каналом без памяти ;
-
число передаваемых кодовых символов m=L ,где L — число уровней
квантования ;
-
интервал дискретизации t=1/Fв=1/100073=9,910-6с
-
вероятность ошибки p=10-6.
Под пропускной способностью дискретного канала связи понимают максимальное количество передаваемой информации. Пропускная способность дискретного канала определяется по следующей формуле:
C= max V [ H(B)-H(B/A) ], (19)
где – число символов, поступающих на вход канала в единицу времени;
H(B)- энтропия на выходе дискретного канала связи;
H(B/A) – условная энтропия, определяющая информацию, содержащуюся выходных символов B при известной последовательности входных символов A.
Число символов, поступающих на вход дискретного канала в единицу времени:
=100073
Энтропия H(B) будет максимальна, если все символы равновероятны, т.е.
max H(B) = log m
max H(B) = log 256 = 8 бит/отсчёт
Величина H(B/A) обусловлена помехами, поэтому в дальнейшем будем называть H(B/A) энтропией шума. Она определяется следующей формулой:
(20)
Вероятность ошибки P – это вероятность того, что при передаче фиксированного символа ai будет принят любой символ, кроме bi . Всего может произойти (m-1) ошибочных переходов, при фиксации символа ai на передаче. Так
как канал симметричен, то вероятность приема фиксированного символа bi при передаче символа ai будет равна .
Следовательно, в m-ичном симметричном канале вероятности переходов удовлетворяют условиям:

(21)
Подставляя эти вероятности в выражение (20) находим энтропию шума:
Выделяя из этой суммы слагаемое с номером i=j, получаем:
Подставляя найденные значения в (19) находим пропускную способность канала:
(22)
C=100073[log256+10-6log10-6/255+(1-10-6 )log(1-10-6 )]= 790,57 кбит/с
Определим пропускную способность для двоичного симметричного канала без памяти (m=2).
Для двоичного симметричного канала без памяти выражение (22) для пропускной способности примет вид:
(23)
CAA= 100073[1+10-6 log10-6+(1-10-6) log(1-10-6 )]= 100,055 кбит/с.
Сравнивая пропускную способность m-ичного дискретного канала и двоичного дискретного канала видим, что m-ичный симметричный дискретный канал обладает большей пропускной способностью по сравнению с двоичным.
5. ОПРЕДЕЛЕНИЕ ОДНОМЕРНОГО РАСПРЕДЕЛЕНИЯ, МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ, ДИСПЕРСИИ, КОРРЕЛЯЦИОННОЙ ФУНКЦИИ НА ВЫХОДЕ СИНХРОННОГО ДЕТЕКТОРА
На вход синхронного детектора поступает случайный процесс
Z(t)=S0S(t)cos(t+)+X x(t)cos(0t+)+Y y(t) sin0t, который представляет собой аддитивную смесь АМ сигнала с подавленной несущей и флуктуационного шума. Здесь S0 – масштаб сигнала, S(t) – случайный модулирующий сигнал с нулевым средним значением. Опорный сигнал U(t)=bcos(0t+).
-
Масштаб сигнала (S0) = 0.1
-
Дисперсия (2) = 1 В2
-
Масштаб независимых квадратурных компонент гауссовского нормального шума; X = 0.005 B, Y = 0.005 B
Определить одномерное распределение выходного продукта, его математическое ожидание и дисперсию; корреляционную функцию и энергетический спектр для флуктуирующей части; отношение сигнал/шум на выходе детектора.
6. РАСЧЕТ ШИРИНЫ СПЕКТРА ИКМ-ЧМ СИГНАЛА.
Сигналы импульсно-кодовой модуляции подается на модулятор с помощью которого осуществляется частотная манипуляция, требуется:
-
рассчитать ширину спектра
сигнала ИКМ-ЧМ;
-
сравнить
с верхней граничной частотой спектра сигнала FB;
-
нарисовать временную диаграмму напряжения на выходе модулятора.
Ширина спектра исходного аналогового сигнала ограничена частотой. FB каждая выборка может принимать одно из 2Fв разрешенных значений называемых уровнями квантования. В свою очередь уровни квантования заменяются при кодировании комбинацией из n=logL двоичных импульсов. Следовательно длительность каждого импульса не может быть больше чем :
и=t/n=t/logL=logL/2=log 256/2=4
сигнала ИКМ-ЧМ будет занимать полосу частот:
=4FBlogL=41000738=3202,336 кГц
Сравнивая с FB мы видим , что
FB на величину 4logL, а так как чем больше L, тем выше помехоустойчивость, то при передаче ИКМ сигналов мы выигрываем в помехоустойчивости но проигрываем в полосе частот , тоесть происходит ”обмен” мощности сигнала на полосу частот.
Временная диаграмма напряжения на выходе модулятора изображена на рис.5.
U(t)
1 0 1
t
U
чм(t)
t
Рис.5.
7. СТРУКТУРНАЯ СХЕМА И АЛГОРИТМ РАБОТЫ ОПТИМАЛЬНОГО ПРИЕМНИКА.
Для некогерентного приема и ЧМ манипуляции требуется :
-
нарисовать структурную схему оптимального приемника и записать
алгоритм работы;
-
вычислить вероятность неправильного приема декретного двоичного
сигнала при отношении энергии сигнала к спектральной плотности
шума на выходе детектора h2=169;
-
построить графики зависимости Pош=f(h) для ЧМ и ФМ и сравнить их.
Целью оптимального приема повышение верности принимаемого сообщения, эта задача решается выбором оптимальной структуры приемника.
Задача приемника заключается в следующем: он анализирует смесь сигнала и шума Z(t) в течение единичного интервала времени и на основании этого анализа принимает решение, какой из возможных сигналов присутствует на входе приемника. Структурная схема оптимального демодулятора, построенного на согласованных фильтрах для приёма ЧМ сигнала приведена на рис.6.
Е1/No
СФ1 АД1 СУ1
Z(t) РУ bi*
СФ2 АД2 СУ2
Е2/No
Рис.6