|
Как найти тангенс угла, если известен косинус? Как найти котангенс угла, если известен косинус?
Итак, читаем внимательно условие вопроса, и вспоминаем, чему нас учили в школе, у нас есть косинус угла, и этого окажется вполне достаточным для того, чтобы мы выполнили задание автора вопроса и нашли тангенс и котангенс данного угла. Вспоминаем, что мы можем найти, зная косинус, конечно-же, мы сразу можем найти синус, это очень легко, и в этом нам поможет вот это волшебное тождество и то, что из него следует, – формула для нахождения синуса: Теперь, зная чему равен синус угла, через косинус, проще простого решать дальше по известным формулам для нахождения тангенса и котангенса, просто подставляя в них эти формулы для синуса, которые я разместила выше: система выбрала этот ответ лучшим
Ксарфакс 5 лет назад Для того, чтобы найти тангенс и котангенс через косинус, достаточно вспомнить тригонометрические формулы: tgα = sinα / cosα. ctgα = cosα / sinα. Так как косинус известен, то синус можно найти из основного тригонометрического тождества: sin²α + cos²α = 1. sinα = √(1 – cos²α), если угол α находится в 1 и 2 четверти. sinα = – √(1 – cos²α), если угол α находится в 3 и 4 четверти. Таким образом: tgα = ± √(1 – cos²α) / cosα. ctgα = ± cosα / √(1 – cos²α). Так как произведение тангенса и котангенса = 1, то ctgα также можно найти из формулы: ctgα = 1 / tgα. Пример Косинус угла α равен 0,94, при этом α находится в 1 четверти (0 < α < 90). Нужно найти тангенс и котангенс. Воспользуемся формулой: tgα = √(1 – cos²α) / cosα. В первой четверти синус и косинус больше 0, поэтому тангенс и котангенс также будут положительными. tgα ≈ 0,34 / 0,94 ≈ 0,36. Соответственно ctgα ≈ 1 / 0,36 ≈ 2,78. Лара Изюминка 6 месяцев назад В школе изучают следующую тригонометрическую формулу: Косинус в квадрате альфа равно единица разделить на сумму единицы и тангенса в квадрате альфа. Из этой формулы легко выразить тангенс в квадрате альфа. Он очевидно равен 1 деленная на косинус в квадрате альфа и из этой дроби нужно вычесть один, а можно еще преобразовать как на картинке. Ну, а для того чтобы выразить котангенс, нужно вспомнить , что произведение тангенса и котангенса равно единице, тогда просто меняем числитель и знаменатель местами и получается формула для нахождения котангенса через косинус. Ну, а знак тангенса и котангенса определяем по той четверти, в которой находится угол. Если это первая и третья четверти, то плюс, иначе минус.
bezdelnik 5 лет назад tg а = Sin a/Cos a. Чтобы выразить тангенс через косинус осталось выразить синус через косинус. Для этого воспользуемся основной тригонометрической формулой (Sin a)^2 +/(Cos a)^2 = 1. Тогда (Sin a)^2 = 1 – (Cos a)^2, Sin a = √(1 – (Cos a)^2), а tg = √(1 – (Cos a)^2)/Cos a. Например, при а= 60 градусов Cos 60° = 0,5, tg = √(1 – 0,25)/0,5 = √(0,75)/0,5 = √(3*0,25)/0,5 = (0,5*√3)/0,5 = √3 = 1,732… . ctg a = Cos a/Sin a, то-есть величина обратная tg а, и при а = 60° ctg 60° = 1/√3 = √3/3 = 0,57735… .
127771 3 года назад Первым делом стоит вспомнить определение тангенса и котангенса, а именно: То есть получаются следующие формулы: tg(x) = sin(x) / cos(x) ctg(x) = cos(x) / sin(x) Из условия задачи нам известен косинус, значит нам нужно будет найти синус. Для этого есть такая формула: sin^2(x) + cos^2(x) = 1 Значит: sin^2(x) = 1 – cos^2(x) sin(x) = √(1 – (Cos a)^2) Теперь у нас есть значения синуса и косинуса, которые можно будет подставить в следующие формулы: Rafail 5 лет назад Наверное все помнят основное тождество тригонометрии: sin^2(x)+cos^2(x)=1. Почему-то также чётко я запомнил следующие простые формулы: tg^2(x)+1=sec^2(x) и ctg^2(x)+1=cosec^2(x). Ну и три определения: sec(x)=1/cos(x), cosec(x)=1/sin(x) и ctg(x)=1/tg(x). Теперь осталось выбрать нужные и применить. Допустим, cos(x)=(√3)/2, тогда sec(x)=2/√3, sec^2(x)=4/3, tg^2(x)=1/3, tg(x)=1/√3, ctg(x)=√3. Зайцевана 5 лет назад Пусть cosa = 1/2, тогда tga^2 = 1/(cosa)^2-1, (tga)^2 =1/0,25 – 1 = 3, tga =корень квадратный из 3, (со знаком + или – в зависимости в какой четверти находится а). ctga = 1/корень из 3.
Синус, косинус, тангенс и котангенс угла – это тригонометрические функции. Можно сказать, что все они связаны между собой. Часто для нахождения одной из этих функций при условии, что известна другая, приходится вспоминать основные тригонометрические равенства или тождества, а также определение самих этих понятий. Зная все перечисленное выше, несложно выразить одну функцию через другую. Тангенс угла – это отношение синуса этого угла к его косинусу. Котангенс угла – это отношение косинуса угла к его синусу. Нам известен косинус, из основного тригонометрического тождества ( sin²α + cos²α = 1 ) выразим синус: sinα = √(1 – cos²α) для α из 1 и 2 четвертей, sinα = -√(1 – cos²α) для α из 3 и 4 четвертей. Подставив формулу для синуса угла в формулу тангенса и котангенса, получим формулы для вычисления значений этих функций: tgα = ± √(1 – cos²α) / cosα, ctgα = ± cosα / √(1 – cos²α). Котангенс, впрочем, можно вычислить путем попроще, вспомнив, что тангенс и котангенс – функции обратные, то есть ctgα = 1 / tgα. Подставляем в формулу значение тангенса и вычисляем котангенс. Если вам требуется найти тангенс и котангенс при помощи косинуса, то вам предстоит воспользоваться определенной тригонометрической формулой:
при которой вы сможете отыскать синус из данной формулы, при том, что мы имеем известный косинус. Получившаяся формула выглядит таким образом:
Теперь, нам следует подставить значение синуса в формулу вычисления тангенса, а именно речь идет о : Теперь подставим аналогичную формулу через косинус для котангенса: TheSun 3 года назад Для нахождения тангенса и котангенса через косинус необходимо воспользоваться приведенной ниже тригонометрической формулой: Находим синус из формулы указанной выше (при условии, что косинус нам известен), получается: Подставляем в формулу вычисления тангенса значение синуса: tg? = sin? / cos? = ± ?(1 – cos??) / cos?. Теперь аналогично для котангенса через косинус. ctg? = cos? / sin? = ± cos? / ?(1 – cos??).
Все функции мы знаем из курса тригонометрии, и в это же время проходят и алгоритм нахождения тангенса/котангенса через косинус. Ну как следует из вопроса косинус нам известен. Если нет, то находим по формулам – Имея на руках значения двух вводных – синуса и косинуса, далее еще проще действовать по формулам нахождения тангенса и котангенса. Знаете ответ? |
как найти тангенс,если известен косинус????
Ксения Емикеева
Профи
(618),
закрыт
11 лет назад
Марина Белова
Мастер
(1963)
11 лет назад
Тангенс угла это отношение синуса этого угла к его косинусу. Синус же угла найдите из основного тригонометрического тождества, а именно, он будет равен корню квадратному из единицы минус квадрат косинуса угла. Это самый простой вариант.
Как найти тангенс, если известен косинус
Понятие тангенса является одним из основных в тригонометрии. Оно обозначает некую тригонометрическую функцию, которая является периодической, но не непрерывной в области определения, как синус и косинус. И имеет разрывы в точках (+,-)Пи*n+Пи/2, где n – это период функции. В России он обозначается как tg(x). Его можно представить через любую тригонометрическую функцию, так как все они тесно взаимосвязаны между собой.

Вам понадобится
- Учебник по тригонометрии.
Инструкция
Для того, чтобы выразить тангенс угла через синус, нужно вспомнить геометрическое определение тангенса. Итак, тангенсом острого угла в прямоугольном треугольнике, называют отношение противолежащего катета к прилежащему.
С другой стороны, рассмотрите декартову систему координат, на которой начерчена единичная окружность с радиусом R=1, и центром О в начале координат. Примите поворот против часовой стрелки, как положительный, а в обратную сторону отрицательный.
Отметьте некую точку M на окружности. Из нее опустите перпендикуляр на ось Ох, назовите ее точкой N. Получился треугольник OMN, у которого угол ONM является прямым.
Теперь рассмотрите острый угол MON, по определению синуса и косинуса острого угла в прямоугольном треугольнике
sin(MON) = MN/OM, cos(MON) = ON/OM. Тогда MN= sin(MON)*OM, а ON = cos(MON)*OM.
Вернувшись к геометрическому определению тангенса (tg(MON) = MN/ON), подставьте полученные выше выражения. Тогда:
tg(MON) = sin(MON)*OM/cos(MON)*OM, сократите OM, тогда tg(MON) = sin(MON)/cos(MON).
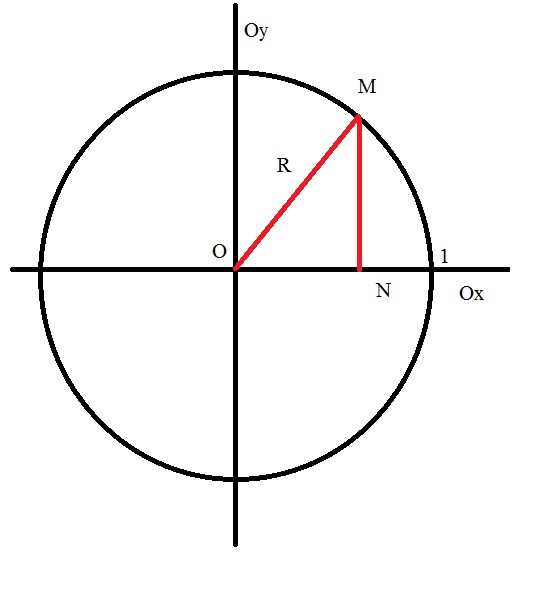
Из основного тригонометрического тождества (sin^2(x)+cos^2(x)=1) выразите косинус, через синус: cos(x)=(1-sin^2(x))^0,5 Подставьте это выражение в полученное на шаге 5. Тогда tg(MON) = sin(MON)/(1-sin^2(MON))^0,5.
Иногда существует потребность в вычисление тангенса двойного и половинчатого угла. Тут тоже выведены соотношения:tg(x/2) = (1-cos(x))/sin(x) = (1-(1-sin^2(x))^0,5)/sin(x);tg(2x) = 2*tg(x)/(1-tg^2(x)) = 2*sin(x)/(1-sin^2(x))^0,5/(1-sin(x)/(1-sin^2(x))^0,5)^2) =
= 2*sin(x)/(1-sin^2(x))^0,5/(1-sin^2(x)/(1-sin^2(x)).
Также возможно выразить квадрат тангенса через двойной угол косинуса, либо синус. tg^2(x) = (1-cos(2x))/(1+cos(2x)) = (1-1+2*sin^2(x))/(1+1-2*sin^2(x)) = (sin^2(x))/(1-sin^2(x)).
Обратите внимание
Обратите внимание на области допустимых значений при решение уравнений и неравенств.
Полезный совет
Знание наизусть основных тождеств, поможет быстро переходить от одних тригонометрических функций к другим.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Найти тангенс фи , если известен косинус фи
Калькулятор коэффициент мощности cos fi в tg fi
Как найти тангенс фи, если известен косинус фи формула:
- tg φ = (√(1-cos²φ))/cos φ
Калькулятор онлайн – косинус в тангенс
cos φ:
tg φ:
Поделиться в соц сетях:
Популярные сообщения из этого блога
Индекс Руфье калькулятор
Проба Руфье калькулятор онлайн. Первые упоминания теста относиться к 1950 году. Именно в это время мы находим первое упоминание доктора Диксона о “Использование сердечного индекса Руфье в медико-спортивном контроле”. Проба Руфье – представляет собой нагрузочный комплекс, предназначенный для оценки работоспособности сердца при физической нагрузке. Индекс Руфье для школьников и студентов. У испытуемого, находящегося в положении лежа на спине в течение 5 мин, определяют число пульсаций за 15 сек (P1); После чего в течение 45 сек испытуемый выполняет 30 приседаний. После окончания нагрузки испытуемый ложится, и у него вновь подсчитывается число пульсаций за первые 15 с (Р2); И в завершении за последние 15 сек первой минуты периода восстановления (Р3); Оценку работоспособности сердца производят по формуле: Индекс Руфье = (4(P1+P2+P3)-200)/10; Индекс Руфье для спортсменов Измеряют пульс в положении сидя (Р1); Спортсмен выполняет 30 глубоких приседаний в
Найти косинус фи (cos φ), через тангенс фи (tg φ)
tg фи=… чему равен cos фи? Как перевести тангенс в косинус формула: cos(a)=(+-)1/sqrt(1+(tg(a))^2) Косинус через тангенс, перевести tg в cos, калькулятор – онлайн tg φ: cos φ: ± Поделиться в соц сетях:
Тригонометрия — это раздел математики, в котором изучаются тригонометрические функции, их свойства, взаимосвязи и применение.
Слово «тригонометрия» образовано от греческих слов «trigonom» (треугольник) и «metreo» (измерять).
Возникновение и развитие тригонометрии связаны с практическими потребностями в измерении и вычислении сначала элементов треугольников на местности, а позднее — в строительстве, мореплавании и астрономии. Современная тригонометрия широко применяется в разных областях математики, в частности в геометрии, других науках, в технике. Например, тригонометрические функции используются при решении задач оптики, задач кинематического анализа и синтеза механизмов, гармонического анализа и других.
Cинус, косинус, тангенс, котангенс острого угла прямоугольного треугольника
Нет понятий «просто синус» или «просто косинус», не имеют смысла записи типа «sin» и «cos» сами по себе, они сами по себе никакой величины не обозначают (точно так же, как и, например, значок квадратного корня сам по себе). Те, кто этого не понимает, часто делает грубую ошибку типа: sin x /cos x = in /co
Есть понятие синуса, косинуса, тангенса, котангенса как тригонометрических функций угла. Здесь угол — аргумент функции. Он может обозначаться «х», «а», «альфа», «бета», «гамма», «фи», «дельта» или ещё какой-нибудь буквой. Суть от этого не меняется.
Для того, чтобы более наглядно представить приведенные ниже определения, начертите прямоугольный треугольник. Это треугольник, один из углов которого — прямой (т.е. один из углов равен 90 градусов). Стороны, прилежащие к прямому углу (перпендикулярные друг другу стороны) — это катеты данного прямоугольного треугольника. Противолежащая прямому углу сторона — это гипотенуза.
Теперь выберите любой из двух других (острых) углов треугольника и обозначьте его, например, альфа. Один из катетов будет примыкать к вершине этого угла (и, собственно, образовывать этот угол вместе с гипотенузой). Это — прилежащий катет. Другой катет не примыкает к вершине этого угла, он находится как бы напротив данной вершины. Это — противолежащий катет.
Кстати, почему-то не все представляют, что такое угол треугольника при данной вершине. У треугольника (обозначим его ABC) есть три вершины: А, В и С. Когда говорят об угле А треугольника, то подразумевают угол, образованный сторонами ВА и АС. Это и есть угол при вершине А.
Итак,
Синусом острого угла называется отношение противолежащего этому углу катета к гипотенузе.
Косинусом острого угла называется отношение прилежащего к этому углу катета к гипотенузе.
Тангенсом острого угла называется отношение противолежащего этому углу катета к прилежащему катету.
Котангенсом острого угла называется отношение прилежащего этому углу катета к противолежащему катету.
Секансом острого угла называется отношение гипотенузы к прилежащему к этому углу катету. Обозначается: sec x.
Косекансом острого угла называется отношение гипотенузы к противолежащему этому углу катету. Обозначается: cosec x.
Как найти углы в прямоугольном треугольнике, если известны стороны?
Дан треугольник АВС, угол С — прямой.
Стороны АВ, АС и ВС известны.
Т.к. угол С — прямой, он равен 90 градусам.
Другие углы можно найти, например, так:
если известен катет и гипотенуза
sinA = BC / AB,
sinB = AC / AB,
если известны два катета
tg A = BC / AC
tg B = AC / BC
Предположим, получили, что sin A = ½. По таблице смотрим, что такому значению sin x соответствует величина угла 30 градусов.
Или, к примеру, получили, что tg B = 1. Значит, угол В равен 45 градусов.
Или, к примеру, мы получили, что sin B = 0,259. По таблице Брадиса или с помощью калькулятора находим, что угол В равен 15 градусов.
sin 15° = 0,259
arcsin0,259 = 15°
Как найти углы в прямоугольном треугольнике, если известен один угол?
Поскольку треугольник прямоугольный, то один из его углов равен 90 градусов. Величина второго угла известна (по условию задачи, обозначим её альфа). В сумме углы треугольника составляют 180 градусов. Значит, третий угол равен 180—90—альфа.
Еединичная окружность (единичный круг)
Единичный круг — это круг с центром в начале координат и радиусом, равным единице (R = 1).
Единичная окружность — это окружность единичного круга (т.е. окружность с центром в начале координат и с радиусом, равным единице).
Единичный радиус-вектор — это вектор, начало которого совпадает с началом координат, а его длина равна единице.
Углы отсчитывают от начального положения подвижного радиуса-вектора (совпадает с положением Ох).
Координатные четверти отсчитываются так:
y
|
|
(II четверть) | (I четверть)
|
________________________ x
|0
|
(III четверть) | (IV четверть)
|
|
Угол первой четверти — от 0 до 90 градусов (от 0 до пи/2).
Угол второй четверти — от 90 до 180 градусов (от пи/2 до пи).
Угол третьей четверти — от 180 до 270 градусов (от пи до 2пи/3).
Угол четвертой четверти — от 270 до 360 градусов (от 2пи/3 до 2пи).
Например:
- углы первой четверти: 30 градусов, 85 градусов, пи/4;
- углы второй четверти: 120 градусов, 178 градусов;
- углы третьей четверти: 205 градусов, 260 градусов;
- углы четвертой четверти: 272 градуса, 305 градусов.
Тригонометрические функции
К тригонометрическим функциям относятся функции:
y = sin x;
y = cos x;
y = tg x;
y = ctg x;
y = sec x;
y = cosec x.
Синусом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Оу к его длине.
Косинусом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Ох к его длине.
Тангенсом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Оу к его проекции на ось Ох.
Котангенсом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Ох к его проекции на ось Оу.
Секансом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение длины этого вектора к его проекции на ось Ох.
Косекансом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение длины этого вектора к его проекции на ось Оу.
Тригонометрические функции связаны между собой, и этим можно воспользоваться для нахождения синуса угла по его косинусу или котангенсу или косинуса угла по его синусу или тангенсу.
Как найти синус угла, если известен косинус?
Нужно воспользоваться основным тригонометрическим тождеством:
sin2a + cos2a = 1
sin2a = 1 − cos2a
|sin a| = КОРЕНЬ(1 − cos2a)
sin a = ± КОРЕНЬ(1 − cos2a)
знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, косинус положительный в I и IV четвертях)
Как найти косинус угла, если известен синус?
Нужно воспользоваться основным тригонометрическим тождеством:
sin2a + cos2a = 1
cos2a = 1 − sin2a
|cos a| = КОРЕНЬ(1 − sin2a)
cos a = ± КОРЕНЬ(1 − sin2a)
знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, косинус положительный в I и IV четвертях)
Как найти синус угла, если известен котангенс?
Нужно воспользоваться тригонометрическим тождеством
1 + ctg2 a = 1/sin2 a
sin2 a = 1 / (1 + ctg2 a)
|sin a| = 1/ КОРЕНЬ(1 + ctg2 a)
sin a = ±1/ КОРЕНЬ(1 + ctg2 a)
знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, котангенс положительный в I и III четвертях)
Как найти косинус угла, если известен тангенс?
Нужно воспользоваться тригонометрическим тождеством
1 + tg2 a = 1/cos2 a
cos2 a = 1 / (1 + tg2 a)
|cos a| = 1/ КОРЕНЬ(1 + tg2 a)
cos a = ±1/ КОРЕНЬ(1 + tg2 a)
знак перед корнем нужно выбрать в соответствии с четвертью данного угла (косинус положительный в I и IV четвертях, тангенс положительный в I и III четвертях)
Тригонометрическое тождество
Тригонометрическим тождеством называется равенство, в которое входят тригонометрические функции и которое удовлетворяется произвольным допустимым значением угла — аргумента тригонометрических функций, но не удовлетворяется, если каждую в отдельности тригонометрическую функцию заменить произвольной величиной.
Основные тригонометрические тождества:
sin2a + cos2a = 1
tg a = sin a / cos a
ctg a = cos a / sin a
sec a = 1 / cos a
cosec a = 1 / sin a
Arcsin, arcos, arctg, arcctg (обратные тригонометрические функции)
- arcsin — читается: арксинус;
- arcos — читается: арккосинус;
- arctg — читается: арктангенс;
- arcctg — читается: арккотангенс.
arcsin, arcos, arctg, arcctg — это обратные тригонометрические функции.
Обратной тригонометрической функцией y = arcsin x называют угол у, взятый на отрезке от –пи/2 до +пи/2, синус которого равен х:
y = arcsin x sin y = x
Обратной тригонометрической функцией y = arccos x называют угол у, взятый на отрезке от –пи до +пи, косинус которого равен х:
y = arccos x cos y = x
Обратной тригонометрической функцией y = arctg x называют угол у, взятый на промежутке от –пи/2 до +пи/2 (исключая концы), тангенс которого равен х:
y = arctg x tg y = x
Обратной тригонометрической функцией y = arcctg x называют угол у, взятый на промежутке от 0 до пи (исключая концы), котангенс которого равен х:
y = arctg x tg y = x
Например,
sin 30° = 0,5
arcsin0,5 = 30°
Синусоида и косинусоида
График функции y = sin x называется синусоидой.
График функции y = cos x называется косинусоидой.
Источники информации:
- Справочник по элементарной математике. Геометрия, тригонометрия, векторная алгебра. Под редакцией П.Ф. Фильчакова. —К.: Наукова думка, 1967. — 442 с.
- В.Д. Гетманцев, О.Ф. Саушкiн. Математика: Тригонометрiя: Посiбник для слухачiв пiдотовчих вiддiлень, вступникiв до вищих навчальних закладiв, студентiв педагогiчних iнститутiв (на укр.). —К.: Либiдь, 1994. — 144 с.
- docme.ru — зачем нужна тригонометрия?
- ru.wikipedia.org — Википедия — тригонометрия;
- ru.wikihow.com — как изучать тригонометрию?













