Таблица синусов, найти угол синуса
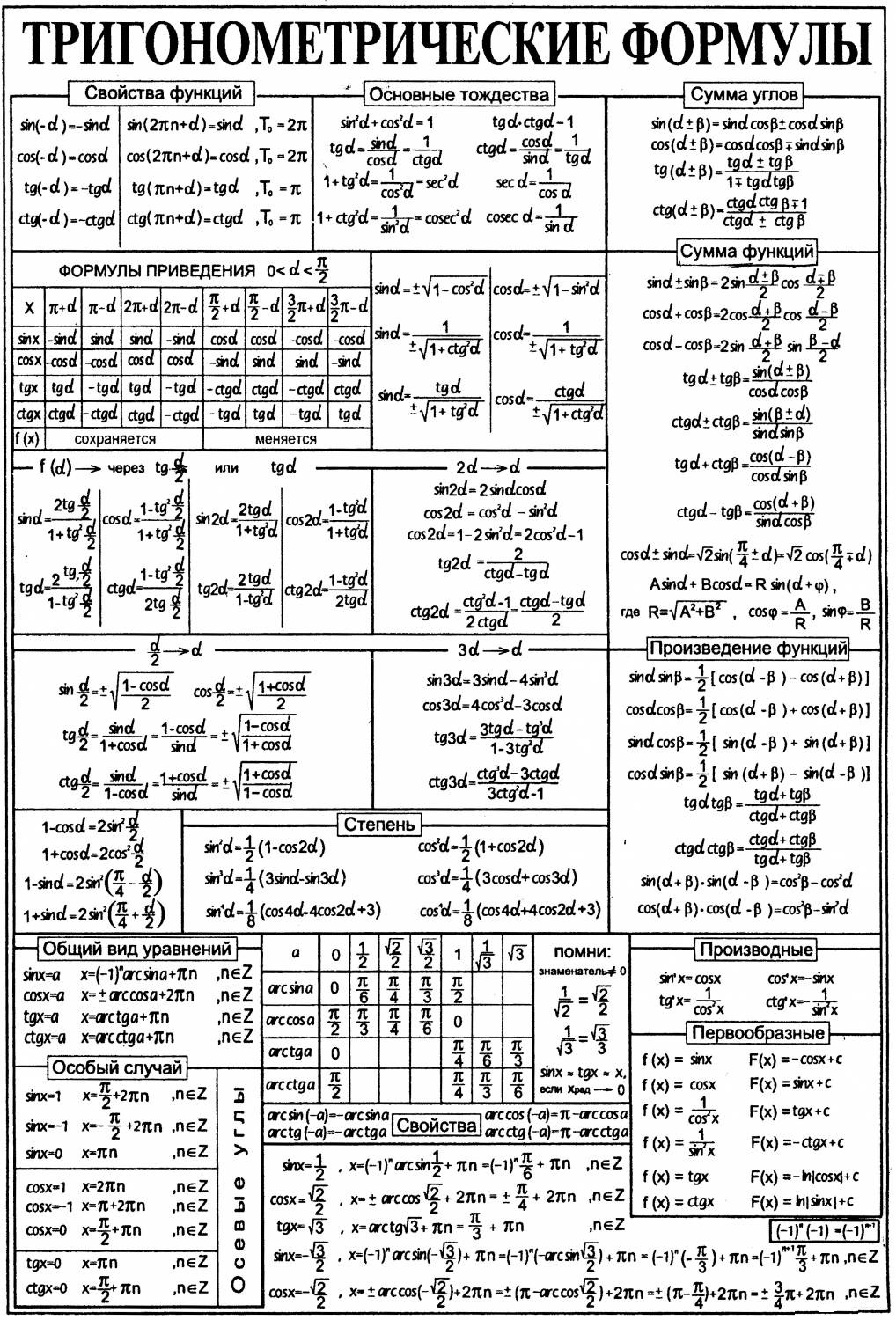
Тригонометрические функции: синус угла
Зачем надо знать значение синуса? Представим ситуацию: известен один из углов (А=60⁰), вписанный в прямоугольный треугольник, и длина гипотенузы. Больше нет никакой информации. Надо узнать вычислить дальний к углу (А) катет. Как поступить?

Ситуация очень простая: смотрим таблицы Брадиса, находим значение sin(60⁰)=0,866, подставляем данные в формулу тригонометрической функции и решаем линейное уравнение. Из школьного курса известно, что sin угла – это отношение дальнего к углу, в данном случае А=60⁰, катета к гипотенузе.
Произвести все расчеты проще, если воспользоваться онлайн калькулятором на сайте. Таким образом можно вычислить длину любой из сторон прямоугольного треугольника. Знаем угол – значит, знаем sin этого угла. И наоборот, знаем sin – найти угол не составит проблемы.
Таблица синусов 0°- 360°
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Таблица синусов углов от 0° – 360°. Углы с шагом в 1°. Вариант для печати.
sin(0°)=sin(360°)=0; точная, но чуть более сложная таблица ( с точностью до 1″) здесь.
|
Углы |
Углы |
Углы |
Углы |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
таблица синусов, синусы углов в угловых градусах, sin α, sinus, сколько составляет синус?, узнать синус, синус градусов
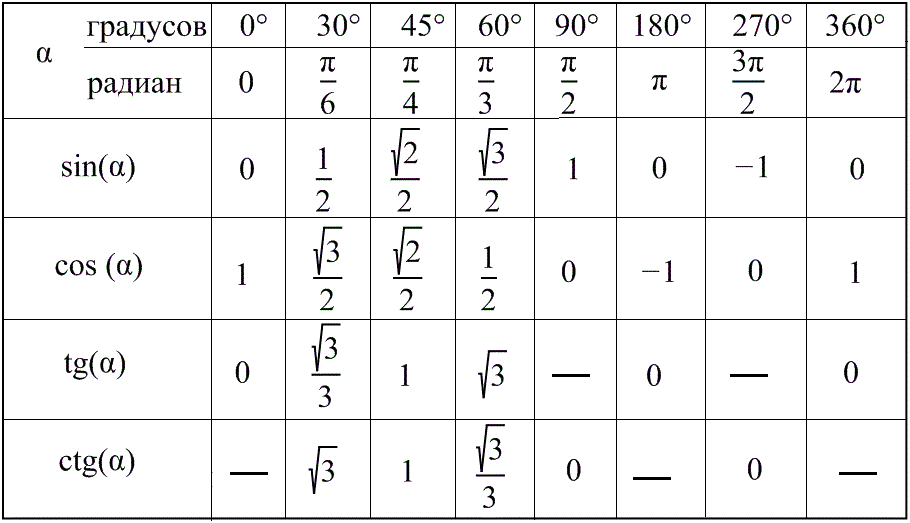
Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций
Доп. Инфо:
- Таблица косинусов углов от 0° – 360°. Углы с шагом в 1°. Таблица значений косинусов.
- Таблица синусов углов от 0° – 360°. Углы с шагом в 1°. Таблица значений синусов.
- Таблица синусов, она-же косинусов точная.
- Таблица тангенсов углов углов от 0° – 360°. Углы с шагом в 1°. Таблица значений тангенса, tg
- Таблица котангенсов углов углов от 0° – 360°. Углы с шагом в 1°. Таблица значений котангенса, ctg
- Таблица тангенсов, она же котангенсов точная.
- Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций.
- Знаки тригонометрических функций синус, косинус, тангенс и котангенс по четвертям в тригонометрическом круге.
- Определение и численные соотношения между единицами измерения углов в РФ. Тысячные, угловые градусы, минуты, секунды, радианы, обороты.
- Таблица соответствия угловых градусов, радиан, оборотов, тысячных (артиллерийских РФ). 0-360 градусов, 0-2π радиан.
Таблица синусов.
Таблица синусов – это записанные в таблицу посчитанные значения синусов углов от 0° до 360°. Используя таблицу синусов вы сможете провести расчеты даже если под руками не окажется инженерного калькулятора. Чтобы узнать значение синуса от нужного Вам угла достаточно найти его в таблице.
Калькулятор – синус угла
sin(°) = 0
Калькулятор – арксинус угла
arcsin() = 90°
Таблица синусов в радианах
| α | 0 | π6 | π4 | π3 | π2 | π | 3π2 | 2π |
| sin α | 0 | 12 | √22 | √32 | 1 | 0 | -1 | 0 |
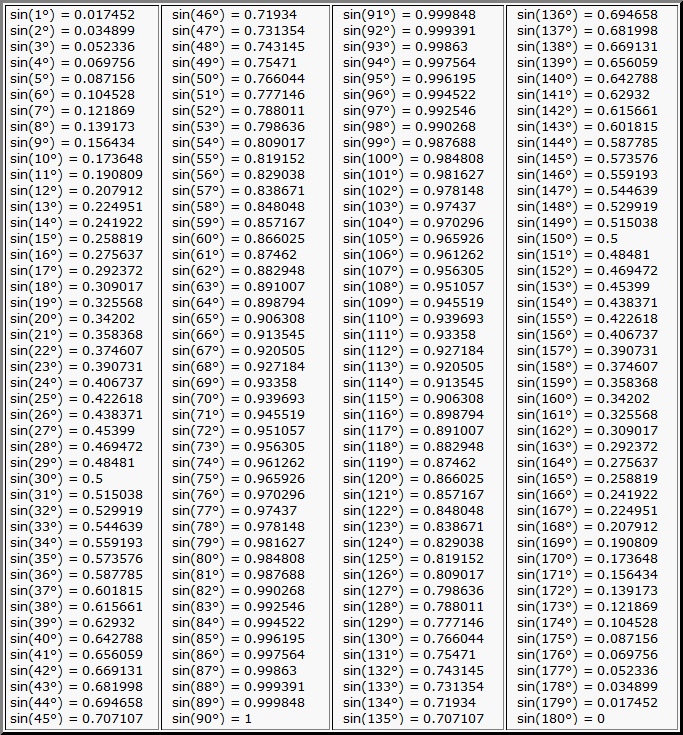
Таблица синусов углов от 0° до 180°
| sin(0°) = 0 sin(1°) = 0.017452 sin(2°) = 0.034899 sin(3°) = 0.052336 sin(4°) = 0.069756 sin(5°) = 0.087156 sin(6°) = 0.104528 sin(7°) = 0.121869 sin(8°) = 0.139173 sin(9°) = 0.156434 sin(10°) = 0.173648 sin(11°) = 0.190809 sin(12°) = 0.207912 sin(13°) = 0.224951 sin(14°) = 0.241922 sin(15°) = 0.258819 sin(16°) = 0.275637 sin(17°) = 0.292372 sin(18°) = 0.309017 sin(19°) = 0.325568 sin(20°) = 0.34202 sin(21°) = 0.358368 sin(22°) = 0.374607 sin(23°) = 0.390731 sin(24°) = 0.406737 sin(25°) = 0.422618 sin(26°) = 0.438371 sin(27°) = 0.45399 sin(28°) = 0.469472 sin(29°) = 0.48481 sin(30°) = 0.5 sin(31°) = 0.515038 sin(32°) = 0.529919 sin(33°) = 0.544639 sin(34°) = 0.559193 sin(35°) = 0.573576 sin(36°) = 0.587785 sin(37°) = 0.601815 sin(38°) = 0.615661 sin(39°) = 0.62932 sin(40°) = 0.642788 sin(41°) = 0.656059 sin(42°) = 0.669131 sin(43°) = 0.681998 sin(44°) = 0.694658 sin(45°) = 0.707107 |
sin(46°) = 0.71934 sin(47°) = 0.731354 sin(48°) = 0.743145 sin(49°) = 0.75471 sin(50°) = 0.766044 sin(51°) = 0.777146 sin(52°) = 0.788011 sin(53°) = 0.798636 sin(54°) = 0.809017 sin(55°) = 0.819152 sin(56°) = 0.829038 sin(57°) = 0.838671 sin(58°) = 0.848048 sin(59°) = 0.857167 sin(60°) = 0.866025 sin(61°) = 0.87462 sin(62°) = 0.882948 sin(63°) = 0.891007 sin(64°) = 0.898794 sin(65°) = 0.906308 sin(66°) = 0.913545 sin(67°) = 0.920505 sin(68°) = 0.927184 sin(69°) = 0.93358 sin(70°) = 0.939693 sin(71°) = 0.945519 sin(72°) = 0.951057 sin(73°) = 0.956305 sin(74°) = 0.961262 sin(75°) = 0.965926 sin(76°) = 0.970296 sin(77°) = 0.97437 sin(78°) = 0.978148 sin(79°) = 0.981627 sin(80°) = 0.984808 sin(81°) = 0.987688 sin(82°) = 0.990268 sin(83°) = 0.992546 sin(84°) = 0.994522 sin(85°) = 0.996195 sin(86°) = 0.997564 sin(87°) = 0.99863 sin(88°) = 0.999391 sin(89°) = 0.999848 sin(90°) = 1 |
sin(91°) = 0.999848 sin(92°) = 0.999391 sin(93°) = 0.99863 sin(94°) = 0.997564 sin(95°) = 0.996195 sin(96°) = 0.994522 sin(97°) = 0.992546 sin(98°) = 0.990268 sin(99°) = 0.987688 sin(100°) = 0.984808 sin(101°) = 0.981627 sin(102°) = 0.978148 sin(103°) = 0.97437 sin(104°) = 0.970296 sin(105°) = 0.965926 sin(106°) = 0.961262 sin(107°) = 0.956305 sin(108°) = 0.951057 sin(109°) = 0.945519 sin(110°) = 0.939693 sin(111°) = 0.93358 sin(112°) = 0.927184 sin(113°) = 0.920505 sin(114°) = 0.913545 sin(115°) = 0.906308 sin(116°) = 0.898794 sin(117°) = 0.891007 sin(118°) = 0.882948 sin(119°) = 0.87462 sin(120°) = 0.866025 sin(121°) = 0.857167 sin(122°) = 0.848048 sin(123°) = 0.838671 sin(124°) = 0.829038 sin(125°) = 0.819152 sin(126°) = 0.809017 sin(127°) = 0.798636 sin(128°) = 0.788011 sin(129°) = 0.777146 sin(130°) = 0.766044 sin(131°) = 0.75471 sin(132°) = 0.743145 sin(133°) = 0.731354 sin(134°) = 0.71934 sin(135°) = 0.707107 |
sin(136°) = 0.694658 sin(137°) = 0.681998 sin(138°) = 0.669131 sin(139°) = 0.656059 sin(140°) = 0.642788 sin(141°) = 0.62932 sin(142°) = 0.615661 sin(143°) = 0.601815 sin(144°) = 0.587785 sin(145°) = 0.573576 sin(146°) = 0.559193 sin(147°) = 0.544639 sin(148°) = 0.529919 sin(149°) = 0.515038 sin(150°) = 0.5 sin(151°) = 0.48481 sin(152°) = 0.469472 sin(153°) = 0.45399 sin(154°) = 0.438371 sin(155°) = 0.422618 sin(156°) = 0.406737 sin(157°) = 0.390731 sin(158°) = 0.374607 sin(159°) = 0.358368 sin(160°) = 0.34202 sin(161°) = 0.325568 sin(162°) = 0.309017 sin(163°) = 0.292372 sin(164°) = 0.275637 sin(165°) = 0.258819 sin(166°) = 0.241922 sin(167°) = 0.224951 sin(168°) = 0.207912 sin(169°) = 0.190809 sin(170°) = 0.173648 sin(171°) = 0.156434 sin(172°) = 0.139173 sin(173°) = 0.121869 sin(174°) = 0.104528 sin(175°) = 0.087156 sin(176°) = 0.069756 sin(177°) = 0.052336 sin(178°) = 0.034899 sin(179°) = 0.017452 sin(180°) = 0 |
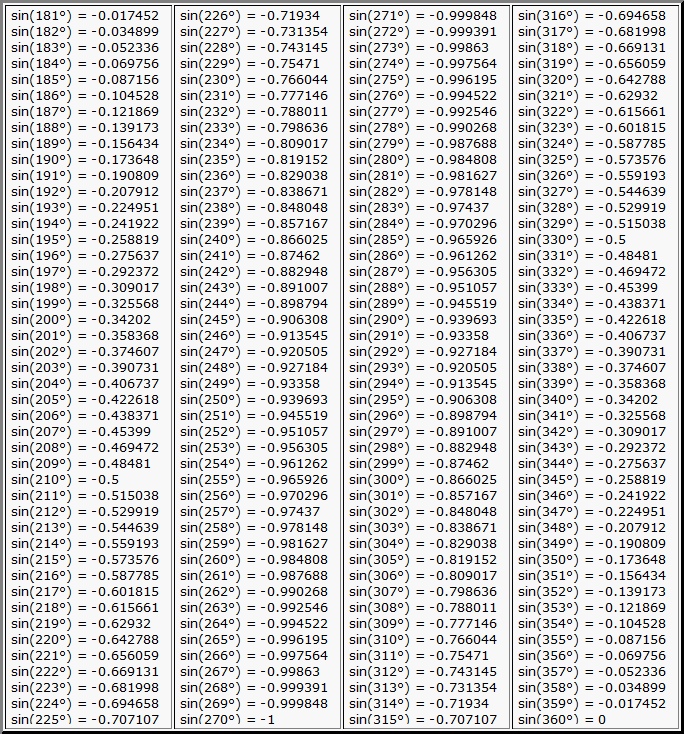
Таблица синусов углов от 181° до 360°
| sin(181°) = -0.017452 sin(182°) = -0.034899 sin(183°) = -0.052336 sin(184°) = -0.069756 sin(185°) = -0.087156 sin(186°) = -0.104528 sin(187°) = -0.121869 sin(188°) = -0.139173 sin(189°) = -0.156434 sin(190°) = -0.173648 sin(191°) = -0.190809 sin(192°) = -0.207912 sin(193°) = -0.224951 sin(194°) = -0.241922 sin(195°) = -0.258819 sin(196°) = -0.275637 sin(197°) = -0.292372 sin(198°) = -0.309017 sin(199°) = -0.325568 sin(200°) = -0.34202 sin(201°) = -0.358368 sin(202°) = -0.374607 sin(203°) = -0.390731 sin(204°) = -0.406737 sin(205°) = -0.422618 sin(206°) = -0.438371 sin(207°) = -0.45399 sin(208°) = -0.469472 sin(209°) = -0.48481 sin(210°) = -0.5 sin(211°) = -0.515038 sin(212°) = -0.529919 sin(213°) = -0.544639 sin(214°) = -0.559193 sin(215°) = -0.573576 sin(216°) = -0.587785 sin(217°) = -0.601815 sin(218°) = -0.615661 sin(219°) = -0.62932 sin(220°) = -0.642788 sin(221°) = -0.656059 sin(222°) = -0.669131 sin(223°) = -0.681998 sin(224°) = -0.694658 sin(225°) = -0.707107 |
sin(226°) = -0.71934 sin(227°) = -0.731354 sin(228°) = -0.743145 sin(229°) = -0.75471 sin(230°) = -0.766044 sin(231°) = -0.777146 sin(232°) = -0.788011 sin(233°) = -0.798636 sin(234°) = -0.809017 sin(235°) = -0.819152 sin(236°) = -0.829038 sin(237°) = -0.838671 sin(238°) = -0.848048 sin(239°) = -0.857167 sin(240°) = -0.866025 sin(241°) = -0.87462 sin(242°) = -0.882948 sin(243°) = -0.891007 sin(244°) = -0.898794 sin(245°) = -0.906308 sin(246°) = -0.913545 sin(247°) = -0.920505 sin(248°) = -0.927184 sin(249°) = -0.93358 sin(250°) = -0.939693 sin(251°) = -0.945519 sin(252°) = -0.951057 sin(253°) = -0.956305 sin(254°) = -0.961262 sin(255°) = -0.965926 sin(256°) = -0.970296 sin(257°) = -0.97437 sin(258°) = -0.978148 sin(259°) = -0.981627 sin(260°) = -0.984808 sin(261°) = -0.987688 sin(262°) = -0.990268 sin(263°) = -0.992546 sin(264°) = -0.994522 sin(265°) = -0.996195 sin(266°) = -0.997564 sin(267°) = -0.99863 sin(268°) = -0.999391 sin(269°) = -0.999848 sin(270°) = -1 |
sin(271°) = -0.999848 sin(272°) = -0.999391 sin(273°) = -0.99863 sin(274°) = -0.997564 sin(275°) = -0.996195 sin(276°) = -0.994522 sin(277°) = -0.992546 sin(278°) = -0.990268 sin(279°) = -0.987688 sin(280°) = -0.984808 sin(281°) = -0.981627 sin(282°) = -0.978148 sin(283°) = -0.97437 sin(284°) = -0.970296 sin(285°) = -0.965926 sin(286°) = -0.961262 sin(287°) = -0.956305 sin(288°) = -0.951057 sin(289°) = -0.945519 sin(290°) = -0.939693 sin(291°) = -0.93358 sin(292°) = -0.927184 sin(293°) = -0.920505 sin(294°) = -0.913545 sin(295°) = -0.906308 sin(296°) = -0.898794 sin(297°) = -0.891007 sin(298°) = -0.882948 sin(299°) = -0.87462 sin(300°) = -0.866025 sin(301°) = -0.857167 sin(302°) = -0.848048 sin(303°) = -0.838671 sin(304°) = -0.829038 sin(305°) = -0.819152 sin(306°) = -0.809017 sin(307°) = -0.798636 sin(308°) = -0.788011 sin(309°) = -0.777146 sin(310°) = -0.766044 sin(311°) = -0.75471 sin(312°) = -0.743145 sin(313°) = -0.731354 sin(314°) = -0.71934 sin(315°) = -0.707107 |
sin(316°) = -0.694658 sin(317°) = -0.681998 sin(318°) = -0.669131 sin(319°) = -0.656059 sin(320°) = -0.642788 sin(321°) = -0.62932 sin(322°) = -0.615661 sin(323°) = -0.601815 sin(324°) = -0.587785 sin(325°) = -0.573576 sin(326°) = -0.559193 sin(327°) = -0.544639 sin(328°) = -0.529919 sin(329°) = -0.515038 sin(330°) = -0.5 sin(331°) = -0.48481 sin(332°) = -0.469472 sin(333°) = -0.45399 sin(334°) = -0.438371 sin(335°) = -0.422618 sin(336°) = -0.406737 sin(337°) = -0.390731 sin(338°) = -0.374607 sin(339°) = -0.358368 sin(340°) = -0.34202 sin(341°) = -0.325568 sin(342°) = -0.309017 sin(343°) = -0.292372 sin(344°) = -0.275637 sin(345°) = -0.258819 sin(346°) = -0.241922 sin(347°) = -0.224951 sin(348°) = -0.207912 sin(349°) = -0.190809 sin(350°) = -0.173648 sin(351°) = -0.156434 sin(352°) = -0.139173 sin(353°) = -0.121869 sin(354°) = -0.104528 sin(355°) = -0.087156 sin(356°) = -0.069756 sin(357°) = -0.052336 sin(358°) = -0.034899 sin(359°) = -0.017452 sin(360°) = 0 |
Синус угла. Таблица синусов.
Синус угла через градусы, минуты и секунды
Синус угла через десятичную запись угла
Как найти угол зная синус этого угла
У синуса есть обратная тригонометрическая функция – arcsin(y)=x
sin(arcsin(y))=y
Пример sin(30°) = 1/2; arcsin(1/2) = 30°
Рассчитать арксинус
Определение синуса
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Синусом угла α называется ордината точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.
sin(α) = BC/AB
sin(-α) = -sin(α)
Периодичность синуса
Функция y = sin(x) периодична, с периодом 2π
sin(α ± 2π) = sin(α)
Пример sin(5π) = sin(4π + π) = sin(π)
Таблица синусов в радианах
sin(0°) = 0sin(π/12) = sin(15°) = 0.2588190451sin(π/6) = sin(30°) = 0.5sin(π/4) = sin(45°) = 0.7071067812sin(π/3) = sin(60°) = 0.8660254038sin(5π/12) = sin(75°) = 0.9659258263sin(π/2) = sin(90°) = 1sin(7π/12) = sin(105°) = 0.9659258263sin(2π/3) = sin(120°) = 0.8660254038sin(3π/4) = sin(135°) = 0.7071067812sin(5π/6) = sin(150°) = 0.5sin(11π/12) = sin(165°) = 0.2588190451sin(π) = sin(180°) = 0sin(13π/12) = sin(195°) = -0.2588190451sin(7π/6) = sin(210°) = -0.5sin(5π/4) = sin(225°) = -0.7071067812sin(4π/3) = sin(240°) = -0.8660254038sin(17π/12) = sin(255°) = -0.9659258263sin(3π/2) = sin(270°) = -1sin(19π/12) = sin(285°) = -0.9659258263sin(5π/3) = sin(300°) = -0.8660254038sin(7π/4) = sin(315°) = -0.7071067812sin(11π/6) = sin(330°) = -0.5sin(23π/12) = sin(345°) = -0.2588190451
Таблица Брадиса синусы
| sin(0) = 0 | sin(120) = 0.8660254038 | sin(240) = -0.8660254038 |
| sin(1) = 0.01745240644 | sin(121) = 0.8571673007 | sin(241) = -0.8746197071 |
| sin(2) = 0.0348994967 | sin(122) = 0.8480480962 | sin(242) = -0.8829475929 |
| sin(3) = 0.05233595624 | sin(123) = 0.8386705679 | sin(243) = -0.8910065242 |
| sin(4) = 0.06975647374 | sin(124) = 0.8290375726 | sin(244) = -0.8987940463 |
| sin(5) = 0.08715574275 | sin(125) = 0.8191520443 | sin(245) = -0.906307787 |
| sin(6) = 0.1045284633 | sin(126) = 0.8090169944 | sin(246) = -0.9135454576 |
| sin(7) = 0.1218693434 | sin(127) = 0.79863551 | sin(247) = -0.9205048535 |
| sin(8) = 0.139173101 | sin(128) = 0.7880107536 | sin(248) = -0.9271838546 |
| sin(9) = 0.156434465 | sin(129) = 0.7771459615 | sin(249) = -0.9335804265 |
| sin(10) = 0.1736481777 | sin(130) = 0.7660444431 | sin(250) = -0.9396926208 |
| sin(11) = 0.1908089954 | sin(131) = 0.7547095802 | sin(251) = -0.9455185756 |
| sin(12) = 0.2079116908 | sin(132) = 0.7431448255 | sin(252) = -0.9510565163 |
| sin(13) = 0.2249510543 | sin(133) = 0.7313537016 | sin(253) = -0.956304756 |
| sin(14) = 0.2419218956 | sin(134) = 0.7193398003 | sin(254) = -0.9612616959 |
| sin(15) = 0.2588190451 | sin(135) = 0.7071067812 | sin(255) = -0.9659258263 |
| sin(16) = 0.2756373558 | sin(136) = 0.6946583705 | sin(256) = -0.9702957263 |
| sin(17) = 0.2923717047 | sin(137) = 0.6819983601 | sin(257) = -0.9743700648 |
| sin(18) = 0.3090169944 | sin(138) = 0.6691306064 | sin(258) = -0.9781476007 |
| sin(19) = 0.3255681545 | sin(139) = 0.656059029 | sin(259) = -0.9816271834 |
| sin(20) = 0.3420201433 | sin(140) = 0.6427876097 | sin(260) = -0.984807753 |
| sin(21) = 0.3583679495 | sin(141) = 0.629320391 | sin(261) = -0.9876883406 |
| sin(22) = 0.3746065934 | sin(142) = 0.6156614753 | sin(262) = -0.9902680687 |
| sin(23) = 0.3907311285 | sin(143) = 0.6018150232 | sin(263) = -0.9925461516 |
| sin(24) = 0.4067366431 | sin(144) = 0.5877852523 | sin(264) = -0.9945218954 |
| sin(25) = 0.4226182617 | sin(145) = 0.5735764364 | sin(265) = -0.9961946981 |
| sin(26) = 0.4383711468 | sin(146) = 0.5591929035 | sin(266) = -0.9975640503 |
| sin(27) = 0.4539904997 | sin(147) = 0.544639035 | sin(267) = -0.9986295348 |
| sin(28) = 0.4694715628 | sin(148) = 0.5299192642 | sin(268) = -0.999390827 |
| sin(29) = 0.4848096202 | sin(149) = 0.5150380749 | sin(269) = -0.9998476952 |
| sin(30) = 0.5 | sin(150) = 0.5 | sin(270) = -1 |
| sin(31) = 0.5150380749 | sin(151) = 0.4848096202 | sin(271) = -0.9998476952 |
| sin(32) = 0.5299192642 | sin(152) = 0.4694715628 | sin(272) = -0.999390827 |
| sin(33) = 0.544639035 | sin(153) = 0.4539904997 | sin(273) = -0.9986295348 |
| sin(34) = 0.5591929035 | sin(154) = 0.4383711468 | sin(274) = -0.9975640503 |
| sin(35) = 0.5735764364 | sin(155) = 0.4226182617 | sin(275) = -0.9961946981 |
| sin(36) = 0.5877852523 | sin(156) = 0.4067366431 | sin(276) = -0.9945218954 |
| sin(37) = 0.6018150232 | sin(157) = 0.3907311285 | sin(277) = -0.9925461516 |
| sin(38) = 0.6156614753 | sin(158) = 0.3746065934 | sin(278) = -0.9902680687 |
| sin(39) = 0.629320391 | sin(159) = 0.3583679495 | sin(279) = -0.9876883406 |
| sin(40) = 0.6427876097 | sin(160) = 0.3420201433 | sin(280) = -0.984807753 |
| sin(41) = 0.656059029 | sin(161) = 0.3255681545 | sin(281) = -0.9816271834 |
| sin(42) = 0.6691306064 | sin(162) = 0.3090169944 | sin(282) = -0.9781476007 |
| sin(43) = 0.6819983601 | sin(163) = 0.2923717047 | sin(283) = -0.9743700648 |
| sin(44) = 0.6946583705 | sin(164) = 0.2756373558 | sin(284) = -0.9702957263 |
| sin(45) = 0.7071067812 | sin(165) = 0.2588190451 | sin(285) = -0.9659258263 |
| sin(46) = 0.7193398003 | sin(166) = 0.2419218956 | sin(286) = -0.9612616959 |
| sin(47) = 0.7313537016 | sin(167) = 0.2249510543 | sin(287) = -0.956304756 |
| sin(48) = 0.7431448255 | sin(168) = 0.2079116908 | sin(288) = -0.9510565163 |
| sin(49) = 0.7547095802 | sin(169) = 0.1908089954 | sin(289) = -0.9455185756 |
| sin(50) = 0.7660444431 | sin(170) = 0.1736481777 | sin(290) = -0.9396926208 |
| sin(51) = 0.7771459615 | sin(171) = 0.156434465 | sin(291) = -0.9335804265 |
| sin(52) = 0.7880107536 | sin(172) = 0.139173101 | sin(292) = -0.9271838546 |
| sin(53) = 0.79863551 | sin(173) = 0.1218693434 | sin(293) = -0.9205048535 |
| sin(54) = 0.8090169944 | sin(174) = 0.1045284633 | sin(294) = -0.9135454576 |
| sin(55) = 0.8191520443 | sin(175) = 0.08715574275 | sin(295) = -0.906307787 |
| sin(56) = 0.8290375726 | sin(176) = 0.06975647374 | sin(296) = -0.8987940463 |
| sin(57) = 0.8386705679 | sin(177) = 0.05233595624 | sin(297) = -0.8910065242 |
| sin(58) = 0.8480480962 | sin(178) = 0.0348994967 | sin(298) = -0.8829475929 |
| sin(59) = 0.8571673007 | sin(179) = 0.01745240644 | sin(299) = -0.8746197071 |
| sin(60) = 0.8660254038 | sin(180) = 0 | sin(300) = -0.8660254038 |
| sin(61) = 0.8746197071 | sin(181) = -0.01745240644 | sin(301) = -0.8571673007 |
| sin(62) = 0.8829475929 | sin(182) = -0.0348994967 | sin(302) = -0.8480480962 |
| sin(63) = 0.8910065242 | sin(183) = -0.05233595624 | sin(303) = -0.8386705679 |
| sin(64) = 0.8987940463 | sin(184) = -0.06975647374 | sin(304) = -0.8290375726 |
| sin(65) = 0.906307787 | sin(185) = -0.08715574275 | sin(305) = -0.8191520443 |
| sin(66) = 0.9135454576 | sin(186) = -0.1045284633 | sin(306) = -0.8090169944 |
| sin(67) = 0.9205048535 | sin(187) = -0.1218693434 | sin(307) = -0.79863551 |
| sin(68) = 0.9271838546 | sin(188) = -0.139173101 | sin(308) = -0.7880107536 |
| sin(69) = 0.9335804265 | sin(189) = -0.156434465 | sin(309) = -0.7771459615 |
| sin(70) = 0.9396926208 | sin(190) = -0.1736481777 | sin(310) = -0.7660444431 |
| sin(71) = 0.9455185756 | sin(191) = -0.1908089954 | sin(311) = -0.7547095802 |
| sin(72) = 0.9510565163 | sin(192) = -0.2079116908 | sin(312) = -0.7431448255 |
| sin(73) = 0.956304756 | sin(193) = -0.2249510543 | sin(313) = -0.7313537016 |
| sin(74) = 0.9612616959 | sin(194) = -0.2419218956 | sin(314) = -0.7193398003 |
| sin(75) = 0.9659258263 | sin(195) = -0.2588190451 | sin(315) = -0.7071067812 |
| sin(76) = 0.9702957263 | sin(196) = -0.2756373558 | sin(316) = -0.6946583705 |
| sin(77) = 0.9743700648 | sin(197) = -0.2923717047 | sin(317) = -0.6819983601 |
| sin(78) = 0.9781476007 | sin(198) = -0.3090169944 | sin(318) = -0.6691306064 |
| sin(79) = 0.9816271834 | sin(199) = -0.3255681545 | sin(319) = -0.656059029 |
| sin(80) = 0.984807753 | sin(200) = -0.3420201433 | sin(320) = -0.6427876097 |
| sin(81) = 0.9876883406 | sin(201) = -0.3583679495 | sin(321) = -0.629320391 |
| sin(82) = 0.9902680687 | sin(202) = -0.3746065934 | sin(322) = -0.6156614753 |
| sin(83) = 0.9925461516 | sin(203) = -0.3907311285 | sin(323) = -0.6018150232 |
| sin(84) = 0.9945218954 | sin(204) = -0.4067366431 | sin(324) = -0.5877852523 |
| sin(85) = 0.9961946981 | sin(205) = -0.4226182617 | sin(325) = -0.5735764364 |
| sin(86) = 0.9975640503 | sin(206) = -0.4383711468 | sin(326) = -0.5591929035 |
| sin(87) = 0.9986295348 | sin(207) = -0.4539904997 | sin(327) = -0.544639035 |
| sin(88) = 0.999390827 | sin(208) = -0.4694715628 | sin(328) = -0.5299192642 |
| sin(89) = 0.9998476952 | sin(209) = -0.4848096202 | sin(329) = -0.5150380749 |
| sin(90) = 1 | sin(210) = -0.5 | sin(330) = -0.5 |
| sin(91) = 0.9998476952 | sin(211) = -0.5150380749 | sin(331) = -0.4848096202 |
| sin(92) = 0.999390827 | sin(212) = -0.5299192642 | sin(332) = -0.4694715628 |
| sin(93) = 0.9986295348 | sin(213) = -0.544639035 | sin(333) = -0.4539904997 |
| sin(94) = 0.9975640503 | sin(214) = -0.5591929035 | sin(334) = -0.4383711468 |
| sin(95) = 0.9961946981 | sin(215) = -0.5735764364 | sin(335) = -0.4226182617 |
| sin(96) = 0.9945218954 | sin(216) = -0.5877852523 | sin(336) = -0.4067366431 |
| sin(97) = 0.9925461516 | sin(217) = -0.6018150232 | sin(337) = -0.3907311285 |
| sin(98) = 0.9902680687 | sin(218) = -0.6156614753 | sin(338) = -0.3746065934 |
| sin(99) = 0.9876883406 | sin(219) = -0.629320391 | sin(339) = -0.3583679495 |
| sin(100) = 0.984807753 | sin(220) = -0.6427876097 | sin(340) = -0.3420201433 |
| sin(101) = 0.9816271834 | sin(221) = -0.656059029 | sin(341) = -0.3255681545 |
| sin(102) = 0.9781476007 | sin(222) = -0.6691306064 | sin(342) = -0.3090169944 |
| sin(103) = 0.9743700648 | sin(223) = -0.6819983601 | sin(343) = -0.2923717047 |
| sin(104) = 0.9702957263 | sin(224) = -0.6946583705 | sin(344) = -0.2756373558 |
| sin(105) = 0.9659258263 | sin(225) = -0.7071067812 | sin(345) = -0.2588190451 |
| sin(106) = 0.9612616959 | sin(226) = -0.7193398003 | sin(346) = -0.2419218956 |
| sin(107) = 0.956304756 | sin(227) = -0.7313537016 | sin(347) = -0.2249510543 |
| sin(108) = 0.9510565163 | sin(228) = -0.7431448255 | sin(348) = -0.2079116908 |
| sin(109) = 0.9455185756 | sin(229) = -0.7547095802 | sin(349) = -0.1908089954 |
| sin(110) = 0.9396926208 | sin(230) = -0.7660444431 | sin(350) = -0.1736481777 |
| sin(111) = 0.9335804265 | sin(231) = -0.7771459615 | sin(351) = -0.156434465 |
| sin(112) = 0.9271838546 | sin(232) = -0.7880107536 | sin(352) = -0.139173101 |
| sin(113) = 0.9205048535 | sin(233) = -0.79863551 | sin(353) = -0.1218693434 |
| sin(114) = 0.9135454576 | sin(234) = -0.8090169944 | sin(354) = -0.1045284633 |
| sin(115) = 0.906307787 | sin(235) = -0.8191520443 | sin(355) = -0.08715574275 |
| sin(116) = 0.8987940463 | sin(236) = -0.8290375726 | sin(356) = -0.06975647374 |
| sin(117) = 0.8910065242 | sin(237) = -0.8386705679 | sin(357) = -0.05233595624 |
| sin(118) = 0.8829475929 | sin(238) = -0.8480480962 | sin(358) = -0.0348994967 |
| sin(119) = 0.8746197071 | sin(239) = -0.8571673007 | sin(359) = -0.01745240644 |
Похожие калькуляторы
В данной таблице приведены значения синусов и косинусов для углов от 0 до 359 градусов. Но если Вам нужно рассчитать значения тригонометрических функций
для более точных углов (с минутами и секундами) или углов больше 360 градусов или углов с отрицательными значениями (например 8° 5′ 53″
или -1775° 15′ 22″ ), то можно воспользоваться тригонометрическим калькулятором.
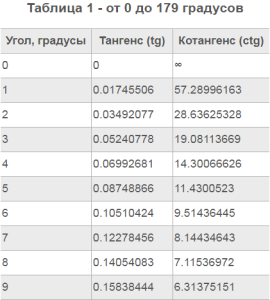
Таблица углов от 0 до 179 градусов
| Угол (градусы) | Синус (Sin) | Косинус (Cos) |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0.01745241 | 0.9998477 |
| 2 | 0.0348995 | 0.99939083 |
| 3 | 0.05233596 | 0.99862953 |
| 4 | 0.06975647 | 0.99756405 |
| 5 | 0.08715574 | 0.9961947 |
| 6 | 0.10452846 | 0.9945219 |
| 7 | 0.12186934 | 0.99254615 |
| 8 | 0.1391731 | 0.99026807 |
| 9 | 0.15643447 | 0.98768834 |
| 10 | 0.17364818 | 0.98480775 |
| 11 | 0.190809 | 0.98162718 |
| 12 | 0.20791169 | 0.9781476 |
| 13 | 0.22495105 | 0.97437006 |
| 14 | 0.2419219 | 0.97029573 |
| 15 | 0.25881905 | 0.96592583 |
| 16 | 0.27563736 | 0.9612617 |
| 17 | 0.2923717 | 0.95630476 |
| 18 | 0.30901699 | 0.95105652 |
| 19 | 0.32556815 | 0.94551858 |
| 20 | 0.34202014 | 0.93969262 |
| 21 | 0.35836795 | 0.93358043 |
| 22 | 0.37460659 | 0.92718385 |
| 23 | 0.39073113 | 0.92050485 |
| 24 | 0.40673664 | 0.91354546 |
| 25 | 0.42261826 | 0.90630779 |
| 26 | 0.43837115 | 0.89879405 |
| 27 | 0.4539905 | 0.89100652 |
| 28 | 0.46947156 | 0.88294759 |
| 29 | 0.48480962 | 0.87461971 |
| 30 | 0.5 | 0.8660254 |
| 31 | 0.51503807 | 0.8571673 |
| 32 | 0.52991926 | 0.8480481 |
| 33 | 0.54463904 | 0.83867057 |
| 34 | 0.5591929 | 0.82903757 |
| 35 | 0.57357644 | 0.81915204 |
| 36 | 0.58778525 | 0.80901699 |
| 37 | 0.60181502 | 0.79863551 |
| 38 | 0.61566148 | 0.78801075 |
| 39 | 0.62932039 | 0.77714596 |
| 40 | 0.64278761 | 0.76604444 |
| 41 | 0.65605903 | 0.75470958 |
| 42 | 0.66913061 | 0.74314483 |
| 43 | 0.68199836 | 0.7313537 |
| 44 | 0.69465837 | 0.7193398 |
| 45 | 0.70710678 | 0.70710678 |
| 46 | 0.7193398 | 0.69465837 |
| 47 | 0.7313537 | 0.68199836 |
| 48 | 0.74314483 | 0.66913061 |
| 49 | 0.75470958 | 0.65605903 |
| 50 | 0.76604444 | 0.64278761 |
| 51 | 0.77714596 | 0.62932039 |
| 52 | 0.78801075 | 0.61566148 |
| 53 | 0.79863551 | 0.60181502 |
| 54 | 0.80901699 | 0.58778525 |
| 55 | 0.81915204 | 0.57357644 |
| 56 | 0.82903757 | 0.5591929 |
| 57 | 0.83867057 | 0.54463904 |
| 58 | 0.8480481 | 0.52991926 |
| 59 | 0.8571673 | 0.51503807 |
| 60 | 0.8660254 | 0.5 |
| 61 | 0.87461971 | 0.48480962 |
| 62 | 0.88294759 | 0.46947156 |
| 63 | 0.89100652 | 0.4539905 |
| 64 | 0.89879405 | 0.43837115 |
| 65 | 0.90630779 | 0.42261826 |
| 66 | 0.91354546 | 0.40673664 |
| 67 | 0.92050485 | 0.39073113 |
| 68 | 0.92718385 | 0.37460659 |
| 69 | 0.93358043 | 0.35836795 |
| 70 | 0.93969262 | 0.34202014 |
| 71 | 0.94551858 | 0.32556815 |
| 72 | 0.95105652 | 0.30901699 |
| 73 | 0.95630476 | 0.2923717 |
| 74 | 0.9612617 | 0.27563736 |
| 75 | 0.96592583 | 0.25881905 |
| 76 | 0.97029573 | 0.2419219 |
| 77 | 0.97437006 | 0.22495105 |
| 78 | 0.9781476 | 0.20791169 |
| 79 | 0.98162718 | 0.190809 |
| 80 | 0.98480775 | 0.17364818 |
| 81 | 0.98768834 | 0.15643447 |
| 82 | 0.99026807 | 0.1391731 |
| 83 | 0.99254615 | 0.12186934 |
| 84 | 0.9945219 | 0.10452846 |
| 85 | 0.9961947 | 0.08715574 |
| 86 | 0.99756405 | 0.06975647 |
| 87 | 0.99862953 | 0.05233596 |
| 88 | 0.99939083 | 0.0348995 |
| 89 | 0.9998477 | 0.01745241 |
| 90 | 1 | 0 |
| 91 | 0.9998477 | -0.01745241 |
| 92 | 0.99939083 | -0.0348995 |
| 93 | 0.99862953 | -0.05233596 |
| 94 | 0.99756405 | -0.06975647 |
| 95 | 0.9961947 | -0.08715574 |
| 96 | 0.9945219 | -0.10452846 |
| 97 | 0.99254615 | -0.12186934 |
| 98 | 0.99026807 | -0.1391731 |
| 99 | 0.98768834 | -0.15643447 |
| 100 | 0.98480775 | -0.17364818 |
| 101 | 0.98162718 | -0.190809 |
| 102 | 0.9781476 | -0.20791169 |
| 103 | 0.97437006 | -0.22495105 |
| 104 | 0.97029573 | -0.2419219 |
| 105 | 0.96592583 | -0.25881905 |
| 106 | 0.9612617 | -0.27563736 |
| 107 | 0.95630476 | -0.2923717 |
| 108 | 0.95105652 | -0.30901699 |
| 109 | 0.94551858 | -0.32556815 |
| 110 | 0.93969262 | -0.34202014 |
| 111 | 0.93358043 | -0.35836795 |
| 112 | 0.92718385 | -0.37460659 |
| 113 | 0.92050485 | -0.39073113 |
| 114 | 0.91354546 | -0.40673664 |
| 115 | 0.90630779 | -0.42261826 |
| 116 | 0.89879405 | -0.43837115 |
| 117 | 0.89100652 | -0.4539905 |
| 118 | 0.88294759 | -0.46947156 |
| 119 | 0.87461971 | -0.48480962 |
| 120 | 0.8660254 | -0.5 |
| 121 | 0.8571673 | -0.51503807 |
| 122 | 0.8480481 | -0.52991926 |
| 123 | 0.83867057 | -0.54463904 |
| 124 | 0.82903757 | -0.5591929 |
| 125 | 0.81915204 | -0.57357644 |
| 126 | 0.80901699 | -0.58778525 |
| 127 | 0.79863551 | -0.60181502 |
| 128 | 0.78801075 | -0.61566148 |
| 129 | 0.77714596 | -0.62932039 |
| 130 | 0.76604444 | -0.64278761 |
| 131 | 0.75470958 | -0.65605903 |
| 132 | 0.74314483 | -0.66913061 |
| 133 | 0.7313537 | -0.68199836 |
| 134 | 0.7193398 | -0.69465837 |
| 135 | 0.70710678 | -0.70710678 |
| 136 | 0.69465837 | -0.7193398 |
| 137 | 0.68199836 | -0.7313537 |
| 138 | 0.66913061 | -0.74314483 |
| 139 | 0.65605903 | -0.75470958 |
| 140 | 0.64278761 | -0.76604444 |
| 141 | 0.62932039 | -0.77714596 |
| 142 | 0.61566148 | -0.78801075 |
| 143 | 0.60181502 | -0.79863551 |
| 144 | 0.58778525 | -0.80901699 |
| 145 | 0.57357644 | -0.81915204 |
| 146 | 0.5591929 | -0.82903757 |
| 147 | 0.54463904 | -0.83867057 |
| 148 | 0.52991926 | -0.8480481 |
| 149 | 0.51503807 | -0.8571673 |
| 150 | 0.5 | -0.8660254 |
| 151 | 0.48480962 | -0.87461971 |
| 152 | 0.46947156 | -0.88294759 |
| 153 | 0.4539905 | -0.89100652 |
| 154 | 0.43837115 | -0.89879405 |
| 155 | 0.42261826 | -0.90630779 |
| 156 | 0.40673664 | -0.91354546 |
| 157 | 0.39073113 | -0.92050485 |
| 158 | 0.37460659 | -0.92718385 |
| 159 | 0.35836795 | -0.93358043 |
| 160 | 0.34202014 | -0.93969262 |
| 161 | 0.32556815 | -0.94551858 |
| 162 | 0.30901699 | -0.95105652 |
| 163 | 0.2923717 | -0.95630476 |
| 164 | 0.27563736 | -0.9612617 |
| 165 | 0.25881905 | -0.96592583 |
| 166 | 0.2419219 | -0.97029573 |
| 167 | 0.22495105 | -0.97437006 |
| 168 | 0.20791169 | -0.9781476 |
| 169 | 0.190809 | -0.98162718 |
| 170 | 0.17364818 | -0.98480775 |
| 171 | 0.15643447 | -0.98768834 |
| 172 | 0.1391731 | -0.99026807 |
| 173 | 0.12186934 | -0.99254615 |
| 174 | 0.10452846 | -0.9945219 |
| 175 | 0.08715574 | -0.9961947 |
| 176 | 0.06975647 | -0.99756405 |
| 177 | 0.05233596 | -0.99862953 |
| 178 | 0.0348995 | -0.99939083 |
| 179 | 0.01745241 | -0.9998477 |
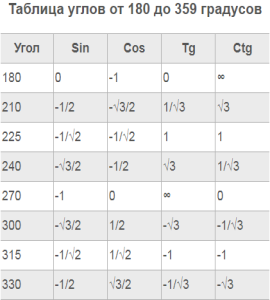
Таблица углов от 180 до 359 градусов
| Угол (градусы) | Синус (Sin) | Косинус (Cos) |
|---|---|---|
| 180 | 0 | -1 |
| 181 | -0.01745241 | -0.9998477 |
| 182 | -0.0348995 | -0.99939083 |
| 183 | -0.05233596 | -0.99862953 |
| 184 | -0.06975647 | -0.99756405 |
| 185 | -0.08715574 | -0.9961947 |
| 186 | -0.10452846 | -0.9945219 |
| 187 | -0.12186934 | -0.99254615 |
| 188 | -0.1391731 | -0.99026807 |
| 189 | -0.15643447 | -0.98768834 |
| 190 | -0.17364818 | -0.98480775 |
| 191 | -0.190809 | -0.98162718 |
| 192 | -0.20791169 | -0.9781476 |
| 193 | -0.22495105 | -0.97437006 |
| 194 | -0.2419219 | -0.97029573 |
| 195 | -0.25881905 | -0.96592583 |
| 196 | -0.27563736 | -0.9612617 |
| 197 | -0.2923717 | -0.95630476 |
| 198 | -0.30901699 | -0.95105652 |
| 199 | -0.32556815 | -0.94551858 |
| 200 | -0.34202014 | -0.93969262 |
| 201 | -0.35836795 | -0.93358043 |
| 202 | -0.37460659 | -0.92718385 |
| 203 | -0.39073113 | -0.92050485 |
| 204 | -0.40673664 | -0.91354546 |
| 205 | -0.42261826 | -0.90630779 |
| 206 | -0.43837115 | -0.89879405 |
| 207 | -0.4539905 | -0.89100652 |
| 208 | -0.46947156 | -0.88294759 |
| 209 | -0.48480962 | -0.87461971 |
| 210 | -0.5 | -0.8660254 |
| 211 | -0.51503807 | -0.8571673 |
| 212 | -0.52991926 | -0.8480481 |
| 213 | -0.54463904 | -0.83867057 |
| 214 | -0.5591929 | -0.82903757 |
| 215 | -0.57357644 | -0.81915204 |
| 216 | -0.58778525 | -0.80901699 |
| 217 | -0.60181502 | -0.79863551 |
| 218 | -0.61566148 | -0.78801075 |
| 219 | -0.62932039 | -0.77714596 |
| 220 | -0.64278761 | -0.76604444 |
| 221 | -0.65605903 | -0.75470958 |
| 222 | -0.66913061 | -0.74314483 |
| 223 | -0.68199836 | -0.7313537 |
| 224 | -0.69465837 | -0.7193398 |
| 225 | -0.70710678 | -0.70710678 |
| 226 | -0.7193398 | -0.69465837 |
| 227 | -0.7313537 | -0.68199836 |
| 228 | -0.74314483 | -0.66913061 |
| 229 | -0.75470958 | -0.65605903 |
| 230 | -0.76604444 | -0.64278761 |
| 231 | -0.77714596 | -0.62932039 |
| 232 | -0.78801075 | -0.61566148 |
| 233 | -0.79863551 | -0.60181502 |
| 234 | -0.80901699 | -0.58778525 |
| 235 | -0.81915204 | -0.57357644 |
| 236 | -0.82903757 | -0.5591929 |
| 237 | -0.83867057 | -0.54463904 |
| 238 | -0.8480481 | -0.52991926 |
| 239 | -0.8571673 | -0.51503807 |
| 240 | -0.8660254 | -0.5 |
| 241 | -0.87461971 | -0.48480962 |
| 242 | -0.88294759 | -0.46947156 |
| 243 | -0.89100652 | -0.4539905 |
| 244 | -0.89879405 | -0.43837115 |
| 245 | -0.90630779 | -0.42261826 |
| 246 | -0.91354546 | -0.40673664 |
| 247 | -0.92050485 | -0.39073113 |
| 248 | -0.92718385 | -0.37460659 |
| 249 | -0.93358043 | -0.35836795 |
| 250 | -0.93969262 | -0.34202014 |
| 251 | -0.94551858 | -0.32556815 |
| 252 | -0.95105652 | -0.30901699 |
| 253 | -0.95630476 | -0.2923717 |
| 254 | -0.9612617 | -0.27563736 |
| 255 | -0.96592583 | -0.25881905 |
| 256 | -0.97029573 | -0.2419219 |
| 257 | -0.97437006 | -0.22495105 |
| 258 | -0.9781476 | -0.20791169 |
| 259 | -0.98162718 | -0.190809 |
| 260 | -0.98480775 | -0.17364818 |
| 261 | -0.98768834 | -0.15643447 |
| 262 | -0.99026807 | -0.1391731 |
| 263 | -0.99254615 | -0.12186934 |
| 264 | -0.9945219 | -0.10452846 |
| 265 | -0.9961947 | -0.08715574 |
| 266 | -0.99756405 | -0.06975647 |
| 267 | -0.99862953 | -0.05233596 |
| 268 | -0.99939083 | -0.0348995 |
| 269 | -0.9998477 | -0.01745241 |
| 270 | -1 | 0 |
| 271 | -0.9998477 | 0.01745241 |
| 272 | -0.99939083 | 0.0348995 |
| 273 | -0.99862953 | 0.05233596 |
| 274 | -0.99756405 | 0.06975647 |
| 275 | -0.9961947 | 0.08715574 |
| 276 | -0.9945219 | 0.10452846 |
| 277 | -0.99254615 | 0.12186934 |
| 278 | -0.99026807 | 0.1391731 |
| 279 | -0.98768834 | 0.15643447 |
| 280 | -0.98480775 | 0.17364818 |
| 281 | -0.98162718 | 0.190809 |
| 282 | -0.9781476 | 0.20791169 |
| 283 | -0.97437006 | 0.22495105 |
| 284 | -0.97029573 | 0.2419219 |
| 285 | -0.96592583 | 0.25881905 |
| 286 | -0.9612617 | 0.27563736 |
| 287 | -0.95630476 | 0.2923717 |
| 288 | -0.95105652 | 0.30901699 |
| 289 | -0.94551858 | 0.32556815 |
| 290 | -0.93969262 | 0.34202014 |
| 291 | -0.93358043 | 0.35836795 |
| 292 | -0.92718385 | 0.37460659 |
| 293 | -0.92050485 | 0.39073113 |
| 294 | -0.91354546 | 0.40673664 |
| 295 | -0.90630779 | 0.42261826 |
| 296 | -0.89879405 | 0.43837115 |
| 297 | -0.89100652 | 0.4539905 |
| 298 | -0.88294759 | 0.46947156 |
| 299 | -0.87461971 | 0.48480962 |
| 300 | -0.8660254 | 0.5 |
| 301 | -0.8571673 | 0.51503807 |
| 302 | -0.8480481 | 0.52991926 |
| 303 | -0.83867057 | 0.54463904 |
| 304 | -0.82903757 | 0.5591929 |
| 305 | -0.81915204 | 0.57357644 |
| 306 | -0.80901699 | 0.58778525 |
| 307 | -0.79863551 | 0.60181502 |
| 308 | -0.78801075 | 0.61566148 |
| 309 | -0.77714596 | 0.62932039 |
| 310 | -0.76604444 | 0.64278761 |
| 311 | -0.75470958 | 0.65605903 |
| 312 | -0.74314483 | 0.66913061 |
| 313 | -0.7313537 | 0.68199836 |
| 314 | -0.7193398 | 0.69465837 |
| 315 | -0.70710678 | 0.70710678 |
| 316 | -0.69465837 | 0.7193398 |
| 317 | -0.68199836 | 0.7313537 |
| 318 | -0.66913061 | 0.74314483 |
| 319 | -0.65605903 | 0.75470958 |
| 320 | -0.64278761 | 0.76604444 |
| 321 | -0.62932039 | 0.77714596 |
| 322 | -0.61566148 | 0.78801075 |
| 323 | -0.60181502 | 0.79863551 |
| 324 | -0.58778525 | 0.80901699 |
| 325 | -0.57357644 | 0.81915204 |
| 326 | -0.5591929 | 0.82903757 |
| 327 | -0.54463904 | 0.83867057 |
| 328 | -0.52991926 | 0.8480481 |
| 329 | -0.51503807 | 0.8571673 |
| 330 | -0.5 | 0.8660254 |
| 331 | -0.48480962 | 0.87461971 |
| 332 | -0.46947156 | 0.88294759 |
| 333 | -0.4539905 | 0.89100652 |
| 334 | -0.43837115 | 0.89879405 |
| 335 | -0.42261826 | 0.90630779 |
| 336 | -0.40673664 | 0.91354546 |
| 337 | -0.39073113 | 0.92050485 |
| 338 | -0.37460659 | 0.92718385 |
| 339 | -0.35836795 | 0.93358043 |
| 340 | -0.34202014 | 0.93969262 |
| 341 | -0.32556815 | 0.94551858 |
| 342 | -0.30901699 | 0.95105652 |
| 343 | -0.2923717 | 0.95630476 |
| 344 | -0.27563736 | 0.9612617 |
| 345 | -0.25881905 | 0.96592583 |
| 346 | -0.2419219 | 0.97029573 |
| 347 | -0.22495105 | 0.97437006 |
| 348 | -0.20791169 | 0.9781476 |
| 349 | -0.190809 | 0.98162718 |
| 350 | -0.17364818 | 0.98480775 |
| 351 | -0.15643447 | 0.98768834 |
| 352 | -0.1391731 | 0.99026807 |
| 353 | -0.12186934 | 0.99254615 |
| 354 | -0.10452846 | 0.9945219 |
| 355 | -0.08715574 | 0.9961947 |
| 356 | -0.06975647 | 0.99756405 |
| 357 | -0.05233596 | 0.99862953 |
| 358 | -0.0348995 | 0.99939083 |
| 359 | -0.01745241 | 0.9998477 |
Другие таблицы