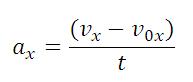Если ускорение отрицательное как найти расстояние

Отрицательное ускорение возникает , когда изменение или изменение скорости в течение определенного периода времени имеет более отрицательный знак. Наблюдайте за собакой на изображении, веселящейся на пляже. Песок замедляет его движение, а это означает, что есть ускорение, противоположное скорости, которую он несет.

Это ускорение можно рассматривать как отрицательное, в отличие от скорости, которая указывается как положительная. Хотя отрицательное ускорение не всегда вызывает снижение скорости.

Собака весело тормозит на песке. Ускорение при торможении можно рассматривать как отрицательное ускорение. Источник: Pixabay.

В одномерном движении направление движения обычно считается положительным, то есть направление скорости. Это то, что считалось ранее: у собаки на рисунке положительное направление – это то, которое идет от хвоста к голове.

Перед тем как погрузить лапы в песок, собака двигалась с определенной скоростью v вперед, то есть положительной. Затем песок замедляется до полной остановки, то есть до нулевой конечной скорости.

Предположим, что все это произошло за промежуток времени Δt. Ускорение за это время будет рассчитываться следующим образом:

В приведенном выше уравнении v> 0, Δt> 0, тогда a <0, то есть отрицательное ускорение (a <0). Поскольку вначале направление скорости было положительным, то отрицательное ускорение означает, что ускорение направлено в сторону от скорости. Таким образом, делается вывод, что:

Следовательно, мы можем установить, что:

• Когда скорость и ускорение имеют одинаковый знак, независимо от знака, скорость увеличивается. В таком случае скорость становится более положительной или более отрицательной, в зависимости от случая.
• Когда скорость и ускорение имеют противоположные знаки, скорость уменьшается.

Формулы для расчета ускорения

Независимо от знака, среднее ускорение a _m между моментами t и t ‘рассчитывается по следующей формуле:

Среднее ускорение предоставляет общую информацию о том, как изменилась скорость за рассматриваемый интервал времени. Со своей стороны, мгновенное ускорение дает подробную информацию о том, как скорость изменяется в каждый момент. Итак, для данного момента t ускорение рассчитывается по следующей формуле:

-Пример 1

В начальный момент t = 0,2 с объект имеет скорость 3 м / с. Позже, в момент t ‘= 0,4 с, он имеет скорость 1 м / с. Вычислите среднее ускорение между моментами времени t и t ‘и интерпретируйте результат.

Ответить

-Пример 2

В начальный момент t = 0,6 с объект имеет скорость -1 м / с. Впоследствии в момент t ‘= 0,8 с он имеет скорость -3 м / с. Вычислите среднее ускорение между моментами t и t ‘. Интерпретируйте результат.

Ответить

В заключение, в конце временного интервала скорость стала еще более отрицательной (-3 м / с).

Значит ли это, что мобильный телефон замедляет свое движение? Нет. Знак минус в скорости означает только то, что он движется назад и быстрее, поскольку скорость -3 м / с идет быстрее, чем -1 м / с, скорость, которая была в начале.

Скорость, которая является модулем скорости, увеличилась, несмотря на отрицательное ускорение. Я имею ввиду, этот объект ускорился. Отсюда делаем вывод:

-Пример 3-Вертикальное подбрасывание.

Рассмотрим следующий пример: объект имеет мгновенную скорость, заданную следующим выражением, со всеми единицами измерения Международной системы:

Найдите скорость и ускорение для времен 0 с, 0,5 с и 1,0 с. В каждом случае укажите, ускоряется или замедляется объект.

Ответить

Скорость в каждый из указанных моментов времени находится путем прямой подстановки t в уравнение. Ускорение находится путем получения данного выражения как функции времени и последующей оценки результата в каждый из заданных моментов времени.

Результаты следующие:

Ускорение постоянное и отрицательное для любого движения. Теперь можно описать, что случилось с мобильным телефоном в процессе его движения.

В момент t = 0 с мобиль замедлял ход. Это следует немедленно, поскольку скорость положительна, а ускорение отрицательна.

В момент t = 0,5 с мобиль остановился, по крайней мере, на мгновение покоился. Мобильный телефон может остановиться даже при ускорении. Самый наглядный пример – вертикальный бросок вверх.

Выпускники наклоняются вертикально к шапкам. Источник: Pexels.

Когда мобильный телефон проецируется вертикально вверх, ему удается достичь максимальной высоты. Если в этом смысле выбрано положительное направление, что происходит почти всегда, в течение времени, необходимого для достижения этой максимальной точки, мобильный телефон будет иметь положительную скорость.

Но гравитация существовала все время. И он всегда направлен вертикально вниз, независимо от того, идет ли объект вверх или вниз. Естественно, ей удается постепенно замедлять работу мобильного телефона, пока он не остановится на мгновение.

Мобайл немедленно меняет скорость и возвращается к земле. В этом случае скорость отрицательна, потому что она также указывает на землю. Следовательно, гравитация заставляет скорость увеличиваться все больше и больше.

Значение ускорения свободного падения оценивается в 9,8 м / с ² , которое для целей расчета округлено до 10 м / с ² . Объект в примере вполне мог быть брошен вверх с начальной скоростью 5 м / с.

Наконец, при t = 1,0 с скорость мобильного телефона отрицательна. Если это вертикальный старт вверх, при отсутствии трения это означает, что он снова проходит через начальную точку, но на этот раз он идет вниз, а не вверх.

В заключение, отрицательное ускорение не обязательно означает, что мобильный телефон тормозит. Напротив, мобильный телефон может работать все быстрее и быстрее. Нужно обратить внимание на то, совпадают ли признаки скорости и ускорения.

Ссылки

1. Уокер, Дж. 2010. Физика. Четвертое издание. Эддисон Уэсли. 26-30.

Ускорение

Говоря простым языком, ускорение — это скорость изменения скорости или изменение скорости за единицу времени.

Ускорение обозначается символом a:

a = ΔV/Δt или a = (V₁ — V₀)/(t₁ — t₀)

Ускорение, как и скорость, является векторной величиной.

Преобразуем формулу ускорения дальше:

a = ΔV/Δt = (ΔS/Δt)/Δt = ΔS/Δt 2

Ускорение — это расстояние, деленное на время в квадрате (м/с 2 ; км/с 2 ; см/с 2 …)

1. Положительное и отрицательное ускорение

Ускорение, как и скорость, обладает знаком.

Если автомобиль разгоняется, его скорость возрастает, а ускорение имеет положительный знак.

При торможении авто, его скорость уменьшается — ускорение имеет отрицательный знак.

Естественно, при равномерном движении ускорение равно нулю.

Но, будьте внимательны! Отрицательное ускорение не всегда означает замедление, а положительное — ускорение! Помните, что скорость (как и перемещение) — это векторная величина. Обратимся к нашему бильярдному шару.

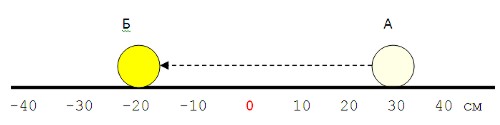
Пусть шар движется с замедлением, но имеет отрицательное перемещение!

Скорость шара уменьшается («минус») и скорость имеет отрицательную величину по направлению («минус»). В итоге, два «минуса» дадут «плюс» — положительное значение ускорения.

Запомните!

2. Среднее и мгновенное ускорение

По аналогии со скоростью ускорение может быть средним и мгновенным.

Среднее ускорение вычисляется как разность конечной и начальной скоростей, которая делится на разность конечного и начального времени:

Среднее ускорение отличается от фактического (мгновенного) ускорения в данный момент времени. Например, при резком нажатии педали тормоза автомобиль получает большое ускорение в первый момент времени. Если же водитель затем отпустит педаль тормоза, то ускорение уменьшится.

3. Равномерное и неравномерное ускорение

Описанный выше случай с торможением характеризует неравномерное ускорение — наиболее часто встречающееся в нашей повседневной жизни.

Однако, существует и равномерное ускорение, самый яркий пример которого — это ускорение свободного падения, которое равно 9,8 м/с 2 , направлено к центру Земли и всегда постоянно.

Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:

Код кнопки:
Политика конфиденциальности Об авторе

Источник

Отрицательное ускорение: формулы, расчет и решаемые упражнения

Содержание:

В отрицательное ускорение Он возникает, когда изменение или изменение скорости в течение определенного периода времени имеет отрицательный знак. Наблюдайте за собакой на изображении, веселящейся на пляже. Песок замедляет его движение, а это означает, что есть ускорение, противоположное скорости, которую он несет.

Это ускорение можно рассматривать как отрицательное, в отличие от скорости, которая указывается как положительная. Хотя отрицательное ускорение не всегда вызывает снижение скорости.

В одномерном движении направление движения обычно считается положительным, то есть направление скорости. Это то, что считалось ранее: у собаки на рисунке положительное направление — это то, которое идет от хвоста к голове.

Прежде чем погрузить лапы в песок, собака с некоторой скоростью приехала v вперед, это положительно. Затем песок замедляется до упора, то есть до нулевой конечной скорости.

Предположим, все это произошло за определенный период времени Δt. Ускорение за это время будет рассчитываться следующим образом:

В предыдущем уравнении v> 0, Δt> 0, тогда a 2 , которое для расчетов округлено до 10 м / с 2 . Объект в примере вполне мог быть брошен вверх с начальной скоростью 5 м / с.

Наконец, при t = 1,0 с скорость мобильного телефона отрицательна. Если это вертикальный бросок вверх, при отсутствии трения это означает, что он снова проходит через начальную точку, но на этот раз он идет вниз, а не вверх.

В заключение, отрицательное ускорение не обязательно означает, что мобильный телефон тормозит. Напротив, мобильный телефон может работать все быстрее и быстрее. Нужно обратить внимание на то, совпадают ли признаки скорости и ускорения.

Источник

Что такое отрицательное ускорение?

Отрицательное ускорение указывает, что скорость объекта изменяется в отрицательном направлении, что может означать, что он движется медленнее или быстрее. Термин «ускорение» используется в физике для описания изменения скорости объекта и представляет собой векторную величину, что означает, что он указывает как величину, так и направление. То, что движется с положительной скоростью, скорость также является вектором, а отрицательное ускорение замедляется. В отличие от этого, объект, который имеет отрицательное ускорение, а также отрицательную скорость, на самом деле движется быстрее.

Часто для кого-то легче понять ускорение в целом и отрицательное ускорение в частности, сначала понимая скорость. Хотя термины «скорость», «скорость» и «ускорение» иногда используются как синонимы в общем разговоре, эти три слова имеют совершенно разные значения применительно к физике. «Скорость» — это измерение того, как далеко объект проходит за определенный период времени, и часто выражается в милях в час (миль в час) или метрах в секунду (м / с).

«Скорость» аналогична скорости, но указывает не только фактическую скорость, но и направление, в котором движется объект, что делает его векторной величиной. Это означает, что объект, движущийся со скоростью 20 м / с, и другой, движущийся со скоростью -20 м / с, движутся с одинаковой скоростью, но в противоположных направлениях. «Ускорение» — это измерение, касающееся изменения скорости объекта, которое часто выражается в метрах в секунду, в секунду (м / с / с или м / с 2 ). Объект, движущийся в покое одну секунду, затем движущийся со скоростью 10 м / с в следующую секунду, 20 м / с в следующую и 30 м / с в следующую секунду, имеет ускорение 10 м / с 2, так как это изменение скорости ,

Один из самых простых способов увидеть отрицательное ускорение — это выбросить что-то в воздух. Когда брошенный объект покидает свою руку, он движется с определенной скоростью, например 40 м / с. Сила гравитации тянет вниз на объект, когда он движется вверх в положительном направлении, давая ему ускорение около -10 м / с 2 . Через одну секунду объект все еще движется со скоростью 30 м / с, еще через секунду он движется со скоростью 20 м / с, а еще через две секунды он останавливается, прежде чем продолжить ускорение вниз.

Отрицательное ускорение просто указывает направление ускорения и может означать, что скорость объекта увеличивается или уменьшается. Объект, движущийся с положительной скоростью, имеющий отрицательное ускорение, замедляется. С другой стороны, объект, который движется с отрицательным ускорением и с отрицательной скоростью, на самом деле движется быстрее. Этот же основной принцип также справедлив для положительного ускорения; когда направление скорости и ускорения одинаковы, объект движется быстрее, а когда они противоположны, объект замедляется.

Источник

ИНФОФИЗ — мой мир.

Весь мир в твоих руках — все будет так, как ты захочешь

Весь мир в твоих руках — все будет так, как ты захочешь

Как сказал.

Если вы студент, значит перед вами стоит тысяча возможностей. Найдите в себе силы, чтобы использовать хотя бы одну из них.

Для всех групп технического профиля

Список лекций по физике за 1,2 семестр

Я учу детей тому, как надо учиться

Часто сталкиваюсь с тем, что дети не верят в то, что могут учиться и научиться, считают, что учиться очень трудно.

Вопрос 2

Вопрос 2. Характеристики механического движения: перемещение, скорость, ускорение. Кинематические уравнения, связывающие перемещение, скорость и ускорение в векторной форме.

Перемещение тела — это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением.

Перемещение векторная величина. (перемещение – вектор, модуль перемещения – скаляр).

Единица измерения перемещения — метр [1 м].

Скорость равномерного прямолинейного движения — это векторная физическая величина, равная отношению перемещения тела S за любой промежуток времен к значению этого промежутка t:

Скорость показывает быстроту изменения координаты: v_х=(х-х₀)/t =Δх/t .

Единица измерения скорости — метр в секунду [1 м/с]

Ускорение — это векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.

Ускорение показывает, как быстро изменяетcя скорость тела. Если ускорение положительно, значит скорость тела увеличивается, движение ускоренное. Если ускорение отрицательно, значит скорость уменьшается, движение замедленное.

Если скорость изменяется одинаково в течение всего времени движения, то такое движение называют равнопеременным.

Тогда ускорение можно рассчитать по формуле:

v _х— конечная скорость тела при равноускоренном движении по прямой

v _0х— начальная скорость тела

a — ускорение тела

t — время движения тела

Единица измерения ускорения в СИ [м/с 2 ].

Ускорение измеряют акселерометром.

Уравнение равномерного движения (перемещение тела при равномерном движении):

Кинематическое уравнение скорости при равноускоренном движении по прямой:

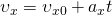
Кинематическое уравнение перемещения при равноускоренном движении по прямой:

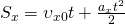
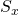— Перемещение тела при равноускоренном движении по прямой

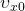— Начальная скорость тела

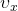— Скорость тела при равноускоренном движении по прямой

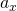— Ускорение тела

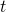— Время движения тела

Источник

Большая Энциклопедия Нефти и Газа

Отрицательное ускорение

Отрицательное ускорение при торможении, в также ускорение разгона при подъеме должны быть ограничены, исходя из условия прочности оборудования и напряжений в элементах перемещаемой бурильной колонны. [1]

Отрицательное ускорение при торможении, а также ускорение разгона при подъеме должны быть ограничены исходя из условия прочности оборудования и напряжений в элементах перемещаемой колонны. [2]

Отрицательное ускорение приводит к уменьшению скорости и тем самым силы сопротивления. [3]

Вследствие огромного отрицательного ускорения при торможении на очень коротком отрезке пути электроны испускают электромагнитные волны с очень большой частотой, порядка 1018 — 10 сек-1. Чем выше приложенное напряжение U, тем ббльшую скорость имеют электроны в момент удара, тем резче они тормозятся и тем более высокую частоту ( и соответственно более короткую длину волны) имеют испускаемые ими рентгеновы лучи. [4]

При отрицательном ускорении давление на стенку скважины может снижаться до значения ниже гидростатического. Эти изменения гидродинамического давления создают знакопеременные нагрузки на пласты. [5]

При отрицательном ускорении ( равномерно-замедленное движение) график скорости также изображается прямой линией, однако прямая наклонена в этом случае вниз. [6]

При отрицательном ускорении ( равнозамедленное движение) график скорости также изображается прямой линией, однако прямая наклонена в этом случае вниз. [8]

При отрицательном ускорении процесса старения СИ межремонтный период увеличивается. СИ работает до тех пор, пока морально не устареет. [9]

Наибольшие величины отрицательного ускорения при шк 12 56 рад / сек приняты в у олэ — 900 и / ОЛ8 — 800 см / сек. В этом случае, в результате расчета, получено, что ползун может двигаться ускоренно менее чем на х / 3 пути, а на остальном пути должен двигаться замедленно. [10]

Это соответствует наибольшему отрицательному ускорению . [11]

Движение с постоянным отрицательным ускорением называют равнозамедленным движением. [12]

В результате решения получается отрицательное ускорение , а в ответе оно положительное. [13]

Найти: 1) отрицательное ускорение поезда , 2) расстояние, пройденное им за время тормо — жения. [14]

Таким образом, наличие отрицательного ускорения при оптимальном движении уменьшает величину потребной тяги для горизонтального полета. [15]

Источник

Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.

При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:

Формула перемещения

Пример №1. По графику определить перемещение тела в момент времени t=3 с.

Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:

Извлекаем из графика необходимые данные:

• Фигура 1. Начальная скорость — 3 м/с. Конечная — 0 м/с. Время — 1,5 с.
• Фигура 2. Начальная скорость — 0 м/с. Конечная — –3 м/с. Время — 1,5 с (3 с – 1,5 с).

Подставляем известные данные в формулу:

Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.

Варианты записи формулы перемещения

Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:

v = v₀ ± at

В итоге получается формула:

Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».

Если начальная скорость равна 0 (v₀ = 0), эта формула принимает вид:

Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:

Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.

Перемещение при разгоне и торможении тела

Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают (а↑↑v). Если векторы имеют противоположное направление (а↑↓v), движение следует описывать в два этапа:

Этап торможения

Время торможения равно разности полного времени движения и времени второго этапа:

t₁ = t – t₂

Когда тело тормозит, через некоторое время t₁ оно останавливается. Поэтому скорость в момент времени t₁ равна 0:

0 = v₀₁ – at₁

При торможении перемещение s₁ равно:

Этап разгона

Время разгона равно разности полного времени движения и времени первого этапа:

t₂ = t – t₁

Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t₂ равна:

v = at₂

При разгоне перемещение s₂ равно:

При этом модуль перемещения в течение всего времени движения равен:

s = |s₁ – s₂|

Полный путь (обозначим его l), пройденный телом за оба этапа, равен:

l = s₁ + s₂

Пример №3. Мальчик пробежал из состояния покоя некоторое расстояние за 5 секунд с ускорением 1 м/с². Затем он тормозил до полной остановки в течение 2 секунд с другим по модулю ускорением. Найти этот модуль ускорения, если его тормозной путь составил 3 метра.

В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:

Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:

v₀₂ = v₀₁ + a₁t₁ = a₁t₁ (так как v₀₁ = 0)

Подставляем выраженные величины в формулу:

Перемещение в n-ную секунду прямолинейного равноускоренного движения

Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:

За первую секунду тело переместится на расстояние, равное:

За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:

За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:

Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:

Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:

Формула перемещения за n-ную секунду

Пример №4. Автомобиль разгоняется с ускорением 3 м/с^2. Найти его перемещение за 6 секунду.

Подставляем известные данные в формулу и получаем:

Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:

где t — время одного промежутка, а n — порядковый номер этого промежутка.

Пример №5. Ягуар ринулся за добычей с ускорением 2,5 м/с². Найти его перемещение за промежуток времени от 4 до 6 секунд включительно.

Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.

Подставляем известные данные в формулу:

Проекция и график перемещения

Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения сонаправлены (v↑↑a), принимает следующий вид:

График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно (v↓↑a), принимает следующий вид:

Определение направления знака проекции ускорения по графику его перемещения:

• Если ветви параболического графика смотрят вниз, проекция ускорения тела отрицательна.
• Если ветви параболического графика смотрят вверх, проекция ускорения тела положительна.

Пример №6. Определить ускорение тела по графику его перемещения.

Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:

Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:

График пути

График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.

В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:

• 1 часть — до момента, когда скорость тела принимает нулевое значение (v = 0). Эта часть графика является частью параболы от начала координат до ее вершины.
• 2 часть — после момента, при котором скорость тела принимает нулевое значение (v = 0). Эта часть является ветвью такой же, но перевернутой параболы. Ее вершина совпадает с вершиной предыдущей параболы, но ее ветвь направлена вверх.

Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.

Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.

При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:

Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

Алиса Никитина | Просмотров: 25.3k