Общее уравнение прямой: описание, примеры, решение задач
Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой. Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и как осуществлять переходы от общего уравнения к другим типам уравнений прямой. Всю теорию закрепим иллюстрациями и решением практических задач.
Общее уравнение прямой: основные сведения
Пусть на плоскости задана прямоугольная система координат O x y .
Любое уравнение первой степени, имеющее вид A x + B y + C = 0 , где А , В , С – некоторые действительные числа ( А и В не равны одновременно нулю) определяет прямую линию в прямоугольной системе координат на плоскости. В свою очередь, любая прямая в прямоугольной системе координат на плоскости определяется уравнением, имеющим вид A x + B y + C = 0 при некотором наборе значений А , В , С .
указанная теорема состоит из двух пунктов, докажем каждый из них.
- Докажем, что уравнение A x + B y + C = 0 определяет на плоскости прямую.
Пусть существует некоторая точка М 0 ( x 0 , y 0 ) , координаты которой отвечают уравнению A x + B y + C = 0 . Таким образом: A x 0 + B y 0 + C = 0 . Вычтем из левой и правой частей уравнений A x + B y + C = 0 левую и правую части уравнения A x 0 + B y 0 + C = 0 , получим новое уравнение, имеющее вид A ( x – x 0 ) + B ( y – y 0 ) = 0 . Оно эквивалентно A x + B y + C = 0 .
Полученное уравнение A ( x – x 0 ) + B ( y – y 0 ) = 0 является необходимым и достаточным условием перпендикулярности векторов n → = ( A , B ) и M 0 M → = ( x – x 0 , y – y 0 ) . Таким образом, множество точек M ( x , y ) задает в прямоугольной системе координат прямую линию, перпендикулярную направлению вектора n → = ( A , B ) . Можем предположить, что это не так, но тогда бы векторы n → = ( A , B ) и M 0 M → = ( x – x 0 , y – y 0 ) не являлись бы перпендикулярными, и равенство A ( x – x 0 ) + B ( y – y 0 ) = 0 не было бы верным.

Следовательно, уравнение A ( x – x 0 ) + B ( y – y 0 ) = 0 определяет некоторую прямую в прямоугольной системе координат на плоскости, а значит и эквивалентное ему уравнение A x + B y + C = 0 определяет ту же прямую. Так мы доказали первую часть теоремы.
- Приведем доказательство, что любую прямую в прямоугольной системе координат на плоскости можно задать уравнением первой степени A x + B y + C = 0 .
Зададим в прямоугольной системе координат на плоскости прямую a ; точку M 0 ( x 0 , y 0 ) , через которую проходит эта прямая, а также нормальный вектор этой прямой n → = ( A , B ) .
Пусть также существует некоторая точка M ( x , y ) – плавающая точка прямой. В таком случае, векторы n → = ( A , B ) и M 0 M → = ( x – x 0 , y – y 0 ) являются перпендикулярными друг другу, и их скалярное произведение есть нуль:
n → , M 0 M → = A ( x – x 0 ) + B ( y – y 0 ) = 0
Перепишем уравнение A x + B y – A x 0 – B y 0 = 0 , определим C : C = – A x 0 – B y 0 и в конечном результате получим уравнение A x + B y + C = 0 .
Так, мы доказали и вторую часть теоремы, и доказали всю теорему в целом.
Уравнение, имеющее вид A x + B y + C = 0 – это общее уравнение прямой на плоскости в прямоугольной системе координат O x y .
Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая.
Из доказательства теоремы также следует, что коэффициенты А и В при переменных x и y являются координатами нормального вектора прямой, которая задана общим уравнением прямой A x + B y + C = 0 .
Рассмотрим конкретный пример общего уравнения прямой.
Пусть задано уравнение 2 x + 3 y – 2 = 0 , которому соответствует прямая линия в заданной прямоугольной системе координат. Нормальный вектор этой прямой – это вектор n → = ( 2 , 3 ) . Изобразим заданную прямую линию на чертеже.

Также можно утверждать и следующее: прямая, которую мы видим на чертеже, определяется общим уравнением 2 x + 3 y – 2 = 0 , поскольку координаты всех точек заданной прямой отвечают этому уравнению.
Мы можем получить уравнение λ · A x + λ · B y + λ · C = 0 , умножив обе части общего уравнения прямой на число λ , не равное нулю. Полученное уравнение является эквивалентом исходного общего уравнения, следовательно, будет описывать ту же прямую на плоскости.
Неполное уравнение общей прямой
Полное общее уравнение прямой – такое общее уравнение прямой A x + B y + C = 0 , в котором числа А , В , С отличны от нуля. В ином случае уравнение является неполным.
Разберем все вариации неполного общего уравнения прямой.
- Когда А = 0 , В ≠ 0 , С ≠ 0 , общее уравнение принимает вид B y + C = 0 . Такое неполное общее уравнение задает в прямоугольной системе координат O x y прямую, которая параллельна оси O x , поскольку при любом действительном значении x переменная y примет значение – C B . Иначе говоря, общее уравнение прямой A x + B y + C = 0 , когда А = 0 , В ≠ 0 , задает геометрическое место точек ( x , y ) , координаты которых равны одному и тому же числу – C B .
- Если А = 0 , В ≠ 0 , С = 0 , общее уравнение принимает вид y = 0 . Такое неполное уравнение определяет ось абсцисс O x .
- Когда А ≠ 0 , В = 0 , С ≠ 0 , получаем неполное общее уравнение A x + С = 0 , задающее прямую, параллельную оси ординат.
- Пусть А ≠ 0 , В = 0 , С = 0 , тогда неполное общее уравнение примет вид x = 0 , и это есть уравнение координатной прямой O y .
- Наконец, при А ≠ 0 , В ≠ 0 , С = 0 , неполное общее уравнение принимает вид A x + B y = 0 . И это уравнение описывает прямую, которая проходит через начало координат. В самом деле, пара чисел ( 0 , 0 ) отвечает равенству A x + B y = 0 , поскольку А · 0 + В · 0 = 0 .
Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой.

Известно, что заданная прямая параллельна оси ординат и проходит через точку 2 7 , – 11 . Необходимо записать общее уравнение заданной прямой.
Решение
Прямая, параллельная оси ординат, задается уравнением вида A x + C = 0 , в котором А ≠ 0 . Также условием заданы координаты точки, через которую проходит прямая, и координаты этой точки отвечают условиям неполного общего уравнения A x + C = 0 , т.е. верно равенство:
Из него возможно определить C , если придать A какое-то ненулевое значение, к примеру, A = 7 . В таком случае получим: 7 · 2 7 + C = 0 ⇔ C = – 2 . Нам известны оба коэффициента A и C , подставим их в уравнение A x + C = 0 и получим требуемое уравнение прямой: 7 x – 2 = 0
Ответ: 7 x – 2 = 0
На чертеже изображена прямая, необходимо записать ее уравнение.

Решение
Приведенный чертеж позволяет нам легко взять исходные данные для решения задачи. Мы видим на чертеже, что заданная прямая параллельна оси O x и проходит через точку ( 0 , 3 ) .
Прямую, которая параллельна очи абсцисс, определяет неполное общее уравнение B y + С = 0 . Найдем значения B и C . Координаты точки ( 0 , 3 ) , поскольку через нее проходит заданная прямая, будут удовлетворять уравнению прямой B y + С = 0 , тогда справедливым является равенство: В · 3 + С = 0 . Зададим для В какое-то значение, отличное от нуля. Допустим, В = 1 , в таком случае из равенства В · 3 + С = 0 можем найти С : С = – 3 . Используем известные значения В и С , получаем требуемое уравнение прямой: y – 3 = 0 .
Ответ: y – 3 = 0 .
Общее уравнение прямой, проходящей через заданную точку плоскости
Пусть заданная прямая проходит через точку М 0 ( x 0 , y 0 ) , тогда ее координаты отвечают общему уравнению прямой, т.е. верно равенство: A x 0 + B y 0 + C = 0 . Отнимем левую и правую части этого уравнения от левой и правой части общего полного уравнения прямой. Получим: A ( x – x 0 ) + B ( y – y 0 ) + C = 0 , это уравнение эквивалентно исходному общему, проходит через точку М 0 ( x 0 , y 0 ) и имеет нормальный вектор n → = ( A , B ) .
Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой.
Даны точка М 0 ( – 3 , 4 ) , через которую проходит прямая, и нормальный вектор этой прямой n → = ( 1 , – 2 ) . Необходимо записать уравнение заданной прямой.
Решение
Исходные условия позволяют нам получить необходимые данные для составления уравнения: А = 1 , В = – 2 , x 0 = – 3 , y 0 = 4 . Тогда:
A ( x – x 0 ) + B ( y – y 0 ) = 0 ⇔ 1 · ( x – ( – 3 ) ) – 2 · y ( y – 4 ) = 0 ⇔ ⇔ x – 2 y + 22 = 0
Задачу можно было решить иначе. Общее уравнение прямой имеет вид A x + B y + C = 0 . Заданный нормальный вектор позволяет получить значения коэффициентов A и B , тогда:
A x + B y + C = 0 ⇔ 1 · x – 2 · y + C = 0 ⇔ x – 2 · y + C = 0
Теперь найдем значение С, используя заданную условием задачи точку М 0 ( – 3 , 4 ) , через которую проходит прямая. Координаты этой точки отвечают уравнению x – 2 · y + C = 0 , т.е. – 3 – 2 · 4 + С = 0 . Отсюда С = 11 . Требуемое уравнение прямой принимает вид: x – 2 · y + 11 = 0 .
Ответ: x – 2 · y + 11 = 0 .
Задана прямая 2 3 x – y – 1 2 = 0 и точка М 0 , лежащая на этой прямой. Известна лишь абсцисса этой точки, и она равна – 3 . Необходимо определить ординату заданной точки.
Решение
Зададим обозначение координат точки М 0 как x 0 и y 0 . В исходных данных указано, что x 0 = – 3 . Поскольку точка принадлежит заданной прямой, значит ее координаты отвечают общему уравнению этой прямой. Тогда верным будет равенство:
2 3 x 0 – y 0 – 1 2 = 0
Определяем y 0 : 2 3 · ( – 3 ) – y 0 – 1 2 = 0 ⇔ – 5 2 – y 0 = 0 ⇔ y 0 = – 5 2
Ответ: – 5 2
Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно
Как мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида.
Для начала рассмотрим переход от общего уравнения вида A x + B y + C = 0 к каноническому уравнению x – x 1 a x = y – y 1 a y .
Если А ≠ 0 , тогда переносим слагаемое B y в правую часть общего уравнения. В левой части выносим A за скобки. В итоге получаем: A x + C A = – B y .
Это равенство возможно записать как пропорцию: x + C A – B = y A .
В случае, если В ≠ 0 , оставляем в левой части общегь уравнения только слагаемое A x , прочие переносим в правую часть, получаем: A x = – B y – C . Выносим – В за скобки, тогда: A x = – B y + C B .
Перепишем равенство в виде пропорции: x – B = y + C B A .
Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому.
Задано общее уравнение прямой 3 y – 4 = 0 . Необходимо преобразовать его в каноническое уравнение.
Решение
Запишем исходное уравнение как 3 y – 4 = 0 . Далее действуем по алгоритму: в левой части остаётся слагаемое 0 x ; а в правой части выносим – 3 за скобки; получаем: 0 x = – 3 y – 4 3 .
Запишем полученное равенство как пропорцию: x – 3 = y – 4 3 0 . Так, мы получили уравнение канонического вида.
Ответ: x – 3 = y – 4 3 0 .
Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям.
Прямая задана уравнением 2 x – 5 y – 1 = 0 . Запишите параметрические уравнения этой прямой.
Решение
Осуществим переход от общего уравнения к каноническому:
2 x – 5 y – 1 = 0 ⇔ 2 x = 5 y + 1 ⇔ 2 x = 5 y + 1 5 ⇔ x 5 = y + 1 5 2
Теперь примем обе части полученного канонического уравнения равными λ , тогда:
x 5 = λ y + 1 5 2 = λ ⇔ x = 5 · λ y = – 1 5 + 2 · λ , λ ∈ R
Ответ: x = 5 · λ y = – 1 5 + 2 · λ , λ ∈ R
Общее уравнение можно преобразовать в уравнение прямой с угловым коэффициентом y = k · x + b , но только тогда, когда В ≠ 0 . Для перехода в левой части оставляем слагаемое B y , остальные переносятся в правую. Получим: B y = – A x – C . Разделим обе части полученного равенство на B , отличное от нуля: y = – A B x – C B .
Задано общее уравнение прямой: 2 x + 7 y = 0 . Необходимо преобразовать то уравнение в уравнение с угловым коэффициентом.
Решение
Произведем нужные действия по алгоритму:
2 x + 7 y = 0 ⇔ 7 y – 2 x ⇔ y = – 2 7 x
Ответ: y = – 2 7 x .
Из общего уравнения прямой достаточно просто получить уравнение в отрезках вида x a + y b = 1 . Чтобы осуществить такой переход, перенесем число C в правую часть равенства, разделим обе части полученного равенства на – С и, наконец, перенесем в знаменатели коэффициенты при переменных x и y :
A x + B y + C = 0 ⇔ A x + B y = – C ⇔ ⇔ A – C x + B – C y = 1 ⇔ x – C A + y – C B = 1
Необходимо преобразовать общее уравнение прямой x – 7 y + 1 2 = 0 в уравнение прямой в отрезках.
Решение
Перенесем 1 2 в правую часть: x – 7 y + 1 2 = 0 ⇔ x – 7 y = – 1 2 .
Разделим на -1/2 обе части равенства: x – 7 y = – 1 2 ⇔ 1 – 1 2 x – 7 – 1 2 y = 1 .
Преобразуем далее в необходимый вид: 1 – 1 2 x – 7 – 1 2 y = 1 ⇔ x – 1 2 + y 1 14 = 1 .
Ответ: x – 1 2 + y 1 14 = 1 .
В общем, несложно производится и обратный переход: от прочих видов уравнения к общему.
Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства:
x a + y b ⇔ 1 a x + 1 b y – 1 = 0 ⇔ A x + B y + C = 0 y = k x + b ⇔ y – k x – b = 0 ⇔ A x + B y + C = 0
Каноническое уравнение преобразуется к общему по следующей схеме:
x – x 1 a x = y – y 1 a y ⇔ a y · ( x – x 1 ) = a x ( y – y 1 ) ⇔ ⇔ a y x – a x y – a y x 1 + a x y 1 = 0 ⇔ A x + B y + C = 0
Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x – x 1 a x = y – y 1 a y ⇔ A x + B y + C = 0
Заданы параметрические уравнения прямой x = – 1 + 2 · λ y = 4 . Необходимо записать общее уравнение этой прямой.
Решение
Осуществим переход от параметрических уравнений к каноническому:
x = – 1 + 2 · λ y = 4 ⇔ x = – 1 + 2 · λ y = 4 + 0 · λ ⇔ λ = x + 1 2 λ = y – 4 0 ⇔ x + 1 2 = y – 4 0
Перейдем от канонического к общему:
x + 1 2 = y – 4 0 ⇔ 0 · ( x + 1 ) = 2 ( y – 4 ) ⇔ y – 4 = 0
Ответ: y – 4 = 0
Задано уравнение прямой в отрезках x 3 + y 1 2 = 1 . Необходимо осуществить переход к общему виду уравнения.
Решение:
Просто перепишем уравнение в необходимом виде:
x 3 + y 1 2 = 1 ⇔ 1 3 x + 2 y – 1 = 0
Ответ: 1 3 x + 2 y – 1 = 0 .
Составление общего уравнения прямой
Выше мы говорили о том, что общее уравнение возможно записать при известных координатах нормального вектора и координатах точки, через которую проходит прямая. Такая прямая определяется уравнением A ( x – x 0 ) + B ( y – y 0 ) = 0 . Там же мы разобрали соответствующий пример.
Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора.
Задана прямая, параллельная прямой 2 x – 3 y + 3 3 = 0 . Также известна точка M 0 ( 4 , 1 ) , через которую проходит заданная прямая. Необходимо записать уравнение заданной прямой.
Решение
Исходные условия говорят нам о том, что прямые параллельны, тогда, как нормальный вектор прямой, уравнение которой требуется записать, возьмем направляющий вектор прямой n → = ( 2 , – 3 ) : 2 x – 3 y + 3 3 = 0 . Теперь нам известны все необходимые данные, чтобы составить общее уравнение прямой:
A ( x – x 0 ) + B ( y – y 0 ) = 0 ⇔ 2 ( x – 4 ) – 3 ( y – 1 ) = 0 ⇔ 2 x – 3 y – 5 = 0
Ответ: 2 x – 3 y – 5 = 0 .
Заданная прямая проходит через начало координат перпендикулярно прямой x – 2 3 = y + 4 5 . Необходимо составить общее уравнение заданной прямой.
Решение
Нормальный вектором заданной прямой будет направляющий вектор прямой x – 2 3 = y + 4 5 .
Тогда n → = ( 3 , 5 ) . Прямая проходит через начало координат, т.е. через точку О ( 0 , 0 ) . Составим общее уравнение заданной прямой:
A ( x – x 0 ) + B ( y – y 0 ) = 0 ⇔ 3 ( x – 0 ) + 5 ( y – 0 ) = 0 ⇔ 3 x + 5 y = 0
Прямая линия. Уравнение прямой.
Свойства прямой в евклидовой геометрии.
Через любую точку можно провести бесконечно много прямых.
Через любые две несовпадающие точки можно провести единственную прямую.
Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются
параллельными (следует из предыдущего).
В трёхмерном пространстве существуют три варианта взаимного расположения двух прямых:
- прямые пересекаются;
- прямые параллельны;
- прямые скрещиваются.
Прямая линия — алгебраическая кривая первого порядка: в декартовой системе координат прямая линия
задается на плоскости уравнением первой степени (линейное уравнение).
Общее уравнение прямой.
Определение. Любая прямая на плоскости может быть задана уравнением первого порядка
причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим
уравнением прямой. В зависимости от значений постоянных А, В и С возможны следующие частные случаи:
• C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат
• А = 0, В ≠0, С ≠0 – прямая параллельна оси Ох
• В = 0, А ≠0, С ≠ 0 – прямая параллельна оси Оу
• В = С = 0, А ≠0 – прямая совпадает с осью Оу
• А = С = 0, В ≠0 – прямая совпадает с осью Ох
Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных
Уравнение прямой по точке и вектору нормали.
Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В)
перпендикулярен прямой , заданной уравнением
Пример. Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору (3, -1).
Решение. Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С
подставим в полученное выражение координаты заданной точки А. Получаем: 3 – 2 + C = 0, следовательно
С = -1. Итого: искомое уравнение: 3х – у – 1 = 0.
Уравнение прямой, проходящей через две точки.
Пусть в пространстве заданы две точки M 1 ( x 1 , y 1 , z 1 ) и M2 ( x 2, y 2 , z 2 ), тогда уравнение прямой,
проходящей через эти точки:
Если какой-либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель. На
плоскости записанное выше уравнение прямой упрощается:
Дробь = k называется угловым коэффициентом прямой.
Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).
Решение. Применяя записанную выше формулу, получаем:
Уравнение прямой по точке и угловому коэффициенту.
Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:
и обозначить , то полученное уравнение называется
уравнением прямой с угловым коэффициентом k.
Уравнение прямой по точке и направляющему вектору.
По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание
прямой через точку и направляющий вектор прямой.
Определение. Каждый ненулевой вектор (α1, α2), компоненты которого удовлетворяют условию
Аα1 + Вα2 = 0 называется направляющим вектором прямой.
Пример. Найти уравнение прямой с направляющим вектором (1, -1) и проходящей через точку А(1, 2).
Решение. Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением,
коэффициенты должны удовлетворять условиям:
1 * A + (-1) * B = 0, т.е. А = В.
Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C / A = 0.
при х = 1, у = 2 получаем С/ A = -3, т.е. искомое уравнение:
Уравнение прямой в отрезках.
Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С, получим:
или , где
Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения
прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.
Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках.
С = 1, , а = -1, b = 1.
Нормальное уравнение прямой.
Если обе части уравнения Ах + Ву + С = 0 разделить на число , которое называется
нормирующем множителем, то получим
xcosφ + ysinφ – p = 0 – нормальное уравнение прямой.
Уравнение прямой

Уравнение прямой на плоскости
Любую прямую на плоскости можно задать уравнением прямой первой степени вида
где A и B не могут быть одновременно равны нулю.

Уравнение прямой с угловым коэффициентом
Общее уравнение прямой при B≠0 можно привести к виду
где k – угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ.

Уравнение прямой в отрезках на осях
Если прямая пересекает оси OX и OY в точках с координатами ( a , 0) и (0, b ), то она может быть найдена используя формулу уравнения прямой в отрезках
Уравнение прямой, проходящей через две различные точки на плоскости
Если прямая проходит через две точки M( x 1, y 1) и N( x 2, y 2), такие что x 1 ≠ x 2 и y 1 ≠ y 2, то уравнение прямой можно найти, используя следующую формулу
| x – x 1 | = | y – y 1 |
| x 2 – x 1 | y 2 – y 1 |

Параметрическое уравнение прямой на плоскости
Параметрические уравнения прямой могут быть записаны следующим образом
x = l t + x 0 y = m t + y 0
где N( x 0, y 0) – координаты точки лежащей на прямой, a = < l , m >- координаты направляющего вектора прямой.
Каноническое уравнение прямой на плоскости
Если известны координаты точки N( x 0, y 0) лежащей на прямой и направляющего вектора a = ( l и m не равны нулю), то уравнение прямой можно записать в каноническом виде, используя следующую формулу
Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки
x – 1 2 – 1 = y – 7 3 – 7
Упростив это уравнение получим каноническое уравнение прямой
Выразим y через x и получим уравнение прямой с угловым коэффициентом
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
x = t + 1 y = -4 t + 7
Решение. Так как M y – N y = 0, то невозможно записать уравнение прямой проходящей через две точки.
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
Уравнение прямой в пространстве
Уравнение прямой, проходящей через две различные точки в пространстве
Если прямая проходит через две точки M( x 1, y 1, z 1) и N( x 2, y 2, z 2), такие что x 1 ≠ x 2, y 1 ≠ y 2 и z 1 ≠ z 2, то уравнение прямой можно найти используя следующую формулу
| x – x 1 | = | y – y 1 | = | z – z 1 |
| x 2 – x 1 | y 2 – y 1 | z 2 – z 1 |
Параметрическое уравнение прямой в пространстве
Параметрические уравнения прямой могут быть записаны следующим образом
 |
x = l t + x 0 |
| y = m t + y 0 | |
| z = n t + z 0 |
где ( x 0, y 0, z 0) – координаты точки лежащей на прямой, – координаты направляющего вектора прямой.
Каноническое уравнение прямой в пространстве
Если известны координаты точки M( x 0, y 0, z 0) лежащей на прямой и направляющего вектора n = , то уравнение прямой можно записать в каноническом виде, используя следующую формулу
| x – x 0 | = | y – y 0 | = | z – z 0 |
| l | m | n |
Прямая как линия пересечения двух плоскостей
Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений
[spoiler title=”источники:”]
http://www.calc.ru/Uravneniye-Pryamoy.html
http://ru.onlinemschool.com/math/library/analytic_geometry/line/
[/spoiler]
Excelsior
Просветленный
(43602)
11 лет назад
Переформулируйте вопрос более аккуратно. Длина прямой бесконечна.
Вообще же, длина участка кривой между точками, задаваемыми значениями параметра а и b, вычисляется по формуле:

Альберт Хаимов
Мастер
(1599)
11 лет назад
Конечно, длину прямой вычислить нельзя. А вот длину отрезка между двумя точками вполне возможно. Если координаты первой и второй точек обозначить соответственно (Х₁; У₁) и (Х₂; У₂), то длина отрезка вычисляется по формуле:
S = √(Х₂ – Х₁)² + (У₂ – У₁)²
Содержание:
Прямая:
Прямая бесконечна (в обе стороны) и разбивает плоскость на две полуплоскости (рис. 24), для которых прямая является границей. Граница принадлежит полуплоскостям. На рисунке 25 точка С лежит на прямой между точками А и В, которые лежат по разные стороны от точки С. Точки С и В лежат по одну сторону от точки А. Из трех точек на прямой одна и только одна точка лежит между двумя другими.
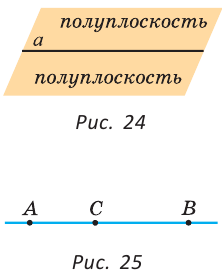
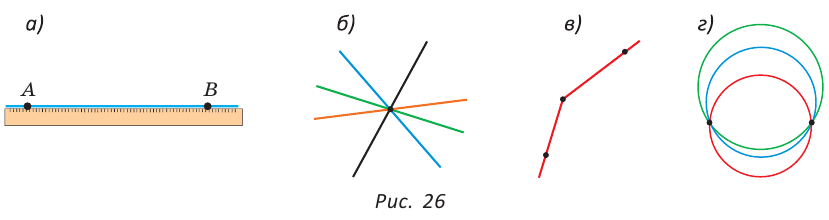
Если на плоскости отметить две точки А и В, то через них всегда можно провести прямую АВ (рис. 26, а). Через одну точку можно провести бесконечно много прямых (рис. 26, б), через три точки не всегда можно провести прямую (рис. 26, в). Через две точки можно провести бесконечно много окружностей (рис. 26, г), а прямую — только одну!
Аксиома прямой. Через любые две точки плоскости можно провести прямую, и притом только одну.
Из аксиомы следует, что если две прямые (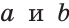 ) имеют общую точку (М), то это единственная общая точка (рис. 27). Если предположить, что существует еще одна общая точка (К), то тогда через две точки (М и К) пройдут две прямые, что по аксиоме прямой невозможно.
) имеют общую точку (М), то это единственная общая точка (рис. 27). Если предположить, что существует еще одна общая точка (К), то тогда через две точки (М и К) пройдут две прямые, что по аксиоме прямой невозможно.
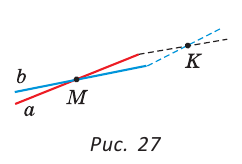
Определение. Две прямые называются пересекающимися, если они имеют общую точку.
Определение. Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.
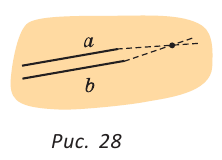
Если прямые 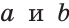 параллельны, то отрезки, изображающие эти прямые, никогда не пересекутся, сколько бы их ни продолжали (рис. 28).
параллельны, то отрезки, изображающие эти прямые, никогда не пересекутся, сколько бы их ни продолжали (рис. 28).
Луч:
Определение. Лучом называется часть прямой, ограниченная одной точкой.
Точка, ограничивающая луч, принадлежит лучу и называется началом луча. Луч бесконечен (в одну сторону). Он обозначается одной малой буквой, или двумя большими буквами, где первой всегда записывается начало луча.
При этом вторая точка может быть не отмечена на луче. Она указывает направление луча, например как точка В на луче АВ (рис. 29).

Определение. Два луча называются дополнительными (противоположными), если они имеют общее начало и лежат на одной прямой.
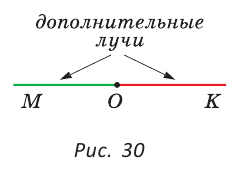
На рисунке 30 изображены дополнительные дополнительные лучи ОМ и ОК. Они дополняют друг друга до прямой. Чтобы построить луч, дополнительный данному, достаточно продлить данный луч за его начало вдоль прямой, на которой лежит данный луч. Любая точка прямой разбивает ее на два дополнительных луча.
Отрезок:
Определение. Отрезком называется часть прямой, ограниченная двумя точками.
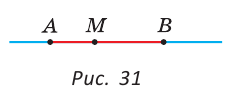
Точки, ограничивающие отрезок, принадлежат отрезку и называются концами отрезка, остальные точки отрезка — его внутренними точками. На рисунке 31 изображен отрезок АВ с концами А и В. Точка М — внутренняя точка отрезка АВ.
Если концы отрезка лежат в разных полуплоскостях относительно прямой, то этот отрезок пересекает прямую, если в одной полуплоскости — то не пересекает. На рисунке 32 концы отрезка АВ лежат в разных полуплоскостях относительно прямой а, и он пересекает прямую 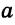 . Концы же отрезка CD лежат в одной полуплоскости, и он не пересекает прямую
. Концы же отрезка CD лежат в одной полуплоскости, и он не пересекает прямую 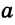 .
.
Если при наложении отрезков их концы совпадут, то по аксиоме прямой эти отрезки совпадут всеми своими точками.
Определение. Два отрезка называются равными, если их можно совместить наложением.
Важной характеристикой отрезка является его длина.
Свойства длины отрезка: каждый отрезок имеет длину, выраженную положительным числом; равным отрезкам соответствуют равные длины, большему отрезку — большая длина. И наоборот.
Аксиома измерения отрезков. Если на отрезке взять точку, то она разобьет данный отрезок на два отрезка, сумма длин которых равна длине данного отрезка.
Аксиома откладывания отрезков. На любом луче от его вершины можно отложить отрезок данной длины, и притом только один.
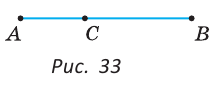
На рисунке 33 точка С лежит на отрезке АВ. По аксиоме измерения отрезков следует, что АС + СВ=АВ.
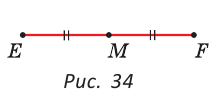
Серединой отрезка называется точка, которая делит отрезок на два равных отрезка. На рисунке 34 точка М — середина отрезка EF, то есть ЕМ = MF.
Определение. Расстоянием между двумя точками называется длина отрезка, соединяющего эти точки.
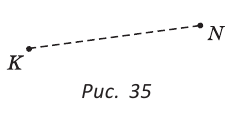
На рисунке 35 расстояние между точками К и N равно длине отрезка KN.
Ломаная:
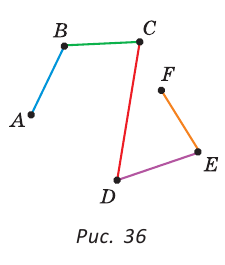
На рисунке 36 отрезки АВ, ВС, CD, DE и EF последовательно соединены своими концами: отрезок ВС соединен с отрезком АВ, отрезок CD соединен с отрезком ВС и так далее. Полученная фигура представляет собой ломаную ABCDEF. Указанные отрезки называются звеньями ломаной, а точки А, В, С, D, Е и F — вершинами ломаной.
Определение. Ломаной называется геометрическая фигура, образованная отрезками, последовательно соединенными своими концами, у которой никакие два соседних звена не лежат на одной прямой. Длиной ломаной называется сумма длин ее звеньев.
Определение. Ломаная называется замкнутой, если начало ее первого звена совпадает с концом последнего. В противном случае она называется незамкнутой. Ломаная называется простой, если она не имеет самопересечений и никакие два ее звена, кроме соседних, не имеют общих точек. В противном случае она называется непростой (рис. 37).
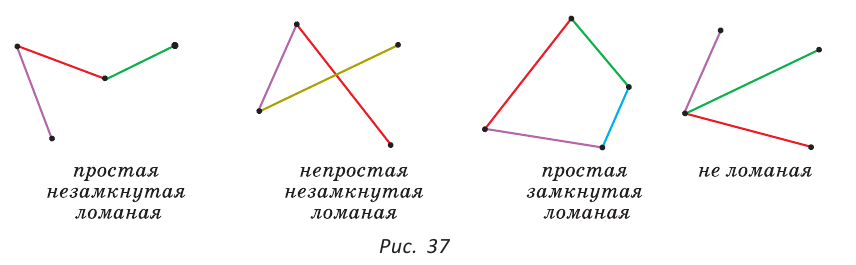
Простая замкнутая ломаная на плоскости называется многоугольником. Звенья этой ломаной называются сторонами этого многоугольника, а вершины — вершинами многоугольника. Периметром многоугольника называется сумма длин его сторон. Часть плоскости, ограниченная многоугольником, называется плоским многоугольником. Слово «плоский» употреблять не будем. Отрезок, соединяющий вершины многоугольника, не принадлежащие одной стороне, называется его диагональю. Если у многоугольника три стороны, то у него три вершины и три угла, и он называется треугольником, если четыре стороны — четырехугольником, если пять — пятиугольником и так далее.
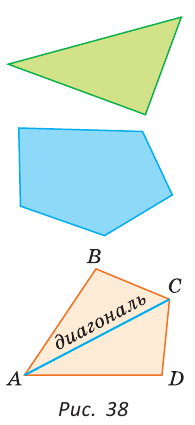
На рисунке 38 изображен четырехугольник ABCD со сторонами АВ, ВС, CD и AD. У него четыре угла: 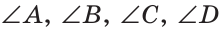 и две диагонали: АС и BD. Периметр этого четырехугольника:
и две диагонали: АС и BD. Периметр этого четырехугольника: 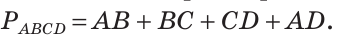
При записи многоугольника его вершины записываются последовательно, начиная с любой вершины и в любом направлении. Например, СBAD — это тот же четырехугольник ABCD.
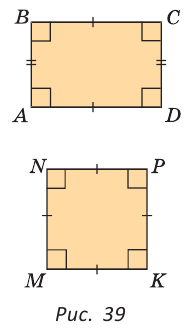
Самые известные четырехугольники — это прямоугольник и квадрат. У прямоугольника все углы прямые, а противоположные стороны равны. Квадрат — это прямоугольник, у которого все стороны равны. На рисунке 39 ABCD — прямоугольник, MNPK — квадрат. Позже мы дадим определение прямоугольника и квадрата и рассмотрим их свойства подробно. А пока будем пользоваться указанными представлениями.
Пример:
На отрезке АВ, равном 24 см, взята точка С. Отрезок АС на 6 см больше отрезка СВ. Найти длину отрезка АС.
Решение:
Пусть СВ = 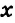 см, тогда АС =
см, тогда АС = 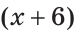 см.
см.
По аксиоме измерения отрезков 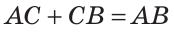 (рис. 40).
(рис. 40).
То есть, 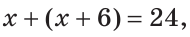
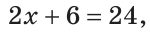
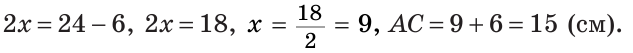
Ответ: 15 см.
Замечание. В дальнейшем при решении задач не будем ссылаться на аксиому измерения отрезков.
Пример:
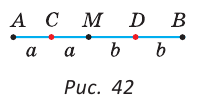
На отрезке АВ отмечены точки С и D (рис. 41). Найти длину отрезка CD, если:
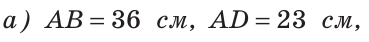
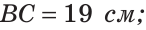
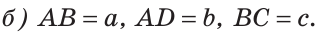
Решение:
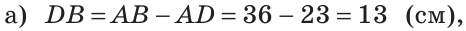
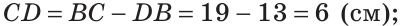
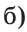 Если сложить отрезки AD и ВС, то получим отрезок АВ плюс отрезок CD. Отсюда
Если сложить отрезки AD и ВС, то получим отрезок АВ плюс отрезок CD. Отсюда 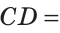
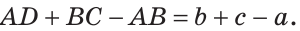
Ответ: а) 6 см; б) 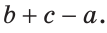
Пример:
На отрезке АВ, равном 42 см, взята точка М. Найти расстояние между серединами отрезков AM и MB.
Решение:
Пусть С — середина отрезка AM, D — середина отрезка MB.
Обозначим 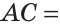
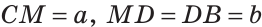 (рис. 42).
(рис. 42).
Тогда 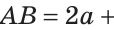
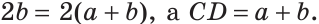
Следовательно, 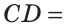
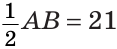 (см).
(см).
Ответ: 21 см.
Замечание. В данной задаче мы доказали свойство: «Если на отрезке отмечена точка, то расстояние между серединами полученных отрезков равно половине данного отрезка». Утверждения, которые будут доказаны нами в ключевых задачах, могут в дальнейшем использоваться как известные свойства.
Прямая в высшей математике
Прямая L в пространстве может быть однозначно определена, если известна точка, принадлежащая прямой, и ненулевой вектор, параллельный прямой (направляющий вектор прямой). Пусть задана такая точка 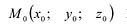 и вектор
и вектор 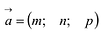 (Рис. 5.1).
(Рис. 5.1).
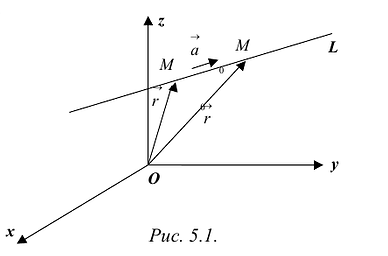
Если М(х, у, z) – произвольная текущая точка прямой L, то вектор 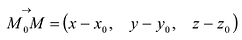 коллииеарен вектору
коллииеарен вектору 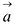 и их соответствующие координаты пропорциональны.
и их соответствующие координаты пропорциональны.
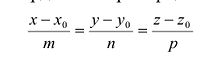
Этим соотношениям удовлетворяют координаты любой точки прямой L и только этой прямой. Равенства (5.1) называются каноническими уравнениями прямой в пространстве.
Обозначим 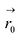 радиус-вектор точки
радиус-вектор точки 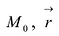 – радиус-вектор точки М. Тогда:
– радиус-вектор точки М. Тогда:
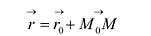 (5.2)
(5.2)
В силу коллинеарности векторов 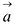 и
и 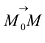 существует число
существует число 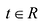 такое, что
такое, что 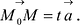 Тогда из (5.2) получим векторное параметрическое уравнение прямой:
Тогда из (5.2) получим векторное параметрическое уравнение прямой:
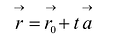 (5-3)
(5-3)
В координатной форме уравнение (5.3) равносильно трем уравнениям:
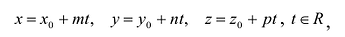 (5.4)
(5.4)
которые называются параметрическими уравнениями прямой в пространстве.
Исключая из уравнений (5.4) параметр t, легко перейти к каноническим уравнениям прямой (5.1).
Обратный переход от (5.1) к (5.4) осуществляют, приравнивая каждое из трех соотношений (5.1) к t. При этом, если знаменатель какого-либо соотношения равен нулю, то необходимо приравнять к нулю его числитель.
Пусть заданы точки 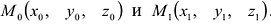 . Составим уравнение прямой, проходящей через заданные точки, пользуясь рис. 5.1.
. Составим уравнение прямой, проходящей через заданные точки, пользуясь рис. 5.1.
Очевидно, что в этом случае направляющим вектором прямой L будет вектор 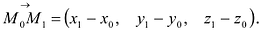 . Используя (5.1), получаем искомые уравнения в виде:
. Используя (5.1), получаем искомые уравнения в виде:
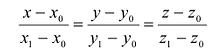
Прямую L в пространстве можно определить как пересечение двух плоскостей. Рассматривая совместно уравнения этих плоскостей, получим уравнение линии L в общем виде:
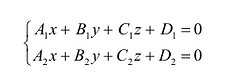 (5.6)
(5.6)
Система двух уравнений первой степени (5.6) определяет прямую линию при условии, что нормальные векторы 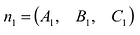 и
и 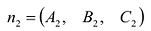 неколлинеарны. Только в этом случае плоскости будут пересекаться. Уравнения (5.6) носят название «общее уравнение прямой в пространстве».
неколлинеарны. Только в этом случае плоскости будут пересекаться. Уравнения (5.6) носят название «общее уравнение прямой в пространстве».
Чтобы перейти от общих уравнений прямой (5.6) к ее каноническим уравнениям (5.1), нужно на прямой найти какую-нибудь точку 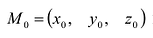 и определить ее направляющий вектор
и определить ее направляющий вектор 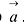 .
.
Точку 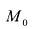 находят, давая произвольное значение одной из переменных х, у или z. Решая систему (5.6), получают значения оставшихся двух переменных.
находят, давая произвольное значение одной из переменных х, у или z. Решая систему (5.6), получают значения оставшихся двух переменных.
Направляющий вектор 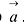 параллелен линии пересечения плоскостей (5.6) и, следовательно, перпендикулярен обоим нормальным векторам плоскостей:
параллелен линии пересечения плоскостей (5.6) и, следовательно, перпендикулярен обоим нормальным векторам плоскостей:
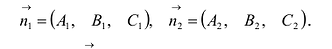
Поэтому в качестве 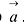 можно взять вектор:
можно взять вектор: 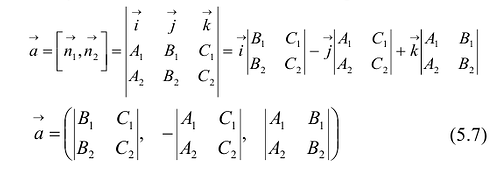
- Заказать решение задач по высшей математике
Понятие прямой
Нормальным вектором прямой называется любой вектор, перпендикулярный прямой.
Направляющим вектором прямой называется любой вектор, лежащий на этой прямой.
Взаимное расположение прямых
Пусть даны две прямые: 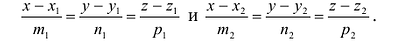
Эти прямые заданы своими точками 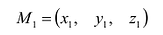 и
и 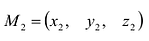 направляющими векторами
направляющими векторами 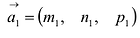 и
и 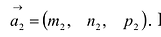 Поэтому:
Поэтому:
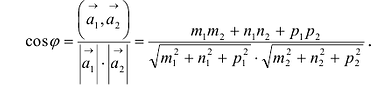
Параллельность или перпендикулярность прямых равносильна, соответственно, параллельности или перпендикулярности их направляющих векторов. Поэтому условие перпендикулярности прямых можно записать в виде:
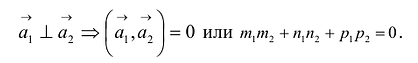
Условие параллельности: 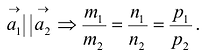
Возможны четыре случая взаимного расположения прямых:
Условие (5.8) выполняется в случаях I-III и означает, что прямые лежат в одной плоскости.
Уравнения прямой на плоскости
1. Па плоскости Оху составим уравнение прямой l, проходящей через точку 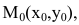 с нормальным вектором n=(А,В) (рис.6).
с нормальным вектором n=(А,В) (рис.6).
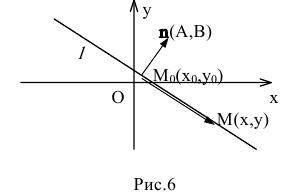 Возьмем любую точку М(х,у), лежащую на прямой l, и рассмотрим вектор
Возьмем любую точку М(х,у), лежащую на прямой l, и рассмотрим вектор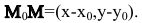 Векторы
Векторы 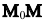 и n будут взаимно перпендикулярными по определению нормального вектора:
и n будут взаимно перпендикулярными по определению нормального вектора: 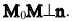 Следовательно, их скалярное произведение будет равно нулю:
Следовательно, их скалярное произведение будет равно нулю: 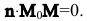
В координатной форме это равенство примет вид:
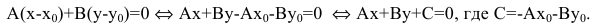
Уравнение Ах+Ву+С=0, где А и В не равны одновременно нулю 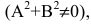 называется общим уравнением прямой.
называется общим уравнением прямой.
Если 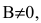 то это уравнение можно представить в виде уравнения с угловым коэффициентом:
то это уравнение можно представить в виде уравнения с угловым коэффициентом:
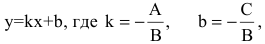
притом 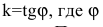 – угол наклона прямой к оси Ох.
– угол наклона прямой к оси Ох.
Вывод. Прямая на плоскости однозначно определяется точкой и нормальным вектором.
2. Па плоскости Оху составим уравнение прямой l, проходящей через точку 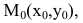 с направляющим вектором
с направляющим вектором 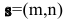 (рис.7).
(рис.7).
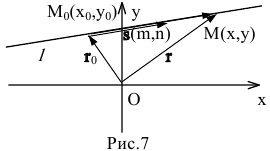
Пусть М(х,у) – произвольная точка прямой l, 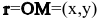 – ее радиус-вектор, а
– ее радиус-вектор, а 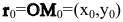 – радиус-вектор точки
– радиус-вектор точки 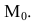 Тогда по правилу треугольника имеем:
Тогда по правилу треугольника имеем:
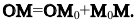
Так как векторы 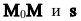 коллинеарны, то
коллинеарны, то 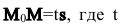 – некоторое число, называемое параметром. Подставляя это выражение в уравнение, получаем векторное уравнение прямой:
– некоторое число, называемое параметром. Подставляя это выражение в уравнение, получаем векторное уравнение прямой:
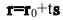
или в координатной форме параметрические уравнения прямой:
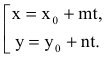
Пусть m и n отличны от нуля. Разрешим каждое из уравнений относительно t: 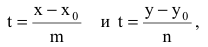
откуда получаем каноническое уравнение прямой:
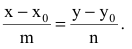
Пусть прямая l проходит через две точки 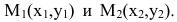 Тогда в качестве направляющего вектора прямой можно взять вектор
Тогда в качестве направляющего вектора прямой можно взять вектор 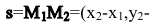
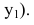 Составим уравнение прямой, проходящей через две точки:
Составим уравнение прямой, проходящей через две точки:
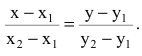
Вывод. Прямая однозначно определяется точкой и направляющим вектором.
Пример:
Вершины треугольника находятся в точках А(2,2), В(1,-2), С(-1,0). Найти проекцию точки А на основание ВС.
Решение:
Построим чертеж.
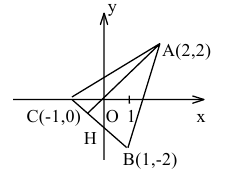
Проекция точки А на ВС есть точка пересечения основания ВС с перпендикуляром, опущенным из А на ВС.
Составим уравнение прямой ВС по двум точкам:
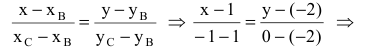
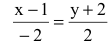 – каноническое уравнение прямой ВС
– каноническое уравнение прямой ВС 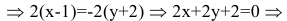
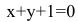 – общее уравнение прямой ВС.
– общее уравнение прямой ВС.
Обозначим искомую проекцию точкой Н(х,у). Т.к. 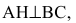 то скалярное произведение векторов
то скалярное произведение векторов
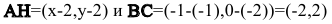 равно нулю:
равно нулю: 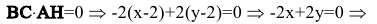
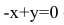 – общее уравнение прямой АН.
– общее уравнение прямой АН.
Теперь найдем проекцию точки А на основание ВС. Для этого решим систему: 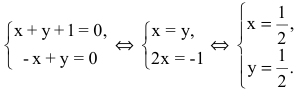 Следовательно,
Следовательно, 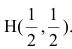 Задача решена.
Задача решена.
Замечание. Уравнение прямой АН можно было находить другими способами. Например, из общего уравнения прямой ВС х+у+1=0 можно выписать координаты нормального вектора 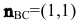 (коэффициенты при х и у соответственно). Т.к.
(коэффициенты при х и у соответственно). Т.к. 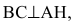 то нормальный вектор прямой ВС будет являться направляющим вектором прямой АН:
то нормальный вектор прямой ВС будет являться направляющим вектором прямой АН: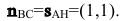
По нормальному вектору 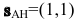 и точке А(2,2) составляем каноническое уравнение прямой АН:
и точке А(2,2) составляем каноническое уравнение прямой АН:
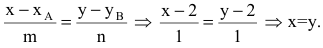
Уравнения прямой в пространстве
Уравнения прямой l, проходящей через точку 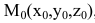 с направляющим вектором
с направляющим вектором 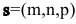 в пространстве Oxyz составляются аналогичным плоскости образом.
в пространстве Oxyz составляются аналогичным плоскости образом.
Пусть M(x,y,z) – произвольная точка прямой 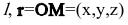 – ее радиус-вектор, a
– ее радиус-вектор, a 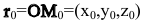 – радиус-вектор точки
– радиус-вектор точки 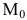 (рис.8).
(рис.8).
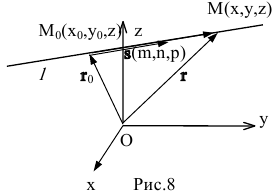
Тогда векторное уравнение прямой останется прежним: 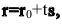 где t – параметр.
где t – параметр.
Параметрические уравнения прямой примут вид:
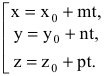
В случае 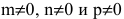 выразим канонические уравнения прямой:
выразим канонические уравнения прямой:
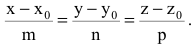
Наконец, составим уравнения прямой, проходящей через две точки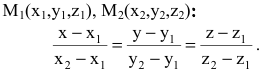
Внимание! В пространстве точка и нормальный вектор однозначным образом определяют плоскость. Поэтому в пространстве общие уравнения прямой будут задаваться линией пересечения двух плоскостей.
- Плоскость – определение, виды и правила
- Кривые второго порядка
- Евклидово пространство
- Матрица – виды, операции и действия с примерами
- Корень из числа – нахождение и вычисление
- Теория множеств – виды, операции и примеры
- Числовые множества
- Вектор – определение и основные понятия
Справедливо
следующее утверждение: если на плоскости
![]()
фиксирована произвольная декартова
прямоугольная система координат
![]() ,
,
то всякое уравнение первой степени с
двумя переменными
![]()
и
![]()
(линейное уравнение) определяет
относительно этой системы координат
прямую линию.
Уравнение
![]() (10)
(10)
с произвольными
коэффициентами
![]()
и
![]()
таким, что
![]()
и
![]()
не равны нулю одновременно, называется
общим
уравнением прямой.
В курсе аналитической
геометрии доказывается, что прямая,
определяемая общим уравнением (10),
перпендикулярна вектору
![]() .
.
Этот вектор называется нормальным
вектором прямой (10).
Каноническим
уравнением прямой
называется уравнение вида
![]() ,
,
(11)
или
![]() ,
,
(12)
Уравнение (11) –
уравнение прямой, проходящей через
заданную точку
![]() ,
,
параллельно некоторому вектору
![]() ,
,
который называется направляющим
вектором
прямой.
Уравнение (12) –
уравнение прямой, проходящей через две
данные точки
![]()
и
![]() .
.
Уравнением прямой
с угловым коэффициентом называется
уравнение
![]() ,
,
(13)
где
![]() угловой
угловой
коэффициент, равный тангенсу угла
наклона прямой к положительному
направлению оси
![]() ордината
ордината
точки
![]() ,
,
в которой прямая, не параллельная оси
![]() ,
,
пересекает эту ось.
Уравнение прямой,
не проходящей через начало координат
и пересекающей оси координат в точках
![]()
и
![]() ,
,
может быть записано в виде (уравнение
в отрезках на осях):
![]() .
.
(14)
Если заданы
произвольная точка
![]()
и произвольный вектор
![]() ,
,
то параметрические уравнения прямой,
проходящей через данную точку, параллельно
данному вектору, имеют вид:
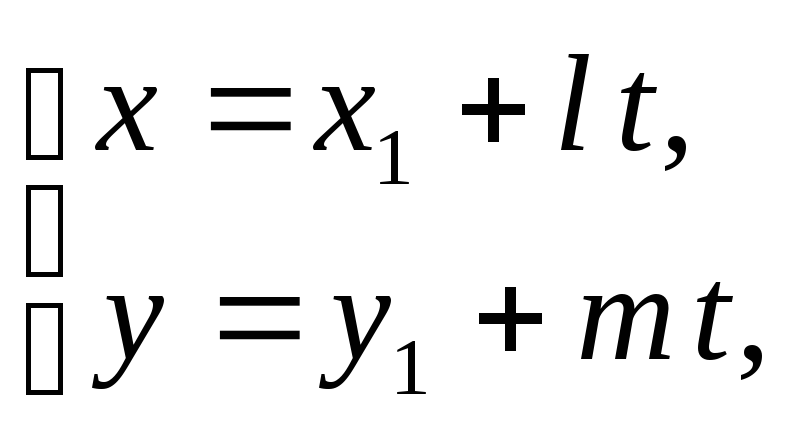 (15)
(15)
где
![]() .
.
Уравнение прямой,
проходящей через заданную точку
![]() ,
,
перпендикулярно вектору
![]() ,
,
имеет вид:
![]() .
.
(16)
Пусть
![]() угол
угол
от положительного направления оси
![]()
до луча
![]() ,
,
проходящего через начало координат,
перпендикулярного к прямой и пересекающего
эту прямую, а
![]() расстояние
расстояние
от начала координат до прямой. Тогда
уравнение прямой может быть записано
в виде:
![]() .
.
(17)
Уравнение (17)
называется нормальным
уравнением
прямой.
Общее уравнение
прямой (10) приводится к виду (17) путём
умножения на нормирующий множитель
![]() .
.
В результате
получается
![]() .
.
Знак нормирующего
множителя противоположен знаку
![]()
в уравнении (10). Если в общем уравнении
![]() ,
,
то знак
![]()
выбирается произвольным образом.
Расстояние
![]()
от точки
![]()
до прямой, заданной общим уравнением
(10) определяется по формуле:
![]() .
.
(18)
Если две прямые
![]()
и
![]()
заданы уравнениями:
![]()
то косинус угла
![]()
между ними определяется по формуле:
![]() .
.
(19)
Условие параллельности
прямых
![]()
и
![]() ,
,
если известны координаты нормальных
векторов
![]()
и
![]() ,
,
эквивалентно условию коллинеарности
векторов
![]()
и
![]() ,
,
заключается в пропорциональности
координат этих векторов, то есть имеет
вид:
![]() .
.
(20)
Условие
перпендикулярности прямых
![]()
и
![]()
выражается равенством нулю скалярного
произведения
![]() .
.
Оно имеет вид:
![]() .
.
(21)
Если известны
координаты направляющих векторов
![]()
и
![]() ,
,
то условия параллельности и
перпендикулярности прямых записываются
аналогично условиям (20) и (21) соответственно.
Если прямые
![]()
и
![]()
заданы уравнениями с угловым коэффициентом
вида (13), то угол между этими прямыми
можно определить по формуле:
![]() .
.
(22)
ПРИМЕРЫ РЕШЕНИЯ
ЗАДАЧ
Задача 1. Записать
уравнение прямой, проходящей через
точку
![]() ,
,
параллельно вектору
![]() .
.
Решение.
Воспользуемся уравнением (11), тогда
уравнение прямой будет иметь вид:
![]() .
.
Задача 2. Составить
уравнение прямой, проходящей через две
точки
![]()
и
![]() .
.
Решение.
Воспользуемся каноническим уравнением
прямой (12):
![]() .
.
Подставляя вместо
![]()
и
![]()
координаты точек
![]()
и
![]()
соответственно, получим:
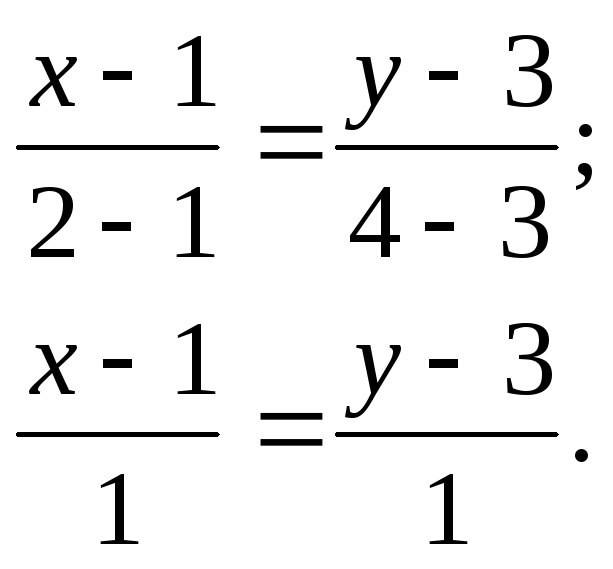
Уравнение прямой
можно записать в общем виде:
![]() .
.
Задача 3. Составить
уравнение прямой, проходящей через
начало координат и наклонённой к оси
![]()
под углом 300.
Решение.
Так как прямая проходит через начало
координат, то в уравнении
![]()
(13),
![]() .
.
Уравнение прямой будет иметь вид
![]() .
.
Так как
![]() ,
,
то окончательно получаем:
![]() .
.
Задача 4. Написать
уравнение прямой, проходящей через
точку
![]()
перпендикулярно вектору
![]() .
.
Решение.
Уравнение прямой запишем в виде (16):
![]() .
.
По условию задачи
![]() .
.
![]() .
.
Раскрыв скобки,
получим общее уравнение прямой:
![]() .
.
Задача 5. Написать
параметрические уравнения прямой,
проходящей через точку
![]()
параллельно вектору
![]() .
.
Решение.
Воспользуемся формулами (15):
![]() ,
,
![]() .
.
Задача 6. Составить
уравнение прямой, отсекающей на осях
координат отрезки 3 и 5.
Решение.
Воспользуемся формулой (14). Уравнение
прямой в отрезках на осях:
![]() .
.
Задача 7. Записать
уравнение прямой
![]()
в отрезках на осях.
Решение.
Разделим обе части уравнения на (-5):
![]() ,
,
![]() .
.
Здесь
![]() .
.
Задача 8. Определить
площадь треугольника, заключённого
между осями координат и прямой
![]() .
.
Решение.
Данный треугольник – прямоугольный,
катеты которого представляют собой
отрезки, отсекаемые прямой на координатных
осях. Запишем уравнение
![]()
в отрезках на осях:
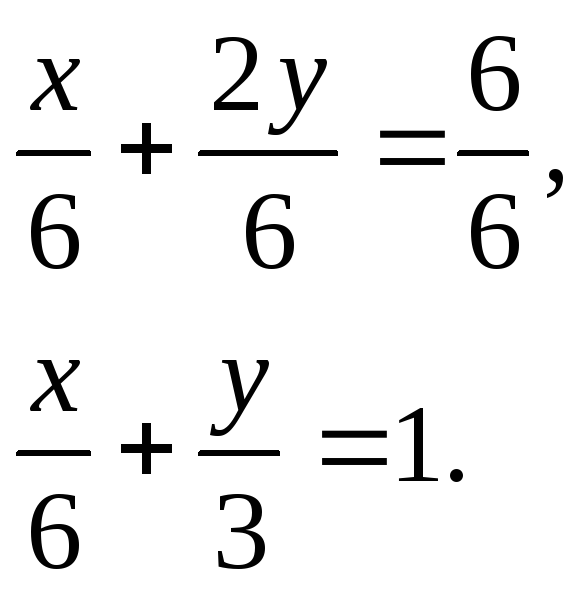
Здесь
![]() .
.
Задача 9. Заданы
прямая
![]() :
:
![]()
и точка
![]() .
.
Требуется:
-
вычислить расстояние
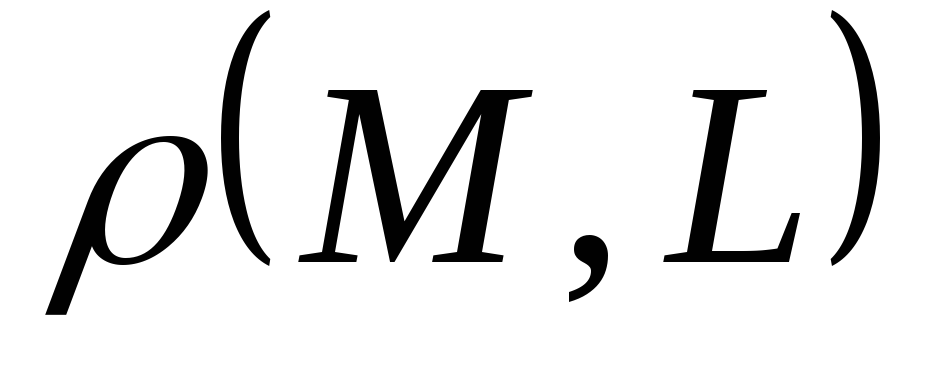
от точки
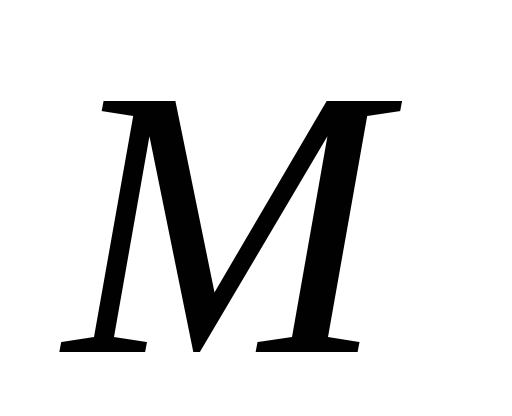
до прямой
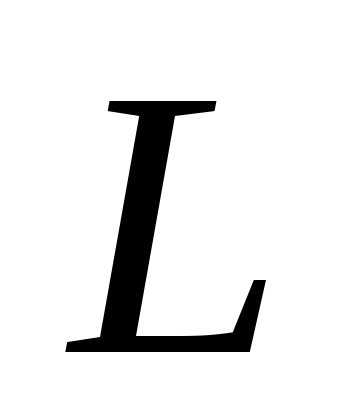 ;
; -
написать уравнение
прямой
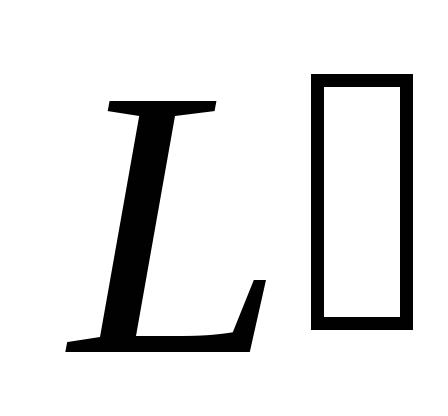 ,
,
проходящей через точку
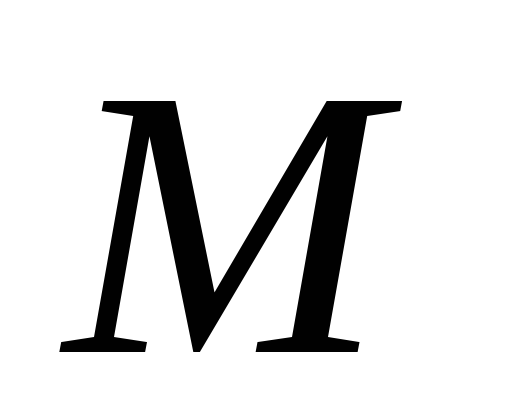
перпендикулярно заданной прямой
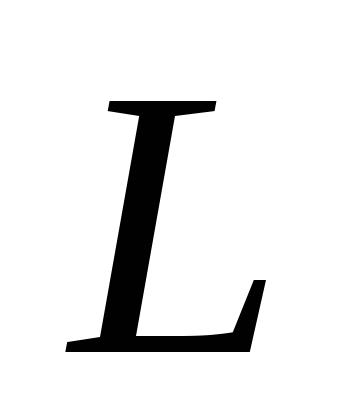 ;
; -
написать уравнение
прямой
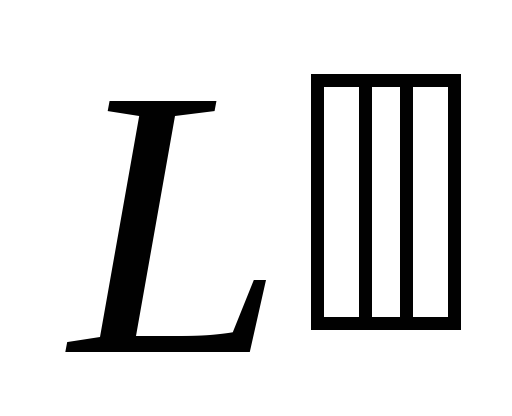 ,
,
проходящей через точку
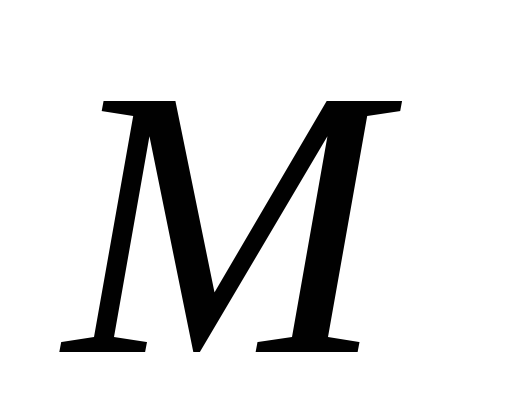
параллельно заданной прямой
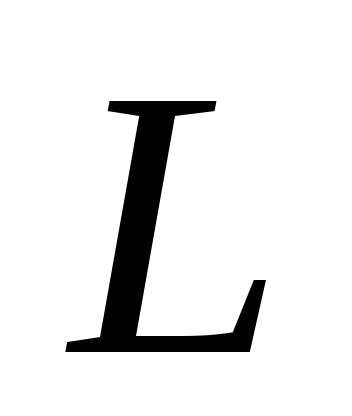 .
.
Решение.
1) Расстояние от
точки
![]()
до прямой
![]()
можно вычислить по формуле (18). По условию
задачи имеем, что
![]() .
.
Подставляя эти значения в данную формулу,
получим:
![]() .
.
2) Нормальный вектор
заданной прямой
![]() :
:
![]() .
.
Так как прямая
![]()
проходит через точку
![]()
перпендикулярно заданной прямой
![]() ,
,
то направляющий вектор
![]()
прямой
![]()
равен нормальному вектору
![]()
прямой
![]() ,
,
т.е.
![]() .
.
Подставляя
координаты точки
![]()
и вектора
![]()
в уравнение (11), получаем
![]() :
:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
3) По условию задачи
прямая
![]()
проходит через точку
![]()
параллельно заданной прямой
![]() ,
,
следовательно, прямые
![]()
и
![]()
имеют один и тот же вектор нормали, т.е.
![]() .
.
Подставляя
координаты точки
![]()
и вектора
![]()
в уравнение 916), получим
![]() :
:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Ответ. 1)
![]() ;
;
2)
![]() :
:
![]() ;
;
3)
![]() :
:
![]() .
.
Задача 10. Установить
взаимное расположение прямых
![]()
и
![]() .
.
Если прямые пересекаются, найти их точку
пересечения.
Решение.
Условия параллельности и перпендикулярности
прямых не выполняются.
Вектор нормали
первой прямой имеет координаты
![]() ,
,
второй прямой –
![]() .
.
![]() и
и
![]() .
.
Следовательно,
прямые пересекаются. Точка пересечения
принадлежит и первой и второй прямой.
Её координаты найдём из системы уравнений:
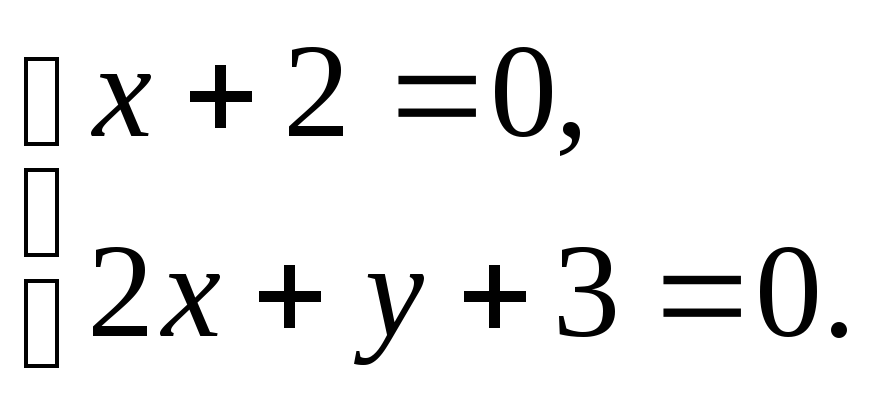
Отсюда получаем
![]() ,
,
![]() .
.
Точка пересечения имеет координаты
![]() .
.
Задача 11. Треугольник
![]()
задан координатами своих вершин:
![]() ,
,
![]()
и
![]() .
.
Требуется:
1) Написать уравнение
стороны
![]() ;
;
2) Написать уравнение
высоты
![]() ,
,
опущенной из вершины
![]()
на сторону
![]()
и вычислить её длину
![]() ;
;
3) Найти угол
![]()
между высотой
![]()
и медианой
![]() .
.
Решение.
1) Воспользуемся
уравнением прямой, проходящей через
две заданные точки (12):
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
2) Уравнение высоты
![]()
есть уравнение прямой, проходящей через
точку
![]()
перпендикулярно
![]() .
.
Нормальный вектор
прямой
![]() ,
,
имеющий координаты
![]()
можно взять в качестве направляющего
вектора искомой прямой, так как он будет
ей перпендикулярен. Подставляя координаты
вектора
![]()
и точки
![]()
в уравнение (11), получаем:
![]() :
:
![]() ;
;
![]() .
.
Раскрыв скобки,
получим уравнение высоты
![]()
в общем виде:
![]() .
.
Длина
![]() это
это
расстояние от точки
![]()
до прямой
![]() .
.
Вычислим его по формуле (18).
![]() .
.
3) По определению
медианы точка
![]() середина
середина
отрезка
![]() .
.
Её координаты находятся по следующим
формулам:
![]() .
.
Подставляя координаты точек
![]()
и
![]() ,
,
получаем:
![]() .
.
Таким образом,
![]() .
.
Составим уравнение
медианы
![]()
как уравнение прямой, проходящей через
две заданные точки (12).
![]() :
:
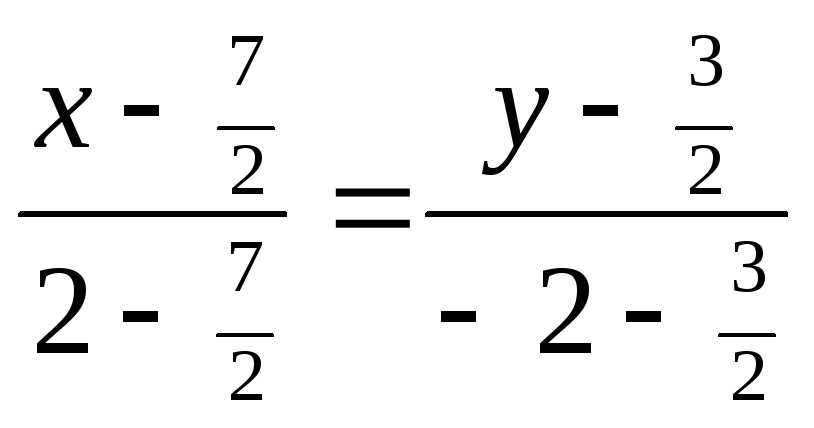 ;
;
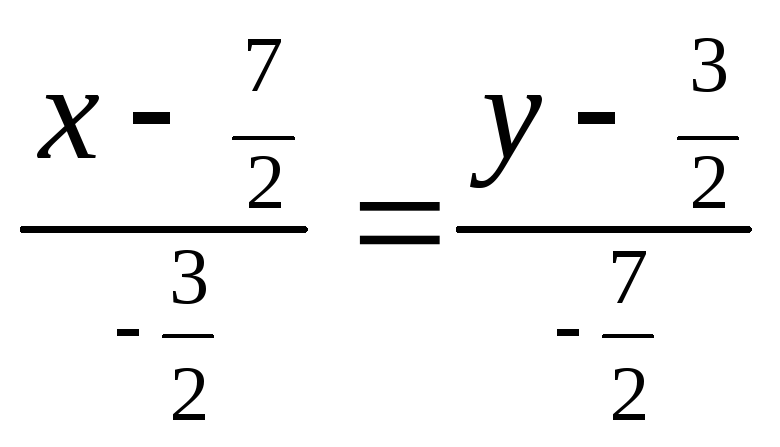 ;
;
![]() ;
;
![]() ;
;
![]() .
.
Чтобы найти угол
между высотой
![]()
и медианой
![]() ,
,
достаточно найти угол между нормальными
векторами этих прямых.
![]() .
.
Подставим координаты
данных векторов в уравнение (7):
![]() .
.
![]() .
.
Ответ. 1)
![]() :
:
![]() ;
;
2)
![]() :
:
![]() ,
,
![]() ;
;
3)
![]() .
.
Задача 12. Определить
положение точки
![]()
относительно прямой
![]() .
.
Решение.
Подставим координаты точки
![]()
в уравнение прямой :
![]() .
.
Следовательно, пара чисел не является
решением уравнения
![]()
и точка
![]()
не принадлежит прямой.
Задача 13. Написать
уравнение прямой, проходящей через
точку
![]()
под углом
![]()
к прямой
![]() :
:
![]() .
.
Решение.
Прямая
![]()
задана параметрическими уравнениями.
Приведём уравнение прямой
![]()
сначала к общему виду, а затем к виду
(13). По условию задачи
![]() ,
,
![]() .
.
Подставим данные значения в (11):
![]() ;
;
![]() .
.
Раскрывая скобки
и приводя подобные, получаем:
![]() .
.
Таким образом,
![]() .
.
Подставим значение угла
![]()
и
![]()
в формулу (22) для определения
![]() :
:
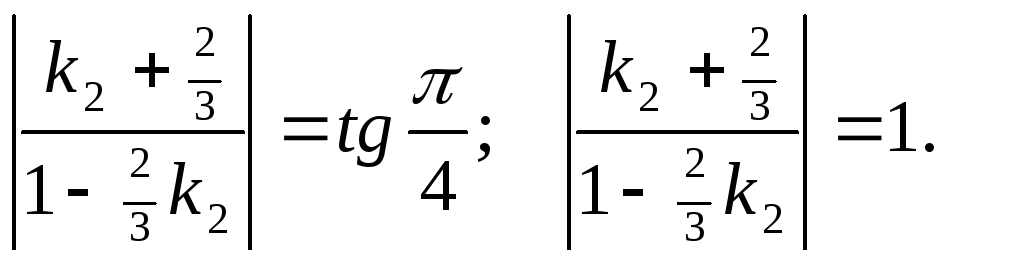
Отсюда:
![]() .
.
(*)
Для нахождения
![]()
необходимо решить уравнение, содержащее
переменную под знаком модуля.
Рассмотрим 3 случая:
![]() 1)
1)
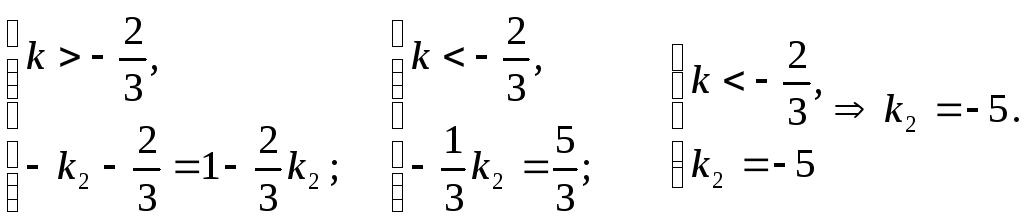
2)
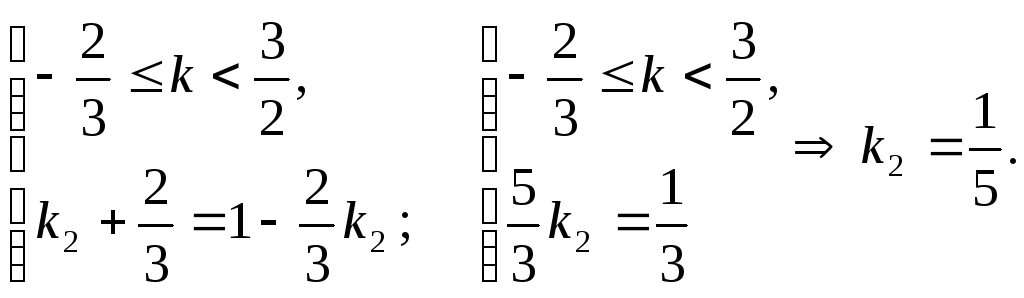
3)
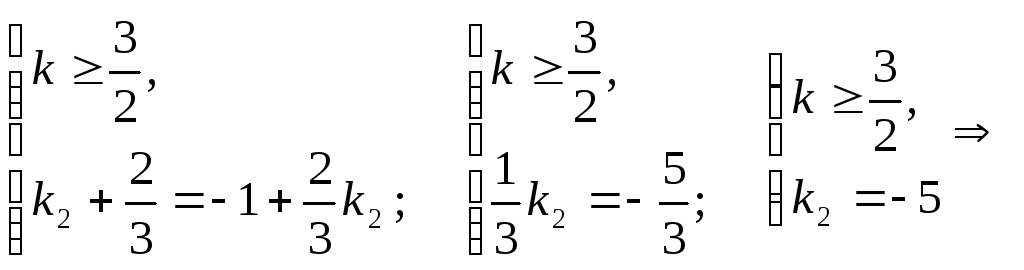 нет
нет
решений.
Таким образом,
получили 2 значения
![]() ,
,
которые являются решением данного
уравнения (*):
![]()
или
![]() .
.
По условию задачи
прямая проходит через точку
![]() .
.
Подставим найденные значения
![]()
в уравнение (13) и определим значение
![]() .
.
1)
![]() :
:
![]()
подставим в это уравнение координаты
точки
![]()
![]()
![]() .
.
Следовательно,
![]() :
:
![]() ;
;
2)
![]() :
:
![]()
подставим в это уравнение координаты
точки
![]()
![]() .
.
Ответ.
![]()
или
![]() .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой (общее уравнение прямой на плоскости и его исследование). Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и его исследование, как осуществлять переходы от общего уравнения к другим типам уравнений прямой (неполного уравнения, полного уравнения). Всю теорию закрепим иллюстрациями и решением практических задач на уравнения.
Общее уравнение прямой: основные сведения
Как найти уравнение прямой? Пусть на плоскости задана прямоугольная система координат Oxy.
Любое уравнение первой степени, имеющее вид Ax+By+C=0, где А, В, С – некоторые действительные числа (А и В не равны одновременно нулю) определяет прямую линию в прямоугольной системе координат на плоскости. В свою очередь, любая прямая в прямоугольной системе координат на плоскости определяется уравнением, имеющим вид Ax+By+C=0 при некотором наборе значений А, В, С.
указанная теорема состоит из двух пунктов, докажем каждый из них.
- Докажем, что уравнение Ax+By+C=0 определяет на плоскости прямую.
Пусть существует некоторая точка М0(x0, y0), координаты которой отвечают уравнению Ax+By+C=0. Таким образом: Ax0+By0+C=0. Вычтем из левой и правой частей уравнений Ax+By+C=0 левую и правую части уравнения Ax0+By0+C=0, получим новое уравнение, имеющее вид A(x-x0)+B(y-y0)=0. Оно эквивалентно Ax+By+C=0.
Полученное уравнение A(x-x0)+B(y-y0)=0 является необходимым и достаточным условием перпендикулярности векторов n→=(A, B) и M0M→=(x-x0, y-y0). Таким образом, множество точек M(x, y) задает в прямоугольной системе координат прямую линию, перпендикулярную направлению вектора n→=(A, B). Можем предположить, что это не так, но тогда бы векторы n→=(A, B) и M0M→=(x-x0, y-y0) не являлись бы перпендикулярными, и равенство A(x-x0)+B(y-y0)=0 не было бы верным.

Следовательно, уравнение A(x-x0)+B(y-y0)=0 определяет некоторую прямую в прямоугольной системе координат на плоскости, а значит и эквивалентное ему уравнение Ax+By+C=0 определяет ту же прямую. Так мы доказали первую часть теоремы.
- Приведем доказательство, что любую прямую в прямоугольной системе координат на плоскости можно задать уравнением первой степени Ax+By+C=0.
Зададим в прямоугольной системе координат на плоскости прямую a; точку M0(x0, y0), через которую проходит эта прямая, а также нормальный вектор этой прямой n→=(A, B).
Пусть также существует некоторая точка M(x, y) – плавающая точка прямой. В таком случае, векторы n→=(A, B) и M0M→=(x-x0, y-y0) являются перпендикулярными друг другу, и их скалярное произведение есть нуль:
n→, M0M→=A(x-x0)+B(y-y0)=0
Перепишем уравнение Ax+By-Ax0-By0=0, определим C: C=-Ax0-By0 и в конечном результате получим уравнение Ax+By+C=0.
Так, без какой-либо помощи онлайн мы смогли доказать и вторую часть теоремы, и доказали всю теорему в целом.
Уравнение, имеющее вид Ax+By+C=0 – это общее уравнение прямой на плоскости в прямоугольной системе координат Oxy (уравнение прямой параллельной оси ox).
Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая.
Из доказательства теоремы также следует, что коэффициенты А и В при переменных x и y являются координатами нормального вектора прямой, которая задана общим уравнением прямой Ax+By+C=0.
Рассмотрим конкретный пример общего уравнения прямой.
Пусть задано уравнение 2x+3y-2=0, которому соответствует прямая линия в заданной прямоугольной системе координат. Нормальный вектор этой прямой – это вектор n→= (2, 3). Изобразим заданную прямую линию из уравнения с вектором на чертеже.

Также можно утверждать и следующее: прямая, которую мы видим на чертеже, определяется общим уравнением 2x+3y-2=0, поскольку координаты всех точек заданной прямой отвечают этому уравнению.
Мы можем получить уравнение λ·Ax+λ·By+λ·C=0, умножив обе части общего уравнения прямой на число λ, не равное нулю. Полученное уравнение является эквивалентом исходного общего уравнения, следовательно, будет описывать ту же прямую на плоскости.
Неполное уравнение общей прямой
Полное общее уравнение прямой – такое общее уравнение прямой Ax+By+C=0, в котором числа А, В, С отличны от нуля. В ином случае уравнение является неполным.
Разберем все вариации неполного общего уравнения прямой.
- Когда А=0, В≠0, С≠0, общее уравнение принимает вид By+C=0. Такое неполное общее уравнение задает в прямоугольной системе координат Oxy прямую, которая параллельна оси Ox, поскольку при любом действительном значении x переменная y примет значение -CB . Иначе говоря, общее уравнение прямой Ax+By+C=0, когда А=0, В≠0, задает геометрическое место точек (x, y), координаты которых равны одному и тому же числу -CB.
- Если А=0, В≠0, С=0, общее уравнение принимает вид y=0. Такое неполное уравнение определяет ось абсцисс Ox.
- Когда А≠0, В=0, С≠0, получаем неполное общее уравнение Ax+С=0, задающее прямую, параллельную оси ординат.
- Пусть А≠0, В=0, С=0, тогда неполное общее уравнение примет вид x=0, и это есть уравнение координатной прямой Oy.
- Наконец, при А≠0, В≠0, С=0, неполное общее уравнение принимает вид Ax+By=0. И это уравнение описывает прямую, которая проходит через начало координат. В самом деле, пара чисел (0, 0) отвечает равенству Ax+By=0, поскольку А·0+В·0=0.
Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой.

Известно, что заданная прямая параллельна оси ординат и проходит через точку 27, -11. Необходимо написать общее уравнение заданной прямой. Попробуем его составить.
Решение
Решение лежит на поверхности. Прямая, параллельная оси ординат, задается уравнением вида Ax+C=0, в котором А≠0. Также условием заданы координаты точки, через которую проходит прямая, и координаты этой точки отвечают условиям неполного общего уравнения Ax+C=0, т.е. верно равенство:
A·27+C=0
Из него возможно определить C, если придать A какое-то ненулевое значение, к примеру, A=7. В таком случае получим: 7·27+C=0⇔C=-2. Нам известны оба коэффициента A и C, подставим их в уравнение Ax+C=0 и получим требуемое уравнение прямой: 7x-2=0
Ответ: 7x-2=0
На чертеже изображена прямая, необходимо записать ее уравнение. Как будем это находить?

Решение
Приведенный чертеж позволяет нам легко взять исходные данные для решения задачи. Мы видим на чертеже, что заданная прямая параллельна оси Ox и проходит через точку (0, 3).
Прямую, которая будет являться параллельной оси абсцисс, определяет неполное общее уравнение By+С=0. Найдем значения B и C. Координаты точки (0, 3), поскольку через нее проходит заданная прямая, будут удовлетворять уравнению прямой By+С=0, тогда справедливым является равенство: В·3+С=0. Зададим для В какое-то значение, отличное от нуля. Допустим, В=1, в таком случае из равенства В·3+С=0 можем найти С: С=-3. Используем известные значения В и С, получаем требуемое уравнение прямой: y-3=0.
Ответ: y-3=0.
Общее уравнение прямой, проходящей через заданную точку плоскости
Пусть заданная прямая проходит через точку М0(x0, y0), тогда ее координаты отвечают общему уравнению прямой, т.е. верно равенство: Ax0+By0+C=0. Отнимем левую и правую части этого уравнения от левой и правой части общего полного уравнения прямой. Получим: A(x-x0)+B(y-y0)+C=0, это уравнение эквивалентно исходному общему, проходит через точку М0(x0, y0) и имеет нормальный вектор n→=(A, B).
Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой.
Даны точка М0(-3, 4), через которую проходит прямая, и нормальный вектор этой прямой n→=(1, -2). Необходимо записать уравнение заданной прямой.
Решение
Исходные условия позволяют нам получить необходимые данные для составления уравнения: А=1, В=-2, x0=-3, y0=4. Тогда:
A(x-x0)+B(y-y0)=0⇔1·(x-(-3))-2·y(y-4)=0⇔⇔x-2y+22=0
Задачу можно решать иначе. Как она будет решаться? Общее уравнение прямой имеет вид Ax+By+C=0. Заданный нормальный вектор (векторная прямая) позволяет получить значения коэффициентов A и B в уравнении прямой, тогда:
Ax+By+C=0⇔1·x-2·y+C=0⇔x-2·y+C=0
Теперь найдем значение С, используя заданную условием задачи точку М0(-3, 4), через которую проходит прямая. Координаты этой точки отвечают уравнению x-2·y+C=0, т.е. -3 – 2·4+С=0. Отсюда С=11. Требуемое уравнение прямой принимает вид: x – 2·y + 11=0.
Ответ: x – 2·y + 11=0.
Задана прямая 23x-y-12=0 и точка М0, лежащая на этой прямой. Известна лишь абсцисса этой точки, и она равна -3. Необходимо определить ординату заданной точки.
Решение
Зададим обозначение координат точки М0 как x0 и y0. В исходных данных указано, что x0=-3. Поскольку точка принадлежит заданной прямой, значит ее координаты отвечают общему уравнению этой прямой. Тогда верным будет равенство:
23×0-y0-12=0
Определяем y0: 23·(-3)-y0-12=0⇔-52-y0=0⇔y0=-52
Ответ: -52
Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно
Как мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида.
Для начала рассмотрим переход от общего уравнения вида Ax+By+C=0 к каноническому уравнению x-x1ax=y-y1ay.
Если А≠0, тогда переносим слагаемое By в правую часть общего уравнения. В левой части выносим A за скобки. В итоге получаем: Ax+CA=-By.
Это равенство возможно записать как пропорцию: x+CA-B=yA .
В случае, если В≠0, оставляем в левой части общегь уравнения только слагаемое Ax, прочие переносим в правую часть, получаем: Ax=-By-C. Выносим –В за скобки, тогда: Ax=-By+CB.
Перепишем равенство в виде пропорции: x-B=y+CBA .
Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому.
Задано общее уравнение прямой 3y-4=0. Необходимо преобразовать его в каноническое уравнение.
Решение
Запишем исходное уравнение как 3y-4=0. Далее действуем по алгоритму: в левой части остаётся слагаемое 0x; а в правой части выносим -3 за скобки; получаем: 0x=-3y-43.
Запишем полученное равенство как пропорцию: x-3=y-430. Так, мы получили уравнение канонического вида.
Ответ: x-3=y-430.
Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям.
Перед нами задание. Прямая задана уравнением 2x-5y-1=0. Запишите параметрические уравнения этой прямой.
Решение
Осуществим переход от общего уравнения к каноническому:
2x-5y-1=0⇔2x=5y+1⇔2x=5y+15⇔x5=y+152
Теперь примем обе части полученного канонического уравнения равными λ, тогда:
x5=λy+152=λ⇔x=5·λy=-15+2·λ, λ∈R
Ответ: x=5·λy=-15+2·λ, λ∈R
Общее уравнение можно преобразовать в уравнение прямой с угловым коэффициентом y=k·x+b, но только тогда, когда В≠0. Для перехода в левой части оставляем слагаемое By, остальные переносятся в правую. Получим: By=-Ax-C. Разделим обе части полученного равенство на B, отличное от нуля: y=-ABx-CB.
Задано общее уравнение прямой: 2x+7y=0. Необходимо преобразовать то уравнение в уравнение с угловым коэффициентом.
Решение
Произведем нужные действия по алгоритму:
2x+7y=0⇔7y-2x⇔y=-27x
Ответ: y=-27x .
Из общего уравнения прямой достаточно просто получить уравнение в отрезках вида xa+yb=1. Чтобы осуществить такой переход, перенесем число C в правую часть равенства, разделим обе части полученного равенства на –С и, наконец, перенесем в знаменатели коэффициенты при переменных x и y:
Ax+By+C=0⇔Ax+By=-C⇔⇔A-Cx+B-Cy=1⇔x-CA+y-CB=1
Необходимо преобразовать общее уравнение прямой x-7y+12=0 в уравнение прямой в отрезках.
Решение
Перенесем 12 в правую часть: x-7y+12=0⇔x-7y=-12.
Разделим на -1/2 обе части равенства: x-7y=-12⇔1-12x-7-12y=1.
Преобразуем далее в необходимый вид: 1-12x-7-12y=1⇔x-12+y114=1.
Ответ: x-12+y114=1.
В общем, несложно производится и обратный переход: от прочих видов уравнения к общему.
Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства:
xa+yb⇔1ax+1by-1=0⇔Ax+By+C=0y=kx+b⇔y-kx-b=0⇔Ax+By+C=0
Каноническое уравнение преобразуется к общему по следующей схеме:
x-x1ax=y-y1ay⇔ay·(x-x1)=ax(y-y1)⇔⇔ayx-axy-ayx1+axy1=0⇔Ax+By+C=0
Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему:
x=x1+ax·λy=y1+ay·λ⇔x-x1ax=y-y1ay⇔Ax+By+C=0
Заданы параметрические уравнения прямой x=-1+2·λy=4. Необходимо записать общее уравнение этой прямой.
Решение
Осуществим переход от параметрических уравнений к каноническому:
x=-1+2·λy=4⇔x=-1+2·λy=4+0·λ⇔λ=x+12λ=y-40⇔x+12=y-40
Перейдем от канонического к общему:
x+12=y-40⇔0·(x+1)=2(y-4)⇔y-4=0
Ответ: y-4=0
Задано уравнение прямой в отрезках x3+y12=1 . Необходимо осуществить переход к общему виду уравнения.
Решение:
Просто перепишем уравнение в необходимом виде:
x3+y12=1⇔13x+2y-1=0
Ответ: 13x+2y-1=0.
Составление общего уравнения прямой
Выше мы говорили о том, что общее уравнение возможно записать при известных координатах нормального вектора и координатах точки, через которую проходит прямая. Такая прямая определяется уравнением A(x-x0)+B(y-y0)=0. Там же мы разобрали соответствующий пример.
Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора.
Задана прямая, параллельная прямой 2x-3y+33=0. Также известна точка M0(4, 1), через которую проходит заданная прямая. Необходимо записать уравнение заданной прямой.
Решение
Исходные условия говорят нам о том, что прямые параллельны, тогда, как нормальный вектор прямой, уравнение которой требуется записать, возьмем направляющий вектор прямой n→=(2, -3): 2x-3y+33=0. Теперь нам известны все необходимые данные, чтобы составить общее уравнение прямой:
A(x-x0)+B(y-y0)=0⇔2(x-4)-3(y-1)=0⇔2x-3y-5=0
Ответ: 2x-3y-5=0.
Заданная прямая проходит через начало координат перпендикулярно прямой x-23=y+45. Необходимо составить общее уравнение заданной прямой.
Решение
Нормальный вектором заданной прямой будет направляющий вектор прямой x-23=y+45.
Тогда n→=(3, 5). Прямая проходит через начало координат, т.е. через точку О(0, 0). Составим общее уравнение заданной прямой:
A(x-x0)+B(y-y0)=0⇔3(x-0)+5(y-0)=0⇔3x+5y=0
Ответ: 3x+5y=0.
