Эволюта эллипса как найти - Сайт, где вы сможете решить свои вопросы

Пусть кривая (Gamma) задана натуральным уравнением. Будем предполагать, что в точке (MinGamma), где (overrightarrow{OM}=textbf{r}(s)), существует кривизна (k=k(s)neq 0). Тогда радиус кривизны кривой (Gamma) в точке (M) равен
$$
R=R(s)=frac{1}{k(s)}.label{ref42}
$$

Отложим на главной нормали кривой (Gamma) (рис. 22.9) в направлении главной нормали (nu=nu(s)) отрезок (MN) длиной (R=R(s)) и назовем точку (N) центром кривизны кривой (Gamma) в точке (M). Пусть (overrightarrow{ON}=rho).

Так как (overrightarrow{MN}=R(s)nu(s)), то получаем:
$$
boldsymbol{rho}=textbf{r}(s)+R(s)boldsymbol{nu}(s).label{ref43}
$$

Рис. 22.9

Используя формулу eqref{ref42} и равенство
$$
frac{d^{2}textbf{r}}{ds^{2}}=frac{dtau}{ds}=k(s)boldsymbolnu(s),nonumber
$$
запишем уравнение eqref{ref43} в следующем виде:
$$
boldsymbolrho=textbf{r}(s)+frac{1}{(k(s))^2}frac{d^2textbf{r}}{ds^2}.label{ref44}
$$

Предполагая, что во всех точках кривой (Gamma) кривизна отлична от нуля, построим для каждой точки кривой центр кривизны и назовем множество всех центров кривизны кривой (Gamma) эволютой этой кривой.

Если кривая (Gamma_1) — эволюта кривой (Gamma), то кривую (Gamma) называют эвольвентой кривой (Gamma_1). Уравнение эволюты кривой (Gamma), заданной натуральным уравнением, имеет вид eqref{ref44}.

Если кривая (Gamma) задана уравнением кривой в векторной форме, то уравнение эволюты этой кривой можно получить, заменив в равенстве eqref{ref44} (k) и (displaystylefrac{d^{2}textbf{r}}{ds^{2}}) их выражениями по формулам отсюда и отсюда.

В случае, когда плоская кривая (Gamma) задана уравнением (Gamma={x=x(t),;y=y(t),;alphaleq tleqbeta}), ее кривизна выражается формулой отсюда, а (displaystyle frac{d^2textbf{r}}{ds^2}) — формулой из этого утверждения, где
$$
textbf{r}’=(x’,y’),quad r″=(x″,y″),quad s’=sqrt{(x’)^{2}+(y’)^{2}},quad s″=frac{x’x″+y’y″}{s},nonumber
$$
и поэтому
$$
frac{d^{2}textbf{r}}{ds^{2}}=left(frac{x″}{(s’)^{2}}-frac{x'(x’x″+y’y″)}{(s’)^{4}},;frac{y″}{(s)^{2}}-frac{y'(x’x″+y’y″)}{(s’)^{4}}right)=\=left(displaystyle y’frac{x″y’-x’y″}{((x’)^{2}+(y’)^{2})^{2}},; x’frac{y″x’-y’x″}{((x’)^{2}+(y’)^{2})^{2}}right).nonumber
$$
Если (boldsymbolrho=(xi,eta)), то уравнение eqref{ref44} в координатной форме примет вид
$$
xi=x-y’frac{(x’)^{2}+(y’)^{2}}{x’y″-y’x″},quad eta=y+x’frac{(x’)^{2}+(y’)^{2}}{x’y″-y’x″}.label{ref45}
$$

Равенства eqref{ref45} задают эволюту кривой (Gamma) в координатной форме.

Замечание 1.

Приведем без доказательства физическое истолкование эволюты и эвольвенты. Пусть на эволюту натянута гибкая нерастяжимая нить. Если эту нить развертывать, оставляя все время натянутой, то конец нити опишет эвольвенту. Этим можно объяснить термины эволюта («развертка») и эвольвента («развертывающаяся»).

Пример 1.

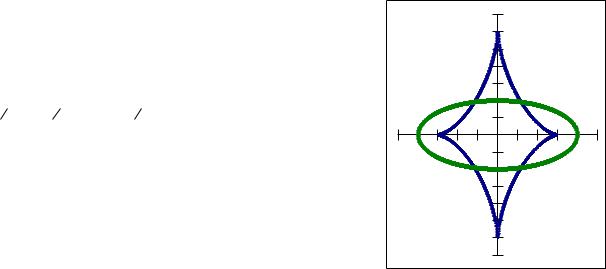
Найти эволюту эллипса (x=acos t, y=bsin t).

Решение.

(triangle) В этом случае (x’=-asin t,;y’=bcos t,;x″=acos t,;y″= -bsin t),и формулы eqref{ref45} принимают вид
$$
xi=frac{a^{2}-b^{2}}{a}cos^3 t,quad eta=frac{b^{2}-a^{2}}{b}sin^{3}t.nonumber
$$
Следовательно, эволютой эллипса является астроида. (blacktriangle)

Рис. 22.10

Если плоская кривая задана уравнением (y=f(x)), то уравнения eqref{ref45} записываются в виде
$$
xi=x-frac{1+(f'(x))^{2}}{f″(x)}f'(x),qquad eta=f(x)+frac{1+(f'(x))^{2}}{f″(x)}.label{ref46}
$$

Пример 2.

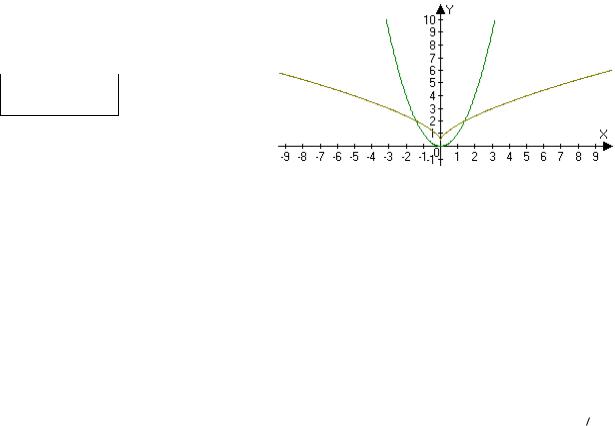
Найти эволюту параболы (y=ax^{2}).

Решение.

Рис. 22.11

(triangle) Используя формулы eqref{ref46}, где (f(x)=ax^{2}), получаем
$$
xi=x-frac{1+4a^{2}x^{2}}{2a}2ax=-4a^{2}x^{3},qquad eta=ax^{2}+frac{1+4a^{2}x^{2}}{2a}=frac{1}{2a}+3ax^{2}.nonumber
$$
Исключая (x), получаем
$$
xi^{2}=frac{16a}{27}left(eta-frac{1}{2a}right)^{3}.nonumber
$$

Следовательно, эволютой параболы является полукубическая парабола. (blacktriangle)

Источник

=	x− y ‘	1 y’ 2
2) если кривая задана явно, то {=		y ‘ ‘	}.
y 1 y’y‘‘ 2

Определение. Эволюта кривой — это линия, состоящая из всех центров кривизны этой кривой. При этом данная кривая для своей эволюты называется эвольвентой.

Свойства эволюты и эвольвенты

1)Касательная к эволюте является нормалью к эвольвенте.

2)Приращение длины дуги эволюты равно приращению радиуса кривизны эвольвенты.

Пример 1. Найти кривизну и эволюту параболы y=x2. Решение.

а). Найдем кривизну по формуле k =

y”

, подставив сюда

y’ =2 x , y’ ‘=2 :

(1+ (

y’)2 )3/ 2

2 3 /2

Отсюда получаем радиус кривизны: R= 2

1 4 x

1 4 x2 3 /2

б). Координаты центра кривизны вычисляются по формулам:

= x− y’ 1 y ‘ 2

= x−2 x

1 4 x2

= −4 x3

y’ ‘

. Это — параметрические

1 y’ 2

4 x2

{ =

= x

= 1/2 3 x

}

y ‘ ‘

уравнения эволюты. Исключая из

системы параметр x, получим явное

уравнение:

x= − 4 , поэтому

2 2

График эволюты изображен на одном чертеже с параболой.

В точке M0(0,0) кривизна равна 2,

радиус кривизны равен 1/2, центр кривизны (0, 1/2). Геометрически это означает, что в малой окрестности точки M0 парабола лучше всего (из всех окружностей) приближается окружностью x−12 2 y2= 14 . ■

Пример 2. Найти кривизну и эволюту эллипса {xy==abcossintt.,}

Решение. Воспользуемся формулой (1): k =		y”(t)x’(t) − y’(t)x”(t)		.

	( (x’(t))2 + (y’(t))2 )3/ 2
Так как {xy’‘==−bacossintt },	{xy’‘ ‘‘==−−abcossin tt },	и	ab
y”(t)x’(t) − y’(t)x”(t) =	− a sint(− bsin t) + a cost bcost = ab , то k =
	.
(a2 sin2 t + b2 cos2 t)3 2

Координаты центра кривизны вычисляются по формулам:

= a cos t−b cost a2 sin2 t b2 cos2 t ab

= b sin t−a sin t a2 sin2 t b2 cos2 t ab

	=	x −y’	x ‘ 2 y ‘ 2
x’ y’ ‘−x ‘ ‘ y’
{
=	y x’	x ‘ 2 y ‘ 2
x’ y’ ‘−x ‘ ‘ y’

Это — параметрические уравнения эволюты. Для исключения из системы параметра t, преобразуем её:

a 2 /3	=	a2 −b2 2/3 cos2 t	},
{b 2 /3	=	b2−a2 2 /3 sin2 t	откуда, складывая
уравнения, получаем неявное уравнение эволюты:
(aξ )23 + (bη )23	= (b2 − a2 )23 — это асторида.
Вершины астроиды:
при	=0	=± a2−b2 ;
				b
при	=0	=±	a2 −b2	.

				a
Если a = 4, b = 2, то вершины астроиды: 0,±6 ,	±3,0 . ■

=	a2−b2 cos3 t	}.
	a
=	b2−b a2 sin3 t
	7
	5
	3
	1

-5 -4 -3 -2 –11 0 1 2 3 4 5

-3

-5

-7

Источник

Построить такой график можно здесь: https://www.desmos.com/

Что мы знаем со школы про эллипс? К сожалению, исходя из своей практики работы с учениками, многие вплоть до 11 класса не сталкиваются с такой замечательной плоской фигурой, впрочем как и с её частным случаем – окружностью. Некоторые знают только примерный вид уравнения…

Кстати, какое оно? Каноническим уравнением эллипса считается следующее уравнение:

Каноническое уравнение эллипса

Почему оно именно такое? Что ж, это можно вывести из определения. Поэтому давайте его напишем.

Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая чем расстояние между фокусами.

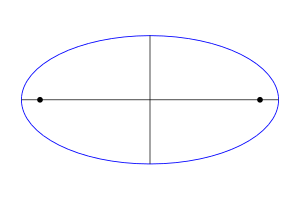
Давайте сделаем рисунок и попробуем вывести каноническое уравнение из определения эллипса.

Математика эллипса: всё, что нужно знать

Обозначим фокусы через F₁ и F₂, расстояние между ними через 2c, а сумму расстояний от произвольной точки эллипса M(x; y) до фокусов – через 2a. По определению 2а > 2c, т.е. а > c.

Для вывода уравнения эллипса выберем систему координат OXY так, чтобы фокусы F₁ и F₂ лежали а оси OX, а начало координат совпадало с серединой отрезка F₁F₂. Тогда фокусы будут иметь следующие координаты: F₁(-c; 0) и F₂(+c; 0).

Тогда, согласно определению эллипса, MF₁ + MF₂ = 2a, то есть:

Мы вывели каноническое уравнение эллипса и доказали, что оно эквивалентно начальному уравнению из определения.

Эллипс – кривая второго порядка.

Исследование формы эллипса по его уравнению

Установим форму эллипса, используя его каноническое уравнение.

1. Каноническое уравнение содержит x и y только в четных степенях, поэтому если точка (x; y) принадлежит эллипсу, то ему также принадлежат точки (x; -y), (-x; y), (-x; -y). Отсюда следует, что эллипс симметричен относительно осей координат Ox и Oy, а также точки O(0; 0), которая является центром эллипса.

2. Точки пересечения эллипса с осями координат. Положив y = 0, находим две точки A₁(a; 0) и A₂(-a;0), в которых ось Ox пересекает эллипс. Положив в уравнении x = 0, находим точки пересечения эллипса с осью Oy: B₁(0; b) и B₂(0; -b). Все эти 4 точки называются вершинами эллипса.

Отрезки A₁A₂ и B₁B₂, а также их длины 2a и 2b называются соответственно большой и малой осями эллипса. Числа a и b называются соответственно большой и малой полуосями эллипса.

3. Также из канонического уравнения следует, что каждое слагаемое в левой части не превосходит единицы, т.е. имеют место неравенства

Следовательно, все точки эллипса лежат внутри прямоугольника, образованного прямыми x = ±a и y = ±b.

4. В каноническом уравнении сумма неотрицательных слагаемых (x/a)² и (y/b)² равна единице. Следовательно, при возрастании одного слагаемого другое будет уменьшаться, т.е. если |x| возрастает, то |y| уменьшается и наоборот.

Дополнительные сведения об эллипсе

Форма эллипса зависит от отношения b/a. При a = b = R эллипс превращается в окружность, уравнение эллипса принимает вид x² + y² = R². Однако, в качестве характеристики формы эллипса чаще используется отношение c/a.

Отношение c/a половины расстояния между фокусами к большей полуоси эллипса называется эксцентриситетом эллипса и обозначается буквой «эпсилон» ε:

Из последней строки видно, что чем меньше эксцентриситет эллипса, тем эллипс будет менее сплющенным, то есть больше походить на окружность, быть ближе к ней по форме. Если положить ε = 0, то эллипс превращается в окружность.

Пусть M(x; y) – произвольная точка эллипса с фокусами F₁ и F₂. Длины отрезков F₁M = r₁ и F₂M = r₂ называются фокальными радиусами точки M.
Очевидно, что r₁ + r₂ = 2a.

Тогда имеют место быть формулы: r₁ = a + εx и r₂ = a + εx

Выведем эти формулы

Прямые x = ±a/ε называются директрисами эллипса. Значение директрисы эллипса выявляется следующим утверждением.

Теорема

Если r – расстояние от произвольной точки эллипса до какого-нибудь фокуса, d – расстояние от этой же точки до соответствующей этому фокусу директрисы, то отношение r/d есть величина постоянная, равная эксцентриситету эллипса: r/d = ε.

Из равенства a² – c² = b² следует, что a > b. Если же a < b, то каноническое уравнение (x/a)² + (y/b)² = 1 определяет эллипс, большая ось которого 2b лежит на оси OY, а малая ось 2a – лежит на оси Ox. Фокусы такого эллипса находятся в точках F₁(0; +c) и F₂(0; -c), где c = √(b² – a²).

Площадь фигуры, ограниченной эллипсом

Допустим, что перед нами стоит следующая задача:
Вычислить площадь фигуры, ограниченной эллипсом.

Решение:

Зададим эллипс параметрическими уравнениями:
x = a⋅cos(t) и y = b ⋅ sin(t). Кстати, выразив косинус и синус из каждого, а потом возведя в квадрат оба уравнения, сложив их, можно прийти к каноническому уравнению эллипса.

В силу симметричности эллипса относительно начала координат, нам достаточно найти площадь 1/4 части эллипса, а затем умножить результат на 4. Сделаем подходящий рисунок.

Здесь x изменяется от 0 до a, следовательно параметр t изменяется от π/2 до 0. Площадь четверти эллипса будем искать с помощью интегрирования функции, задающей эллипс в первой четверти координат.

Вывод формулы для площади эллипса

Длина дуги эллипса (периметр эллипса)

Вывод длины дуги эллипса через эллиптический интеграл

Ознакомиться с эллиптическими интегралами

Стоит заметить, что для окружности всё получается гораздо проще, и мы легко выводим формулу, знакомую нам со школы C = 2πR.

Вывод длины дуги окружности

Приближённые формулы для периметра

Точные формулы для периметра

Джеймс Айвори и Фридрих Бессель независимо друг от друга получили формулу для периметра эллипса:

Площадь сегмента эллипса

Площадь сегмента между дугой, выпуклой влево, и вертикальной хордой , проходящей через точки (x; y) и (x; -y) можно определить по формуле:

Если эллипс задан уравнением Ax² + Bxy + Cy² = 1, то площадь можно определить по формуле

Физический смысл фокусов

1. Свет от источника, находящегося в одном из фокусов, отражается эллипсом так, что отраженные лучи пересекутся во втором фокусе.

2. Свет от источника, находящегося вне любого из фокусов, отражается эллипсом так, что отраженные лучи ни в каком фокусе не пересекутся.

3. Если F₁ и F₂ — фокусы эллипса, то для любой точки M, принадлежащей эллипсу, угол между касательной в этой точке и прямой F₁M равен углу между касательно и прямой F₂M.

4. Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.

5. Эволютой эллипса является астроида , вытянутая вдоль вертикальной оси. Эволюта плоской кривой — геометрическое место точек , являющихся центрами кривизны кривой. По отношению к своей эволюте любая кривая является эвольвентой .

6. Среди всех выпуклых замкнутых кривых, ограничивающих данную площадь, эллипсы и только они имеет максимальную аффинную длину .
Аффинная длина — параметр плоской кривой , который сохраняется при эквиаффинных преобразованиях (то есть аффинных преобразованиях , сохраняющих площадь ).

7. Если лестницу (бесконечно тонкий отрезок прямой) прислонить к вертикальной стенке с горизонтальным полом, и один конец лестницы будет скользить по стенке (всё время касаясь её) а второй конец лестницы будет скользить по полу (всё время касаясь его), тогда любая фиксированная точка лестницы (не на её концах), будет двигаться по дуге некоторого эллипса. Это свойство остаётся верным, если мы возьмём точку не внутри лестницы-отрезка, а на её мыслимом продолжении. Последнее свойство используется в описанном выше эллипсографе.

Построение эллипса с помощью иголок, нитки и карандаша.

Построение эллипса с помощью иголок, нитки и карандаша.

Эллипсы в астрономии. Все планеты и другие небесные тела Солнечной системы движутся вокруг Солнца по эллиптическим орбитам, в одном из фокусов – Солнце. Этот закон был открыт ещё Кеплером. Ближайшую точку к Солнцу Земля проходит 4 января, таким образом, для северного полушария зима чуть теплее, чем для южного. К тому же, из-за такой формы орбиты, зима для северного полушария чуть короче, то есть период между осенним и весенним равноденствием не ровно 1/2 года, а меньше. Действительно, на южном полюсе температуры бывают ниже, чем на северном полюсе.

Физическое свойство фокусировки. Лучи, испущенные из одного фокуса, после отражения соберутся во втором фокусе. Название «фокус» как раз и связано со словом «фокусировка» лучей. Если на орбите Земли расположить зеркала, так чтобы они были повёрнуты ровно по касательной к орбите, то все лучи соберутся во 2 фокусе, то есть из той точки будет видно, что вся орбита светится.

Последнее свойство используется в физике для построение оптических резонаторов в лазерной технике. Лампа накачки размещается вдоль одной из фокальных осей зеркально отражающего эллиптического цилиндра, а лазерный стержень располагается вдоль другой фокальной оси. На второй фокальной оси помещают активную среду. А свойства эллиптической поверхности помогают быть уверенными в том, что вся энергия лампы накачки соберется в области активной среды.

Почитать подробнее здесь

Поместим в одном из фокусов зеркального эллипса лампочку
и проследим за выпущенными из неё лучами света. Отразившись от эллипса, они соберутся в другом фокусе. Причём окажутся там одновременно:

Зрительно напомним геометрическое определение эллипса: эллипс есть множество точек M плоскости, сумма расстояний от которых до данных точек A и B постоянна:

Решим вспомогательную задачу. Даны две точки по одну сторону от прямой. Мы хотим пройти из A в B, набрав по пути воды из реки l.

Мы хотим пройти из A в B, набрав по пути воды из реки l. В какой точке M надо набирать воду, чтобы общий путь имел минимальную длину?

Рассмотрим точку B’, симметричную точке B. Тогда XB = XB’. Длина AX+XB = AX+XB’ минимальна, когда ломаная AXB’ превращается в прямую.

Мы хотим пройти из A в B, набрав по пути воды из реки l. В какой точке набирать воду? Ответ: в точке пересечения l с AB’ (где B’ симметрична B относительно l). Заодно мы доказали равенство углов. Мы хотим пройти из A в B, набрав по пути воды из реки l. Где набирать воду?
Ответ 1: в точке пересечения l с AB’.
Ответ 2: там, где «угол падения равен углу отражения».

Принцип Ферма: свет выбирает кратчайший путь между двумя точками.

Вернемся к доказательству оптического свойства эллипса. На эллипсе сумма AM+MB постоянна. А для точек вне эллипса эта сумма больше, AX+XB > AM+MB.

В частности, если провести в точке M касательную к эллипсу, то для любой другой точки X на этой касательной AX+XB > AM+MB. Значит, по предыдущей задаче «угол падения равен углу отражения».

…по предыдущей задаче «угол падения равен углу отражения». Оптическое свойство эллипса доказано.

Многофокусные эллипсы

N-эллипс — обобщение эллипса , имеющее более двух фокусов. N-эллипсы называют также мультифокальными эллипсами , полиэллипсами, k -эллипсами, эллипсами Чирнхауса . Впервые такие фигуры исследовал Джеймс Максвелл в 1846 году.

Пусть на плоскости задано n точек (ui , vi ) (фокусы ), тогда n -эллипс является геометрическим местом точек плоскости, для которых сумма расстояний до n фокусов является постоянной величиной d . В виде формулы данное утверждение записывается как

1-эллипс представляет собой окружность , 2-эллипс — обычный эллипс. Обе данные кривые являются алгебраическими кривыми степени 2.

Для любого числа n фокусов n -эллипс представляет собой замкнутую выпуклую кривую. Кривая является гладкой вне окрестностей фокуса.

Эллипс с 4-мя фокусами и фокусным расстоянием d = 7

Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в VK
Репетитор IT mentor в Instagram
Репетитор IT mentor в telegram

Источник

Эллипс, его фокусы и главные оси

Эллипс как коническое сечение, его фокусы и директрисы, получаемые геометрически с помощью шаров Данделена.

Э́ллипс (др.-греч. ἔλλειψις «опущение; нехватка, недостаток (эксцентриситета до 1)») — замкнутая кривая на плоскости, которая может быть получена как пересечение плоскости и кругового цилиндра или как ортогональная проекция окружности на плоскость.

Окружность является частным случаем эллипса с эксцентриситетом e=0 . Наряду с гиперболой и параболой, эллипс является коническим сечением и квадрикой.

Определение[править | править код]

Эллипс — геометрическое место точек M евклидовой плоскости, для которых сумма расстояний до двух данных точек $F_{1}$ и $F_{2}$ (называемых фокусами) постоянна и больше расстояния между фокусами, то есть

${displaystyle |F_{1}M|+|F_{2}M|=2cdot a}$

, причём ${displaystyle |F_{1}F_{2}|<2cdot a.}$

Другие определения[править | править код]

Эллипс также можно определить как:

фигуру, которую можно получить из окружности, применяя аффинное преобразование
ортогональную проекцию окружности на плоскость
пересечение плоскости и кругового цилиндра.

Связанные определения[править | править код]

Проходящий через фокусы эллипса отрезок AB, концы которого лежат на эллипсе, называется большой осью данного эллипса. Длина большой оси равна 2a в вышеприведённом уравнении.
Отрезок CD, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса.
Точка пересечения большой и малой осей эллипса называется его центром.
Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b.
Расстояния $r_{1}$ и $r_{2}$ от каждого из фокусов до данной точки на эллипсе называются фокальными радиусами в этой точке.
Расстояние $c={frac {|F_{1}F_{2}|}{2}}$ называется фокальным расстоянием.
Величина $e={frac {c}{a}}={sqrt {1-{frac {b^{2}}{a^{2}}}}}$ называется эксцентриситетом.
Диаметром эллипса называют произвольную хорду, проходящую через его центр. Сопряжёнными диаметрами эллипса называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.
Радиус эллипса в данной точке это отрезок, соединяющий центр эллипса с точкой, а также его длина, которая вычисляется по формуле $r={frac {ab}{sqrt {b^{2}cos ^{2}varphi +a^{2}sin ^{2}varphi }}}={frac {b}{sqrt {1-e^{2}cos ^{2}varphi }}}$ , где — угол между радиусом и большой полуосью.
Фокальным параметром $p={frac {b^{2}}{a}}$ называется половина длины хорды, проходящей через фокус и перпендикулярной большой оси эллипса.
Отношение длин малой и большой полуосей называется коэффициентом сжатия эллипса или эллиптичностью: ${displaystyle k={frac {b}{a}}}$ . Величина, равная $(1-k)={frac {a-b}{a}},$ называется сжатием эллипса. Для окружности коэффициент сжатия равен единице, сжатие — нулю. Коэффициент сжатия и эксцентриситет эллипса связаны соотношением ${displaystyle k^{2}=1-e^{2}.}$
Для каждого из фокусов существует прямая, называемая директрисой, такая, что отношение расстояния от произвольной точки эллипса до его фокуса к расстоянию от этой точки до данной прямой равно эксцентриситету эллипса. Весь эллипс лежит по ту же сторону от такой прямой, что и фокус. Уравнения директрис эллипса в каноническом виде записываются как ${displaystyle x=pm {frac {p}{eleft(1-e^{2}right)}}}$ для фокусов ${displaystyle left(pm {frac {pe}{1-e^{2}}},,0right)}$ соответственно. Расстояние между фокусом и директрисой равно ${displaystyle {frac {p}{e}}}$ .

Соотношения между элементами эллипса[править | править код]

Части эллипса (описание см. в разделе «Связанные определения»)

— большая полуось;
— малая полуось;
— фокальное расстояние (полурасстояние между фокусами);
— фокальный параметр;
${displaystyle {boldsymbol {r}}_{p}}$ — перифокусное расстояние (минимальное расстояние от фокуса до точки на эллипсе);
${displaystyle {boldsymbol {r}}_{a}}$ — апофокусное расстояние (максимальное расстояние от фокуса до точки на эллипсе);

${displaystyle a^{2}=b^{2}+c^{2};}$

${displaystyle e={frac {c}{a}}={sqrt {1-{frac {b^{2}}{a^{2}}}}};;;(0leqslant e<1);}$

${displaystyle p={frac {b^{2}}{a}}.}$

					${displaystyle {boldsymbol {r_{p}}}}$	${displaystyle {boldsymbol {r_{a}}}}$
— большая полуось		${displaystyle a={frac {b}{sqrt {1-e^{2}}}}}$	${displaystyle a={frac {c}{e}}}$	${displaystyle a={frac {p}{1-e^{2}}}}$	${displaystyle a={frac {r_{p}}{1-e}}}$	${displaystyle a={frac {r_{a}}{1+e}}}$
— малая полуось	${displaystyle b=a{sqrt {1-e^{2}}}}$		${displaystyle b={frac {c~{sqrt {1-e^{2}}}}{e}}}$	${displaystyle b={frac {p}{sqrt {1-e^{2}}}}}$	${displaystyle b=r_{p}{sqrt {frac {1+e}{1-e}}}}$	${displaystyle b=r_{a}{sqrt {frac {1-e}{1+e}}}}$
— фокальное расстояние		${displaystyle c={frac {be}{sqrt {1-e^{2}}}}}$		${displaystyle c={frac {pe}{1-e^{2}}}}$	${displaystyle c={frac {r_{p}e}{1-e}}}$	${displaystyle c={frac {r_{a}e}{1+e}}}$
— фокальный параметр	${displaystyle p=a(1-e^{2})}$	${displaystyle p=b~{sqrt {1-e^{2}}}}$	${displaystyle p=c~{frac {1-e^{2}}{e}}}$		${displaystyle p=r_{p}(1+e)}$	${displaystyle p=r_{a}(1-e)}$
${displaystyle {boldsymbol {r}}_{p}}$ — перифокусное расстояние	${displaystyle r_{p}=a(1-e)}$	${displaystyle r_{p}=b~{sqrt {frac {1-e}{1+e}}}}$	${displaystyle r_{p}=c~{frac {1-e}{e}}}$	${displaystyle r_{p}={frac {p}{1+e}}}$	${displaystyle {boldsymbol {r}}_{p}}$	${displaystyle r_{p}=r_{a}{frac {1-e}{1+e}}}$
${displaystyle {boldsymbol {r}}_{a}}$ — апофокусное расстояние	${displaystyle r_{a}=a(1+e)}$	${displaystyle r_{a}=b~{sqrt {frac {1+e}{1-e}}}}$	${displaystyle r_{a}=c~{frac {1+e}{e}}}$	${displaystyle r_{a}={frac {p}{1-e}}}$	${displaystyle r_{a}=r_{p}~{frac {1+e}{1-e}}}$	${displaystyle {boldsymbol {r}}_{a}}$

Координатное представление[править | править код]

Эллипс как кривая второго порядка[править | править код]

Эллипс является центральной невырожденной кривой второго порядка и удовлетворяет общему уравнению вида

${displaystyle a_{11}x^{2}+a_{22}y^{2}+2a_{12}xy+2a_{13}x+2a_{23}y+a_{33}=0}$

при инвариантах D>0 и , где:

$Delta ={begin{vmatrix}a_{11}&a_{12}&a_{13}\a_{12}&a_{22}&a_{23}\a_{13}&a_{23}&a_{33}end{vmatrix}},$

$D={begin{vmatrix}a_{11}&a_{12}\a_{12}&a_{22}end{vmatrix}}=a_{11}a_{22}-a_{12}^{2},$

${displaystyle I=operatorname {tr} {begin{pmatrix}a_{11}&a_{12}\a_{12}&a_{22}end{pmatrix}}=a_{11}+a_{22}.}$

Соотношения между инвариантами кривой второго порядка и полуосями эллипса (верно только при условии, что центр эллипса совпадает с началом координат и $a_{{33}}=-1$ ):

${displaystyle Delta =-{frac {1}{a^{2}}}{frac {1}{b^{2}}},}$

${displaystyle D={frac {1}{a^{2}}}{frac {1}{b^{2}}},}$

${displaystyle I={frac {1}{a^{2}}}+{frac {1}{b^{2}}}.}$

Соотношения

Если переписать общее уравнение в виде

$AX^{2}+BXY+CY^{2}+DX+EY+F=0,$

то координаты центра эллипса:

$h={frac {BE-2CD}{4AC-B^{2}}},k={frac {BD-2AE}{4AC-B^{2}}},$

угол вращения определяется из выражения

$tg(2Theta )={frac {B}{A-C}}.$

Направления векторов осей:

${displaystyle {begin{pmatrix}B&(C-A+{sqrt {(C-A)^{2}+B^{2}}})end{pmatrix}},{begin{pmatrix}B&(C-A-{sqrt {(C-A)^{2}+B^{2}}})end{pmatrix}},}$

отсюда

${displaystyle operatorname {tg} Theta ={frac {C-Apm {sqrt {(C-A)^{2}+B^{2}}}}{B}}.}$

Длины полуосей определяются выражениями

${displaystyle a={sqrt {frac {2F'({sqrt {(A-C)^{2}+B^{2}}}+A+C)}{4AC-B^{2}}}},}$

${displaystyle b={sqrt {{frac {2F'}{{sqrt {(A-C)^{2}+B^{2}}}+A+C}}.}}}$

Обратное соотношение — коэффициенты общего уравнения из параметров эллипса — можно получить, подставив в каноническое уравнение (см. раздел ниже) выражение для поворота системы координат на угол Θ и переноса в точку ${displaystyle (x_{c},,y_{c})}$ :

${displaystyle {frac {x'^{2}}{a^{2}}}+{frac {y'^{2}}{b^{2}}}=1,}$

${displaystyle x'=(x-x_{c})cos Theta +(y-y_{c})sin Theta ,}$

${displaystyle y'=-(x-x_{c})sin Theta +(y-y_{c})cos Theta .}$

Выполнив подстановку и раскрыв скобки, получим следующие выражения для коэффициентов общего уравнения:

${displaystyle A=a^{2}sin ^{2}Theta +b^{2}cos ^{2}Theta ,}$

${displaystyle B=2(b^{2}-a^{2})sin Theta cos Theta ,}$

${displaystyle C=a^{2}cos ^{2}Theta +b^{2}sin ^{2}Theta ,}$

${displaystyle D=-2Ax_{c}-By_{c},}$

${displaystyle E=-Bx_{c}-2Cy_{c},}$

${displaystyle F=Ax_{c}^{2}+Cy_{c}^{2}+Bx_{c}y_{c}-a^{2}b^{2}.}$

Если ввести только угол, а центр эллипса оставить в начале координат, то

${displaystyle F=-a^{2}b^{2}.}$

Следует заметить, что в уравнении общего вида эллипса, заданного в декартовой системе координат, коэффициенты (или, что то же самое, ${displaystyle a_{11},2a_{12},a_{22},2a_{13},2a_{23},a_{33}}$ ) являются определёнными с точностью до произвольного постоянного множителя, то есть приведённая выше запись и

${displaystyle AkX^{2}+BkXY+CkY^{2}+DkX+EkY+Fk=0,}$

где являются эквивалентными. Нельзя ожидать, что выражение

$1/a^{2}+1/b^{2}=Ak+Ck$

будет выполняться при любом .

Соотношение между инвариантой и полуосями в общем виде выглядит следующим образом:

${displaystyle {frac {1}{a^{2}}}+{frac {1}{b^{2}}}={frac {A+C}{Fcdot (Acdot h^{2}+Bcdot hcdot k+Ccdot k^{2}-1)}}={frac {I}{F'}},}$

где $F'=Fcdot (Acdot h^{2}+Bcdot hcdot k+Ccdot k^{2}-1)$ — коэффициент при переносе начала координат в центр эллипса, когда уравнение приводится к виду

${displaystyle AX^{2}+BXY+CY^{2}+F'=0.}$

Другие инварианты находятся в следующих соотношениях:

${displaystyle -{frac {Delta }{F'^{3}}}={frac {D}{F'^{2}}}={frac {1}{a^{2}}}{frac {1}{b^{2}}}.}$

Каноническое уравнение[править | править код]

Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением:

${frac {x^{2}}{a^{2}}}+{frac {y^{2}}{b^{2}}}=1.$

Это уравнение называется каноническим уравнением эллипса. Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат^{[Комм. 1]}.

Соотношения[править | править код]

Для определённости положим, что
В этом случае величины и — соответственно, большая и малая полуоси эллипса.

Зная полуоси эллипса, можно вычислить:

его фокальное расстояние и эксцентриситет ${displaystyle left|F_{1}F_{2}right|=2{sqrt {a^{2}-b^{2}}},;;;e={frac {sqrt {a^{2}-b^{2}}}{a}}<1,}$
координаты фокусов эллипса

Эллипс имеет две директрисы, уравнения которых можно записать как

$x={frac {a}{e}},;;;x=-{frac {a}{e}}.$

Фокальный параметр (то есть половина длины хорды, проходящей через фокус и перпендикулярной оси эллипса) равен

$p={frac {b^{2}}{a}}.$

Фокальные радиусы, то есть расстояния от фокусов до произвольной точки кривой :

$r_{1}=a+ex,;;;r_{2}=a-ex.$

Уравнение диаметра, сопряжённого хордам с угловым коэффициентом :

$y=-{frac {b^{2}}{a^{2}k}}x.$

Уравнение касательной к эллипсу в точке $(x_{0},y_{0})$ имеет вид:

${frac {xx_{0}}{a^{2}}}+{frac {yy_{0}}{b^{2}}}=1.$

Условие касания прямой y=mx+k и эллипса ${frac {x^{2}}{a^{2}}}+{frac {y^{2}}{b^{2}}}=1$ записывается в виде соотношения ${displaystyle k^{2}=m^{2}a^{2}+b^{2}.}$

Уравнение касательных, проходящих через точку :

${displaystyle {frac {y-y_{1}}{x-x_{1}}}={frac {-x_{1}y_{1}pm {sqrt {b^{2}x_{1}^{2}+a^{2}y_{1}^{2}-a^{2}b^{2}}}}{a^{2}-x_{1}^{2}}}.}$

Уравнение касательных, имеющих данный угловой коэффициент :

${displaystyle y=kxpm {sqrt {k^{2}a^{2}+b^{2}}},}$

точки касания такой прямой эллипса (или что то же самое, точки эллипса, где касательная имеет угол с тангенсом, равным ):

$x=mp {frac {ka^{2}}{sqrt {k^{2}a^{2}+b^{2}}}},y=pm {frac {b^{2}}{sqrt {k^{2}a^{2}+b^{2}}}}.$

Уравнение нормали в точке $left(x_{1},y_{1}right):$

${frac {y-y_{1}}{x-x_{1}}}={frac {a^{2}y_{1}}{b^{2}x_{1}}}.$

Уравнения в параметрической форме[править | править код]

Геометрическая иллюстрация параметризации эллипса (анимация)

Каноническое уравнение эллипса может быть параметризовано:

${begin{cases}x=a,cos t\y=b,sin tend{cases}};;;0leqslant tleqslant 2pi ,$

где — параметр.

Только в случае окружности (то есть при a=b ) параметр является углом между положительным направлением оси абсцисс и радиус-вектором данной точки.

В полярных координатах[править | править код]

Если принять фокус эллипса за полюс, а большую ось — за полярную ось, то его уравнение в полярных координатах будет иметь вид

$rho ={frac {p}{1pm ecos varphi }},$

где e — эксцентриситет, а p — фокальный параметр.
Знак минус соответствует помещению полюса полярных координат в левый фокус, а знак плюс — в правый.

Вывод уравнения[править | править код]

Пусть r₁ и r₂ — расстояния до данной точки эллипса от первого и второго фокусов.
Пусть также полюс системы координат находится в первом фокусе, а угол varphi отсчитывается от направления на второй фокус.
Тогда из определения эллипса следует, что

${displaystyle r_{1}+r_{2}=2a}$

Отсюда ${displaystyle r_{2}^{2}=left(2a-r_{1}right)^{2}=4a^{2}-4ar_{1}+r_{1}^{2}}$ .
С другой стороны, из теоремы косинусов

$r_{2}^{2}=r_{1}^{2}+4c^{2}-4r_{1}ccos varphi .$

Исключая $r_{2}$ из последних двух уравнений, получаем

${displaystyle r_{1}={frac {a^{2}-c^{2}}{a-ccos varphi }}={frac {a(1-c^{2}/a^{2})}{1-c/acos varphi }}.}$

Учитывая, что ${displaystyle p=a(1-e^{2})}$ и $e=frac{c}{a}$ , получаем искомое уравнение.

Если принять центр эллипса за полюс, а большую ось — за полярную ось, то его уравнение в полярных координатах будет иметь вид

$rho ={frac {b}{sqrt {1-e^{2}cos ^{2}varphi }}}={frac {ab}{sqrt {a^{2}sin ^{2}varphi +b^{2}cos ^{2}varphi }}}.$

Длина дуги эллипса (

s) в зависимости от его параметра (

θ)

Длина дуги эллипса[править | править код]

Длина дуги плоской линии определяется по формуле:

$l=int limits _{t_{1}}^{t_{2}}{sqrt {left({frac {dx}{dt}}right)^{2}+left({frac {dy}{dt}}right)^{2}}},dt.$

Воспользовавшись параметрическим представлением эллипса, получаем следующее выражение:

$l=int limits _{t_{1}}^{t_{2}}{sqrt {a^{2}sin ^{2}t+b^{2}cos ^{2}t}},dt.$

После замены $b^{2}=a^{2}left(1-e^{2}right)$ выражение для длины дуги принимает окончательный вид:

$l=aint limits _{t_{1}}^{t_{2}}{sqrt {1-e^{2}cos ^{2}t}},dt,;;;e<1.$

Получившийся интеграл принадлежит семейству эллиптических интегралов, которые в элементарных функциях не выражаются, и сводится к эллиптическому интегралу второго рода . В частности, периметр эллипса равен:

${displaystyle L=4aint limits _{0}^{pi /2}{sqrt {1-e^{2}cos ^{2}t}},dt=4aE(e),}$

где — полный эллиптический интеграл второго рода.

Приближённые формулы для периметра[править | править код]

$Lapprox 4{frac {pi ab+(a-b)^{2}}{a+b}}.$

Максимальная погрешность этой формулы при эксцентриситете эллипса (соотношение осей ).
Погрешность всегда положительна.

Приблизительно в два раза меньшие погрешности в широком диапазоне эксцентриситетов дает формула:
$Lapprox 4cdot left(a^{x}+b^{x}right)^{left(1/xright)}$ , где $x={frac {ln 2}{ln {frac {pi }{2}}}}.$
Максимальная погрешность этой формулы при эксцентриситете эллипса (соотношение осей )
Погрешность также всегда положительна.

Существенно лучшую точность при обеспечивает формула Рамануджана:

При эксцентриситете эллипса (соотношение осей ) погрешность составляет .
Погрешность всегда отрицательна.

Ещё точней оказалась вторая формула Рамануджана:
${displaystyle Lapprox pi (a+b)left[1+{frac {3left({frac {a-b}{a+b}}right)^{2}}{10+{sqrt {4-3left({frac {a-b}{a+b}}right)^{2}}}}}right].}$

Точные формулы для периметра[править | править код]

Джеймс Айвори^[1] и Фридрих Бессель^[2] независимо друг от друга получили формулу для периметра эллипса:

${displaystyle L=pi (a+b)left[1+sum limits _{n=1}^{infty }left[{frac {(2n-1)!!}{(2n-1)cdot 2^{n}cdot n!}}left({frac {a-b}{a+b}}right)^{n}right]^{2}right].}$

Альтернативная формула

${displaystyle L={frac {2pi aN(1-e^{2})}{M({sqrt {1-e^{2}}})}},}$

где M(x) — арифметико-геометрическое среднее 1 и ,
а N(x) — модифицированное арифметико-геометрическое среднее 1 и , которое было введено С. Ф. Адлаем в статье 2012 года^[3].

Площадь эллипса и его сегмента[править | править код]

Площадь эллипса вычисляется по формуле

Площадь сегмента между дугой^[en], выпуклой влево, и вертикальной хордой, проходящей через точки и можно определить по формуле^[4]:

$S={frac {pi ab}{2}}-{frac {b}{a}}left(x,{sqrt {a^{2}-x^{2}}}+a^{2}arcsin {frac {x}{a}}right).$

Если эллипс задан уравнением
$Ax^{2}+Bxy+Cy^{2}=1$ , то площадь можно определить по формуле

${displaystyle S={frac {2pi }{sqrt {4AC-B^{2}}}}.}$

Другие свойства[править | править код]

Оптические
- Свет от источника, находящегося в одном из фокусов, отражается эллипсом так, что отраженные лучи пересекутся во втором фокусе.
- Свет от источника, находящегося вне любого из фокусов, отражается эллипсом так, что отраженные лучи ни в каком фокусе не пересекутся.
Если $F_{1}$ и $F_{2}$ — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой $(F_{1}X)$ равен углу между этой касательной и прямой $(F_{2}X)$ .
Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
- Эквивалентная формулировка: через середины двух любых параллельных хорд эллипса проходит какой-либо диаметр эллипса. В свою очередь, любой диаметр эллипса всегда проходит через центр эллипса.
Эволютой эллипса является астроида, вытянутая вдоль вертикальной оси.
Точки пересечения эллипса с осями являются его вершинами.
Эксцентриситет эллипса, то есть отношение $e={frac {c}{a}}={sqrt {1-{frac {b^{2}}{a^{2}}}}};;;(0leqslant e<1),$ характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
- Если эксцентриситет эллипса равен нулю (что то же самое, что фокальное расстояние равно нулю: $F_{1}F_{2}=0$ ), то эллипс вырождается в окружность.
Экстремальные свойства^[5]

где

обозначает площадь фигуры

Более того, равенство достигается в том и только в том случае, если ограничено эллипсом.

Среди всех выпуклых замкнутых кривых, ограничивающих данную площадь, эллипсы и только они имеет максимальную аффинную длину.

Если произвольный эллипс вписан в треугольник ABC и имеет фокусы P и Q, тогда для него справедливо соотношение^[6]

${frac {{overline {PA}}cdot {overline {QA}}}{{overline {CA}}cdot {overline {AB}}}}+{frac {{overline {PB}}cdot {overline {QB}}}{{overline {AB}}cdot {overline {BC}}}}+{frac {{overline {PC}}cdot {overline {QC}}}{{overline {BC}}cdot {overline {CA}}}}=1.$

Если лестницу (бесконечно тонкий отрезок прямой) прислонить к вертикальной стенке с горизонтальным полом, и один конец лестницы будет скользить по стенке (всё время касаясь её) а второй конец лестницы будет скользить по полу (всё время касаясь его), тогда любая фиксированная точка лестницы (не на её концах), будет двигаться по дуге некоторого эллипса. Это свойство остаётся верным, если мы возьмём точку не внутри лестницы-отрезка, а на её мыслимом продолжении. Последнее свойство используется в описанном выше^[⇦] эллипсографе.

Касательная, проходящая через точку $(x_{0},y_{0})$ , принадлежащую эллипсу, имеет следующее уравнение:

${displaystyle {frac {xx_{0}}{a^{2}}}+{frac {yy_{0}}{b^{2}}}=1.}$

Построение эллипса[править | править код]

Построение эллипса с помощью иголок, нитки и карандаша

Инструментами для рисования эллипса являются:

эллипсограф
две иголки, воткнутые в фокусы эллипса и соединённые ниткой длиной 2a, которую оттягивают карандашом. Способ был придуман Джеймсом Максвеллом в возрасте 14 лет и при запросе его отца в Эдинбургское королевское общество оказался ранее неизвестным^[7].

При помощи циркуля или циркуля и линейки можно построить любое количество точек, принадлежащих эллипсу, но не весь эллипс целиком.

Эллипсы, связанные с треугольником[править | править код]

Эллипс Брокара — эллипс с фокусами в точках Брокара
Эллипс Мандарта
Эллипс Штейнера

См. также[править | править код]

Кривая второго порядка
Парабола
Каустика
Эллипсоид
Эллипсограф
Гипербола
Окружность Аполлония
Овал Кассини

Комментарии[править | править код]

↑ Если же в правой части стоит единица со знаком минус, то получившееся уравнение

${displaystyle {frac {x^{2}}{a^{2}}}+{frac {y^{2}}{b^{2}}}=-1}$

описывает мнимый эллипс, он не имеет точек на вещественной плоскости.

Примечания[править | править код]

↑ Ivory J. A new series for the rectification of the ellipsis (англ.) // Transactions of the Royal Society of Edinburgh. — 1798. — Vol. 4. — P. 177—190. — doi:10.1017/s0080456800030817.
↑ Bessel F. W. Über die Berechnung der geographischen Längen und Breiten aus geodätischen Vermesssungen (нем.) // Astron. Nachr.. — 1825. — Bd. 4. — S. 241—254. — doi:10.1002/asna.18260041601. — Bibcode: 1825AN……4..241B. В англ. переводе: Bessel F. W. The calculation of longitude and latitude from geodesic measurements (1825) (англ.) // Astron. Nachr.. — 2010. — Vol. 331. — P. 852—861. — doi:10.1002/asna.201011352. — arXiv:0908.1824.
↑ Adlaj S. An eloquent formula for the perimeter of an ellipse (англ.) // Notices of the AMS. — 2012. — Vol. 76, iss. 8. — P. 1094—1099. — doi:10.1090/noti879.
↑ Корн, 1978, с. 68.
↑ Фейеш Тот Л. Глава II, §§ 4, 6 // Расположения на плоскости, на сфере и в пространстве. — М.: Физматгиз, 1958. — 364 с.
↑ Allaire P. R., Zhou J., Yao H. Proving a nineteenth century ellipse identity (англ.) // Mathematical Gazette. — 2012. — Vol. 96, no. 535. — P. 161—165.
↑ Карцев В. П. Максвелл. — М.: Молодая гвардия, 1974. (Серия «Жизнь замечательных людей»). С. 26—28.

Литература[править | править код]

Корн Г., Корн Т. Свойства окружностей, эллипсов, гипербол и парабол // Справочник по математике. — 4-е издание. — М.: Наука, 1978. — С. 70—73.
Селиванов Д. Ф. Эллипс // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
А. В. Акопян, А. А. Заславский. Геометрические свойства кривых второго порядка, — М.: МЦНМО, 2007. — 136 с.
И. Бронштейн. Эллипс // Квант, № 9, 1970.
А. И. Маркушевич. Замечательные кривые // «Популярные лекции по математике», выпуск 4.

Ссылки[править | править код]

S.Sykora, Approximations of Ellipse Perimeters and of the Complete Elliptic Integral E(x). Review of known formulae (англ.)
Grard P. Michon. Perimeter of an Ellipse (Final Answers) (англ.), 2000—2005. — 20 c.
Видео: Как нарисовать эллипс

Источник

Макеты страниц

Определение. Величина R, обратная кривизне К линии в данной точке М, называется радиусом кривизны этой линии в рассматриваемой точке:

или

Построим в точке М нормаль к кривой (рис. 146), направленную в сторону вогнутости кривой, и отложим на этой нормали отрезок МС, равный радиусу R кривизны кривой в точке М.

Рис. 146.

Рис. 147.

Точка С называется центром кривизны данной кривой в точке М, круг радиуса R с центром в точке С (проходящий через точку М) называется кругом кривизны данной кривой в точке М.

Из определения круга кривизны следует, что в данной точке кривизна кривой и кривизна круга кривизны равны между собой.

Выведем формулы, определяющие координаты центра кривизны.

Пусть кривая задана уравнением

Зафиксируем на кривой точку (х, у) и определим координаты центра кривизны, соответствующего этой точке (рис. 147). Для этого напишем уравнение нормали к кривой в точке М:

(Здесь X и Y — текущие координаты точки нормали.)

Так как точка лежит на нормали, то ее координаты должны удовлетворять уравнению (4):

Далее, точка находится от точки на расстоянии, равном радиусу кривизны

Решая совместно уравнения (5) и (6), определим а и Р:

отсюда

а так как , то

Чтобы решить вопрос о том, верхние или нижние знаки следует брать в последних формулах, нужно рассмотреть случай и случай . Если , то в этой точке кривая вогнута и, следовательно, и поэтому следует брать нижние знаки. Учитывая, что в этом случае формулы координат центра запишем в следующем виде:

Аналогично можно показать, что формулы (7) будут справедливы и в случае

Если кривая задана параметрическими уравнениями

то координаты центра кривизны легко получить из формул (7), подставляя в них вместо их выражения через параметр:

Тогда

Пример 1. Определить координаты центра кривизны параболы

а) в произвольной точке ; б) в точке ); в) в точке .

Решение. Подставляя значения и в формулы (7), получим (рис. 148)

a) ; б) при находим при имеем .

Если в точке данной линии кривизна отлична от нуля, то этой точке соответствует вполне определенный центр кривизны . Совокупность всех центров кривизны данной линии образует некоторую новую линию, называемую эволютой по отношению к первой.

Рис. 148.

Рис. 149.

Таким образом, геометрическое место центров кривизны данной линии называется ее эволютой. По отношению к своей эволюте данная линия называется эвольвентой или инволютой (или разверткой)

Если данная кривая определяется уравнением , то уравнения (7) можно рассматривать как параметрические уравнения эволюты с параметром х. Исключая из этих уравнений параметр это возможно), получим непосредственную зависимость между текущими координатами эволюты . Если же кривая задана параметрическими уравнениями , то уравнения (7) дают параметрические уравнения эволюты (так как величины являются функциями от ).

Пример 2. Найти уравнение эволюты параболы .

Решение. На основании примера 1 имеем для любой точки раболы Исключая из этих уравнений параметр получим то — уравнение полукубической параболы (рис. 149).

Пример 3. Найти уравнение эволюты эллипса, заданного параметрическими уравнениями

Решение. Вычисляем производные от х и у по

Подставляя выражения производных в формулы (7), получим

Таким образом,

Аналогично получаем:

Исключив параметр t, получаем уравнение эволюты эллипса в виде

Здесь — текущие кооординаты эволюты (рис. 150).

Рис. 150.

Пример 4. Найти параметрические уравнения эволюты циклоиды

Решение.

Подставив полученные выражения в формулу (7), находим

Сделаем преобразование переменных, положив

тогда уравнения эволюты примут вид

они определяют в координатах циклоиду с тем же производящим кругом радиуса а. Таким образом, эволютой циклоиды является такая же циклоида, но смещенная по оси Ох на величину — и по оси Оу на величину – (рис. 151).

Рис. 151.

Источник

Исследование формы эллипса по его уравнению

Дополнительные сведения об эллипсе

Площадь фигуры, ограниченной эллипсом

Длина дуги эллипса (периметр эллипса)

Площадь сегмента эллипса

Физический смысл фокусов

Многофокусные эллипсы

Определение[править | править код]

Другие определения[править | править код]

Связанные определения[править | править код]

Соотношения между элементами эллипса[править | править код]

Координатное представление[править | править код]

Эллипс как кривая второго порядка[править | править код]

Каноническое уравнение[править | править код]

Соотношения[править | править код]

Уравнения в параметрической форме[править | править код]

В полярных координатах[править | править код]

Вывод уравнения[править | править код]

Длина дуги эллипса[править | править код]

Приближённые формулы для периметра[править | править код]

Точные формулы для периметра[править | править код]

Площадь эллипса и его сегмента[править | править код]

Другие свойства[править | править код]

Построение эллипса[править | править код]

Эллипсы, связанные с треугольником[править | править код]

См. также[править | править код]

Комментарии[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Вам также может понравиться

Как найти налог по номеру налогового уведомления

Как найти ответы на олимпиаду 2021

Как составить игру на знакомство

Добавить комментарий Отменить ответ