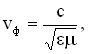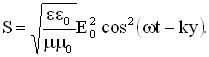Фазовая скорость распространения волны как найти

Фазовая скорость распространения волны как найти

Формула скорости волны в физике

Формула скорости волны

Определение

Фронт волны (волновая поверхность) – это геометрическое место точек среды, для которых в некоторый момент времени фаза волны
имеет одно и то же значение.

Скоростью волны называют скорость, с которой движется фронт волны.

Формула фазовой скорости волны

Рассмотрим одномерный случай для гармонической волны. Уравнение волновой поверхности при это запишем как:

[Ф_s=omega t-kx+varphi left(1right),]

где${ Ф}_s$ – фаза волны; $k=frac{2pi }{lambda }$ – волновое число; $lambda $ – длина волны; $omega $ – циклическая частота; $varphi $ – начальная фаза. Уравнению (1) в каждый момент времени соответствует только одна точка оси X координата которой, равна:

[x=frac{omega t+varphi -Ф_s}{k}left(2right).]

Разным значениям фазы волны $Ф_s$ соответствуют разные волновые поверхности, каждая из которых в одномерной волне превращается в точку. Из формулы (2) видно, что волновые поверхности перемещаются в среде со скоростью:

[frac{dx}{dt}=frac{omega }{k}=frac{lambda }{T}=v left(3right),]

где $T$ – период колебаний точек в волне.

Если волны гармонические, то скорость движения волновой поверхности равна скорости распространения волны. Скорость, которую определяет выражение (3) является фазовой скоростью.

Фазовая скорость гармонической волны совпадает со скорость распространения энергии волны.

Скорость волны зависит от вещества, в котором распространяется волна и типа волны. Скорость волны – это не то же самое, что скорость колебания частиц среды в волне.

Формула для вычисления фазовой скорости распространения продольных волн

Скорость распространения продольных упругих волн в однородных в газах или жидкостях может быть вычислена как:

[v=sqrt{frac{K}{rho }}left(4right),]

где $K$ – модуль объемной упругости вещества; $rho =const$ – плотность среды. В газах формула (4) выполняется, если избыточное давление много меньше, равновесного давление газа в невозмущенном состоянии.

Для нахождения скорости распространения продольных волн в газе применяют выражение:

[v=sqrt{frac{gamma p}{rho }}left(5right),]

где $gamma $ – показатель адиабаты; $p$ – давление газа.

Продольные механические волны могут распространяться в твердых телах, их фазовая скорость равна:

[v=sqrt{frac{E}{rho }}left(6right),]

где $E$ – модуль Юнга вещества стержня.

Формула для фазовой скорости распространения поперечных волн

Поперечные механические волны способны распространяться только в твердых телах. Скорость ($v$) распространения поперечных волн в бесконечной изотропной среде при этом можно найти как:

[v=sqrt{frac{G}{rho }left(7right),}]

где $G$ – модуль сдвига среды; $rho $ – плотность вещества.

Упругие свойства и плотность твердого тела зависит от химического состава вещества, и она несущественно изменяется при изменении давления и температуры. Поэтому в большинстве случаев скорость распространения волны можно считать постоянной.

Формула для групповой скорости волн

Кроме фазовой скорости для описания распространения диспергирующих волн применяют понятие групповой скорости. При этом фазовая скорость может зависеть от частоты, при этом в веществе распространяются волны сложного негармонического характера, тогда с групповую скорость проще использовать, как характеристику скорости распространения волн.

Групповой скоростью называют скорость перемещения группы (цуга) волн, которые создают в каждый момент времени, локализованный в пространстве, волновой пакет. Любая реальная волна представляет собой суперпозицию гармонических волн. Скорость, с которой такая волна распространяется в веществе, имеющем дисперсию, равна фазовой скорости накрадывающихся волн. Распространение волны определяют перемещением энергии колебаний, которую переносит группа вол от источника.

Групповая скорость ($u$) связана с фазовой скоростью ($v$) формулой:

[u=v-frac{dv}{dlambda }left(8right).]

Если дисперсия отсутствует, то $frac{dv}{dlambda }=0$, тогда фазовая и групповая скорости равны и не зависят от длины волны.

Примеры задач с решением

Пример 1

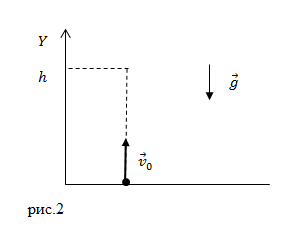
Задание. За время равное $t=20$ c волне совершается $N=$100 колебаний, при этом расстояние между соседними максимумами волны составляет 1 м. Какова скорость распространения волны?

Решение. Сделаем рисунок.

Формула скорости волны, пример 1

В качестве основы для решения задачи используем формулу для вычисления фазовой скорости волны вида:

[v=frac{lambda }{T} left(1.1right).]

Найдем период колебаний как время одного полного колебания:

[T=frac{t}{N} left(1.2right).]

Используя формулу (1.2) скорость будем вычислять, применяя формулу:

[v=frac{lambda N}{t}.]

Вычислим искомую скорость:

[v=frac{1cdot 100}{20}=5left(frac{м}{с}right).]

Ответ. $v=5frac{м}{с}$

Пример 2

Задание. Уравнение плоской волны, которая распространяется вдоль положительного направления оси X, имеет вид: $xi left(x,tright)=2{cos left[omega left(t-frac{x}{v}right)right] }left(мright).$ Частота колебаний $nu =450$Гц, длина волны $lambda =0,8 $м. Какова скорость распространения волны, какой будет максимальная скорость колебания частиц среды?

Решение. Фазовую скорость движения волны найдем как:

[v=frac{lambda }{T}=lambda nu left(2.1right),]

где период – величина обратная частоте колебаний:

[T=frac{1}{nu }left(2.2right).]

Вычислим фазовую скорость:

[v=450cdot 0,8=360 left(frac{м}{с}right).]

Скорость колебания частиц равна:

[frac{dxi }{dt}=frac{d}{dt}left(2{cos left[omega left(t-frac{x}{v}right)right] }right)=-2omega {sin left[omega left(t-frac{x}{v}right)right]left(2.3right). }]

Максимальное значение скорости колебаний частиц в волне из (2.3) равно:

[{left(frac{dxi }{dt}right)}_{max}=left|2omega right|left(2.4right).]

Циклическую частоту найдем как:

[omega =2pi nu ,]

тогда:

[{left(frac{dxi }{dt}right)}_{max}=left|2cdot 2pi nu right|=4pi nu .]

Вычислим максимальную скорость колебаний частиц:

[{left(frac{dxi }{dt}right)}_{max}=4pi cdot 450=5,65cdot {10}^3left(frac{м}{с}right).]

Ответ. $v=360 frac{м}{с}$, ${left(frac{dxi }{dt}right)}_{max}=5,65cdot {10}^3frac{м}{с}$

Читать дальше: формула скорости свободного падения.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник

Фазовая скорость вдоль направления, отклонённого от волнового вектора на угол α. Рассматривается монохроматическая плоская волна

Фа́зовая ско́рость — скорость перемещения точки, обладающей постоянной фазой колебательного движения в пространстве, вдоль заданного направления. Обычно рассматривают направление, совпадающее с направлением волнового вектора, и фазовой называют скорость, измеренную именно в этом направлении, если противное не указано явно (то есть если явно не указано направление, отличное от направления волнового вектора). Фазовая скорость по направлению волнового вектора совпадает со скоростью движения фазового фронта (поверхности постоянной фазы). Её можно рассматривать при желании как векторную величину.

Наиболее употребительное обозначение: v_{phi } .

Строго говоря, понятие фазы применимо только при описании гармонических или монохроматических (то есть синусоидальных {displaystyle sin(phi )} или являющихся мнимыми экспонентами e^{iphi }) волн, а также — приближенно — для волн близкой формы (например, почти монохроматических волновых пакетов) или легко сводящихся к синусоидальным (например, сферических волн вида cos(phi )/r), или, что менее корректно, при описании периодических волн другой формы. Тем не менее, волну (практически) любой формы с помощью преобразования Фурье можно представить как сумму монохроматических волн, и тогда к каждой из этих волн понятие фазы и фазовой скорости применимо вполне строго (впрочем, тогда у каждой монохроматической волны в разложении будет, вообще говоря, своя фазовая скорость, не совпадающая с другими; только в частных случаях они могут все точно совпадать или быть близки).

Для описания волн, отличных от гармонических, (особенно для описания волновых пакетов), используют, кроме понятия фазовой скорости, понятие скорости групповой (описывающей движение не отдельного гребня в волновом пакете, а его огибающей, например, максимума огибающей).

Формулы[править | править код]

Основная формула, определяющая фазовую скорость (монохроматической) волны в одномерном пространстве или фазовую скорость вдоль волнового вектора для волны в пространстве большей размерности:

{displaystyle v_{phi }=omega /k}

которая является прямым следствием того факта, что фаза плоской волны в однородной среде есть

phi =omega t-kx для одномерного случая

или phi =omega t-{vec k}cdot {vec x} для размерности, большей единицы.

Конкретное соотношение между omega и k — так называемый закон дисперсии — для каждого конкретного типа волн получают обычно из дифференциального уравнения, описывающего данный тип волн, подставляя в него монохроматическую (чаще всего плоскую) волну[1].

В случае, когда фазовая скорость не зависит для данного типа волн от частоты или волнового числа (и направления волнового вектора), групповая скорость совпадает с фазовой.

Фазовая скорость электромагнитной волны[править | править код]

В вакууме для электромагнитной волны любой частоты (по крайней мере в тех диапазонах частот и интенсивностей, которые исследованы) фазовая скорость, измеренная в направлении волнового вектора, всегда равна одной и той же величине — скорости света в вакууме, универсальной константе.

В средах закон дисперсии электромагнитных волн достаточно сложен (см. Дисперсия света), и фазовая скорость может заметно меняться, вплоть до отрицательных[2] значений.

Для волнового уравнения[править | править код]

Любая волна, описываемая волновым уравнением

{frac {partial ^{2}f}{partial t^{2}}}=C^{2}{frac {partial ^{2}f}{partial x^{2}}},

имеет фазовую скорость С (причём C здесь — некий постоянный коэффициент; этот коэффициент равен скорости света в волновом уравнении для электромагнитных волн).

Такой результат получается прямой подстановкой в это уравнение монохроматической волны вида cos(kx-omega t) и затем вычислением
omega /k.

Этот результат верен не только для волнового уравнения на одномерном пространстве (мы его использовали выше лишь для краткости; всё остаётся совершенно аналогичным при любом количестве производных по координатам в правой части).

Для уравнения Клейна—Гордона[править | править код]

Уравнение Клейна — Гордона

{displaystyle {frac {partial ^{2}f}{partial t^{2}}}=C^{2}{frac {partial ^{2}f}{partial x^{2}}}+C^{4}m^{2}f},

отличающееся только последним членом, даёт при аналогичной подстановке

{displaystyle omega ^{2}=C^{2}k^{2}+C^{4}m^{2}},

откуда:

omega ={sqrt {C^{2}k^{2}+C^{4}m^{2}}}

и

v_{varphi }=omega /k=C{sqrt {1+C^{2}m^{2}/k^{2}}}.

Это выражение при ненулевых вещественных m всегда больше, чем C, и может быть сколь угодно большим при k → 0.

Фазовая скорость как вектор[править | править код]

В некотором смысле фазовая скорость не является вектором. Говоря так, имеют в виду тот факт, что фазовые скорости по разным направлениям (например, по направлениям координатных осей), определяемые так, как это описано выше, не являются ни координатами, ни проекциями[3] никакого вектора[4]. В том числе, очевидно, они не являются проекциями или координатами вектора, совпадающего по направлению с волновым вектором, и с абсолютной величиной, равной фазовой скорости в этом направлении.

Но это, конечно, не мешает при желании ввести чисто формально вектор фазовой скорости, по определению совпадающий по направлению с волновым вектором и с абсолютной величиной, равной фазовой скорости в этом направлении. Вопрос о том, корректно ли называть такой вектор вектором фазовой скорости, является чисто терминологическим (конвенциональным). Фактом является лишь то, что проекции этого «вектора» на оси координат или компоненты по этим осям не будут соответствовать фазовой скорости вдоль этих направлений в соответствии с определением фазовой скорости по направлению, данным в начале статьи (и вообще с каким-то разумным определением, кроме чисто формального, описанного в данном абзаце).

Конкретно же, для случая плоской гармонической волны фазовую скорость вдоль волнового вектора можно выразить следующим образом:

{displaystyle v_{phi }equiv v_{phi ,0}=omega /k},

где k — волновое число, omega  — угловая частота.
При этом фазовая скорость вдоль направления, отклонённого от волнового вектора на угол alpha , будет равна:

v_{{phi ,alpha }}={frac {v_{{k}}}{cos alpha }}

Непонимание этого факта часто служит причиной недоразумений и ошибок. Например, из приведённого выше ясно, что фазовая скорость может быть больше скорости света (это вытекает прямо из написанной выше формулы, учитывая, что cos alpha может принимать сколь угодно малые значения при стремлении угла к прямому, и, соответственно, фазовая скорость по направлению, близкому к ортогональному, оказывается сколь угодно велика, стремясь к бесконечности)[5].

Может ли фазовая скорость превосходить скорость света[править | править код]

Фазовая скорость может превосходить скорость света в вакууме, и нередко её превосходит. Это никак не противоречит известному принципу максимальности скорости света, необходимость которого возникает, чтобы одновременно соблюдались принцип причинности (чтобы не возникало причинных парадоксов) и принцип относительности (лоренц-инвариантность).

Дело в том, что эти принципы накладывают ограничение только на скорость распространения таких физических объектов, посредством которых можно передать информацию. А фазовая скорость[6] не относится к скоростям таковых объектов. Чисто монохроматическая (синусоидальная) волна бесконечна в пространстве и во времени, не может никак измениться, чтобы передать информацию (если мы промодулируем волну, она перестанет быть монохроматической, а скорость распространения модуляции не совпадает с фазовой скоростью, обычно совпадая со скоростью групповой для почти монохроматических волн).

Фазовая скорость по направлению, не совпадающему с волновым вектором[править | править код]

Поскольку фазовая скорость, измеренная вдоль произвольного направления, не совпадающего с волновым вектором и направлением распространения волны, не является скоростью движения «физического объекта», то есть объекта, состояние которого в последующие моменты времени причинно обусловлено состоянием в предыдущие, а по сути характеризует просто состояние осциллирующего поля в искусственно выбранных точках, часто (а именно если выбрать достаточно большой угол с волновым вектором) фазовая скорость по данному направлению любой, даже сколь угодно медленной (как показано в параграфе выше) волны может превышать скорость света, стремясь к бесконечности при стремлении угла к прямому.

В частности, фазовая скорость света (или вообще любой бегущей электромагнитной волны) в вакууме, измеренная по любому направлению, не совпадающему с её волновым вектором, всегда больше скорости света.

Но дело не ограничивается фазовой скоростью по произвольному направлению. Скорость света может быть превзойдена даже и фазовой скоростью, измеренной вдоль волнового вектора.

Фазовая скорость для квантовой частицы[править | править код]

Фазовая скорость квантовой «волны», соответствующей любой массивной частице (то есть частице, имеющей массу больше нуля), всегда больше скорости света. Это легко видеть из формул v_{phi }=omega /k, E = hbar omega и p=hbar k, из чего v_{phi }=E/p, в то время как E для массивных частиц всегда больше p за счёт массы (энергии покоя).

Однако эта фазовая скорость в принципе не может наблюдаться (так как в квантовой физике фаза ненаблюдаема вообще). Доступна же наблюдению лишь групповая скорость, которая и является квантовым аналогом обычной скорости классической частицы.

Фазовая скорость для уравнения Клейна — Гордона[править | править код]

Но дифференциальные уравнения, описывающие квантовые частицы, могут быть реализованы в принципе и на других физических системах (например, на достаточно простых механических моделях). В этом случае фазовая скорость вполне доступна наблюдению.

Тем не менее и здесь фазовая скорость может быть сделана сколь угодно большой (достаточно подобрать достаточно малое k), и в принципе её нетрудно сделать большей, чем скорость света.

Этот на вид парадоксальный результат связан с тем, что «распространение» такой волны является иллюзией[7] в том смысле, что между разными частями волны нет причинной связи (состояние волны, продвинувшейся вправо, не определяется тем, какой она была слева).

Примечания[править | править код]

  1. ↑ cos(kx-omega t) или exp(i(kx-omega t)) или аналогичный многомерный вариант.
  2. ↑ Логотип YouTube Материалы с отрицательным показателем преломления — Виктор Веселаго
  3. ↑ В случае использования, например, косоугольных координат понятия координаты вектора и проекции на ось не совпадают.
  4. ↑ Конечно, в определённой фиксированной системе координат любая тройка (будем говорить для определённости о трёхмерном случае) чисел определяет вектор; однако если мы имеем дело с настоящим вектором, то при смене системы координат (например, при повороте осей) мы должны получить согласованные по определённым правилам результаты для любой системы координат, а уже такое оказывается для рассматриваемой нами тройки чисел неверным.
  5. ↑ Это не противоречит теории относительности. См. следующий параграф.
  6. ↑ Как, например, и скорость зайчика на экране — см. статью Сверхсветовое движение.
  7. ↑ Распространение как факт, конечно, имеет место; под иллюзией здесь понимается то, что мы склонны интуитивно вкладывать в этот факт больше, чем в нём реально есть, а именно мы интуитивно склонны считать, что для волны, движущейся слева направо, предыдущие состояния волны слева являются причиной последующих состояний справа, что не так. На самом деле более верным было бы сказать, что разные части этой волны колеблются независимо друг от друга, и наложение таких колебаний и даёт бегущую волну (действительно, чем-то похоже на оптический обман).

Ссылки[править | править код]

  • Физическая энциклопедия OnLine. Том 5, стр.266.
Источник

Волны,
образованные внешним воздействием,
приложенным к упругой среде,
называются бегущими
волнами:
они “бегут” от создающего их источника.
Если внешняя сила совершает гармонические
колебания, то вызванные ею волны
называются гармоническими
бегущими волнами.

Фазовая
скорость волны.

Фазовая
скорость  –
это скорость распространения данной
фазы колебаний, т.е. скорость волны.

Связь
длины волны ,
фазовой скорости  и
периода колебаний Т задается соотношением:

.

Учитывая,
что ,
где  – линейная
частота волны,  –
период, а циклическая
частота волны ,
получим разные формулы для фазовой
скорости:

.

Для
волнового процесса характерна
периодичность по времени и по пространству.

Т
– период колебаний точек среды. Роль
пространственного периода играет длина
волны . Соотношение
между периодом и циклической частотой
задается формулой: .
Аналогичное соотношение можно записать
для длины волны и величиной k,
называемой волновым
числом: .

еще
одно уравнение для фазовой скорости:

.

Фазовая
скорость различна для разных сред. В
случае упругих поперечных волн (в твердом
теле) фазовая скорость равна:

 ,

где –
модуль сдвига среды,  -ее
плотность в невозбужденном состоянии
(т.е. когда в этой среде не распространяется
упругая волна).

Фазовая
скорость упругих продольных волн в
твердом теле равна

,

где
Е – модуль Юнга, –
плотность невозмущенной среды (твердого
тела до момента распространения по нему
волны).

Фазовая
скорость продольных волн в жидкости и
газе определяется соотношением:

,

где
К – модуль
объемной упругости среды –
величина, характеризующая способность
среды сопротивляться изменению ее
объема, –
плотность невозмущенной среды.

Фазовая
скорость продольных волн в идеальном
газе задается формулой:

,

 –
показатель адиабаты, –
молярная масса, Т – абсолютная температура,
R – универсальная газовая постоянная.
Фазовая скорость в газе зависит от сорта
газа ()
и от его термодинамического состояния
(Т).

Уравнение
бегущей волны.
уравнение
бегущей волны в
одномерном пространстве, которое
предполагаем изотропным и однородным.
Кроме того, силы сопротивления в среде
считаем пренебрежимо малыми (т.е. нет
затухания колебаний). Пусть точка О –
центр (источник) колебаний, она колеблется
по закону:

,

где  –
смещение точки О от положения равновесия, –
частота, А – амплитуда колебаний. Часы
или секундомер №1 включаются сразу, как
только начинаются колебаний точки О, и
отсчитывают время t (Рисунок 2.1.1). Ось ОУ
совпадает с направлением распространения
волны.

Через
промежуток времени  процесс
колебаний дойдет до точки В, и она будет
колебаться по закону:

.


Амплитуда
колебаний в случае отсутствия затухания
процесса будет такой же как и амплитуда
точки О. Часы или секундомер №2 включаются
тогда, когда колебательный процесс
дойдет до точки В (т.е. когда начинает
колебаться точка В), и отсчитывают
время .
Моменты времени t и  связаны
между собой соотношением  или .
Расстояние между точками О и В обозначим .
Фазовая скорость волны равна ,
тогда .
Учитывая соотношения для  и  и
формулы  и ,
можно записать уравнение колебаний
точки В в разных видах:

.

Аналогично
уравнению колебаний точки В запишем
уравнение колебаний любой точки среды,
расположенной на расстоянии y от источника
колебаний:

,

где  –
волновое число (см. определение выше).

Это
уравнение и есть уравнение для
смещения  любой
точки пространства в любой момент
времени, т.е. уравнение бегущей волны,
где А – амплитуда, величина  –
фаза волны, которая в

Билет
40

СЛОЖЕНИЕ
ВОЛН

Сложение
в пространстве двух (или нескольких)
волн, при котором образуется постоянное
во времени распределение амплитуды
результирующих колебаний в различных
точках пространства, называется
интерференцией.

СТОЯЧИЕ
ВОЛНЫ

Частным
случаем интерференции являются стоячие
волны – волны, образующиеся при наложении
двух бегущих волн, распространяющихся
навстречу друг другу волн с одинаковыми
амплитудами и частотами.

Для
вывода уравнения стоячей волны примем:
1) волны распространяются в среде без
затухания; 2) А1 =
А2 =А –
имеют равные амплитуды; 3) ω1 =
ω2=
ω – равные частоты; 4)φ10 =
φ20 =
0.

Уравнение
бегущей волны, распространяющейся вдоль
положительного направления оси х (т.е.
уравнение падающей волны):

(1)

Уравнение
бегущей волны, распространяющейся в
отрицательном направлении оси х (т.е.
уравнение отраженной волны):

(2)

Сложив
(1) и (2) получим уравнение стоячей волны:

Особенностью
 стоячей волны является то, что
амплитуда зависит от координаты х.
При перемещении от одной точки к другой
амплитуда меняется по закону:

ДИСПЕРСИЯ
И ГРУППОВАЯ СКОРОСТЬ ВОЛНЫ

Дисперсия
волн – ,зависимость фазовой скорости
гармонических волн в среде от частоты
их колебаний. Дисперсия волн наблюдается
для волн любой природы. Наличие дисперсии
волн приводит к искажению формы сигнала
(напр., звукового импульса) при
распространении в среде. 

Групповая
скорость – ,величина, приближенно
характеризующая распространение
негармонической волны (она является
суперпозицией группы гармонических
волн). Если форма волны изменяется в
результате дисперсии волн в среде не
очень быстро, то можно рассматривать
распространение негармонической волны
как целого с групповой скоростью,
отличной от фазовых скоростей ее
гармонических составляющих. Групповая
скорость характеризует скорость переноса
энергии волной. 

Билет
41

ИНТЕРФЕРЕНЦИЯ
СВЕТА

Интерференция
– явление, имеющее место при наложении
(суперпозиции) когерентных волн и
состоящее в увеличении амплитуды
результирующих колебаний в одних точках
пространства при одновременном ослаблении
колебаний в других точках. Таким образом,
при интерференции происходит
пространственное перераспределение
энергии накладывающихся волн.

Интерференция
света
– частный случай общего явления
интерференции волн. При интерференции
света возникает интерференционная
картина – чередование областей с
повышенной и пониженной освещенностью,
например, кольца Ньютона, наблюдаемые
в данной работе. Устойчивая интерференция
возможна лишь в случае, когда в любой
точке области наложения волн их разность
фаз постоянна во времени (волны взаимно
когерентны).

РАСЧЁТ
ИНТЕРФЕРЕНЦИОННОЙ КАРТИНЫ ОТ ДВУХ
КОГЕРЕНТНЫХ ИСТОЧНИКОВ

Пусть
в некоторую точку пространства M
приходят световые волны от двух взаимно
когерентных источников

и

(рисунок 1), или, что равноценно, от одного
источника, но прошедшие до места встречи
разные пути. Через

и

обозначим оптические пути, пройденные
волнами от источников до точки
:

,
где

– расстояния, пройденные волнами,

– показатели преломления сред, через
которые шли волны.

Рисунок
1 – Ход лучей при интерференции.

В
точке M
каждая из этих волн вызывает колебания
напряженности электрического поля,
описывающиеся уравнениями:

,

, (1)

где


– мгновенные значения напряженностей
электрических полей обеих волн,

– амплитуды напряженностей,

– циклическая частота,

– время,

– волновое число,

– длина световой волны в вакууме,

– начальные фазы волн (для упрощения
далее полагаем, что
).

Амплитуда


результирующего колебания в точке

такова:

, (2)

где


– разность фаз волн в точке M;


– оптическая разность хода волн.

Из
формулы (2) следует, что волны усилят
друг друга, и в точке

возникнет интерференционный максимум
освещенности, если
,
то есть
,
где
,
или
,
следовательно:

. (3)

Последнее
равенство есть условие интерференционного
максимума: две волны при наложении
усилят друг друга, если их оптическая
разность хода равна нулю или на ней
укладывается целое число длин волн
.
В этом случае
,
а если
,
то
.

Из
(2) также следует, что взаимное ослабление
волн и образование в точке

интерференционного минимума имеет
место, если
,
то есть
,
где
.
При этом

,
то есть:

. (4)

Последнее
равенство есть условие интерференционного
минимума: две волны при наложении ослабят
друг друга, если на оптической разности
хода укладывается нечетное число длин
полуволн
.
В этом случае
,
а при

происходит полное гашение:
.

БИЛЕТ
42

ПОЛОСЫ
РАВНОЙ ТОЛЩИНЫ И РАВНОГО НАКЛОНА

Различают
интерференционные картины двух типов:
полосы
равного наклона,
когда на плоскопараллельный слой падает
расходящийся пучок лучей, и полосы
равной толщины,
когда пучок параллельных лучей падает
на слой с непараллельными поверхностями
(клин).

Частным
случаем полос равной толщины являются
кольца
Ньютона.
Для их наблюдения плосковыпуклую линзу
с большим радиусом кривизны

помещают на гладкую стеклянную пластину
(см. рисунок 2). Между линзой и пластиной
вокруг точки их соприкосновения

имеется тонкий воздушный клин. На линзу
направляют пучок параллельных лучей.
В отраженном свете полосы равной толщины
возникают в результате интерференции
луча 1, отраженного в точке

от нижней поверхности линзы, и луча 2,
отраженного в точке

от верхней поверхности пластинки, то
есть от поверхностей воздушного клина.
Ввиду малости кривизны линзы лучи 1 и 2
фактически совпадают и накладываются
на падающий луч (на рисунке 2 углы
отражения лучей 1 и 2 преувеличены для
наглядности). Толщина воздушного зазора


определяется расстоянием

до точки касания, поэтому полосы равной
толщины имеют вид концентрических
колец.

Рисунок
2 – Ход лучей при наблюдении колец Ньютона.

Как
видно из рисунка 2, оптическая разность
хода лучей 1 и 2 такова:

, (5)

(
добавляется вследствие потери полуволны
при отражении света от оптически более
плотной среды в точке B).
Поскольку клин воздушный, то
.
Выведем формулу, связывающую радиус

темного кольца номер
,
радиус кривизны линзы

и длину световой волны
.
Соединим центр кривизны линзы C
с точками A
и O.
Для прямоугольного треугольника ACD
имеем:

.

Пренебрежем
величиной

ввиду ее малости ()
и получим
,
откуда
.
Подставляя это выражение для

в формулу (5), получаем:

. (6)

Темные
кольца проходят там, где величина

удовлетворяет условию минимума (4).
Приравняем правые части равенств (4) и
(6):

.

и
получим из последнего равенства формулу
для радиусов темных колец в отраженном
свете:

. (7)

БИЛЕТ
43

принцип
Гюйгенса-Френеля

В
соответствии с принципом Гюйгенса-Френеля
каждая щель дифракционной решетки
становится источником вторичных волн.
Следовательно, решетку можно представить
как набор когерентных источников,
расположенных в щелях решетки и
испускающих световые лучи, отклоняющиеся
вправо и влево от первоначального
направления на различные углы в пределах
от 0 до 90°.

В
фокальной плоскости линзы, помещенной
за решеткой, наблюдается дифракционная
картина, обусловленная двумя факторами:
дифракцией света от каждой щели и
многолучевой интерференцией света от
всех щелей.

Рисунок
1 – Ход лучей в дифракционной решетке. 1
– дифракционная решетка, 2 – собирающая
линза, 3 – экран.

максимумы
будут наблюдаться под углами
,
определяемыми следующим условием
(формулой дифракционной решетки):

(1)

где


– номер максимума или порядок спектра.

Формула
для нахождения длин световых волн

.

ДИФРАКЦИЯ
ФРЕНЕЛЯ НА КРУГЛОМ ОТВЕРСТИИ

 Весь
фронт волны  разбивается на
бесконечное количество узких колечек.
Сумма изображается на графике –в
пределе  получается спираль
(рис.4).

        Действие
отверстия в точке наблюдения, находящейся
на оси картины,  зависит от того,
сколько зон Френеля укладывается в
отверстии. Если число зон нечетное –
действие больше, чем без экрана. Больше
всего – если открыта одна зона. Если
открыта только первая зона, то, как видно
из рисунка, амплитуда примерно в два
раза больше, чем если бы был открыт весь
фронт, а интенсивность – в четыре раза
больше. Если открыто четное число зон
– меньше, чем без экрана. Меньше всего
– если открыты 2 зоны. Это все хорошо
видно из графического рассмотрения
(рис.4). Амплитуда определяется как длина
вектора  ON с
началом в точке О,
а конец – там, где кончается последняя
открытая зона. Вокруг центральной точки
будут темные и светлые кольца – это
ясно из осевой симметрии картинки.

БИЛЕТ
44

ДИФРАКЦИЯ
ФРАУНГОФЕРРА НА ЩЕЛИ И ДИФРАКЦИОННОЙ
РЕШЁТКЕ

Дифракция
Фраунгофера —
случай дифракции, при котором дифракционная
картина наблюдается на значительном
расстоянии от отверстия или преграды. 

Оптическая
разность хода волн, идущих от краев щели
в произвольном направлении ,
равна

.                                       (1.9)

После
прохождения через линзу Л они
собираются на экране в точке Р и
интерферируют. Для выяснения вида
интерференционной картины разобьем
открытую поверхность волнового фронта
АВ на зоны Френеля (разность хода от
краев соседних зон равна ),
параллельные краям щели. Всего на
ширине  щели уместится

  зон.                               (1.10)

Так
как на щель падает плоская волна, то
площади всех зон одинаковы,  значит,
одинакова амплитуда колебаний,
возбуждаемых в точке Р действием
каждой зоны Френеля, а фазы колебаний,
создаваемых соседними зонами,
противоположны. Следовательно, колебания
каждой пары соседних зон будут гасить
друг друга.

Поэтому,
если на ширине щели укладывается четное
число зон Френеля, то амплитуда
результирующего колебания в точке Р равна
0 и наблюдается минимум интенсивности
света.

Из
(1.10) следует условие образования
дифракционного минимума:

(k=1,2,…)                      (1.11)

Дифракционный
максимум возникает при нечетном числе
зон Френеля, укладывающихся на ширине
щели

(k=1,2,…),                       (1.12)

Одномерная
дифракционная решетка
– это система параллельных щелей равной
ширины а,
лежащих в одной плоскости и разделенных
равными по ширине непрозрачными
промежутками b.
Величина

(1.15)

называется
постоянной (периодом) дифракционной
решетки.

При
падении на решетку плоской монохроматической
волны в фокальной плоскости линзы
наблюдается дифракционная картина.

Она
является результатом двух процессов:
дифракции света от каждой щели и
интерференции пучков света,
дифрагированных от всех щелей.

Для
выяснения характера картины на экране
рассмотрим дифракцию от двух щелей
(рис5).

Очевидно,
что в тех направлениях,  в которых
ни

одна
из щелей не распространяет света, он не
будет распространяться и при двух щелях,
т.е. прежние минимумы интенсивности
будут возникать в направлениях,
определяемых условием (1.11)

(k=1,2,…).

Кроме
того, в некоторых других направлениях
вторичные волны, идущие от двух щелей,
будут гасить друг друга вследствие
интерференции, т.е. будут наблюдаться
дополнительные минимумы. Они возникают
в направлениях, отвечающих условию

(m=0,1,2,…),               (1.16)

где  –
разность хода лучей, идущих от
краев А и В щелей.
Действие одной щели будет усиливать
действие другой, если в разности хода
укладывается целое число длин волн:

(m=0,1,2,…).            (1.17)

Формула
(1.17) – условие образования главных
максимумов.

БИЛЕТ
45

ДИФРАКЦИЯ
НА ПРОСТРАНСТВЕННОЙ РЕШЁТКЕ. ФОРМУЛА
ВУЛЬФА-БРЭГТА.

Дифракционную
картину могут дать не только рассмотренные
выше одномерные структуры, но также
двумерные и трехмерные периодические
структуры, например, кристаллические
тела. Однако период кристаллических
тел d мал,
составляет единицы ангстрем (1 =10-4 мкм),
т.е. значительно меньше длин волн видимого
света (0,4-0,8 мкм).
Поэтому для видимого света кристаллы
являются однородной средой, и дифракция
не наблюдается.

Вто
же время для значительно более
коротковолнового рентгеновского
излучения( 10-9 –
10-11 м)
кристаллы представляют собой
естественные дифракционные решетки
(см. рис.6).

Абсолютный
показатель преломления рентгеновского
излучения близок к единице, поэтому
оптическая разность хода между лучами

Рис.6

1- и 2-,
отражающимися от кристаллографических
плоскостей CD+DE=2dsin,
где d –
расстояние между плоскостями, в которых
лежат узлы (атомы) кристаллической
решетки,  –
угол скольжения лучей.

Условию
интерференционных максимумов удовлетворяет
[см.(3,15)] формула Вульфа-Брэгга

2dsin =m ,
m=1,2,3– (13)

где
m – порядок дифракционного максимума.

МЕТОД
ДЕБАЯ – ШЕРРЕРА

Метод
Дебая — Шеррера –
один из методов рентгеноструктурного
анализа.
Также называется методом порошка.

Монохроматический
пучок рентгеновского излучения,
направляется на образец исследуемого
материала, растертого в порошок. На
фотопленке, свернутой цилиндром вокруг
образца, изображение (дебаеграмма)
получается в виде колец. Расстояние
между линиями одного и того же кольца
на дебаеграмме позволяет найти брэгговские
углы отражения. Затем, по формуле Брэгга
– Вульфа  можно
получить отношение  расстояния
между отражающими плоскостями к порядку
отражения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

From Wikipedia, the free encyclopedia

Frequency dispersion in groups of gravity waves on the surface of deep water. The ■ red square moves with the phase velocity, and the ● green circles propagate with the group velocity. In this deep-water case, the phase velocity is twice the group velocity. The red square overtakes two green circles when moving from the left to the right of the figure.

New waves seem to emerge at the back of a wave group, grow in amplitude until they are at the center of the group, and vanish at the wave group front.

For surface gravity waves, the water particle velocities are much smaller than the phase velocity, in most cases.

Propagation of a wave packet demonstrating a phase velocity greater than the group velocity without dispersion.

This shows a wave with the group velocity and phase velocity going in different directions. The group velocity is positive, while the phase velocity is negative.[1]

The phase velocity of a wave is the rate at which the wave propagates in any medium. This is the velocity at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave (for example, the crest) will appear to travel at the phase velocity. The phase velocity is given in terms of the wavelength λ (lambda) and time period T as

v_{mathrm {p} }={frac {lambda }{T}}.

Equivalently, in terms of the wave’s angular frequency ω, which specifies angular change per unit of time, and wavenumber (or angular wave number) k, which represent the angular change per unit of space,

v_{mathrm {p} }={frac {omega }{k}}.

To gain some basic intuition for this equation, we consider a propagating (cosine) wave A cos(kx − ωt). We want to see how fast a particular phase of the wave travels. For example, we can choose kx – ωt = 0, the phase of the first crest. This implies kx = ωt, and so v = x / t = ω / k.

Formally, we let the phase φ = kx – ωt and see immediately that ω = -dφ / dt and k = dφ / dx. So, it immediately follows that

{displaystyle {frac {partial x}{partial t}}=-{frac {partial phi }{partial t}}{frac {partial x}{partial phi }}={frac {omega }{k}}.}

As a result we observe a inverse relation between the angular frequency and wavevector. If the wave has higher frequency oscillations, the wave length must be shortened for the phase velocity to remain constant.[2] Additionally, the phase velocity of electromagnetic radiation may – under certain circumstances (for example anomalous dispersion) – exceed the speed of light in vacuum, but this does not indicate any superluminal information or energy transfer.[citation needed] It was theoretically described by physicists such as Arnold Sommerfeld and Léon Brillouin.

The previous definition of phase velocity has been demonstrated for an isolated wave. However, such a definition can be extended to a beat of waves, or to a signal composed of multiple waves. For this it is necessary to mathematically write the beat or signal as a low frequency envelope multiplying a carrier. Thus the phase velocity of the carrier determines the phase velocity of the wave set.[3]

Group velocity[edit]

A superposition of 1D plane waves (blue) each traveling at a different phase velocity (traced by blue dots) results in a Gaussian wave packet (red) that propagates at the group velocity (traced by the red line).

The group velocity of a collection of waves is defined as

{displaystyle v_{g}={frac {partial omega }{partial k}}.}

When multiple sinusoidal waves are propagating together, the resultant superposition of the waves can result in an “envelope” wave as well as a “carrier” wave that lies inside the envelope. This commonly appears in wireless communication when modulation (a change in amplitude and/or phase) is employed to send data. To gain some intuition for this definition, we consider a superposition of (cosine) waves f(x, t) with their respective angular frequencies and wavevectors.

{displaystyle {begin{aligned}f(x,t)&=cos(k_{1}x-omega _{1}t)+cos(k_{2}x-omega _{2}t)\&=2cos left({frac {(k_{2}-k_{1})x-(omega _{2}-omega _{1})t}{2}}right)cos left({frac {(k_{2}+k_{1})x-(omega _{2}+omega _{1})t}{2}}right)\&=2f_{1}(x,t)f_{2}(x,t).end{aligned}}}

So, we have a product of two waves: an envelope wave formed by f1 and a carrier wave formed by f2 . We call the velocity of the envelope wave the group velocity. We see that the phase velocity of f1 is

{displaystyle {frac {omega _{2}-omega _{1}}{k_{2}-k_{1}}}.}

In the continuous differential case, this becomes the definition of the group velocity.

Refractive index[edit]

In the context of electromagnetics and optics, the frequency is some function ω(k) of the wave number, so in general, the phase velocity and the group velocity depend on specific medium and frequency. The ratio between the speed of light c and the phase velocity vp is known as the refractive index, n = c / vp = ck / ω.

In this way, we can obtain another form for group velocity for electromagnetics. Writing n = n(ω), a quick way to derive this form is to observe

{displaystyle k={frac {1}{c}}omega n(omega )implies dk={frac {1}{c}}left(n(omega )+omega {frac {partial }{partial omega }}n(omega )right)domega .}

We can then rearrange the above to obtain

{displaystyle v_{g}={frac {partial w}{partial k}}={frac {c}{n+omega {frac {partial n}{partial omega }}}}.}

From this formula, we see that the group velocity is equal to the phase velocity only when the refractive index is a constant dn / dk = 0. When this occurs, the medium is called non-dispersive, as opposed to dispersive, where various properties of the medium depend on the frequency ω. The relation ω = ω(k) is known as the dispersion relation of the medium.

See also[edit]

  • Cherenkov radiation
  • Dispersion (optics)
  • Group velocity
  • Propagation delay
  • Shear wave splitting
  • Wave propagation
  • Wave propagation speed
  • Planck constant
  • Speed of light
  • Matter wave#Phase velocity

References[edit]

Footnotes[edit]

  1. ^ Nemirovsky, Jonathan; Rechtsman, Mikael C; Segev, Mordechai (9 April 2012). “Negative radiation pressure and negative effective refractive index via dielectric birefringence”. Optics Express. 20 (8): 8907–8914. Bibcode:2012OExpr..20.8907N. doi:10.1364/OE.20.008907. PMID 22513601.
  2. ^ “Phase, Group, and Signal Velocity”. Mathpages.com. Retrieved 2011-07-24.
  3. ^ “Phase Velocity: Waves and Signals”. electroagenda.com.

Bibliography[edit]

  • Crawford jr., Frank S. (1968). Waves (Berkeley Physics Course, Vol. 3), McGraw-Hill, ISBN 978-0070048607 Free online version
  • Brillouin, Léon (1960), Wave Propagation And Group Velocity, New York and London: Academic Press Inc., ISBN 978-0-12-134968-4
  • Main, Iain G. (1988), Vibrations and Waves in Physics (2nd ed.), New York: Cambridge University Press, pp. 214–216, ISBN 978-0-521-27846-1
  • Tipler, Paul A.; Llewellyn, Ralph A. (2003), Modern Physics (4th ed.), New York: W. H. Freeman and Company, pp. 222–223, ISBN 978-0-7167-4345-3
Источник

1. Упругие волны

1.1. Упругие продольные и поперечные волны

1.2. Характеристики бегущих волн

1.2.1. Длина волны

1.2.2. Фазовая скорость волны

1.2.3. Фазовая скорость различна для разных сред

1.2.4. Фронт волны. Волновая поверхность

1.2.5. Уравнение бегущей волны

1.2.6. Волновое уравнение

1.2.7. Скорость и ускорение колеблющейся точки. Относительное смещение точек среды

1.3. Энергия упругих волн

1.4. Принцип суперпозиции волн. Групповая скорость

1.5. Интерференция волн. Стоячие волны

2. Звуковые волны

3. Электромагнитные волны

Как происходит распространение колебаний? Необходима среда для передачи колебаний или они могут передаваться без нее? Как звук от звучащего камертона доходит до слушателя? Каким образом быстропеременный ток в антенне радиопередатчика вызывает появление тока в антенне приемника? Как свет от далеких звезд достигает нашего глаза? Для рассмотрения подобного рода явлений необходимо ввести новое физическое понятие – волна. Волновые процессы представляют общий класс явлений, несмотря на их разную природу.

Процесс распространения колебаний в пространстве называется волной.

Волны, образованные внешним воздействием, приложенным к упругой среде, называются бегущими волнами: они “бегут” от создающего их источника. Важное свойство бегущих волн заключается в том, что они переносят энергию и импульс. Если внешняя сила совершает гармонические колебания, то вызванные ею волны называются гармоническими бегущими волнами.

Волновой процесс обусловлен наличием связей между отдельными частями системы, в зависимости от которых, мы имеем упругую волну той или иной природы.

1. Упругие волны

1. Упругими или механическими волнами называются механические возмущения (деформации), распространяющиеся в упругой среде.

Деформации в теле или среде называются упругими, если они полностью исчезают после прекращения внешних воздействий.

Тела, которые воздействуют на среду, вызывая колебания, называются источниками волн. Распространение упругих волн не связано с переносом вещества, но волны переносят энергию, которой обеспечивает волновой процесс источник колебаний.

2. Среда называется однородной, если ее физические свойства, рассматриваемые в данной задаче, не изменяются от точки к точке.

Среда называется изотропной, если ее физические свойства, рассматриваемые в задаче, одинаковы по всем направлениям.

Среда называется линейной, если между величинами, характеризующими внешнее воздействие на среду, которое и вызывает ее изменение, существует прямо пропорциональная связь. Например, выполнение закона Гука означает, что среда линейна по своим механическим свойствам.

1.1. Упругие продольные и поперечные волны

Все волны делятся на продольные и поперечные.

Поперечные волны – упругие волны, при распространении которых частицы среды совершают колебания в направлении, перпендикулярном направлению распространения волны.

Продольные волны – упругие волны, при распространении которых частицы среды совершают колебания вдоль направления распространения волны.

Поперечные упругие волны возникают только в твердых телах, в которых возможны упругие деформации сдвига. Продольные волны могут распространяться в жидкостях или газах, где возможны объемные деформации среды, или в твердых телах, где возникают деформации удлинения или сжатия. Исключение составляют поперечные поверхностные волны. Простые продольные колебания – это процесс распространения в пространстве областей сжатий и растяжений среды. Сжатия и растяжения среды образуются при колебаниях ее точек (частиц) около своих положений равновесия.

1.2. Характеристики бегущих волн

1.2.1. Длина волны

Минимальное расстояние, на которое распространяется волна за время, равное периоду колебания точки среды около положения равновесия, называется длиной волны.

Длиной волны называется наименьшее расстояние между двумя точками среды, совершающими колебания в фазе (т.е. разность их фаз равна ).

Если точки разделены расстоянием , их колебания происходят в противофазе.

1.2.2. Фазовая скорость волны

Из повседневного опыта известно, что бегущие по воде волны распространяются с постоянной скоростью, пока свойства среды, например, глубина воды, не меняется, что говорит о том, что скорость распространения волнового процесса в пространстве остается постоянной. В случае гармонических бегущих волн (см. определение выше) эта скорость называется фазовой.

Фазовая скорость – это скорость распространения данной фазы колебаний, т.е. скорость волны.

Связь длины волны , фазовой скорости и периода колебаний Т задается соотношением:

.

Учитывая, что , где – линейная частота волны, – период, а циклическая частота волны , получим разные формулы для фазовой скорости:

.

Для волнового процесса характерна периодичность по времени и по пространству.

Т – период колебаний точек среды. Роль пространственного периода играет длина волны . Соотношение между периодом и циклической частотой задается формулой: . Аналогичное соотношение можно записать для длины волны и величиной k, называемой волновым числом: .

Таким образом. Можно добавить еще одно уравнение для фазовой скорости:

.

1.2.3. Фазовая скорость различна для разных сред

В случае упругих поперечных волн (в твердом теле) фазовая скорость равна:

,

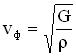
где – модуль сдвига среды, -ее плотность в невозбужденном состоянии (т.е. когда в этой среде не распространяется упругая волна).

Фазовая скорость упругих продольных волн в твердом теле равна

,

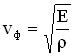
где Е – модуль Юнга, – плотность невозмущенной среды (твердого тела до момента распространения по нему волны).

Фазовая скорость продольных волн в жидкости и газе определяется соотношением: ,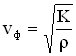

где К – модуль объемной упругости среды – величина, характеризующая способность среды сопротивляться изменению ее объема, – плотность невозмущенной среды.

Фазовая скорость продольных волн в идеальном газе задается формулой: ,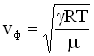

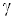
– показатель адиабаты, – молярная масса, Т – абсолютная температура, R – универсальная газовая постоянная. Фазовая скорость в газе зависит от сорта газа () и от его термодинамического состояния (Т).

1.2.4. Фронт волны. Волновая поверхность

При прохождении волны по среде ее точки вовлекаются в колебательный процесс последовательно друг за другом.

Геометрическое место точек, до которого к некоторому моменту времени дошел колебательный процесс, называется волновым фронтом.

Геометрическое место точек, колеблющихся в фазе, называется волновой поверхностью.

Волновой фронт – частный случай волновой поверхности. Волновой фронт все время перемещается. Волновые поверхности остаются неподвижными. Они проходят через положения равновесия частиц среды, которые колеблются в одинаковой фазе.

При описании распространения волн широко используют понятие луча. Направления, в которых распространяются колебания, называются лучами. В изотропной среде (см. определение выше) лучи перпендикулярны волновым поверхностям (фронту) и имеют вид прямых линий. В анизотропной среде, а также при дифракции волн, лучи могут искривляться.

Форма волнового фронта определяет вид волны: сферические (от точечного источника в изотропной среде), эллиптические (в анизотропной среде), цилиндрические (от протяженных источников), плоские и другие. На достаточно большом расстоянии от источника небольшой участок любого фронта можно считать плоским.

Если известно положение фронта волны в некоторый момент времени и скорость волны , то его положение в последующий момент времени можно определить на основе принципа Гюйгенса. Согласно этому принципу все точки поверхности волнового фронта являются источниками вторичных волн. Искомое положение волнового фронта совпадает с поверхностью, огибающей фронты вторичных волн.

1.2.5. Уравнение бегущей волны

Уравнением упругой волны называется зависимость от координат и времени скалярных или векторных величин, характеризующих колебания среды при прохождении по ней волны.

Так, для волн в твердом теле такой величиной является смещение от положения равновесия любой точки тела в произвольный момент времени. Для характеристики продольных волн в жидкости или газе используют понятие избыточного давления. Избыточное давление равно разности между давлением в данный момент времени, когда по среде проходит волна, и равновесным, когда возмущений в среде нет.

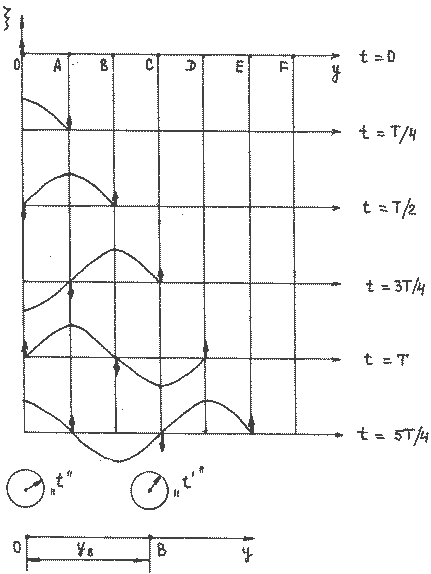
Получим уравнение бегущей волны в одномерном пространстве, которое предполагаем изотропным и однородным (см. определения выше). Кроме того, силы сопротивления в среде считаем пренебрежимо малыми (т.е. нет затухания колебаний). Пусть точка О – центр (источник) колебаний, она колеблется по закону:

,

где – смещение точки О от положения равновесия, – частота, А – амплитуда колебаний. Часы или секундомер №1 включаются сразу, как только начинаются колебаний точки О, и отсчитывают время t (Рисунок 2.1.1). Ось ОУ совпадает с направлением распространения волны.

Через промежуток времени процесс колебаний дойдет до точки В, и она будет колебаться по закону: .

Рисунок 2.1.1.

Амплитуда колебаний в случае отсутствия затухания процесса будет такой же как и амплитуда точки О. Часы или секундомер №2 включаются тогда, когда колебательный процесс дойдет до точки В (т.е. когда начинает колебаться точка В), и отсчитывают время . Моменты времени t и связаны между собой соотношением или . Расстояние между точками О и В обозначим . Фазовая скорость волны равна , тогда . 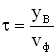Учитывая соотношения для и и формулы и , можно записать уравнение колебаний точки В в разных видах:

.

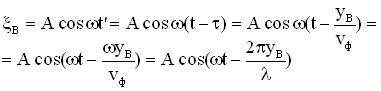
Аналогично уравнению колебаний точки В запишем уравнение колебаний любой точки среды, расположенной на расстоянии y от источника колебаний:

,

где – волновое число (см. определение выше).

Это уравнение и есть уравнение для смещения любой точки пространства в любой момент времени, т.е. уравнение бегущей волны, где А – амплитуда, величина – фаза волны, которая в отличии от фазы колебаний зависит и от времени “t”, и от расстояния “y” колеблющейся точки от источника колебаний.

Вернемся к разделению волн по форме фронта волны и к понятию луча, как направления распространения колебательного процесса. Учтем, что в изотропной среде лучи перпендикулярны фронту и имеют вид прямых линий. Тогда уравнение бегущей волны, полученное выше, есть уравнение плоской бегущей волны, т.е. когда фронт волны – плоскость.

Уравнение плоской отраженной волны в одномерном пространстве легко получить, если представить ее как бегущую волну в отрицательном направлении оси ОУ, что приведет к замене в уравнении бегущей волны координаты “y” на “-y”:

.

Упругая волна называется синусоидальной или гармонической, если соответствующие ей колебания частиц среды являются гармоническими. Так, рассмотренные выше бегущая и отраженная волны являются гармоническими волнами.

1.2.6. Волновое уравнение

Когда мы рассматривали колебания, то для любой колебательной системы получали дифференциальное уравнение, для которого соответствующее уравнение колебаний являлось решением. Аналогично уравнение бегущей и отраженной волны являются решениями дифференциального уравнения второго порядка в частных производных, называемого волновым уравнением и имеющего вид:

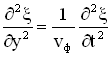
, где – фазовая скорость волны.

Уравнения бегущей и отраженной волн и волновое уравнение представлены для случая одного измерения, т.е. распространения волны вдоль оси ОУ. В волновое уравнение входят вторые частные производные по времени и координате от смещения потому, что есть функция двух переменных t и y.

1.2.7. Скорость и ускорение колеблющейся точки. Относительное смещение точек среды

Если смещение любой точки среды с координатой y в момент времени t задано уравнением:

,

то скорость этой точки есть величина , а ускорение – :

,

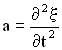
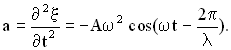
1.3. Энергия упругих волн

В среде распространяется плоская упругая волна и переносит энергию, величина которой в объеме равна: , где – объемная плотность среды.

Если выбранный объем записать как , где S – площадь его поперечного сечения, а – его длина, то среднее количество энергии, переносимое волной за единицу времени через поперечное сечение S, называется потоком через его поверхность:

.

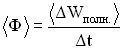
Количество энергии, переносимое волной за единицу времени через единицу площади поверхности, расположенной перпендикулярно направлению распространения волны, называется плотностью потока энергии волны.

Эта величина определяется соотношением:

,

где 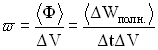-объемная плотность энергии волны, – фазовая скорость волны. Так как фазовая скорость волны – вектор, направление которого совпадает с направлением распространения волны, то можно величине плотности потока энергии I придать смысл векторной величины:

.

Величина , вектор плотности энергии волны, впервые была введена Н.А. Умовым в 1984 году и получила название вектора Умова. Подобная величина для электромагнитных волн называется вектором Умова – Пойнтинга.

Интенсивностью волны называется модуль среднего значения вектора Умова .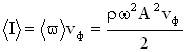

1.4. Принцип суперпозиции волн. Групповая скорость

Принцип суперпозиции (наложения) волн установлен на опыте. Он состоит в том, что в линейной среде волны от разных источников распространяются независимо, и накладываясь, не изменяют друг друга. Результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые частица получит, участвуя в каждом из слагаемых волновых процессов.

Согласно принципу суперпозиции накладываться друг на друга без взаимного искажения могут волны любой формы. В результате наложения волн результирующее колебание каждой частицы среды может происходить по любому сложному закону. Такое образование волн называется волновым пакетом. Скорость движения волнового пакета не совпадает со скоростью ни с одной из слагаемых волн. В этом случае говорят о скорости волнового пакета. Скорость перемещения максимума группы волн (волнового пакета) называется групповой скоростью. Она равна скорости переноса энергии волнового пакета.

На практике мы всегда имеем дело с группой волн, так как синусоидальных волн, бесконечных в пространстве и во времени, не существует. Любая ограниченная во времени и пространстве синусоидальная волна есть волновой пакет (его называют цуг волны). Групповая скорость такого пакета совпадает с фазовой скоростью бесконечных синусоидальных волн, результатом сложения которых он является.

В общем виде связь между групповой и фазовой скоростями имеет вид:

.

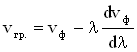
1.5. Интерференция волн. Стоячие волны

1. Интерференцией волн называется явление наложение двух и более волн, при котором в зависимости от соотношения между фазами этих волн происходит устойчивое во времени их взаимное усиление в одних точках пространства и ослабление в других.

В пространстве всегда найдутся такие точки, в которых разность фаз складываемых колебаний равна величине , где k – целое число, т.е. волны (от разных источников) приходят в такие точки в фазе. В них будет наблюдаться устойчивое, неизменно продолжающееся все время усиление колебаний частиц. Найдутся в пространстве, где распространяется несколько волн, и такие точки, где разность фаз будет равна , т.е. волны приходят в эти точки в противофазе. В таких точках пространства будет наблюдаться устойчивое ослабление колебаний частиц.

Устойчивая интерференционная картина возникает только при наложении таких волн, которые имеют одинаковую частоту, постоянную во времени разность фаз в каждой точке пространства. Волны, удовлетворяющие этим условиям и источники, создающие такие волны, называются когерентными. Плоские синусоидальные волны, частоты которых одинаковы, когерентны всегда.

2. Запишем условия максимумов и минимумов при интерференции. Когерентные точечные источники и испускают волны по всем направлениям. До точки наблюдения М расстояние от первого источника , а от второго – .

Колебания точки М под действием волн от двух источников и описываются уравнениями:

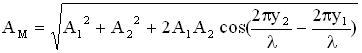
, . Амплитуда результирующего колебания в точке М определится следующим образом (см. раздел “Сложение колебаний”): . Амплитуда колебаний точки М максимальна (), если , где Величина называется разностью хода двух волн. Условие максимума при интерференции имеет вид: . Если целое число волн укладывается на разности хода двух волн, то при их сложении наблюдается интерференционный максимум. Амплитуда колебаний точки М минимальна (), если , (). Условие минимума при интерференции имеет вид: .   Если нечетное число полуволн укладывается на разности хода двух волн, то при их сложении наблюдается интерференционный минимум. 3. Простейший случай интерференции наблюдается при наложении бегущей и отраженной волн, что приводит к образованию стоячей волны. Уравнения бегущей и отраженной волны имеют вид: , Суммарное смещение частицы среды, находящейся на расстоянии y от источника колебаний, равно сумме смещений и : .

Это и есть уравнение стоячей волны. Величина 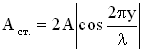– амплитуда, а () – фаза стоячей волны. Можно сказать, что частицы в стоячей волне имеют одну фазу колебаний. Амплитуда колебаний частиц в стоячей волне зависит от их координат (расстояний до источника колебаний), но не зависит от времени. Знак модуля поставлен в формуле для амплитуды стоячей волны, потому что амплитуда – величина положительная.

В стоячей волне есть точки, которые все время остаются неподвижными. Такие точки называются узлами смещения, их положение определяется из условия:

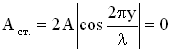
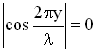
, отсюда следует . Выполнение этого соотношения будет при условии для Итак, координаты узлов задаются формулой:

.

Расстояние между двумя соседними узлами равно .

Точки среды, колеблющиеся с наибольшей амплитудой, называются пучностями стоячей волны, их положение (координаты) определяются соотношением:

.

Это уравнение можно получить из условия максимума амплитуды

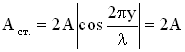
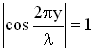
, т.е. . Последнее соотношение выполняется при значениях аргумента ().

Расстояние между двумя соседними пучностями равно .

4. Изменение фазы волны при ее отражении.

Как отмечалось ранее, стоячая волна образуется при сложении бегущей и отраженной волн. Отраженную волну можно рассматривать как бегущую волну, распространяющуюся в обратном направлении и ее можно получить при отражении бегущей волны от границы двух сред. Для синусоидальных волн это означает, что при отражении от более плотной среды фаза волны скачком изменяется на радиан, а при отражении от менее плотной среды фаза волны не изменяется. Изменение фазы на радиан соответствует появлению дополнительного хода луча, равного .

2. Звуковые волны

1. Важным видом продольных волн являются звуковые волны. Так называются волны с частотами 17 – 20000 Гц. Учение о звуке называется акустикой. В акустике изучаются волны, которые распространяются не только в воздухе, но и в любой другой среде. Упругие волны с частотой ниже 17 Гц называются инфразвуком, а с частотой выше 20000 Гц – ультразвуком.

Звуковые волны – упругие колебания, распространяющиеся в виде волнового процесса в газах, жидкостях, твердых телах.

2. Избыточное звуковое давление. Уравнение звуковой волны.

Уравнение упругой волны позволяет вычислить смещение любой точки пространства, по которому проходит волна, в любой момент времени. Но как говорить о смещении частиц воздуха или жидкости от положения равновесия? Звук, распространяясь в жидкости или газе, создает области сжатия и разряжение среды, в которых давление соответственно повышается или понижается по сравнению с давлением невозмущенной среды.

Если – давление и плотность невозмущенной среды (среды, по которой не проходит волна), а – давление и плотность среды при распространении в ней волнового процесса, то величина называется избыточным давлением. Величина есть максимальное значение избыточное давление (амплитуда избыточного давления).

Изменение избыточного давления для плоской звуковой волны (т.е. уравнение плоской звуковой волны) имеет вид:

,

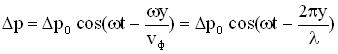
где y – расстояние от источника колебаний точки, избыточное давление в которой мы определяем в момент времени t.

Если ввести величину избыточной плотности и ее амплитуды так же, как мы вводили величину избыточного звукового давления, то уравнение плоской звуковой волны можно было бы записать так: . 3. Объективные и субъективные характеристики звука.

Само слово “звук” отражает два различных, но взаимосвязанных понятия: 1)звук как физическое явление; 2)звук – то восприятие, которое испытывает слуховой аппарат (человеческое ухо) и ощущения, возникающие у него при этом. Соответственно характеристики звука делятся на объективные, которые могут быть измерены физической аппаратурой, и субъективные, определяемые восприятием данного звука человеком.

К объективным (физическим) характеристикам звука относятся характеристики, которые описывают любой волновой процесс: частота, интенсивность и спектральный состав. В таблицу 3 включены сравнительные данные объективных и субъективных характеристик.

Таблица 3.

Субъективные Характеристики Объективные характеристики
Высота звука Высота звука определяется частотой волны
Тембр (окраска звука) Тембр звука определяется его спектром
Громкость (сила звука) Сила звука определяется нтенсивностью волны (или квадратом ее амплитуды)

Остановимся на некоторых определениях.

Частота звука измеряется числом колебаний частиц среды, участвующих в волновом процессе, в 1 секунду.

Интенсивность волны измеряется энергией, переносимой волной в единицу времени через единичную площадь (расположенную перпендикулярно направлению распространению волны).

Спектральный состав (спектр) звука указывает из каких колебаний состоит данный звук и как распределены амплитуды между отдельными его составляющими.

Различают сплошные и линейчатые спектры. Для субъективной оценки громкости используются величины, называемые уровнем силы звука и уровнем громкости. Все акустические величины и их размерности в СИ приведены в приложении.

3. Электромагнитные волны

1. Электромагнитными волнами называются возмущения электромагнитного поля (т.е. переменное электромагнитное поле), распространяющиеся в пространстве.

Утверждение о существовании электромагнитных волн является непосредственным следствием решения системы уравнений Максвелла. Согласно этой теории следует, что переменное электромагнитное поле распространяется в пространстве в виде волн, фазовая скорость которых равна:

где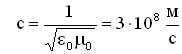 – скорость света в вакууме, , – электрическая и магнитная постоянные, , – соответственно диэлектрическая и магнитная проницаемость среды.

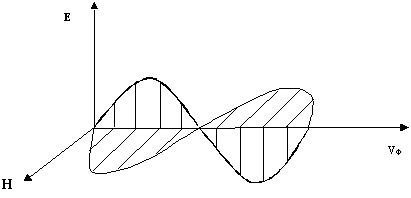
2. Электромагнитные волны – поперечные волны. Векторы Е и Н поля электромагнитной волны взаимно перпендикулярны друг другу. Вектор скорости волны и векторы Е и Н образуют правую тройку векторов (Рисунок 2.1.4).

Для сравнения ориентации тройки векторов , Е и Н на рисунке приведено расположение осей декартовой системы координат. Такое сопоставление уместно и в дальнейшем будет использовано для определения проекций векторов Е и Н на координатные оси.

Рисунок 2.1.4

Взаимно перпендикулярные векторы Е и Н колеблются в одной фазе (их колебания синфазные). Модули этих векторов связаны соотношением:

которое справедливо для любой бегущей электромагнитной волны независимо от формы ее волновых поверхностей.

3. По форме волновых поверхностей волны могут быть плоские, эллиптические, сферические и т.д..

Монохроматической волной называется электромагнитная волна одной определенной частоты. Монохроматическая волна не ограничена в пространстве и во времени. В каждой точке электромагнитного поля монохроматической волны проекции векторов Е и Н на оси координат совершают гармонические колебания одинаковой частоты . Например, для плоской монохроматической волны, распространяющейся вдоль положительного направления оси ОУ, как показано на рисунке 2.1.3.,ее уравнение имеет вид:

Такие волны называются плоско (или линейно) поляризованными волнами.

Плоскость, в которой происходит колебание вектора Е называют плоскостью поляризации линейно поляризованной волны, а плоскость колебаний вектора Н – плоскостью колебаний. Ранее эти названия были обратными (см. [1]).

4. Все сказанное о стоячих волнах в упругих средах относится и к электромагнитным волнам. В этом случае, однако, волна характеризуется не одним вектором, а двумя взаимно перпендикулярными векторами Е и Н.

Стоячая электромагнитная волна состоит из двух стоячих волн – магнитной и электрической, колебания которых сдвинуты по фазе на .

5. Энергия электромагнитных волн. Объемная плотность энергии электромагнитного поля в линейной изотропной среде задается соотношением: 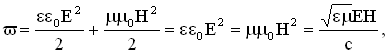с – скорость света в вакууме.

В случае плоской линейно поляризованной монохроматической волны, распространяющейся вдоль положительного направления ОY, напряженность электрического поля задается уравнением:

соответственно объемная плотность энергии этой волны

Значение объемной плотности энергии волны меняется за период от 0 до .Среднее за период значение энергии равно:

.

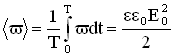
6. Вектор плотности потока энергии электромагнитной волны называется вектором Умова – Пойнтинга:

Для линейно поляризованной монохроматической волны вектор Пойнтинга направлен в сторону распространения волны и численно равен:

Интенсивность электромагнитной волны равна модулю среднего значения вектора Пойнтинга за период его полного колебания:

Интенсивностью электромагнитной волны называется физическая величина, численно равная энергии, переносимая волной за единицу времени через единицу площади поверхности, расположенной перпендикулярно к направлению распространения волны.

Интенсивность бегущей монохроматической волны: – фазовая скорость волны, среднее значение объемной плотности энергии поля волны.

Интенсивность света (электромагнитных волн, рассматриваемых в оптике) прямо пропорциональна квадрату амплитуды колебаний вектора напряженности Е поля световой волны.

Источник

Добавить комментарий