В древности объём измеряли в сиеках, горстках, тинах, пурах, цибах, штофах, ложках.
(1) тина (= 3) пура (= 9) сиеков (= 720) горсток (= 162) штофа (= 208) литров.
Многие из этих мер давно уже забыты.
В международной системе единиц (СИ) единицей объёма является метр кубический
м3
.
Рис. (1). Кубический метр
В повседневной жизни встречается единица объёма литр
л
. Она названа именем французского винодела Литра.
Обрати внимание!
Литр является кубическим дециметром:
1 л=1 дм3
.
Деления мензурки обычно выражаются в миллилитрах (мл):
1 мл=1см3
.
В физике важно умение перейти от одной единицы измерения к другой. Рассмотрим следующие соотношения:
1м3=10дм⋅10дм⋅10дм=1000дм3;1м3=100см⋅100см⋅100см=1000000см3;1м3=1000мм⋅1000мм⋅1000мм=1000000000мм3.
1 дм3=110м⋅110м⋅110м=11000м3=0,001м3.
Определение объёма
Рис. (2). Прямоугольный параллелепипед
Объём тела вычисляют по формулам.
Для прямоугольного параллелепипеда:
объём=длина⋅ширина⋅высота.
Если длина равна
l1
, ширина
l2
, высота
l3
, тогда объём будет
V=l1⋅l2⋅l3
.
Объём тел неправильной формы определяют методом погружения.
- В мензурку наливают воду и определяют её объём.
- В воду погружают тело и определяют общий объём тела и воды.
- Объём тела определяют, вычитая из общего объёма начальный объём.
Рис. (3). Погружение в жидкость тела неправильной формы
Некоторые английские неметрические единицы объёма
Акрофут (= 1233,48)
м3
.
Кубический дюйм (= 16,39)
см3
.
Баррель нефти (= 158,99)
дм3
.
Бушель (США) (= 35,24)
дм3
.
Галлон жидкости (США) (= 3,78)
дм3
.
Источники:
Рис. 1. Кубический метр. © ЯКласс.
Рис. 2. Прямоугольный параллелепипед. © ЯКласс.
Рис. 3. Погружение в жидкость тела неправильной формы. © ЯКласс.
Обновлено: 16.05.2023
Чтобы вычислить объем тела, нужно массу тела разделить на его плотность: v = m : p. Для правильного решения задач нужно уметь верно переводить единицы измерения величин в Международную систему единиц: 1 г = 0,001 кг, 1 л = 1 дм3 = 0,001 м3, 1 см3 = 0,000 001 м3, 1 г/см3 = 1000 кг/м3.
Что такое объем в физике 7 класс?
Объём — количественная характеристика пространства, занимаемого телом или веществом. С понятием объёма тесно связано понятие вместимости — объёма внутреннего пространства сосуда, упаковочного ящика и т. п. Объём тела (как и вместимость сосуда) определяется его формой и линейными размерами.
Чему равен объем 7 класс?
Объём тела вычисляют по формулам: Для прямоугольного параллелепипеда: объём = длина ⋅ ширина ⋅ высота . Если длина равна l 1 , ширина l 2 , высота l 3 , тогда объём будет V = l 1 ⋅ l 2 ⋅ l 3 .
Как найти n в физике 7 класс?
Измерение физических величин
- из значения верхней границы (ВГ) шкалы вычесть значение нижней границы (НГ) шкалы и результат разделить на количество делений (N);
- найти разницу между значениями двух соседних числовых меток (А и Б) шкалы и разделить на количество делений между ними (n).
Что такое МЮ в физике 7 класс?
Масса (m) — мера инертности тела, определяемая при его взвешивании как отношение силы тяжести (P) к коэффициенту (g). Плотность (ρ) — масса единицы объёма вещества, численно равная отношению массы (m) вещества к его объёму (V).
Как найти объем в физике через массу?
Отсюда видно, что для определения объема тела надо массу этого тела разделить на его плотность. Чтобы определить массу тела, надо плотность тела умножить на его объем. 1.
Как измеряется объем в физике?
Единицей объема в СИ считается кубический метр, его производные – кубический сантиметр, кубический дециметр и т. д. Жидкость измеряется в литрах. Для жидких и сыпучих веществ в разных странах используют различные внесистемные единицы – галлон, баррель.
Как вычислить массу?
Вес можно рассчитать по формуле: m=V*p, где р – плотность, V – объем материала. Например, 10 м3 речного песка весят 13 тонн. Если известна масса материала, то объем можно узнать по формуле: V = m/ p.
Как найти объем по формуле?
По какой формуле можно найти объем?
- Зная массу и плотность V = m/ρ, где m — масса, а ρ — плотность
- Для геометрических фигур, например куб V = a^3 перемножить три стороны, а для цилиндра V = S*H площадь основания помножить на высоту
Как можно найти массу вещества?
И наоборот, массу вещества определяют как произведение молярной массы на количество вещества: m = n . M. Так, масса 0,1 моля Na составляет 0,1 моль×23 г/моль = 2,3 Молярная масса численно всегда совпадает с молекулярной массой (или атомной массой — если вещество состоит не из молекул, а из атомов).
Что такое сила в физике 7 класс?
Си́ла — физическая векторная величина, являющаяся мерой воздействия на данное тело со стороны других тел или полей. Приложение силы обусловливает изменение скорости тела или появление деформаций и механических напряжений.
Как найти F в физике 7 класс?
A = Fs, где А — работа, F — сила и s — пройденный путь.
Как найти P в физике 7 класс?
Если высоту столба жидкости, находящейся в сосуде, обозначить буквой h, а площадь дна сосуда S, то V = S·h. Масса жидкости m = ρ·V, или m = ρ·S·h . Вес этой жидкости P = g·m, или P = g·ρ·S·h. p = g·ρ·h.
В повседневной жизни встречается единица объёма литр л . Она названа именем французского винодела Литра.
Литр является кубическим дециметром 1 л = 1 дм 3 .
Деления мензурки обычно выражаются в миллилитрах (мл) 1 мл = 1 см 3 .
1 м 3 = 10 дм ⋅ 10 дм ⋅ 10 дм = 1000 дм 3 1 м 3 = 100 см ⋅ 100 см ⋅ 100 см = 1000 000 см 3 1 м 3 = 1000 мм ⋅ 1000 мм ⋅ 1000 мм = 1000 000 000 мм 3
1 см 3 = 1 100 м ⋅ 1 100 м ⋅ 1 100 м = 1 1000 000 м 3 = 0,000 001 м 3
1 мм 3 = 1 1000 м ⋅ 1 1000 м ⋅ 1 1000 м = 1 1000 000 000 м 3 = 0,000 000 001 м 3
- В мензурку наливают воду и определяют её объём.
- В воду погружают тело и определяют общий объём тела и воды.
- Объём тела определяют, вычитая из общего объёма начальный объём.
Рис. 1. Кубический метр. © ЯКласс.
Рис. 2. Прямоугольный параллелепипед. © ЯКласс.
Рис. 3. Погружение в жидкость тела неправильной формы. © ЯКласс.
Объём — количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами. С понятием объёма тесно связано понятие вместимость, то есть объём внутреннего пространства сосуда, упаковочного ящика и т. п. Синонимом вместимости частично является ёмкость, но словом ёмкость обозначают также сосуды и качественную характеристику конденсаторов.
Принятые единицы измерения — в СИ и производных от неё — кубический метр, кубический сантиметр, литр (кубический дециметр) и т. д. Внесистемные — галлон, баррель.
Содержание
Вычисление объёма
Математически
В общем случае математически объём тела вычисляется по следующей интегральной формуле:
,
где — характеристическая функция геометрического образа тела.
Для ряда тел с простой формой более удобным является использование специальных формул. Например, объём куба с длиной стороны, равной a, равен .
Через плотность
Единицы объёма жидкости
Английские внесистемные
- 1 пинта = 0,57 л
- 1 Кварта = 2 пинты = 1,23 л
- 1 галлон = 8 пинтам = 4,55 л (Имперский галлон)
Американские внесистемные
- 1 американский галлон = 3,785 л (Распространён в США)
Античные внесистемные
Древнееврейские
-
= 24 883 см³ (Эйфа́)
- Омер = 1 /10 эйфы
- Гин = 4147 см³ [1]
- Кав = 1382 см³
Русские внесистемные
-
= 40 вёдер = 492 л = 4 четверти = 8 штофов = 12,3 л = 10 чарок = 20 шкаликов = 1,23 л
- Бутылка (винная) = 1/16 Ведра = 0,77 л
- Бутылка (пивная) = 1/20 Ведра = 0,61 л = 4,7 ведра = 2 шкалика = 0,123 л = 4 бутылки = 3,075 л (косушка) = пол чарки = 0,0615 л = 1,54 л
Единицы сыпучих веществ
Английские внесистемные
- 1 бушель = 36,36872 литров = 8 галлонов = 3,63687·10 −2 м³
- 1 баррель = 0,16365 м³. (для сыпучих веществ)
Русские внесистемные
Молярный объём
Vm — величина, равная отношению объёма V системы (тела) к её количеству вещества n:
Молярный объем для газов при нормальных условиях: Vm = 22,4 л/моль
Прочие единицы измерения
- 1 дюйм кубический = 1,63871·10 −5 м³
- 1 литр = 1·10 −3 м³
- Лямбда 1 λ = 1·10 −9 м³
- 1 унция = 2,841·10 −5 м³ (анг.)
- 1 унция = 2,957·10 −5 м³ (амер.)
- 1 фут кубический = 2,83168·10 −2 м³
- 1 ярд кубический = 0,76455 м³
- 1 стер = 1 м³
- 1 ае кубическая =3,348071936e+40 км³
- 1 км кубический = 1 000 000 000 м³
- 1 световой год кубический = 8,46590536e+38 км³
- 1 пк кубический = 2,9379989989648103256576e+40 км³
- 1 мпк кубический =1 000 000 000 пк³=2,9379989989648103256576e+49 км³
Примечания
Литература
- Проставив сноски, внести более точные указания на источники.
- Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное.
- Добавить иллюстрации.
- Физические величины по алфавиту
- Единицы измерения объёма
Wikimedia Foundation . 2010 .
Полезное
Смотреть что такое “Объём” в других словарях:
объём — объём, а … Русский орфографический словарь
объём — объём … Словарь употребления буквы Ё
объём — объём/ … Морфемно-орфографический словарь
объём — сущ., м., употр. сравн. часто Морфология: (нет) чего? объёма, чему? объёму, (вижу) что? объём, чем? объёмом, о чём? об объёме; мн. что? объёмы, (нет) чего? объёмов, чему? объёмам, (вижу) что? объёмы, чем? объёмами, о чём? об объёмах 1. В… … Толковый словарь Дмитриева
объём — а; м. 1. Величина чего л. в длину, высоту и ширину, измеряемая в кубических единицах. О. геометрического тела. О. куба, цилиндра. О. здания. О. полтора кубометра. В объёме (в трёх измерениях; объёмно). 2. Содержание чего л. с точки зрения… … Энциклопедический словарь
ОБЪЁМ — ОБЪЁМ, а, муж. 1. Величина чего н. в длину, высоту и ширину, измеряемая в кубических единицах. О. пирамиды. О. здания. 2. Вообще величина, количество. Большой о. работ. О. информации. О. знаний. | прил. объёмный, ая, ое (к 1 знач.). Объёмное… … Толковый словарь Ожегова
объём — ОБЪЁМ1, а, м Величина или вместимость предмета, определяемая произведением длины, высоты и ширины и измеряемая в кубических единицах. Объем бассейна в новой школе составляет 300 кубических метров. ОБЪЁМ2, а, м Количество или величина чего л.… … Толковый словарь русских существительных
ОБЪЁМ — ОБЪЁМ, мера части пространства, занимаемого телом. Единицей измерения служит объём единичного куба … Современная энциклопедия
объ — объ. Пишется вм. (об) перед е, ю, я, напр. объехать, объявить.Примечание. Вм. этой приставки и следующей за ней буквы и пишется обы, напр. обыграть. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
объ… — Пишется вместо об… перед е, ю, я, напр. объехать, объявить. Примечание. вместо этой приставки и следующей за ней буквы и пишется обы, напр. обыграть. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
Физика. Наука, изучающая явления природы, свойства и строение материи.
Материя . Всё, что есть во Вселенной.
Молекула . Мельчайшая частица данного вещества.
Диффузия . Взаимное перемешивание молекул одного вещества с молекулами другого.
Механическое движение . Изменение положения тела относительно других тел с течением времени.
Путь . Длина траектории.
Траектория . Линия, по которой движется тело.
Равномерное движение. Движение, при котором тело за любые равные промежутки времени проходит одинаковые пути.
Скорость . Величина, равная отношению пути ко времени, за которое этот путь пройден.
Инерция . Явление сохранения скорости тела при отсутствии действия на него других тел.
Тормозной путь . Путь, который проходит автомобиль после выключения двигателя до полной остановки.
Плотность . Физическая величина, равная отношению массы тела к его объёму.
Сила. Мера механического воздействия на тело со стороны других тел.
Масса. Мера инертности.
Вес. Сила, с которой тело вследствие притяжения к Земле действует на горизонтальную опору или подвес.
Равнодействующая сила . Сила, которая производит на тело такое же действие, как несколько одновременно действующих сил.
Сила трения . Сила, возникающая при движении одного тела по поверхности другого и направленная против движения.
Давление . Величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности.
Атмосфера . Воздушная оболочка Земли.
Архимедова сила . Сила, выталкивающая тело из жидкости или газа.
Работа. Величина, равная произведению приложенной силы на пройденный путь.
Мощность. Величина, равная отношению работы ко времени, за которое она была совершена.
Рычаг. Твёрдое тело, которое может вращаться вокруг неподвижной опоры.
КПД. Отношение полезной работы к полной работе.
Потенциальная энергия . Энергия взаимодействия.
Кинетическая энергия . Энергия движения.
Определения и формулы
Измерение физических величин
Измерение физических величин
- из значения верхней границы (ВГ) шкалы вычесть значение нижней границы (НГ) шкалы и результат разделить на количество делений (N);
- найти разницу между значениями двух соседних числовых меток (А и Б) шкалы и разделить на количество делений между ними (n).
ЦД = (ВГ — НГ) / N
ЦД = (Б — А) / n
Механическое движение
Скорость (ʋ) — физическая величина, численно равна пути (S), пройденного телом за единицу времени (t).
Путь (S) — длина траектории, по которой двигалось тело, численно равен произведению скорости (ʋ) тела на время (t) движения.
Время движения (t) — равно отношению пути (S), пройденного телом, к скорости (ʋ) движения.
Средняя скорость (ʋ ср ) — равна отношению суммы участков пути (S1, S2, S3, …), пройденного телом, к промежутку времени (t1 + t2+ t3+ …), за который этот путь пройден.
ʋср = (S1 + S2 + S3 + …) / (t1 + t2 + t3 + …)
Сила тяжести, вес, масса, плотность
Сила тяжести — сила (FТ), с которой Земля притягивает к себе тело, равная произведению массы (т) тела на коэффициент пропорциональности (g) — постоянную величину для Земли. (g = 9,8 H/кг)
FТ = m*g
Вес (Р) — сила, с которой тело действует на горизонтальную опору или вертикальный подвес, равная произведению массы (т) тела на коэффициент (g).
Масса (т) — мера инертности тела, определяемая при его взвешивании как отношение силы тяжести (Р) к коэффициенту (g).
т = Р / g
Плотность (ρ) — масса единицы объёма вещества, численно равная отношению массы (т) вещества к его объёму (V).
Механический рычаг, момент силы
Момент силы (М) равен произведению силы (F) на сё плечо (l)
М = F*l
Условие равновесия рычага — рычаг находится в равновесии, если плечи (l1, l2)действующих на него двух сил (F1, F2) обратно пропорциональны значениям сил.
a) F1 / F2 = l1 / l2
Давление, сила давления
Давление (р) — величина, численно равная отношению силы (F), действующей перпендикулярно поверхности, к площади (S) этой поверхности
Сила давления (F) — сила, действующая перпендикулярно поверхности тела, равная произведению давления (р) на площадь этой поверхности (S)
Давление газов и жидкостей
Давление однородной жидкости (р) — на дно сосуда зависит только от её плотности (ρ) и высоты столба жидкости (h).
Закон Архимеда — на тело, погруженное в жидкость (или газ), действует выталкивающая сила — архимедова сила (FВ). равная весу жидкости (или газа), в объёме (VТ) этого тела.
FВ = ρ*g*Vт
Условие плавания тел — если архимедова сила (FВ) больше силы тяжести (FТ)тела, то тело всплывает.
FВ > FТ
Закон гидравлической машины — силы (F1, F2), действующие на уравновешенные поршни гидравлической машины, пропорциональны площадям (S1, S2) этих поршней.
F1 / F2 = S1 / S2
Закон сообщающихся сосудов — однородная жидкость в сообщающихся сосудах находится на одном уровне (h)
Работа, энергия, мощность
Механическая работа — Работа (A) — величина, равная произведению перемещения тела (S) на силу (F), под действием которой это перемещение произошло.
Формула:
А = F*S
Коэффициент полезного действия механизма (КПД) — коэффициент полезного действия (КПД) механизма — число, показывающее, какую часть от всей выполненной работы (АВ) составляет полезная работа (АП).
ɳ = АП / АВ *100%
Потенциальная энергия (Е П ) тела, поднятого над Землей, пропорциональна его массе (т) и высоте (h) над Землей.
Формула:
ЕП = m*g*h
Кинетическая энергия (Е К ) движущегося тела пропорциональна его массе (m) и квадрату скорости (ʋ 2 ).
ЕК = m*ʋ 2 / 2
Сохранение и превращение механической энергии — Сумма потенциальной (ЕП) и кинетической (ЕК) энергии в любой момент времени остается постоянной.
EП + EК = const
Мощность (N) — величина, показывающая скорость выполнения работы и равная:
а) отношению работы (А) ко времени (t), за которое она выполнена;
б) произведению силы (F), под действием которой перемещается тело, на среднюю скорость (ʋ) его перемещения.
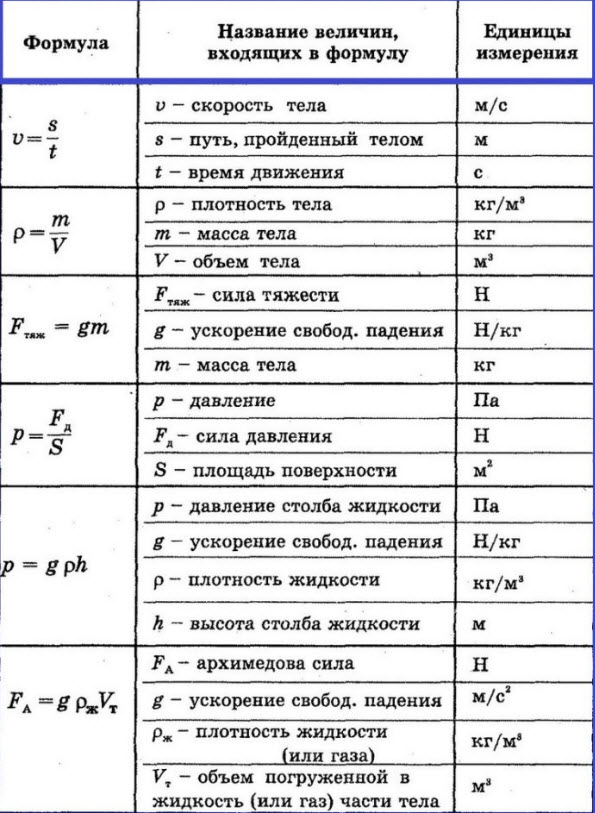
Формулы меры длины и веса и соотношения между единицами
12 самых востребованных формул по физике в 7 классе
Тест для закрепления материала
- Сколько в теле молекул
- Чему равна масса тела из данного вещества
- Что массы разных тел неодинаковы
- Отношение массы тела к его объему
2 Вычислите скорость (в м/с) равномерного полёта воздушного шара в течение 1,5 мин., за которые он пролетел 540 м
Объем – мера в трехмерном пространстве, занимаемом объектом (длина, ширина и высота).
Задача обучения
- Понять, как геометрически можно измерить объем.
Основные пункты
- В качестве единицы чаще всего используют м 3 . Но для жидкостей – литр (0.001 м 3 ).
- Можно воспринимать как количество жидкости, вытесненной погруженным телом.
- Объем можно вычислить у геометрических объектов по формулам. В случае со сложными объектами следует измерить вытесненную жидкость.
Термины
- Поперечное сечение – срез, образованный плоскостью, прорезающей предмет под прямым углом.
- Измерение – мера пространственной протяженности в конкретном направлении (высота, ширина и глубина).
Объем в физике – мера трехмерного пространства, ограниченного чертой. В нем может вмещаться определенное вещество или отображает форму. В чем измеряется объем в физике? В качестве единицы используют м 3 , но для жидкостей – литр (0.001 м 3 ).
Геометрически определяется через умножение трех измерений объекта (длина, ширина и высота). Как провести измерение объема? Некоторые объемы вычисляются как:
- объем куба: две ширины, одна высота.
- объем цилиндра: площадь поперечного сечения превосходит высоту цилиндра.
- объем сферы: в 4/3 раза больше радиуса куба.
Объем твердого тела вычисляется через объем жидкости, которую вытесняет при погружении.
Объем сосуда можно определить как его емкость, то есть количество вмещаемой жидкости. Таким же образом работают и измерительные чаши: площадь поперечного сечения умножается на переменную высоту. Жидкость всегда будет покрывать поперечное сечение, а добавление увеличит высоту внутри контейнера.
Мерную чашу используют для определения объемов жидкостей. Единицами служат унции, чаши и миллилитры
Жидкость расплывается по форме контейнера, заполняя минимально требуемую высоту. Газы же стараются заполнить собою все максимально. Поэтому измерить объем жидкости очень просто, ведь газ всегда равномерно распространяется по пространству.
Читайте также:
- Какие черты характера раскрывают поведение бирюка в грозовую ночь кратко
- Презентация отчет по проекту пдд в детском саду
- Исследовательская деятельность в средней школе
- Как жизнедеятельность живых организмов повлияла на изменение геологических оболочек земли кратко
- Какие события связаны с правлением князя игоря княгини ольги князя святослава кратко
Цель работы:
Научиться определять объём тела с помощью измерительного цилиндра.
Приборы и материалы:
Измерительный цилиндр (мензурка), тела неправильной формы небольшого объёма (гайки, фарфоровые ролики, кусочки металла и др.), нитки.
Указания к работе:
1. Определите цену деления мензурки.
2. Налейте в мензурки столько воды, чтобы тело можно было полностью погрузить в воду, и измерьте её объём.
3. Опустите тело, объём которого надо измерить, в воду, удерживая его за нитку (рис. 201), и снова измерьте объём жидкости.
4. Проделайте опыты, описанные в пунктах 2 и 3, с некоторыми другими имеющимися у вас телами.
5. Результаты измерений запишите в таблицу 9.
Дополнительное задание.
Если тело неправильной формы не входить в мензурку, то его объём можно определить с помощью отливного сосуда (рис. 202). Перед измерением сосуд наполняют водой до отверстия отливной трубки. При погружении в него тела часть воды, равная объёму тела, выливается. Измерив мензуркой её объём, определяют объём погружённого в жидкость тела.
Таблица 9.
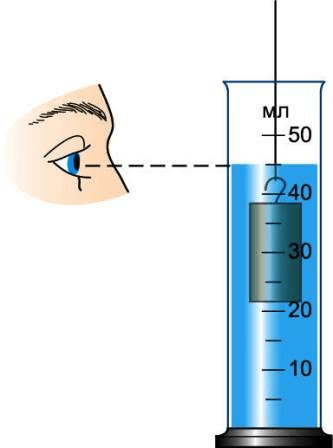
рис. 201
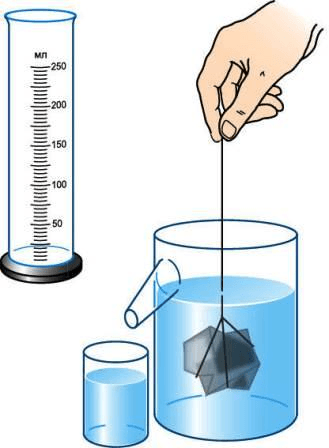
рис. 202
reshalka.com
ГДЗ учебник по физике 7 класс Перышкин. №4 Измерение объема тела. Номер №1
Решение
Объём тела неправильной формы точно измерить с помощью измерительных приборов нельзя. Поэтому для измерения объема воспользуемся мензуркой. Тело, полностью погружённое в жидкость, вытесняет объём жидкости, который равен объёму самого тела. Воспользуемся этим законом и найдем объёмы некоторых тел следующим образом. Нальем достаточное количество воды в мензурку, а затем погрузим полностью туда наше тело. Разница между первоначальным объёмом и объёмом жидкости, в которое погружено тело, равна объёму этого тела.
V
=
V
2
−
V
1
, где
V
2
− объём воды и тела,
V
1
− начальный объём воды в мензурке.
- Прежде чем проводить измерения физической величины с помощью измерительного прибора нужно определите цену деления его шкалы.
Для определения цены деления необходимо взять 2 соседних числа, найти их разницу (от большего отнять меньшее), а затем разделить полученное число на количество маленьких штрихов между этими числами.
На шкале цилиндра возьмём, к примеру, числа 20 и 30.
Таким образом, цена каждого деления будет равна
30
−
202
=
10
= 5 мл.
2 - В мензурку нальём столько воды, чтобы тело можно было полностью погрузить в воду. Начальный объём воды равен 70
с
м
3
. - Опустим тело, объём которого надо измерить (шарик, брусок, цилиндр), в воду, удерживая его за нитку, и снова измерим объём жидкости.
Вычисления.
V
б
р
=
95
−
70
=
25с
м
3
V
ц
=
85
−
65
=
20с
м
3
V
ш
=
75
−
60
=
15с
м
3
- Результаты измерений запишем в таблицу 9.
Таблица 9.
| № опыта | Название тела | Начальный объём воды в мензурке
V 1 , с м 3 |
Объём воды и тела
V 2 , с м 3 |
Объём тела V,
с м 3 V = V 2 − 1 |
|---|---|---|---|---|
| 1 | Брусок | 70 | 95 | 25 |
| 2 | Цилиндр | 65 | 85 | 20 |
| 3 | Шарик | 60 | 75 | 15 |
Вывод. В ходе лабораторной работы мы научились измерять объёмы тел с помощью измерительного цилиндра и выяснили, что объём тел равен разнице объёма воды, в которое погружено тело, и первоначального объёма воды.
Для того чтобы определить плотность вещества, надо массу тела разделить на его объем:
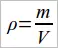(10.1)
Массу тела можно определить с помощью весов. А как найти объем тела?
Если тело имеет форму прямоугольного параллелепипеда (рис. 24), то его объем находится по формуле
V = аbс.
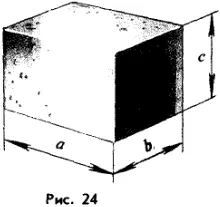
Если же у него какая-то другая форма, то его объем можно найти методом, который был открыт древнегреческим ученым Архимедом в III в. до н. э.
Архимед родился в Сиракузах на острове Сицилия. Его отец, астроном Фидий, был родственником Гиерона, ставшего в 270 г. до н. э. царем города, в котором они жили.
До нас дошли не все сочинения Архимеда. О многих его открытиях стало известно благодаря более поздним авторам, в сохранившихся трудах которых описываются его изобретения. Так, например, римский архитектор Витрувий (I в. до н. э.) в одном из своих сочинений рассказал следующую историю:
«Что касается Архимеда, то изо всех его многочисленных и разнообразных открытий то открытие, о котором я расскажу, представляется мне сделанным с безграничным остроумием.
Во время своего царствования в Сиракузах Гиерон после благополучного окончания всех своих мероприятий дал обет пожертвовать в какой-то храм золотую корону бессмертным богам. Он условился с мастером о большой цене за работу и дал ему нужное по весу количество золота. В назначенный день мастер принес свою работу царю, который нашел ее отлично исполненной; после взвешивания вес короны оказался соответствующим выданному весу золота.
После этого был сделан донос, что из короны была взята часть золота и вместо него примешано такое же количество серебра. Гиерон разгневался на то, что его провели, и, не находя способа уличить это воровство, попросил Архимеда хорошенько подумать об этом. Тот, погруженный в думы по этому вопросу, как-то случайно пришел в баню и там, опустившись в ванну, заметил, что из нее вытекает такое количество воды, каков объем его тела, погруженного в ванну. Выяснив себе ценность этого факта, он, не долго думая, выскочил с радостью из ванны, пошел домой голым и громким голосом сообщал всем, что он нашел то, что искал. Он бежал и кричал одно и то же по-гречески: «Эврика, эврика! (Нашел, нашел!)».
Затем, пишет Витрувий, Архимед взял сосуд, доверху наполненный водой, и опустил в него золотой слиток, равный по весу короне. Измерив объем вытесненной воды, он снова наполнил сосуд водой и опустил в него корону. Объем воды, вытесненной короной, оказался больше объема воды, вытесненной золотым слитком. Больший объем короны означал, что в ней присутствует менее плотное, чем золото, вещество. Поэтому опыт, проделанный Архимедом, показал, что часть золота была похищена.
Итак, для определения объема тела, имеющего неправильную форму, достаточно измерить объем воды, вытесняемой данным телом. Располагая измерительным цилиндром (мензуркой), это сделать несложно.
В тех случаях, когда известны масса и плотность тела, его объем можно найти по формуле, вытекающей из формулы (10.1):
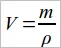(10.2)
Отсюда видно, что для определения объема тела надо массу этого тела разделить на его плотность.
Если, наоборот, объем тела известен, то, зная, из какого вещества оно состоит, можно найти его массу:
m = ρV. (10.3)
Чтобы определить массу тела, надо плотность тела умножить на его объем.
1. Какие способы определения объема вы знаете? 2. Что вам известно об Архимеде? 3. Как можно найти массу тела по его плотности и объему?
Экспериментальное задание. Возьмите кусок мыла, имеющий форму прямоугольного параллелепипеда, на котором обозначена его масса. Проделав необходимые измерения, определите плотность мыла.
На прошлом уроке мы познакомились с определением плотности тела, узнали формулу, по которой можно ее рассчитать: $rho = frac{m}{V}$.
Сейчас нам предстоит взглянуть на эту формулу с других сторон. Мы научимся находить объем и массу по известной плотности материала тела, решать задачи, используя полученные знания.
Расчет массы тела по его плотности
Знание плотности веществ очень важно для многих практических целей. Для инженеров и строителей, например, знание плотности имеет колоссальное значение — так они могут рассчитать массу будущего механизма или строения.
Как вычисляется масса тела по его плотности и объему?
Плотность определяется по формуле $rho = frac{m}{V}$. Выразим отсюда массу:
$m = rho V$.
Чтобы рассчитать массу тела, если известны его объем и плотность, нужно плотность умножить на объем.
Задача на расчет массы
Рассмотрим пример задачи на расчет массы.
Рассчитайте массу детали, изготовленной из латуни, объемом $0.15 space м^3$.
Из таблицы 1 предыдущего урока берем значение плотности латуни. Она равна $8500 frac{кг}{м^3}$.
Дано:
$rho = 8500 frac{кг}{м^3}$
$V = 0.15 space м^3$
$m -?$
Показать решение и ответ
Скрыть
Решение:
$m = rho cdot V$,
$m = 8500 frac{кг}{м^3} cdot 0.15 space м^3 = 1275 space кг approx 1.3 space т$.
Ответ: $m = 1275 space кг approx 1.3 space т$.
Расчет объема тела по его плотности
По какой формуле можно определить объем тела?
Подобным образом выразим из формулы плотности объем:
$V = frac{m}{rho}$.
Чтобы рассчитать объем тела, если известны его масса и плотность, нужно массу разделить на плотность.
Данной формулой для определения объема часто пользуются в тех случаях, когда тела имеют сложную неправильную форму.
Задача на расчет объема
Рассмотрим пример задачи на расчет объема.
Молоко в бутылке имеет массу $1.03 space кг$. Рассчитайте объем бутылки.
В таблице 2 прошлого параграфа находим молоко: его плотность равна $1030 frac{кг}{м^3}$.
Дано:
$rho = 1030 frac{кг}{м^3}$
$m = 1.03 space кг$
$V -?$
Решение:
$V = frac{m}{rho}$,
$V = frac{1.03 space кг}{1030 frac{кг}{м^3}} = 0.001 space м^3 = 1 space л$.
Ответ: $V = 1 space л$.
Дополнительные задачи
Задача №1
На рисунке 1 изображен кусок хозяйственного мыла в упаковке. По данным производителя размеры размеры его полиэтиленовой упаковки составляют 6 см x 9 см x 5,5 см.
Масса одного куска 200 г. Масса брутто (масса товара вместе с упаковкой) указан 211 г. Найдите объем куска мыла без упаковки. Выразите ответ в СИ.
Обозначим стороны упаковки как $a, b space и space с$, массу куска была $m_м$, массу куска мыла в упаковке — $m$, а общую массу мыла в упаковке — $m_{уп}$.
Объем куска мыла будем обозначать как $V_м$, а вместе с упаковкой — $V$.
Дано:
$a = 6 space см$
$b = 9 space см$
$c = 5.5 space см$
$m_м = 200 space г$
$m = 211 space г$
$V_м -?$
Показать решение и ответ
Срыть
Решение:
Найдем массу упаковки:
$m_{уп} = m — m_м$,
$m_{уп} = 211 space г — 200 space г = 11 space г$.
Общий объем упаковки и мыла:
$V = a cdot b cdot c$,
$V = 6 space см cdot 9 space см cdot 5.5 space см = 297 space см^3$.
Указано, что упаковка изготовлена из полиэтилена (из таблицы 1 предыдущего параграфа его плотность $rho_п$ равна $0.92 frac{г}{см^3}$).
Найдем объем упаковки $V_{уп}$:
$V_{уп} = frac{m_{уп}}{rho_{уп}}$,
$V_{уп} = frac{11 space г}{0.92 frac{г}{см^3}} approx 12 space см^3$.
Общий объем куска мыла в упаковке складывается из объема самого куска и объема упаковки. Так мы можем найти объем куска мыла:
$V_м = V — V_{уп}$,
$V_м = 297 space см^3 — 12 space см^3 = 285 space см^3$.
Выразим в СИ:
$285 space см^3 = 285 cdot 1 space см cdot 1 space см cdot 1 space см = 285 cdot 0.01 space м cdot 0.01 space м cdot 0.01 space м = 285 cdot 0.000001 space м^3 = 0.000285 space м^3$.
Ответ: $V_м = 0.000285 space м^3$
Задача №2
Масса чугунного шара составляет 800 г. Его объем — $125 space см^3$. Будет ли этот шар сплошным (отлитым полностью из одного материала) или полым (иметь пространство внутри, заполненное, например, воздухом)?
Показать решение
Скрыть
Проверить это достаточно просто: рассчитаем плотность этого шара:
$rho = frac{m}{V}$,
$rho = frac{800 г}{125 space см^3} = 6.4 frac{г}{см^3}$.
Сравним полученное значение с табличной плотностью чугуна:
$rho = 7 frac{г}{см^3}$
Сколько бы тогда весил сплошной шар?
$m = rho V$,
$m = 7 frac{г}{см^3} cdot 125 space см^3 = 875 space г$.
Разница между массами реального и предполагаемого сплошного шара составляет 75 г.
Следовательно, реальный шар имеет внутри какую-то полость, он не полностью выполнен из чугуна.
Задача №3
В грузовой автомобиль загрузили 48 сосновых бревен. Масса каждого соснового бревна составляет $20 space дм^3$. На сколько увеличилась масса автомобиля после загрузки?
Из таблицы 1 предыдущего параграфа возьмем плотность сухой сосны ($400 frac{кг}{м^3}$). Переведем $20 space дм^3$ в $м^3$:
$20 space дм^3 = 20 cdot 0.1 space м cdot 0.1 space м cdot 0.1 space м = 20 cdot 0.001 space м^3 = 0.02 space м^3$.
Количество брусков — $n$.
Дано:
$V = 20 space дм^3$
$rho = 400 frac{кг}{м^3}$
$n = 48$
СИ:
$V = 0.02 space м^3$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем массу одного соснового бревна:
$m = rho cdot V$,
$m = 400 frac{кг}{м^3} cdot 0.02 space м^3 = 8 space кг$.
Масса всех сосновых бревен (M) будет равна:
$M = n cdot m$,
$M = 48 cdot 8 space кг = 384 space кг$
Ответ: масса автомобиля после загрузки увеличится на 384 кг.
Упражнения
Упражнение №1
Какова масса $0.5 space л$ спирта, молока, ртути?
Дано:
$V = 0.5 space л$
$rho_1 = 800 frac{кг}{м^3}$
$rho_2 = 1030 frac{кг}{м^3}$
$rho_3 = 13600 frac{кг}{м^3}$
СИ:
$V = 5 cdot 10^{-4} space м^3$
$m_1 — ?$
$m_2 — ?$
$m_3 — ?$
Показать решение и ответ
Скрыть
Решение:
Зная объем и плотность тела, мы может рассчитать его массу по формуле: $m = rho V$.
Рассчитаем массу спирта:
$m_1 = rho_1 V$,
$m_1 = 800 frac{кг}{м^3} cdot 5 cdot 10^{-4} space м^3 = 0.4 space кг$.
Рассчитаем массу молока:
$m_2 = rho_2 V$,
$m_2 = 1030 frac{кг}{м^3} cdot 5 cdot 10^{-4} space м^3 = 0.515 space кг$.
Рассчитаем массу ртути:
$m_3 = rho_3 V$,
$m_3 = 13600 frac{кг}{м^3} cdot 5 cdot 10^{-4} space м^3 = 6.8 space кг$.
Ответ: $m_1 = 0.4 space кг$, $m_2 = 0.515 space кг$, $m_3 = 6.8 space кг$.
Упражнение №2
Определите объем льдинки, масса которой $108 space г$.
Дано:
$m = 108 space г$
$rho = 900 frac{кг}{м^3}$
СИ:
$m = 0.108 space кг$
$V — ?$
Показать решение и ответ
Скрыть
Решение:
Зная массу и плотность льда, рассчитаем его объем:
$V = frac{m}{rho}$,
$V = frac{0.108 space кг}{900 frac{кг}{м^3}} = 0.00012 space м^3 = 120 space см^3$.
Ответ: $V = 120 space см^3$.
Упражнение №3
Сколько килограммов керосина входит в пятилитровую бутыль?
Дано:
$V = 5 space л$
$rho = 800 frac{кг}{м^3}$
СИ:
$V = 5 cdot 10^{-3} space м^3$
$m — ?$
Показать решение и ответ
Скрыть
Решение:
Зная плотность и объем, найдем массу керосина:
$m = rho V$,
$m = 800 frac{кг}{м^3} cdot 5 cdot 10^{-3} space м^3 = 4 space кг$.
Ответ: $m = 4 space кг$.
Упражнение №4
Грузоподъемность лифта составляет $3 space т$. Сколько листов железа можно погрузить в лифт, если длина каждого листа равна $3 space м$, ширина — $60 space см$ и толщина — $4 space мм$?
Дано:
$M = 3 space т$
$a = 60 space см$
$b = 4 space мм$
$c = 3 space м$
$rho = 7800 frac{кг}{м^3}$
СИ:
$M = 3000 space кг$
$a = 0.6 space м$
$b = 0.004 space м$
$n — ?$
Показать решение и ответ
Скрыть
Решение:
Сначала рассчитаем массу одного железного листа. Для этого нам нужно знать его объем (плотность мы взяли из таблицы). Объем мы может вычислить, перемножив друг на друга ширину, высоту и длину: $V = a cdot b cdot c$.
Масса железного листа:
$m = rho V = rho cdot a cdot b cdot c$,
$m = 7800 frac{кг}{м^3} cdot 0.6 space м cdot 0.004 space м cdot 3 space м = 56.16 space кг$.
Теперь разделим грузоподъемность лифта на массу одного лифта. Полученное целое число и будет ответом на вопрос задачи:
$n = frac{M}{m}$,
$n = frac{3000 space кг}{56.16 space кг} approx 53$.
Ответ: $n = 53$.
Упражнение №5
Кружка доверху наполнена молоком. Определите объем кружки, если масса молока в кружке $515 space г$, плотность молока найдите в таблице.
Дано:
$m = 515 space г$
$rho = 1030 frac{кг}{м^3}$
СИ:
$m = 0.515 space кг$
$V — ?$
Показать решение и ответ
Скрыть
Решение:
Зная массу и плотность молока, найдем объем, который оно занимает в кружке:
$V = frac{m}{rho}$,
$V = frac{0.515 space кг}{1030 frac{кг}{м^3}} = 0.0005 space м^3 = 0.5 space л$.
Ответ: $V = 0.5 space л$.
Задание
Возьмите баночку из-под меда. Рассмотрите внимательно этикетку. Найдите на ней, какова масса меда и объем баночки. Затем рассчитайте плотность меда. Полученный результат проверьте по таблице.
Дано:
$m = 800 space г$
$V = 500 space мл$
СИ:
$m = 0.8 space кг$
$V = 0.0005 space м^3$
$rho — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем плотность меда:
$rho = frac{m}{V}$,
$rho = frac{0.8 space кг}{0.0005 space м^3} = 1600 frac{кг}{м^3}$.
По таблице плотность меда составляет $1350 frac{кг}{м^3}$. Существует множество различных сортов меда, плотность которых отличается друг от друга. Наше значение плотности не сильно отличается от табличного, поэтому можно сказать, что результат получен правильный.
Ответ: $rho = 1600 frac{кг}{м^3}$.
