Задачи на Сопротивление проводников с решениями
Формулы, используемые на уроках «Задачи на сопротивление проводников»:
Название величины |
Обозначение |
Единица измерения |
Формула |
Сила тока |
I |
А |
I = U / R |
Напряжение |
U |
В |
U = IR |
Сопротивление |
R |
Ом |
R = U/I |
Длина проводника |
l |
м |
l = RS / p |
Площадь поперечного сечения проводника |
S |
мм2 |
S = pl / R |
Удельное сопротивление вещества |
p |
Ом • мм2 /м
|
p = RS / l |
Сопротивление проводника |
R |
Ом |
R = pl / S |
Площадь поперечного сечения измеряют в мм2, поэтому в справочниках значения удельного сопротивления проводника приводятся не только в единицах СИ Ом • м, но в Ом • мм2 / м.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Длина алюминиевого провода 500 м, площадь его поперечного сечения 4 мм2 , Чему равно сопротивление провода?
Задача № 2.
Медный провод с площадью поперечного сечения 0,85 мм2 обладает сопротивлением 4 Ом. Какова длина провода?
Задача № 3.
Длина серебряного провода 0,6 м, а сопротивление 0,015 Ом. Определите площадь поперечного сечения провода.
Задача № 4.
Жила алюминиевого провода, используемого для электропроводки, имеет площадь поперечного сечения 2 мм2. Какой площадью поперечного сечения должен обладать никелиновый провод, чтобы длина и сопротивление линии не изменились?
Задача № 5.
Площади поперечных сечений стальных проволок с одинаковыми длинами равны 0,05 и 1 мм2. Какая из них обладает меньшим сопротивлением; во сколько раз?
Задача № 6.
Сопротивление проволоки длиной 1 км равно 5,6 Ом. Определите напряжение на каждом участке проволоки длиной 100 м, если сила тока в ней 7 мА.
Задача № 7.
Имеются два однородных проводника, однако первый в 8 раз длиннее второго, который имеет вдвое большую площадь поперечного сечения. Какой из проводников обладает большим сопротивлением; во сколько раз?
Задача № 8.
Шнур, употребляемый для подводки тока к телефону, для гибкости делают из многих тонких медных проволок. Рассчитайте сопротивление такого провода длиной 3 м, состоящего из 20 проволок площадью поперечного сечения 0,05 мм2 каждая.
Задача № 9.
Определите силу тока, проходящего через реостат, изготовленный из никелиновой проволоки длиной 50 м и площадью поперечного сечения 1 мм2, если напряжение на зажимах реостата равно 45 В.
Задача № 10.
Сопротивление проволоки, у которой площадь поперечного сечения 0,1 мм2, равно 180 Ом. Какой площади поперечного сечения надо взять проволоку той же длины и из того же материала, чтобы получить сопротивление 36 Ом?
Краткая теория для решения
Задачи на Сопротивление проводников.
Таблица удельного электрического сопротивления
некоторых веществ при 20 °С.
Это конспект по теме «ЗАДАЧИ на Сопротивление проводников». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на Последовательное соединение проводников
- Посмотреть конспект по теме Электрическое сопротивление
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
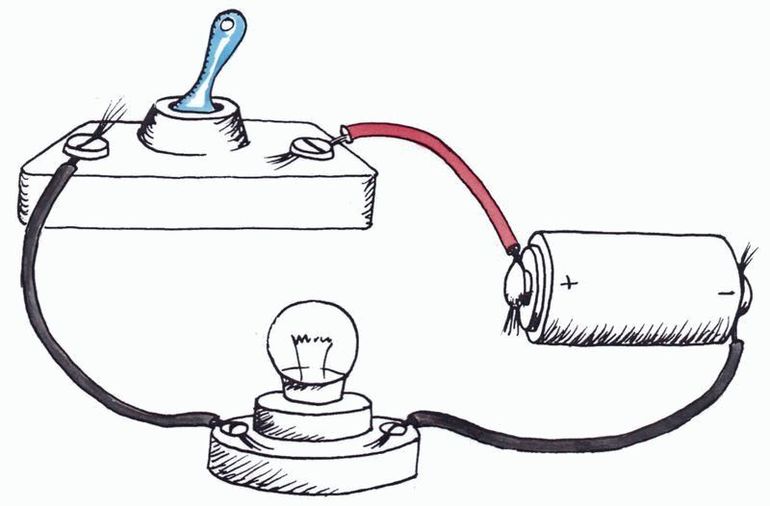
Для изучения зависимости электрических параметров соберём электрическую цепь, изображённую на схеме (рис.(1)).
Состав схемы (по часовой стрелке по ходу электрического тока):
- источник электрического напряжения (тока);
- электрический ключ для размыкания;
- последовательно подключённый амперметр для измерения силы тока в цепи;
- сопротивление (спираль никелиновой проволоки);
- вольтметр, подключённый параллельно к сопротивлению.
Рис. (1). Первая схема электрической цепи
При замыкании цепи отметим показания приборов. Используя регулятор напряжения на источнике, изменим напряжение в два раза. При этом показания вольтметра и амперметра также изменятся в два раза. Продолжим увеличивать напряжение на источнике. Наблюдения показывают, что при увеличении напряжения в (3) раза, вольтметр покажет увеличение напряжения на спирали в три раза. Во столько же раз увеличится и сила тока.
Опыт показывает зависимость изменения силы тока от приложенного напряжения.
Сила тока в проводнике прямо пропорциональна напряжению на концах проводника: (Ibacksim U).
Эту зависимость можно изобразить графически:
Рис. (2). График зависимости силы тока в проводнике от напряжения между концами этого проводника
При включении в электрическую цепь источника тока различных проводников и амперметров увидим, что для разных проводников показания амперметров различны, значит, сила тока для каждого проводника отличается.
Рис. (3). Электрическая схема с набором различных сопротивлений (AB), (CD), (EF)
Графики тоже будут отличаться.
Рис. (4). Графики зависимости силы тока от напряжения для сопротивлений (AB), (CD), (EF)
Вольтметр подключим поочерёдно к концам этих проводников. Увидим равные значения напряжения. Значение силы тока на участке цепи пропорционально разности потенциалов на его концах и зависит от рода вещества проводника. Отличие электрических параметров (U) и (I) связано с тем, что проводники имеют разное электрическое сопротивление.
Сопротивление проводника равно (1) Ом, если в проводнике при напряжении на концах (1) вольт протекает сила тока (1) ампер:
([R]=1) Ом;
(R=frac{U}{I});
Единицы измерения применяют с кратными приставками: миллиом (мОм), килоом (кОм), мегаом (МОм).
(1) мОм = (0,001) Ом;
(1) кОм = (1000) Ом;
(1) МОм = (1 000 000) Ом.
Почему существует сопротивление? Движению электронов под действием поля мешают ионы кристаллической решётки металла.
Электрический ток — направленное движение заряженных частиц.
В середине (XIX) века Джеймс Кларк Максвелл объединил исследования Вольта, Эрстеда, Ампера, Ома, Фарадея в классическую электродинамику. Учёные придерживались гипотезы, что электричество переносят положительные частицы. Все законы строились на этом предположении.
За направление электрического тока принимают движение положительно заряженных частиц.
(29) апреля (1897) года Джозеф Джон Томсон выступил на заседании Королевского общества с докладом о катодных лучах, что и считается датой открытия электрона.
Электронный ток — направленное движение электронов.
В металлах электрический ток переносится электронами. Положительные ионы, связанные узлами кристаллической решётки, перемещаться не могут. Электроны, перемещаясь между ионами, сталкиваются с ними, отскакивают обратно, что уменьшает общий поток электронов.
Электрическое сопротивление — физическая величина, отражающая свойство проводника препятствовать электронному току.
(R=frac{U}{I});
([R]=1~frac{В}{А}=1~Ом).
Чтобы узнать, как зависит сила тока в цепи от сопротивления, обратимся к опыту (рис.(4)).
Рис. (5). Электрическая цепь с аккумулятором
На рисунке изображена электрическая цепь, источником тока в которой является аккумулятор.
- Напряжение (2) В на концах резисторов постоянно. Это подтверждают показания вольтметра, подключенного параллельно к резистору.
- Используются три постоянных резистора сопротивлениями (1), (2) и (4) Ом, которые подключаются в цепь поочерёдно.
- Сила тока в цепи измеряется амперметром, который подключен последовательно с резистором.
Таблица (1). Результаты опыта
| Напряжение на концах проводника, В | Сопротивление проводника, Ом | Сила тока в цепи, А |
|
(2) |
(1) |
(2) |
|
(2) |
(2) |
(1) |
|
(2) |
(4) |
(0,5) |
По опытным данным (табл.(1)) прослеживается закономерность, которую обнаружил ещё в (1827) году Георг Ом.
Сила тока в проводнике обратно пропорциональна сопротивлению проводника: (Ibacksim frac{1}{R}).
В честь этого ученого открытый им закон называют его именем — закон Ома для участка цепи.
Сила тока на участке цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению участка цепи:
где I — сила тока, U — напряжение, R — сопротивление.
При изменяющемся сопротивлении и постоянном напряжении на участке зависимость силы тока от сопротивления будет гиперболической:
Рис. (6). График зависимости силы тока от сопротивления проводника
Определить сопротивление проводника можно несколькими способами:
1. при помощи амперметра и вольтметра;
2. при помощи омметра;
3. при помощи мультиметра, который эксплуатируется в режиме омметра.
Таблица (2). Способы измерения сопротивления
|
амперметр и вольтметр |
омметр |
мультиметр в режиме омметра |
|
Рис. 7. Амперметр и вольтметр |
Рис. 8. Омметр |
Рис. 9. Мультиметр |
|
|
|
|

Рис. 10. Обозначение омметра в цепи (или мультиметра в режиме измерения сопротивления)
Источники:
Рис. 2. График зависимости силы тока в проводнике от напряжения между концами этого проводника. © ЯКласс.
Рис. 4. Графики зависимости силы тока от напряжения для сопротивлений AB, CD, EF. © ЯКласс.
Рис. 6. График зависимости силы тока от сопротивления проводника. © ЯКласс.
Рис. 7. Старые советские измерительные приборы, Creative Commons Zero 1.0 License, https://openclipart.org/detail/205486/voltmeter-and-ammeter.
Рис. 8. Автор: Сергин Владимир Александрович – Собственный фотоснимок автора, Общественное достояние, https://commons.wikimedia.org/w/index.php?curid=4353228.
Рис. 9. Мультиметр. © ЯКласс.
Рис. 10. Указание авторства не требуется: 2021-06-07, бесплатно для коммерческого использования, https://clck.ru/VLDy3/.
Сила тока в цепи определяется электрическим зарядом, проходящим через поперечное сечение проводника за единицу времени: $I = frac{q}{t}$.
Электрическое напряжение — это еще одна физическая величина, характеризующая электрическое поле. Она равна отношению работы тока на данном участке к электрическому заряду, прошедшему по этому участку: $U = frac{A}{q}$.
Электрическое сопротивление — величина, зависящая от свойств проводника. На значение сопротивления не влияет ни значение силы тока в проводнике, ни значение напряжения на его концах. Его можно рассчитать по формуле $R = frac{rho l}{S}$, где $rho$ — удельное сопротивление проводника, $l$ — длина проводника, $S$ — площадь его поперечного сечения. Значение удельного сопротивления для определенного вещества можно посмотреть в таблице 1 в уроке «Расчет сопротивления проводника. Удельное сопротивление».
Эти три физические величины (силу тока, напряжение и сопротивление) связывает между собой закон Ома для участка цепи: $I = frac{U}{R}$. Сила тока в проводнике прямо пропорциональна напряжению на его концах и обратно пропорциональна его сопротивлению.
В данном уроке вы научитесь использовать эти знания для решения задач. Мы рассмотрим несколько примеров, а затем перейдем к упражнениям и их подробным решениям.
Пример задачи №1
Длина медного провода, использованного в осветительной сети, $100 space м$, площадь поперечного сечения его $2 space мм^2$. Чему равно сопротивление такого провода?
Для того, чтобы рассчитать сопротивление такого проводника, нам понадобится значение его удельного сопротивления. Удельное сопротивление меди равно $0.017 frac{Ом cdot мм^2}{м}$. Так как эта величина нам дана именно в этих единицах измерения, мы не будем переводить в СИ значение площади поперечного сечения, выраженное в $мм^2$.
Теперь мы можем записать условие задачи и решить ее.
Дано:
$l = 100 space м$
$S = 2 space мм^2$
$rho = 0.017 frac{Ом cdot мм^2}{м}$
$R — ?$
Решение:
Формула для расчета сопротивления проводника:
$R = frac{rho l}{S}$.
Рассчитаем его:
$R = frac{0.017 frac{Ом cdot мм^2}{м} cdot 100 space м}{2 space мм^2} = frac{1.7 space Ом}{2} = 0.85 space Ом$.
Ответ: $R = 0.85 space Ом$.
Пример задачи №2
Никелиновая проволока длиной $120 space м$ и площадью поперечного сечения $0.5 space мм^2$ включена в цепь с напряжением $127 space В$. Определить силу тока в проволоке.
Табличное значение удельного сопротивления никелина равно $0.4 frac{Ом cdot мм^2}{м}$.
Перейдем к записи условия задачи и ее решению.
Дано:
$l = 120 space м$
$S = 0.5 space мм^2$
$U = 127 space В$
$rho = 0.4 frac{Ом cdot мм^2}{м}$
$I — ?$
Решение:
Силу тока мы можем рассчитать, используя формулу закона Ома для участка цепи:
$I = frac{U}{R}$.
Но мы не знаем значения сопротивления проводника. Его мы тоже можем вычислить:
$R = frac{rho cdot l}{S}$,
$R = frac{0.4 frac{Ом cdot мм^2}{м} cdot 120 space м}{0.5 space мм^2} = frac{48 space Ом}{0.5} = 96 space Ом$.
Теперь мы можем рассчитать силу тока:
$I = frac{127 space В}{96 space Ом} approx 1.3 space А$.
Ответ: $I approx 1.3 space А$.
Пример задачи №3
Манганиновая проволока длиной $8 space м$ и площадью поперечного сечения $0.8 space мм^2$ включена в цепь аккумулятора. Сила тока в цепи $0.3 space А$. Определить напряжение на полюсах аккумулятора.
Табличное значение удельного сопротивления манганина равно $0.43 frac{Ом cdot мм^2}{м}$.
Запишем условие задачи и решим ее.
Дано:
$l = 8 space м$
$S = 0.8 space мм^2$
$I = 0.3 space А$
$rho = 0.43 frac{Ом cdot мм^2}{м}$
$U — ?$
Решение:
Если в условии задачи сказано, что проводник включен в цепь аккумулятора, это означает, что напряжение на полюсах аккумулятора будет равно напряжению на концах проволоки.
Почему? Взгляните на такую электрическую цепь (рисунок 1). Она состоит только из проводника и аккумулятора.
Если мы захотим измерить напряжение на полюсах аккумулятора c помощью вольтметра, то параллельно подключим его в эту цепь (рисунок 2). А если захотим измерить напряжение на концах проводника? Мы подключим вольтметр точно так же. Получается, что вольтметр подключен параллельно одновременно и к источнику тока, и к проводнику. Поэтому напряжение на концах проводника — это то же самое напряжение на полюсах аккумулятора.
Запишем закон Ома:
$I = frac{U}{R}$.
Выразим из него напряжение, которое нужно найти:
$U = IR$.
Сопротивление проводника рассчитаем по формуле $R = frac{rho cdot l}{S}$.
$R = frac{0.43 frac{Ом cdot мм^2}{м} cdot 8 space м}{0.8 space мм^2} = frac{3.44 space Ом}{0.8} = 4.3 space Ом$.
Теперь мы можем рассчитать напряжение:
$U = 0.3 space А cdot 4.3 space Ом = 1.29 space В approx 1.3 space В$.
Ответ: $U approx 1.3 space В$.
Упражнения
Упражнение №1
Длина одного провода $20 space см$, другого — $1.6 space м$. Площадь сечения и материал проводов одинаковы. У какого провода сопротивление больше и во сколько раз?
Обратите внимание, что если материал проводников один и тот же, то одинаковы и значения удельных сопротивлений $rho$ для этих проводников.
Дано:
$l_1 = 20 space см$
$l_2 = 1.6 space м$
$S_1 = S_2 = S$
$rho_1 = rho_2 = rho$
СИ:
$l_1 = 0.2 space м$
$frac{R_2}{R_1} — ?$
Показать решение и ответ
Скрыть
Решение:
Сопротивление проводника рассчитывается по формуле $R = frac{rho cdot l}{S}$.
Сопротивление первого провода:
$R_1 = frac{rho_1 l_1}{S_1} = frac{rho l_1}{S}$.
Сопротивление второго провода:
$R_2 = frac{rho_2 l_2}{S_2} = frac{rho l_2}{S}$.
Теперь сравним их между собой:
$frac{R_2}{R_1} = frac{frac{rho l_2}{S}}{frac{rho l_1}{S}} = frac{l_2}{l_1}$.
Подставим численные значения длины проводов:
$frac{R_2}{R_1} = frac{1.6 space м}{0.2 space м} = 8$.
Получается, что сопротивление второго провода больше сопротивления первого в 8 раз.
Это логично, ведь вы знаете, что чем больше длина проводника, тем больше его сопротивление.
Ответ: сопротивление второго провода больше сопротивления первого в 8 раз.
Упражнение №2
Рассчитайте сопротивления следующих проводников, изготовленных из:
- Алюминиевой проволоки длиной $80 space см$ и площадью поперечного сечения $0.2 space мм^2$
- Никелиновой проволоки длиной $400 space см$ и площадью поперечного сечения $0.5 space мм^2$
- Константановой проволоки длиной $50 space см$ и площадью поперечного сечения $0.005 space см^2$
Для решения этой задачи нам понадобятся табличные значения удельного сопротивления для веществ, из которых изготовлены проволоки. Удельное сопротивление алюминия — $0.028 frac{Ом cdot мм^2}{м}$, никелина — $0.4 frac{Ом cdot мм^2}{м}$, константана — $0.5 frac{Ом cdot мм^2}{м}$.
Обратите внимание на единицы измерения удельных сопротивлений, длин и площадей проводников. Для корректных расчетов длину каждой проволоки мы переведем в СИ (в $м^2$). Площади поперечных сечений должны быть выражены в $мм^2$. Для третьего задания переведем $см^2$ в $см^2$.
Дано:
$l_1 = 80 space см$
$l_2 = 400 space см$
$l_3 = 50 space см$
$S_1 = 0.2 space мм^2$
$S_2 = 0.5 space мм^2$
$S_3 = 0.005 space см^2 = 0.5 space мм^2$
$rho_1 = 0.028 frac{Ом cdot мм^2}{м}$
$rho_2 = 0.4 frac{Ом cdot мм^2}{м}$
$rho_3 = 0.5 frac{Ом cdot мм^2}{м}$
СИ:
$l_1 = 0.8 space м$
$l_2 = 4 space м$
$l_3 = 0.5 space м$
$R_1 — ?$
$R_2 — ?$
$R_3 — ?$
Показать решение и ответ
Скрыть
Решение:
Формула для расчета сопротивления проводника: $R = frac{rho l}{S}$.
Рассчитаем по ней сопротивление каждого проводника.
$R_1 = frac{rho_1 l_1}{S_1}$,
$R_1 = frac{0.028 frac{Ом cdot мм^2}{м} cdot 0.8 space м}{0.2 space мм^2} = frac{0.0224 space Ом}{0.2} = 0.112 space Ом$.
$R_2 = frac{rho_2 l_2}{S_2}$,
$R_2 = frac{0.4 frac{Ом cdot мм^2}{м} cdot 4 space м}{0.5 space мм^2} = frac{1.6 space Ом}{0.5} = 3.2 space Ом$.
$R_3 = frac{rho_3 l_3}{S_3}$,
$R_2 = frac{0.5 frac{Ом cdot мм^2}{м} cdot 0.5 space м}{0.5 space мм^2} = frac{0.25 space Ом}{0.5} = 0.5 space Ом$.
Ответ: $R_1 = 0.112 space Ом$, $R_2 = 3.2 space Ом$, $R_3 = 0.5 space Ом$.
Упражнение №3
Спираль электрической плитки изготовлена из нихромовой проволоки длиной $13.75 space м$ и площадью поперечного сечения $0.1 space мм^2$. Плитка рассчитана на напряжение $220 space В$. Определите силу тока в спирали плитки.
Удельное сопротивление нихрома равно $1.1 frac{Ом cdot мм^2}{м}$.
Дано:
$l = 13.75 space м$
$S = 0.1 space мм^2$
$U = 220 space В$
$rho = 1.1 frac{Ом cdot мм^2}{м}$
$I — ?$
Показать решение и ответ
Скрыть
Решение:
Силу тока в спирали плитки мы можем рассчитать, используя формулу закона Ома для участка цепи: $I = frac{U}{R}$.
Неизвестное сопротивление нихромовой проволоки рассчитаем по формуле $R = frac{rho l}{S}$.
$R = frac{1.1 frac{Ом cdot мм^2}{м} cdot 13.75 space м}{0.1 space мм^2} = frac{15.125 space Ом}{0.1} = 151.25 space Ом$.
Рассчитаем теперь силу тока:
$I = frac{220 space В}{151.25 space Ом} approx 1.5 space А$.
Ответ: $I approx 1.5 space А$.
Упражнение №4
Сила тока в железном проводнике длиной $150 space мм$ и площадью поперечного сечения $0.02 space мм^2$ равна $250 space мА$. Каково напряжение на концах проводника?
Для решения задачи нам понадобится значение удельного сопротивления. Для железа оно равна $0.1 frac{Ом cdot мм^2}{м}$.
Дано:
$I = 250 space мА$
$l = 150 space мм$
$S = 0.02 space мм^2$
$rho = 0.1 frac{Ом cdot мм^2}{м}$
СИ:
$I = 0.25 space А$
$l = 0.15 space м$
$U — ?$
Показать решение и ответ
Скрыть
Решение:
Закон Ома для участка цепи: $I = frac{U}{R}$.
Выразим отсюда напряжение: $U = IR$.
Рассчитаем сопротивление проводника:
$R = frac{rho l}{S}$,
$R = frac{0.1 frac{Ом cdot мм^2}{м} cdot 0.15 space м}{0.02 space мм^2} = frac{0.015 space Ом}{0.02} = 0.75 space Ом$.
Теперь мы можем рассчитать напряжение на концах проводника:
$U = 0.25 space А cdot 0.75 space Ом approx 0.2 space В$.
Ответ: $U approx 0.2 space В$.
Какие есть формулы для вычисления сопротивления резистора
Содержание
- 1 Что такое резистор
- 2 Сопротивление резистора
- 3 Последовательная цепь источника и сопротивлений
- 4 Параллельная схема элементов
- 5 Расчет смешанного соединения элементов схемы
- 6 Мощность рассеивания
- 7 Параметры резисторов
- 8 Определение параметров по маркировке и схеме
- 9 Видео по теме
Сопротивление направленному движению электронов (электрическому току) в проводах электроснабжения чаще всего провоцирует потери. Они зависят от площади сечения (S), длины (L), удельного сопротивления вещества провода (ρ). Однако, сопротивление послужило созданию самого распространенного элемента в электронике — резистора.
Что такое резистор
Деталь электрической или электронной схемы, сопротивляющаяся прохождению электрического тока, называется резистор (от латинского resisto — сопротивляюсь). Падение или изменение напряжения на этом элементе используется в схемотехнике для получения нужных процессов управления автоматикой или преобразования электричества в свет, тепло, звук или движение.
Наиболее удобно классифицировать резисторы по следующим признакам:
- назначение. Для различных сфер используют элементы с
общими свойствами или специфическими по частоте тока, точности изготовления или ограничения по напряжению;
- способ управления сопротивлением. Постоянные резисторы в определенном диапазоне напряжения и тока не меняют сопротивление. У переменных можно менять вручную данный параметр с целью управления процессами. Подстроечные используются для корректировки режимов при наладке и после ремонта;
- материал рабочей части резистора. Металлы, их окислы и сплавы, графитовые или композитные смеси;
- вид резистивных тел. Проволока, фольга или ленты из метала, напыление пленки на керамику, интегрированные каналы в микросхеме;
- способ размещения. Резисторы могут быть впаяны в электронную плату, устанавливаться отдельно на панели управления или закладываться при создании микросхемы внутри изделия;
- характер изменения падения напряжения на элементе от внешних условий (ВАХ). Вольт-амперная характеристика в рабочем диапазоне резистора может быть линейной или нелинейной.
Нелинейная ВАХ отражает изменение сопротивления компонента от внешних условий. Такие резисторы служат датчиками напряжения (варисторы), магнитного поля (магниторезисторы), уровня освещенности (фоторезисторы), перепада температуры (терморезисторы), изменения деформации (тензорезисторы).
Сопротивление резистора
У тех, кто только начинает изучать азы электротехники, часто возникает вопрос, а чем отличается резистор от сопротивления. Разница в том, что резистор является пассивным элементом электроцепи, а сопротивление — это характеристика данного элемента, которую можно рассчитать, определить по маркировке или измерить. Но зачастую сопротивление используется в качестве синонима слова «резистор».
Рассчитать внутреннее сопротивление резистора в сети постоянного тока помогает формула закона Ома для элемента цепи:
Эту формулу применяют также для расчета активного сопротивления в сети переменного тока, но используют действующий ток через элемент. Он равен постоянному току, при котором выделяется на резисторе столько же теплоты, сколько за одинаковое время при прохождении импульсного или синусоидального тока различной частоты.
Суммарное электрическое сопротивление в сетях переменного тока вычисляется при учете активной и реактивной составляющей участка цепи. Любой вид сопротивления измеряется в омах.
Одинокий резистор в схеме часто используется как ограничитель тока. На электронных платах этих элементов много. Друг с другом они соединяются в различных комбинациях: последовательно, параллельно или по смешанной системе.
Последовательная цепь источника и сопротивлений
В замкнутом контуре из последовательно соединенных резисторов и батареи ток в разных точках цепи имеет одинаковое значение. Показание вольтметра на отдельном резисторе будет отражать произведение его внутреннего сопротивления на ток в контуре. Суммарные показания вольтметров будут равны напряжению источника, а для определения общего сопротивления резисторов надо сложить сопротивления всех элементов.
Последовательную цепочку сопротивлений часто используют как делитель напряжения в маломощных измерительных или задающих ступенчатое управление параметрами устройствах. Сопротивление нагрузки Rн, подключенной параллельно R1 вместо вольтметра, должно быть немного больше, чтобы делитель работал стабильно.
Параллельная схема элементов
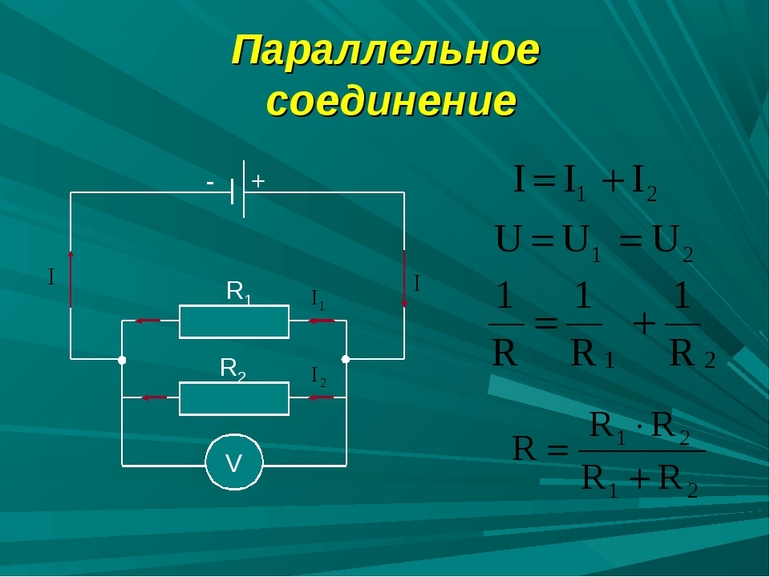
При параллельном соединении на каждом элементе присутствует напряжение источника, общий ток равен сумме токов резисторов. Расчет сопротивления участка цепи осуществляется по формуле R = (R1 • R2) / (R1 + R2).
Отличие параллельного соединения от последовательного заключается в том, что каждый резистор получает напряжение, которое равно напряжению источника, а общее сопротивление участка меньше меньшего из его составляющих.
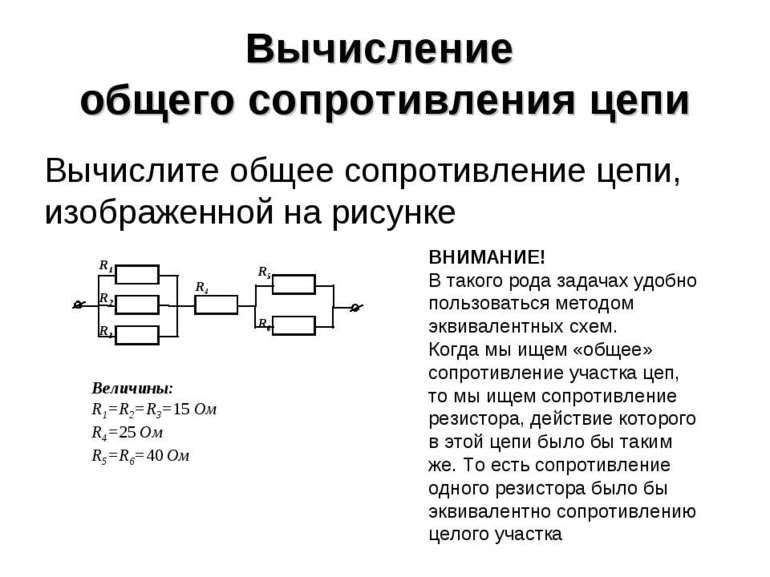
Расчет смешанного соединения элементов схемы
Перед тем как рассчитать общее сопротивление схемы, состоящей из параллельных и последовательных участков, используют методы упрощения. На каждом шаге упрощенные эквивалентные схемы можно посчитать по уже известным формулам. Полученный в результате резистор будет обладать общим сопротивлением исходной схемы.
Мощность рассеивания
Для надежной работы электрической схемы нужно знать и сопротивление резистора, и мощность рассеивания, формула для вычисления последней имеет вид:
Правильно подобранный элемент схемы должен рассеять мощность Р (Вт) не разрушаясь и не нагревая другие детали.
Параметры резисторов
Выбор резисторов происходит чаще всего по следующим основным параметрам:
- номинальному сопротивлению. Подбирается или подгоняется ближайшее к расчетному;
- допуску — характеристика, отражающая точность при изготовлении номинального сопротивления. Она составляет 5–20%;
- номинальной мощности рассеивания. Наибольшая величина рассеянного тепла без изменения характеристик меньше номинала элемента;
- предельному рабочему напряжению. Приложенное к выводам резистора наибольшее напряжение, которое не разрушает его;
- температурный коэффициент. Показывает, как изменится сопротивление резистора при колебании на один градус температуры среды.
Для переменных резисторов учитывают ряд дополнительных характеристик:
- износоустойчивость — число циклов;
- функцию изменения сопротивления (линейная, логарифмическая, обратнологарифмическая);
- уровень шума при движении ползунка.
Определение параметров по маркировке и схеме
Некоторые из параметров наносятся непосредственно на резисторы, например, сопротивление и допуск. Раньше для информации о них использовали буквы и цифры. Номинальное сопротивление резисторов имеет диапазон от 0.01 Ом до 1 ГОм. Цифры в маркировке обозначают номинал, а буквы — множитель. Конкретная величина получается умножением или делением цифр.
Буквенно-цифровая маркировка предполагает использование букв Е и R для сопротивлений до 99 Ом, выше — К, а уровень мегаомов обозначается буквой М. В зависимости от того, какую позицию занимает буква в цифровом коде, определяются целые числа или дробные. Узнать, какому множителю соответствует определенная буква, поможет специальная таблица, которую можно найти в любом справочном пособии.
Элементы с цифро-буквенной маркировкой сейчас можно найти преимущественно в старой аппаратуре. В ходе ее ремонта часто приходится менять резисторы, поэтому необходимо уметь расшифровывать такое обозначение.
Сейчас в угоду минимизации отказались от буквенно-цифровых обозначений. На поверхность резисторов наносится маркировка кольцами или точками разных цветов. Чтобы определить по полоскам сопротивление резистора, следует начинать со смещенной к одному из выводов или самой широкой цветной полоски.
Набор цветов первых трех колец при 5 и 6-полосной раскраске означает шифр сопротивления резистора, цвет четвертого кольца обозначает определенное значение множителя для него. Цвет пятого кольца показывает точность изготовления резистора. При шестиполосной окраске цвет последнего кольца обозначает изменение сопротивления (процент) при перепаде температуры окружающей среды на 1 градус. Четырех и пятиполосная раскраска его не имеет.
При четырехполосной маркировке сопротивление резисторов определяется по цветам первых двух. Цвет третьей полосы — это множитель для точного определения сопротивления. Последняя полоса своей расцветкой говорит о допуске в процентах от номинала.
На электрической схеме резистор изображается в виде прямоугольника с размерами 4×10 мм. Рядом с изображением указывается буква R и цифра, обозначающая порядковый номер элемента на схеме, например, R1. Указывается также номинальное сопротивление. Как определить его по буквенно-цифровой маркировке, было рассказано выше.
Мощность рассеивания указывается на графическом изображении специальными метками, если этот параметр меньше 1 ватта. Как узнать мощность по ним подскажет таблица, приведенная ниже.
Если мощность рассеивания выше одного ватта, то внутри прямоугольника ставят римскую цифру. Например, V используется для мощности величиной 5 Вт, Х — 10 Вт и т. п.
Бывают случаи, когда нет возможности воспользоваться маркировкой, например, если она повреждена или стерта. В таком случае нужно знать, как измерить сопротивление специальным прибором. Это может быть омметр или мультиметр. Они мало чем отличаются, но последний является многофункциональным прибором. Принцип измерений основывается на законе Ома. Перед тем как проверить резистор, следует выставить рабочий режим и диапазон измеряемого сопротивления.
Алгоритм по измерению сопротивления используется такой:
Резистор является довольно простым элементом и по своему устройству, и по принципу работы. Поэтому его сопротивление определяется также довольно просто. Еще больше облегчают задачу онлайн-калькуляторы. Ими можно воспользоваться, если возникает необходимость рассчитывать сопротивление многих элементов, для соединения которых применяются разные способы, а также для расшифровки маркировки в виде цветных полос.
Видео по теме
Общие сведения
Прохождение электрического тока через проводник зависит от его проводимости. Это параметр пропорционален силе тока. Другими словами, он определяет способность вещества пропускать через себя электричество без потерь. Зависит проводимость от физических свойств материала, температуры, степени воздействия внешних сил. Обратной ей величиной является сопротивление, то есть характеристика проводника, показывающая его возможность сопротивляться прохождению тока.
Связь между фундаментальными параметрами электротока экспериментально установил Симон Ом. Он выяснил, что сила тока в замкнутой цепи пропорциональна разности потенциалов (напряжению) и обратно пропорциональна сопротивлению: I = U / R. Так, если R равно нулю, то сила тока будет бесконечной.
Способность веществ препятствовать прохождению электротока используется при построении электрических цепей. Так, радиоэлемент, который называется резистором, установленный в определённом месте электроцепи, позволяет получить на нагрузке нужное значение напряжения или тока. Радиодеталь представляет собой двухполюсник, который имеет установленное значение сопротивления или может изменять его.
Реальная замкнутая электрическая цепь состоит из множества активных и пассивных радиоэлементов. Каждый из них обладает каким-то значением сопротивления. В этом случае говорят о внутреннем сопротивлении прибора.
Расчёт выходных характеристик цепи, а именно величин тока и напряжения, требует знания общего сопротивления всей замкнутой цепочки. Иными словами, все элементы, начиная от источника питания и заканчивая нагрузкой, заменяются эквивалентными резисторами. Для цепи сначала считают общее значение сопротивления, а затем вычисляют нужные характеристики. Относительно источника тока, нагрузки и других элементов каждый резистор может быть подключён:
- последовательно;
- параллельно.
Вид подключения влияет на общее сопротивление. Формула для его нахождения может быть довольно громоздкой из-за смешанного соединения, поэтому чаще расчёт ведётся в несколько этапов, на каждом из которых выполняется объединение одного или нескольких элементов.
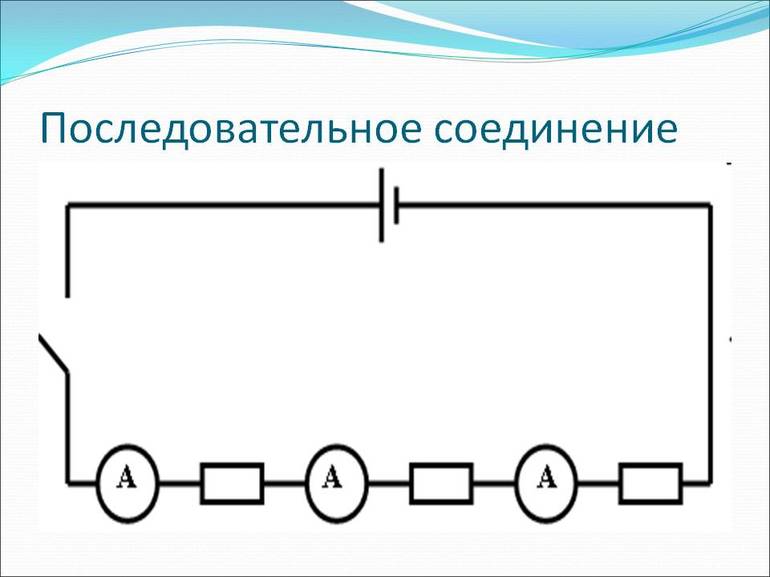
Последовательное подключение
Для удобства при изображении разветвлённой электрической цепи все сопротивления чертят в виде прямоугольников, которые являются резисторами. У любого такого элемента можно выделить два вывода. Один является началом, а другой — концом. С учетом сказанного можно сформулировать определение для последовательного соединения проводников: подключение, при котором конец предыдущего элемента соединён с началом последующего, называют последовательным.
Любой проводник обладает электрическим сопротивлением. Целью преобразования является замена чередующейся последовательности одним резистором. При этом по своим электрическим свойствам он должен не отличаться от всей цепочки. Простыми словами это можно пояснить так: если взять два чёрных ящика, у которых есть по паре выводов, причём один будет содержать всю электроцепь, а другой быть её эквивалентом, то определить, в каком из них находится схема, а где эквивалент, будет невозможно.
При последовательном соединении происходят следующие явления. Пусть имеется прямая цепочка, содержащая n резисторов: R1 + R2 + … +Rn. Сила тока — это величина, которая равняется заряду, протекающему за единицу времени. Можно представить, что в первом резисторе значение электротока будет больше, чем во втором. В результате возникнет «пробка», и скорость движения зарядов замедлится.
В точке соединения элементов произойдёт накопление электронов, что приведёт в ней к росту напряжения. Соответственно, сила тока на первом резисторе будет уменьшаться, а на втором, наоборот, увеличиваться. Это приведёт к выравниванию количества проходящих через резисторы зарядов, поэтому сила тока практически за мгновение во всей последовательной цепи станет одинаковой.
Напряжение — это работа, выполняемая по переносу заряда. По закону сохранения энергии общее её значение равняется их сумме на различных этапах. Общую разность потенциалов можно будет определить, сложив напряжения на каждом элементе. Такой вид подключения описывается следующими выражениями:
- I = I 1 = I 2 = … = In;
- U = U1 + U2 + … +Un.
Эти равенства являются фундаментальными для нахождения параметров при повторении резисторов в цепи. Используя закон Ома, можно найти, чему будет равняться сопротивление цепи. Формула для его нахождения будет выглядеть так: Rпос = R 1 + R 2 +… + Rn.
Параллельное соединение
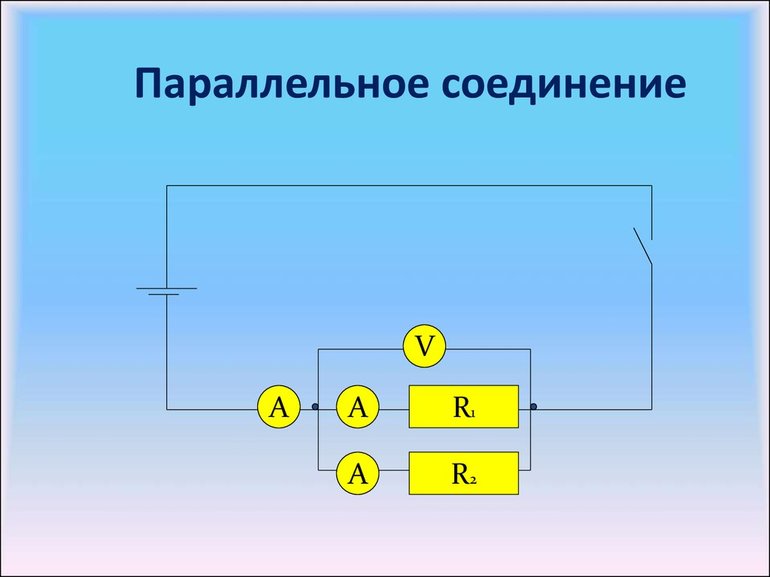
По распространённости такой вид соединения чаще встречается, чем последовательное подключение. При нём проводники соединены так, что начала всех резисторов сводятся в одну точку электрической цепи, а концы — в другую. Для того чтобы заменить разветвлённое подключение одним эквивалентным элементом, нужно знать, как правильно рассчитать ток и напряжение.
Пусть имеется цепь, состоящая из R1 + R2 + … +Rn параллельно включённых радиоэлементов. На неё подаётся напряжение U. На вход схемы поступает ток с силой I. Используя закон сохранения зарядов, можно выполнить следующие рассуждения: ток втекает в узел, к которому подсоединены начала всех резисторов, затем он растекается по их выводам.
В результате через первую ветвь потечёт ток I1, вторую — I2, в энную — In. Поскольку заряд не может пропасть, то какое его количество втекло в узел, такое же должно разойтись по всем ветвям для одного и того же момента времени. Значит, сумма токов на всех выводах будет равняться поступающему на них значению.
Электростатическое поле является потенциальным, то есть работа по перемещению заряда из одной точки в другую не зависит от траектории, по которой перемещается носитель. Следовательно, при переносе одного кулона по любой ветви нужно будет совершить одинаковую работу. Из приведённых рассуждений следует, что при параллельном соединении формулы, с помощью которых можно рассчитать характеристики электрической цепи, будут следующими:
- I = I1 + I2 + … +In;
- U1 = U2 = … = Un.
Таким образом, вычисление эквивалентного сопротивления, которым можно будет заменить всю цепь в соответствии с законом Ома, выполняется по формуле: 1 / R пар = 1 / R 1 + 1 / R 2 + … + 1 / Rn. Для одинаковых проводников при вычислении сопротивления можно использовать приведённую формулу. Это позволяет в некоторых случаях упростить расчёт.
Согласно правилу сложения дробей c одинаковым знаменателем можно записать равенство: 1 / R1 + 1 / R2 + … + 1 / Rn = N / R1. Отсюда следует, что Rпар = R1 / N, где N равно числу резисторов. По аналогии можно посчитать общее сопротивление по упрощённой формуле для двух элементов: (1 / R1) + (1 / R2) = (R 2 + R 1) / R 1 * R 2. Это довольно удобные формулы для практического применения.
Решение задач
Для вычисления сопротивления любого смешанного соединения нужно запомнить всего две формулы — выражения для нахождения величины при последовательном и параллельном подключении. Поочерёдно комбинируя их применение, сложную схему можно заменить одним сопротивлением. Но не всегда приходится применять формулы. Есть задания, в которых неизвестную величину можно вычислить в уме.
Например, пусть имеется параллельное подключение из четырёх резисторов. Сопротивления проводников равняются 10 Ом, 12 Ом, 15 Ом, 20 Ом. Нужно образовать из них резистор, не изменяющий характеристики электрической цепи. Чтобы выполнить расчёт в уме, следует каждый элемент представить в виде комбинации из 60-омных резисторов. Тогда к первому нужно будет добавить шесть, ко второму — пять, к третьему — четыре, к четвёртому — три. Общее количество резисторов получится 18. Значит, Rобщ = 60 / 18 = 10 / 3 = 3,3 Ом.
Из типовых задач, в которых необходимо найти сопротивление цепи, предлагающихся в школе на уроках физики, можно привести следующие:
- Найдите ток в цепи, если вольтметр, подключённый к одному из трёх последовательно соединённых проводников, показывает 100 В. Сопротивление элементов составляет: R1 = R2 = 5 Ом, R3 = 15 Ом. В задаче три резистора подключены в линию, значит, их полное сопротивление равно: R = R 1 + R 2 + R 3 = 25 Ом. У вольтметра r внутреннее равно бесконечности. Следовательно, I = U / R = 100 / 25 = 4 A.
-
Каково будет сопротивление каждого из резисторов, если при их последовательном соединении ток равен 3A, а при параллельном — 16A. Напряжение в сети составляет 120 В. При первом способе соединения Iпосл = U / (R1 + R2), при втором Iпар = U / Rпар = U * (R1 + R2) / R1 * R2. Из первой формулы следует, что R1 + R2 = U / Iпос. Тогда: I пар = U 2 / Iпос * R 1 * R 2 → R 1 * R 2 = U 2 / I пар * I пос. Используя теорему Виета, можно составить квадратное уравнение. После его решения искомые величины будут равны: R 1 = 30 Ом, R 2 = 10 Ом.
Следует отметить, что приборы для измерения тока, напряжения и даже ёмкости используют особенности вычисления сопротивления цепи. Так, вольтметр имеет бесконечно большой внутренний импеданс, что позволяет подключать его параллельно к измеряемым точкам без внесения изменения в протекающий сигнал.
Амперметр же, наоборот, характеризуется пренебрежимо малой величиной внутреннего сопротивления, поэтому и подключают его в разрыв линии, на которой выполняют измерения.