Оглавление:
- Основные теоретические сведения
- Импульс тела
- Закон сохранения импульса
- Сохранение проекции импульса
- Многомерный случай ЗСИ. Векторный метод
Основные теоретические сведения
Импульс тела
К оглавлению…
Импульсом (количеством движения) тела называют физическую векторную величину, являющуюся количественной характеристикой поступательного движения тел. Импульс обозначается р. Импульс тела равен произведению массы тела на его скорость, т.е. он рассчитывается по формуле:
Направление вектора импульса совпадает с направлением вектора скорости тела (направлен по касательной к траектории). Единица измерения импульса – кг∙м/с.
Общий импульс системы тел равен векторной сумме импульсов всех тел системы:
Изменение импульса одного тела находится по формуле (обратите внимание, что разность конечного и начального импульсов векторная):
где: pн – импульс тела в начальный момент времени, pк – в конечный. Главное не путать два последних понятия.
Абсолютно упругий удар – абстрактная модель соударения, при которой не учитываются потери энергии на трение, деформацию, и т.п. Никакие другие взаимодействия, кроме непосредственного контакта, не учитываются. При абсолютно упругом ударе о закрепленную поверхность скорость объекта после удара по модулю равна скорости объекта до удара, то есть величина импульса не меняется. Может поменяться только его направление. При этом угол падения равен углу отражения.
Абсолютно неупругий удар – удар, в результате которого тела соединяются и продолжают дальнейшее своё движение как единое тело. Например, пластилиновый шарик при падении на любую поверхность полностью прекращает свое движение, при столкновении двух вагонов срабатывает автосцепка и они так же продолжают двигаться дальше вместе.
Закон сохранения импульса
К оглавлению…
При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, такая система называется замкнутой.
В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой. Этот фундаментальный закон природы называется законом сохранения импульса (ЗСИ). Следствием его являются законы Ньютона. Второй закон Ньютона в импульсной форме может быть записан следующим образом:
Как следует из данной формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:
Аналогично можно рассуждать для равенства нулю проекции силы на выбранную ось. Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:
Аналогичные записи можно составить и для остальных координатных осей. Так или иначе, нужно понимать, что при этом сами импульсы могут меняться, но именно их сумма остается постоянной. Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны.
Сохранение проекции импульса
К оглавлению…
Возможны ситуации, когда закон сохранения импульса выполняется только частично, то есть только при проектировании на одну ось. Если на тело действует сила, то его импульс не сохраняется. Но всегда можно выбрать ось так, чтобы проекция силы на эту ось равнялась нулю. Тогда проекция импульса на эту ось будет сохраняться. Как правило, эта ось выбирается вдоль поверхности по которой движется тело.
Многомерный случай ЗСИ. Векторный метод
К оглавлению…
В случаях если тела движутся не вдоль одной прямой, то в общем случае, для того чтобы применить закон сохранения импульса, нужно расписать его по всем координатным осям, участвующим в задаче. Но решение подобной задачи можно сильно упростить, если использовать векторный метод. Он применяется если одно из тел покоится до или после удара. Тогда закон сохранения импульса записывается одним из следующих способов:
В этих формулах буквой υ обозначены скорости тел до соударения, а буквой u обозначены скорости тел после соударения. Из правил сложения векторов следует, что три вектора в этих формулах должны образовывать треугольник. Для треугольников применяется теорема косинусов. Если правильно записать соответствующую теорему косинусов, то зачастую получается уравнение из которого можно найти нужную величину. Однако, иногда к правильно записанной теореме косинусов еще нужно будет добавить правильно записанный закон сохранения энергии (смотрите следующий раздел). В этом случае получится система уравнений из которых наверняка можно будет найти нужную величину.
как найти скорость тела если известно импульс тела и масса тела ?
El_Nano
Гуру
(2974),
на голосовании
7 лет назад
Голосование за лучший ответ
Допустимое отклонение
Искусственный Интеллект
(111186)
8 лет назад
подели импульс на массу
El_NanoГуру (2974)
8 лет назад
о спасибо тогда еще несколько вопросов электические заряды имеются один +10 другой -20 и они слились что будет? ответ будет же -10 ??
Допустимое отклонение
Искусственный Интеллект
(111186)
Сложно себе представить “слившиеся” заряды, но если ты говоришь о заряде системы из этих двух зарядов, то да, они просто складываются.
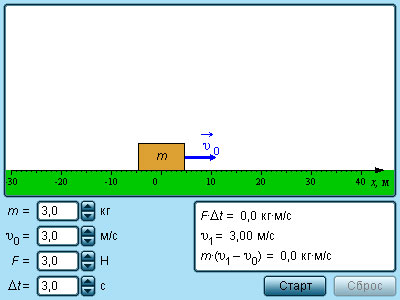
Если на тело массой m за определенный промежуток времени Δt действует сила F→, тогда следует изменение скорости тела ∆v→=v2→-v1→. Получаем, что за время Δt тело продолжает движение с ускорением:
a→=∆v→∆t=v2→-v1→∆t.
Основываясь на основном законе динамики, то есть втором законе Ньютона, имеем:
F→=ma→=mv2→-v1→∆t или F→∆t=mv2→-mv1→=m∆v→=∆mv→.
Изменение импульса
Импульс тела, или количество движения – это физическая величина, равная произведению массы тела на скорость его движения.
Импульс тела считается векторной величиной, которая измеряется в килограмм-метр в секунду (кг м/с).
Импульс силы – это физическая величина, равняющаяся произведению силы на время ее действия.
Импульс относят к векторным величинам. Существует еще одна формулировка определения.
Изменение импульса тела равняется импульсу силы.
При обозначении импульса p→ второй закон Ньютона записывается как:
F→∆t=∆p→.
Данный вид позволяет формулировать второй закон Ньютона. Сила F→ является равнодействующей всех сил, действующих на тело. Равенство записывается как проекции на координатные оси вида:
FxΔt=Δpx; FyΔt=Δpy; FzΔt=Δpz.
Рисунок 1.16.1. Модель импульса тела.
Изменение проекции импульса тела на любую из трех взаимно перпендикулярных осей равно проекции импульса силы на эту же ось.
Одномерное движение – это движение тела по одной из координатный осей.
На примере рассмотрим свободное падение тела с начальной скоростью v0 под действием силы тяжести за промежуток времени t. При направлении оси OY вертикально вниз импульс силы тяжести Fт=mg, действующий за время t, равняется mgt. Такой импульс равняется изменению импульса тела:
Fтt=mgt=Δp=m(v–v0), откуда v=v0 + gt.
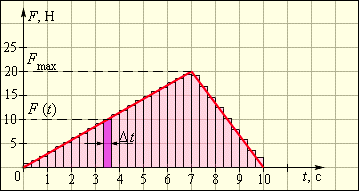
Запись совпадает с кинематической формулой определения скорости равноускоренного движения. По модулю сила не изменяется из всего интервала t. Когда она изменяема по величине, тогда формула импульса требует подстановки среднего значения силы Fср из временного промежутка t. Рисунок 1.16.2 показывает, каким образом определяется импульс силы, которая зависит от времени.
Рисунок 1.16.2. Вычисление импульса силы по графику зависимости F(t)
Необходимо выбрать на временной оси интервал Δt, видно, что сила F(t) практически неизменна. Импульс силы F(t)Δt за промежуток времени Δt будет равняться площади заштрихованной фигуры. При разделении временной оси на интервалы на Δti на промежутке от от 0 до t, сложить импульсы всех действующих сил из этих промежутков Δti, тогда суммарный импульс силы будет равняться площади образования при помощи ступенчатой и временной осей.
Применив предел (Δti→0), можно найти площадь, которая будет ограничиваться графиком F(t) и осью t. Использование определения импульса силы по графику применимо с любыми законами, где имеются изменяющиеся силы и время. Данное решение ведет к интегрированию функции F(t) из интервала [0; t].
Рисунок 1.16.2 показывает импульс силы, находящийся на интервале от t1=0 с до t2=10.
Из формулы получим, что Fср(t2-t1)=12Fmax(t2-t1)=100 Н·с=100 кг·м/с.
То есть, из примера видно Fср=12Fmax=10 Н.
Определение средней силы
Имеются случаи, когда определение средней силы Fср возможно при известных времени и данных о сообщенном импульсе. При сильной ударе по мячу с массой 0,415 кг можно сообщить скорость, равную v=30 м/с. Приблизительным временем удара является значение 8·10–3 с.
Тогда формула импульса приобретает вид:
p=mv=12,5 кг·м/с.
Чтобы определить среднюю силу Fср во время удара, необходимо Fср=p∆t=1,56·103 Н.
Получили очень большое значение, которое равняется телу массой 160 кг.
Когда движение происходит по криволинейной траектории, то начальное значение p1→ и конечное
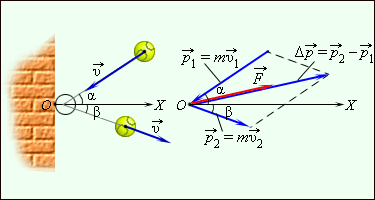
p2→ могут быть различны по модулю и по направлению. Для определения импульса ∆p→ применяют диаграмму импульсов, где имеются векторы p1→ и p2→, а ∆p→=p2→-p1→ построен по правилу параллелограмма.
Для примера приводится рисунок 1.16.2, где нарисована схема импульсов мяча, отскакивающего от стены. При подаче мяч с массой m со скоростью v1→ налетает на поверхность под углом α к нормали и отскакивает со скоростью v2→ с углом β. При ударе в стену мяч подвергался действию силы F→, направленной также, как и вектор ∆p→.
Рисунок 1.16.3. Отскакивание мяча от шероховатой стенки и диаграмма импульсов.
Если происходит нормальное падение мяча с массой m на упругую поверхность со скоростью v1→=v→, тогда при отскоке она изменится на v2→=-v→. Значит, за определенный промежуток времени импульс изменится и будет равен ∆p→=-2mv→. Используя проекции на ОХ, результат запишется как Δpx=–2mvx. Из рисунка 1.16.3 видно, что ось ОХ направлена от стенки, тогда следует vx<0 и Δpx>0. Из формулы получим, что модуль Δp связан с модулем скорости, который принимает вид Δp=2mv.
Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
p = mv
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
10 г = 0,01 кг
Импульс равен:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Относительный импульс
Определение
Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p1отн2 = m1v1отн2 = m1(v1 – v2)
p1отн2 — импульс первого тела относительно второго, m1 — масса первого тела, v1отн2 — скорость первого тела относительно второго, v1 и v2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
15 т = 15000 кг
p1отн2 = m1(v1 – v2) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙103 (кг∙м/с)
Изменение импульса тела
ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:
∆p = p – p0 = p + (– p0)
∆p — изменение импульса тела, p — конечный импульс тела, p0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар |
|
|
|
Конечная скорость после удара:
v = 0. Конечный импульс тела: p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0. |
Абсолютно упругий удар |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p. |
Пуля пробила стенку |
|
|
|
Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p0 – p = m(v0 – v) |
Радиус-вектор тела повернул на 180 градусов |
|
|
|
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p = 2mv0 |
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой:
|
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:
Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:
Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:
Подставим это выражение во второй закон Ньютона и получим:
Или:
F∆t — импульс силы, ∆p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:
Реактивное движение
Определение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:
Реактивная сила:
Второй закон Ньютона для ракеты:
Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
V = a∆t
Выразим ускорение из второго закона Ньютона для ракеты:
Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:
Отсюда ускорение равно:
Выразим формулу для скорости и сделаем вычисления:
Суммарный импульс системы тел
Определение
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:
Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:
Закон сохранения импульса
Закон сохранения импульсаПолный импульс замкнутой системы сохраняется:
Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
- положителен, если его направление совпадает с направлением оси ОХ;
- отрицателен, если он направлен противоположно направлению оси ОХ.
Важно!
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
m2v2 = (m1 + m2)v
Отсюда скорость равна:
Задание EF17556
Импульс частицы до столкновения равен −p1, а после столкновения равен −p2, причём p1 = p, p2 = 2p, −p1⊥−p2. Изменение импульса частицы при столкновении Δ−p равняется по модулю:
а) p
б) p√3
в) 3p
г) p√5
Алгоритм решения
1.Записать исходные данные.
2.Построить чертеж, обозначить векторы начального и конечного импульсов, а также вектор изменения импульса. Для отображения вектора изменения импульса использовать правило сложения векторов методом параллелограмма.
3.Записать геометрическую формулу для вычисления длины вектора изменения импульса.
4.Подставить известные значения и вычислить.
Решение
Запишем исходные данные:
• Модуль импульса частицы до столкновения равен: p1 = p.
• Модуль импульса частицы после столкновения равен: p2 = 2p.
• Угол между вектором начального и вектором конечного импульса: α = 90о.
Построим чертеж:
Так как угол α = 90о, вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:
Δp=√p21+p22
Подставим известные данные:
Δp=√p2+(2p)2=√5p2=p√5
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17695
На рисунке приведён график зависимости проекции импульса на ось Ox тела, движущегося по прямой, от времени. Как двигалось тело в интервалах времени 0–1 и 1–2?
а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено
Алгоритм решения
1.Записать формулу, связывающую импульс тема с его кинематическими характеристиками движения.
2.Сделать вывод о том, как зависит характер движения от импульса.
3.На основании вывода и анализа графика установить характер движения тела на интервалах.
Решение
Импульс тела есть произведение массы тела на его скорость:
p = mv
Следовательно, импульс и скорость тела — прямо пропорциональные величины. Если импульс с течением времени не меняется, то скорость тоже. Значит, движение равномерное. Если импульс растет линейно, то и скорость увеличивается линейно. В таком случае движение будет равноускоренным.
На участке 0–1 импульс тела не менялся. Следовательно, на этом участке тело двигалось равномерно. На участке 1–2 импульс тела увеличивался по линейной функции, следовательно, на этом участке тело двигалось равноускорено.
Верный ответ: б.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22730
Камень массой 3 кг падает под углом α = 60° к горизонту в тележку с песком общей массой 15 кг, покоящуюся на горизонтальных рельсах, и застревает в песке (см. рисунок). После падения кинетическая энергия тележки с камнем равна 2,25 Дж. Определите скорость камня перед падением в тележку.
Алгоритм решения
1.Записать исходные данные.
2.Записать закон сохранения импульса применительно к задаче.
3.Записать формулу кинетической энергии тела.
4.Выполнить общее решение.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса камня: m1 = 3 кг.
• Масса тележки с песком: m2 = 15 кг.
• Кинетическая энергия тележки с камнем: Ek = 2,25 Дж.
Так как это абсолютно неупругий удар, закон сохранения импульса принимает вид:
m1v1+m2v2=(m1+m2)v
Учтем, что скорость тележки изначально была равна нулю, а к ее движению после столкновения привела только горизонтальная составляющая начальной скорости камня:
m1v1cosα=(m1+m2)v
Выразить конечную скорость системы тел после столкновения мы можем через ее кинетическую энергию:
Ek=(m1+m2)v22
Отсюда скорость равна:
v=√2Ekm1+m2
Выразим скорость камня до столкновения через закон сохранения импульса и подставим в формулу найденную скорость:
v1=(m1+m2)vm1cosα=(m1+m2)m1cosα·√2Ekm1+m2
Подставим известные данные и произведем вычисления:
v1=(3+15)3cos60o·√2·2,253+15=12·√0,25=12·0,5=6 (мс)
Ответ: 6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22520
Снаряд, имеющий в точке О траектории импульсp0, разорвался на два осколка. Один из осколков имеет импульс −p1
. Импульс второго осколка изображается вектором:
а) −−→AB
б) −−→BC
в) −−→CO
г) −−→OD
Алгоритм решения
1.Сформулировать закон сохранения импульса и записать его в векторной форме.
2.Применить закон сохранения импульса к задаче.
3.Выразить из закона импульс второго осколка и найти на рисунке соответствующий ему вектор.
Решение
Согласно закону сохранения импульса, импульс замкнутой системы тел сохраняется. Записать его можно так:
−p1+−p2=−p′
1+−p′2
Можем условно считать осколки замкнутой системой, так как они не взаимодействуют с другими телами. Применяя к ним закон сохранения импульса, получим:
−p0=−p1+−p2
Отсюда импульс второго осколка равен векторной разности импульса снаряда и импульса первого осколка:
−p2=−p0−−p1
Известно, что разностью двух векторов является вектор, начало которого соответствует вычитаемому вектору, а конец — вектору уменьшаемому. В нашем случае вычитаемый вектор — вектор импульса первого осколка. Следовательно, начало вектора импульса второго осколка лежит в точке А. Уменьшаемый вектор — вектор импульса снаряда. Следовательно, конец вектора лежит в точке В. Следовательно, искомый вектор — −−→AB.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18122
Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в груз неподвижно висящий на нити длиной 40 см, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова масса груза?
Ответ:
а) 27 г
б) 64 г
в) 81 г
г) 100 г
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Сделать чертеж, отобразив начальное, промежуточное и конечное положение тел.
3.Записать закон сохранения импульса для момента столкновения и закон сохранения механической энергии для момента максимального отклонения нити от положения равновесия.
4.Выполнить решение задачи в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса пластилиновой пули: m = 9 г.
• Скорость пластилиновой пули: v = 20 м/с.
• Максимальный угол отклонения нити: α = 60°.
Переведем единицы измерения величин в СИ:
Сделаем чертеж:
Нулевой уровень — точка А.
После неупругого столкновения пули с грузом они начинают двигаться вместе. Поэтому закон сохранения импульса для точки А выглядит так:
mv=(m+M)V
После столкновения система тел начинается двигаться по окружности. Точка В соответствует верхней точке траектории. В этот момент скорость системы на мгновение принимает нулевое значение, а потенциальная энергия — максимальное.
Закон сохранения энергии для точки В:
(m+M)V22=(m+M)gh
V22=gh
Высоту h можно определить как произведение длины нити на косинус угла максимального отклонения. Поэтому:
V=√2glcosα
Подставим это выражение в закон сохранения импульса для точки А и получим:
Выразим массу груза:
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 20.1k
