Цена деления мензурки определяется точно также как цена деления любого измерительного прибора. Иначе говоря мы должны от большего значения отнять меньшее и поделить разность на количество делений, которые находятся в промежутке между этими значениями.
Поясним это на простых примерах. Вот рисунок, на котором показаны четыре мензурки:
Первая мензурка проградуирована от 10 до 50 мл. Отнимем от сорока двадцать 40-20=20. В этом промежутке двадцать делений. Делим 20/20=1. Цена деления 1 мл.
Для второй мензурке делаем тоже самое: 12-10=2 2/5=0.4. Цена деления 0.4 мл
Берем третью мензурку. 100-20=80. 80/16=5. Цена деления 5 мл.
И четвертая мензурка 60-30=30. 30/15=2. Цена деления этой мензурки 2 мл.
система выбрала этот ответ лучшим
Чосик
[208K]
более года назад
Мензурки имеют различный размер и потому цена делений у них может отличаться. Не у каждого деления есть рядом надпись, потому, чтобы узнать размер отмерянной порции, необходимо найти цену деления.
Для этого берем два соседних значения, которые указаны на мензурке и отнимает от большего меньшее. Затем считаем число промежутков между ними (или же число делений плюс один). И делим полученное число на число промежутков.
Например, возьмем верхние значения – 500 и 400. Считаем разницу и получим 100. Между ними 4 промежутка. 100/4 = 25. То есть, каждая черточка прибавляет 25 мл. И если надо 475 мл, то набираем до 400 и после доводим объем до третьей черточки.
СТЭЛС
[309K]
более года назад
Как минимум есть шкала, с цифрами (чаще это целые части), промежуточными делениями, и указана мера, в данном случае миллилитры, вот их и ищем.
Берем любой отрезок между делениями подписанными цифрами. Считаем сколько между ними “периодов” между промежуточными черточками.
Теперь смотрим на разницу цифр подписанных по краям этого отрезка, и делим ее на количество этих самый периодов.
Пример:
Взяли отрезок между цифрами 300 и 400 мл. Между ними четыре “периода” Разница между 300 и 400, будет 100. Делим 100 на 4, получаем 25 мл. одно деление.
Assorti
[106K]
6 лет назад
Для того, чтобы разобраться с ценой деления, давайте посмотрим на ту самую мензурку, что изображена на картинке.. Самое нижнее деление обозначено, как 5 миллилитров, это и есть цена деления этой мензурки. Значит от каждой метки до следующей вы будете наливать ровно 5 миллилитров. Когда будете наливать жидкость следите за тем, чтобы нижний мениск жидкости совпадал с этой самой меткой, тогда это будет точно 5 мл.
владсандрович
[766K]
более года назад
Вам для этого нужно произвести такой вот расчет, а именно возьмите верхние показатели и от большего отнимите меньший, а потом итоговое число делите на то количество, которое у вас получится от общей совокупности делений, то есть если мерных уровней 5, то делите на пять. В итоге получите верный ответ в миллилитрах.
Красное облако
[248K]
более года назад
Цена деления мензурок может быть разной, так как сами мензурки разные.
Смотрите на самое нижнее деление, это и будет та самая “цена” например 10 мл.
Ну или берем два соседних значения, от большего значения отнимаем меньшее и делим полученную цифру на количество делений.
Знаете ответ?
Опубликовано: 04.06.2021
Обновлено: 07.06.2022
Кол-во просмотров: 62947
Читать: 1 минут
Мензурка — сосуд с делениями для измерения объема жидкостей. Используется в лабораториях медицинских, учебных и промышленных предприятий, а также в быту. При пользовании мензуркой, как и любой другой мерной посуды с градуировкой, важно точно определить цену деления. Рассказываем по порядку.
Что такое цена деления и как ее определить
Цена деления показывает, скольким миллилитрам жидкости соответствует каждая метка, нанесенная на шкалу. В случае с мензуркой эта величина помогает вычислить погрешность. А зная погрешность, легко определить объем жидкости в сосуде.
В определении цены деления помогают любые две соседние цифры на шкале мензурки. Алгоритм такой:
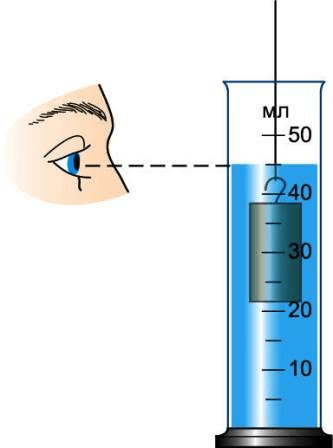
- Взять любые две находящиеся ближе всего друг к другу отметки, возле которых указаны цифры. На рисунке это 60 и 40.
- Вычесть из большего меньшее. 60 – 40 = 20.
- Посчитать, сколько промежутков между этими отметками на шкале. На рисунке между отметками 60 и 40 — 4 промежутка.
- Разделить разность из второго пункта на число промежутков. 20 : 4 = 5. Это и есть величина, которую мы искали.
Цена деления нашей мензурки — 5 мл.

Как определить погрешность и объем жидкости
Погрешность равна половине цены деления мензурки. В нашем случае погрешность составляет 2,5 мл.
Чтобы определить объем, берем ближайшее число от верхней границы жидкости (на рисунке — это значение 40 мл) и прибавляем количество штрихов (на рисунке — 2 штриха) по 5 мл:
V = 40 + 2 × 5 = 50 мл.
С учетом погрешности объем жидкости в сосуде, изображенном на рисунке, равен 50 ± 2,5 мл. Знак ± означает, что действительный объем может составлять от 47,5 до 52,5 мл с учетом погрешности.
В нашем интернет-магазине вы можете приобрести широкий ассортимент мензурок по низким ценам.
Обращайтесь!
Цель работы:
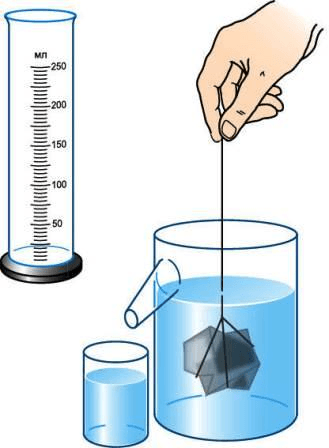
Научиться определять объём тела с помощью измерительного цилиндра.
Приборы и материалы:
Измерительный цилиндр (мензурка), тела неправильной формы небольшого объёма (гайки, фарфоровые ролики, кусочки металла и др.), нитки.
Указания к работе:
1. Определите цену деления мензурки.
2. Налейте в мензурки столько воды, чтобы тело можно было полностью погрузить в воду, и измерьте её объём.
3. Опустите тело, объём которого надо измерить, в воду, удерживая его за нитку (рис. 201), и снова измерьте объём жидкости.
4. Проделайте опыты, описанные в пунктах 2 и 3, с некоторыми другими имеющимися у вас телами.
5. Результаты измерений запишите в таблицу 9.
Дополнительное задание.
Если тело неправильной формы не входить в мензурку, то его объём можно определить с помощью отливного сосуда (рис. 202). Перед измерением сосуд наполняют водой до отверстия отливной трубки. При погружении в него тела часть воды, равная объёму тела, выливается. Измерив мензуркой её объём, определяют объём погружённого в жидкость тела.
Таблица 9.
рис. 201
рис. 202
reshalka.com
ГДЗ учебник по физике 7 класс Перышкин. №4 Измерение объема тела. Номер №1
Решение
Объём тела неправильной формы точно измерить с помощью измерительных приборов нельзя. Поэтому для измерения объема воспользуемся мензуркой. Тело, полностью погружённое в жидкость, вытесняет объём жидкости, который равен объёму самого тела. Воспользуемся этим законом и найдем объёмы некоторых тел следующим образом. Нальем достаточное количество воды в мензурку, а затем погрузим полностью туда наше тело. Разница между первоначальным объёмом и объёмом жидкости, в которое погружено тело, равна объёму этого тела.
V
=
V
2
−
V
1
, где
V
2
− объём воды и тела,
V
1
− начальный объём воды в мензурке.
- Прежде чем проводить измерения физической величины с помощью измерительного прибора нужно определите цену деления его шкалы.
Для определения цены деления необходимо взять 2 соседних числа, найти их разницу (от большего отнять меньшее), а затем разделить полученное число на количество маленьких штрихов между этими числами.
На шкале цилиндра возьмём, к примеру, числа 20 и 30.
Таким образом, цена каждого деления будет равна
30
−
202
=
10
2= 5 мл. - В мензурку нальём столько воды, чтобы тело можно было полностью погрузить в воду. Начальный объём воды равен 70
с
м
3
. - Опустим тело, объём которого надо измерить (шарик, брусок, цилиндр), в воду, удерживая его за нитку, и снова измерим объём жидкости.
Вычисления.
V
б
р
=
95
−
70
=
25с
м
3
V
ц
=
85
−
65
=
20с
м
3
V
ш
=
75
−
60
=
15с
м
3
- Результаты измерений запишем в таблицу 9.
Таблица 9.
| № опыта | Название тела | Начальный объём воды в мензурке
V 1 , с м 3 |
Объём воды и тела
V 2 , с м 3 |
Объём тела V,
с м 3 V = V 2 − 1 |
|---|---|---|---|---|
| 1 | Брусок | 70 | 95 | 25 |
| 2 | Цилиндр | 65 | 85 | 20 |
| 3 | Шарик | 60 | 75 | 15 |
Вывод. В ходе лабораторной работы мы научились измерять объёмы тел с помощью измерительного цилиндра и выяснили, что объём тел равен разнице объёма воды, в которое погружено тело, и первоначального объёма воды.
Для измерения физических величин используют измерительные приборы. Например, для измерения высоты мы будем использовать такой измерительный прибор как линейка, для измерения массы тела – весы, для измерения температуры – термометр, а для измерения времени – часы и т.д..
Многие измерительные приборы имеют шкалу. Шкала измерительного прибора представляет собой совокупность отметок (точек, штрихов) вместе со связанной с ними нумерацией (числами). Для того, чтобы определить с какой точностью может измерить тот или иной прибор, необходимо знать его цену деления.
Ценой деления шкалы прибора называет расстояние между двумя ближайшими штрихами на шкале прибора. Для того чтобы определить цену деления (С) надо найти два ближайших штриха шкалы, возле которых написаны значения величины;
вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.
Например, рассмотрим такой измерительный прибор как шприц. Шприц нужен для измерения такой физической величины как объем (V). Рассмотрим шкалу шприца и определить ее цену деления (см.рис.).
Для того, чтобы определить цену деления данной шкалы мы возьмем два ближайших штриха, возле которых написаны значения, например 7 и 8.
Далее выполним вычитание, как указано в инструкции выше: 8-7=1. Затем, посчитаем сколько делений между большими штрихами (на рисунке отмечены зелеными черточками и подписаны цифрами снизу). У нас получилось 5 делений.
Разделим получившуюся разницу на 5: 1/5=0,2. Значит цена деления шкалы нашего измерительного прибора равна 0,2 мл.
Запишем наши вычисления формулой: С=(8-7)/5=0,2 мл.
Пример с мензуркой
С = 40 – 30/2 = 5 мл.
Если данную мензурку наполнить полностью жидкостью, то ее объем будет равен 50 мл. А если налить жидкость до первого значения, отличного от нуля, то её объем будет равен 5 мл. Между штрихами 40 и 30 вмещается 10 мл жидкости. Между самыми близкими штрихами объем налитой жидкости будет равен 5 мл. Эта величина и будет являться ценой деления мензурки.
Для основных и производных единиц измерения в системе СИ используют дольные и кратные десятичные приставки для удобной записи чисел. Например: 6000000000=10М (приставки обозначают числа).
Задание. Приведите примеры известных Вам внесистемных единиц и соотношение их с единицами системы СИ.
В большинстве задач, где не дано обратное, желательно переводить скорость в метры/секунду (м/с). Для этого вспоминаем, что
1 км = 1000 м = 100 000 см = 1 000 000 мм
1 ч = 60 мин = 3600 с
Допустим, нам необходимо перевести 72 км/ч в метры в секунду.
Километры у нас находятся в числителе, часы в знаменателе, поэтому
72 км/ч * 1000 (домножаем на 1000, чтобы получить метры)
= 72000 м/ч / 3600 (делим на количество секунд в часе, чтобы получить из часов секунды; делим, поскольку часы у нас в знаменателе (снизу дроби), а не в числителе) = 20 м/с
Преобразовать – сначала перевести величину измерения в систему СИ, а потом преобразовать в стандартный вид.
Для того, чтобы определить, что такое миллисекунда, нужно понять, что представляет собой приставка “милли”. С помощью данной приставки образуются дольные единицы измерения в системе СИ. Приставка “милли” имеет латинское происхождение и означает “mille” – тысяча. Таким образом, единица измерения, образованная с помощью “милли” будет равна 0,001 от исходной единицы. Итак, миллисекунда – это одна из единиц измерения времени, она равна тысячной доле от 1 секунды.
Обозначается: мс (русский язык), ms (английский язык).
Чтобы перевести миллисекунды в секунды и наоборот, нужно помнить, что:
1 секунда = 1000 миллисекунд.
1 миллисекунда = 0,001 секунды.
Если нужно перевести миллисекунды в секунды, то достаточно заданное количество миллисекунд разделить на 1000. Например:
20 миллисекунд = 20 / 1000 = 0,02 секунды.
2000 миллисекунд = 2000 / 1000 = 2 секунды.
Если наоборот нужно перевести секунды в миллисекунды, то умножаем имеющееся число секунд на 1000. Например:
3 секунды = 3 * 1000 = 3000 миллисекунд.
0,05 секунды = 0,05 * 1000 = 50 миллисекунд.
0,15 : 1000=0,00015
Физические величины при измерениях и вычислениях обычно выражают числами. Они могут значительно отличаться друг от друга и выражаться как чрезвычайно малыми, так и гигантскими числами. Например, размеры различных тел лежат в пределах от микроскопических до космических масштабов и различаются в 1000000000000000000000000000000… раз (всего надо написать 60 нулей) – такое число даже сложно прочитать!
Как же записать очень малое или очень большое число, чтобы сэкономить бумагу и чтобы легко оперировать этими числами – складывать, вычитать, умножать, делить, да и вообще быстро прочитать и понять записанное?
Наиболее удобный способ записи малых и больших чисел заключается в использовании множителя 10 в некоторой степени. Например, число 2000 можно записать как 2·1000 или 2·10^3. Степень десяти (в данном случае «3») показывает, сколько нулей нужно приписать справа за первым множителем (в нашем примере «2»). Это называют записью числа в стандартной форме. Если число содержит более, чем одну значащую цифру, например 21500, то его можно записать как 21500·10^0 или 2150·10^1 или 215·10^2 или 21,5·10^3 или 2,15·10^4 или 0,215·10^5 или 0,0215·10^6 и так далее.
Запомним: в стандартной форме числа до запятой всегда оставляют только одну цифру, отличную от нуля, а остальные цифры записывают после запятой. Например, в стандартной форме число 21500 = 2,15·10^4.
math-prosto@mail.ru
Материал взят с инета.
Люди! Как определить цену деления мензурки?! Расскажите, пожалуйста по подробней!!! И лучше еще с примером. Спасибо
Мастер
(1980),
на голосовании
6 лет назад
Голосование за лучший ответ
Анна Бочкова
Знаток
(295)
6 лет назад
Чтобы определить цену деления мензурки, надо взять два рядом стоящих числа на шкале, от большего отнимаешь меньшее и делишь всё на количество делений между числами.
Пределы измерения определяются цифрами у первой и последней отметок (точек, штрихов) шкалы прибора
Цена деления – это разность значений величины, соответствующих двум соседним отметкам.
Например : Мензурка имеет предел измерения от 0 до 50 мл, цена деления её шкалы составляет 2,5 мл. a = (30 мл – 10 мл) /4 = 5 мл.
©lidell1996