Физика как найти цену деления вольтметра

Как определить цену деления амперметра и вольтметра? Школьный вопрос. Запомнила еще с 7 класса, когда нам объяснял физик. Теперь пользуюсь всегда, даже когда готовлю что-нибудь и нужно понять, какова цена деления, например, измерительного пластикового контейнера в мультиварке. Из большего значения вычитаю меньшее, а после делю на количество промежутков между “черточками”. Например, здесь. 120 мл минус 60 мл = 60 мл. Делим на три и получаем 20 мл. То есть цена одного деления равняется 20 мл. автор вопроса выбрал этот ответ лучшим Есть что-то общее между всеми измерительными приборами – это шкала, которая разбита делениями. Например обычные ручные часы, мы привыкли, что на циферблате показаны шестьдесят делений, каждое из которых равно одной минуте. Но что делать если на современных часах всего четыре деления? Пятнадцать, тридцать, сорок пять и шестьдесят. Чему тогда равно деление? Все очень, мы отнимаем от большего меньшее, например от 45 отнимем 15 и получим разность между делениями – 30. Теперь чтобы узнать цену деления мы должны эту разность поделить на 2 – число взятых делений. Получаем на таких часах цена деления равна 15 минутам. Аналогично решаем задачу с любым измерительным прибором, амперметров или вольтметром. Отнимаем от большего обозначенного на шкале значения меньшее, и делим на количество необозначенных черточек-делений между ними. Azama­tik [55.3K] 6 лет назад  Цену деления как амперметра, так и вольтметра будем определять по следующей формуле: Ч2 – Ч1/n, где Ч2 и Ч1 – это соседние значения (числа), которые написаны на приборе; а n – это количество делений между ними. Определим цену деления приборов, изображенных на рисунке: Амперметр: Ч2 – это, к примеру, три, а Ч1 – два. Отнимаем от большего меньшее и получаем единицу. Единицу делим на есть и поучаем 0,2. Цена деления апмерметра 0,2. Вольтметр: от ста (Ч2) отнимаем пятьдесят (Ч1) и делим на десять (n). Получаем результат 5. Цена деления вольтметра равна 5. Nelli­4ka [114K] 6 лет назад  Давайте разберемся на конкретном примере. Берем пару любых соседних чисел – будь то 0 и 2, 2 и 4, 4 и 6 и т.д. Находим разницу между этими числами. В нашем случае это 2. Затем нужно посчитать, сколько делений находится между этими цифрами. Деления – это не сами полоски, а пространство между ними. У нас получается 4. Далее мы делим на это число получившуюся ранее разницу: 2:4 = получаем 0,5. Таким образом, цена деления – 0,5. Чтобы определить цену деления какого-то прибора (амперметра, вольтметра и т.д.), нужно найти два соседних числа, отнять от большего меньшее и поделить получившееся число на количество промежутков между делениями (которые расположены между двумя этими числами). Пример из фото: 10-5=5 5:5=1 Цена деления=1. Сахар­ный имбир­ь [3.6K] 4 года назад  Возьмем, допустим, мерный стакан. На нем указаны следующие числа: 0, 50, 100, 150, 200. Между этими числами расположено четыре черточки, плюс напротив самих чисел они также имеются. То есть между числами у нас есть пять делений, и нам нужно понять, чему они соответствуют. Берем любые два соседних числа и отнимаем от большего меньшее. Например, от 150 отнимаем 100, получается 50. Потом это число делим на количество делений между “соседями”, то есть в нашем случае на 5. Получается 10 – это и есть цена деления на нашем мерном стакане. Werte­p75 [1.5K] 4 года назад  Первое действие – вычитание. Естественно, вычитать нужно меньшее из большего, а не наоборот, нам нужно найти положительное значение. Второе действие – деление. Делить нужно то число, что стало результатом первого действия. Делить надо на число, соответствующее количеству промежутков (не чёрточек!) между двумя значениями. MMM DANON­E [27.1K] 4 года назад  Цену деления данных приборов найти легко, пригодятся элементарные знания с уроков физики. Посчитайте, сколько делений у вас находятся между соседними числами. Затем произведите разность между соседними числами на шкале (от большего вычесть меньшее), полученную цифру поделите на высчитанное заранее число делений. Нужно из максимального значения шкалы прибора, вычесть минимальное (начальное) Полученный результат разделить на количество самых маленьких делений имеющихся на шкале. Полученный результат и будет ценой каждого деления в отдельности. Нэпэй­шни [18.2K] 6 лет назад  Цена деления амперметраа и вольтметра? вычисляется по простой формуле.Число1-Число2/n(число делений у шкалы.Например амперметр (число делений5):Ч1 это 4 Ч2 это 2.Отнимает и получаем 2.Двойку делим на n выходит единица. Чтобы определить цену деления нужно посчитать количество делений между двумя соседними числами.Затем вычесть из большего числа меньшее и разделить на количество делений. Знаете ответ?

Амперметр

Для измерения силы тока используется амперметр. В идеале собственное сопротивление амперметра стремится к нулю, и оно никак не влияет на значение силы тока. Он включается в цепь последовательно с соблюдением полярности:

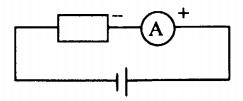
Вольтметр

Для измерения напряжения участка цепи используется вольтметр. В идеале собственное сопротивление вольтметра стремится к бесконечности, и устройство не проводит через себя ток. Он включается в электрическую цепь параллельно участку, в котором будет измеряться напряжение, с соблюдением полярности:

Как правильно записывать показания измерительных приборов с учетом погрешности

При записи величин (с учетом погрешности) следует пользоваться формулой:

A=a±Δa 

где A — измеряемая величина, a — результат измерений, Δa — погрешность измерений.

Важно!

Погрешность измерений равна половине цены деления шкалы измерительного прибора, если в задаче не указана другая величина погрешности.

Цена деления шкалы — разность значений величины, соответствующих двум соседним отметкам шкалы. Чтобы найти цену деления шкалы, нужно:

1. Найти два ближайших штриха шкалы, возле которых написаны значения величин.
2. Вычесть из большего значения меньшее.
3. Полученное число разделить на число делений (промежутков), находящихся между ними.

Пример №1. Определите показания вольтметра (см. рисунок), если погрешность прямого измерения напряжения составляет половину цены деления вольтметра.

Видно, что стрелка вольтметра встала на значении «2,0» Вольт. Она немного не дотягивает до штриха «2», но к нему она находится ближе, чем к предыдущему штриху.

Два ближайших штриха шкалы с указанными значениями имеют значения 1 и 2 В. Всего между ними 5 промежутков. Следовательно, цена деления шкалы равна: (2 – 1)/5 = 0,2 (Вольт).

Так как по условию задачи погрешность равна половине цене деления шкалы, то она равна 0,1 Вольтам. Следовательно, вольтметр показывает: 2,0 ± 0,1 В.

Задание EF18821

Определите показания вольтметра (см. рисунок), если погрешность прямого измерения напряжения равна цене деления вольтметра.

Ответ: (____± ____) В.

---

Алгоритм решения

1.Определить цену деления шкалы измерительного прибора.

2.Определить погрешность измерений.

3.Определить показания прибора.

4.Записать показания прибора с учетом погрешности измерений.

Решение

Так как два ближайших штриха, обозначенными числовыми значениями, показывают 1 и 2 Вольта, а между ними 5 делений, то цена деления шкалы равна:

2−15=0,2 (В)

Согласно условию задачи, погрешность измерений равна цене деления шкалы. Стрелка вольтметра стоит в трех делениях от штриха, обозначенном цифрой «1». 3 деления по 0,2 Вольта равны 0,6 Вольтам. Следовательно, вольтметр показывает 1,6 В. С учетом погрешности: V = 1,6 ± 0,2 В.

Внимание! При записи ответа нужно использовать только десятичные числа без пробелов и знака «±».

Ответ: 1,60,2

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18883

Определите показания амперметра (см. рисунок), если погрешность прямого измерения силы тока равна цене деления амперметра.

Ответ: ( ____± ____) А.

---

Алгоритм решения

1.Определить цену деления шкалы измерительного прибора.

2.Определить погрешность измерений.

3.Определить показания прибора.

4.Записать показания прибора с учетом погрешности измерений.

Решение

Так как два ближайших штриха, обозначенными числовыми значениями, показывают 0 и 0,2 Ампера, а между ними 10 делений, то цена деления шкалы равна:

0,2−010=0,02 (А)

Согласно условию задачи, погрешность измерений равна цене деления шкалы. Стрелка амперметра стоит на штрихе, обозначенном числом «0,2». Следовательно, амперметр показывает 0,2 А. Так как при измерении учитываются сотые доли Амперов, правильно результат измерения записывается так: I = 0,20 А. С учетом погрешности: I = 0,20 ± 0,02 А.

Внимание! При записи ответа нужно использовать только десятичные числа без пробелов и знака «±».

Ответ: 0,200,02

pазбирался: Алиса Никитина | обсудить разбор

Задание EF19038

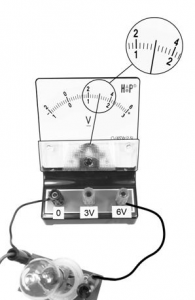Определите напряжение на лампочке (см. рисунок), если погрешность прямого измерения напряжения равна цене деления вольтметра.

Ответ: ( ____±____ ) В.

---

Алгоритм решения

1.Определить цену деления шкалы измерительного прибора.

2.Определить погрешность измерений.

3.Определить показания прибора.

4.Записать показания прибора с учетом погрешности измерений.

Решение

Так как два ближайших штриха, обозначенными числовыми значениями, показывают 2 и 4 Вольта, а между ними 10 делений, то цена деления шкалы равна:

4−210=0,2 (В)

Согласно условию задачи, погрешность измерений равна цене деления шкалы. Стрелка вольтметра стоит в пяти делениях от штриха, обозначенном цифрой «2». 5 делени1 по 0,2 Вольта равны 1 Вольту. Следовательно, вольтметр показывает 3 В. Так как при измерении учитываются сотые доли Вольтов, правильно результат измерения записывается так: U = 3 В.С учетом погрешности: U = 3,0 ± 0,2 В.

Внимание! При записи ответа нужно использовать только десятичные числа без пробелов и знака «±».

Ответ: 3,00,2

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 7.3k

Для характеристики электрического тока в цепи у нас есть уже две физические величины: сила тока ($I$) и напряжение ($U$).

Для измерения силы тока мы используем амперметр. Значит, существует прибор и для измерения электрического напряжения. 

Как называют прибор для измерения напряжения? Он называется вольтметром.
На данном уроке мы рассмотрим его применение, правила подключения в электрическую цепь и другие его характеристики.

Вольтметр

Вольтметр — это прибор для измерения напряжения на полюсах источника тока или на каком-либо другом участке цепи.

Вольтметры по внешнему виду очень похожи на амперметры. Как их различать тогда? Если на шкале амперметра стоит буква $A$, то на шкале вольтметра будет обязательно стоять буква $V$.

Вольтметры бывают разных видов. Это зависит от их назначения. Вы чаще всего будете встречать или демонстрационный вольтметр (рисунок 1, а) или лабораторный (рисунок 1, б).

Как можно догадаться из названий приборов, демонстрационный вольтметр используется для демонстрации опытов, а лабораторный вы будете использовать при выполнении лабораторных работ.

На шкале каждого вольтметра есть высшее (максимальное) значение напряжения, которое он способен измерить. Превышение этого предела может привести к выходу прибора из строя.

Вольтметр в электрической цепи

Вольтметр подключают в электрическую цепь на определенный ее участок, на котором необходимо измерить напряжение. 

Обратите внимание на то, что если амперметр, последовательно подключенный в электрическую цепь, будет показывать одинаковое значение силы тока на всех участках цепи, то с вольтметром у нас совершенно другая история. Он предназначен для измерения напряжения на определенном участке цепи.

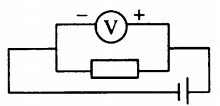
Для обозначения на схемах электрических цепей у вольтметра имеется свой условный знак (рисунок 2). Выглядит он, как кружок с буквой $V$ посередине.

Правила подключения вольтметра в электрическую цепь

• Зажимы вольтметра нужно подсоединять к тем точкам цепи, между которыми надо измерить напряжение. Такое подключение называется параллельным (рисунок 3).

Подробнее об особенностях параллельного подключения приборов вы узнаете в следующих уроках.

• У одного из зажимов вольтметра стоит знак “+”. Провод, подключенный к этому зажиму, необходимо соединять с проводом, идущим от положительного полюса источника тока (рисунок 4). Если подключить прибор неправильно, то стрелка вольтметра просто начнет отклоняться в другую сторону.

Измерение напряжения вольтметром в электроприборе

Используя вышеприведенные правила, давайте попробуем на практическом опыте измерить напряжение. 

Допустим, его необходимо измерить на электрической лампе. Соберем электрическую цепь, состоящую из ключа, электрической лампы, источника тока. Подключим последовательно в эту цепь амперметр. Вольтметр подсоединяем параллельно к зажимам лампы (рисунок 5).

Схема такой электрической цепи будет выглядеть следующим образом (рисунок 6).

Обратите внимание, что амперметром здесь мы измеряем силу тока в электрической лампе. Вольтметром мы измеряем ее напряжение. 

Амперметр подключается последовательно, а вольтметр — параллельно.

А какой должна быть сила тока, проходящего через вольтметр, по сравнению с силой тока в цепи? Отличается ли она от силы тока во всей цепи?

Да, отличается. Вольтметр устроен таким образом, что сила тока, проходящего через него, крайне мала по сравнению с силой тока в самой электрической цепи. Это позволяет исключить изменение напряжения между теми точками, к которым подсоединен вольтметр. Это же и способствует получению более точных значений напряжения.

Измерение напряжения вольтметром на полюсах источника тока

Как с помощью вольтметра измерить напряжение на полюсах источника тока?

Чтобы узнать напряжение на полюсах источника тока, мы можем подключить вольтметр непосредственно к нему (рисунок 7). Не забывайте соблюдать полярность при подключении! Амперметр же включать в подобную цепь нельзя.

Это интересно: вольтамперметр

Упражнения

Определим цену деления такого вольтметра. Возьмем значения 0 и 3. От 0 до 3 у нас всего два деления. Получается, что $frac{3 space В — 0 space В}{2} = 1.5 space В$.
Цена деления этого вольтметра равна $1.5 space В$.

На рисунке 8 изображены показания этого вольтметра при:
$U_1 = 4.5 space В$ (рисунок 8, а);
$U_2 = 7.5 space В$ (рисунок 8, б);
$U_3 = 10.5 space В$ (рисунок 8, в).

Шкала вольтметра на рисунке 5 идентична шкале вольтметра на рисунке 1, а. Ее цену деления мы уже определили в предыдущем упражнении. Цена деления этого вольтметра равна $1.5 space В$.

На рисунке 5 вольтметр показывает значение напряжения, равное $1.5 space В$.

Схема такой цепи изображена на рисунке 9. Обратите внимание, что амперметр подключен в цепь последовательно, а вольтметр — параллельно.

Шкала измерительных приборов служит для количественной оценки величин. Линейка числовых значений может быть нанесена на прямую линию, на окружность или часть окружности. Для использования обязательно наличие движущегося по шкале указателя.

ИнструкцияДля определения цены деления шкалы недостаточно видеть только голую разметку без каких-либо обозначений. Необходимо знать, какую именно величину измеряет шкала. Можно определять количество золота меркой для зерна, но результат такого измерения будет весьма приблизительным. Шкалы измерительных приборов снабжены обозначениями величины, для определения которой используется данный прибор. Например, V проставляется на вольтметрах. Надпись t◦С означает, что перед вами термометр со шкалой Цельсия.

Кроме измеряемой величины, необходимо знать единицы измерения этой величины. Конечно, на глаз отличитьсантиметр от дюйма легко и заблудиться в единицах измерения на обычной чертежной линейке невозможно. Но без специальной маркировки вы не узнаете, что за прибор перед вами — амперметр или миллиамперметр. А путаница с электроизмерительными приборами чревата замыканием цепи.

Необходимо знать пределы измеряемой величины. Уличный термометр способен измерить отрицательную температуру воздуха, а термометр для ванной предназначен для измерения узкого диапазона температур в пределах нескольких градусов от температуры человеческого тела.

В разных случаях требуется разная точность измерения одной и той же величины. Уличный термометра определяет температуру воздуха с точностью до целого градуса, а медицинский термометр способен отследить изменения температуры тела с точностью до десятой доли градуса.

Чтобы определить цену деления маркированной шкалы, сначала определите количественное значение между двумя подписанными метками как разность двух соседних чисел. Например, на ученической линейке разность между двумя любыми цифрами – один сантиметр. А на спидометре разница между цифрами может быть десять километров в час.

Сосчитайте количество делений в границах выбранного участка шкалы. Разделите числовое значение интервала на количество промежутков между мелкими делениями. Если на линейке между двумя цифрами десять маленьких делений, цена одного такого деления будет равна одной десятой части сантиметра, или одному миллиметру.

Если на спидометре между двумя цифрами с разницей в десять километров в час только одно деление, промежуток нужно разделить пополам. Полученная цена деления – пять километров в час.

Таким образом, цена деления шкалы может быть равна единице измерения по данной шкале или содержать несколько единиц. И возможна цена деления в долях единицы измерения. Любой измерительный прибор сам по себе не приносит большой пользы.

Необходимо умение им пользоваться. Для этого следует научиться определять цену деления измерительного прибора, то есть значение самой маленькой черточки его разметки.

ИнструкцияВозьмите в руки измерительный прибор (к примеру,школьную линейку), внимательно осмотрите его. Вы увидите деления – одни побольше, другие поменьше. Деления могут быть разных цветов, некоторые из них подписаны. На школьной линейке, к примеру, первое подписанное деление – один сантиметрОтметьте для себя отрезок до первого подписанного деления. Сосчитайте количество маленьких делений, находящихся в этом отрезке (к примеру, на школьной линейке в отрезке, равном одному сантиметру, находится десять маленьких делений и два дополнительных деления средней величины).

Определите цену самого маленького деления. Для этого разделите величину первого подписанного деления на количество маленьких делений внутри этого отрезка. На школьной линейке, к примеру, один сантиметр нужно разделить на десять делений. Получится один миллиметр. Итак, цена маленького деления на школьной линейке равна одному миллиметру.

Теперь определите цену дополнительных делений, если они имеются на измерительном приборе. К примеру, на школьной линейке два дополнительных деления в одном сантиметре. Следовательно, нужно один сантиметр разделить на два деления – получится пять миллиметров. Итак, цена дополнительного деления на линейке – пять миллиметров.

None Источники:

• цена деления измерительных приборов

Измерительные приборы, как правило, имеют шкалу. Это значит, что на нем нанесены штриховые деления, а рядом написаны числовые значения величин, соответствующие делениям. Расстояния между двумя штрихами, возле которых написаны значения физической величины, могут быть дополнительно разделены еще на несколько делений, не подписанных числами. Расстояние между двумя ближайшими штрихами называется ценой деления шкалы прибора, которую необходимо определить перед использованием самого оборудования.

ИнструкцияПеред тем, как находить цену деления, внимательно рассмотрите сам прибор: что он измеряет, в каких единицах, его исправность. Это позволит нарисовать полную картину проводимого опыта по определению той или иной величины. Найдите на шкале два ближайших штриха, возле которых написаны числовые значения величины. Посчитайте сколько между ними делений (но не штрихов).

Пример. Пусть нужно определить цену деления бытового термометра. Соседние подписанные штрихи 10 и 20 градусов Цельсия. Между ними помещается десять делений.Найдите положительную разность между выбранными числовыми значениями величины, для этого отнимите от большего числа меньшее число. Полученную разницу разделите на количество делений, находящихся между ними. Полученное частное является ценой деления, без знания которой не определить показания измерительного прибора.

Пример. 20-10=10 градусов Цельсия. Разность, равная десяти градусам Цельсия, делится на десять делений между штрихами: 10/10=1 градус Цельсия.

Значит, цена деления выбранного термометра равна один градус Цельсия. Видео по темеОбратите вниманиеУ разных приборов, называющихся одинаково, может быть разная шкала, следовательно, и цена деления может отличаться.

Источники:

• Опыт работы учителем физики.
• цена деления термометра

После ремонта или замены шкалы амперметра требуется ее проверка и градуировка. Существует несколько способов сделать такое тестирование. В зависимости от наличия необходимых приборов и требуемых показателей точности градуировки, воспользуйтесь одним из способов, описанных ниже.

Вам понадобится.

• зарядное устройство со встроенным амперметром и аккумулятор, источник питания 9 Вольт, переменный проволочный резистор 1 кОм, эталонный амперметр, соединительные провода, измерительный прибор для питания цепей переменного и постоянного токов типа УИ300.1.

ИнструкцияПервый способ можно использовать, если есть зарядное устройство и аккумулятор. Соедините последовательно зарядное устройство, проверяемый амперметр и аккумулятор. Поставьте на минимальный ток регулятор зарядного тока в зарядном устройстве. Включите зарядное устройство. Поставьте регулятор зарядного тока в такое положение, чтобы амперметр зарядного устройства показывал 1 Ампер. Отметьте на шкале проверяемого

амперметра

положение его стрелки. Повторите эту операцию, последовательно устанавливая с помощью регулятора зарядного устройства и контролируя по показаниям амперметра токи в 2, 3, 4 Ампера и т. д. Когда стрелка проверяемого амперметра дойдет до края шкалы, выключите зарядное устройство, предварительно установив регулятор тока на минимум. Затем отметьте на шкале промежуточные значения. У данного способа низкая точность градуировки, которая ограничивается точностью амперметра зарядного устройства.

Большей точности градуировки можно добиться, используя эталонный амперметр. Соберите схему, соединив последовательно эталонный амперметр, проверяемый амперметр и переменный проволочный резистор. Вывод ползунка резистора должен идти к источнику питания.

Подключите собранную схему к источнику питания 9 Вольт. Поворачивая ручку резистора, увеличьте ток в цепи до 1 Ампера. Отметьте местоположение стрелки проверяемого амперметра.

Повторите эту операцию, устанавливая значения токов на эталонном амперметре в 2, 3, 4 Ампера и т. д. Блок питания должен обеспечивать ток, немного больший, чем тот, на который рассчитаны эталонный и проверяемый амперметр.

Высокую точность градуировки обеспечивает использование измерительного прибора для питания цепей переменного и постоянного токов типа УИ300.1. Подключите к нему амперметр и пользуясь инструкцией, разметьте прибор. Обратите вниманиеЕсли при подключении в первом, втором и третьем варианте стрелка проверяемого и эталонного прибора отклоняется влево, следует изменить полярность подключения амперметра, поменяв местами провода на нем.

Источники:

После замены шкалы или другого ремонта нужно проверить точность показаний или отградуировать шкалу вольтметра. Такую проверку можно сделать несколькими несложными способами. В зависимости от необходимой точности и доступных приборов, используйте один из способов, описанных ниже.

Вам понадобится.

• блок питания с встроенным вольтметром, источник питания 12 Вольт, переменный проволочный резистор на 1 кОм, лампочка на 12 Вольт, эталонный вольтметр, соединительные провода, измерительный прибор для питания цепей переменного и постоянного токов типа УИ300.1.

ИнструкцияПодключите проверяемый вольтметр к блоку питания со встроенным вольтметром. Регулятором выходного напряжения блока установите выходное напряжение 1 Вольт. Отметьте на шкале проверяемого вольтметра положение, на котором остановилась его стрелка. Последовательно выполняя эту операцию с шагом в 1 Вольт, разметьте всю шкалу второго прибора. После этого сбросьте напряжение с блока питания до минимума и отключите его. Затем разметьте промежуточные значения шкалы вольтметра. Если шкалаполучается нелинейной, разметку промежуточных значений наносите пропорционально расположения основной разметки. Данный способ дает разметку с низкой точностью градуировки, которая ограничивается точностью показаний вольтметра на блоке питания.

Большую точность градуировки дает второй способ, в котором используется эталонный вольтметр. Соедините последовательно переменный резистор и лампочку на 12 Вольт. Параллельно к лампочке подсоедините эталонный и проверяемый вольтметры.

Свободный вывод резистора и второй провод от лампочки подключите к источнику питания. Поворачивая ручку резистора, считывайте показания напряжения с эталонного вольтметра и ориентируясь на них, наносите разметку на шкалу размечаемого прибора с шагом в 1 Вольт. Если проверяемый прибор рассчитан на большее напряжение, используйте блок питания, эталонный вольтметр и лампочку на соответственно большее напряжение.

Использование для градуировки измерительного прибора для питания цепей переменного и постоянного токов типа УИ300.1 даст высокую точность разметки проверяемого вольтметра. Подключите к этому прибору вольтметр и воспользовавшись указаниями инструкции по эксплуатации на УИ300.1, отградуируйте его.

Если измерения производятся приборами с цифровыми табло, то показания можно снимать без всяких проблем. Если же на измерительные приборы нанесены шкалы, то для того чтобы точно измерить величину, нужно знать цену деления прибора. Иногда она указывается на шкале, если же ее там нет, рассчитайте ее самостоятельно.

Вам понадобится.

• – приборы с различными шкалами.

ИнструкцияВнимательно осмотрите шкалу аналогового прибора, которым производится измерение. На ней нанесены единицы измерения, с которыми работает данный прибор. На любой шкале нанесены числовые значения измеряемой величины, между которыми находятся деления без количественных показателей. Величина, заключенная между ними, является наименьшей, которую можно измерить с помощью прибора. Цена деления прибора – это наименьшая величина, которую можно измерить прибором с данной шкалой. Эта наименьшая цена заключена в наименьшем делении шкалы прибора.

На шкале найдите два ближайших цифровых значений. При этом совершенно не важен их порядок. Например, если на мерном цилиндре, с помощью которого можно измерить объем жидкости в мл, нанесены числовые значения 0, 100, 200, 300, 400, 500, то можно взять пары чисел 0 и 100, 100 и 200 или 400 и 500 либо любую другую пару чисел по такому принципу. Отнимите от большего числового значения меньшее.

Посчитайте деления между ближайшими числовыми значениями на шкале. При подсчете учитывайте, что делением называется расстояние между двумя ближайшими линиями шкалы, а не сами эти линии. Рассчитайте цену деления прибора, поделив разность двух ближайших числовых значений шкалы на количество делений между ними. Это и будет минимальная величина, измеряемая прибором.

Например, чтобы найти цену деления шкалы вольтметра, который измеряет напряжение в вольтах, с числами 0, 2, 4, 6, 8 и пятью делениями между двумя ближайшими числовыми значениями, проделайте определенную последовательность действий. Возьмите два ближайших числовых значения – пусть это будут 4 и 6. Теперь от большего числа отнимите меньшее – получится 2.

Это число поделите на количество делений между этими значениями (по условию оно равно 5). Получится 2/5=0,4 вольта. Цена деления вольтметра равна 0,4 В.

Источники:

Приборы, в которых для измерений используется шкала, имеют большое количество делений, не все из которых пронумерованы. Определение цены деления шкалы необходимо для повышения точности измерений, если измеряемая величина находится между пронумерованными делениями.

Вам понадобится.

• – прибор со шкалой;
• – калькулятор;
• – тонкий предмет для отсчета делений (игла).

ИнструкцияВозьмите прибор со шкалой, цену деления которой необходимо определить. Внимательно осмотрите ее, она должна равномерно делить поле для измерений и не быть поврежденной. Если каждое деление шкалы пронумеровано, то для того, чтобы найти цену деления, возьмите два ближайших числовых значения и от большего вычтите меньшее.

Например, если каждая риска (черточка) на шкале пронумерована числами 0, 100, 200, 300, 400. То возьмите любые два рядом стоящие числа, подходят 200 и 300, и из большего вычтите меньшее 300-200=100. Это и будет цена деления такой шкалы. Обратите внимание, в каких единицах измеряются величины, такая же размерность будет и у цены деления.

Если у прибора между основными пронумерованными делениями есть более мелкие, не пронумерованные, заметьте два ближайших числовых значения. После этого подсчитайте количество делений, которые заключены между этими числовыми значениями. В случае, если шкала мелкая, воспользуйтесь иголкой. Обязательно считайте деления между рисками шкалы, а не сами риски (черточки), поскольку их будет на одну больше.

Для расчета цены деления, возьмите два замеченных ранее числовых значения, отнимите от большего значения меньшее. Полученный результат поделите на количество раннее подчитанных делений, которые находились между числовыми значениями на шкале, полученный результат и будет ценой деления данной шкалы.

Например, если шкала состоит из числовых делений 0, 20, 40, 60, 80, 100, возьмите два ближайших числовых значения. Для этого подойдут числа 60 и 80. Тщательно подсчитайте между ними количество делений.

Предположим, что между ними 10 делений. Для того чтобы подсчитать цену деления от большего числа вычтите меньшее 80-60=20. Полученный результат поделите на количество делений 20/10=2.

Видео по теме

Перед началом эксперимента необходимо определить цену деления измерительных приборов.

Цена деления шкалы микроамперметра АМикроамперметр А1 измеряет силу тока до 50 мкА. Шкала прибора содержит 5 больших делений, каждое из которых разделено еще на 10 делений. Таким образом, цена большого деления шкалы микроамперметра равна , цена наименьшего деления микроамперметра равна . Для того, чтобы определить показание микроамперметра необходимо умножить цену деления на количество делений шкалы, соответствующих отклонению стрелки прибора.

Пример 1.Отклонение стрелки соответствует 2 большим или 20 маленьким делениям. Показание микроамперметра равно или .

Цена деления шкалы миллиамперметра АМиллиамперметр А2 измеряет силу тока до 2 мА. Шкала прибора содержит 5 больших делений, каждое из которых разделено еще на 10 делений. Таким образом, цена большого деления шкалы миллиамперметра равна , цена наименьшего деления микроамперметра равна . Определяем показание миллиамперметра, умножив цену деления на количество делений шкалы, соответствующих отклонению стрелки прибора.

Пример 2.Стрелка миллиамперметра отклонилась на 0,6 больших или 6 маленьких делений. Показание миллиамперметра соответствует или .

Цена деления шкалы вольтметра V

Вольтметр V измеряет напряжение до 0,5 В. Шкала прибора содержит 5 больших делений, каждое из которых разделено еще на 10 делений. Таким образом, цена большого деления шкалы вольтметра равна , цена наименьшего деления вольтметра равна . Показание вольтметра равно произведению цены деления на количество делений шкалы, соответствующих отклонению стрелки прибора.

Пример 3.Стрелка вольтметра отклонилась на 3,2 большого или 32 маленьких деления. Показание вольтметра соответствует или .

Цена деления шкалы вольтметра V

Вольтметр V измеряет напряжение до 12 В. Верхняя шкала прибора содержит 6 больших делений, каждое из которых разделено еще на 10 делений. Таким образом, цена большого деления верхней шкалы вольтметра равна , цена наименьшего деления вольтметра равна . Показание вольтметра равно произведению цены деления на количество делений шкалы, соответствующих отклонению стрелки прибора.

Пример 4.Стрелка вольтметра отклонилась на 4,5 большого или 45 маленьких делений. Показание вольтметра соответствует или .

Не нашли то, что искали? Воспользуйтесь поиском:

Как определить цену деления амперметра и вольтметра?

• Чтобы определить цену деления нужно посчитать количество делений между двумя соседними числами.Затем вычесть из большего числа меньшее и разделить на количество делений.

• Запомнила еще с 7 класса, когда нам объяснял физик. Теперь пользуюсь всегда, даже когда готовлю что-нибудь и нужно понять, какова цена деления, например, измерительного пластикового контейнера в мультиварке. Из большего значения вычитаю меньшее, а после делю на количество промежутков между quot;черточкамиquot;.

  Например, здесь. 120 мл минус 60 мл = 60 мл. Делим на три и получаем 20 мл. То есть цена одного деления равняется 20 мл.

• Цену деления как амперметра, так и вольтметра будем определять по следующей формуле: Ч2 Ч1/n,где Ч2 и Ч1 – это соседние значения (числа), которые написаны на приборе; а n это количество делений между ними.

  Определим цену деления приборов, изображенных на рисунке:

  Амперметр: Ч2 – это, к примеру, три, а Ч1 – два. Отнимаем от большего меньшее и получаем единицу. Единицу делим на есть и поучаем 0,2.

  Цена деления апмерметра 0,2. Вольтметр: от ста (Ч2) отнимаем пятьдесят (Ч1) и делим на десять (n). Получаем результат 5.

• Цена деления амперметраа и вольтметра? вычисляется по простой формуле. Число1-Число2/n(число делений у шкалы.

  Например амперметр (число делений5):Ч1 это 4 Ч2 это 2. Отнимает и получаем 2. Двойку делим на n выходит единица.

• Нужно из максимального значения шкалы прибора, вычесть минимальное (начальное) Полученный результат разделить на количество самых маленьких делений имеющихся на шкале. Полученный результат и будет ценой каждого деления в отдельности.

• Давайте разберемся на конкретном примере. Берем пару любых соседних чисел – будь то 0 и 2, 2 и 4, 4 и 6 и т.д.

  Находим разницу между этими числами. В нашем случае это 2. Затем нужно посчитать, сколько делений находится между этими цифрами.

  Деления – это не сами полоски, а пространство между ними. У нас получается 4.

  Далее мы делим на это число получившуюся ранее разницу: 2:4 = получаем 0,5. Таким образом, цена деления – 0,5.

  None

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ«Информационно – измерительная техника»1. Определить цену деления CIмногопредельного электромагнитного прибора Э377 при включении его на пределы измерения 300; 750; 1500 мА. Полное число делений шкалы N=75,Решение. Ценой деления шкалы прибора называют отношение предела измерения прибора (нормирующее значение шкалы) А к полному числу делений шкалы N.

В данном случае цена деления шкалы миллиамперметра на каждом из его трех пределов измерения равна:

2. Электродинамический ваттметр Д5016/2 имеет два предала измерения по току: IN = 2.5; 5А — и шесть – по напряжению: UN = 30; 75; 150; 300; 450; 600 В. Шкала ваттметра односторонняя с числом делений N = I50, Определить цену деления ваттметра CW для всех возможных комбинаций включения прибора.

Решение.

IN,А

UNВ

СW , Вт/дел

3. Для измерения напряжения U = 3300 В вольтметр Д5015/2 с нормирующими значениями шкалы U_N = 75; 150; 300; 600 В, включен через измерительный трансформатор напряжения U510. Шкала вольтметра имеет 150 делений. Определить цену деления вольтметра С_V на всех пределах измерения, если коэффициент трансформация К 6000/100.

Решение.

	UN,В
CVВ/дел				240. 4. Амперметр Д5014/2 с пределами измерений 2. 5; 5 А.   С односторонней шкалой на 100 делений включен во вторичную обмотку трансформатора тока И515М. Определить цену деления амперметра CA если коэффициент трансформация   K = 50/5.

Решение.

5.  При поверке амперметра переменного тока методом сличения поверяемый прибор А показал I = 5.00 A, a образцовый A = 5.12 А. Нормирующее значение шкалы поверяемого прибора I_N = 10 А. Считая показания образцового прибора (I) соответствующим действительному значению измеряемого тока, найти абсолютную и приведенную погрешности поверяемого прибора. Присвоить поверяемому прибору класс точности, считая, что найденная погрешность наибольшая. Решение.  Абсолютная погрешность прибора представляет собой разность между показанием прибора и действительным значением измеряемой величины (показанием образцового прибора):

ΔIII = 5.00 – 5.12 = -0.12  A,Приведенная погрешность прибора определяется отношением модуля абсолютной погрешности к нормирующему значению шкалы прибора:

γ = |ΔII_NКласс точности прибора характеризует его свойство в отношении точности и определяется пределами допускаемой приведенной погрешности прибора. Согласно ГОСТ 8711-78 (“Амперметры и вольтметры”) приняты следующие классы точности для указанных приборов: 0.05; 0.1; 0.2; 0.5; 1.0; 1.5; 2.5; 4.0 и 5.0.

Таким образом, обращаясь к принятому ряду классов точности, выбираем ближайшее большее к γ число, т.е. при γ = 1,2 % класс точности прибора К = 1.5.

6.  Для измерения напряжения в электрической цепи используется вольтметр класса точности 1.0 с пределом измерения U_N = З00 В. Показание вольтметра U=100 В. Определить абсолютную и относительную δ погрешность измерения и действительную величину измеряемого напряжения.

Решение.  Так как истинное (действительное) значение измеряемой величины неизвестно, для определения абсолютной погрешности измерения используем класс точности прибора:

Приведенная погрешность прибора равна его классу точности, т.е. γ = 1 %Относительная погрешность Следовательно, измеренное значение напряжения U=100 В может отличаться от его действительного значения не более чем на 3 %7. Предельное значений тока, измеряемое миллиамперметром, сопротивление которого RА= 5 Ом, равно 4·10-3 А, Определить сопротивление RШ шунта

Источники:

• www.kakprosto.ru
• studopedia.ru
• info-4all.ru
• vunivere.ru

Как определить цену деления амперметра и вольтметра?

Если на шкале 100 делений, а переключатель пределов измерения стоит на 1000, то цена одного деления = 1000 / 100 = 10 единиц измерения. Если переключатель пределов стоит на 100, то цена деления соответственно 1 ед. Если переключатель на 10, то цена равна 0,1 единицы и т. д.

Внимательно посмотреть на шкалу и вспомнить арифметику.

берешь 2 цифры на нем написаные, 5 и 10 к примеру. вычитаешь из большего меньшее (10-5) и делишь на количество промежутков между делениями.
Например. 0 l l l l 5 l l l l 10 — цена деления 1 (10-5/5)

Погрешности измерений, представление результатов эксперимента

Определяется несовершенством методов и допущениями в методике.

Погрешность теории (модели)

Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.

Погрешность оператора

Определяется субъективным фактором, ошибками экспериментатора.

Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.

В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:

• определение длины с помощью линейки или мерной ленты;
• определение объема с помощью мензурки.

Пример получения результатов прямых измерений с помощью линейки:

Измерим длину бруска линейкой, у которой пронумерованы сантиметры и есть только одно деление между пронумерованными делениями. Цена деления такой линейки: begin triangle=frac= frac>=0,5 text end Инструментальная погрешность: begin d=frac=frac=0,25 text end Истинное значение: (L_0=4 text) Результат измерений: $$ L=L_0pm d=(4,00pm 0,25) text $$ Относительная погрешность: $$ delta=fraccdot 100text=6,25textapprox 6,3text $$

Теперь возьмем линейку с n=9 мелкими делениями между пронумерованными делениями. Цена деления такой линейки: begin triangle=frac= frac>=0,1 text end Инструментальная погрешность: begin d=frac=frac=0,05 text end Истинное значение: (L_0=4,15 text) Результат измерений: $$ L=L_0pm d=(4,15pm 0,05) text $$ Относительная погрешность: $$ delta=fraccdot 100textapprox 1,2text $$

Второе измерение точнее, т.к. его относительная погрешность меньше.

п.5. Абсолютная погрешность серии измерений

Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).

Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.

Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.

Составим расчетную таблицу:

№ опыта	1	2	3	Сумма
Масса, г	99,8	101,2	100,3	301,3
Абсолютное отклонение, г	0,6	0,8	0,1	1,5

Сначала находим среднее значение всех измерений: begin m_0=frac=fracapprox 100,4 text end Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности (m_0) и измерения. begin triangle_1=|100,4-99,8|=0,6\ triangle_2=|100,4-101,2|=0,8\ triangle_3=|100,4-100,3|=0,1 end Находим среднее абсолютное отклонение: begin triangle_=frac=frac=0,5 text end Мы видим, что полученное значение (triangle_) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: begin triangle m=maxleft; dright>=maxleft\ text end Записываем результат: begin m=m_0pmtriangle m\ m=(100,4pm 0,5) text end Относительная погрешность (с двумя значащими цифрами): begin delta_m=fraccdot 100textapprox 0,050text end

п.6. Представление результатов эксперимента

Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.

• абсолютная погрешность их суммы равна сумме абсолютных погрешностей

• абсолютная погрешность их разности также равна сумме абсолютных погрешностей

• относительная погрешность их произведения равна сумме относительных погрешностей

• относительная погрешность их частного также равна сумме относительных погрешностей

• относительная погрешность квадрата (a^2) равна удвоенной относительной погрешности

• относительная погрешность куба (a^3) равна утроенной относительной погрешности

• относительная погрешность произвольной натуральной степени (a^n) равна

Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.

п.7. Задачи

Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно?

Составим таблицу для расчета цены деления:

№ мензурки	a, мл	b, мл	n	(triangle=frac), мл
1	20	40	4	(frac=4)
2	100	200	4	(frac=20)
3	15	30	4	(frac=3)
4	200	400	4	(frac=40)

Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):

№ мензурки	Объем (V_0), мл	Абсолютная погрешность (triangle V=frac), мл	Относительная погрешность (delta_V=fraccdot 100text)
1	68	2	3,0%
2	280	10	3,6%
3	27	1,5	5,6%
4	480	20	4,2%

Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.

Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка

Задача 2. В двух научных работах указаны два значения измерений одной и той же величины: $$ x_1=(4,0pm 0,1) text, x_2=(4,0pm 0,03) text $$ Какое из этих измерений точней и почему?

Мерой точности является относительная погрешность измерений. Получаем: begin delta_1=fraccdot 100text=2,5text\ delta_2=fraccdot 100text=0,75text end Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: (delta_2lt delta_1), второе измерение точней.

Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.

Абсолютная погрешность скорости каждой машины равна инструментальной, т.е. половине деления спидометра: $$ triangle v_1=frac=5 (text), triangle v_2=frac=0,5 (text) $$ Показания каждого из спидометров: $$ v_1=(54pm 5) text, v_2=(72pm 0,5) text $$ Скорость сближения равна сумме скоростей: $$ v_0=v_+v_, v_0=54+72=125 text $$ Для суммы абсолютная погрешность равна сумме абсолютных погрешностей слагаемых. $$ triangle v=triangle v_1+triangle v_2, triangle v=5+0,5=5,5 text $$ Скорость сближения с учетом погрешности равна: $$ v=(126,0pm 5,5) text $$ Относительная погрешность: $$ delta_v=fraccdot 100textapprox 4,4text $$ Ответ: (v=(126,0pm 5,5) text, delta_vapprox 4,4text)

Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.

Инструментальная погрешность линейки (d=frac=0,05 text)
Результаты прямых измерений длины и ширины: $$ a=(90,20pm 0,05) text, b=(60,10pm 0,05) text $$ Относительные погрешности (не забываем про правила округления): begin delta_1=fraccdot 100textapprox 0,0554textapprox uparrow 0,056text\ delta_2=fraccdot 100textapprox 0,0832textapprox uparrow 0,084text end Площадь столешницы: $$ S=ab, S=90,2cdot 60,1 = 5421,01 text^2 $$ Для произведения относительная погрешность равна сумме относительных погрешностей слагаемых: $$ delta_S=delta_a+delta_b=0,056text+0,084text=0,140text=0,14text $$ Абсолютная погрешность: begin triangle S=Scdot delta_S=5421,01cdot 0,0014=7,59approx 7,6 text^2\ S=(5421,0pm 7,6) text^2 end Ответ: (S=(5421,0pm 7,6) text^2, delta_Sapprox 0,14text)

Шкала измерительного прибора, цена деления шкалы

Стрелочные измерительные приборы: вольтметры, амперметры, омметры и т. д., — обладают шкалами.

Шкала — плоская или цилиндрическая поверхность, относительно которой движется стрелка, на которой нанесены деления.

Иногда шкала у прибора всего одна, а иногда их несколько, при этом индикатором измерений служит всего одна стрелка. Давайте же разберемся, что это за шкалы, и как ими пользоваться, чтобы ничего не напутать.

Для начала отметим, что шкалы эти бывают разными. Во-первых, более распространенными являются именованные шкалы, то есть шкалы, на которых деления проградуированы соответствующими единицами измеряемых величин, это градуированные шкалы.

Во-вторых, встречаются условные шкалы. Если прибор имеет несколько переключаемых пределов измерений, то шкала будет наверняка условной, и одни и те же деления будут иметь разные значения в каждом из установленных пользователем пределов.

Для того, чтобы по условной шкале прибора определить точно значение измеряемой в данный момент величины, необходимо, зная цену деления, количество делений до того места, куда отклонилась, и где остановилась в данный момент стрелка, умножить на цену деления.

Если цена деления не ясна, то ее можно легко найти, для этого берется разность между двумя известными значениями на шкале, и делится на количество делений между этими значениями. Например, известно, что красная шкала имеет ширину 10 вольт, а количество делений 50, значит цена деления для красной шкалы составляет 200 мВ.

Если на шкале есть отметка ноль, то шкала называется нулевой. Если нуля нет, то шкала называется безнулевой. Что касается нулевых шкал, то они, в свою очередь, подразделяются на односторонние и двухсторонние. На фото выше можно видеть сразу семь нулевых шкал.

У односторонних ноль размещен в самом начале шкалы (как на рисунке, головка вольтметра с односторонней шкалой), а у двухсторонних — по центру или между конечной и начальной отметками. Так, в зависимости от расположения нуля, двухсторонние шкалы подразделяются на несимметричные и симметричные.

Симметричная шкала ноль имеет по центру, несимметричная — не по центру шкалы. Если шкала безнулевая, то крайние отметки обозначают верхний и нижний пределы измерений. На фото выше изображен миллиамперметр с симметричной двухсторонней шкалой, цена деления составляет 50 мкА, поскольку 0,5 мА / 10 = 0,05 мА или 50 мкА.

В зависимости от характера связи угловых и линейных расстояний между двумя соседними делениями шкалы с измеряемыми величинами, шкалы бывают неравномерными, равномерными, логарифмическими, степенными и т. д. Для более точных измерений предпочтительней равномерные шкалы.

Когда отношение ширины самого широкого деления к самому узкому не более 1,3 при неизменной цене деления, шкалу уже можно считать равномерной.

На лицевой стороне измерительного прибора, недалеко от шкалы, как правило, размещены необходимые маркировки: единица величины измерения, ГОСТ, класс точности прибора, число фаз и род тока, категория защищенности данного измерительного прибора от внешних электрических и магнитных полей, условия эксплуатации, рабочее положение, предельное напряжение прочности изоляции измерительных цепей (на фото — в звездочке «2», значит 2 кВ), номинальная частота тока, если отличается от промышленных 50 Гц, например 500 Гц, положение относительно Земли, тип, система прибора, год выпуска, заводской номер, и прочие важные параметры.

В этой таблице приведены расшифровки основных обозначений, которые можно встретить на шкалах. Надеемся, что эта краткая статья поможет вам научиться правильно проводить измерения при помощи стрелочных измерительных приборов.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!