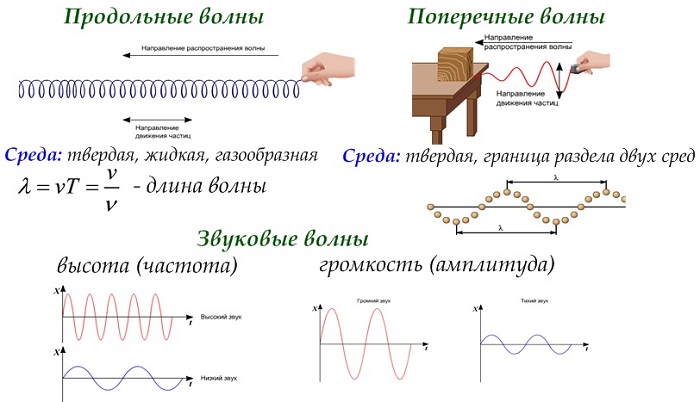
График волны функции (например, физической величины) y, распространяющейся вдоль оси Оx, построенный в фиксированный момент времени (t = const). Длина волны λ может быть измерена как расстояние между парой соседних максимумов y (x) либо минимумов, либо как удвоенное расстояние между соседними точками, в которых y = 0
Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе[1][2].
Длина́ волны́ (в линии передачи) — расстояние в линии передачи, на котором фаза электромагнитной волны вдоль направления распространения меняется на 2π[3].
Длину волны можно также определить:
- как расстояние, измеренное в направлении распространения волны, между двумя точками в пространстве, в которых фаза колебательного процесса отличается на
; - как путь, который проходит фронт волны за интервал времени, равный периоду колебательного процесса;
- как пространственный период волнового процесса.
Представим себе волны, возникающие в воде от равномерно колеблющегося поплавка, и мысленно остановим время. Тогда длина волны — это расстояние между двумя соседними гребнями волны, измеренное в радиальном направлении. Длина волны — одна из основных характеристик волны наряду с частотой, амплитудой, начальной фазой, направлением распространения и поляризацией. Для обозначения длины волны принято использовать греческую букву 
, размерность длины волны — метр ([м]).
Как правило, длина волны используется применительно к гармоническому или квазигармоническому (например, затухающему или узкополосному модулированному) волновому процессу в однородной, квазиоднородной или локально однородной среде. Однако формально длину волны можно определить по аналогии и для волнового процесса с негармонической, но периодической пространственно-временной зависимостью, содержащей в спектре набор гармоник. Тогда длина волны будет совпадать с длиной волны основной (наиболее низкочастотной, фундаментальной) гармоники спектра.
Длина волны — пространственный период волнового процесса[править | править код]
Волна — колебательный процесс, развивающийся (распространяющийся) в пространстве и во времени, в связи с этим изменяющаяся в волновом процессе физическая величина является функцией пространственных координат и времени (то есть особого вида пространственно-временной функцией). Волновой процесс в частности может быть периодическим (например, гармоническим). По аналогии с периодом колебаний 
[с] (интервалом времени, за который периодический колебательный процесс повторяется и размерность которого — секунда), длину волны [м] можно рассматривать как пространственный период волнового процесса. Следует заметить, что круговой частоте колебания 
[радиан/с], показывающей, на сколько радиан изменится фаза колебания за 1 с в фиксированной точке (в множестве точек если твердое тело), соответствует «пространственная круговая частота» 
[радиан/м], называемая волновым числом и показывающая, на сколько радиан отличаются фазы колебательного процесса в двух точках пространства, расположенных вдоль направления распространения волны на расстоянии 1 м друг от друга. При этом очевидно, что фазы колебательного процесса в двух таких точках, расположенных друг от друга на расстоянии в [м], отличаются ровно на 
.
Связь с частотой[править | править код]
Получить соотношение, связывающее длину волны с фазовой скоростью 
и частотой 
можно из определения. Длина волны соответствует пространственному периоду волны, то есть расстоянию, которое точка с постоянной фазой «проходит» за интервал времени, равный периоду колебаний, поэтому
Для электромагнитных волн в вакууме скорость в этой формуле равна скорости света (299 792 458 м/с), и длина волны
. Если значение подставить в герцах, то будет выражена в метрах.
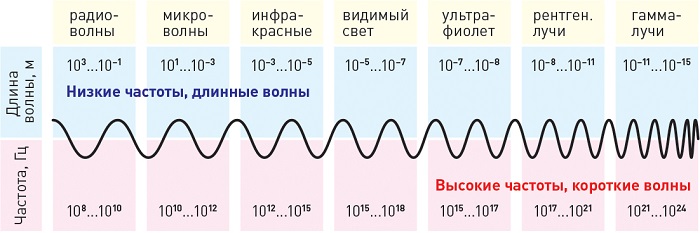
Радиоволны делят на диапазоны по значениям длин волн, например, 10…100 м — декаметровые (короткие) волны, 1…10 м — метровые, 0.1…1,0 м — дециметровые и т. п. Механизмы и условия распространения радиоволн, степень проявления эффекта дифракции, отражающие свойства объектов, предельная дальность радиосвязи и радиолокации сильно зависят от длины волны. Как правило, габаритные размеры антенн сравнимы либо (справедливо всегда для антенн направленного действия) превышают рабочую длину волны радиоэлектронного средства. Магнитная антенна средневолнового радиоприёмника имеет габарит на порядки меньше длины волны, и при этом, тем не менее, обладает пространственной селективностью.
Длина волны в среде[править | править код]
В оптически более плотной среде (слой выделен тёмным цветом) длина электромагнитной волны сокращается. Синяя линия — распределение мгновенного (t = const) значения напряжённости поля волны вдоль направления распространения. Изменение амплитуды напряжённости поля, обусловленное отражением от границ раздела и интерференцией падающей и отражённых волн, на рисунке условно не показано.
Длина электромагнитной волны в среде короче, чем в вакууме:
- где — показатель преломления среды;
- — относительная диэлектрическая проницаемость среды;
- — относительная магнитная проницаемость среды.
Величины 
, 
и 
могут существенно зависеть от частоты 
(явление дисперсии). Поскольку для большинства сред в радиочастотном диапазоне 
(для диэлектриков 
, для ферромагнетиков с ростом частоты 
), то в инженерной практике используют величину 
, которую называют коэффициентом укорочения. Она равна отношению длины волны в среде к длине волны в вакууме. Например, для полиэтилена (используется в радиочастотном диапазоне как изоляционный материал с малыми потерями) = 2,56, и коэффициент укорочения 
= 1/1,6 = 0,625.
Напротив, длина электромагнитной волны (поперечномагнитной, поперечноэлектрической) в волноводах может быть не только больше, чем в среде с тем же значением , но и больше, чем вакууме, поскольку фазовая скорость электромагнитной волны в волноводе превышает скорость электромагнитной волны в среде с тем же .
Волны де Бройля[править | править код]
Волнам де Бройля также соответствует определённая длина волны. Частице с энергией 
и импульсом 
, соответствуют:
- частота:
- длина волны:
- где — постоянная Планка.
Примеры[править | править код]
Приближённо, с погрешностью около 0,07 % рассчитать длину радиоволны в свободном пространстве можно так: 300 000 делим на частоту в килогерцах, получаем длину волны в метрах. Другой способ — запомнить какую-нибудь удобную пару ↔ , например, частоте 100 МГц соответствует длина волны 3 м; тогда оценив, во сколько раз требуемая частота выше или ниже 100 МГц, можно определить длину волны. Например, 1 МГц ниже 100 МГц в 100 раз, значит 1 МГц ↔ 3 м × 100 = 300 м
Примеры характерных частот и длин волн: частоте 50 Гц (частота тока в электросети) соответствует длина радиоволны 6000 км; частоте 100 МГц (радиовещательный FM-диапазон) — 3 м; 900 (1800) МГц (мобильные телефоны) —
33,3 (16,7) см; 2,4 ГГц (Wi-Fi) — 12,5 см; 10 ГГц (бортовые радиолокационные станции системы управления вооружением современных самолётов-истребителей) — 3 см. Видимый свет представляет собой электромагнитное излучение c длинами волн от 380 до 780 нм[4].
Примечания[править | править код]
- ↑ Колебания и волны // Физика : Учебник для 11 класса общеобразовательных учреждений / Г. Я. Мякишев, Б. Б. Буховцев. — 12-е изд. — М. : Просвещение, 2004. — С. 121. — 336 с. — 50 000 экз. — ISBN 5-09-013165-1.
- ↑ Определение не вполне корректно, поскольку (1) в одинаковой фазе колебания происходят и на фронте волны, и расстояние между точками на фронте может быть произвольным, в том числе и нулевым; (2) чтобы расстояние между двумя точками равнялось длине волны, колебание должно происходить не в одинаковой фазе, а со сдвигом фаз в , и расположены точки должны быть вдоль линии распространения
- ↑ ГОСТ 18238-72. Линии передачи сверхвысоких частот. Термины и определения.
- ↑ ГОСТ 7601-78. Физическая оптика. Термины, буквенные обозначения и определения основных величин Архивная копия от 23 марта 2013 на Wayback Machine
Литература[править | править код]
- Волны де Бройля / В. И. Григорьев // Вешин — Газли. — М. : Советская энциклопедия, 1971. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 5).
- Длина волны // Дебитор — Евкалипт. — М. : Советская энциклопедия, 1972. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 8).
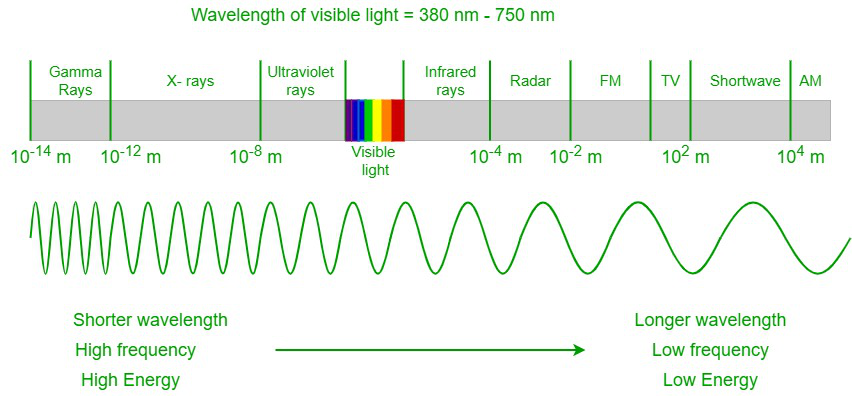
All electromagnetic radiation is light, and it occurs over an extremely wide range of wavelengths, from high-energy gamma waves with shorter wavelengths to low-energy radio waves with longer wavelengths. But the human eye can detect only a small portion of the radiation, and that portion is referred to as visible light. In an electromagnetic spectrum, the visible spectrum lies in between the infrared spectrum and the UV spectrum. Visible light ranges between a wavelength of 400 nm and 700 nm. The human eye cannot detect other electromagnetic radiation as the radiation has either large or small wavelengths and is out of biological limitations.
Electromagnetic spectrum
When a visible spectrum travels through a prism, the light gets separated into a spectrum of colors of different wavelengths. The violet color has the shortest wavelength of around 380 nm, and the red color has the longest wavelength of around 700 nm. Our eyes can detect the outer-most layer of the sun, the corona, in visible light.
Wavelength
A wavelength is one of the properties of a wave and is defined as the distance between the two successive crests or troughs of a wave, where a crest is the highest point of the wave, and a trough is the lowest point of the wave. Since wavelength is a distance or length between two points, it is measured in meters, centimeters, millimeters, micrometers, etc. It is denoted by the symbol Lambda ‘λ’.
Wave
Frequency
Frequency (f) is defined as the total number of wave cycles or oscillations produced per unit of time. Frequency is measured in terms of Hertz (Hz) or s-1.
The formula for the frequency:
Frequency (f) = 1/period(T)
f = 1/T
- A period is defined as the time taken to complete an oscillation.
- From the equation of frequency, we can conclude that the frequency of a wave is inversely proportional to its period.
- 1 Hertz = 1 oscillation/second
Wave velocity
The velocity of a wave or wave velocity is defined as the distance traveled by the wave in a unit of time. The S.I. unit of wave velocity is ms-1.
- Light travels with a speed in the vacuum of 29,97,92,458 m/s, i.e., approximately 3 × 108 m/s, and it is represented by the symbol c.
Wavelength of the light
We know that light possesses the characteristics of both a wave and a particle. So, the wavelength of a light wave is given as;
λ =
Where λ is the wavelength of light
c is the velocity of light and
f is the frequency of the light
The energy of a photon is given as,
E = h × f =
Where E is the energy of a photon
h is the Planck’s constant i.e., h = 6.64 × 10-34 joule-second
Wavelength, Frequency, and Energy of the visible light spectrum
| Colour | Wavelength | Frequency | The energy of a photon |
| Violet | 380 – 450 nm | 668-789 THz |
2.75 – 3.26 eV |
| Blue | 450-495 nm | 606-668 THz |
2.50 – 2.75 eV |
| Green | 495-570 nm | 526-606 THz |
2.17 – 2.50 eV |
|
Yellow |
570-590 nm | 508-526 THz |
2.10 – 2.17 eV |
|
Orange |
590-620 nm | 484-508 THz |
2.00 – 2.10 eV |
|
Red |
620-750 nm | 400-484 THz |
1.65 – 2.00 eV |
Sample Problems
Problem 1: Calculate the wavelength of the visible light with a frequency of 5.36 × 1014 Hz.
Solution:
Given the frequency of light = 5.36 × 1014 Hz
We know, that the velocity of light (c) = 3 × 108 m/s
Now, the wavelength of light (λ) =
⇒ λ =
⇒ λ = 5.60 × 10-7 m
Hence, the wavelength is 5.60 × 10-7 m
Problem 2: If a microwave oven emits microwave energy of 1.64 × 10-24 J, then calculate the wavelength of the microwave emitted.
Solution:
Given data,
The energy of microwave emitted = 1.64 × 10-24 J
We know, that the energy of a photon =
h = 6.64 × 10-34 joule-second
⇒ 1.64 × 10-24 =
⇒ λ =
⇒ λ = 12.146 × 10-2 m = 12.15 cm
Hence, the wavelength of the microwave emitted is 12.15 cm.
Problem 3: If a radio station broadcasts at a frequency of 555 kHz, then calculate the wavelength of radio waves emitted.
Solution:
Given,
Frequency of radio waves = 555 KHz
We know, that the velocity of light (c) = 3 × 108 m/s
Now, the wavelength of light (λ) =
⇒ λ =
⇒ λ = 540 m
Hence the wavelength of radio waves emitted is 540 m.
Problem 4: Calculate the wavelength of yellow light emitted from a sodium lamp at a frequency of 5.15 × 1014 Hz.
Solution:
Given,
The frequency of yellow light = 5.15 × 1014 Hz
We know, that the velocity of light (c) = 3 × 108 m/s
Now, the wavelength of light (λ) =
⇒ λ =
⇒ λ = 582.5 × 10-9 m = 582.5 nm
Hence, the wavelength of the yellow light is 582.5 nm.
Problem 5: Calculate the wavelength of a photon with an energy of 3.35 × 10-19 Joules.
Solution:
Given,
The energy of a photon = 3.35 × 10-19 Joules.
We know, that the energy of a photon =
h = 6.64 × 10-34 joule-second
⇒ 3.35 × 10-19 =
⇒ λ =
⇒ λ= 5.94 × 10-7 m = 594 nm
Hence, the wavelength of the photon is 594 nm.
Problem 6: The broadcasting frequency of a radio station is 101 MHz. What will be the wavelength of the wave if the broadcast wave is an electromagnetic wave?
Solution:
Given data, Frequency of the wave = 101 MHz = 101 × 106 Hz
Speed of light = 3 × 108 m/s
Now, the wavelength of light (λ) = c/f
⇒ λ = (3 × 108)/(101 × 106)
⇒ λ = 2.97 m
Hence, the wavelength of the broadcast wave is 2.97m
Last Updated :
15 May, 2022
Like Article
Save Article
Длина волны света
4.3
Средняя оценка: 4.3
Всего получено оценок: 87.
4.3
Средняя оценка: 4.3
Всего получено оценок: 87.
Свет – это распространяющиеся в пространстве электромагнитные волны. И как и любой другой волновой процесс, свет обладает всеми характеристиками волнового процесса. Рассмотрим такую характеристику, как длина волны света.
Свет как волновой процесс
При изучении света И. Ньютон открыл явление дисперсии – изменение показателя преломления света для разных цветов. Другим открытым им же явлением стала интерференционная картина «колец Ньютона» – линза, соприкасающаяся с плоским стеклом, дает вокруг точки касания ряд концентрических темных колец, причем радиус колец меняется, если освещать линзу светом различных цветов.
Дать удовлетворительное объяснение открытым явлениям И. Ньютон не смог. Это сделал позже другой физик – Т. Юнг. Он предположил, что свет является волной. А значит, ему должны быть присущи все явления, присущие волнам, в частности сложение с появлением интерференционной картины. Зависимость радиуса колец Ньютона от цвета освещения может быть объяснено разностью длины волны различных цветов.
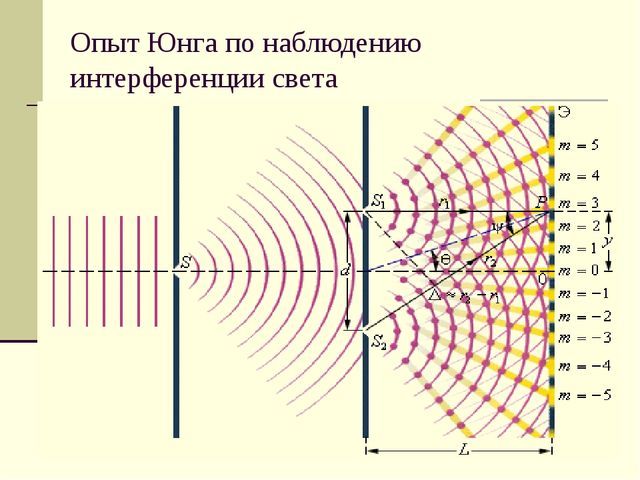
Опыт Т. Юнга
Для демонстрации явления интерференции и для определения длины волны света Т.Юнг поставил специальный эксперимент.
Для получения четкой интерференционной картины необходимо иметь два когерентных световых луча, то есть, луча, обладающих одинаковой длиной волны и имеющих постоянную разность фаз. Освещая две близких щели, можно за ними на экране получить условия для сложения и вычитания световых волн – интерференцию. Главная идея опыта Юнга была в том, чтобы для освещения щелей использовать не простой световой луч, который использовали исследователи до Юнга, а луч, прошедший через маленькое отверстие, за которым, в соответствии с принципом Гюйгенса будет возбуждена единая когерентная волна, и именно она должна использоваться для освещения двух щелей, с получением за ними интерференционной картины.
Длина волны света
Измерив оптическую разность хода световых лучей и расстояние между интерференционными полосами в опыте Юнга, можно получить формулу, по которой рассчитывается длина световой волны. Другим вариантом определения длины света является измерение радиуса колец Ньютона, и вычисление разности оптического хода волн, исходя из геометрии линзы.
Оказалось, что свет представляет собой волны очень небольшой длины – от $4×10^{-7}м$ для фиолетового до $8×10^{-7}м$ для красного цветов.
Волновой характер световых волн и их длина накладывают ограничение на предельное увеличение светового микроскопа. Объекты, имеющие величину меньше длины световой волны, будут «огибаться» световыми волнами, и увидеть их будет невозможно. Поэтому для большего увеличения в электронных микроскопах применяется поток электронов, которые в соответствии с принципом корпускулярно-волнового дуализма обладают свойствами волн с очень малой длиной.
Что мы узнали?
Свет является электромагнитным излучением с малой длиной волны. Длина световых волн впервые были измерена в опытах Т. Юнга. Были получены значения от $4×10^{-7}м$ для фиолетового до $8×10^{-7}м$ для красного цветов.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.3
Средняя оценка: 4.3
Всего получено оценок: 87.
А какая ваша оценка?
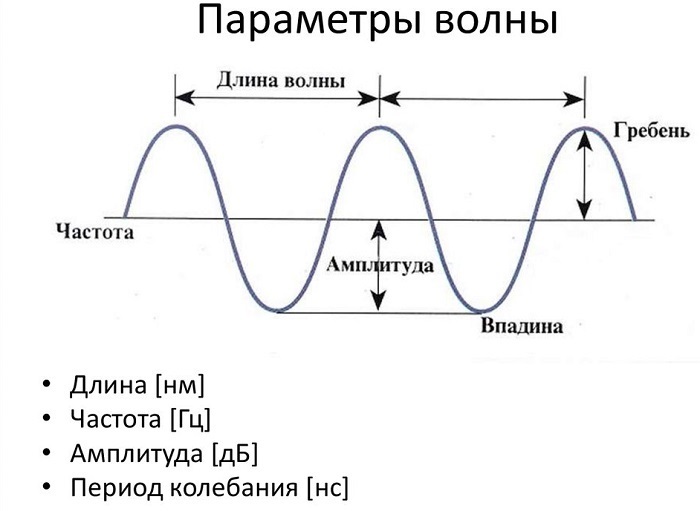
Длина волны – это расстояние между двумя последовательными пиками (гребнями) или впадинами. Самое высокое положение волны называется пиком. Самое нижнее положение волны называется впадиной.
Цикл – это полное колебание, например, кривая между двумя гребнями или двумя впадинами. Максимальное расстояние волны от равновесного положения называется амплитудой.
На рисунке показаны основные параметры волны, используемые в физике:
Определение и формула длины волн
Волна – это возмущение, распространяющееся от точки, в которой она возникла, в окружающую среду. Такое возмущение переносит энергию без чистого переноса вещества.
Длина представляет собой фактическое расстояние, пройденное волной, которое не всегда совпадает с расстоянием среды, или частиц, в которых распространяется волна. Ее также определяют как пространственный период волнового процесса.
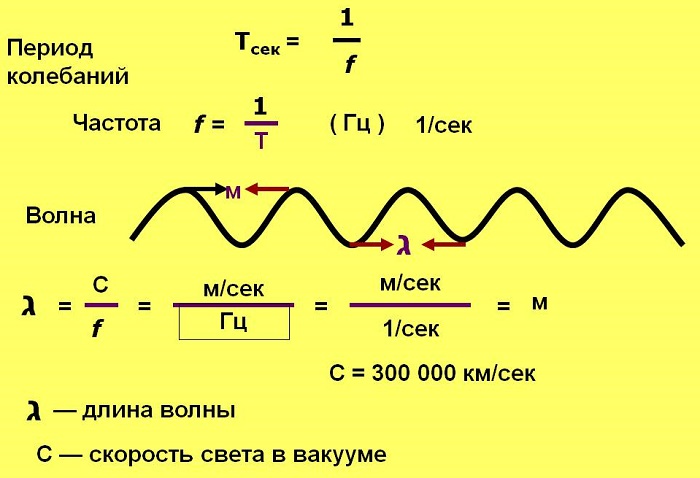
Греческая буква “λ” (лямбда) в физике используется для обозначения длины в уравнениях. Она обратно пропорциональна частоте волны.
Период Т — время завершения полного колебания, единица измерения секунды (с).
Длинная волна соответствует низкой частоте, а короткая – высокой. Длина измеряется в метрах. Количество волн, излучаемых в каждую секунду, называется частотой и обратно пропорционально периоду.
У различных длин разная скорость распространения. Например, скорость света в воде равна 3/4 от скорости в вакууме.
Пространственный период волны – это расстояние, которое точка с постоянной фазой «пролетает» за интервал времени, соответствующий периоду колебаний.
Частота f — количество полных колебаний в единицу времени. Измеряется в Герцах (Гц).
При одном полном колебании в секунду f = 1 Гц; при 1000 колебаний в секунду f = 1 килогерц (кГц); 1 млн. колебаний в секунду f = 1 мегагерц (1 МГц).
Зная, что скорость света в вакууме с — 300 000 км/с, или 300 000 000 м/с, то для перевода длины волны в частоту нужно 3 х 108 м/с поделить на длину в метрах.
Единицы измерения длины волны λ – нанометры и ангстремы, где нанометр является миллиардной частью метра (1 м = 109 нм) и ангстрем является десятимиллиардной частью метра (1 м = 1010 А), то есть нанометр эквивалентен 10 ангстрем (1 нм = 10 А).
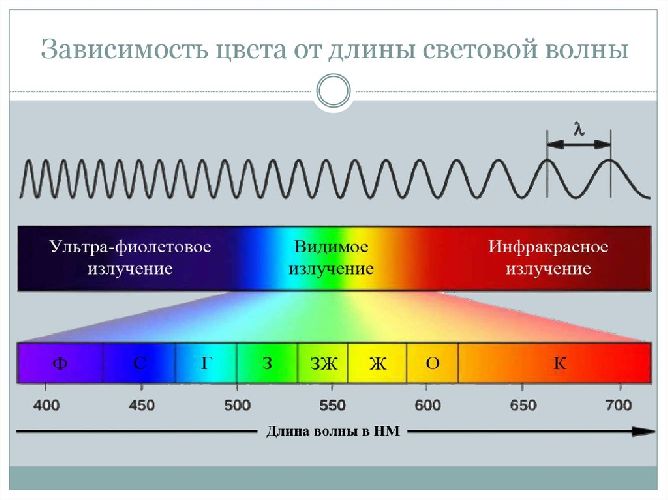
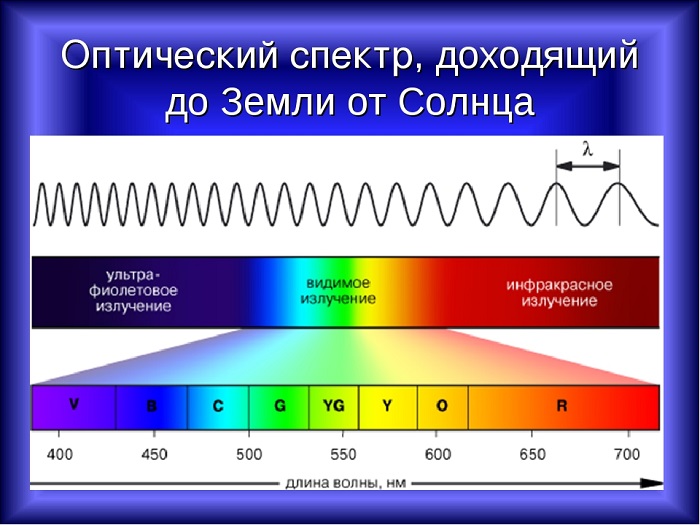
Свет, который исходит от Солнца, является электромагнитным излучением, которое движется со скоростью 300 000 км/с, но длина не одинакова для любого фотона, а колеблется между 400 нм и 700 нм. Длина световой волны влияет на цвет.
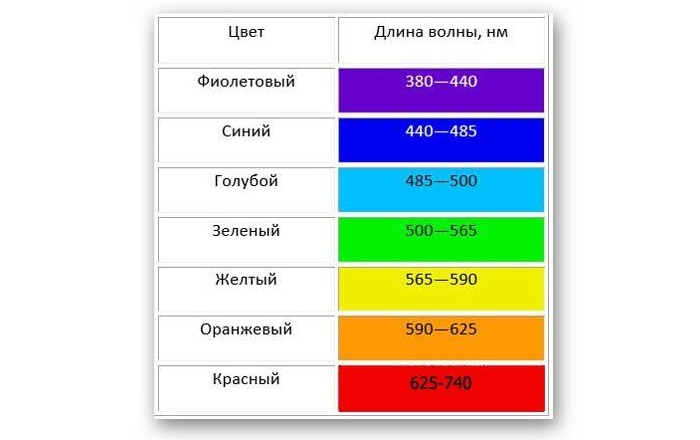
Белый свет разлагается на спектр различных цветных полос, каждая из которых определяется своей длиной волны. Таким образом, светом с наименьшей длиной является фиолетовый, который составляет около 400 нм, а светом с наибольшей длиной – красный, который составляет около 700 нм.
Таблица показывает длину волны в зависимости от цвета:
Излучения с длиной меньше фиолетового называются ультрафиолетовым излучением, рентгеновским и гамма-лучами в порядке уменьшения. Излучения больше красного называются инфракрасными, микроволнами и радиоволнами, в порядке возрастания.
Предельная дальность связи зависит от длины. Размеры антенны часто превышают рабочую длину радиоэлектронного средства.
Рисунок показывает длину волн и частоту (нм), исходящих от различных источников:
Примеры расчета длины волны для звуковых, электромагнитных и радиоволн
Задача №1
Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?
Задача №2
Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с. прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.
Задача №3
Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.
Длина волны – одно из важнейших понятий в физике и технике. Это свойство волны, характеризующее расстояние между двумя соседними точками на волне, на которых фаза колебаний совпадает.
Длина волны является одним из основных параметров, определяющих свойства волн, таких как скорость, частота и амплитуда.
В данной статье мы рассмотрим, что такое длина волны, как ее измерять и как она используется в различных областях науки и техники.
Основы световых волн
Свет – это электромагнитное излучение, распространяющееся в пространстве в виде волн. В оптике, длина волны – это расстояние между двумя соседними точками на волне, которые находятся в фазе. Другими словами, это расстояние между двумя соседними максимумами или минимумами на волне.
Длина волны света обычно измеряется в нанометрах (нм), и она имеет прямую связь с частотой волны. Частота волны – это количество колебаний, происходящих за единицу времени. Чем выше частота, тем короче длина волны.
Для световых волн длина волны связана с их цветом. Видимый свет включает в себя волны с длинами от приблизительно 400 нм до 700 нм. Красный цвет соответствует длине волны около 700 нм, а фиолетовый цвет – длине волны около 400 нм. Все остальные цвета радуги находятся между этими двумя крайними точками.
Понимание длины волны света является важным для понимания различных оптических явлений, таких как дифракция, интерференция, и поляризация.
Формула длины волны
Формула длины волны связывает длину волны света с его частотой. Длина волны обозначается символом λ (ламбда) и измеряется в метрах (м), а частота обозначается символом ν (ню) и измеряется в герцах (Гц).
Формула выглядит следующим образом:
λ = c / ν,
где c – скорость света, которая равна приблизительно 299792458 метров в секунду.
С помощью этой формулы можно вычислить длину волны для любой электромагнитной волны, включая световые волны.
Например, для световой волны с частотой 500 TГц (терагерц), длина волны будет:
λ = 299792458 м/с / (500 * 1012 Гц) ≈ 599.6 нм
Также можно использовать эту формулу для расчета частоты световой волны, если известна ее длина:
ν = c / λ
Например, для световой волны длиной 600 нм, ее частота будет:
ν = 299792458 м/с / (600 * 10-9 м) ≈ 500 ТГц
Формула длины волны также применяется в других областях физики, таких как акустика и радиофизика. В этих областях она используется для расчета длин волн звуковых и радиоволн.
Единицы измерения длины волны
Длина волны – это расстояние между двумя точками на одной волне, которые находятся в одной фазе. Единица измерения длины волны зависит от контекста, в котором она используется.
В общей физике и оптике, наиболее распространенными единицами измерения длины волны являются нанометры (нм), микрометры (мкм) и ангстремы (Å).
Нанометр (1 нм) – это одна миллиардная часть метра, и он используется для измерения длины волн в видимом и ультрафиолетовом диапазонах. Например, длина волны красного света составляет около 700 нм, а ультрафиолетового света около 300 нм.
Микрометр (1 мкм) – это одна миллионная часть метра, и он используется для измерения длины волн в инфракрасном диапазоне. Например, длина волны инфракрасного излучения от тела с температурой 1000 К составляет около 3 мкм.
Ангстрем (1 Å) – это 0,1 нм, и он используется для измерения длины волн в рентгеновском диапазоне. Например, длина волны рентгеновского излучения обычно составляет от 0,1 до 1 Å.
Единицы измерения длины волны
Обратите внимание, что научные и технические измерения длины волн могут использовать любую из этих единиц в зависимости от конкретного контекста и диапазона длин волн, которые измеряются. Например, нанометры часто используются для измерения длины волн света, в то время как миллиметры могут быть использованы для измерения длины радиоволн.
Значение длины волны в науке и технологии
Длина волны является одной из ключевых характеристик световых, радиоволновых и других типов волн. Ее значение широко применяется в различных научных и технических областях.
В физике длина волны используется для определения энергии квантов, связанных с электромагнитным излучением, и для изучения поведения света в различных средах. Длина волны также используется в оптике для описания оптических явлений, таких как дифракция и интерференция.
В радиоэлектронике длина волны используется для определения частоты сигналов, передаваемых через антенны, и для расчета размеров антенн.
В области связи длина волны играет ключевую роль при передаче информации через оптические волокна, где она определяет скорость передачи данных и возможности мультиплексирования.
Также длина волны используется для создания различных типов световых и радиоволновых приборов, таких как лазеры и радиомаяки.
Использование длины волны также находит применение в медицине, где ее значение используется для создания изображений с помощью медицинской оптики, например, в эндоскопии.
Применение длины волны в повседневной жизни
Длина волны играет важную роль не только в науке и технологии, но и в повседневной жизни. Многие явления, которые мы наблюдаем вокруг себя, связаны с длиной волны.
Применение длины волны в повседневной жизни может быть обнаружено во многих зрительных и звуковых эффектах.
Например, цвета, которые мы видим в окружающей нас природе, на самом деле являются результатом различных длин волн света, которые поглощаются и отражаются различными поверхностями.
Это также может быть заметно в эффектах, связанных с преломлением света, например, в появлении радуги или в способности линзы фокусировать свет на определенной точке.
Длина звуковой волны также играет важную роль в нашей повседневной жизни. Например, музыкальные инструменты создают звуковые волны различных длин, которые мы слышим в виде различных звуков и тональностей. Кроме того, в зависимости от длины звуковой волны, звук может иметь различные характеристики, такие как громкость, тон и частота.
Также длина волны имеет практическое применение в медицине, в частности, в области ультразвуковых исследований, где длина волны используется для создания изображений внутренних органов и тканей.
Еще одним интересным примером применения длины волны в повседневной жизни является использование инфракрасных волн для передачи информации в виде сигналов в телевизионных пультах. Каждая кнопка на пульте имеет свой уникальный код в виде последовательности инфракрасных импульсов различной длины волны.
Таким образом, длина волны является важным параметром, который играет роль в многих аспектах нашей жизни, от цвета, который мы видим, до звука, который мы слышим, и до передачи информации с помощью электромагнитных волн.
Заключение
Длина волны является важной характеристикой для описания различных типов волн и находит широкое применение в научных и технических областях, таких как физика, оптика, радио, связь и многие другие.
Кроме того, понимание длины волны и ее свойств может помочь лучше понять различные зрительные и звуковые эффекты, которые мы наблюдаем в повседневной жизни.
Различные единицы измерения длины волны используются в разных областях науки и техники, и важно иметь представление о том, как они соотносятся между собой. Понимание длины волны помогает нам лучше понимать мир вокруг нас и его фундаментальные свойства.
