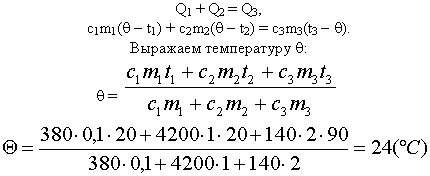Thermodynamics is the field of physics concerned with temperature, heat and, ultimately, energy transfers. Although the laws of thermodynamics can be a little tricky to follow, the first law of thermodynamics is a simple relationship between the work done, heat added, and the change in internal energy of a substance. If you have to calculate a change in temperature, it’s either a simple process of subtracting the old temperature from the new one, or it may involve the first law, the amount of energy added as heat, and the specific heat capacity of the substance in question.
TL;DR (Too Long; Didn’t Read)
A simple change in temperature is calculated by subtracting the final temperature from the initial temperature. You may need to convert from Fahrenheit to Celsius or vice-versa, which you can do using a formula or an online calculator.
When heat transfer is involved, use this formula: change in temperature = Q / cm to calculate the change in temperature from a specific amount of heat added. Q represents the heat added, c is the specific heat capacity of the substance you’re heating, and m is the mass of the substance you’re heating.
What’s the Difference Between Heat and Temperature?
The key bit of background you need for a temperature calculation is the difference between heat and temperature. The temperature of a substance is something you are familiar with from everyday life. It’s the quantity you measure with a thermometer. You also know that the boiling points and melting points of substances depend on their temperature. In reality, temperature is a measure of the internal energy a substance has, but that information isn’t important for working out the change in temperature.
Heat is a bit different. This is a term for the transfer of energy through thermal radiation. The first law of thermodynamics says that the change in energy equals the sum of the heat added and the work done. In other words, you can give more energy to something by warming it up (transferring heat to it) or by physically moving or stirring it (doing work on it).
Simple Change in Temperature Calculations
The simplest temperature calculation you may have to do involves working out the difference between a starting and finishing temperature. This is easy. You subtract the final temperature from the starting temperature to find the difference. So if something starts at 50 degrees Celsius and finishes at 75 degrees C, then the change in temperature is 75 degrees C – 50 degrees C = 25 degrees C. For decreases in temperature, the result is negative.
The biggest challenge for this type of calculation occurs when you need to do a temperature conversion. Both temperatures must be either Fahrenheit or Celsius. If you have one of each, convert one of them. To switch from Fahrenheit to Celsius, subtract 32 from the amount in Fahrenheit, multiply the result by 5, and then divide it by 9. To convert from Celsius to Fahrenheit, first multiply the amount by 9, then divide it by 5, and finally add 32 to the result. Alternatively, just use an online calculator.
Calculating Temperature Change From Heat Transfer
If you’re doing a more complicated problem involving heat transfer, calculating the change in temperature is more difficult. The formula you need is:
Change in temperature = Q / cm
Where Q is the heat added, c is the specific heat capacity of the substance, and m is the mass of the substance you’re heating up. The heat is given in joules (J), the specific heat capacity is an amount in joules per kilogram (or gram) °C, and the mass is in kilograms (kg) or grams (g). Water has a specific heat capacity of just under 4.2 J/g °C, so if you’re raising the temperature of 100 g of water using 4,200 J of heat, you get:
Change in temperature = 4200 J ÷ (4.2 J/g °C × 100 g) = 10 °C
The water increases in temperature by 10 degrees C. The only thing you need to remember is that you have to use consistent units for mass. If you have a specific heat capacity in J/g °C, then you need the mass of the substance in grams. If you have it in J/kg °C, then you need the mass of the substance in kilograms.
Как найти в физике начальную и конечную температуру через количество теплоты, удельную теплоту и массу?
Домашние задания
Николай Маслихов
21 декабря 2020 · 3,6 K
Ответить1Уточнить
Сергей Иванов
Математика
158
Мне интересно и нравятся: математика. физика. астрономия, информатика, астрофизика, науки… · 26 дек 2020 · ivanov610.narod.ru
Формула связи такая Q = cm(t2-t1). Если даны: количество теплоты, удельную теплоту и массу, то из этой формулы можно выразить только изменение температуры. t2-t1 =Q/cm. Чтобы найти конечную или начальную температуры, нужно какую-то из них тоже знать. Знаем конечную, найдем начальную и наоборот.
4,2 K
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
Содержание:
Температура:
Перед тем как, например, пойти на пляж, многие интересуются прогнозом погоды. И если ожидается температура воздуха 10 °С, то, скорее всего, планы будут изменены. А стоит ли отказываться от прогулки, если прогнозируется температура 300 К (кельвинов)? И что на самом деле вкладывают физики в понятие «температура»?

Что такое температура
Эксперименты показывают, что макроскопическая система может переходить из одного состояния в другое. Например, если в морозный день занести в комнату шарик, наполненный гелием, то гелий в шарике будет нагреваться и при этом будут изменяться давление, объем и некоторые другие параметры газа. После того как шарик пробудет в комнате некоторое время, изменения прекратятся. Один из постулатов молекулярной физики и термодинамики — его еще называют нулевое начало термодинамики — гласит: любое макроскопическое тело или система тел при неизменных внешних условиях самопроизвольно переходит в термодинамическое равновесное состояние (состояние теплового равновесия), после достижения которого все части системы имеют одинаковую температуру. Нулевое начало термодинамики фактически вводит и определяет понятие температуры.
Температура — физическая величина, характеризующая состояние теплового равновесия макроскопической системы.
Состояние теплового равновесия — это такое состояние макроскопической системы, при котором все макроскопические параметры системы остаются неизменными сколь угодно долго.
В состоянии теплового равновесия все части системы имеют одинаковую температуру; другие макроскопические параметры неизменны, но могут быть разными. Вспомните пример с шариком: после того как установится тепловое равновесие, температура окружающего воздуха и температура гелия в шарике будут одинаковыми, а давление, плотность и объем — разными.
Как работают термометры
Температура — это физическая величина, и ее можно измерять. Для этого нужно установить шкалу температур. Самые распространенные температурные шкалы — шкалы Цельсия, Кельвина, Фаренгейта (рис. 29.1).
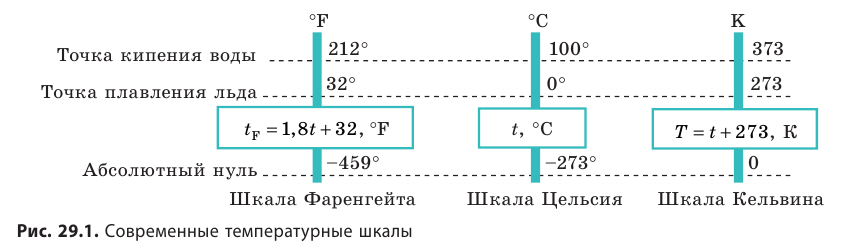
Построение шкалы температур начинается с выбора реперных (опорных) точек, которые должны быть однозначно связаны с какими-либо физическими процессами, которые легко воспроизвести. Например, за нулевую точку температурной шкалы Цельсия принята температура таяния льда при нормальном атмосферном давлении ( t = 0 °С). Температуре кипения воды при нормальном атмосферном давлении приписывают значение t =100 °С. Единица температуры по шкале Цельсия — градус Цельсия: 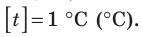 .
.

Рис. 29.2. различные виды термометров: а — жидкостный (принцип действия: изменение объема жидкости при изменении температуры); б — термометр сопротивления (изменение электрического сопротивления проводника при изменении температуры); в — биметаллический деформационный (изменение длин двух разных металлических пластин при изменении температуры)
Приборы для измерения температуры — термометры (рис. 29.2). Основные части любого термометра — термометрическое тело (ртуть или спирт в жидкостном термометре, биметаллическая пластина в металлическом деформационном термометре и т. д.) и шкала. Если термометрическое тело привести в контакт с телом, температуру которого нужно измерить, система придет в неравновесное состояние. При переходе в равновесное состояние будут изменяться некоторые параметры термометрического тела (объем, сопротивление и т. п.). Зная, как эти параметры зависят от температуры, определяют температуру тела.
Обратите внимание!
- Термометр фиксирует собственную температуру, равную температуре тела, с которым термометр находится в термодинамическом равновесии.
- Термометрическое тело не должно быть массивным, иначе оно существенно изменит температуру тела, с которым контактирует.
Температура и средняя кинетическая энергия молекул
То, что температура тела должна быть связана с кинетической энергией его молекул, следует из простых соображений. Например, с увеличением температуры увеличивается скорость движения броуновских частиц, ускоряется диффузия, повышается давление газа, а это значит, что молекулы движутся быстрее и их кинетическая энергия становится больше. Можно предположить: если газы находятся в состоянии теплового равновесия, средние кинетические энергии молекул этих газов одинаковы. Но как это доказать, ведь непосредственно измерить эти энергии невозможно?
Обратимся к основному уравнению МКТ идеального газа: 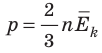 . По определению
. По определению 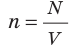 , поэтому
, поэтому 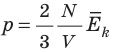 . После преобразований получим:
. После преобразований получим: 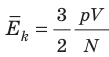 .
.
Таким образом, чтобы экспериментально убедиться в равенстве средних кинетических энергий молекул различных газов при одинаковой температуре, нужно измерить объемы (V), давления (p) и массы (m) газов и, зная их молярную массу (M), найти число молекул каждого газа (N) по формуле 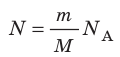 .
.
Чтобы обеспечить одинаковую температуру, можно, например, погрузить баллоны с различными газами в сосуд с водой и дождаться состояния теплового равновесия (рис. 29.3).
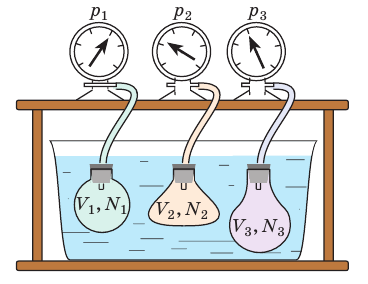
Рис. 29.3. опыт, позволяющий установить связь между температурой и средней кинетической энергией поступательного движения молекул газа. Газы в сосудах находятся в состоянии теплового равновесия со средой, а следовательно, и друг с другом
Эксперименты показывают, что для всех газов в состоянии теплового равновесия отношение 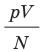 одинаково, а следовательно, одинаковыми являются и средние кинетические энергии молекул газов. (Отношение
одинаково, а следовательно, одинаковыми являются и средние кинетические энергии молекул газов. (Отношение 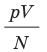 часто обозначают символом θ (тета).)
часто обозначают символом θ (тета).)
Например, при температуре 0 °С (сосуды с газами погрузили в тающий лед) 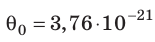 , Дж, то есть
, Дж, то есть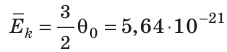 Дж; при температуре 100 °С (сосуды погрузили в кипящую воду)
Дж; при температуре 100 °С (сосуды погрузили в кипящую воду) 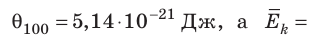
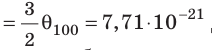 Дж. Так как в состоянии теплового равновесия значение θ для любых газов одинаково, то температуру можно измерять в джоулях.
Дж. Так как в состоянии теплового равновесия значение θ для любых газов одинаково, то температуру можно измерять в джоулях.
Абсолютная шкала температур
Понятно, что в джоулях представлять температуру неудобно (прежде всего потому, что значения θ очень малы), к тому же неудобно полностью отказываться от шкалы Цельсия. В 1848 г. английский физик Уильям Томсон (лорд Кельвин) (1824–1907) предложил абсолютную шкалу температур (сейчас ее называют шкалой Кельвина).
Температуру Т, измеренную по шкале кельвина, называют абсолютной температурой.
Единица абсолютной температуры — кельвин — основная единица СИ: [T] = 1 К (К).
Шкала Кельвина построена следующим образом:
- изменение температуры по шкале Кельвина равно изменению температуры по шкале Цельсия: ∆ = T t ∆ , то есть цена деления шкалы Кельвина равна цене деления шкалы Цельсия: 1 °С = 1 К; температуры, измеренные по шкалам Кельвина и Цельсия, связаны соотношениями:
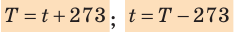
- температура по шкале Кельвина связана с величиной
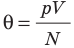 соотношением θ = kT, где k — постоянная Больцмана — коэффициент пропорциональности, не зависящий ни от температуры, ни от состава и количества газа:
соотношением θ = kT, где k — постоянная Больцмана — коэффициент пропорциональности, не зависящий ни от температуры, ни от состава и количества газа: 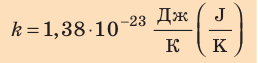
- абсолютная температура имеет глубокий физический смысл: средняя кинетическая энергия поступательного движения молекул идеального газа прямо пропорциональна абсолютной температуре:
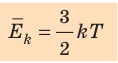 (1) То есть, если газ охладить до температуры T= 0 К, движение его молекул должно прекратиться (
(1) То есть, если газ охладить до температуры T= 0 К, движение его молекул должно прекратиться (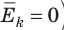 ). Таким образом, нулевая точка шкалы Кельвина — это самая низкая теоретически возможная температура. На самом деле движение молекул не прекращается никогда, поэтому достичь температуры 0 К (–273 °С) невозможно.
). Таким образом, нулевая точка шкалы Кельвина — это самая низкая теоретически возможная температура. На самом деле движение молекул не прекращается никогда, поэтому достичь температуры 0 К (–273 °С) невозможно.
Абсолютный нижний предел температуры, при котором движение молекул и атомов должно прекратиться, называют абсолютным нулем температуры. Давление p газа полностью определяется его абсолютной температурой T и концентрацией n молекул газа: p=nkT (2).
Выводы:
- Физическая величина, характеризующая состояние теплового равновесия макроскопической системы, называется температурой. Абсолютный нижний предел температуры, при котором движение молекул и атомов должно прекратиться, называют абсолютным нулем температуры. Шкала, за нулевую точку которой взят абсолютный нуль температуры, называется абсолютной шкалой температур (шкалой Кельвина). Единица абсолютной температуры — кельвин (К) — основная единица СИ. Температуры по шкале Кельвина и Цельсия связаны соотношением: T=t + 273; t=T – 273.
- Средняя кинетическая энергия поступательного движения молекул идеального газа прямо пропорциональна абсолютной температуре, а давление газа определяется абсолютной температурой и концентрацией молекул газа:
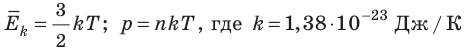 — постоянная Больцмана.
— постоянная Больцмана.
- Парообразование и конденсация
- Тепловое равновесие в физике
- Изопроцессы в физике
- Твердые тела и их свойства в физике
- Механизмы, работающие на основе правила моментов
- Идеальный газ в физике
- Уравнение МКТ идеального газа
- Уравнение состояния идеального газа
 Уравнение теплового баланса:
Уравнение теплового баланса:
− r m п + c в m п ( t − t к и п ) + λ m л + c в m л ( t − t п л ) = 0
Пример №2. В кастрюлю, где находится вода объемом 2 л при температуре 25 о С, долили 3 л кипятка. Какая температура воды установилась?
Количество теплоты, отданное кипятком, равно количеству теплоты, принятому более прохладной водой. Поэтому:
c m 1 ( t − t 0 ) = − c m 2 ( t − t к и п )
m 1 ( t − t 0 ) = − m 2 ( t − t к и п )
m 1 t + m 2 t = m 1 t 0 + m 2 t к и п
( m 1 + m 2 ) t = m 1 t 0 + m 2 t к и п
t = m 1 t 0 + m 2 t к и п m 1 + m 2 . .
t = 2 · 25 + 3 · 100 2 + 3 . . = 350 5 . . = 70 ( ° C )
Взаимные превращения механической и внутренней энергии
Если в тексте задачи указан процент одного вида энергии, перешедший в другой, то он указывается в виде десятичной дроби перед этой энергией, которой тело обладало вначале.
Частные случаи закона сохранения энергии
m v 2 2 . . = c m Δ t
0 , 5 ( m v 2 0 2 . . − m v 2 2 . . ) = c m Δ t
m v 2 2 . . = c m Δ t + λ m
0 , 6 m g h = c m Δ t + r m
q m т о п = m р g h
0 , 25 q m т о п m с v 2 2 . .
Пример №3. Свинцовая дробинка, летящая со скоростью 100 м/с, попадает в доску и входит в нее. 52% кинетической энергии дробинки идет на ее нагревание. На сколько градусов нагрелась дробинка? Удельная теплоемкость свинца 130 Дж/(кг∙К).
Запишем закон сохранения энергии для этого случая:
0 , 52 m v 2 2 . . = c m Δ t
Δ t = 0 , 52 v 2 2 c . . = 0 , 52 · 100 2 2 · 130 . . = 20 ( К )
Примеры КПД
| При неупругом ударе о стенку пуля нагрелась |
| Тело падает с некоторой высоты и в момент падения нагревается |
| В результате того, что пуля пробивает стену, ее скорость уменьшается, 50% выделившейся при этом энергии идет на нагревание пули |
| Летящая пуля при ударе о стенку расплавилась. Начальная температура пули меньше температуры плавления |
| Капля воды, падая с некоторой высоты, в момент удара испарилась. Температура капли у поверхности земли меньше температуры кипения. На нагрев пошло 60% выделившейся механической энергии |
| Вследствие сгорания топлива ракета поднялась на некоторую высоту |
| Вследствие сгорания топлива снаряд приобрел некоторую скорость, и на это было затрачено 25% энергии |
Q п о л е з н = c m Δ T
Q п о л е з н = c m Δ T + r m
( п р о и з в е д е н и е м о щ н о с т и н а в р е м я )
η = c m Δ T P t . . 100 %
Q п о л е з н = c m Δ T
Q з а т р = q m т о п
η = c m Δ T q m т о п . . 100 %
A п о л е з н = N t = N s v . .
Q з а т р = q m т о п
η = c m Δ T v q m т о п . . 100
E п о л е з н = m v 2 2 . .
Q з а т р = q m п о р
η = m v 2 2 q m п о р . . 100
Внимание! Если в задаче указано время, в течение которого происходит один тепловой процесс, а спрашивают о времени протекания другого, то считайте, что мощность нагревателя или холодильника постоянна:
Q 1 t 1 . . = Q 2 t 2 . .
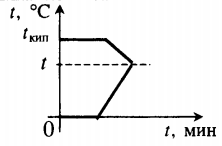
Пример №4. Для нагревания на электроплитке некоторого количества воды от 20 до 100 о С потребовалась 21 минута. Сколько времени после этого необходимо для полного испарения воды? Удельная теплоемкость воды 4200 Дж (кг∙К), удельная теплота парообразования 2,24 МДж/кг.
Будем считать, что мощность электроплитки постоянна. Поэтому:
Q 1 t 1 . . = Q 2 t 2 . .
Количество теплоты, сообщенное воде при нагревании:
Q 1 = с m ( t 2 − t 1 )
Количество теплоты, которое нужно сообщить, чтобы вода полностью испарилась:
с m ( t 2 − t 1 ) t 1 . . = r m t 2 . .
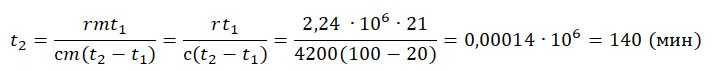
Кусок льда, имеющий температуру 0°С, помещён в калориметр с электронагревателем. Чтобы превратить этот лёд в воду с температурой 12°С, требуется количество теплоты 80 кДж. Какая температура установится внутри калориметра, если лёд получит от нагревателя количество теплоты 60 кДж? Теплоёмкостью калориметра и теплообменом с внешней средой пренебречь.
Алгоритм решения
Решение
Запишем исходные данные:
Составим уравнение теплового баланса для первого случая:
Q 1 = λ m + c m t 1
Внимание! Вместо разности температур используется значение только конечной температуры, так как начальная температура равна 0.
Найдем массу льда из уравнения теплового баланса для первого случая. Учтем что:
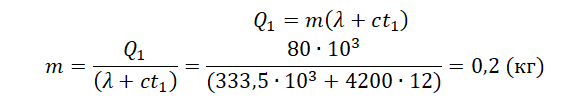
Чтобы расплавить кусок льда массой 0,5 кг, нужно затратить следующее количество теплоты:
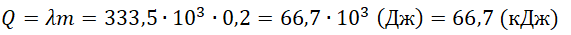
Лед не расплавится весь, так как ему будет сообщено лишь 60 кДж теплоты. Поэтому в калориметре температура будет равна 0 о С.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Внимательно прочитайте текст задания и выберите верный ответ из списка
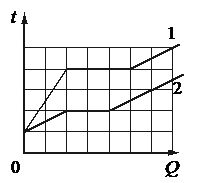 На рисунке представлены графики зависимости температуры t двух тел одинаковой массы от сообщённого им количества теплоты Q. Первоначально тела находились в твёрдом агрегатном состоянии.
На рисунке представлены графики зависимости температуры t двух тел одинаковой массы от сообщённого им количества теплоты Q. Первоначально тела находились в твёрдом агрегатном состоянии.
Используя данные графиков, выберите из предложенного перечня два верных утверждения и укажите их номера. Ответ: а) Температура плавления первого тела в 1,5 раза больше, чем второго. б) Тела имеют одинаковую удельную теплоёмкость в твёрдом агрегатном состоянии. в) Удельная теплоёмкость второго тела в твёрдом агрегатном состоянии в 3 раза больше, чем первого. г) Оба тела имеют одинаковую удельную теплоту плавления. д) Тела имеют одинаковую удельную теплоёмкость в жидком агрегатном состоянии.
Алгоритм решения
- Проанализировать каждое из утверждений.
- Проверить истинность утверждений с помощью графика.
- Выбрать и записать верные утверждения.
Решение
Проверим первое утверждение, согласно которому, температура плавления первого тела в 1,5 раза больше, чем второго.
Если это было бы так, то количество клеток до горизонтального участка графика 1 относилось к количеству клеток до горизонтального участка графика 2 как 3 к 2. Но мы видим, что до 1 графика 4 клетки, до 1 — 2. Следовательно, температура плавления первого тела в 2 раза больше, чем второго.
Первое утверждение неверно.
Проверим второе утверждение, согласно которому тела имеют одинаковую удельную теплоёмкость в твёрдом агрегатном состоянии.
Если бы это было так, то соответствующие участки графиков совпадали бы. Только в таком случае температура тел увеличивалась на одну и ту же температуру при получении одного и того же количества теплоты. Но мы видим, что это не так.
Второе утверждение неверно.
Проверим третье утверждение, согласно которому удельная теплоёмкость второго тела в твёрдом агрегатном состоянии в 3 раза больше, чем первого.
Если это было бы так, то первое тело при сообщении телам одинакового количества теплоты нагревалось бы втрое быстрее второго. И это действительно так, потому что температура второго во время нагревания в твердом состоянии увеличилась только на 1 клетку, в то время как температура первого тела — на 2 клетки.
Третье утверждение верно.
Проверим четвертое утверждение, согласно которому оба тела имеют одинаковую удельную теплоту плавления.
Если это было бы так, то протяженность горизонтальных участков обоих графиков была бы одинаковой. Но это не так. Протяженность этого участка для тела 1 составляет 3 клетки, для тела 2 — 2 клетки.
Четвертое утверждение верно.
Проверим пятое утверждение, согласно которому тела имеют одинаковую удельную теплоёмкость в жидком агрегатном состоянии.
Если бы это было так, то соответствующие участки графиков были параллельными. Только при таком условии при повышении температуры на одно и то же количество градусов тела бы получли одинаковое количество теплоты. И это действительно так.
Пятое утверждение верно.
Вывод: верным утверждения «в» и «д».
pазбирался: Алиса Никитина | обсудить разбор | оценить
В сосуде лежит кусок льда. Температура льда t 1 = 0 «> t 1 = 0 °C. Если сообщить ему количество теплоты Q = 50 «> Q = 50 кДж, то 3/4 льда растает. Какое количество теплоты q надо после этого сообщить содержимому сосуда дополнительно, чтобы весь лёд растаял и образовавшаяся вода нагрелась до температуры t 2 = 20 «> t 2 = 20 °C? Тепловыми потерями на нагрев сосуда пренебречь.
Теплотехника

Теплотехника (нем. Wärmetechnik) — общетехническая дисциплина, изучающая методы получения, преобразования, передачи и использования теплоты, а также принцип действия и конструктивные особенности тепло- и парогенераторов тепловых машин, агрегатов и устройств. wikipedia.org/wiki/Теплотехника
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Введение в теплотехнику
Теплотехника представляет собой науку, которая изучает законы распространения и передачи теплоты между телами. Вместе с термодинамикой учение о теплообмене составляет теоретические основы теплотехники.
Различают три вида теплообмена: теплопроводность (или кондук-ция), конвекция и тепловое излучение. Теплопроводностью называется перенос теплоты, возникающий при непосредственном соприкосновении между частицами тела.
В жидкостях наряду с теплопроводностью теплота может распространяться также путем перемещения и перемешивания между собой более или менее нагретых частиц самой жидкости. Такой вид распространения теплоты называется конвекцией. В целом явление передачи теплоты при соприкосновении стенки с жидкостью путем теплопроводности и дальнейшее распространение ее в жидкости за счет конвекции (а также процесс, протекающий в обратном направлении) называется конвективным теплообменом, или теплоотдачей.
Тепловым излучением, или лучеиспусканием, называется перенос энергии в виде электромагнитных волн между двумя взаимно излучающими поверхностями. При этом происходит двойное превращение энергии: тепловой энергии в лучистую на поверхности тела, излучающего теплоту, и лучистой энергии в тепловую на поверхности тела, поглощающего лучистую теплоту.
Частные процессы переноса теплоты
Частные процессы переноса теплоты — теплопроводность, конвекция и лучеиспускание обычно происходят одновременно. Например, в топочных устройствах различных технологических установок конвективный перенос теплоты сопровождается тепловым излучением. В этом случае процесс переноса теплоты называется сложным теплообменом.
В теплообменных аппаратах, как правило, происходят одновременно различные виды теплообмена. Например, в паровом котле теплота передается от продуктов сгорания топлива к стенкам кипятильных труб путем излучения и конвекции, через металл стенок труб теплота распространяется путем теплопроводности, и далее осуществляется процесс теплоотдачи кипящей воде или пару. Такой процесс переноса теплоты от греющей среды через стенку к нагреваемой среде называется теплопередачей.
Необходимо отметить, что в тепловых установках, используемых в производстве строительных материалов и изделий, процессы теплообмена являются решающими, так как интенсивность и качество тепловой обработки строительных изделий в значительной мере зависят от правильной работы теплоиспользующей аппаратуры. Очень важно при организации теплообмена в промышленных условиях обеспечить равномерность тепловой обработки во всем объеме камеры или на отдельных
участках непрерывно действующих установок. В противном случае в общей массе обработанной продукции будет содержаться как перегретый, так и недогретый материал. При этом нужно иметь в виду, что тепловая обработка многих строительных изделий сопровождается сложными физико-химическими процессами экзо- или эндотермического характера, учет которых в расчете теплообмена обязателен.
Известно, что процесс распространения теплоты в пространстве неразрывно связан с распределением температуры в нем. Совокупность значений температуры в каждый момент времени для всех точек рассматриваемого пространства называется температурным полем.
Математически оно выражается уравнением 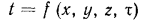 , где, x, у, z — координаты точки, а
, где, x, у, z — координаты точки, а  — время. Если температура во времени не меняется, то поле называется установившимся, или стационарным. Если температура зависит от времени, поле называется неустановившимся, а протекающие в таких условиях тепловые процессы — нестационарными, например нагревание или охлаждение тел.
— время. Если температура во времени не меняется, то поле называется установившимся, или стационарным. Если температура зависит от времени, поле называется неустановившимся, а протекающие в таких условиях тепловые процессы — нестационарными, например нагревание или охлаждение тел.
Температурное поле может быть функцией трех, двух и одной координаты. Соответственно оно называется трех, двух- и одномерным. Наиболее простой вид имеет уравнение одномерного стационарного температурного поля t=f(x). Все точки пространства, имеющие одинаковую температуру, образуют изотермическую поверхность.
Естественно, что изменение температуры в теле может наблюдаться лишь в направлениях, пересекающих изотермические поверхности (например, направление х, (рис. 13.1). При этом наиболее резкое изменение получается в направлении нормали n к изотермическим поверхностям. Предел отношения изменения температуры 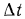 к расстоянию между изотермами по нормали
к расстоянию между изотермами по нормали 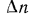 при условии, что
при условии, что 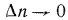 , называется температурным градиентом, т.е.
, называется температурным градиентом, т.е.
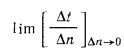
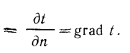
Частная производная применена здесь потому, что в общем случае температура может изменяться не только в пространстве, но и во времени (при нестационарном режиме).
Температурный градиент
Температурный градиент — это вектор с положительным знаком при возрастании температуры и с отрицательным при ее падении. Градиент температуры численно равен производной температуры по нормали.
Количество переносимой теплоты в единицу времени называют тепловым потоком Q, который измеряется вДж/с (Вт). Тепловой поток, отнесенный в единице поверхности тела, называют по верх постной плотностью теплового потока (или просто плотностью теп-
лового потока) q Q/S, которая измеряется в 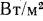
Величина q является вектором, направление которого противоположно направлению градиента температуры, так как тепловая энергия самостоятельно распространяется всегда только в сторону убывания температуры (см. рис. 13.1).
Исследуя явления теплопроводности в твердых телах, Фурье установил, что тепловая мощность, передаваемая теплопроводностью, пропорциональна градиенту температуры и площади сечения, перпендикулярного направлению теплового потока, т. е.
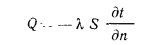
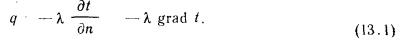
Множитель пропорциональности  , входящий в это уравнение, характеризует способность вещества, из которою состоит рассматриваемое тело, проводить теплоту и называется коэффициентом теплопроводности, или просто теплопроводностью. Из уравнения (13.1), которое является математическим выражением основного закона распространения теплоты путем теплопроводности (закон Фурье), следует, что теплопроводность
, входящий в это уравнение, характеризует способность вещества, из которою состоит рассматриваемое тело, проводить теплоту и называется коэффициентом теплопроводности, или просто теплопроводностью. Из уравнения (13.1), которое является математическим выражением основного закона распространения теплоты путем теплопроводности (закон Фурье), следует, что теплопроводность  ,
, 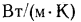 , определяет мощность теплового потока, проходящего через 1
, определяет мощность теплового потока, проходящего через 1 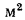 поверхности при градиенте температуры 1 К/м.
поверхности при градиенте температуры 1 К/м.
Возможно эта страница вам будет полезна:
Для различных тел теплопроводность имеет определенное значение и зависит от структуры, плотности, влажности, давления и температуры веществ этих тел. Точные значения  определяют на основе специальных лабораторных опытов. При технических расчетах обычно используют ориентировочные значения теплопроводности
определяют на основе специальных лабораторных опытов. При технических расчетах обычно используют ориентировочные значения теплопроводности  ,
, 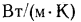

Таким образом, наиболее высокая теплопроводность у металлов, значительно ниже у неметаллических строительных материалов и самые низкие значения у пористых материалов, применяемых специально для тепловой изоляции. У теплоизоляционных материалов 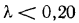 Вт/(м • К) .
Вт/(м • К) .
У большинства металлов с повышением температуры теплопроводность убывает. Содержание примесей в металлах резко снижает их теплопроводность. Например, для стали при 0,1% углерода  =53, а при 1% углерода
=53, а при 1% углерода  = 39
= 39 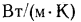 . Для строительных и теплоизоляционных материалов теплопроводность возрастает с увеличением температуры (исключение составляют магнезитовые огнеупоры). Зависимость
. Для строительных и теплоизоляционных материалов теплопроводность возрастает с увеличением температуры (исключение составляют магнезитовые огнеупоры). Зависимость  от температуры для этих материалов может быть выражена равенством
от температуры для этих материалов может быть выражена равенством
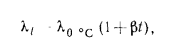
где 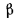 — температурный коэффициент, представляющий собой приращение
— температурный коэффициент, представляющий собой приращение  материала при повышении его температуры на
материала при повышении его температуры на 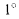 .
.
У различных строительных материалов в интервале температур 0—100° С 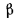 = 0,0025. Для капельных жидкостей с повышением температуры теплопроводность убывает. Исключение составляют лишь вода и глицерин.
= 0,0025. Для капельных жидкостей с повышением температуры теплопроводность убывает. Исключение составляют лишь вода и глицерин.
У газов с повышением температуры теплопроводность возрастает и практически не зависит от давления, за исключением очень высоких (более 200МПа) и очень низких (менее 0,003 МПа) давлений. На теплопроводность влияют общая пористость материала, размер и степень замкнутости пор.
Для пористых материалов теплопроводность находится в обратной зависимости от их общей пористости и в прямой— от размеров пор. Это объясняется увеличением передачи теплоты конвекцией и излучением в общем процессе теплообмена пористого материала и свидетельствует о том, что теплоизоляционные материалы, используемые при высоких температурах, должны иметь мелкопористое строение.
Поры, сообщающиеся между собой и с поверхностью материала, создают более благоприятные условия для увлажнения материала и тем самым для увеличения его теплопроводности, поэтому теплоизоляционные материалы должны иметь по возможности замкнутые поры.
Для пористых материалов  является условной величиной, так как наличие пор в материале не позволяет рассматривать его как сплошное тело. Поэтому
является условной величиной, так как наличие пор в материале не позволяет рассматривать его как сплошное тело. Поэтому  пористых материалов представляет собой теплопроводность некоторого однородного тела, через которое при одинаковых форме, размерах и температурах на границе его поверхности с окружающей средой передаётся та же тепловая мощность, что и через пористое тело.
пористых материалов представляет собой теплопроводность некоторого однородного тела, через которое при одинаковых форме, размерах и температурах на границе его поверхности с окружающей средой передаётся та же тепловая мощность, что и через пористое тело.
Материалы с большей плотностью, как правило, обладают большей теплопроводностью, однако нужно иметь в виду, что теплопроводные свойства материала зависят не только от объема воздуха, заключенного в порах, но главным образом от равномерного распределения воздуха в пористом материале.
С этой точки зрения крупнопористый материал будет менее эффективным теплоизолятором, чем мелкопористый материал с той же плотностью. Среди строительных материалов встречаются такие, которые, имея меньшую плотность, обладают большей теплопро-
водностью, чем материалы с большей плотностью. Примерами могут служить минеральная вата, торфяная крошка, употребляемая в качестве теплоизоляционного сыпучего материала, и др. В частности, у минеральной ваты при плотности около 125 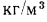 теплопроводность наименьшая.
теплопроводность наименьшая.
При меньшей плотности теплопроводность возрастает в результате увеличения передачи теплоты конвекцией в порах вследствие меньшего уплотнения ваты.
Теплопроводность строительных материалов
Теплопроводность строительных материалов резко возрастает при их увлажнении, гак как значительно отличаются теплопроводности воздуха и воды: теплопроводность воздуха в порах материала 0,025— 0,028, а воды 0,55 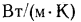 ), т. е. почти в 20 раз больше, чем воздуха. Материал становится еще более теплопроводным, если влага, находящаяся в его порах, замерзает, так как теплопроводность льда равна 2,5
), т. е. почти в 20 раз больше, чем воздуха. Материал становится еще более теплопроводным, если влага, находящаяся в его порах, замерзает, так как теплопроводность льда равна 2,5 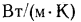 , т. е. примерно в 4 раза выше, чем у воды, и в 80 раз выше, чем у воздуха.
, т. е. примерно в 4 раза выше, чем у воды, и в 80 раз выше, чем у воздуха.
Повышение теплопроводности влажных материалов обусловливается также увеличением контактирующих поверхностей частиц основного вещества материала. Это приводит к тому, что теплопроводность влажного материала значительно выше, чем сухого и воды в отдельности.
Например, для сухого кирпича  равна 0,35, для воды 0,55, а для влажного кирпича 1
равна 0,35, для воды 0,55, а для влажного кирпича 1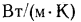 . Поэтому строительные и особенно теплоизоляционные материалы необходимо предохранять от увлажнения, иначе сильно снижаются их теплозащитные свойства.
. Поэтому строительные и особенно теплоизоляционные материалы необходимо предохранять от увлажнения, иначе сильно снижаются их теплозащитные свойства.
Для анизотропных материалов, которые имеют неодинаковую структуру в различных направлениях (древесина, волокнистые и прессованные материалы, кристаллы), теплопроводность зависит от направления теплового потока. Например, у сосновой древесины при направлении теплового потока параллельно направлению волокон  увеличивается вдвое по сравнению с теплопроводностью при направлении теплового потока перпендикулярно волокнам.
увеличивается вдвое по сравнению с теплопроводностью при направлении теплового потока перпендикулярно волокнам.
- Это объясняется тем, что при направлении, перпендикулярном волокнам, тепловому потоку приходится пересекать большое количество воздушных зазоров, находящихся как внутри волокон древесины, так и между ними и оказывающих сопротивление прохождению теплоты. При направлении теплового потока параллельно волокнам влияние воздуха, заключенного в древесине,, будет значительно меньше.
Расчетные формулы при стационарной теплопроводности
Рассмотрим формулы, по которым можно рассчитать количество-теплоты, передаваемой путем теплопроводности через стенки различной конфигурации (плоскую, цилиндрическую; сферическую), и установим для них уравнения температурных полей.
Однородная плоская стенка. Рассмотрим явление теплопроводности в однородной плоской стенке толщиной 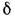 (рис. 13.2). Теплопроводность материала стенки
(рис. 13.2). Теплопроводность материала стенки  , и пусть на поверхностях стенки поддерживаются постоянные температуры
, и пусть на поверхностях стенки поддерживаются постоянные температуры 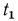 и
и 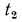 (режим стационарный), причем температурное поле одномерно и меняется только в направлении оси х. Внутренние источники теплоты в стенке отсутствуют. На основа нии уравнения (13.1) для бесконечно тонкого слоя стенки dx взятого на расстоянии от поверхности, будем иметь:
(режим стационарный), причем температурное поле одномерно и меняется только в направлении оси х. Внутренние источники теплоты в стенке отсутствуют. На основа нии уравнения (13.1) для бесконечно тонкого слоя стенки dx взятого на расстоянии от поверхности, будем иметь:
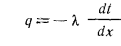 или
или 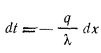 и
и 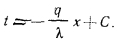
Постоянная интегрирования С определяется из граничных условий: при 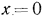
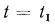 ,
, 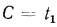 при
при 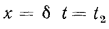
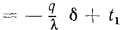 , откуда определяют плотность теплового потока
, откуда определяют плотность теплового потока
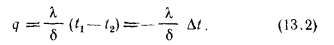
Разность температур 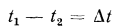 называется температурным напором. Отношение
называется температурным напором. Отношение 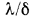
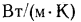 , называется тепловой проводимостью стенки, показывающей, какое количество теплоты проводит 1
, называется тепловой проводимостью стенки, показывающей, какое количество теплоты проводит 1 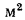 стенки за единицу времени при температурном напоре, равном одному градусу. Обратная величина тепловой проводимости
стенки за единицу времени при температурном напоре, равном одному градусу. Обратная величина тепловой проводимости 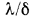
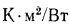 , называется
, называется
термическим сопротивлением стенки, которое определяет падение температуры при прохождении через стенку теплового потока плотностью, равной единице. Подобное название 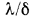 обусловлено тем, что формула (13.2), написанная в виде
обусловлено тем, что формула (13.2), написанная в виде 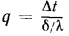 аналогична по форме закону Ома для постоянного тока, и отношение
аналогична по форме закону Ома для постоянного тока, и отношение 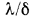 , соответствующее омическому сопротивлению в формуле закона Ома, называют термическим сопротивлением теплопроводности.
, соответствующее омическому сопротивлению в формуле закона Ома, называют термическим сопротивлением теплопроводности.
Если в выражение 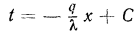 подставить значения
подставить значения 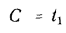 и
и 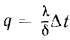 , то получим уравнение температурной кривой
, то получим уравнение температурной кривой

Уравнение (13.3) показывает, что при постоянном значении  внутри однородной плоской стенки температура изменяется по закону прямой линии. В действительности теплопроводность зависит от температуры, поэтому температура изменяется не по прямой, а по кривой.
внутри однородной плоской стенки температура изменяется по закону прямой линии. В действительности теплопроводность зависит от температуры, поэтому температура изменяется не по прямой, а по кривой.
Зная по уравнению (13.2) величину q, легко определить и общее количество теплоты Q, переданное через плоскую стенку с площадью поверхности S в течение времени  :
:

Многослойная плоская стенка. В строительстве наиболее распространенный тип ограждения — многослойные конструкции. Например, стены жилых домов на основном кирпичном слое с одной стороны имеют внутреннюю штукатурку, а с другой — внешнюю облицовку. Обмуровка топок и печей, используемых в промышленности строительных материалов, также обычно состоит из нескольких слоев: слоя огнеупорной кладки, слоя обычного кирпича и слоя тепловой изоляции.
Рассмотрим плоскую стенку, составленную из нескольких например трех, разнородных, плотно прилегающих друг к другу слоев (рис. 13.3). Толщины слоев и соответствующие значения теплопроводности составляют 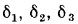 и
и 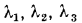 .
.
Кроме того, заданы температуры наружных поверхностей стенки 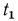 и
и 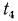 . Соприкасающиеся поверхности слоев имеют температуры
. Соприкасающиеся поверхности слоев имеют температуры 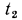 и
и 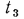 , но значения их неизвестны Поскольку мы рассматриваем стационарный режим, то плотность теплового потока q , проходящего через каждый слой стенки, по величине одинакова. На основании формулы (13.2) для каждого слоя можно написать:
, но значения их неизвестны Поскольку мы рассматриваем стационарный режим, то плотность теплового потока q , проходящего через каждый слой стенки, по величине одинакова. На основании формулы (13.2) для каждого слоя можно написать:
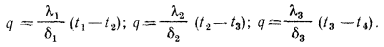
Исходя из написанных уравнений, находим изменения температуры в каждом слое и, складывая их, получим температурный напор 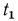 —
— 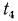 =
= 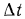 т. е.
т. е.
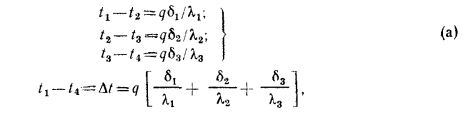
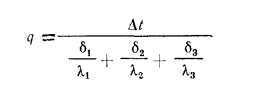
По аналогии для n-слойной стенки расчетную формулу можно написать так:

Из полученного уравнения следует, что общее термическое сопротивление многослойной стенки равно сумме частных термических сопротивлений.
Если значение теплового потока, определенного по формуле (13.5), подставить в равенство (а), можно найти неизвестные температуры 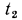 и
и 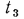 :
:
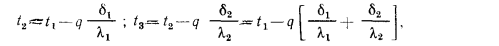
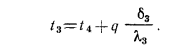
Внутри каждого слоя температура изменяется по закону прямой линии (при  = const), а для многослойной стенки она представляет собой ломаную линию (см. рис. 13.3), так как каждый слой стенки имеет свое значение
= const), а для многослойной стенки она представляет собой ломаную линию (см. рис. 13.3), так как каждый слой стенки имеет свое значение  .
.
Возможно эта страница вам будет полезна:
В некоторых случаях многослойную стенку рассчитывают как однослойную однородную стенку с такой же толщиной  , т.е.
, т.е. 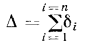 .
.
При этом в расчет вводится так называемая эквивалентная теплопроводность 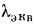 , определяемая из соотношения
, определяемая из соотношения
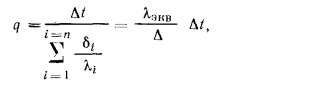

Однослойная цилиндрическая стенка
Рассмотрим однородную цилиндрическую стенку (трубу) длиной l с внутренним диаметром 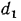 и наружным
и наружным 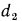 . Теплопроводность материала имеет постоянное значение и равна
. Теплопроводность материала имеет постоянное значение и равна  . На внутренней и наружной поверхностях трубы поддерживаются постоянные температуры
. На внутренней и наружной поверхностях трубы поддерживаются постоянные температуры 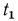 и
и 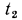 (рис. 13.4), причем
(рис. 13.4), причем 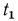
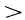
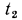 . Температурное поле считаем одномерным, т. е. температура меняется только в радиальном направлении. В этом случае изотермические поверхности будут представлять собой цилиндрические поверхности, имеющие общую ось с трубой. Внутри рассматриваемой стенки выделим кольцевой слой радиусом r и толщиной dr. Тогда, по закону Фурье, количество теплоты, проходящей через этот слой за единицу времени,
. Температурное поле считаем одномерным, т. е. температура меняется только в радиальном направлении. В этом случае изотермические поверхности будут представлять собой цилиндрические поверхности, имеющие общую ось с трубой. Внутри рассматриваемой стенки выделим кольцевой слой радиусом r и толщиной dr. Тогда, по закону Фурье, количество теплоты, проходящей через этот слой за единицу времени,
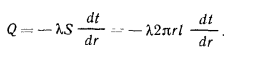
Разделяя переменные и интегрируя, получим:
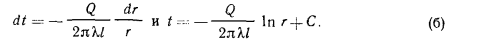
Используя граничные условия, находим: при 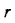
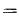
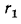
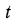
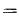
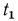 и при
и при 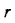
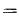
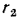
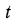
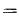
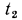 .
.
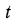
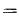
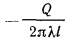
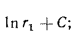
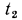
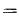
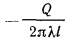
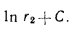
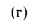
Вычитая из равенства (в) равенство (г), получим:
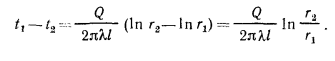
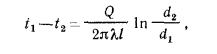

Полученное уравнение является расчетной формулой теплопроводности цилиндрической стенки. Оно будет справедливо и при 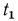
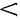
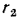 , т. е, когда тепловой поток направлен от наружной поверхности к внутренней.
, т. е, когда тепловой поток направлен от наружной поверхности к внутренней.
Для определения закона изменения температуры по толщине цилиндрической стенки подставим в равенство 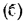 значения С из равенства (в) и Q из уравнения (13.7):
значения С из равенства (в) и Q из уравнения (13.7):
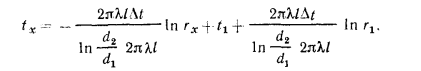
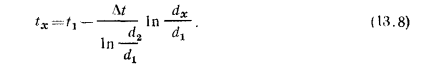
Равенство (13.8) представляет собой уравнение логарифмической кривой. При 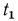
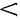
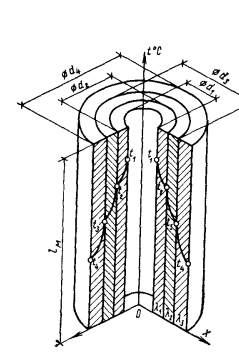 Рис. 13.5. Многослойная цилиндрическая стенка
Рис. 13.5. Многослойная цилиндрическая стенка
Плотность теплового потока для цилиндрической стенки может быть отнесена к единице внутренней поверхности 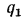 или к единице наружной поверхности
или к единице наружной поверхности 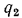 либо чаще всего к 1 пог. м длины трубы
либо чаще всего к 1 пог. м длины трубы 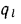 . В последнем случае
. В последнем случае
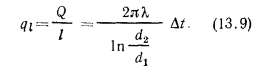
Соотношения между 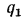
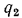 и
и 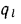 получают из равенства
получают из равенства
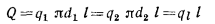
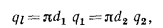
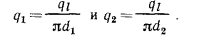
Величину 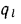 , Вт/м, называют линейной плотностью теплового потока.
, Вт/м, называют линейной плотностью теплового потока.
Факторы, влияющие на процесс теплоотдачи
Процесс теплообмена между жидкостью и стенкой, которую эта жидкость омывает, называется конвективным теплообменом, или процессом теплоотдачи. В этом процессе теплота передается одновременно путем теплопроводности и конвекции, и поэтому такой вид теплообмена представляет собой сложный процесс, зависящий от большего числа факторов по сравнению с процессом чистой теплопроводности.
- Конвективный теплообмен характерен для большинства процессов тепловой обработки строительных материалов и изделий, связанных с прохождением газов через слой материала, через садку изделий, над уровнями жидкостей при сушке и т. д.
Факторы, влияющие на процесс теплоотдачи, условно можно разделить на следующие группы.
I. Природа возникновения движения жидкости вдоль стенки.В зависимости от причины, вызывающей движение жидкости, различают два вида движения — свободное и вынужденное. Свободное движение, называемое иначе естественной конвекцией, вызывается подъемной силой, обусловленной разностью плотностей холодных и нагретых частиц жидкости. Интенсивность свободного движения зависит от вида жидкости, разности температур между отдельными ее частицами и объема пространства, в котором протекает процесс.
Вынужденное движение жидкости, или вынужденная конвекция, обусловлено работой внешних агрегатов (насоса, вентилятора и т. п.). Движущая сила при этом виде движения возникает вследствие разности давлений, устанавливающихся на входе и выходе из канала, по которому перемещается жидкость. Если скорость вынужденного движения небольшая и есть разница температур между отдельными частицами жидкости, то наряду с вынужденным движением может наблюдаться и свободное движение.
II. Режим движения жидкости. Движение жидкости может иметь ламинарный или турбулентный характер. В первом случае частицы жидкости в форме отдельных несмешивающихся струй следуют очертаниям канала или стенки и профиль скоростей на достаточном удалении от начала трубы имеет вид правильной параболы. Подобное распределение установившихся скоростей обусловливается наличием сил внутреннего трения (вязкости) между частицами жидкости. При этом максимальная скорость движения частиц жидкости, перемещающейся по оси трубы, в 2 раза больше средней скорости их движения, получаемой в результате деления секундного объема жидкости на площадь поперечного сечения трубы (рис. 14.1, а).
Турбулентный режим движения характеризуется непостоянством скорости движения частиц жидкости в рассматриваемой точке пространства. Из-за непрерывного перемешивания жидкости в ней нельзя выделить отдельные струи, и такое движение лишь условно можно назвать стационарным, считая для каждой частицы жидкости характерными не мгновенные, а усредненные за некоторый промежуток времени значения скорости. В этом случае профиль скоростей по сечению трубы будет иметь вид усеченной параболы и максимальная скорость, наблюдаемая у частиц жидкости, движущихся по оси трубы, будет всего в 1,2— 1,3 раза больше средней скорости. Характерно, что не все частицы жидкости при турбулентном режиме имеют неупорядоченное движение. Вблизи стенок, ограничивающих потоки, вследствие вязкости жидкости пульсации скорости уменьшаются, и около самой стенки сохраняется тонкий пограничный слой, движущийся ламинарно. В пределах этого слоя, который имеет толщину не более нескольких тысячных долей диаметра трубы, скорость движения частиц жидкости резко меняется от нуля на самой стенке до 0,4—0,7 средней скорости на условной границе с турбулентным ядром потока (рис. 14.1, б).
Строго говоря, турбулентные пульсации проникают и в ламинарный подслой и затухают в нем вследствие действия сил вязкости. Поэтому термин «ламинарный подслой» правильнее заменять термином «вязкий подслой».
Английский физик Рейнольдс установил, что при движении жидкости в трубах переход из ламинарного режима в турбулентный определяется значением безразмерного комплекса 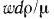 , в который входят средняя скорость w, диаметр трубы d*, плотность
, в который входят средняя скорость w, диаметр трубы d*, плотность 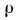 и динамическая вязкость жидкости
и динамическая вязкость жидкости 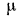 . Этот комплекс называют числом Рейнольдса и обозначают символом Re. При
. Этот комплекс называют числом Рейнольдса и обозначают символом Re. При 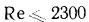 движение жидкости в трубах имеет ламинарный характер, а при
движение жидкости в трубах имеет ламинарный характер, а при 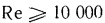 — турбулентный, т е. критическая скорость, позволяющая определить переход любой жидкости из ламинарного режима в турбулентный для трубы любого диаметра, может быть найдена из соотношения
— турбулентный, т е. критическая скорость, позволяющая определить переход любой жидкости из ламинарного режима в турбулентный для трубы любого диаметра, может быть найдена из соотношения 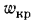
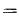
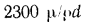 .
.
Следует также отметить, что наряду с описанным процессом формирования гидродинамического пограничного слоя происходит аналогичный процесс формирования и теплового пограничного слоя, в пределах
которого температура меняется от 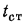 до
до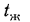 . Характер распределения температуры в тепловом пограничном слое зависит от режима течения жидкости в динамическом пограничном слое.
. Характер распределения температуры в тепловом пограничном слое зависит от режима течения жидкости в динамическом пограничном слое.
При ламинарном течении перенос теплоты между слоями жидкости осуществляется путем теплопроводности. В турбулентном пограничном слое основное изменение температуры происходит в пределах тонкого вязкого подслоя около стенки, через который теплота также передается путем теплопроводности.
В турбулентном ядре пограничного слоя вследствие интенсивного перемешивания жидкости температура изменяется незначительно (см. рис. 14.2, б) и поле температур имеет ровный пологий характер, т. е. отмечается качественное сходство в пограничном слое между распределением температур и скоростей.
III. Физические свойства жидкостей. На процесс теплоотдачи непосредственно влияют следующие физические параметры жидкостей: теплопроводность  , удельная теплоемкость с,
, удельная теплоемкость с,
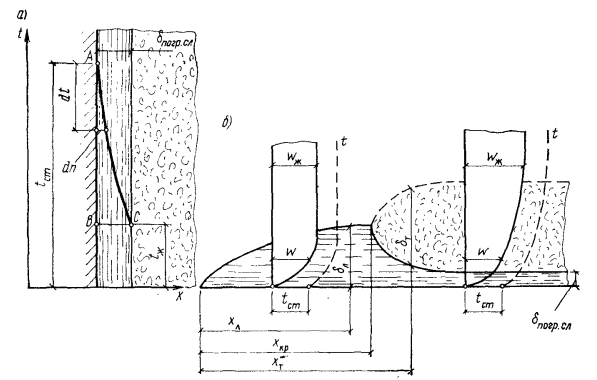 Рис. 14.2. Характер изменения температуры в пограничном слое (а) и скорости в тепловом и динамическом пограничных слоях (б)
Рис. 14.2. Характер изменения температуры в пограничном слое (а) и скорости в тепловом и динамическом пограничных слоях (б)
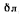 ,
,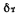 — толщина пограничного слоя соответственно ламинарного и турбулентного
— толщина пограничного слоя соответственно ламинарного и турбулентного
плотность р, а также вязкость и температуропроводность. Известно, что все жидкости обладают вязкостью, т. е. между отдельными частицами или слоями, перемещающимися с различными скоростями, всегда возникает сила внутреннего трения, противодействующая движению. По закону Ньютона, эта сила F, отнесенная к единице поверхности, пропорциональна градиенту скорости 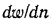 , т. е. F =
, т. е. F = 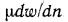 .
.
Коэффициент пропорциональности jx в этом уравнении называется коэффициентом . внутреннего трения или динамической вязкостью. При 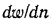 =1.
=1.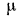 = F, т. е. динамическая вязкость численно равна силе трения, приходящейся на единицу поверхности соприкосновения двух слоев жидкости, скользящих один по другому, при условии, что на единицу длины нормали к поверхности скольжения скорость движения изменяется на единицу .Отношение
= F, т. е. динамическая вязкость численно равна силе трения, приходящейся на единицу поверхности соприкосновения двух слоев жидкости, скользящих один по другому, при условии, что на единицу длины нормали к поверхности скольжения скорость движения изменяется на единицу .Отношение 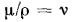 называется кинематической вязкостью. Если в комплексе
называется кинематической вязкостью. Если в комплексе 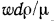 заменить отношение
заменить отношение 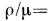
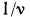 то число Рейнольдса принимает вид
то число Рейнольдса принимает вид 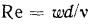 .
.
- Понятие температуропроводности тел связано с протеканием в них нестационарных тепловых процессов, наблюдаемых обычно при нагревании или охлаждении.
Скорость теплового процесса при нестационарном режиме определяется отношением 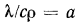 , которое называется температуропроводностью. Температуропроводность характеризует скорость выравнивания температуры в различных точках тела. Чем больше величина а, тем быстрее все точки какого-либо тела при его остывании или нагревании достигнут одинаковой температуры.
, которое называется температуропроводностью. Температуропроводность характеризует скорость выравнивания температуры в различных точках тела. Чем больше величина а, тем быстрее все точки какого-либо тела при его остывании или нагревании достигнут одинаковой температуры.
Единицей измерения динамической (абсолютной) вязкости 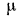 . служит
. служит 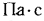 , а единицей измерения v и а —
, а единицей измерения v и а — 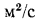 .
.
В настоящее время опытное определение коэффициента теплоотдачи производится, как правило, не на самих образцах тепловых устройств, а на их упрощенных моделях, более удобных для экспериментирования.
Результаты опытов, проведенных на моделях, обобщают, используя тепловую теорию подобия. Основной вывод, который делают на основе этой теории, заключается в том, что нет необходимости искать зависимость коэффициента теплоотдачи от каждого из тех факторов, которые на него влияют, а достаточно найти зависимость между определенными безразмерными комплексами величин, характерных для рассматриваемых условий процесса теплоотдачи.
Эти безразмерные комплексы величин называют критериями подобия. Составленные из размерных величин критерии подобия отражают физическую сущность, или, как говорят, модель процесса. Следовательно, задача заключается в том, чтобы найти вид зависимостей между критериями подобия, называемых критериальными уравнениями.
Теория из учебников тут.
Составляют критерии подобия с помощью дифференциальных уравнений конвективного теплообмена, т. е. уравнений, которые дают аналитическую зависимость между параметрами, характеризующими процесс теплоотдачи в дифференциальной форме.






















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
источники:
http://spadilo.ru/fazovye-perexody-i-uravnenie-teplovogo-balansa/
http://lfirmal.com/predmet-teplotekhnika/
| Устройство | Полезная энергия (работа), затраченная энергия (полная работа) | КПД |
| Электронагреватель, электроплитка, электрочайник, кипятильник. | ||
| Газовая горелка, паровая турбина, спиртовка, плавильная печь. | ||
| Двигатель автомобиля, самолета. | ||
| Ружье с пороховым зарядом, пушка |
Пособие рекомендовано учащимся, желающим
получить практические навыки в решении задач на
теплообмен, и может быть полезным для учителей и
абитуриентов.
При соприкосновении тел, имеющих разные
температуры, между этими телами происходит
теплообмен. С точки зрения
молекулярно-кинетической теории, это
объясняется так: молекулы более нагретого тела
имеют большую кинетическую энергию, чем молекулы
тела, менее нагретого. При “столкновениях”
молекул соприкасающихся тел происходит процесс
выравнивания их средних кинетических энергий.
Молекулы более нагретого тела теряют часть своей
кинетической энергии, при этом нагретое тело
будет остывать. Кинетическая энергия молекул
холодного тела возрастает, поэтому температура
этого тела будет увеличиваться. В конечном итоге
кинетические энергии молекул обоих тел
сравняются, и температуры тел станут
одинаковыми. На этом теплообмен прекращается.
Энергию, которую тело получает или отдаёт в
процессе теплообмена, называют количеством
теплоты (Q).
Количество теплоты, как и все другие виды
энергии, измеряется в системе СИ в Джоулях: [Q] = Дж.
(Здесь и в дальнейшем единицы измеряются в
системе СИ.)
Нагревание или охлаждение
При нагревании или охлаждении тела количество
теплоты, поглощаемое или выделяемое им,
рассчитывается по формуле:
Q = сm(t2 – t1), (1)
где m – масса тела, кг;
(t2 – t1) – разность температур
тела,° С (или К);
с – удельная теплоёмкость вещества, из
которого состоит тело,
Удельная теплоёмкость вещества – это
количество теплоты, которое нужно сообщить
одному килограмму данного вещества, чтобы
увеличить его температуру на 1° С (или это
количество теплоты, которое выделяет один
килограмм данного вещества, остывая на 1° С).
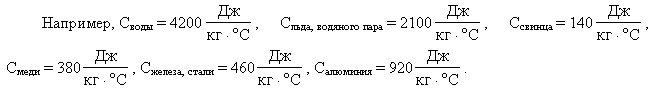
Значения удельных теплоемкостей других
веществ можно найти в справочниках, а также в
школьном учебнике или задачнике.
При нагревании тела его внутренняя энергия
увеличивается. Это требует притока энергии к
телу от других тел. Значит, оно поглощает
некоторое количество теплоты, принимая его от
других тел, участвующих в теплообмене.
При охлаждении тела его внутренняя энергия
уменьшается. Поэтому остывающее тело отдаёт
кому-либо некоторое количество теплоты.
Обычно конечную температуру, установившуюся в
результате теплообмена, обозначают греческой
буквой ![]() (тэта).
(тэта).
В формуле (1) произведение cm для каждого
конкретного тела есть величина постоянная. Её
называют теплоёмкостью тела и обозначают С:
C = c m.(2)
Размерность теплоемкости: ![]() Теплоемкость тела показывает,
Теплоемкость тела показывает,
сколько энергии нужно подвести к данному телу,
чтобы нагреть его на 1° С (или сколько энергии
выделяет это тело, остывая на 1° С).
Теплообмен между телами, имеющими одинаковые
температуры, не происходит, даже если
контактируют вещества, находящиеся в разных
агрегатных состояниях. Например, при температуре
плавления (0° С) лёд и вода могут находиться
бесконечно долго, при этом количество льда и
количество воды останутся неизменными.
Аналогично ведут себя пар и жидкость,
находящиеся при температуре кипения. Теплообмен
между ними не происходит.
Плавление или кристаллизация
Если при нагревании тела его температура
достигнет температуры плавления, то начинает
происходить процесс перехода этого вещества из
твердого состояния в жидкое. При этом идут
изменения в расположении и характере
взаимодействия молекул. Температура при
плавлении не изменяется. Это означает, что
средние кинетические энергии молекул жидкости и
твердого тела при температуре плавления
одинаковы. Однако внутренняя энергия тела при
плавлении возрастает за счет увеличения энергии
взаимодействия молекул. Количество теплоты,
поглощаемое телом при плавлении, рассчитывается
по формуле
![]() (3)
(3)
где m – масса тела, кг;
![]() –
–
удельная теплота плавления, ![]()
При кристаллизации, наоборот, внутренняя
энергия тела уменьшается на величину ![]() и эта теплота данным
и эта теплота данным
телом выделяется. Она поглощается другими
телами, участвующими в теплообмене.
Удельная теплота плавления показывает,
сколько энергии нужно сообщить одному
килограмму данного вещества, взятого при
температуре плавления, чтобы полностью
превратить его при этой температуре в жидкость
(или сколько энергии выделяет 1 кг жидкости,
взятой при температуре кристаллизации, если вся
она при этой температуре полностью превратится в
твёрдое тело).
Удельную теплоту плавления любого вещества
можно найти в справочниках. Для льда же ![]()
Температура плавления у каждого вещества своя.
Её также можно найти в справочниках. Важно
подчеркнуть, что температура плавления вещества
равна температуре кристаллизации этого же
вещества. У льда tпл = 0° С.
Кипение или конденсация
При достижении жидкостью температуры кипения
начинает происходить другой фазовый переход –
кипение, при котором расстояния между молекулами
значительно увеличиваются, а силы
взаимодействия молекул уменьшаются. Вся
подводимая к жидкости теплота идет на разрыв
связей между молекулами. При конденсации пара в
жидкость, наоборот, расстояния между молекулами
значительно сокращаются, а силы взаимодействия
молекул увеличиваются. Для кипения жидкости
энергию к жидкости нужно подводить, при
конденсации пара энергия выделяется. Количество
теплоты, поглощаемое при кипении или выделяемое
при конденсации, рассчитывается по формуле:
![]()
где m – масса тела, кг; L – удельная
теплота парообразования, ![]()
Удельная теплота парообразования
показывает, сколько энергии нужно сообщить
одному килограмму жидкости, взятой при
температуре кипения, чтобы при этой температуре
полностью превратить её в пар (для конденсации:
сколько энергии выделяет один килограмм пара,
взятого при температуре конденсации, полностью
превращаясь в жидкость).
При одинаковом давлении температура кипения и
температура конденсации одного и того же
вещества одинаковы.
Температуры кипения и удельные теплоты
парообразования также можно найти в
справочниках. Для воды же они соответственно
равны: рис. 9 (при нормальном атмосферном
давлении).
Уравнение теплового баланса
Тела, участвующие в теплообмене, представляют
собой термодинамическую систему.
Термодинамическая система называется теплоизолированной,
если она не получает энергию извне и не отдаёт её;
теплообмен происходит только между телами,
входящими в эту систему. Для любой
теплоизолированной системы тел справедливо
следующее утверждение: количество теплоты,
отданное одними телами, равно количеству
теплоты, принимаемому другими телами.
Qотд. = Qполуч. (5)
Это утверждение описывает частный случай
закона сохранения и превращения энергии в
применении к процессу теплообмена. А формула (5)
является одним из видов уравнения теплового
баланса.
При решении задач с помощью данного вида
уравнения теплового баланса в формуле (1) в
качестве t2 следует брать большую
температуру, а в качестве t1 – меньшую.
Тогда разность (t2 – t1) будет
положительна и всё произведение cm(t2–t1)
также будет положительным. Все теплоты, отданные
и полученные, будут положительными.
Уравнение теплового баланса можно записать и в
таком виде:
Q1+ Q2+…+ Qn= 0, (6)
где n – количество тел системы.
Алгебраическая сумма всех количеств теплоты
(поглощенных и выделенных) в теплоизолированной
системе равна нулю.
Q1, Q2, …, Qn – это теплоты,
поглощаемые или выделяемые участниками
теплообмена. Очевидно, что в этом случае какие-то
теплоты должны быть положительны, а какие-то –
отрицательны. При записи уравнения теплового
баланса в виде (6) всегда t2 – конечная
температура, а t1 – начальная.
Если тело нагревается, то разность (t2 – t1)
положительна и все произведение cm(t2 – t1)
положительно. То есть Q > 0 тогда, когда теплота к
данному телу подводится.
А если t2 < t1 (тело остывает), то
разность (t2 – t1) отрицательна, то есть
Q < 0. В этом случае тело энергию выделяет.
Если при фазовом переходе энергия к телу
подводится (плавление, кипение), то Q > 0; если
тело выделяет энергию (кристаллизация,
конденсация), то Q < 0.
В принципе уравнения (5) и (6) равносильны.
Результат решения задачи не зависит от того,
каким видом уравнения пользуемся. Выбор способа
решения – за читателем.
Применим уравнение теплового баланса для
решения ряда задач (здесь приводим лишь одну
задачу, остальные материалы можно найти по
адресу http:// kirov-festival.nm.ru).
Задача 1
В медном калориметре массой 100 г находится 1 кг
воды при температуре 20° С. В воду опускают
свинцовую деталь массой 2 кг, имеющую температуру
90° С. До какой температуры нагреется вода? (В этой
и последующих задачах потерями теплоты в
калориметре пренебречь.)
Решение
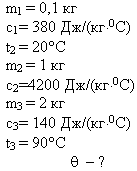 |
Проведём анализ:
Вода и калориметр При опускании в воду с температурой 20° С |
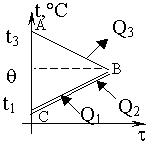 |
Изменение температур тел с течением времени удобно изображать на графике зависимости t(t ). Отрезок АВ соответствует |
| Два параллельных отрезка СВ соответствуют графикам изменения температур калориметра и воды. Стрелки, идущие к ним, показывают, что для нагревания калориметра и воды требуется энергия Q1 и Q2, которую они поглощают. |
|
| Решим задачу с использованием уравнения теплового баланса в виде (5):
|
Решим задачу с использованием уравнения
теплового баланса в виде (6):
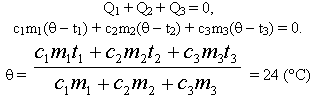
Ответ: Вода нагреется до 24° С.
Предлагаю читателю самостоятельно сделать
проверку размерности.
Напомним, остальной материал (полноценную
версию пособия) можно найти по адресу http:// kirov-festival.nm.ru.