Физика как найти кпд цикла

Полное условие задачи

Найдите КПД цикла, изображенного на рисунке для идеального одноатомного газа.

Краткое условие задачи

Решение задачи

КПД цикла находим по формуле:

где работа определяется как площадь прямоугольника 1234:

Для определения затраченного количества теплоты нужно выяснить, в каких процессах газ получал теплоту. Для этого воспользуемся первым законом термодинамики, формулой для изменения внутренней энергии и уравнением состояния идеального газа:

Рассмотрим каждый процесс по отдельности.

В процессе 1 – 2 начальная температура меньше конечной:

поэтому изменение внутренней энергии больше нуля:

а работа равна нулю, поскольку процесс изохорный:

Отсюда следует, что газ в процессе 1 – 2 получал тепло:

Найдем это тепло:

Разность температур найдем используя уравнение состояния идеального газа. Запишем его для состояния 1 и для состояния 2:

Вычитаем из второго уравнения первое и находим разность температур:

Подставим в формулу для теплоты:

В процессе 2 – 3 начальная температура также меньше конечной:

поэтому изменение внутренней энергии также больше нуля:

а работа в этом процессе больше нуля (газ совершает работу):

поскольку объем увеличивается:

Отсюда следует, что газ в процессе 2 – 3 тоже получал тепло:

Найдем это тепло:

Разность температур найдем используя уравнение состояния идеального газа. Запишем его для состояния 2 и для состояния 3:

Вычитаем из второго уравнения первое и находим разность температур:

Подставим в формулу для теплоты:

В процессе 3 – 4 начальная температура больше конечной:

поэтому изменение внутренней энергии меньше нуля:

а работа равна нулю, поскольку процесс изохорный:

Отсюда следует, что газ в процессе 3 – 4 отдает тепло:

В процессе 4 – 1 начальная температура также больше конечной:

поэтому изменение внутренней энергии также меньше нуля:

работа в этом процессе тоже меньше нуля (над газом совершают работу):

поскольку объем уменьшается:

Отсюда следует, что газ в процессе 4 – 1 тоже отдает тепло:

Таким образом затраченная теплота равна:

Искомый КПД равен:

Или

Ответ: 17 %.

Речь в статье пойдет о КПД различных циклов, проводимых с газом. При этом давайте помнить, что внутренняя энергия изменяется тогда, когда изменяется температура, а в адиабатном процессе передачи тепла не происходит, то есть для совершения работы в таком процессе газ “изыскивает внутренние резервы”. Кроме того, работа численно равна площади под кривой процесса, а работа за цикл – площади внутри цикла.

Задача 1.

На рисунке представлена диаграмма цикла с одноатомным идеальным газом. Участки и – адиабаты.  Вычислите КПД данной тепловой машины и максимально возможный КПД .

КПД тепловой машины можно вычислить как

Машина получает тепло только на участке AB, и, так как работы здесь не совершается, то можно вычислить количество теплоты, полученное газом, как увеличение его внутренней энергии:

Работа численно равна площади, ограниченной циклом. Поэтому

Участк и по условию – адиабаты, то есть передачи тепла газу на этих участках не происходит, следовательно, работа будет совершена за счет «внутренних резервов» – то есть внутренней энергии. Нужно, следовательно, найти, как она изменилась.

Задачу можно решить двумя способами. Во-первых, просто определить температуры в точках и , и , это легко сделать из данных графика с помощью уравнения Менделеева-Клапейрона, и затем посчитать . Но, так как , а ,то изменение внутренней энергии будет равно

Определим максимальный КПД. Посчитаем его как КПД цикла Карно. Максимальная температура газа будет достигнута в точке , а минимальная – в точке :

Ответ: , .

Задача 2.

Над идеальным одноатомным газом проводят цикл, включающий изобару, изохору, изотерму, при этом работа газа за цикл равна кДж.  В процессе изотермического сжатия (3-1) внешние силы совершают над газом положительную работу кДж. Найдите КПД данной тепловой машины.

Работа газа в процессе 1-2– площадь под линией процесса 1-2. Работа внешних сил – площадь под циклом (под линией 3-1). Поэтому полная работа за цикл – это разность работы газа и работы внешних сил, площадь, ограниченная линиями цикла. Она будет равна 5 кДж.

Работа газа в процессе 1-2, таким образом, равна 8 кДж. А поскольку процесс изобарный, то кДж. Тогда КПД

Ответ: .

Задача 3.

КПД  тепловой машины, работающей по циклу, включающему изотермический (1-2) и адиабатный (3-1) процессы, равен , причем работа, совершенная 2 моль одноатомного идеального газа в изотермическом процессе кДж. Найдите разность максимальной и минимальной  температур  газа в цикле.

Полная площадь под кривой процесса 1-2 равна кДж. При этом, так как КПД машины 25%, то площадь внутри цикла равна , а под кривой 3-1  – .  В процессе 1-2 изменения внутренней энергии не было, так как температура не менялась, а в процессе 3-1 газу не передавали тепло, следовательно, работа совершена за счет внутренней энергии. Т.е.

Ответ: 500 K.

У нас уже была внутренняя энергия и первое начало термодинамики, а сегодня разберемся с задачами на КПД теплового двигателя. Что поделать: праздники праздниками, но сессию ведь никто не отменял.

Присоединяйтесь к нам в телеграме и получайте полезную рассылку каждый день. А приступая к практике, не забывайте держать под рукой памятку по задачам и полезные формулы.

Задачи по физике на КПД теплового двигателя

Задача на вычисление КПД теплового двигателя №1

Условие 

Вода массой 175 г подогревается на спиртовке. Пока вода нагрелась от t1=15 до t2=75 градусов Цельсия, масса спиртовки уменьшилась с 163 до 157 г Вычислите КПД установки.

Решение

Коэффициент полезного действия можно вычислить как отношение полезной работы и полного количества теплоты, выделенного спиртовкой:

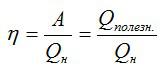
Полезная работа в данном случае – это эквивалент количества теплоты, которое пошло исключительно на нагрев. Его можно вычислить по известной формуле:

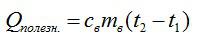
Полное количество теплоты вычисляем, зная массу сгоревшего спирта и его удельную теплоту сгорания.

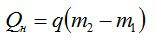
Подставляем значения и вычисляем:

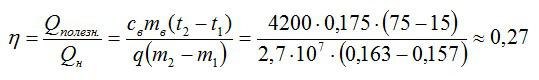
Ответ: 27%

Задача на вычисление КПД теплового двигателя №2

Условие

Старый двигатель совершил работу 220,8 МДж, при этом израсходовав 16 килограмм бензина. Вычислите КПД двигателя.

Решение

Найдем общее количество теплоты, которое произвел двигатель:

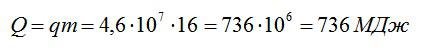
Теперь можно рассчитать КПД:

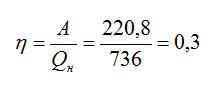
Или, умножая на 100, получаем значение КПД в процентах:

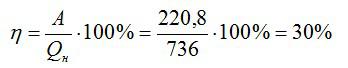
Ответ: 30%.

Задача на вычисление КПД теплового двигателя №3

Условие

Тепловая машина работает по циклу Карно, при этом 80% теплоты, полученной от нагревателя, передается холодильнику. За один цикл рабочее тело получает от нагревателя 6,3 Дж теплоты. Найдите работу и КПД цикла.

Решение

КПД идеальной тепловой машины:

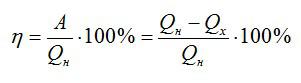
По условию:

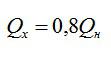
Вычислим сначала работу, а затем КПД:

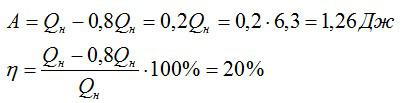
Ответ: 20%; 1,26 Дж.

Задача на вычисление КПД теплового двигателя №4

Условие

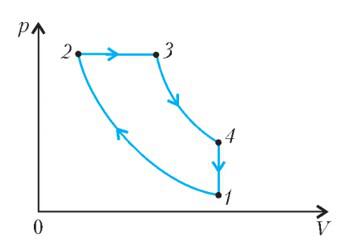
На диаграмме изображен цикл дизельного двигателя, состоящий из адиабат 1–2 и 3–4, изобары 2–3 и изохоры 4–1. Температуры газа в точках 1, 2, 3, 4 равны T1 , T2 , T3 , T4 соответственно. Найдите КПД цикла.

Решение

Проанализируем цикл, а КПД будем вычислять через подведенное и отведенное количество теплоты. На адиабатах тепло не подводится и не отводится. На изобаре 2 – 3 тепло подводится, объем растет и, соответственно, растет температура. На изохоре 4 – 1 тепло отводится, а давление и температура падают.

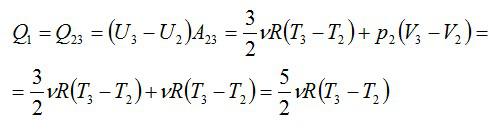
Аналогично:

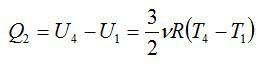
Получим результат:

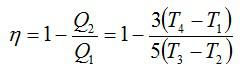
Ответ: См. выше.

Задача на вычисление КПД теплового двигателя №5

Условие

Тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 2,94 кДж и отдаёт за один цикл охладителю количество теплоты Q2 = 13,4 кДж. Найдите КПД цикла.

Решение

Запишем формулу для КПД:

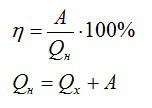
Отсюда:

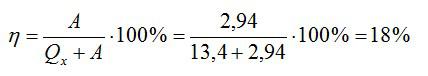
Ответ: 18%

Вопросы на тему тепловые двигатели

Вопрос 1. Что такое тепловой двигатель?

Ответ. Тепловой двигатель – это машина, которая совершает работу за счет энергии, поступающей к ней в процессе теплопередачи. Основные части теплового двигателя: нагреватель, холодильник и рабочее тело.

Вопрос 2. Приведите примеры тепловых двигателей.

Ответ. Первыми тепловыми двигателями, получившими широкое распространение, были паровые машины. Примерами современного теплового двигателя могут служить:

• ракетный двигатель;
• авиационный двигатель;
• газовая турбина.

Вопрос 3. Может ли КПД двигателя быть равен единице?

Ответ. Нет. КПД всегда меньше единицы (или меньше 100%). Существование двигателя с КПД равным единице противоречит первому началу термодинамики.

КПД реальных двигателей редко превышает 30%.

Вопрос 4. Что такое КПД?

Ответ. КПД (коэффициент полезного действия) – отношение работы, которую совершает двигатель, к количеству теплоты, полученному от нагревателя.

Вопрос 5. Что такое удельная теплота сгорания топлива?

Ответ. Удельная теплота сгорания q – физическая величина, которая показывает, какое количество теплоты выделяется при сгорании топлива массой 1 кг. При решении задач КПД можно определять по мощности двигателя N и сжигаемому за единицу времени количеству топлива.

Задачи и вопросы на цикл Карно

Затрагивая тему тепловых двигателей, невозможно оставить в стороне цикл Карно – пожалуй, самый знаменитый цикл работы тепловой машины в физике. Приведем дополнительно несколько задач и вопросов на цикл Карно с решением.

Цикл (или процесс) Карно – это идеальный круговой цикл, состоящий из двух адиабат и двух изотерм. Назван так в честь французского инженера Сади Карно, который описал данный цикл в своем научном труде «О движущей силе огня и о машинах, способных развивать эту силу» (1894).

Задача на цикл Карно №1

Условие

Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 73,5 кДж. Температура нагревателя t1 =100° С, температура холодильника t2 = 0° С. Найти КПД цикла, количество теплоты, получаемое машиной за один цикл от нагревателя, и количество теплоты, отдаваемое за один цикл холодильнику.

Решение

Рассчитаем КПД цикла: 

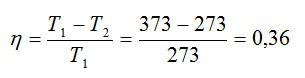
С другой стороны, чтобы найти количество теплоты, получаемое машиной, используем соотношение:

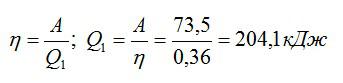
Количество теплоты, отданное холодильнику, будет равно разности общего количества теплоты и полезной работы:

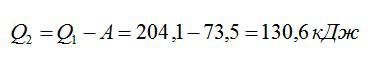
Ответ: 0,36; 204,1 кДж; 130,6 кДж.

Задача на цикл Карно №2

Условие

Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А=2,94 кДж и отдает за один цикл холодильнику количество теплоты Q2=13,4 кДж. Найти КПД цикла.

Решение

Формула для КПД цикла Карно:

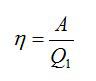
Здесь A – совершенная работа, а Q1 – количество теплоты, которое понадобилось, чтобы ее совершить. Количество теплоты, которое идеальная машина отдает холодильнику, равно разности двух этих величин. Зная это, найдем:

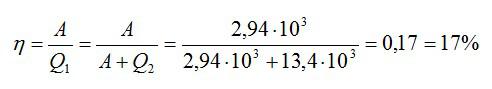
Ответ: 17%.

Задача на цикл Карно №3

Условие

Изобразите цикл Карно на диаграмме и опишите его

Решение

Цикл Карно на диаграмме PV выглядит следующим образом:

• 1-2. Изотермическое расширение, рабочее тело получает от нагревателя количество теплоты q1;
• 2-3. Адиабатическое расширение, тепло не подводится;
• 3-4. Изотермическое сжатие, в ходе которого тепло передается холодильнику;
• 4-1. Адиабатическое сжатие.

Ответ: см. выше.

Вопрос на цикл Карно №1

Сформулируйте первую теорему Карно

Ответ. Первая теорема Карно гласит: КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела.

Вопрос на цикл Карно №2

Может ли коэффициент полезного действия в цикле Карно быть равным 100%?

Ответ. Нет. КПД цикла карно будет равен 100% только в случае, если температура холодильника будет равна абсолютному нулю, а это невозможно.

Если у вас остались вопросы по теме тепловых двигателей и цикла Карно, вы можете смело задавать их в комментариях. А если нужна помощь в решении задач или других примеров и заданий, обращайтесь в профессиональный студенческий сервис.

Цикл
Карно—
это обратимый круговой процесс, состоящий
из двух адиабатических и двух изотермических
процессов. В процессе Карно термодинамическая
система выполняет механическую работу
и обменивается теплотой с
двумя тепловыми резервуарами, имеющими
постоянные, но различающиеся температуры.
Резервуар с более высокой температурой
называется нагревателем, а с более
низкой температурой — холодильником.

КПД
для идеального газа—
Вычислим
КПД цикла Карно для идеального газа.
При изотермическом процессе внутренняя
энергия идеального газа остаётся
постоянной. Поэтому количество полученной
газом теплоты  равно
работе ,
совершаемой газом при переходе из
состояния 1 в состояние 2.(рис 2)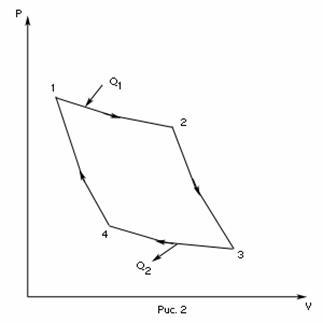Эта работа равна

,

где  –
масса идеального газа в тепловой машине.

Количество
отдаваемой холодильнику теплоты  равно
работе ,
затраченной на сжатие газа при переходе
его из состояния 3 в состояние 4. Эта
работа равна

.

Для
того чтобы цикл был замкнутым, состояние
1 и 4 должны лежать на одной и той же
адиабате. Отсюда вытекает условие

.

Аналогично
для состояний 2 и 3 должно вытекать
условие

.

Разделив
одно соотношение на другое, приходим к
условию замкнутости цикла

.

Теперь
подставляя  и  в
выражение для КПД, получим

. 
(2)

В
результате получим формулу для КПД
цикла Карно:

26. Барометрическая формула. Распределение Больцмана.

При
выводе основного уравнения
молекулярно-кинетической теории газов
и максвелловского распределения молекул
по скоростям делалось предположение,
что внешние силы не действуют на молекулы
газа, поэтому молекулы равномерно
распределены по объему. Но молекулы
любого газа находятся в потенциальном
поле тяготения Земли. Сила тяжести, с
одной стороны, и тепловое движение
молекул — с другой, приводят газ к
некоторому стационарному состоянию,
при котором давление газа с высотой
уменьшается. 

Выведем
закон изменения давления с высотой,
предполагая при этом, что масса всех
молекул одинакова, поле тяготения
однородно и температура постоянна.

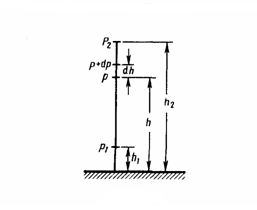
Рис.1

Если
атмосферное давление на высоте h равно
р (рис. 1), то на высоте h+dh оно равно p+dp
(при dh>0 dp<0, так как давление с высотой
уменьшается). Разность давлений р и p+dp
равна весу газа, заключенного в объеме
цилиндра высотой dh с основанием площадью
1 м²: 

 

где
ρ — плотность газа на высоте h (dh настолько
мало, что при изменении высоты в этом
интервале плотность газа можно считать
постоянной). Значит, 

 (1) 

Зная
уравнение состояния идеального газа
pV=(m/M) RT (m — масса газа, М — молярная масса
газа), находим, что 

 

Подставив
это выражение в (1), получим 

 или 

С
изменением высоты от h₁ до
h₂ давление
изменяется от р₁ до
р₂ (рис.
67), т. е. 

 

или 

 (2) 

Выражение
(2) называется барометрической
формулой.
Она позволяет вычислить атмосферное
давление в зависимости от высоты или,
измеряя давление, найти высоту: Так как
высоты считаются относительно уровня
моря, где давление считается нормальным,
то выражение (2) может быть представлено
в виде 

 (3) 

где
р — давление на высоте h. 

Прибор
для определения высоты над земной
поверхностью называется высотомером (или альтиметром).
Его работа основана на применении
формулы (3). Из этой формулы следует, что
чем тяжелее газ, тем давление с высотой
убывает тем быстрее. 

Барометрическую
формулу (3) можно преобразовать, если
воспользоваться формулой p=nkT: 

 

где
n – концентрация молекул на высоте h,
n₀ –
то же, на высоте h=0. Так как M=m₀N_A (N_A –
постоянная Авогадро, m₀ –
масса одной молекулы), a R=kN_A,
то 

 (4) 

где
m₀gh=P
— потенциальная энергия молекулы в
поле тяготения, т. е. 

 (5) 

Выражение
(5) называется распределением
Больцмана для
внешнего потенциального поля. Из него
видно, что при постоянной температуре
плотность газа больше там, где меньше
потенциальная энергия его молекул. 

Если
частицы находятся в состоянии хаотического
теплового движения и имеют одинаковую
массу и , то распределение Больцмана
(5) применимо в любом внешнем потенциальном
поле, а не только в поле сил тяжести.

Соседние файлы в предмете Физика

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Большинство современных двигателей преобразуют внутреннюю энергию углеводородного топлива в механическую энергию. То есть являются тепловыми машинами. Первым ученым, который задался вопросом о создании самой эффективной тепловой машины стал французский физик Сади Карно. В 1824 в его работе – «Размышления о движущей силе огня и о машинах, способных развивать эту силу», предложен идеальный термодинамический цикл тепловой машины. Цикл, позволяющий получить максимальный теоретический КПД, затем назвали именем Карно. 

Главной характеристикой, на которую обращают внимание при проектировании любого двигателя является коэффициент полезного действия или КПД. Коэффициент КПД показывает, насколько эффективно протекает трансформация тепловой энергии в системе в полезную механическую работу. КПД любого цикла вычисляется путем отношения полезной работы к затраченной энергии (которую передают системе).

• Полезная работа – та, которую получаем на выходе системы в результате выполнения цикла.
• Затраченная энергия – та, что была подведена к системе за цикл.

Термодинамические процессы и циклы.

Цикл Карно состоит из двух изотермических и двух адиабатных процессов. Чтобы понять, что из себя представляют эти процессы, обратимся к первому закону термодинамики:

∆U = A + Q,

где ∆U – внутренняя энергия рабочего тела или системы,

A – совершаемая в цикле работа,

Q – количество теплоты, переданное за цикл, системе.

Формулировка первого закона термодинамики: при переходе системы из одного состояния в другое, изменение внутренней энергии системы равно сумме количества теплоты, переданного системе, и работы внешних сил.

Что такое изотермический и адиабатный процессы?

Изотермический процесс

Изотермический процесс – процесс, перехода рабочего тела из одного состояния в другое без изменения температуры ∆T=0.  

Например, изменение объёма и давления газа при неизменной температуре.

При постоянной температуре изменение внутренней энергии газа ∆U будет равно нулю, так как ∆T = 0.

Тогда, согласно первому закону термодинамики: Q = A.  Это значит:

• получая теплоту, газ будет расширяться, совершая положительную работу. При этом всё количество тепла будет потрачено на совершение работы.
• и наоборот, при отдаче теплоты объем газа будет уменьшаться.

Адиабатный процесс

Адиабатный процесс – такой процесс, который протекает без передачи или получения тепла Q от окружающей среды. То есть, процесс протекает в теплоизолированной системе или с бесконечно большой скоростью, при которой теплообменом можно пренебречь Q = 0.

Согласно первому закону термодинамики: A = -∆U.

Это значит:

• работу газ совершает за счет уменьшения внутренней энергии;
• и наоборот, приложенная к системе работа, затрачивается только на повышение внутренней энергии.

Из каких процессов состоит цикл Карно

Главная особенность всех круговых процессов или циклов состоит в том, что их работа невозможна, если приводить рабочее тело в контакт только с одним источником теплоты. Любой тепловой двигатель устроен таким образом, что за счет теплообмена между двумя источниками теплоты он способен преобразовать тепло в механическую работу. Температуры этих источников должны отличаться, но, при этом, быть постоянными.

Чтобы понять, как работает цикл Карно, нужно представить простой тепловой двигатель, например цилиндр с поршнем, внутри которого находится газ. К газу может подводиться и отводится тепло. Источники тепла, при этом, называются:

• нагреватель – источник, имеющий высокую постоянную температуру T_Н
• холодильник – с постоянной низкой температурой T_Х.

Цикл Карно имеет четыре обратимых процесса – два изотермических, и два – адиабатных.

Изотермические процессы протекают при постоянной температуре T. Адиабатные процессы – при постоянной энтропии S, без теплообмена с окружающей средой.

Для удобства, цикл Карно представляют в:

• T-S координатах – зависимость энтропии S от температуры T.
• p-V координатах – зависимость давления p от удельного объёма V.

Изотермическое расширение

Изотермическое расширение или изотермический подвод тепла – показано процессом AB. В начале рабочее тело находится в точке A. На данном этапе рабочее тело или газ имеет начальную температуру T_Н. Затем, к телу подводится энергия в виде теплоты Q₁. Снижение температуры при расширении отсутствует, так как подводится теплота Q₁, от нагревателя. Увеличения температуры тоже не будет, так как совершается работа A₁=Q₁. Поэтому, при расширении рабочего тела его температура остается постоянной – изотермическое расширение T_Н=const. При этом, энтропия рабочего тела увеличивается, из-за увеличения его объема. Происходит это за счет совершения механической работы.

Адиабатическое расширение

Адиабатическое расширение – показано процессом BC. После окончания изотермического подвода тепла газ находится в состоянии, характеризуемом точкой B. Далее следует адиабатическое расширение рабочего тела. На этом этапе газ в двигателе изолирован от обоих тепловых источником – как от горячего, так и от холодного. Поэтому ни источники, ни рабочее тело получают и не теряют тепло. Такой процесс называется адиабатическим. Из-за отсутствия теплообмена с окружающей средой Q=0 энтропия рабочего тела остается постоянной S=const. Работа осуществляется только за счет внутренней энергии A = -∆U. Поэтому происходит снижение температуры газа.

Рабочее тело, расширяясь, заставляет поршень двигаться вверх. Давление газа под поршнем постепенно снижается. Выталкивая подвижный поршень вверх, рабочее тело совершает механическую работу, в результате чего теряет определенное количество внутренней энергии. Количество этой энергии равно проделанной работе A = -∆U. В процессе расширения рабочего тела его температура уменьшается и становится равной T_Х.

Изотермическое сжатие

Изотермическое сжатие – процесс CD. На данном этапе рабочее передаёт тепло холодному источнику при температуре T_Х. К газу подводится работа сжатия путем перемещения поршня вниз. В результате этого процесса, рабочее тело передает холодильнику количество теплоты равное подводимой работе Q₂=А₂. Изменения внутренней энергии не будет ∆U=0. Поэтому, этот процесс считается изотермическим сжатием T_Х=const. Энтропия газа уменьшается.

Адиабатическое сжатие

Адиабатическое сжатие – процесс DA. После завершения отвода тепла, газ находится в состоянии, характеризуемом точкой D. На последней стадии цикла рабочее тело снова остается изолированным обоих источников Q=0. Предполагается, что поршень движется без трения, а процесс является обратимым. Работа продолжает подводиться и поршень движется вниз, сжимая газ. В результате этого внутренняя энергия газа возрастает A = +∆U. Под давлением поршня температура рабочего тела поднимается до температуры нагревателя T_Н, но энтропия остается неизменной. Итогом этого этапа является то, что рабочее тело возвращается к своему изначальному состоянию в точку А.

Поскольку цикл Карно идеальный, то принято допущение, что температуры рабочего тела в процессах AB и CD равна температуре горячего и холодного источника или отличаются на бесконечно малую величину.

Формула расчета цикла Карно

Коэффициент КПД показывает, насколько совершенен цикл и входящие в него термодинамические процессы. Термический КПД любого термодинамического цикла рассчитывается по формуле:

Где Q₁ – тепло, подведенное к рабочему телу от нагревателя;

Q₂ – тепло, отведенное от рабочего тела к холодильнику.

Применительно для расчета КПД цикла Карно используется формула:

Где T_Н -температура горячего источника;

T_Х -температура холодно источника.

Температура формуле вычисления КПД цикла Карно в кельвинах [К].

Обратный цикл Карно

Описанный выше цикл теплового двигателя Карно полностью обратим. Это значит, что можно пройти все процессы в обратном направлении:

• процесс отвода тепла станет процессом подвода тепла
• процесс сжатия – расширением.

При проходе процессов в обратном направлении получим циклом холодильной машины Карно или теплового насоса. Диаграммы остаются абсолютно такими же, измениться лишь направление процессов.

Единственное отличие обратного цикла Карно — это противоположные направления всех четырёх термодинамических процессов.

Тепло в обратном цикле Карно будет поглощаться из холодильника, и далее отводиться к нагревателю. Чтобы это осуществить, в соответствии со вторым законом термодинамики, необходимо затратить работу. Работа затрачивается на сжатие газа.

В результате того, что к данной системе прикладывается работа, тепло перемещается от холодного источника к горячему.

Подробнее про обратный цикл Карно и холодильные машины рекомендуем прочитать в статье.

Теорема Карно

Теорема Карно – это теорема, выявляющая некоторые ограничения для предела КПД реальных тепловых машин. Описал ее Сади Карно в своем труде о движущей силе огня. Но некоторые из современных авторов считают, что рассуждения Карно позволяют сформулировать сразу две теоремы. Звучат они так:

1. КПД любого обратимого теплового двигателя, работающего по циклу Карно, не зависит от природы рабочего тела и конструкции самой машины, а является лишь функцией температур нагревателя и холодильника:

Из этой теоремы можно сделать вывод, что самую большую роль, определяющую КПД тепловой машины, играет разница температур горячего и холодного источников.

1. КПД любого теплового двигателя, работающего по необратимому циклу, должен быть меньше КПД двигателя с обратимым циклом Карно, при условии равных температур нагревателей и холодильников.

Эта трактовка теоремы дает понять, что реальные двигатели неидеальны, в отличии от теоретической модели Карно. Поэтому, из-за наличия неизбежных потерь энергии, КПД реального двигателя будет снижаться в зависимости от объема этих потерь.

Исходя из этого, уравнение расчета КПД цикла Карно показывает максимальную эффективность работы для любого двигателя, в котором задействованы соответствующие температурные параметры.

Следствие теоремы Карно – все обратимые двигатели, которые работают между идентичными источниками тепла, имеют одинаковую эффективность.

Отсюда можно сделать вывод: понижение температуры холодного резервуара сильнее влияет на максимальный КПД тепловой машины, чем увеличение температуры горячего резервуара на такую же величину. На практике добиться этого довольно сложно, так как чаще всего источником для охлаждения является окружающая среда со своей температурой.

Максимальный КПД достигается только в том случае, когда значение энтропии не изменяется в течение цикла. Например, в течение цикла энтропия может изменяться при наличии трения, в результате которого при механической работе выделяется тепло. В данной ситуации цикл нельзя назвать обратимым.

Обобщенный цикл Карно

Согласно описанной ранее теореме Карно, КПД абсолютно любого реального цикла не может быть выше КПД в цикле Карно при идентичных температурных параметрах. Несмотря на это существуют примеры, термический КПД которых, при определенных условиях, равен циклу Карно. Такие циклы имеют отличия в изображении на T-S диаграмме. В данных циклах используется регенерация теплоты, поэтому они называются регенеративными.

Термодинамический цикл с регенерацией теплоты

Происходит процесс регенерации следующим образом. Доля тепла, отдаваемая рабочим телом холодильнику, переходит обратно к рабочему телу для его нагревания. Такой метод повышает термический КПД рабочего цикла, позволяя сделать расход теплоты более выгодным, и используется в теплосиловых устройствах. Например, в современных тепловых электрических станциях.

Рассмотрим T-S диаграмму регенеративного цикла.

Данный цикл состоит из двух изотермических (1-2) и (3-4) и двух политропных (произвольных) (2-3) и (4-1) обратимых и эквидистантных процессов.

1. Горячий источник (нагреватель), имея начальную температуру T₁, по изотерме (1-2) передает теплоту рабочему телу.
2. В точке 2 начинается расширение рабочего тела в направлении (2-3) – политропный процесс. На данной кривой происходит отвод теплоты регенерации q_рег.
3. Точка 3 на диаграмме находится левее, чем в диаграмме для идеального цикла Карно, поскольку вследствие отвода теплоты регенерации уменьшается энтропия рабочего тела.
4. Далее, на изотермической прямой (3-4) происходит сжатие рабочего тела и отведение теплоты к холодному источнику с температурой T₂ (холодильник).
5. В точке 4 начинается политропный процесс сжатия по кривой (4-1). Одновременно с этим к рабочему телу подводится теплота q_рег.

Рабочее тело принимает и отдает равное количество теплоты q_рег, значит в данном процессе происходит перенос теплоты из одной части цикла в другую, это и называется процессом регенерации.

Термический КПД регенеративного цикла

Термический КПД регенеративного цикла будет равен термическому КПД Карно при идентичных параметрах температуры. Поэтому такой регенеративный цикл так же называют обобщенным циклом Карно (только если он обратим). Подобные явления находят массовое практическое применение на различных промышленных объектах и предприятиях.

К примеру, по принципу регенерации происходит подогрев воды в паровых турбинах и подогрев воздуха в газовых турбинах. 

Говоря об обобщенном цикле Карно, стоит отметить, что его реализация в идеальном виде невозможна. Обусловлено это тем, что в идеале такая система должна содержать бесконечно большое количество промежуточных регенераторов. При этом, для каждого из них температура отводимой и подводимой теплоты должна быть определенной. Любые методы регенерации, которые используются на практике, являются в определенной мере приближенными к идеальному циклу.

Эффективность реальных тепловых двигателей.

Обратимые двигатели в реальности невозможны. Реальные машины имеют еще меньший КПД, чем КПД машины Карно. Помимо этого, реальные двигатели, работающие по принципу Карно, можно встретить крайне редко. Несмотря на это, данное уравнение не теряет своей актуальности для определения максимального КПД, который можно спрогнозировать для определенной пары источников теплоты. Двигатель, работающий по принципу Карно должен рассматриваться как теоретическая модель тепловых двигателей.

Важнейшей технической задачей является повышение КПД тепловых двигателей и приближение этого значение к максимально возможному. Сравним значения термических КПД некоторых тепловых двигателей:

• Паровой двигатель – 8%
• Газотурбинная установка – 25-38%
• Паротурбинная установка – 40-50%

Начальные и конечные температуры пара для паровой турбины имеют такие приблизительные значения: T_н = 800 К, T_х = 300 К. Максимальное теоретическое значение КПД при данных температурах – 62%. Но, вследствие различных потерь энергии, в реальности экономичность достигает 45%.

На сегодня, КПД самых экономичных паротурбинных блоков на сверхперегретом паре с развитой системой регенерации и промежуточным перегревом пара достигает 52%.

Заключение

Модель работы идеального теплового двигателя, предложенная Сади Карно почти 200 лет назад, хоть и нереализуема на практике, но определенно остается актуальной и в нынешнее время.

Цикл Карно – теоретический инструмент, позволяющий рассчитать максимальную эффективность для любого теплового двигателя, что является немаловажной задачей для каждого инженера, занимающегося разработкой и моделированием термодинамических систем.