Коэффицие́нт поле́зного де́йствия (КПД) — характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии. Определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой; обозначается обычно η («эта»)[1]. КПД является безразмерной величиной и часто выражается в процентах. Часто применяется в переносном смысле как метафора эффективности чего-либо без привязки к расчётам.
Определение[править | править код]
Математически КПД определяется как
где А — полезная работа (энергия), а Q — затраченная энергия.
Если КПД выражается в процентах, эту формулу иногда записывают в виде
.
Здесь умножение на 

В силу закона сохранения энергии и в результате неустранимых потерь энергии КПД реальных систем всегда меньше единицы, то есть невозможно получить полезной работы больше или столько, сколько затрачено энергии.
КПД теплово́го дви́гателя — отношение совершённой полезной работы двигателя к энергии, полученной от нагревателя. КПД теплового двигателя может быть вычислен по следующей формуле
,
где 

.
Другие похожие показатели[править | править код]
Не все показатели, характеризующие эффективность энергетических процессов, соответствуют вышеприведённому описанию. Даже если они традиционно или ошибочно называются «коэффициент полезного действия», они могут иметь другие свойства, в частности, превышать 100 %.
КПД котлов[править | править код]
КПД котлов на органическом топливе традиционно рассчитывается по низшей теплоте сгорания; при этом предполагается, что влага продуктов сгорания покидает котёл в виде перегретого пара. В конденсационных котлах эта влага конденсируется, теплота конденсации полезно используется. При расчёте КПД по низшей теплоте сгорания он в итоге может получиться больше единицы. В данном случае корректнее было бы считать его по высшей теплоте сгорания, учитывающей теплоту конденсации пара; однако при этом показатели такого котла трудно сравнивать с данными о других установках.
Тепловые насосы и холодильные машины[править | править код]
Достоинством тепловых насосов как нагревательной техники является возможность получать больше теплоты, чем расходуется энергии на их работу. Холодильная машина может отвести от охлаждаемого конца больше теплоты, чем затрачивается энергии на организацию процесса.
Эффективность машин характеризует холодильный коэффициент[en]
,
где 

Для тепловых насосов используют термин коэффициент трансформации
,
где 

В идеальной машине 

Наилучшими показателями производительности для холодильных машин обладает обратный цикл Карно: в нём холодильный коэффициент
,
где 

Примечания[править | править код]
- ↑ Зубарев Д. Н. Коэффициент полезного действия // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 484—485. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
- ↑ Холодильный коэффициент // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
Литература[править | править код]
- Пёрышкин А. В. Физика. 8 класс. — Дрофа, 2005. — 191 с. — 50 000 экз. — ISBN 5-7107-9459-7..
Формула КПД (коэффициента полезного действия) в физике
Формула КПД (коэффициента полезного действия)
В реальной действительности работа, совершаемая при помощи какого – либо устройства, всегда больше полезной работы, так как часть работы выполняется против сил трения, которые действуют внутри механизма и при перемещении его отдельных частей. Так, применяя подвижный блок, совершают дополнительную работу, поднимая сам блок и веревку и, преодолевая силы трения в блоке.
Введем следующие обозначения: полезную работу обозначим $A_p$, полную работу – $A_{poln}$. При этом имеем:
[A_p < A_{poln} ; frac{A_p}{A_{poln}}<1left(1right).]
Определение и формула КПД
Определение
Коэффициентом полезного действия (КПД) называют отношение полезной работы к полной. Обозначим КПД буквой $eta $, тогда:
[eta =frac{A_p}{A_{poln}} left(2right).]
Чаще всего коэффициент полезного действия выражают в процентах, тогда его определением является формула:
[eta =frac{A_p}{A_{poln}}cdot 100% left(2right).]
При создании механизмов пытаются увеличить их КПД, но механизмов с коэффициентом полезного действия равным единице (а тем более больше единицы) не существует.
И так, коэффициент полезного действия – это физическая величина, которая показывает долю, которую полезная работа составляет от всей произведенной работы. При помощи КПД оценивают эффективность устройства (механизма, системы), преобразующей или передающей энергию, совершающего работу.
Для увеличения КПД механизмов можно пытаться уменьшать трение в их осях, их массу. Если трением можно пренебречь, масса механизма существенно меньше, чем масса, например, груза, который поднимает механизм, то КПД получается немного меньше единицы. Тогда произведенная работа примерно равна полезной работе:
[A_papprox A_{poln}left(3right).]
Золотое правило механики
Необходимо помнить, что выигрыша в работе, используя простой механизм добиться нельзя.
Выразим каждую из работ в формуле (3) как произведение соответствующей силы на путь, пройденный под воздействием этой силы, тогда формулу (3) преобразуем к виду:
[F_1s_1approx F_2s_2left(4right).]
Выражение (4) показывает, что используя простой механизм, мы выигрываем в силе столько же, сколько проигрываем в пути. Данный закон называют «золотым правилом» механики. Это правило сформулировал в древней Греции Герон Александрийский.
Это правило не учитывает работу по преодолению сил трения, поэтому является приближенным.
КПД при передаче энергии
Коэффициент полезного действия можно определить как отношение полезной работы к затраченной на ее выполнение энергии ($Q$):
[eta =frac{A_p}{Q}cdot 100% left(5right).]
Для вычисления коэффициента полезного действия теплового двигателя применяют следующую формулу:
[eta =frac{Q_n-Q_{ch}}{Q_n}left(6right),]
где $Q_n$ – количество теплоты, полученное от нагревателя; $Q_{ch}$ – количество теплоты переданное холодильнику.
КПД идеальной тепловой машины, которая работает по циклу Карно равно:
[eta =frac{T_n-T_{ch}}{T_n}left(7right),]
где $T_n$ – температура нагревателя; $T_{ch}$ – температура холодильника.
Примеры задач на коэффициент полезного действия
Пример 1
Задание. Двигатель подъемного крана имеет мощность $N$. За отрезок времени равный $Delta t$ он поднял груз массой $m$ на высоту $h$. Каким является КПД крана?textit{}
Решение. Полезная работа в рассматриваемой задаче равна работе по подъему тела на высоту $h$ груза массы $m$, это работа по преодолению силы тяжести. Она равна:
[A_p=mgh left(1.1right).]
Полную работу, которая выполняется при поднятии груза, найдем, используя определение мощности:
[N=frac{A_{poln}}{Delta t}to A_{poln}=NDelta tleft(1.2right).]
Воспользуемся определением коэффициента полезного действия для его нахождения:
[eta =frac{A_p}{A_{poln}}cdot 100%left(1.3right).]
Формулу (1.3) преобразуем, используя выражения (1.1) и (1.2):
[eta =frac{mgh}{NDelta t}cdot 100%.]
Ответ. $eta =frac{mgh}{NDelta t}cdot 100%$
Пример 2
Задание. Идеальный газ выполняет цикл Карно, при этом КПД цикла равно $eta $. Какова работа в цикле сжатия газа при постоянной температуре? Работа газа при расширении равна $A_0$
Решение. Коэффициент полезного действия цикла определим как:
[eta =frac{A_p}{Q}left(2.1right).]
Рассмотрим цикл Карно, определим, в каких процессах тепло подводят (это будет $Q$).
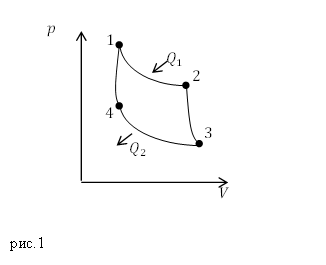
Так как цикл Карно состоит из двух изотерм и двух адиабат, можно сразу сказать, что в адиабатных процессах (процессы 2-3 и 4-1) теплообмена нет. В изотермическом процессе 1-2 тепло подводят (рис.1 $Q_1$), в изотермическом процессе 3-4 тепло отводят ($Q_2$). Получается, что в выражении (2.1) $Q=Q_1$. Мы знаем, что количество теплоты (первое начало термодинамики), подводимое системе при изотермическом процессе идет полностью на выполнение газом работы, значит:
[Q=Q_1=A_{12}left(2.2right).]
Газ совершает полезную работу, которую равна:
[A_p=Q_1-Q_2left(2.3right).]
Количество теплоты, которое отводят в изотермическом процессе 3-4 равно работе сжатия (работа отрицательна) (так как T=const, то $Q_2=-A_{34}$). В результате имеем:
[A_p=A_{12}+A_{34}left(2.4right).]
Преобразуем формулу (2.1) учитывая результаты (2.2) – (2.4):
[eta =frac{A_{12}+A_{34}}{A_{12}}to A_{12}eta =A_{12}+A_{34}to A_{34}=(eta -1)A_{12}left(2.4right).]
Так как по условию $A_{12}=A_0, $окончательно получаем:
[A_{34}=left(eta -1right)A_0.]
Ответ. $A_{34}=left(eta -1right)A_0$
Читать дальше: формула линейной скорости.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Формула КПД и как его вычислить для тепловой машины или механизма
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Эта аббревиатура вряд ли требует расшифровки: она неизвестна разве что тем, у кого в школе был «неуд» по физике.
Но для забывчивых всё же напомним, что под этим сокращением скрывается коэффициент полезного действия. Что же собой представляет эта величина?

Поговорим о ней простым и понятным языком – это может пригодиться даже в повседневной жизни.
Что такое КПД в физике и какова его формула
Для выполнения какой-либо работы необходимо затратить определённое количество энергии. Чтобы ехал велосипед, вы тратите мышечную энергию крутя педали. Чтобы двигался автомобиль, используется энергия сжигаемого топлива (бензина, солярки или газа).
Для горения лампочки требуется энергия электрического тока. Список можно продолжать до бесконечности. Точку можно поставить на солнечной энергии, благодаря которой существует жизнь на Земле.
Далее возникает логичный вопрос: а насколько эффективно расходуется эта энергия? В идеале хотелось бы, чтобы вся она шла «в дело», то есть использовалась только по прямому назначению. Но, к сожалению, на практике такого не бывает.
Затраченная энергия будет всегда больше, чем полезная работа, так как для достижения основной цели (движение, подъём груза, освещение, отопление и т.д.) часть энергии неизбежно уйдёт на неустранимые потери (преодоление силы трения, нагрев электропроводки, выброс продуктов горения в атмосферу и т.д.). Понятно, что чем меньше такие потери, тем лучше.
Критерием того, насколько эффективно работает система (устройство, агрегат, двигатель, машина и т.д.), служит показатель, получивший название коэффициент полезного действия (КПД).

Иными словами, коэффициент полезного действия показывает, какова доля полезной работы в общих энергозатратах. Математически КПД (чаще всего обозначается символом ŋ) определяется по формуле:
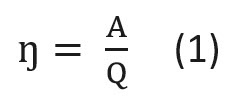
где A — полезная энергия (работа);
Q — энергия, затраченная на совершение полезной работы.
Понятно, что ŋ – величина безразмерная и не может быть больше единицы (да и равной единице она может быть чисто теоретически).
Выражается она в виде десятичной дроби либо в процентах (в последнем случае в формулу вставляется множитель х100).
Так, если КПД равен 0,9 (90%), то это значит, что 10% полезной мощности составили безвозвратные потери.
КПД теплового двигателя (машины)
Под тепловым двигателем понимается машина (агрегат), в которой энергия, высвобождающаяся в процессе расширения рабочего тела, преобразуется в механическую работу.
В качестве рабочего тела обычно выступает газ или газообразные вещества (пары бензина, водяной пар и т.п.).
Тепловые машины работают по замкнутому циклу. Это значит, что процесс преобразования энергии и сопутствующей теплопередачи периодически повторяется, а рабочее тело совершает круговой цикл, возвращаясь в исходное состояние.
К тепловым двигателям относятся:
- поршневые (паровые машины, двигатели внутреннего сгорания);
- роторные/турбинные (газовые или паровые турбины АЭС и ТЭЦ);
- реактивные (авиация);
- ракетные (космическая техника).
Используя положения предыдущего параграфа, КПД тепловой машины можно сформулировать как отношение полезной работы, совершённой за один цикл, к энергии (количеству теплоты), поступившей от энергоносителя (нагревателя).
Тогда формулу (1) можно преобразовать следующим образом:
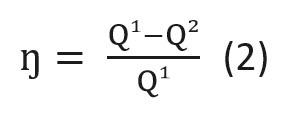
где Q1 — количество теплоты, полученное двигателем от нагревателя за цикл;
Q2 — количество теплоты, отданное двигателем охладителю (холодильнику) за цикл;
Q1 – Q2 – количество теплоты, которое пошло на совершение работы.
Предположим, что Q1 = Q2, то есть на совершение полезной работы ничего не осталось – вся энергия «ушла в трубу». Тогда и КПД будет нулевым. Если же Q2 = 0, то есть вся энергия отдана полезной работе (потери отсутствуют), то коэффициент полезного действия будет равен 1.
Но это теория, на практике ни то ни другое нереалистично. В первом случае двигатель просто бесполезен, во втором – идеален, но недосягаем.
Значения КПД для различных типов тепловых двигателей приведены ниже.

Самым большим КПД обладают тепловые двигатели, работающие на основе цикла Карно (процесс назван в честь французского инженера, открывшего это явление в 1824 г.). В термодинамике оно характеризует круговой цикл, включающий в себя две стадии: расширение и сжатие рабочего тела.
Причём на протяжении обеих стадий попеременно проходят два процесса: изотермический (протекающий при постоянной температуре), и адиабатический (протекающий без теплообмена с окружающей средой). Максимальное значение КПД здесь достигается за счёт того, что тела с разной температурой не контактируют, а значит, без осуществления работы теплопередача исключается.
КПД механизма — по какой формуле вычисляют
Человек придумал разнообразные механизмы, с помощью которых можно поднимать тяжёлые грузы на определённую высоту. Так, для подъёма ведра с водой из колодца изобрели ворот, для подъёма автомобиля – домкрат. При помощи лебёдки и наклонной плоскости египтяне построили свои грандиозные пирамиды.
Пользуясь этими приспособлениями, человек редко вспоминает об их КПД. В качестве примера рассмотрим этот показатель для наклонной плоскости.
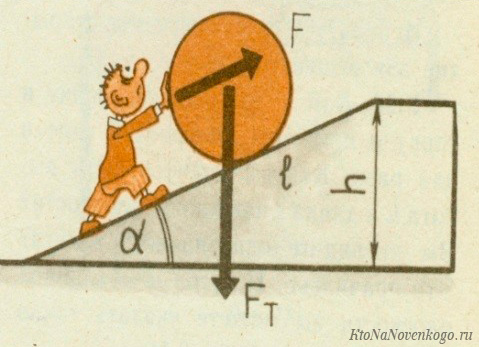
Принцип расчёта КПД остаётся неизменным: нужно найти отношение полезной работы ко всей затраченной энергии. То есть опять-таки используем общую формулу (1), сделав соответствующие преобразования.
Предположим, тело массой m нужно поднять (точнее затолкать или затянуть) на высоту h. При постоянной скорости подъёма полезная работа будет равна произведению силы тяжести (mg) на высоту (h).
Затраченная работа определяется произволением силы толчка или тяги F на длину наклонной плоскости L. Заметим, что толчковое (тяговое) усилие идёт на преодоление силы трения Fтр.
Таким образом, КПД такого простейшего механизма можно посчитать по формуле:
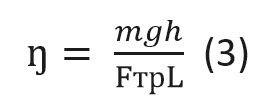
Несложный анализ показывает, что коэффициент полезного действия наклонной плоскости обратно пропорционален силе трения и длине аппарели. Последняя, в свою очередь, зависит от угла наклона: чем он больше, тем короче аппарель.
Как можно увеличить КПД
Современная наука постоянно ищет пути повышения коэффициента полезной модности двигателей и отдельных механизмов, внедряя новые технические решения и технологические инновации.
Чем выше будет КПД, тем экономичней будет двигатель, тем больше энергоресурсов удастся сберечь.
Тепловой двигатель
Из формулы (2) следует, что для увеличения КПД есть два пути: а) повышение температуры нагревателя; б) понижение температуры холодильника. Оба пути малоперспективны.
Нагреватель нельзя разогревать до бесконечности, так как любой материал имеет предел жаропрочности. Холодильником почти всегда служит окружающая среда, а внедрение в систему дополнительного теплообменника (например, баллона с жидким азотом) нецелесообразно: это резко увеличит вес, габариты и стоимость двигателя.
Установлено, что на коэффициент полезного действия не влияют характеристики рабочего тела. Что же остаётся?
А остаётся немало практически реализуемых способов, таких как уменьшение трения в механических узлах, минимизация теплопотерь путём достижения максимально полного сгорания топлива, создание обтекаемых форм для снижения лобового сопоставления (воздуха или воды) и т.д.
Учитывая, что в механике хорошим показателем на сегодняшний день считается КПД 30-40%, учёным и практикам есть над чем работать.
Наклонная плоскость
Из формулы (3) следует, что для повышения КПД нужно снижать силу трения (прежде всего, путём создания гладких соприкасающихся поверхностей) и увеличивать угол наклона. Но! При крутом уклоне силёнок для поднятия тяжёлого груза может и не хватить.
В заключение отметим, что в электротехнике ситуация с КПД обстоит гораздо лучше (показатель в 95% для электродвигателя – норма). На то есть объективные причины, объяснение которых выходит за рамки рассматриваемой темы.
Выбирая техническое устройство, всегда обращают внимание на эффективность его работы. Иными словами, насколько высока энергоэффективность. Получить ответ на этот вопрос можно, если произвести вычисление коэффициента его полезного действия. Тогда становится понятным, насколько затраченные усилия будут обеспечивать полезный результат работы.
Понятие КПД (коэффициента полезного действия)
Термин «КПД» широко используется не только среди профессионалов, но и в быту. Под ним понимают, насколько совершенная работа превышает полезную, т.е. ту, ради которой механизм или прибор приобретается.
Учеными разработана специальная формула, из которой следует, что КПД всегда меньше единицы. Чтобы рассчитать коэффициент, нужно полезную работу, выраженную в Джоулях, разделить на энергию, которая затрачена на эту работу. Поскольку энергия также выражается в Джоулях, конечная расчетная величина безразмерна.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Объяснить бытовым языком данное понятие можно так: энергия, выделяемая от плиты, на которой должен закипеть чайник, расходуется не только на его нагревание. Она должна нагреть саму посудину, воздух вокруг нее, сам нагревательный элемент. И только ее часть будет расходоваться на передачу воде. Чтобы сориентироваться, насколько долго будет закипать чайник одного объема на различного вида печах, нужно знать их КПД.
В поисках наиболее эффективного прибора не стоит стремиться к единице. Такого не бывает. Например, КПД атомной электростанции примерно равно 35%.
Происходит это по двум причинам:
- Исходя из закона сохранения энергии, получить больше работы, чем затрачено энергии, невозможно.
- Любая работа сопровождается определенными потерями, будь-то нагревание тары или преодоление сил трения при движении по поверхности.
Термин КПД применим практически к каждому процессу, в котором имеется затраченная и полезная работа.
Применение в различных сферах физики
Характеризуя КПД, следует учитывать, что он не является константой, поскольку в каждом случае свои особенности энергозатрат. С другой стороны, он не может быть установлен изолированно от конкретных процессов. Если рассмотреть работу электродвигателя, величина его КПД сложится исходя из преобразования энергии тока в механическую работу.
В данном случае КПД рассматривается не как соотношение полезной и общей работы, а как соотношение отдаваемой мощности и подводимой к рабочему механизму.
В формулу (η=P2/P1) должны быть включены P1 – первичная мощность и P2 – мощность прибора.
В качестве первого примера выведем формулу КПД для варианта определения с величинами работы и затраченной энергии (формула для определения КПД теплового двигателя). Условными обозначениями в ней будут являться:
Ап – работа полезная;
- Q1 – количество энергии (или тепла), полученной от нагревающего устройства;
- Q2 – количество энергии (или тепла), отданное в процессе деятельности;
- Q1 – Q2 – та энергия (или тепло), которая пошла на процесс.
В итоге получится выражение:
Теперь выразим формулу через соотношение мощностей. Условные обозначения следующие:
Ротд – полезная (эффективная) мощность;
Рподв – номинальная мощность.
Формула будет выглядеть так:
Если затрата или передача энергии происходит неоднократно, общий КПД равен сумме КПД на каждом участке процесса:
Какой буквой обозначается, единицы измерения
В вышеприведенной формуле искомая величина коэффициента полезного действия обозначается буквой η, которая произносится “эта”.
Для упрощения понимания величины, КПД чаще выражается в процентах.
Физическая формула КПД
С учетом изложенных выше особенностей и необходимости выражения результата в %, физические формулы приобретают усовершенствованный внешний вид:
или
Примеры расчета КПД
Формула применяется для расчетов коэффициентов машин различного типа.
Задача 1
Имеется 10 кг дров, теплота сгорания которых составляет 95 Дж/кг. При их сгорании в помещении объемом 75 м3 установилась температура 22оС (допускаем, что удельная теплоемкость воздуха равна 1,3 кДж/ кгхград).
Решение состоит из нескольких действий:
- 1300 Дж умножить на 75 (объем) и 22 (температуру). Получаем 2 145 кДж. Это то тепло, выраженное в кДж, которое поступило в воздух помещения.
- 10700000Дж умножаем на 10 (количество дров) =10х107 кДж.
- При делении полезного тепла и полного, выработанного обогревателем, получаем значение 2,5%. Это говорит о низкой эффективности прибора и большой затрате дров и необходимости внесения конструктивных изменений, например, оборудования возможности дымоходам нагревать не только воздух, но и предметы в помещении.
Задача 2
В доме установлен электробойлер объемом 80 литров. Нагревательный элемент имеет мощность 2 кВт. Было замечено, что для нагревания воды от 12оС до 70оС уходит 3 часа. Нужно определить КПД прибора.
Дополнительные данные: плотность воды составляет 1000 кг/м3, ее теплоемкость – 4200 Дж/кг*оС.
Решать задачу нужно по формуле:
(eta=Q_{пол}div Q_{зат}times100%)
(Q_{зат}=Ntimes t=10800(сек))
(Q_{пол}=ctimes mtimes(T_2-T_1))
(m=rhotimes V)
(T_1=12) oC
(T_2=70) oC
Конечная формула:
(eta=(ctimesrhotimes Vtimes(T_2-T_1)div Ntimes t)times100%=90%)
Задача 3
Температура воды, налитой в котел паровой машины, составляет 160оС. Температура холодильника – 10оС. Коэффициент полезного действия машины – 60%. В топке сжигается 200 кг угля. Его удельная теплота сгорания – 2,9 • 107 Дж/кг. О какой максимальной работе может идти речь для данной машины?
Решение следующее. Амакс возможна для идеальной тепловой машины, которая функционирует по циклу Карно. Ее КПД равно (Т1-Т2)/Т1. В этой формуле Т1 и Т2 – температуры нагревателя, холодильника.
Определяем КПД, пользуясь формулой: ( eta;=;Adiv Q_1). В этой формуле А – работа тепловой машины, Q1 – теплота, полученная от нагревателя. С другой стороны, она равна (eta_1times mtimes q).
(Q_1;=;eta_1times mtimes q)
((T_1-T_2)div T_1=Adiveta_1times mtimes g)
Итоговая формула:
(А;=;eta_1times mtimes qtimes(1;-;Т_2div Т_1))
Подставив значение, получаем ответ: 1,2*109 Дж.
Тепловой двигатель состоит из нагревателя, рабочего тела и холодильника.
Для характеристики работоспособности двигателей введено понятие коэффициента полезного действия (КПД). Впервые ввёл в науку и технику понятие КПД двигателя французский инженер Сади Карно.

Отношение совершённой полезной работы двигателя к энергии, полученной от нагревателя, называют коэффициентом полезного действия теплового двигателя.
КПД теплового двигателя определяют по формуле:
или
КПД=Q1−Q2Q1⋅100%
.
— полезная работа, совершенная тепловым двигателем;
— количество теплоты, полученное рабочим телом от нагревателя;
— количество теплоты, отданное рабочим телом холодильнику (т.е. окружающей среде);
— количество теплоты, которое пошло на совершение тепловым двигателем полезной работы.
Обрати внимание!
Коэффициент полезного действия не имеет единицы измерения, но может выражается в процентах, или записывается в виде десятичной дроби.
В этом случае он будет меньше единицы, т.е. менее (100)%.
Например, КПД двигателей внутреннего сгорания не превышает (20 )— (40)%, а КПД паровых турбин чуть выше (30)%.

