Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 27 июля 2020 года; проверки требуют 25 правок.
У этого термина существуют и другие значения, см. Напряжение.
| Напряже́ние | |
|---|---|
| U, V | |
| Размерность | L2MT-3I-1 |
| Единицы измерения | |
| СИ | вольт |
| Классическая электродинамика |
|---|
 |
| Электричество · Магнетизм |
|
Электростатика Закон Кулона |
|
Магнитостатика Закон Био — Савара — Лапласа |
|
Электродинамика Векторный потенциал |
|
Электрическая цепь Закон Ома |
|
Ковариантная формулировка Тензор электромагнитного поля |
| См. также: Портал:Физика |
Электри́ческое напряже́ние между точками A и B электрической цепи или электрического поля — скалярная физическая величина, значение которой численно равно работе эффективного электрического поля (включающего сторонние поля), совершаемой при переносе единичного пробного электрического заряда из точки A в точку B[1][2], деленной на величину этого заряда.
При этом считается, что перенос пробного заряда не изменяет распределения зарядов на источниках поля (по определению пробного заряда). Напряжение в общем случае формируется из вкладов двух работ: работы электрических сил 









Определение электрического напряжения можно записать в другой форме. Для этого нужно представить работу 



Размерность электрического напряжения в Международной системе величин (англ. International System of Quantities, ISQ), на которой основана Международная система единиц (СИ), — L2MT-3I-1. Единицей измерения напряжения в СИ является вольт (русское обозначение: В; международное: V).
Понятие напряжение ввёл Георг Ом в работе 1827 года, в которой предлагалась гидродинамическая модель электрического тока для объяснения открытого им в 1826 году эмпирического закона Ома: 
Напряжение в цепях постоянного тока[править | править код]

Исторически принято, что направление тока совпадает с направлением движения положительных зарядов в проводнике (Б. Франклин).
Напряжение в цепи постоянного тока между точками A и B — работа, которую совершает электрическое поле при переносе пробного положительного заряда из точки A в точку B.
Напряжение может быть условно отрицательным, например, при двуполярном питании.
При однополярном источнике питания обычно «землёй» считают один из выводов источника, чаще отрицательный вывод.
Например, в автомобилях «землёй» принято читать корпус автомобиля, который соединяют с отрицательной (тонкой) клеммой свинцового аккумулятора (так было не всегда).
При двуполярном источнике за землю принимают его среднюю точку, соответственно появляется условно положительное напряжение, — от средней точки источника до плюсовой клеммы, и условно отрицательное — от средней точки до минусовой клеммы. Это условное соглашение называют «полярностью напряжения».
Напряжение в цепях переменного тока[править | править код]

Для описания цепей переменного тока применяются следующие напряжения:
- мгновенное напряжение;
- амплитудное значение напряжения;
- среднее значение напряжения;
- среднеквадратическое значение напряжения;
- средневыпрямленное значение напряжения.
Мгновенное напряжение есть разность потенциалов между двумя точками, измеренная в данный момент времени. Зависит от времени (является функцией времени):
Амплитудное значение напряжения есть максимальное по модулю значение мгновенного напряжения за весь период колебаний:
Для гармонических (синусоидальных) колебаний напряжения мгновенное значение напряжения выражается как:
Для сети переменного синусоидального напряжения со среднеквадратическим значением 220 В амплитудное напряжение равно приблизительно 311 В.
Амплитудное напряжение можно измерить с помощью осциллографа.
Среднее значение напряжения (постоянная составляющая напряжения) есть напряжение, определяемое за весь период колебаний, как:
Для синусоиды среднее значение напряжения равно нулю.
Среднеквадратическое значение напряжения (электротехнические наименования: действующее, эффективное) есть напряжение, определяемое за весь период колебаний, как:
Среднеквадратическое значение напряжения наиболее удобно для практических расчётов, так как на линейной активной нагрузке оно совершает ту же работу (например, лампа накаливания имеет ту же яркость свечения, нагревательный элемент выделяет столько же тепла), что и равное ему постоянное напряжение.
Для синусоидального напряжения справедливо равенство:
В технике и быту при использовании переменного тока под термином «напряжение» имеется в виду именно среднеквадратическое значение напряжения, и все вольтметры проградуированы, исходя из его определения. Однако конструктивно большинство приборов фактически измеряют не среднеквадратическое, а средневыпрямленное (см. ниже) значение напряжения, поэтому для несинусоидального сигнала их показания могут отличаться от истинного значения.
Средневыпрямленное значение напряжения есть среднее значение модуля напряжения:
Для синусоидального напряжения справедливо равенство:
На практике используется редко, однако большинство вольтметров переменного тока (те, в которых ток перед измерением выпрямляется) фактически измеряют именно эту величину, хотя их шкала и проградуирована по среднеквадратическим значениям.
Напряжение в цепях трёхфазного тока[править | править код]
В цепях трёхфазного тока различают фазное и линейное напряжения. Под фазным напряжением понимают среднеквадратичное значение напряжения на каждой из фаз нагрузки относительно нейтрали, а под линейным — напряжение между подводящими фазными проводами. При соединении нагрузки в треугольник фазное напряжение равно линейному, а при соединении в звезду (при симметричной нагрузке или при глухозаземлённой нейтрали) линейное напряжение в 
На практике напряжение трёхфазной сети обозначают дробью, в числителе которой стоит фазное при соединении в звезду (или, что то же самое, потенциал каждой из линий относительно земли), а в знаменателе — линейное напряжение. Так, в России наиболее распространены сети с напряжением 220/380 В; также иногда используются сети 127/220 В и 380/660 В.
Характерные значения и стандарты[править | править код]
| Объект | Тип напряжения | Значение (на вводе потребителя) | Значение (на выходе источника) |
|---|---|---|---|
| Электрокардиограмма | Импульсное | 1—2 мВ | – |
| Телевизионная антенна | Переменное высокочастотное | 1—100 мВ | – |
| Гальванический цинковый элемент типа АА («пальчиковый») | Постоянное | 1,5 В | – |
| Литиевый гальванический элемент | Постоянное | 3—3,5 В (в исполнении пальчикового элемента, на примере Varta Professional Lithium, AA) | – |
| Логические сигналы компьютерных компонентов | Импульсное | 3,3 В; 5 В | – |
| Батарейка типа 6F22 («Крона») | Постоянное | 9 В | – |
| Силовое питание компьютерных компонентов | Постоянное | 5 В, 12 В | – |
| Электрооборудование автомобилей | Постоянное | 12/24 В | – |
| Блок питания ноутбука и жидкокристаллических мониторов | Постоянное | 19 В | – |
| Сеть «безопасного» пониженного напряжения для работы в опасных условиях | Переменное | 12—42 В | – |
| Напряжение наиболее стабильного горения свечи Яблочкова | Постоянное | 55 В | – |
| Напряжение в телефонной линии (при опущенной трубке) | Постоянное | 60 В | – |
| Напряжение в электросети Японии | Переменное трёхфазное | 100/172 В | – |
| Напряжение в домашних электросетях США | Переменное трёхфазное | 120 В / 240 В (сплит-фаза[en]) | – |
| Напряжение в бытовых электросетях России | Переменное трёхфазное | 220/380 В | 230/400 В |
| Разряд электрического ската | Постоянное | до 200—250 В | – |
| Контактная сеть трамвая и троллейбуса | Постоянное | 550 В | 600 В |
| Разряд электрического угря | Постоянное | до 650 В | – |
| Контактная сеть метрополитена | Постоянное | 750 В | 825 В |
| Контактная сеть электрифицированной железной дороги (Россия, постоянный ток) | Постоянное | 3 кВ | 3,3 кВ |
| Распределительная воздушная линия электропередачи небольшой мощности | Переменное трёхфазное | 6—20 кВ | 6,6—22 кВ |
| Генераторы электростанций, мощные электродвигатели | Переменное трёхфазное | 10—35 кВ | – |
| На аноде кинескопа | Постоянное | 7—30 кВ | – |
| Статическое электричество | Постоянное | 1—100 кВ | – |
| На свече зажигания автомобиля | Импульсное | 10—25 кВ | – |
| Контактная сеть электрифицированной железной дороги (Россия, переменный ток) | Переменное | 25 кВ | 27,5 кВ |
| Пробой воздуха на расстоянии 1 см | 10—20 кВ | – | |
| Катушка Румкорфа | Импульсное | до 50 кВ | – |
| Пробой слоя трансформаторного масла толщиной 1 см | 100—200 кВ | – | |
| Воздушная линия электропередачи большой мощности | Переменное трёхфазное | 35 кВ, 110 кВ, 220 кВ, 330 кВ | 38 кВ, 120 кВ, 240 кВ, 360 кВ |
| Электрофорная машина | Постоянное | 50—500 кВ | – |
| Воздушная линия электропередачи сверхвысокого напряжения (межсистемные) | Переменное трёхфазное | 500 кВ, 750 кВ, 1150 кВ | 545 кВ, 800 кВ, 1250 кВ |
| Трансформатор Тесла | Импульсное высокочастотное | до нескольких МВ | – |
| Генератор Ван де Граафа | Постоянное | до 7 МВ | – |
| Грозовое облако | Постоянное | От 2 до 10 ГВ | – |
См. также[править | править код]
- Источник напряжения
- Список параметров напряжения и силы электрического тока
- Закон Пашена
Примечания[править | править код]
- ↑ Миллер М. А., Пермитин Г. В. Напряжение электрическое // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 244—245. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
- ↑ Напряжение электрическое / Юрьев Ю. В. // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
- ↑ Детлаф А. А., Яворский Б. М., Милковская Л. Б. Курс физики. — 1977. — Т. 2.
Литература[править | править код]
- Миллер М. А., Пермитин Г. В. Напряжение электрическое // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 244—245. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
- Детлаф А. А., Яворский Б. М., Милковская Л. Б.. Курс физики. Электричество и магнетизм. — М.: “ВЫСШАЯ ШКОЛА”, 1977. — Т. 2.
Ссылки[править | править код]
- Электрическое напряжение // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Про разность потенциалов, электродвижущую силу и напряжение
- «Глоссарий.ру»: Словарь по естественным наукам.
Одним из самых фундаментальных терминов в электротехнике является термин «электрическое напряжение». В этой статье мы объясним, что это такое и как его рассчитать.
Объяснение простыми словами
Электрическое напряжение U является той самой причиной, которая «заставляет» протекать электрический ток I. Электрическое напряжение всегда возникает, когда заряды разделены друг от друга, то есть все отрицательные заряды на одной стороне, а все положительные — на другой. Если соединить эти две стороны электропроводящим материалом, потечет электрический ток.
Общепринятое определение термина «электрическое напряжение».
Электрическое напряжение (или просто напряжение) — это разность потенциалов между двумя точками в электрическом поле. Это движущая сила для электрического заряда.
Потенциал в электрическом поле — это энергия заряженного тела, не зависящая от его электрического заряда. Для пояснения вы можете посмотреть на сравнение с водяным контуром чуть ниже в статье.
Есть другое определение (из учебника по физике 8 класса):
Напряжение — это физическая велuчuна, характеризующая электрическое поле. Электрическое напряжение между двумя точками электрического поля численно равно работе, совершенной при переносе между ними заряда 1 Кл силами электрического поля.
Сравнение с использованием модели протекания воды.
Хорошей аналогией, которая поможет вам представить себе электрическое напряжение и потенциал, является водяной контур. В этой схеме у вас есть два бассейна на разной высоте, которые соединены трубой. В этой трубе вода может перетекать из верхнего бассейна в нижний. Затем вода перекачивается обратно в верхний бассейн с помощью насоса, как показано на рисунке ниже.
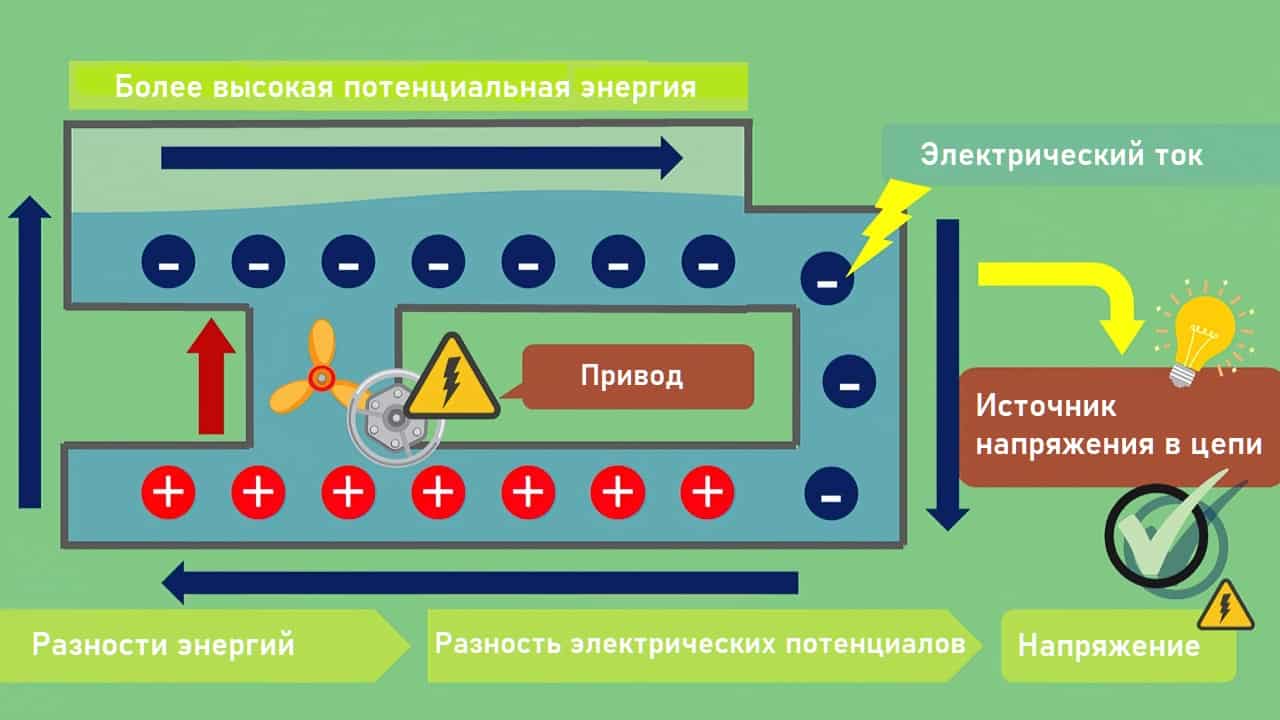
В своих размышлениях вы теперь легко можете сравнить насос с источником электрического напряжения. Кроме того, поток воды можно сравнить с электрическим током. Насос транспортирует воду из нижнего бассейна в верхний. Оттуда она самостоятельно течет обратно в нижний бассейн. В данном примере насос является приводом для потока. Чем больше разница в высоте, тем сильнее поток. Решающим фактором является потенциальная энергия верхнего бассейна. Вы можете сравнить разность энергий двух бассейнов с разностью электрических потенциалов. Проще говоря, большая разница в высоте соответствует большему электрическому напряжению.
Формула
Формула для электрического напряжения U, согласно закона Ома для участка цепи, имеет вид
U = R * I .
Как видно из этой формулы, если электрическое напряжение остается неизменным, то чем больше электрическое сопротивление (R), тем меньше сила тока (I).
Другая формула для расчета электрического напряжения такова:
U = P / I .
То есть электрическое напряжение U равно мощности деленной на силу тока I.
Единица измерения электрического напряжения
Единицей измерения электрического напряжения в СИ является Вольт, сокращенно В (в честь итальянского учёного А. Вольта).
1 вольт (1 В) — это напряжение между двумя точками электрического поля, при переносе между которыми заряда 1 Кл совершается работа 1 Дж.
[U] = 1 В
Теперь вы можете объяснить смысл надписи 4,5 В или 9 В на круглой или плоской батарейке. Смысл в том, что при переносе с одного полюса источника на другой (через спираль лампочки или другой проводник) заряда 1 Кл силами электрического поля может быть совершена работа соответственно 4,5 Дж или 9 Дж.
В электротехнике напряжение может варьироваться от микровольт (1 мкВ = 1 * 10-6 В) и миливольт (1 мВ = 10-3 В), до киловольт (1 кВ = 1 * 103 В) и мегавольт (1 МВ = 106 В)
Вы можете преобразовать отдельные единицы измерения следующим образом:
1 В = 1000 мВ, 1 мВ = 1000 мкВ, 1 МВ = 1000 кВ, 1 кВ = 1000 В.
Электрическое напряжение в цепи
Для источников напряжения в схемах обычно используется один из следующих символов.

Источник напряжения всегда имеет два соединения/полюса. Полюс «плюс» и полюс «минус». Само напряжение обозначено стрелкой напряжения (UQ). Для источников оно всегда отображается от плюса к минусу.
Электрическое напряжение, падающее на резисторе, также можно обозначить стрелкой напряжения (на схеме обозначена как красная стрелка UR ). Это указывает на техническое направление электрического тока.
Также часто можно услышать термин «напряжение холостого хода» или «напряжение источника». Это выходное напряжение ненагруженного источника, т.е. источника, к которому ничего не подключено. Если цепь замкнута с нагрузкой, то можно измерить только напряжение на полюсах источника.
Электрические напряжения при последовательном и параллельном соединении
У нас уже есть статья о последовательном и параллельном соединении проводников, в котором мы обсуждаем эту тему более подробно. Поэтому здесь мы рассмотрим лишь некоторые основы.
При последовательном соединении компоненты подключаются в ряд.

Здесь электрическое напряжение источника делится на резисторы. Этот момент также описывается вторым правилом Кирхгофа. Здесь применимо следующее:
UQ = U1 + U2 + U3
то есть напряжение источника равно сумме электрических напряжений на отдельных резисторах. Напряжение источника по-разному распределяется по разным резисторам.
В электрической цепи с параллельным соединением компоненты расположены, соответственно, параллельно друг относительно друга. Это можно увидеть на следующей схеме.

Здесь гораздо проще определить электрические напряжения на резисторах, так как при параллельном соединении:
UQ = U1 = U2 = U3
Поэтому электрическое напряжение на резисторах такое же высокое, как и электрическое напряжение источника.
Измерение электрического напряжения
Приборы для измерения напряжения, также называемые вольтметрами, всегда подключаются параллельно потребителю, на котором необходимо измерить электрическое напряжение.
Одним из наиболее часто используемых вольтметров является цифровой мультиметр (DMM), поэтому мы покажем вам процедуру измерения напряжения с помощью DMM. Сначала необходимо установить тип электрического напряжения (DC — постоянный ток или AC — переменный ток).
Для постоянного тока необходимо обратить внимание на правильную полярность, т.е. подключить плюс к положительному полюсу. На следующем этапе необходимо выбрать правильный диапазон измерения. Если вы не можете оценить, насколько велика измеряемая величина, установите наибольший возможный диапазон и двигайтесь от него вниз, пока не найдете нужный. Наконец, вам нужно только «считать» электрическое напряжение прибором.
Примеры типовых значений электрического напряжения
Для некоторых применений соответствующее электрическое напряжение можно найти в таблице ниже.
| Светодиод | 1,2 — 1,5 В |
| Зарядное устройство USB | 5 В |
| Напряжение автомобильного аккумулятора | 12, 4 — 12,8 В |
| Напряжение в розетке (среднеквадратичное или действующее значение) | 230 В |
| Высоковольтные линии электропередач (ЛЭП) | 60 кВ — 1 МВ |
Вы можете видеть, что на высоковольтных линиях присутствует напряжение до мегавольт. Такие большие электрические напряжения используются для того, чтобы уменьшить потери в длинных линиях.
Решающим фактором для потребителя является мощность P, которую можно рассчитать для постоянного напряжения с помощью формулы:
P = U * I
Это означает, что электрический ток I так же важен для потребителя, как и электрическое напряжение. Согласно закону Ома, зависимость между током и напряжением имеет вид:
U = R * I .
Если напряжение остается неизменным, сопротивление определяет величину тока. Чтобы проиллюстрировать это, представьте следующее. У вас есть три разных бассейна, которые заполнены одинаковым количеством воды. Каждый бассейн имеет слив, который различается по сечению, т.е. в одном бассейне сливная труба очень маленькая, а в другом — очень большая.
Постоянное электрическое напряжение можно определить по тому, что все емкости заполнены на одинаковую высоту. Если слив узкий в нижней части, он представляет собой большое сопротивление. Ток здесь может течь только медленно. Если сечение сливной трубы больше, то сопротивление меньше и, соответственно, может протекать больший ток.
Пробовали ли вы когда-нибудь надувать воздушные шарики на время? Один надувает быстро, а другой за это же время надувает гораздо меньше. Без сомнения, первый совершает большую работу, чем второй.

Рис. (1). Надувание шара
С источниками напряжения происходит точно так же. Чтобы обеспечить движение частиц в проводнике, надо совершить работу. И эту работу совершает источник. Работу источника характеризует напряжение. Чем оно больше, тем большую работу совершает источник, тем ярче будет гореть лампочка в цепи (при других одинаковых условиях).

Рис. (2). Лампа в цепи
Напряжение равно отношению работы электрического поля по перемещению заряда
к величине перемещаемого заряда на участке цепи.
U=Aq
, где (U) — напряжение, (A) — работа электрического поля, (q) — заряд.
Обрати внимание!
Единица измерения напряжения в системе СИ — [(U)] = (1) B (вольт).
(1) вольт равен электрическому напряжению на участке цепи, где при протекании заряда, равного (1) Кл, совершается работа, равная (1) Дж: (1) В (= 1) Дж/1 Кл.
Все видели надпись на домашних бытовых приборах «(220) В». Она означает, что на участке цепи совершается работа (220) Дж по перемещению заряда (1) Кл.
Кроме вольта, применяют дольные и кратные ему единицы — милливольт и киловольт.
(1) мВ (= 0,001) В, (1) кВ (= 1000) В или (1) В (= 1000) мВ, (1) В (= 0,001) кВ.
Для измерения напряжения используют прибор, который называется вольтметр.
Обозначаются все вольтметры латинской буквой (V), которая наносится на циферблат приборов и используется в схематическом изображении прибора.

Рис. (3). Обозначение вольтметра
В школьных условиях используются вольтметры, изображённые на рисунке:


Рис. (4). Вольтметры
Основными элементами вольтметра являются корпус, шкала, стрелка и клеммы. Клеммы обычно подписаны плюсом или минусом и для наглядности выделены разными цветами: красный — плюс, черный (синий) — минус. Сделано это с той целью, чтобы заведомо правильно подключать клеммы прибора к соответствующим проводам, подключённым к источнику.
Обрати внимание!
В отличие от амперметра, который включается в разрыв цепи последовательно, вольтметр включается в цепь параллельно.
Рис. (5). Электроцепь с подключенным вольтметром и амперметром
Включая вольтметр в цепь постоянного тока, необходимо соблюдать полярность.
Сборку электрической цепи лучше начинать со всех элементов, кроме вольтметра, а его уже подключать в самом конце.
Вольтметры делятся на приборы постоянного тока и переменного тока.
Если прибор предназначен для цепей переменного тока, то на циферблате принято изображать волнистую линию. Если прибор предназначен для цепей постоянного тока, то линия будет прямой.
Таблица (1). Вольтметры
|
Рис. (6). Вольтметр постоянного тока |
Рис. (7). Вольтметр переменного тока |
|
|
|
|
|
|
Можно обратить внимание на клеммы прибора. Если указана полярность («(+)» и «(-)»), то это прибор для измерения постоянного напряжения.
Иногда используют буквы (AC/DC). В переводе с английского (AC) (alternating current) — переменный ток, а (DC) (direct current) — постоянный ток.
В цепь переменного тока включается вольтметр для измерения переменного тока. Он полярности не имеет.
Рис. (8). Электроцепь с переменным источником тока
Обрати внимание!
Для измерения напряжения можно использовать и мультиметр.
Перед измерением необходимо прочитать инструкцию, чтобы правильно подключить прибор.

Рис. (9). Мультиметр
Следует помнить, что высокое напряжение опасно.
Что будет с человеком, который окажется рядом с упавшим оголённым кабелем, находящимся под высоким напряжением?
Так как земля является проводником электрического тока, вокруг упавшего оголённого кабеля, находящегося под напряжением, может возникнуть опасное для человека шаговое напряжение.
При попадании под шаговое напряжение даже небольшого значения возникают непроизвольные судорожные сокращения мышц ног. Обычно человеку удаётся в такой ситуации своевременно выйти из опасной зоны.
Обрати внимание!
Однако нельзя выбегать оттуда огромными шагами, шаговое напряжение при этом только увеличится! Выходить надо обязательно быстро, но очень мелкими шагами или скачками на одной ноге!
Существует много знаков, предупреждающих о высоком напряжении. Вот некоторые из них.




Рис. (10). Предупреждающие об опасности знаки
Источники:
Рис. 5. Электроцепь с подключенным вольтметром и амперметром. © ЯКласс.
Рис. 8. Электроцепь с переменным источником тока. © ЯКласс.
Формула напряжения в физике — это представление электрической потенциальной энергии на единицу заряда. Если ток был размещен в определенном месте, напряжение указывает на ее потенциальную энергию в этой точке. Другими словами, это измерение силы, содержащейся в электрическом поле или цепи в данной точке. Он равен работе, которую нужно было бы выполнить за единицу заряда против электрического поля, чтобы переместить его из одной точки в другую.
Напряжение является скалярной величиной, у него нет направления. Закон Ома гласит, что интенсивность равна текущему временному сопротивлению.
Сопротивление
Формула механической мощности — средняя и мгновенная мощность
Любой проводник в цепи препятствует прохождению через себя тока. Данная характеристика определяет такую физическую величину, как сопротивление. Исходя из величины сопротивления, все вещества относят к проводникам или изоляторам. Точная граница весьма расплывчата, поэтому при некоторых условиях некоторые вещества можно отнести как к изоляторам, так и к проводникам. Участок электросхемы может иметь элемент с определенным значением величины, который именуется резистор.

Резисторы различных типов
Для переменного тока
Нужно понимать, что закон не применим напрямую к переменным цепям, например, с катушками индуктивности, конденсаторами или линиям передач. Закон может использоваться только для чисто резистивных цепей переменного тока без каких-либо изменений. В цепи RLC противодействие току является импедансом Z, который образует комбинацию двух ортогональных частей сопротивления.
Переменный ток
Im=Vm/Z
В этом случае Vm связано с Im с помощью константы пропорциональности Z (импеданса) и константы пропорциональности R. Для чисто резистивных линий, где (Z = R).
Vm = ImZ и Vm = ImR
Z — это общее сопротивление участка к переменному току, состоящее из реальной части — сопротивления и мнимой — реактивности.
Формула ее определяется теоремой Пифагора, поскольку угол Ф зависит от реактивной составляющей.
Интегральная форма
Взаимосвязь параметров электрической цепи
Все параметры любой электрической цепи строго взаимосвязаны, поэтому в любой момент времени можно точно определить величину любого из них, зная остальные.
К сведению. Основополагающий закон, по которому производится большинство расчетов, – закон Ома, согласно которому сила тока обратно пропорциональна его сопротивлению и прямо пропорциональна приложенной разности потенциалов.

Формула напряжения тока закона Ома выглядит следующим образом:
I=U/R.
Так, цепь с большим напряжением пропускает больший ток, а при одинаковом напряжении ампераж будет больше там, где меньше сопротивление.
Принятые обозначения в формуле расчета напряжения и тока понятны во всем мире:
- I – сила тока;
- U – напряжение;
- R – сопротивление.
Путем простейшего математического преобразования находится формула расчета сопротивления через силу тока и напряжение.
Кроме закона Ома, используется формула расчета мощности:
P=U∙I.
Символом P здесь обозначена мощность тока.
Любая схема может содержать участки, где имеется последовательное соединение, или есть элемент, подключенный параллельно. Расчеты при этом усложняются, но базовые формулы остаются одинаковыми.
Закон Ома для неоднородного участка цепи
Физическая величина, равная отношению работы сторонних сил Aст при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой (ЭДС) источника Eэдс:
$ E_{эдс} = {A_{cт}over q} $ (1).
Таким образом, ЭДС равна работе, совершаемой сторонними силами при перемещении единичного положительного заряда. При перемещении единичного положительного заряда по замкнутой цепи постоянного тока работа электростатического поля равна нулю, а работа сторонних сил равна сумме всех ЭДС, действующих в этой цепи.
Работа электростатических сил по перемещению единичного заряда равна разности потенциалов $ Δφ = φ_1 – φ_2 $ между начальной и конечной точками 1 и 2 неоднородного участка. Работа сторонних сил равна, по определению, электродвижущей силе Eэдс, действующей на данном участке. Поэтому полная работа равна:
$ U_п = φ_1 – φ_2 + E_{эдc} $ (2).
Величина Uп называется напряжением на участке цепи 1–2. В случае однородного участка напряжение равно разности потенциалов:
$ U_п = φ_1 – φ_2 $ (3).
Немецкий исследователь Георг Симон Ом в начале XIX века установил, что сила тока I, текущего по однородному проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:
$ I = {U over R} $ (4).
Рис. 2. Портрет Георга Ома.
Величина R — это электрическое сопротивление. Уравнение (4) выражает закон Ома для однородного участка цепи. Для участка цепи, содержащего ЭДС, закон Ома записывается в следующем виде:
$ U_п = I * R = φ_1 – φ_2 + E_{эдс} = Δ φ_{12} + E_{эдс}$ (5).
Данное уравнение называется обобщенным законом Ома для неоднородного участка цепи.
Как работает закон в реальной жизни
Используя совместно формулу расчета мощности и закон Ома, можно производить вычисления, не зная одной из величин. Самый простой пример – для лампы накаливания известны только ее мощность и напряжение. Применяя приведенные выше формулы, можно легко определить параметры нити накаливания и ток через нее.

Сила тока формула через мощность:
I=P/U;
Сопротивление:
R=U/I.
Такой же результат можно найти из мощности, не прибегая к промежуточным расчетам:
R=U2/P.
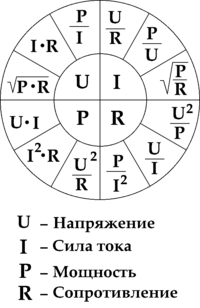
Аналогично можно вычислить любую величину, зная только две из них. Для упрощения преобразований имеется мнемоническое отображение формул, позволяющее находить любые величины.

Внимательно посмотрев на формулы, можно заметить, что, если уменьшить напряжение на лампе в два раза, ожидаемая мощность не снизится аналогично в два раза, а в четыре, согласно формуле:
P=U2/R.
Это довольно распространенная ошибка среди далеких от электротехники людей, которые неправильно соотносят мощность и напряжение, а также их действие на остальные параметры.
Кстати. Сила тока, найденная через сопротивление и напряжение, справедлива как для постоянного, так и для переменного тока, если в ней не используются такие элементы, как конденсатор или индуктивность.
Облегчить расчеты можно, используя онлайн калькулятор.
Определение через разложение электрического поля
Используя приведенное выше понятие, потенциал не находится на одном месте, когда магнитные поля меняются со временем. В физике иногда полезно обобщать электрическое значение, рассматривая только консервативную часть поля. Это делается с помощью следующего разложения, используемого в электродинамике.

В показанной выше формуле Е — индуцированный — вращательное электрическое поле, обусловленное изменяющимися во времени магнитными фонами. В этом случае сила между точками всегда определяется однозначно.
Пример с обычной водой
Существуют вещества, которые можно отнести одновременно к проводникам и изоляторам. Самый простой пример – обыкновенная вода. Дистиллированная вода является хорошим изолятором, но наличие в ней практически любых примесей делает ее проводником. Особенно это относится к солям различных металлов. При растворении в воде соли диссоциируются на ионы, их наличие – прямой повод для возникновения тока. Чем больше концентрация солей, тем меньшим сопротивлением будет обладать вода.

Для наглядности можно взять дистиллированную воду для приготовления электролита для автомобильных аккумуляторных батарей. Опустив щупы омметра в воду, можно увидеть, что его показания велики. Добавление всего нескольких кристаллов поваренной соли через некоторое время вызывает резкое уменьшение сопротивления, которое будет тем меньше, чем больше соли перейдет в раствор.
Различные используемые величины
Кроме основных величин: вольт, ампер, ом, ватт, используют кратные, большие или меньшие. Для обозначений применяют соответствующие приставки:
- Кило – 1000;
- Мега – 1000000;
- Гига – 1000000000;
- Милли – 0.001.
Таким образом, получается:
- Киловольт (кВ) – тысяча вольт;
- Мегаватт (Мвт) – миллион ватт;
- Миллиом (мОм) – одна тысячная Ом;
- Гигаватт (ГВт) – тысяча мегаватт или миллиард ватт.
Как найти напряжение
Формула нахождения напряжения как разности потенциалов в электрическом поле:
U=ϕA-ϕB, где ϕAи ϕB – потенциалы в точках А и В, соответственно.
Также можно записать напряжение как работу по переносу единицы заряда из точки А в точку В в электрическом поле:
U=A/q, где q – величина заряда.
Работа тем больше, чем выше напряженность электрического поля Е, то есть сила, действующая на неподвижный заряд.
Потенциальную энергию заряда в электростатическом поле называют электростатический потенциал.
Единицы измерения в формуле
Вам будет интересно:Антиклиналь + синклиналь – это складчатые горы

В формуле, определяющей напряжение, значением СИ является вольт. Таким образом, что 1В = 1 джоуль/кулон. Вольт назван в честь итальянского физика Алессандро Вольта, который изобрел химическую батарею.
Это означает, что в формуле напряжения в физике один кулон заряда получит один джоуль потенциальной энергии, когда он будет перемещен между двумя точками, где разность электрических потенциалов составляет один вольт. При напряжении 12, один кулон заряда получит 12 джоулей потенциальной энергии.
Батарея на шесть вольт имеет потенциал для одного кулона заряда, чтобы получить шесть джоулей потенциальной энергии между двумя местоположениями. Батарея на девять вольт имеет потенциал для одного кулона заряда, чтобы получить девять джоулей потенциальной энергии.
Гидравлическая аналогия
Чтобы легче усвоить законы электрических цепей, можно представить себе аналогию с гидравлической системой, в которой соединение насоса и трубопроводов образует замкнутую систему. Для этого нужны следующие соответствия:
- Источник питания – насос;
- Проводники – трубы;
- Электроток – движение воды.
Без особых усилий становится понятнее, что чем меньше диаметр труб, тем медленнее по ним движется вода. Чем мощнее насос, тем большее количество воды он способен перекачать. При одинаковой мощности насоса уменьшение диаметра труб приведет к снижению потока воды.

Измерительные приборы
Для измерения параметров электрических цепей служат измерительные приборы:
- Вольтметр;
- Амперметр;
- Омметр.
Наиболее часто используется класс комбинированных устройств, в которых переключателем выбирается измеряемая величина – ампервольтомметры или авометры.

Закон Ома назван в честь своего открывателя это ученый Георг Симон Ом. Свои эксперименты в области электричества он начал вдохновляясь опытами Фурье. Ом проводил свои опыты с различными материалами и изучение их электропроводности. Так была разработана знаменитая формула, которая стала краеугольной в современной физике, которая вошла в школьные учебники: I=U/R. Сила тока пропорциональна величине напряжения и имеет обратную пропорциональность сопротивлению.
В статье подробно разобраны области теории и практического применения принципов закона Ома в современной электротехнике. В качестве дополнения, в материале содержатся два обучающих видеоролика и один научный материал на тему статьи.
Закон Ома
Закон Ома показывает отношения между напряжением (U), током (I) и сопротивлением (R). Записано это может быть тремя разными способами:
U = I × R
или
I = V/R
или
R = V/I
Где:
- V – напряжение в вольтах (В);
- I – сила тока в амперах (А);
- R – сопротивление в омах (Ом);
Для большинства схем амперы – слишком большие величины, а омы – слишком маленькие. Поэтому в формулу можно подставлять миллиамперы и килоомы. Если силу тока подставлять в миллиамперах (мА), то сопротивление обязательно должно быть в килоомах (кОм) и наоборот. Напряжение – всегда в вольтах.
Чтобы проще запомнить три разные версии определения Закона Ома, можно воспользоваться «VIR-треугольником».
- Если надо вычислить напряжение, закрываем пальцем V. У нас остаются I и R. Они на одном уровне, значит между ними ставим знак умножения. Получается: V = I × R .
- Если вычисляем ток, закрываем пальцем I. У нас остаётся V над R. Значит напряжение делится на сопротивление: I = V/R .
- Аналогичным образом поступаем при вычислении сопротивления. Закрываем R. Остаётся V над I. Значит: R = V/I .
Закон Ома, определение: Сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению. Есть также частный случай – Закон Ома для участка цепи – сила тока в участке цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна сопротивлению этого участка.
Закон Ома для цепи
Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит. Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).
Итак, закон Ома для рассматриваемого участка цепи имеет вид:
φ1-φ2=I*R, где
- I – ток, протекающий по участку цепи.
- R – сопротивление этого участка.
- φ1-φ2 – разность потенциалов между точками 1-2.
Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R. Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).
В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:
- U1=I*R1
- U2=I*R2
- Un=I*Rn
- U=I*(R1+R2+…+Rn
Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:
U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn
Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.
Для ЭДС
Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:
Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.
Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.
Для полной цепи
Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.
Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.
Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:
I = U / (R + r)
Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.
Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.
Для переменного тока
Переменный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).
Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.
Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.
Для замкнутой цепи
На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие активного сопротивления от реактивного в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.
Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.
Формула для расчета падения напряжения на индуктивном сопротивлении:
U = I ⋅ ωL
Где L – индуктивность реактивного сопротивления, а ω – угловая частота (производная по времени от фазы колебания).
Формула для расчета падения напряжения на емкостном сопротивлении:
U = I / ω ⋅ С
С – емкость реактивного сопротивления.
Эти две формулы – частные случаи закона Ома для переменных цепей.
Полный же будет выглядеть следующем образом:
I = U / Z
Здесь Z – полное сопротивление переменной цепи известное как импеданс.
Сфера применения
Закон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:
- Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
- В сверхпроводниках;
- Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
- В вакуумных и газовых радиолампах;
- В диодах и транзисторах.
Последовательное и параллельное включение элементов
Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение. Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.
Цепь последовательно включенных резистивных элементов
Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:
- I = I1= I2 ;
- U = U1+ U2 ;
- R = R1+ R2
Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения. Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.
При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx. Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.
Цепь параллельно включенных резистивных элементов
На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:
- I = I1+ I2 … ;
- U = U1= U2 … ;
- 1 / R = 1 / R1+ 1 / R2 + …
Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение. Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.
Интегральная и дифференциальная формы закона
Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры. Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.
Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.
Под дифференциальный расчет берется формула: J = ό * E. Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.












