Чтобы определить площадь тела, используют формулы: площадь прямоугольника S можно рассчитать, умножив длину прямоугольника на ширину прямоугольника. S = l 1 ⋅ l 2 . Площадь треугольника S = ah 2 , где a — сторона, h — высота, проведённая к данной стороне.
Как найти S в физике 7 класс?
Путь (s) — длина траектории, по которой двигалось тело, численно равен произведению скорости (v) тела на время (t) движения.
A = Fs, где А — работа, F — сила и s — пройденный путь. За единицу работы принимается работа, совершаемая силой в 1Н, на пути, равном 1 м.
Как найти P в физике 7 класс?
Если высоту столба жидкости, находящейся в сосуде, обозначить буквой h, а площадь дна сосуда S, то V = S·h. Масса жидкости m = ρ·V, или m = ρ·S·h . Вес этой жидкости P = g·m, или P = g·ρ·S·h. p = g·ρ·h.
Что значит V в физике 7 класс?
В физике величиной, характеризующей быстроту движения, называется скорость. … Чтобы определить скорость при равномерном движении, надо путь, пройденный телом за какой-то промежуток времени, разделить на этот промежуток времени: скорость = путь/время. Скорость обозначают буквой v, путь — s, время — t.
Как найти L по физике?
Формула:T = 2π√L/g.
Что означают буквы в физике 7 класс?
А также: A — работа; В — магнитная индукция; С — электроемкость конденсатора; D — оптическая сила; Е — напряженность электрического поля, энергия (в электростатике W); F — сила, фокусное расстояние линзы, постоянная Фарадея; K — Кельвин, кинетическая энергия: G — гравитационная постоянная; H — высота, напряженность …
Чему равна сила в физике?
Сила равна массе тела, умноженной на его ускорение. – ускорение. Единица измерения силы – Н (ньютон). Вектор силы направлен туда же, куда и ускорение.
Как найти P в физике электричество?
Мощность электрического тока обозначают буквой Р: P = A t = U ⋅ I ⋅ t t = U ⋅ I . Таким образом: Мощность электрического тока равна произведению напряжения на силу тока: P = U ⋅ I .
Как найти объем по физике?
По какой формуле можно найти объем?
- Зная массу и плотность V = m/ρ, где m — масса, а ρ — плотность
- Для геометрических фигур, например куб V = a^3 перемножить три стороны, а для цилиндра V = S*H площадь основания помножить на высоту
Как найти H по физике?
В данном случае можем воспользоватся формулой H = (g*t^2) / 2. Где H — искомая высота g-ускорение свободного падения равное 9.8 м/c^2 t-время падения. Тогда скорость сможем рассчитать по формуле V=g*t.
- Главная
- Справочник
- Как найти площадь прямоугольника
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость
Как найти площадь прямоугольника
Содержание:
- Формула
- Примеры вычисления площади прямоугольника
Формула
Чтобы найти площадь прямоугольника (рис. 1), надо его длину умножить на ширину, то есть
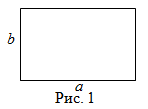
Прямоугольником называется четырехугольник, у которого все углы равны. Все углы в прямоугольнике прямые, то есть равны $90^{circ}$.
Примеры вычисления площади прямоугольника
Пример
Задание. Найти площадь прямоугольника, если одна его сторона равна 3 см, а вторая, смежная с ней – 5 см.
Решение. Искомая площадь прямоугольника равна произведению двух заданных сторон:
$S=3 cdot 5=15$ (см2)
Ответ. $S=15$ (см2)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти площадь прямоугольника, если одна его сторона равна 3 м, а диагональ – 5 м.
Решение. Сделаем чертеж (рис. 2).
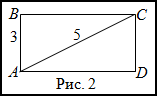
Рассмотрим прямоугольный треугольник $ABC$, из которого по
теореме Пифагора найдем длину катета $BC$ :
$B C=sqrt{A C^{2}-A B^{2}}=sqrt{5^{2}-3^{2}}=sqrt{25-9}=sqrt{16}=4$ (м)
Тогда искомая площадь равна
$S=3 cdot 4=12$ (м2)
Ответ. $S=12$ (м2)
Читать дальше: как найти площадь параллелограмма.
Статьи по теме
- Как найти площадь
- Как найти площадь треугольника
- Как найти площадь ромба
- Как найти площадь эллипса
- Как найти площадь прямоугольного треугольника
- Все темы раздела “Как найти площадь”

Разделы
- Формулы сокращенного умножения
- Формулы по физике
- Логарифмы
- Векторы
- Матрицы
- Комплексные числа
- Пределы
- Производные
- Интегралы
- СЛАУ
- Числа
- Дроби
Все еще сложно?
Не получается написать работу самому?
Доверь это кандидату наук!
Ищещь ответ на вопрос с которым нужна помощь?
80% ответов приходят в течение 10 минут
250 ответов по вашей теме сегодня
2 специалиста свободны онлайн
Ответы приходят уже через 10 минут
90% ответов положительные
Выбирайте формулу, ориентируясь на известные величины.
1. Если известны две соседние стороны
Просто перемножьте две стороны прямоугольника.
- S — искомая площадь прямоугольника;
- a и b — соседние стороны.
2. Если известны любая сторона и диагональ
Найдите квадраты диагонали и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте длину известной стороны на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).
3. Если известны любая сторона и диаметр описанной окружности
Найдите квадраты диаметра и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте известную сторону на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- D — диаметр описанной окружности.
4. Если известны любая сторона и радиус описанной окружности
Найдите квадрат радиуса и умножьте результат на 4.
Отнимите от полученного числа квадрат известной стороны.
Найдите корень из результата и умножьте на него длину известной стороны.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- R — радиус описанной окружности.
5. Если известны любая сторона и периметр
Умножьте периметр на длину известной стороны.
Найдите квадрат известной стороны и умножьте полученное число на 2.
От первого произведения отнимите второе и разделите результат на 2.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- P — периметр прямоугольника (равен сумме всех сторон).
6. Если известны диагональ и угол между диагоналями
Найдите квадрат диагонали.
Разделите полученное число на 2.
Умножьте результат на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- d — любая диагональ прямоугольника;
- α — любой угол между диагоналями прямоугольника.
7. Если известны радиус описанной окружности и угол между диагоналями
Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.
Умножьте полученное число на 2, а потом на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- R — радиус описанной окружности;
- α — любой угол между диагоналями прямоугольника.
Читайте также 🎓❓📐
- ТЕСТ: Умеете ли вы считать в уме?
- Как легко и быстро считать проценты в уме
- Как найти площадь любого треугольника
- ТЕСТ: Сколько центнеров в тонне? А сантиметров в дециметре? Проверьте, умеете ли вы переводить единицы измерения
- Как освоить устный счёт школьникам и взрослым
Что такое прямоугольник
Определение
Прямоугольник — параллелограмм, в котором все углы прямые.
В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые, тогда четвёртый угол в силу теоремы о сумме углов многоугольника также будет равен 90°.
Свойства
- Противоположные стороны попарно равны.
- Диагонали равны. Они пересекаются и точкой пересечения делятся пополам.
- Биссектриса отсекает от прямоугольника равнобедренный треугольник.
- Стороны прямоугольника являются его высотами.
- Квадрат диагонали прямоугольника равен сумме квадратов двух его соседних сторон.
- Около любого прямоугольника можно описать окружность, при этом ее диаметр численно равен диагонали прямоугольника.
Признаки
Параллелограмм является прямоугольником при выполнении одного из следующих условий:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- Диагонали параллелограмма равны.
- Сумма квадратов соседних сторон параллелограмма равна квадрату диагонали.
- Все углы параллелограмма равны.
Формулы для нахождения площади
Через две стороны
Площадь прямоугольника через две стороны можно вычислить по формуле:
(S=ab)
где a, b — соседние стороны прямоугольника.
Через диагонали и синус угла между ними
Для того, чтобы найти площадь прямоугольника через диагонали и синус угла, нужно воспользоваться формулой:
(S=frac{d^2sinalpha}2)
где (d ) — диагональ, (alpha) — угол между диагоналями (острый).
Через любую сторону и диагональ
Чтобы определить площадь прямоугольника через любую сторону и диагональ, нужно воспользоваться формулой:
(S=asqrt{d^2-a^2}=bsqrt{d^2-b^2})
где a, b — соседние стороны прямоугольника, d — диагональ.
Через сторону и диаметр описанной окружности
Чтобы узнать площадь прямоугольника через сторону и диаметр описанной окружности, нужно воспользоваться формулой:
(S=asqrt{D^2-a^2}=bsqrt{D^2-b^2})
где a, b — соседние стороны прямоугольника, D — диаметр описанной окружности.
Через сторону и радиус описанной окружности
Вычисление площади прямоугольника через сторону и радиус описанной окружности происходит по формуле:
(S=asqrt{4R^2-a^2}=bsqrt{4R^2-b^2})
где a, b — соседние стороны прямоугольника, R — радиус описанной окружности.
Через сторону и периметр
Чтобы посчитать площадь прямоугольника через сторону и периметр, нужно воспользоваться формулой:
(S=frac{Pa-2a^2}2=frac{Pb-2b^2}2)
где a, b — соседние стороны прямоугольника, Р — периметр.
Через радиус описанной окружности и синус угла между диагоналями
Способ нахождения площади прямоугольника через радиус окружности и синус угла между диагоналями происходит по формуле:
(S=frac{4R^2sinalpha}2)
где (R) — радиус описанной окружности, (alpha) — угол между диагоналями (острый).

{S = a cdot b}
Найти площадь прямоугольника
Найти площадь прямоугольника вы сможете с помощью калькуляторов или по формулам вручную. Для этого мы подготовили 6 формул и калькулятор, который позволяет произвести расчет по любой из них.
Прямоугольник — четырехугольник, у которого все углы равны 90° (прямые).
Содержание:
- калькулятор площади прямоугольника
- формула площади прямоугольника через стороны
- формула площади прямоугольника через сторону и диагональ
- формула площади прямоугольника через диагонали и угол
- формула площади прямоугольника через сторону и периметр
- формула площади прямоугольника через сторону и радиус описанной окружности
- формула площади прямоугольника через радиус описанной окружности и угол между диагоналями
- примеры задач
Формула площади прямоугольника через стороны

S = a cdot b
a, b – стороны прямоугольника (длина и ширина)
Формула площади прямоугольника через сторону и диагональ
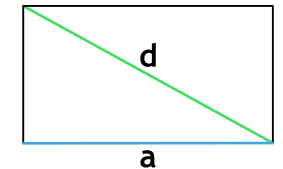
S=a cdot sqrt{d^2 – a^2}
d – диагональ прямоугольника
a – сторона прямоугольника
Формула площади прямоугольника через диагонали и угол
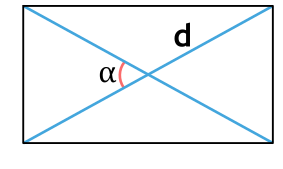
S = dfrac{1}{2} cdot d^2 cdot sin(alpha)
d – диагональ прямоугольника
α – угол между диагоналями
Формула площади прямоугольника через сторону и периметр

S = dfrac{a cdot P – 2a^2}{2}
a – сторона прямоугольника
P – периметр прямоугольника
Формула площади прямоугольника через сторону и радиус описанной окружности
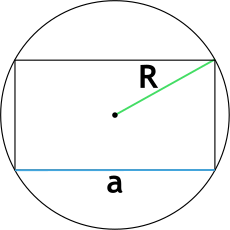
S = a cdot sqrt{4R^2 – a^2}
R – радиус описанной окружности
a – сторона прямоугольника
Формула площади прямоугольника через радиус описанной окружности и угол между диагоналями
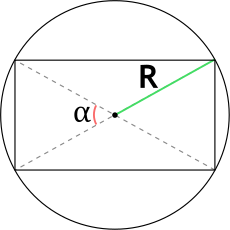
S = 2R^2 cdot sin{alpha}
R – радиус описанной окружности
α – угол между диагоналями
Примеры задач на нахождение площади сектора круга
Задача 1
Найдите площадь прямоугольника диагональ которого равна 10 см, а угол между диагоналями равен 30°.
Решение
Так как в условии нам даны диагональ и угол, нам подойдет третья формула.
S = dfrac{1}{2} cdot d^{: 2} cdot sin(alpha) = dfrac{1}{2} cdot 10^2 cdot sin(30°) = dfrac{1}{2} cdot 100 cdot sin(30°) = 50 cdot dfrac{1}{2} = 25 : см^2
Ответ: 25 см²
Для проверки результата воспользуемся калькулятором .
Задача 2
Найдите площадь прямоугольника со сторонами 4 см и 13 см.
Решение
Используем первую формулу.
S = a cdot b = 4 cdot 13 = 52 : см^2
Ответ: 52 см²
Проверим ответ на калькуляторе .
Задача 3
Найдите площадь прямоугольника если его длина 2 дм а ширина 4 см.
Решение
Задача аналогична предыдущей. Тоже воспользуемся первой формулой. Учтем, что 2 дм = 20 см.
S = a cdot b = 20 cdot 4 = 80 : см^2
Ответ: 80 см²
Проверим ответ на калькуляторе .
Задача 4
Найдите площадь прямоугольника, если его длина равна 7 см а ширина 4 см.
Решение
И снова однотипная задача. Решим ее как и две решенные выше.
S = a cdot b = 7 cdot 4 = 28 : см^2
Ответ: 28 см²
Проверка .
