Работа сил электростатического поля. Понятие потенциала
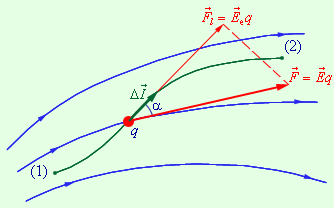
Когда пробный заряд q перемещается в электрическом поле, можно говорить о работе, совершаемой в данный момент электрическими силами. Для малого перемещения ∆l→ формулу работы можно записать так: ∆A=F·∆l·cos α=Eq∆lcos α=Elq∆l.
Рисунок 1.4.1. Малое перемещение заряда и работа, совершаемая в данный момент электрическими силами.
Теперь посмотрим, какую работу по перемещению заряда совершают силы в электрическом поле, которое создается распределенным зарядом, не изменяющимся во времени. Такое поле еще называют электростатическим. У него есть важное свойство, о котором мы поговорим в этой статье.
При перемещении заряда из одной точки электростатического поля в другую работа сил электрического поля будет зависеть только от величины этого заряда и положением начальной и конечной точки в пространстве. Форма траектории при этом не имеет значения.
У гравитационного поля есть точно такое же свойство, что неудивительно, поскольку соотношения, с помощью которых мы описываем кулоновские и гравитационные силы, одинаковы.
Исходя из того, что форма траектории не имеет значения, мы можем также сформулировать следующее утверждение:
Когда заряд в электростатическом поле перемещается по любой замкнутой траектории, работа сил поля равна 0. Поле, обладающее таким свойством, называется консервативным, или потенциальным.
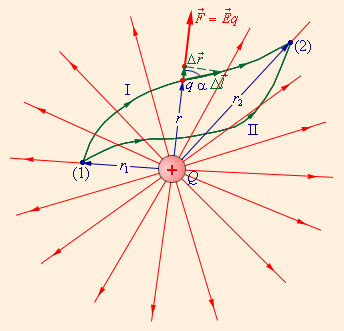
Ниже приведена иллюстрация силовых линий в кулоновском поле, образованных точечным зарядом Q, а также две траектории перемещения пробного заряда q в другую точку. Символом ∆l→ на одной из траекторий обозначается малое перемещение. Запишем формулу работы кулоновских сил на нем:
∆A=F∆lcos α=Eq∆r=14πε0Qqr2∆r.
Следовательно, зависимость существует только между работой и расстоянием между зарядами, а также их изменением Δr. Проинтегрируем данное выражение на интервале от r=r1 до r=r2 и получим следующее:
A=∫r1r2E·q·dr=Qq4πε01r1-1r2.
Рисунок 1.4.2. Траектории перемещения заряда и работа кулоновских сил. Зависимость от расстояния между начальной и конечной точкой траектории.
Результат применения данной формулы не будет зависеть от траектории. Для двух различных траекторий перемещения заряда, указанных на изображении, работы кулоновских сил будут равны. Если же мы изменим направление на противоположное, то и работа также поменяет знак. А если траектории будут соединены, т.е. заряд будет перемещаться по замкнутой траектории, то работа кулоновских сил будет нулевой.
Вспомним, как именно создается электростатическое поле. Оно представляет собой сочетание точечных разрядов. Значит, согласно принципу суперпозиции, работа результирующего поля, совершаемая при перемещении пробного заряда, будет равна сумме работ кулоновских полей тех зарядов, из которых состоит электростатическое поле. Соответственно, величина работы каждого заряда не будет зависеть от того, какой формы траектория. Значит, и полная работа не будет зависеть от пути – важно лишь местоположение начальной и конечной точки.
Поскольку у электростатического поля есть свойство потенциальности, мы можем добавить новое понятие – потенциальная энергия заряда в электрическом поле. Выберем какую-либо точку, поместим в нее разряд и примем его потенциальную энергию за 0.
Потенциальная энергия заряда, помещенного в любую точку пространства относительно нулевой точки, будет равна той работе, которая совершается электростатическим полем при перемещении заряда из этой точки в нулевую.
Обозначив энергию как W, а работу, совершаемую зарядом, как A10, запишем следующую формулу:
Wp1=A10.
Обратите внимание, что энергия обозначается именно буквой W, а не E, поскольку в электростатике E – это напряженность поля.
Потенциальная энергия электрического поля является определенной величиной, которая зависит от выбора точки отсчета (нулевой точки). На первый взгляд в таком определении есть заметная неоднозначность, однако на практике она, как правило, не вызывает недоразумений, поскольку сама по себе потенциальная энергия физического смысла не имеет. Важна лишь разность ее значений в начальной и конечной точке пространства.
Чтобы вычислить работу, которая совершается электростатическим полем при перемещении точечного заряда из точки 1 в точку 2, нужно найти разность значений потенциальной энергии в них. Путь перемещения и выбор нулевой точки значения при этом не имеют.
A12=A10+ A02= A10 – A20 =Wp1 – Wp2.
Если мы поместим заряд q в электростатическое поле, то его потенциальная энергия будет прямо пропорциональна его величине.
Понятие потенциала электрического поля
Потенциал электрического поля – это физическая величина, значение которой можно найти, разделив величину потенциальной энергии электрического заряда в электростатическом поле на величину этого заряда.
Он обозначается буквой φ. Это важная энергетическая характеристика электростатического поля.
φ=Wpq.
Если мы умножим величину заряда на разность потенциалов начальной и конечной точки перемещения, то мы получим работу, совершаемую при этом перемещении.
A12=Wp1–Wp2=qφ1–qφ2=q(φ1 – φ2).
Потенциал электрического поля измеряется в вольтах (В).
1 В=1 Дж1 Кл.
Разность потенциалов в формулах обычно обозначается Δφ.
Чаще всего при решении задач на электростатику в качестве нулевой берется некая бесконечно удаленная точка. Учитывая это, мы можем переформулировать определение потенциала так:
Потенциал электростатического поля точечного заряда в некоторой точке пространства будет равен той работе, которая совершается электрическими силами тогда, когда единичный положительный заряд удаляется из этой точки в бесконечность.
φ∞=A∞q.
Чтобы вычислить потенциал точечного заряда на расстоянии r, на котором размещается бесконечно удаленная точка, нужно использовать следующую формулу:
φ=φ∞=1q∫r∞Edr=Q4πε0∫r∞drr2=14πε0Qr
С помощью нее мы также можем найти потенциал поля однородно заряженной сферы или шара при r≥R, что следует из теоремы Гаусса.
Изображение электрических полей с помощью эквипотенциальных поверхностей
Чтобы наглядно изобразить электростатические поля, кроме силовых линий используются поверхности, называемые эквипотенциальными.
Эквипотенциальная поверхность (поверхность равного потенциала) – это такая поверхность, у которой во всех точкам потенциал электрического поля одинаков.
Эквипотенциальные поверхности и силовые линии на изображении всегда находятся перпендикулярно друг другу.
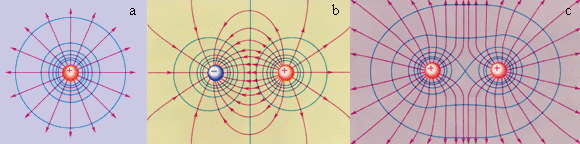
Если мы имеем дело с точечным зарядом в кулоновском поле, то эквипотенциальные поверхности в данном случае являются концентрическими сферами. На изображениях ниже показаны простые электростатические поля.
Рисунок 1.4.3. Красным показаны силовые линии, а синим – эквипотенциальные поверхности простого электрического поля. На первом рисунке изображен точечный заряд, на втором –электрический диполь, на третьем – два равных положительных заряда.
Если поле однородное, то его эквипотенциальные поверхности являются параллельными плоскостями.
В случае малого перемещения пробного заряда q вдоль силовой линии из начальной точки 1 в конечную точку 2 мы можем записать такую формулу:
ΔA12=qEΔl=q(φ1–φ2)=–qΔφ,
где Δφ=φ1-φ2 – изменение потенциала. Отсюда выводится, что:
E=-∆φ∆l, (∆l→0) или E=-dφdl.
Это соотношение передает связь между потенциалом поля и его напряженностью. Буквой l обозначена координата, которую следует отсчитывать вдоль силовой линии.
Зная принцип суперпозиции напряженности полей, которые создаются электрическими разрядами, мы можем вывести принцип суперпозиции для потенциалов:
φ=φ1+φ2+φ3+…
Работа сил электрического поля. Напряжение
План урока
- Работа электрического поля
- Напряжение
Цели урока
- Знать: формулы для расчета работы электрического поля; понятие напряжения; формулу напряжения; связь между работой электрических сил и напряжением
- Уметь: проводить аналогию между работой силы тяжести и работой электрической силы; выводить формулу для расчета работы однородного электрического поля
Разминка
- По какой формуле рассчитывается работа в механике?
- Может ли электрическое поле совершить механическую работу?
- Что общего между гравитационным полем Земли и электрическим полем?
Работа электрического поля
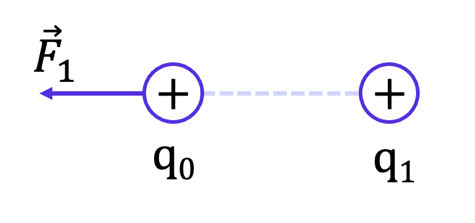
Рис. 1. Взаимодействие двух положительных зарядов
Рассмотрим систему, состоящую из двух положительных зарядов q0 и q1 (рис. 1). Нам уже известно, что сила Кулона, действующая на заряд q0, будет направлена от заряда q1, в нашем случае – влево.
Из механики нам известно, что работу можно найти по следующей формуле:
A=F·∆x,
где F – модуль постоянной силы, действующей на тело, ∆x – перемещение тела.
Если направления движения тела и действующей на него силы совпадают, то работа такой силы положительна.
Если же направления приложенной силы и движения тела противоположны, то работа такой силы отрицательна.
Соответственно, если заряд q0 перемещается влево, по направлению силы, то электрическая сила Fэл→ совершает положительную работу. Потенциальная энергия такой системы уменьшается.
В противном случае, если заряд q0 перемещается вправо, против направления действия силы, то электрическая сила совершает отрицательную работу.
Потенциальная энергия системы увеличивается, подобно энергии сжатой пружины.
Формула подразумевает действие постоянной силы, в приведенном примере сила, равная Fэл=E·q0 будет уменьшаться по мере удаления от заряда q1 вместе с модулем напряженности. Расчет работы электрического поля в данном случае будет очень трудоемок, поэтому мы рассмотрим работу однородного поля, в котором вектор напряженности не меняется E=const, следовательно, и значение силы также не будет меняться с течением времени.
Как вы уже знаете, однородное электрическое поле существует между двумя разноименно заряженными пластинами. В этом случае силу, действующую на пробный заряд q0, можно найти по формуле:
Fэл→=E→·q0.
Проведем аналогию между однородным электрическим полем и гравитационным полем Земли. Известно, что сила тяжести находится по следующей формуле:
Fтяж→=m·g→.
Сила тяжести прямо пропорциональная массе тела m и сонаправлена с вектором ускорения свободного падения g→; электрическая сила прямо пропорциональна величине пробного заряда q и сонаправлена с вектором напряженности E→.
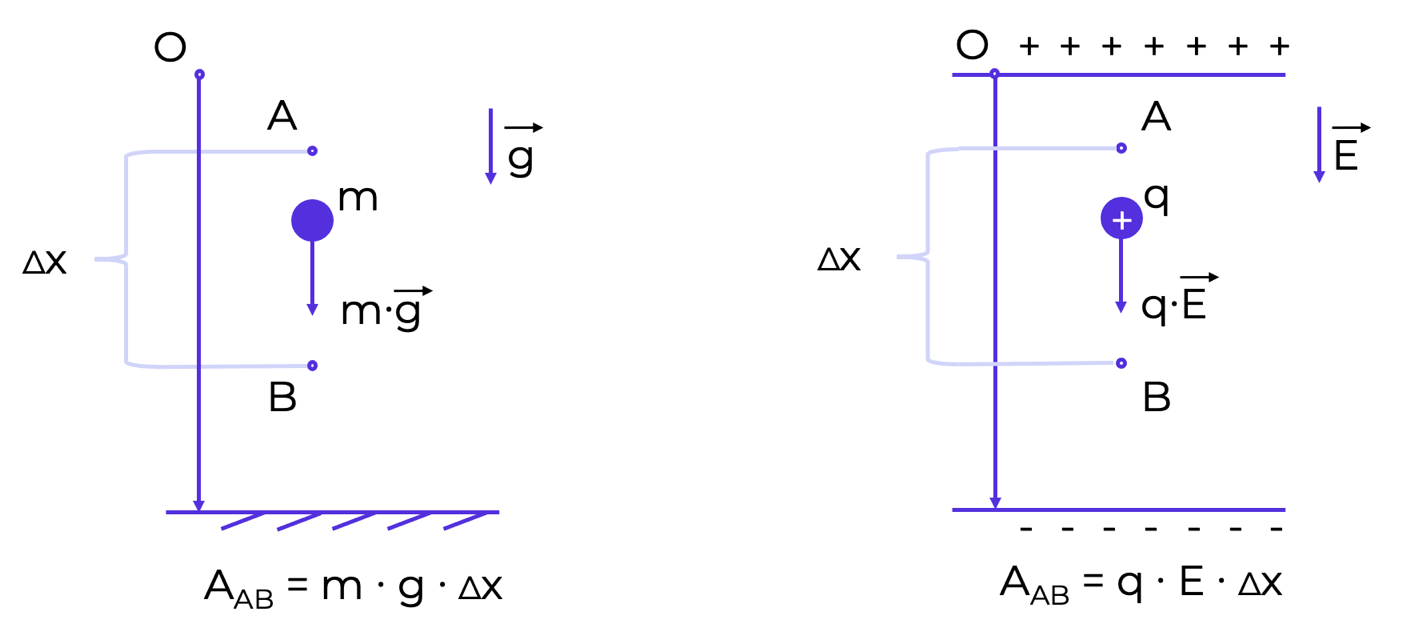
Сравним работу силы тяжести и работу электрической силы в случае, когда вектор напряженности направлен вертикально вниз (рис. 2).
Рис. 2. Сравнение работы силы тяжести и работы электрической силы при перемещении положительного заряда
Пусть тело массой m под действием силы тяжести перемещается из точки A в точку B. Тогда перемещение этого тела равно:
∆x=xB-xA.
В соответствии с формулами выше работа силы тяжести будет равна:
A=m·g·∆x.
Пусть теперь точечный положительный заряд q перемещается из точки A в точку B вдоль силовой линии электрического поля, то есть по направлению действия силы Fэл=q·E.
A=Fэл·∆x=E·q·∆x.
Если вместо положительного заряда q перемещается отрицательный заряд -q, то действующая на него электрическая сила будет направлена в сторону, противоположную перемещению. Поэтому работа электрической силы в этом случае будет отрицательна:
A=Fэл·∆x=-E·q·∆x.
Напряжение
Из последнего выражения видно, что работа электрического поля прямо пропорциональна величине заряда q. Отношение работы электрической силы к величине заряда называется напряжением:
U=Aq,
где U [В] – напряжение;
A [Дж] – работа электрического поля по перемещению заряда q0;
q [Кл] – величина заряда.
Напряжение
– скалярная физическая величина, равная отношению работы сил электрического поля по перемещению точечного заряда q к величине этого заряда:
U=Aq.
В СИ единица измерения напряжения – вольт (В).
Если напряженность – силовая характеристика поля, то напряжение – это энергетическая характеристика электрического поля.
С одной стороны, при перемещении положительного заряда q по линии напряженности однородного поля на расстояние ∆x электрическая сила Fэл→ совершает работу, равную
A=Fэл·∆x=E·q·∆x.
С другой стороны, работа электрической силы поля может быть найдена по известному напряжению U между начальной и конечной точками перемещения:
A=q·U.
Приравнивая правые части выражений для работы, получаем, что напряжение U между двумя точками в однородном электрическом поле, расположенными на одной линии напряженности, равно произведению модуля вектора напряженности E→ поля на расстояние ∆x между этими точками:
U=E·∆x.
Отсюда для напряженности однородного электрического поля получаем выражение
E=U∆x.
Таким образом единицей измерения напряженности, кроме Н/Кл, также справедливо называть В/м.
Пример 1
Тело, двигаясь равномерно прямолинейно вдоль направления электрического поля со скоростью v = 15 м/с в течение 2 минут, совершило работу 7,2 кДж. Определить модуль вектора напряжённости электрического поля E, если заряд тела равен 4 Кл.
Решение
1. Запишем исходные данные:
v = 15 м/с; t = 2 мин = 120 с; A = 3,6 кДж = 3600 Дж; q = 4 Кл.
2. Запишем выражение для работы электрической силы:
A=E·q·∆x.
3. Поскольку заряд двигается вдоль направления электрического поля E→, то знак работы электрической силы будет иметь положительное значение.
4. Заряд двигался равномерно, значит его перемещение равно ∆x=v·t. Теперь перепишем формулу для работы электрического поля:
A=E·q·v·t.
5. Выразим напряжённость электрического поля из уравнения выше:
E=Aq·v·t=36004·15·120=0,5 Вм.
Ответ: E=0,5 Вм.
Итоги
- Работу электрического поля напряженностью E по перемещению заряда q можно найти по следующей формуле: A=E·q·∆x.
Напряжение
– скалярная физическая величина, равная отношению работы сил электрического поля по перемещению точечного заряда q к величине этого заряда: U=Aq=E·∆x.- Напряжение не зависит от величины перемещаемого заряда q.
- Напряжение – это энергетическая характеристика электрического поля.
Контрольные вопросы
1. Приведите пример, когда электрическое поле совершает отрицательную работу.
2. Как найти работу электрической силы?
3. От каких физических величин зависит напряжение?
Чем на самом деле является напряжение? Это способ описания и измерения напряженности электрического поля. Само по себе напряжение не может существовать без электронного поля вокруг положительных и отрицательных зарядов. Так же, как магнитное поле окружает Северный и Южный полюса.
По современным понятиям, электроны не оказывают взаимного влияния. Электрическое поле – это нечто, что исходит от одного заряда и его присутствие может ощущаться другим.
О понятии напряженности можно сказать то же самое! Просто это помогает нам представить, как электрическое поле может выглядеть. Честно говоря, оно не обладает ни формой, ни размером, ничем подобным. Но поле функционирует с определённой силой на электроны.
Силы и их действие на заряженную частицу
На заряженный электрон, воздействует сила с некоторым ускорением, заставляя его перемещаться все быстрее и быстрее. Этой силой совершается работа по передвижению электрона.
Силовые линии – это воображаемые очертания, которые возникают вокруг зарядов (определяется электрическим полем), и если мы поместим какой-либо заряд в эту область, он испытает силу.
Свойства силовых линий:
- путешествуют с севера на юг;
- не имеют взаимных пересечений.
Почему у двух силовых линий не возникает пересечений? Потому что не бывает этого в реальной жизни. То, о чём говорится, является физической моделью и не более. Физики изобрели её для описания поведения и характеристик электрического поля. Модель очень хороша при этом. Но помня, что это всего лишь модель, мы должны знать о том, для чего такие линии нужны.
Силовые линии демонстрируют:
- направления электрических полей;
- напряженность. Чем ближе линии, тем больше сила поля и наоборот.
Если нарисованные силовые линии нашей модели пересекутся, расстояние меж ними станет бесконечно малыми. Из-за силы поля, как формы энергии, и из-за фундаментальных законов физики это невозможно.
Что такое потенциал?
Потенциалом называется энергия, которая затрачивается на передвижение заряженной частицы из первой точки, имеющей нулевой потенциал во вторую точку.
Разность потенциалов меж пунктами А и Б – это работа, производимая силами для передвижения некоего положительного электрона по произвольной траектории из А в Б.
Чем больший потенциал у электрона, чем больше плотность потока на единицу площади. Такое явление подобно гравитации. Чем больше масса, тем больше потенциал, тем интенсивнее и плотнее гравитационное поле на единицу площади.
Небольшой заряд с низким потенциалом, с прореженной плотностью потока показан на следующем рисунке.
А ниже показан заряд с большим потенциалом и плотностью потока.
Например: во время грозы электроны истощаются в одной точке и собираются в другой, образуя электрическое поле. Когда сила станет достаточной, чтобы сломать диэлектрическую проницаемость, получается удар молнии (состоящий из электронов). При выравнивании разности потенциалов электрическое поле разрушается.
Электростатическое поле
Это разновидность электрического поля, неизменного повремени, образуемого зарядами, которые не двигаются. Работа передвижения электрона определяется соотношениями,
где r1 и r2 – расстояния заряда q до начальной и конечной точки траектории движения. По полученной формуле видно, что работа при перемещении заряда из точки в точку не зависит от траектории, а зависит лишь от начала и конца перемещения.
На всякий электрон действует сила, и поэтому при перемещении электрона в поле выполняется определенная работа.
В электростатическом поле работа зависит лишь от конечных пунктов следования, а не от траектории. Поэтому, когда движение происходит по замкнутому контуру, заряд приходит в исходное положение, и величина работы становится равной нулю. Это происходит потому, что падение потенциала нулевое (поскольку электрон возвращается в ту же самую точку). Так как разность потенциалов нулевая, чистая работа будет также нулевой, ведь потенциал падения равен работе, деленной на значение заряда, выраженное в кулонах.
Об однородном электрическом поле
Однородным называется электрическое поле меж двух противоположно заряженных плоских металлических пластин, где линии напряженности параллельны между собой.
Почему сила действия на заряд в таком поле всегда одинаковая? Благодаря симметрии. Когда система симметрична и есть только одна вариация измерения, всякая зависимость исчезает. Есть много других фундаментальных причин для ответа, но фактор симметрии – самый простой.
Работа по передвижению положительного заряда
Электрическое поле – это поток электронов от «+» до «-», приводящий к высокой напряженности области.
Поток – это количество линий электрического поля, проходящих через него. В каком направлении будут положительные электроны двигаться? Ответ: по направлению электрического поля от положительного (высокого потенциала) к отрицательному (низкому потенциалу). Поэтому положительно заряженная частица будет двигаться именно в этом направлении.
Интенсивность поля во всякой точке определяется как сила, воздействующая на положительный заряд, помещенный в эту точку.
Работа заключается в переносе электронных частиц по проводнику. По закону Ома, можно определить работу разными вариациями формул, чтобы провести расчет.
Из закона сохранения энергии следует, что работа – это изменение энергии на отдельном отрезке цепи. Перемещение положительного заряда против электрического поля требует совершения работы и в результате получается выигрыш в потенциальной энергии.
Заключение
Из школьной программы мы помним, что электрическое поле образуется вокруг заряженных частиц. На любой заряд в электрическом поле воздействует сила, и вследствие этого при движении заряда выполняется некоторая работа. Большим зарядом создается больший потенциал, который производит более интенсивное или сильное электрическое поле. Это означает, что возникает больший поток и плотность на единицу площади.
Важный момент заключается в том, что должна быть выполнена определенной силой работа по перемещению заряда от высокого потенциала к низкому. Тем самым уменьшается разница заряда между полюсами. Перемещение электронов от токи до точки требует энергии.
Загляните на карту сайта Электронщик, буду рад если вы найдете на моем сайте еще что-нибудь полезное. Делитесь информацией в соцсетях, ставьте лайки, если вам понравилось – это поможет развитию канала
From Wikipedia, the free encyclopedia
For other examples of “work” in physics, see Work (physics).
Electric field work is the work performed by an electric field on a charged particle in its vicinity. The particle located experiences an interaction with the electric field. The work per unit of charge is defined by moving a negligible test charge between two points, and is expressed as the difference in electric potential at those points. The work can be done, for example, by electrochemical devices (electrochemical cells) or different metals junctions[clarification needed] generating an electromotive force.
Electric field work is formally equivalent to work by other force fields in physics,[1] and the formalism for electrical work is identical to that of mechanical work.
Physical process[edit]
Particles that are free to move, if positively charged, normally tend towards regions of lower electric potential (net negative charge), while negatively charged particles tend to shift towards regions of higher potential (net positive charge).
Any movement of a positive charge into a region of higher potential requires external work to be done against the electric field, which is equal to the work that the electric field would do in moving that positive charge the same distance in the opposite direction. Similarly, it requires positive external work to transfer a negatively charged particle from a region of higher potential to a region of lower potential.
Kirchhoff’s voltage law, one of the most fundamental laws governing electrical and electronic circuits, tells us that the voltage gains and the drops in any electrical circuit always sum to zero.
The formalism for electric work has an equivalent format to that of mechanical work. The work per unit of charge, when moving a negligible test charge between two points, is defined as the voltage between those points.
where
- Q is the electric charge of the particle
- E is the electric field, which at a location is the force at that location divided by a unit (‘test’) charge
- FE is the Coulomb (electric) force
- r is the displacement
is the dot product operator
Mathematical description[edit]
Given a charged object in empty space, Q+. To move q+ closer to Q+ (starting from 
Where U(r) is the potential energy of q+ at a distance r from the source Q. So, integrating and using Coulomb’s Law for the force:
Now, use the relationship
To show that the external work done to move a point charge q+ from infinity to a distance r is:
This could have been obtained equally by using the definition of W and integrating F with respect to r, which will prove the above relationship.
In the example both charges are positive; this equation is applicable to any charge configuration (as the product of the charges will be either positive or negative according to their (dis)similarity).
If one of the charges were to be negative in the earlier example, the work taken to wrench that charge away to infinity would be exactly the same as the work needed in the earlier example to push that charge back to that same position.
This is easy to see mathematically, as reversing the boundaries of integration reverses the sign.
Uniform electric field[edit]
Where the electric field is constant (i.e. not a function of displacement, r), the work equation simplifies to:
or ‘force times distance’ (times the cosine of the angle between them).
Electric power[edit]
The electric power is the rate of energy transferred in an electric circuit. As a partial derivative, it is expressed as the change of work over time:
,
where V is the voltage. Work is defined by:
Therefore
References[edit]
- ^ Debora M. Katz (1 January 2016). Physics for Scientists and Engineers: Foundations and Connections. Cengage Learning. pp. 1088–. ISBN 978-1-337-02634-5.