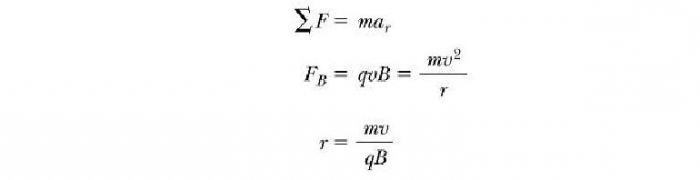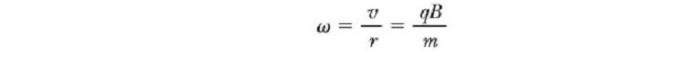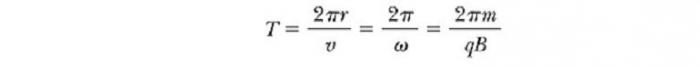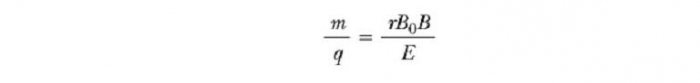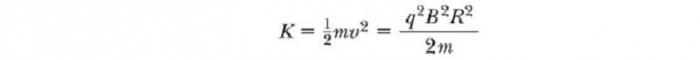Физика как найти скорость частицы

Как найти скорость частицы

Часто при изучении школьного курса электромагнетизма или при научных исследованиях возникает необходимость установить скорость, с которой двигалась какая-нибудь элементарная частица, например, электрон или протон.

Инструкция

Допустим, дана следующая задача: электрическое поле с напряженностью Е и магнитное поле с индукцией В, возбуждены перпендикулярно друг другу. Перпендикулярно им, равномерно и прямолинейно движется заряженная частица с зарядом q и скоростью v. Требуется определить ее скорость.

Решение очень простое. Если частица по условиям задачи движется равномерно и прямолинейно, значит, ее скорость v постоянная. Таким образом, в соответствии с первым законом Ньютона, величины действующих на нее сил взаимно уравновешены, то есть в сумме они равны нулю.

Какие силы действуют на частицу? Во-первых, электрическая составляющая силы Лоренца, которая вычисляется по формуле: Fэл = qE. Во-вторых, магнитная составляющая силы Лоренца, которую вычисляют по формуле: Fм = qvBSinα. Поскольку по условиям задачи частица движется перпендикулярно магнитному полю, угол α = 90 градусам, и соответственно, Sinα = 1. Тогда магнитная составляющая силы Лоренца Fм = qvB.

Электрическая и магнитная составляющие уравновешивают друг друга. Следовательно, величины qE и qvB численно равны. То есть Е = vB. Следовательно, скорость частицы вычисляется по такой формуле: v = E/B. Подставив в формулу значения Е и В, вы вычислите искомую скорость.

Или, например, у вас такая задача: частица с массой m и зарядом q, двигаясь со скоростью v, влетела в электромагнитное поле. Его силовые линии (как электрические, так и магнитные) параллельны. Частица влетала под углом α к направлению силовых линий и после этого началась двигаться с ускорением а. Требуется вычислить, с какой скоростью она двигалась первоначально. Согласно второму закону Ньютона, ускорение тела с массой m вычисляется по формуле: a = F/m.

Массу частицы вы знаете по условиям задачи, а F – результирующая (суммарная) величина сил, действующих на нее. В данном случае на частицу действуют электрическая и магнитная оставляющие силы Лоренца: F = qE + qBvSinα.

Но поскольку силовые линии полей (по условию задачи) параллельны, то вектор электрической силы перпендикулярен вектору магнитной индукции. Следовательно, суммарная сила F вычисляется по теореме Пифагора: F = [(qE)^2 + (qvBSinα)^2]^1/2

Преобразуя, получите: am = q[E^2 +B^2v^2Sin^2α]^1/2. Откуда: v^2 = (a^2m^2 – q^2E^2)/(q^2B^2Sin^2α). После вычисления и извлечения квадратного корня, получите искомую величину v.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Как найти скорость частицы

Движение заряженной частицы в магнитном поле: формулы. Движение заряженных частиц в однородном магнитном поле

Как известно, электрическое поле принято характеризовать величиной силы, с которой оно действует на пробный единичный электрический заряд. Магнитное поле традиционно характеризуют силой, с которой оно действует на проводник с «единичным» током. Однако при его протекании происходит упорядоченное движение заряженных частиц в магнитном поле. Поэтому мы можем определить магнитное поле B в какой-то точке пространства с точки зрения магнитной силы F_B, которую поле оказывает на частицу при ее движении в нем со скоростью v.

Общие свойства магнитной силы

Эксперименты, в которых наблюдалось движение заряженных частиц в магнитном поле, дают такие результаты:

Величина F_B магнитной силы, действующей на частицу пропорциональна заряду q и скорости v частицы.
Если движение заряженной частицы в магнитном поле происходит параллельно вектору этого поля, то сила, действующая на нее, равна нулю.
Когда вектор скорости частицы составляет любой Угол θ ≠ 0 с магнитным полем, то сила действует в направлении, перпендикулярном к v и B; то есть, F_B перпендикулярна плоскости, образованной v и B (см.рис. ниже).
Величина и направление F_B зависит от скорости частицы и от величины и направления магнитного поля B.
Направление силы, действующей на положительный заряд, противоположно направлению такой же силы, действующей на отрицательный заряд, движущийся в ту же сторону.
Величина магнитной силы, действующей на движущуюся частицу, пропорциональна sinθ угла θ между векторами v и B.

Сила Лоренца

Мы можем суммировать вышеперечисленные наблюдения путем записи магнитной силы в виде F_B = qv х B.

Когда происходит движение заряженной частицы в магнитном поле, сила Лоренца F_B при положительном q направлена вдоль векторного произведения v x B. Оно по определению перпендикулярно как v, так и B. Считаем это уравнение рабочим определением магнитного поля в некоторой точке в пространстве. То есть оно определяется в терминах силы, действующей на частицу при ее движении. Таким образом, движение заряженной частицы в магнитном поле кратко можно определить как перемещение под действием этой силы.

Заряд, движущийся со скоростью v в присутствии как электрического поля E, так и магнитного B, испытывает действие как электрической силы qE, так и магнитной qv х В. Полное приложенное к нему воздействие равно F_Л = qE + qv х В. Его принято называть так: полная сила Лоренца.

Движение заряженных частиц в однородном магнитном поле

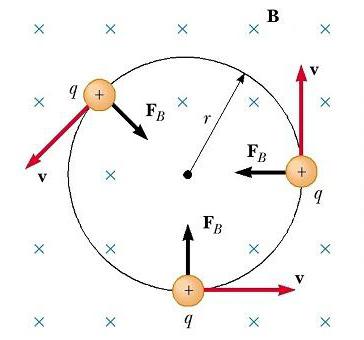
Рассмотрим теперь частный случай положительно заряженной частицы, движущейся в однородном поле, с начальным вектором скорости, перпендикулярным ему. Предположим, что вектор B поля направлен за страницу. Рисунок ниже показывает, что частица движется по кругу в плоскости, перпендикулярной к B.

Движение заряженной частицы в магнитном поле по окружности происходит потому, что магнитная сила F_B направлена под прямым углом к v и B и имеет постоянную величину qvB. Поскольку сила отклоняет частицы, направления v и F_B изменяются непрерывно, как показано на рисунке. Так как F_B всегда направлена к центру окружности, она изменяет только направление v, а не ее величину. Как показано на рисунке, движение положительно заряженной частицы в магнитном поле происходит против часовой стрелки. Если q будет отрицательным, то вращение произойдет по часовой стрелке.

Динамика кругового движения частицы

Какие же параметры характеризуют вышеописанное движение заряженной частицы в магнитном поле? Формулы для их определения мы можем получить, если возьмем предыдущее уравнение и приравняем F_B центробежной силе, требуемой для сохранения круговой траектории движения:

То есть радиус окружности пропорционален импульсу mv частицы и обратно пропорционален величине ее заряда и величине магнитного поля. Угловая скорость частицы

Период, с которым происходит движение заряженной частицы в магнитном поле по кругу, равен длине окружности, разделенной на ее линейную скорость:

Эти результаты показывают, что угловая скорость частицы и период кругового движения не зависит от линейной скорости или от радиуса орбиты. Угловую скорость ω часто называют циклотронной частотой (круговой), потому что заряженные частицы циркулируют с ней в типе ускорителя под названием циклотрон.

Движение частицы под углом к вектору магнитного поля

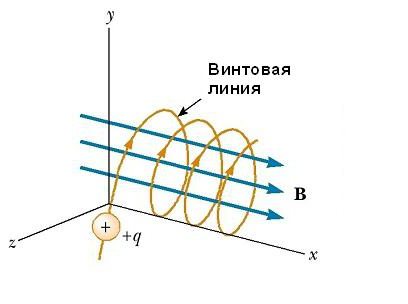
Если вектор v скорости частицы образует некоторый произвольный угол по отношению к вектору B, то ее траектория является винтовой линией. Например, если однородное поле будет направлено вдоль оси х, как показано на рисунке ниже, то не существует никакой компоненты магнитной силы F_B в этом направлении. В результате составляющая ускорения a_x= 0, и х-составляющая скорости движения частицы является постоянной. Однако магнитная сила F_B = qv х В вызывает изменение во времени компонентов скорости v_y и v_z. В результате имеет место движение заряженной частицы в магнитном поле по винтовой линии, ось которой параллельна магнитному полю. Проекция траектории на плоскости yz (если смотреть вдоль оси х) представляет собой круг. Проекции ее на плоскости ху и xz являются синусоидами! Уравнения движения остаются такими же, как и при круговой траектории, при условии, что v заменяется на ν_⊥ = √(ν_у 2 + ν_z 2 ).

Неоднородное магнитное поле: как в нем движутся частицы

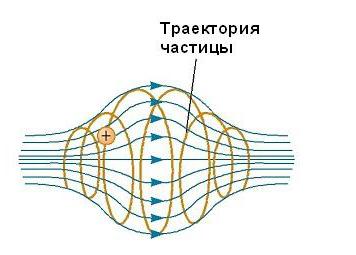
Движение заряженной частицы в магнитном поле, являющемся неоднородным, происходит по сложным траекториям. Так, в поле, величина которого усиливается по краям области его существования и ослабляется в ее середине, как, например, показано на рисунке ниже, частица может колебаться вперед и назад между конечными точками.

Как Земля влияет на движение космических частиц

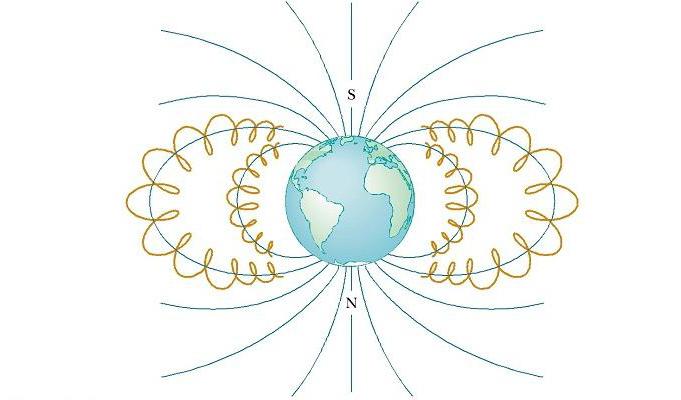
Околоземные пояса Ван Аллена состоят из заряженных частиц (в основном электронов и протонов), окружающих Землю в форме тороидальных областей (см. рис. ниже). Движение заряженной частицы в магнитном поле Земли происходит по по спирали вокруг силовых линий от полюса до полюса, покрывая это расстояние в несколько секунд. Эти частицы идут в основном от Солнца, но некоторые приходят от звезд и других небесных объектов. По этой причине они называются космическими лучами. Большинство их отклоняется магнитным полем Земли и никогда не достигает атмосферы. Тем не менее, некоторые из частиц попадают в ловушку, именно они составляют пояса Ван Аллена. Когда они находятся над полюсами, иногда происходят столкновения их с атомами в атмосфере, в результате чего последние излучают видимый свет. Так возникают красивые Полярные сияния в Северном и Южном полушариях. Они, как правило, происходят в полярных регионах, потому что именно здесь пояса Ван Аллена расположены ближе всего к поверхности Земли.

Иногда, однако, солнечная активность вызывает большее число заряженных частиц, входящих в эти пояса, и значительно искажает нормальные силовые линии магнитного поля, связанные с Землей. В этих ситуациях полярное сияние можно иногда увидеть в более низких широтах.

Селектор скоростей

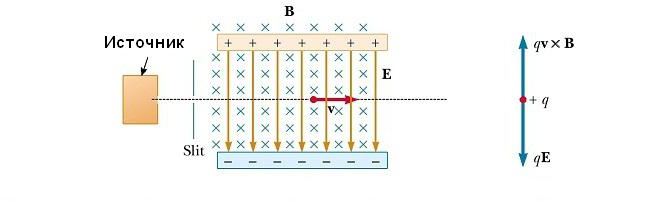
Во многих экспериментах, в которых происходит движение заряженных частиц в однородном магнитном поле, важно, чтобы все частицы двигались с практически одинаковой скоростью. Это может быть достигнуто путем применения комбинации электрического поля и магнитного поля, ориентированного так, как показано на рисунке ниже. Однородное электрическое поле направлено вертикально вниз (в плоскости страницы), а такое же магнитное поле приложено в направлении, перпендикулярном к электрическому (за страницу).

Масс-спектрометр

Этот прибор разделяет ионы в соответствии с соотношением их массы к заряду. По одной из версий этого устройства, известного как масс-спектрометр Бэйнбриджа, пучок ионов проходит сначала через селектор скоростей и затем поступает во второе поле B₀, также однородное и имеющее то же направление, что и поле в селекторе (см. рис. ниже). После входа в него движение заряженной частицы в магнитном поле происходит по полукругу радиуса r перед ударом в фотопластинку Р. Если ионы заряжены положительно, луч отклоняется вверх, как показано на рисунке. Если ионы заряжены отрицательно, луч будет отклоняться вниз. Из выражения для радиуса круговой траектории частицы, мы можем найти отношение m/q

и затем, используя уравнение v=E/B, мы находим, что

Таким образом, мы можем определить m/q путем измерения радиуса кривизны, зная поля величин B, B₀, и E. На практике, так обычно измеряет массы различных изотопов данного иона, поскольку все они несут один заряд q. Таким образом, отношение масс может быть определено, даже если q неизвестно. Разновидность этого метода была использована Дж. Дж. Томсоном (1856-1940) в 1897 году для измерения отношение е/m_е для электронов.

Циклотрон

Он может ускорить заряженные частицы до очень высоких скоростей. И электрические, и магнитные силы играют здесь ключевую роль. Полученные высокоэнергетические частицы используются для бомбардировки атомных ядер, и тем самым производят ядерные реакции, представляющие интерес для исследователей. Ряд больниц использует циклотронное оборудование для получения радиоактивных веществ для диагностики и лечения.

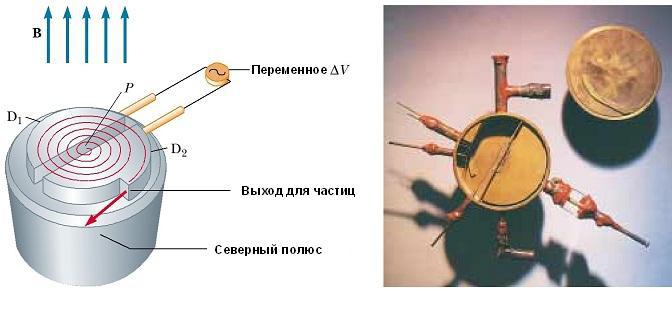
Схематическое изображение циклотрона показан на рис. ниже. Частицы движутся внутри двух полуцилиндрических контейнеров D 1 и D 2, называемых дуантами. Высокочастотная переменная разность потенциалов приложена к дуантам, разделенным зазором, а однородное магнитное поле направлено вдоль оси циклотрона (южный полюс его источника на рис. не показан).

Положительный ион, выпущенный из источника в точке Р вблизи центра устройства в первом дуанте, перемещается по полукруглой траектории (показана пунктирной красной линией на рисунке) и прибывает обратно в щель в момент времени Т / 2, где Т — время одного полного оборота внутри двух дуантов.

Частота приложенной разности потенциалов регулируется таким образом, что полярность дуантов меняется на обратную в тот момент времени, когда ион выходит из одного дуанта. Если приложенная разность потенциалов регулируется таким образом, что в этот момент D₂ получает более низкий электрический потенциал, чем D₁ на величину qΔV, то ион ускоряется в зазоре перед входом в D₂, и его кинетической энергии увеличивается на величину qΔV. Затем он движется вокруг D₂ по полукруглой траектории большего радиуса (потому что его скорость увеличилась).

Через некоторое время T / 2 он снова поступает в зазор между дуантами. К этому моменту полярность дуантов снова изменяется, и иону дается еще один «удар» через зазор. Движение заряженной частицы в магнитном поле по спирали продолжается, так что при каждом проходе одного дуанта ион получает дополнительную кинетическую энергию, равную qΔV. Когда радиус его траектории становится близким к радиусу дуантов, ион покидает систему через выходную щель. Важно отметить, что работа циклотрона основана на том, что Т не зависит от скорости иона и радиуса круговой траектории. Мы можем получить выражение для кинетической энергии иона, когда он выходит из циклотрона в зависимости от радиуса R дуантов. Мы знаем, что скорость кругового движения частицы — ν = qBR /m. Следовательно, ее кинетическая энергия

Когда энергии ионов в циклотрон превышает около 20 МэВ, в игру вступают релятивистские эффекты. Мы отмечаем, что T увеличивается, и что движущиеся ионы не остаются в фазе с приложенной разностью потенциалов. Некоторые ускорители решают эту проблему, изменяя период прикладываемой разности потенциалов, так что она остается в фазе с движущимися ионами.

Эффект Холла

Когда проводник с током помещается в магнитное поле, то дополнительная разность потенциалов создается в направлении, перпендикулярном к направлению тока и магнитного поля. Это явление, впервые наблюдаемое Эдвином Холлом (1855-1938) в 1879 году, известно как эффект Холла. Он всегда наблюдается, когда происходит движение заряженной частицы в магнитном поле. Это приводит к отклонению носителей заряда на одной стороне проводника в результате магнитной силы, которую они испытывают. Эффект Холла дает информацию о знаке носителей заряда и их плотности, он также может быть использован для измерения величины магнитных полей.

Устройство для наблюдения эффекта Холла состоит из плоского проводника с током I в направлении х, как показано на рисунке ниже.

Физика. 10 класс

§ 30. Сила Лоренца. Движение заряженных частиц в магнитном поле

Поскольку электрический ток представляет собой упорядоченное движение заряженных частиц, то это означает, что магнитное поле, действуя на проводник с током, действует тем самым на каждую из этих частиц. Таким образом, силу Ампера можно рассматривать как результат сложения сил, действующих на отдельные движущиеся заряженные частицы. Как можно определить силу, действующую со стороны магнитного поля на заряженную частицу, движущуюся в этом поле?

Сила Лоренца. Силу, которой магнитное поле действует на заряженную частицу, движущуюся в этом поле, называют силой Лоренца в честь выдающегося нидерландского физика Хендрика Антона Лоренца ( 1853–1928 ).

Модуль силы Лоренца можно определить по формуле , где N — общее число свободных заряженных одинаковых частиц на прямолинейном участке проводника длиной Δl ( рис. 167 ). Если модуль заряда одной частицы q, а модуль суммарного заряда всех частиц Nq, то согласно определению силы тока , где Δt — промежуток времени, за который заряженная частица проходит участок проводника длиной Δl. Тогда

Поскольку – модуль средней скорости упорядоченного движения заряженной частицы в стационарном * электрическом поле внутри проводника, то формулу для определения модуля силы Лоренца можно записать в виде:

где α — угол между направлениями индукции магнитного поля и скорости упорядоченного движения заряженной частицы.

Из формулы (30.1) следует, что сила Лоренца максимальна в случае, когда заряженная частица движется перпендикулярно направлению индукции магнитного поля (α = 90°). Когда частица движется вдоль линии индукции поля (α = 0° или α = 180°), сила Лоренца на неё не действует. Сила Лоренца зависит от выбора инерциальной системы отсчёта, так как в разных системах отсчёта скорость движения заряженной частицы может отличаться.

Направление силы Лоренца, действующей на заряженную частицу, как и направление силы Ампера, определяют по правилу левой руки (рис. 168): если левую руку расположить так, чтобы составляющая индукции магнитного поля, перпендикулярная скорости движения частицы, входила в ладонь, а четыре пальца были направлены по движению положительно заряженной частицы (против движения отрицательно заряженной частицы), то отогнутый на 90° в плоскости ладони большой палец укажет направление действующей на частицу силы Лоренца.

Сила Лоренца перпендикулярна как направлению скорости движения частицы, так и направлению индукции магнитного поля.

На рисунке 169 представлены направления индукции магнитного поля, скорости движения частицы в данный момент времени и силы Лоренца , действующей на частицу со стороны магнитного поля. Определите знак заряда частицы.

* Электрическое поле, создаваемое и поддерживаемое источником тока в течение длительного промежутка времени и обеспечивающее постоянный электрический ток в проводнике, называют стационарным электрическим полем. ↑

Источник

From Wikipedia, the free encyclopedia

Sound measurements
Characteristic	Symbols
Sound pressure	p, SPL,L_PA
Particle velocity	v, SVL
Particle displacement	δ
Sound intensity	I, SIL
Sound power	P, SWL, L_WA
Sound energy	W
Sound energy density	w
Sound exposure	E, SEL
Acoustic impedance	Z
Audio frequency	AF
Transmission loss	TL

v t e

Particle velocity is the velocity of a particle (real or imagined) in a medium as it transmits a wave. The SI unit of particle velocity is the metre per second (m/s). In many cases this is a longitudinal wave of pressure as with sound, but it can also be a transverse wave as with the vibration of a taut string.

When applied to a sound wave through a medium of a fluid like air, particle velocity would be the physical speed of a parcel of fluid as it moves back and forth in the direction the sound wave is travelling as it passes.

Particle velocity should not be confused with the speed of the wave as it passes through the medium, i.e. in the case of a sound wave, particle velocity is not the same as the speed of sound. The wave moves relatively fast, while the particles oscillate around their original position with a relatively small particle velocity. Particle velocity should also not be confused with the velocity of individual molecules, which depends mostly on the temperature and molecular mass.

In applications involving sound, the particle velocity is usually measured using a logarithmic decibel scale called particle velocity level. Mostly pressure sensors (microphones) are used to measure sound pressure which is then propagated to the velocity field using Green’s function.

Mathematical definition[edit]

Particle velocity, denoted , is defined by

$mathbf v = frac{partial mathbf delta}{partial t}$

where delta is the particle displacement.

Progressive sine waves[edit]

The particle displacement of a progressive sine wave is given by

$delta(mathbf{r},, t) = delta_mathrm{m} cos(mathbf{k} cdot mathbf{r} - omega t + varphi_{delta, 0}),$

where

It follows that the particle velocity and the sound pressure along the direction of propagation of the sound wave x are given by

${displaystyle v(mathbf {r} ,,t)={frac {partial delta (mathbf {r} ,,t)}{partial t}}=omega delta cos !left(mathbf {k} cdot mathbf {r} -omega t+varphi _{delta ,0}+{frac {pi }{2}}right)=v_{mathrm {m} }cos(mathbf {k} cdot mathbf {r} -omega t+varphi _{v,0}),}$

${displaystyle p(mathbf {r} ,,t)=-rho c^{2}{frac {partial delta (mathbf {r} ,,t)}{partial x}}=rho c^{2}k_{x}delta cos !left(mathbf {k} cdot mathbf {r} -omega t+varphi _{delta ,0}+{frac {pi }{2}}right)=p_{mathrm {m} }cos(mathbf {k} cdot mathbf {r} -omega t+varphi _{p,0}),}$

where

$v_{{mathrm {m}}}$ is the amplitude of the particle velocity;
$varphi _{{v,0}}$ is the phase shift of the particle velocity;
${displaystyle p_{mathrm {m} }}$ is the amplitude of the acoustic pressure;
$varphi _{{p,0}}$ is the phase shift of the acoustic pressure.

Taking the Laplace transforms of and with respect to time yields

${hat {v}}({mathbf {r}},,s)=v_{{mathrm {m}}}{frac {scos varphi _{{v,0}}-omega sin varphi _{{v,0}}}{s^{2}+omega ^{2}}},$

${hat {p}}({mathbf {r}},,s)=p_{{mathrm {m}}}{frac {scos varphi _{{p,0}}-omega sin varphi _{{p,0}}}{s^{2}+omega ^{2}}}.$

Since $varphi _{{v,0}}=varphi _{{p,0}}$ , the amplitude of the specific acoustic impedance is given by

$z_{{mathrm {m}}}({mathbf {r}},,s)=|z({mathbf {r}},,s)|=left|{frac {{hat {p}}({mathbf {r}},,s)}{{hat {v}}({mathbf {r}},,s)}}right|={frac {p_{{mathrm {m}}}}{v_{{mathrm {m}}}}}={frac {rho c^{2}k_{x}}{omega }}.$

Consequently, the amplitude of the particle velocity is related to those of the particle displacement and the sound pressure by

$v_mathrm{m} = omega delta_mathrm{m},$

$v_{{mathrm {m}}}={frac {p_{{mathrm {m}}}}{z_{{mathrm {m}}}({mathbf {r}},,s)}}.$

Particle velocity level[edit]

Sound velocity level (SVL) or acoustic velocity level or particle velocity level is a logarithmic measure of the effective particle velocity of a sound relative to a reference value.
Sound velocity level, denoted L_v and measured in dB, is defined by^[1]

$L_{v}=ln !left({frac {v}{v_{0}}}right)!~{mathrm {Np}}=2log _{{10}}!left({frac {v}{v_{0}}}right)!~{mathrm {B}}=20log _{{10}}!left({frac {v}{v_{0}}}right)!~{mathrm {dB}},$

where

v is the root mean square particle velocity;
v₀ is the reference particle velocity;
1 Np = 1 is the neper;
1 B = 1/2 ln 10 is the bel;
1 dB = 1/20 ln 10 is the decibel.

The commonly used reference particle velocity in air is^[2]

$v_{0}=5times 10^{{-8}}~{mathrm {m/s}}.$

The proper notations for sound velocity level using this reference are L_{v/(5 × 10⁻⁸ m/s)} or L_v (re 5 × 10⁻⁸ m/s), but the notations dB SVL, dB(SVL), dBSVL, or dB_SVL are very common, even though they are not accepted by the SI.^[3]

References[edit]

^ “Letter symbols to be used in electrical technology – Part 3: Logarithmic and related quantities, and their units”, IEC 60027-3 Ed. 3.0, International Electrotechnical Commission, 19 July 2002.
^ Ross Roeser, Michael Valente, Audiology: Diagnosis (Thieme 2007), p. 240.
^ Thompson, A. and Taylor, B. N. sec 8.7, “Logarithmic quantities and units: level, neper, bel”, Guide for the Use of the International System of Units (SI) 2008 Edition, NIST Special Publication 811, 2nd printing (November 2008), SP811 PDF

External links[edit]

Ohm’s Law as Acoustic Equivalent. Calculations
Relationships of Acoustic Quantities Associated with a Plane Progressive Acoustic Sound Wave
The particle Velocity Can Be Directly Measured with a Microflown
Particle velocity measured with Weles Acoustics sensor – working principle
Acoustic Particle-Image Velocimetry. Development and Applications

Источник

101

Министерство
образования Российской Федерации

Тульский
государственный университет

Кафедра
физики

Лекции по физике

Под
редакцией Пекара Ю.А.

Тула
2000

Разработали:
Ю.А.Пекар, доцент кафедры физики

Ю.Н.Колмаков,
доцент кафедры физики

Л.С.Лежнева,
доцент кафедры физики

И.М.Лагун,
доцент кафедры физики

Рассмотрено
на заседании кафедры

Протокол
N8 от 14 июня 2000г.

Зав.
каф. физики
Д.М.
Левин

Семестр
2.

Механика. Молекулярная физика. Кинематика

Основные понятия и величины

Классическая
механика изучает механическое движение
частиц (материальных точек) и тел, т.е.
изменение положения их в пространстве
с течением времени.

Частица
(материальная точка) — это тело, размерами
которого в условиях

данной
задачи можно пренебречь. Одно и то же
тело в различных условиях либо может
считаться частицей, либо — нет.

Другая
абстракция — абсолютно твердое тело
— это система частиц,

расстояния
между которыми в процессе движения
тела остаются неизменными.

При
этом постулируется, что:

1)
пространство является бесконечным,
однородным, изотропным;

2)
время является однородным, течет только
в одном направлении, а ход времени не
зависит от состояния движения тел.

Механическое
движение тел рассматривается в системе
отсчета.

Кинематика
— это раздел механики, рассматривающий
движение тел вне

зависимости
от причин, вызывающих это движение.

2. Кинематика частицы. Перемещение, скорость, ускорение

Существуют
различные способы определения положения
частицы.

1) Векторный способ описания движения.

В
этом случае положение частицы задается
её радиус-вектором
.
Геометрическое место концов радиус-вектора
представляет кривую,

называемую
траекторией.

Зависимость
радиус-вектора частицы от времени

называется
кинематическим
уравнением движения.
С геометрической

точки
зрения — это уравнение траектории.

Изменение
радиус-вектора
за время ∆t называетсяперемещением:
.
Длина дуги траектории между этими
точками ∆l
назывется путем.

Важнейшей
кинематической характеристикой движения
является скорость.

Скоростью
частицы называется векторная величина,
определяемая

равенством

иначе
говоря, скорость
— это производная от радиус-вектора по
времени.

Из
определения следует, что скорость
направлена по касательной

к
траектории. Величина скорости

где
l
— путь, пройденный вдоль траектории.

Иногда
используется понятие средней
скорости:
это векторная

величина,
равная отношению перемещения ко времени,
т.е.

Скорость
изменения скорости частицы по времени,
т.е. вектор

называется
ускорением частицы.

Таким
образом, зная кинематический закон
движения, можно простым

дифференцированием
по времени найти скорость и ускорение
в любой

момент
времени (так называемая прямая задача
кинематики).

Наоборот,
зная ускорение частицы, а также начальные
условия,

т.е.
положение
и скоростьчастицы в начальный момент времени,

можно
найти траекторию движения частицы
(обратная задача

кинематики).

Источник

Условие задачи:

Определить скорость частицы, при движении с которой её динамическая масса превышает массу покоя в 3 раза.

Задача №11.5.5 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(m=3m_0) кг, (upsilon-?)

Решение задачи:

Релятивистскую (она же динамическая, как это говорится в условии) массу (m), т.е. массу частицы, движущейся относительно наблюдателя с некоторой скоростью (upsilon), можно определить по формуле:

[m = frac{{{m_0}}}{{sqrt {1 – frac{{{upsilon ^2}}}{{{c^2}}}} }};;;;(1)]

Здесь (m_0) – масса покоя, (upsilon) – скорость движения частицы относительно наблюдателя, (c) – скорость света в вакууме, равная 3·10⁸ м/с.

По условию задачи динамическая масса (m) превышает массу покоя (m_0) в 3 раза, то есть (m=3m_0), поэтому равенство (1) примет вид:

[3{m_0} = frac{{{m_0}}}{{sqrt {1 – frac{{{upsilon ^2}}}{{{c^2}}}} }}]

Откуда получим:

[sqrt {1 – frac{{{upsilon ^2}}}{{{c^2}}}} = frac{1}{3}]

Возведем в квадрат обе части полученного равенства:

[1 – frac{{{upsilon ^2}}}{{{c^2}}} = frac{1}{9}]

Значит:

[frac{{{upsilon ^2}}}{{{c^2}}} = frac{8}{9}]

Извлечем квадратный корень из обеих частей:

[frac{upsilon }{c} = frac{{2sqrt 2 }}{3}]

Окончательно имеем:

[upsilon = frac{{2sqrt 2 }}{3}c]

Численный ответ задачи равен:

[upsilon = frac{{2sqrt 2 }}{3} cdot 3 cdot {10^8} = 2,83 cdot {10^8};м/с]

Ответ: 2,83·10⁸ м/с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

11.5.4 Частица движется со скоростью 0,75 скорости света для неподвижного наблюдателя
11.5.6 Тело с массой покоя 1 кг движется со скоростью 2*10^8 м/с. Определить массу этого
11.5.7 Чему равна скорость протона, движущегося в ускорителе, если его масса в 1,25 раз

Источник

Как найти скорость частицы

Как найти скорость частицы

Движение заряженной частицы в магнитном поле: формулы. Движение заряженных частиц в однородном магнитном поле

Общие свойства магнитной силы

Сила Лоренца

Движение заряженных частиц в однородном магнитном поле

Динамика кругового движения частицы

Движение частицы под углом к вектору магнитного поля

Неоднородное магнитное поле: как в нем движутся частицы

Как Земля влияет на движение космических частиц

Селектор скоростей

Масс-спектрометр

Циклотрон

Эффект Холла

Физика. 10 класс

§ 30. Сила Лоренца. Движение заряженных частиц в магнитном поле

Mathematical definition[edit]

Progressive sine waves[edit]

Particle velocity level[edit]

See also[edit]

References[edit]

External links[edit]

Лекции по физике

Механика. Молекулярная физика. Кинематика

Основные понятия и величины

2. Кинематика частицы. Перемещение, скорость, ускорение

1) Векторный способ описания движения.

Условие задачи:

Дано:

Решение задачи:

Ответ: 2,83·10⁸ м/с.

Смотрите также задачи:

Добавить комментарий Отменить ответ

Как найти скорость частицы

Как найти скорость частицы

Движение заряженной частицы в магнитном поле: формулы. Движение заряженных частиц в однородном магнитном поле

Общие свойства магнитной силы

Сила Лоренца

Движение заряженных частиц в однородном магнитном поле

Динамика кругового движения частицы

Движение частицы под углом к вектору магнитного поля

Неоднородное магнитное поле: как в нем движутся частицы

Как Земля влияет на движение космических частиц

Селектор скоростей

Масс-спектрометр

Циклотрон

Эффект Холла

Физика. 10 класс

§ 30. Сила Лоренца. Движение заряженных частиц в магнитном поле

Mathematical definition[edit]

Progressive sine waves[edit]

Particle velocity level[edit]

See also[edit]

References[edit]

External links[edit]

Лекции по физике

Механика. Молекулярная физика. Кинематика

Основные понятия и величины

2. Кинематика частицы. Перемещение, скорость, ускорение

1) Векторный способ описания движения.

Условие задачи:

Дано:

Решение задачи:

Ответ: 2,83·108 м/с.

Смотрите также задачи:

Вам также может понравиться

Как найти объем куда

Как исправить близорукость у подростка упражнения

Как найти момент силы стержня

Добавить комментарий Отменить ответ

Ответ: 2,83·10⁸ м/с.