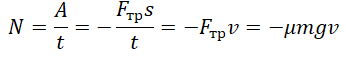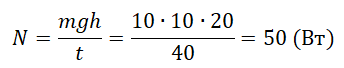п.1. Полезная работа и затраченная работа
Полезной называется работа по подъёму грузов или преодолению какого-либо сопротивления.
Затраченной (полной) называется работа, совершённая приложенной силой.
Примеры полной и полезной работы
Затраченная работа равна сумме:
- полезной работы;
- работы против силы трения в различных частях механизма;
- работы по перемещению различных составных элементов механизма.
Поэтому всегда (A_text{полезная}lt A_text{затраченная})
п.2. КПД механизма
Коэффициент полезного действия механизма – это отношение его полезной работы к затраченной работе. $$ eta=frac{A_text{п}}{A_text{з}}cdot 100text{%} $$
Поскольку в реальных механизмах всегда (A_text{п}lt A_text{з}), $$ frac{A_text{п}}{A_text{з}}lt 1. $$
Следовательно КПД реальных механизмов (etalt 100text{%}).
Только в идеальном механизме, в котором нет потерь на трение, и все составные элементы не имеют веса, (A_text{п}=A_text{з}) и (eta=100text{%}).
КПД никогда не может быть выше (100text{%}).
КПД реальных механизмов можно увеличить за счет снижения трение в подвижных узлах и уменьшения веса всех составных элементов конструкции.
Для этого нужны новые смазочные вещества и лёгкие, но прочные конструкционные материалы.
п.3. Задачи
Задача 1. По наклонной плоскости поднимают груз массой 50 кг, прикладывая к нему силу 250 Н, направленную вдоль плоскости. Чему равен КПД плоскости, если её длина 10 м, а высота 3 м?
Дано:
(m=50 text{кг})
(gapprox 10 text{м/с}^2)
(F=250 text{Н})
(L=10 text{м})
(h=3 text{м})
__________________
(eta-?)
Полезная работа по подъему груза begin{gather*} A_text{п}=mgh. end{gather*} Затраченная работа на перемещение груза вдоль наклонной плоскости begin{gather*} A_text{з}=FL. end{gather*} КПД плоскости: begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{mgh}{FL}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{50cdot 10cdot 3}{250cdot 10}cdot 100text{%}=60text{%} end{gather*} Ответ: 60%
Задача 2. С помощью подвижного блока поднимают груз массой 200 кг, прикладывая силу 1200 Н. Чему равен КПД блока?
Дано:
(m=200 text{кг})
(gapprox 10 text{м/с}^2)
(F=1200 text{Н})
__________________
(eta-?)
Полезная работа по подъему груза на высоту (h): begin{gather*} A_text{п}=mgh. end{gather*} Подвижный блок дает выигрыш в силе в 2 раза и проигрыш в расстоянии. Т.е. при работе нужно вытянуть трос длиной (2h). Затраченная работа: begin{gather*} A_text{з}=Fcdot 2h. end{gather*} КПД блока begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{mgh}{2Fh}cdot 100text{%}=frac{mg}{2F}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{200cdot 10}{2cdot 1200}cdot 100text{%}approx 83,3text{%} end{gather*} Ответ: 83,3%
Задача 3. Груз массой 245 кг с помощью рычага равномерно подняли на высоту 6 см. При этом к длинному плечу рычага была приложена сила 500 Н, а точка приложения силы опустилась на 30 см. Найдите КПД рычага.
Дано:
(m=245 text{кг})
(gapprox 10 text{м/с}^2)
(h_2=6 text{см}=0,6 text{м})
(F_1=500 text{Н})
(h_1=30 text{см}=0,3 text{м})
__________________
(eta-?)
Полезная работа по подъему груза на высоту (h_2): begin{gather*} A_text{п}=mgh_2. end{gather*} Затраченная работа по опусканию длинного плеча рычага: begin{gather*} A_text{з}=F_1h_1. end{gather*} КПД рычага begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{mgh_2}{F_1h_1}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{245cdot 10cdot 0,06}{500cdot 0,3}cdot 100text{%}=frac{147}{150}cdot 100text{%}=98text{%} end{gather*} Ответ: 98%
Задача 4. Чему равен КПД гидравлической машины, если для равномерного подъема груза массой 1,2 т к меньшему поршню прикладывают силу 160 Н? Площади поршней равны 5 см2 и 500 см2.
Дано:
(m=1,2 text{т}=1200 text{кг})
(gapprox 10 text{м/с}^2)
(F_1=160 text{Н})
(S_1=5 text{см}^2=5cdot 10^{-4} text{м}^2)
(S_2=500 text{см}^2=5cdot 10^{-2} text{м}^2)
__________________
(eta-?)
При опускании малого поршня на высоту (h_1) из малого в большой цилиндр вытекает объем жидкости равный $$ V=S_1h_1=S_2h_2Rightarrow frac{h_2}{h_1}=frac{S_1}{S_2} $$ Полезная работа по подъему груза на высоту (h_2): begin{gather*} A_text{п}=mgh_2. end{gather*} Затраченная работа по опусканию поршня малого цилиндра: begin{gather*} A_text{з}=F_1h_1. end{gather*} КПД гидравлической машины begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{mgh_2}{F_1h_1}cdot 100text{%}=frac{mgS_1}{F_1S_2}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{1200cdot 10cdot 5cdot 10^{-4}}{160cdot 5cdot 10^{-2}}cdot 100text{%}=frac{600}{800}cdot 100text{%}=75text{%} end{gather*} Ответ: 75%
Задача 5*. Груз массой 12 кг поднимают с помощью подвижного блока массой 3 кг. Чему равен КПД блока?
Дано:
(M=12 text{кг})
(m=3 text{кг})
__________________
(eta-?)
Полезная работа по подъему груза на высоту (h): begin{gather*} A_text{п}=Mgh. end{gather*} Подвижный блок дает выигрыш в силе в 2 раза. Поэтому достаточно приложить силу, равную половине суммы весов груза и блока: begin{gather*} F=frac 12(M+m)g end{gather*} При этом будет проигрыш в расстоянии. Потребуется вытянуть трос длиной (2h). Затраченная работа, приложенная к тросу: begin{gather*} A_text{з}=Fcdot 2h=frac 12(M+m)gcdot 2h=(M+m)gh. end{gather*} КПД подвижного блока begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{Mgh}{(M+m)gh}cdot 100text{%}=frac{M}{M+m}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{12}{12+3}cdot 100text{%}=80text{%} end{gather*} Ответ: 80%
Задача 6. Сколько воды можно поднять из колодца глубиной 36 м за 1 ч, если мощность электродвигателя равна 5 кВт, КПД всей установки равно 70%?
Дано:
(N=5 text{кВт}=5cdot 10^3 text{Вт})
(eta=70text{%}=0,7)
(h=36 text{м})
(t=1 text{ч}=3600 text{с})
(gapprox 10 text{м/с}^2)
__________________
(m-?)
Полезная работа по подъему груза на высоту (h): begin{gather*} A_text{п}=Mgh. end{gather*} Затраченная работа электродвигателя: begin{gather*} A_text{з}=Nt. end{gather*} КПД установки begin{gather*} eta=frac{A_text{п}}{A_text{з}}=frac{mgh}{Nt} end{gather*} Масса воды begin{gather*} m=frac{eta Nt}{gh} end{gather*} Получаем: begin{gather*} m=frac{0,7cdot 5cdot 10^3cdot 3600}{10cdot 36}=35cdot 10^3 (text{кг})=35 text{т} end{gather*} Ответ: 35 т
Задача 7*. КПД подвижного блока при подъеме первого груза равен 80%, а при подъеме второго груза – 90%. Масса какого груза больше и во сколько раз? Трением в блоке можно пренебречь.
Дано:
(eta_1=80text{%}=0,8)
(eta_2=90text{%}=0,9)
__________________
(frac{M_2}{M_1}-?)
КПД подвижного блока массой (m), с помощью которого поднимают груз массой (M) begin{gather*} eta=frac{M}{M+m} end{gather*} (см. Задачу 5 выше). Масса груза begin{gather*} eta(M+m)=MRightarrow eta m=(1-eta)MRightarrow M=frac{eta}{1-eta}m end{gather*} Получаем: begin{gather*} M_1=frac{0,8}{1-0,8}m=4m,\[6pt] M_2=frac{0,9}{1-0,9}m=9m end{gather*} Масса второго груза больше.
Отношение масс begin{gather*} frac{M_2}{M_1}=frac{9m}{4m}=2,25 (text{раз}) end{gather*} Ответ: масса второго груза больше в 2,25 раз
п.4. Лабораторная работа №13. Определение КПД наклонной плоскости
Цель работы
Научиться проводить измерения и рассчитывать КПД простого механизма на примере наклонной плоскости. Исследовать зависимость КПД наклонной плоскости от высоты.
Теоретические сведения

Работа по подъему тела весом (P) вертикально на высоту (h) (из точки C в точку B): $$ A_text{CB}=Ph $$
Работа по перемещению того же тела силой (F), направленной вдоль наклонной плоскости длиной (L) (из точки A в точку B): $$ A_text{AB}=FL $$
В обоих случаях тело перемещается с нулевого уровня AC, где (h_0=0), на уровень с высотой (h) в точку B. Работа сторонних сил в этом случае равна изменению потенциальной энергии тела: $$ A=A_text{CB}=A_text{AB}=Delta E_p $$
Получаем уравнение для идеальной наклонной плоскости (без трения): $$ Ph=FL $$
При наличии трения получаем неравенство: $$ Phlt FL $$
Полезная и затраченная работа для наклонной плоскости: $$ A_text{п}=Ph, A_text{з}=FL $$
КПД наклонной плоскости: $$ eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{Ph}{FL}cdot 100text{%} $$
Затраченная работа равна сумме полезной работы и работы по преодолению силы трения: $$ A_text{з}=A_text{п}+F_text{тр}L $$
Откуда сила трения равна: $$ F_text{тр}=frac{A_text{з}-A_text{п}}{L}=frac{FL-Ph}{L}=F-Pfrac hL $$
Вес (P) и сила (F) определяются в работе с помощью динамометра с ценой деления (d=0,1 text{Н}).
Абсолютная погрешность прямых измерений $$ Delta_F=Delta_P=frac d2=0,05 text{Н}. $$
Сила (F) определяется в серии из пяти опытов с вычислением средних величин.
Высота наклонной плоскости (h) и длина наклонной плоскости (L) определяются с помощью мерной ленты с ценой деления (d=5 text{мм}). Абсолютная погрешность (Delta_L=2,5 text{мм}).
Относительные погрешности измерений вычисляются как обычно.
Относительная погрешность расчета КПД: $$ delta_eta=delta_F+delta_P+delta_h+delta_L $$
Абсолютная погрешность расчета КПД: $$ Delta_eta=etacdot delta_eta $$
Приборы и материалы
Доска длиной от 70 см, штатив с муфтой и лапкой, брусок массой не менее 300 г, мерная лента, динамометр.
Ход работы
1. Измерьте мерной лентой длину доски (L).
2. Определите вес бруска (P) с помощью динамометра.
3. Соберите наклонную плоскость: закрепите один конец доски в лапке штатива на высоте около (h=frac L3.)
4. Положите брусок на наклонную плоскость, прикрепите к нему динамометр и равномерно тяните по наклонной плоскости. Следите, чтобы динамометр располагался параллельно наклонной плоскости. Запишите измеренное значение (F). Повторите измерение (F) в серии из пяти опытов.
5. Соберите новую наклонную плоскость: закрепите один конец доски в лапке штатива на высоте около (h=frac L4). Перейдите на шаг 4 и повторите серию опытов для определения (F).
6. Рассчитайте КПД для двух исследованных наклонных плоскостей. Найдите относительные и абсолютные погрешности расчетов КПД.
7. Для каждой из наклонных плоскостей укажите величину полезной и затраченной работы, найдите силу трения.
8. Сделайте выводы о зависимости силы трения и КПД от высоты наклонной плоскости.
Результаты измерений и вычислений
Длина наклонной плоскости (доски) begin{gather*} L=80 text{см}=800 text{мм},\[7pt] Delta_L=2,5 text{мм},\[6pt] delta_L=frac{Delta_L}{L}=frac{2,5}{800}approx 0,0031=0,31text{%} end{gather*}
Вес бруска begin{gather*} P=4,4 text{Н},\[7pt] Delta_P=0,05 text{Н},\[6pt] delta_P=frac{Delta_P}{P}=frac{0,05}{4,4}approx 0,0011=1,1text{%} end{gather*}
1. Наклонная плоскость высотой (h=27 text{см})
Высота наклонной плоскости begin{gather*} h=27 text{см}=270 text{мм},\[7pt] Delta_h=2,5 text{мм},\[6pt] delta_h=frac{Delta_h}{h}=frac{2,5}{270}approx 0,0093=0,93text{%} end{gather*}
Определение силы тяги (F) в серии опытов
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| $$ F, H $$ | 2,9 | 2,8 | 3,0 | 2,7 | 2,8 | 14,2 |
| $$ Delta_F, H $$ | 0,06 | 0,04 | 0,16 | 0,14 | 0,04 | 0,44 |
begin{gather*} F_text{ср}=frac{sum F_i}{5}=frac{14,2}{5}=2,84 (text{Н}),\[6pt] Delta_{Ftext{ср}}=frac{sum Delta_{Fi}}{5}=frac{0,44}{5}approx 0,09 (text{Н}),\[6pt] F=(2,84pm 0,09) text{Н},\[7pt] delta_F=frac{0,09}{2,84}approx 0,032=3,2text{%} end{gather*}
Полезная работа: $$ A_text{П}=Ph=4,4cdot 0,27=1,188 (text{Дж}) $$
Затраченная работа: $$ A_text{З}=FL=2,84cdot 0,8=2,272 (text{Дж}) $$
Сила трения: $$ F_text{тр}=F-Pfrac hL=2,84-4,4cdot frac{0,27}{0,8}approx 1,36 (text{Н}) $$
КПД наклонной плоскости: $$ eta=frac{A_text{П}}{A_text{З}}=frac{1,188}{2,272}approx 0,523=52,3text{%} $$
Погрешности расчета КПД: $$ delta_eta=delta_F+delta_P+delta_h+delta_L=0,032+0,011+0,0093+0,0031=0,0554approx 0,056=5,6text{%} $$
При расчете (delta_eta) использовали округление с избытком. $$ Delta_eta=0,523cdot 0,056approx 0,029=2,9text{%} $$
Окончательно получаем: $$ eta=(52,3pm 2,9)text{%}, delta_eta=5,6text{%} $$
2. Наклонная плоскость высотой (h=20 text{см})
Высота наклонной плоскости begin{gather*} h=20 text{см}=200 text{мм},\[7pt] Delta_h=2,5 text{мм},\[6pt] delta_h=frac{Delta_h}{h}=frac{2,5}{200}approx 0,013=1,3text{%} end{gather*}
Определение силы тяги (F) в серии опытов
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| $$ F, H $$ | 2,4 | 2,6 | 2,5 | 2,6 | 2,5 | 12,6 |
| $$ Delta_F, H $$ | 0,12 | 0,08 | 0,02 | 0,08 | 0,02 | 0,32 |
begin{gather*} F_text{ср}=frac{sum F_i}{5}=frac{12,6}{5}=2,52 (text{Н}),\[6pt] Delta_{Ftext{ср}}=frac{sum Delta_{Fi}}{5}=frac{0,32}{5}approx 0,06 (text{Н}),\[6pt] F=(2,52pm 0,06) text{Н},\[7pt] delta_F=frac{0,06}{2,52}approx 0,024=2,4text{%} end{gather*}
Полезная работа: $$ A_text{П}=Ph=4,4cdot 0,2=0,88 (text{Дж}) $$
Затраченная работа: $$ A_text{З}=FL=2,52cdot 0,8=2,016 (text{Дж}) $$
Сила трения: $$ F_text{тр}=F-Pfrac hL=2,52-4,4cdot frac{0,2}{0,8}approx 1,42 (text{Н}) $$
КПД наклонной плоскости: $$ eta=frac{A_text{П}}{A_text{З}}=frac{0,88}{2,016}approx 0,437=43,7text{%} $$
Погрешности расчета КПД: $$ delta_eta=delta_F+delta_P+delta_h+delta_L=0,024+0,011+0,013+0,0031=0,0511approx 0,052=5,2text{%} $$
При расчете (delta_eta) использовали округление с избытком. $$ Delta_eta=0,437cdot 0,052approx 0,023=2,3text{%} $$
Окончательно получаем: $$ eta=(43,7pm 2,3)text{%}, delta_eta=5,2text{%} $$
Выводы
На основании полученных результатов можно сделать следующие выводы.
В работе проводился расчет КПД наклонной плоскости постоянной длины, но разной высоты.
Для высоты около (h=frac L3):
- полезная и затраченная работы: (A_text{П}=1,188 (text{Дж}), A_text{З}=2,272 (text{Дж}))
- сила трения: (F_text{тр}=1,36 (text{Н}))
- КПД: (eta=(52,3pm 2,9)text{%}, delta_eta=5,6text{%})
Для высоты около (h=frac L4):
- полезная и затраченная работы: (A_text{П}=0,88 (text{Дж}), A_text{З}=2,016 (text{Дж}))
- сила трения: (F_text{тр}=1,42 (text{Н}))
- КПД: (eta=(43,7pm 2,3)text{%}, delta_eta=5,2text{%})
Таким образом, с уменьшением высоты:
- сила трения растет;
- КПД наклонной плоскости падает.
Все задачи, поставленные перед исследованием, успешно выполнены.
Полезная и затраченная работа
На предыдущих занятиях при рассмотрении устройства и работы простейших механизмов не учитывали трение между деталями механизмов, вес механизмов – это идеализированные условия. На практике работа, совершаемая приложенной к телу силой, называется затраченной, она всегда больше работы, которая совершается по перемещению груза, поднятию груза или преодолению сопротивления, эта работа называется полезной. Полезная работа меньше затраченной.
Коэффициент полезного действия
Отношение полезной работы к затраченной работе, выраженной в процентах, называется коэффициентом полезного действия (КПД): ![]() .
.
КПД выражается в процентах, и для того чтобы его рассчитать, необходимо знать работу полезную и работу затраченную. При этом золотое правило механики не нарушается, потому что часть работы необходимо затратить, например, на трение, и, если сложить эти расходы, получается затраченная работа.
Эксперимент
На наклонной плоскости перемещаем каретку с грузом, с помощью динамометра узнаем вес каретки с грузом, в нашем случае вес 3 Н (рис.1).
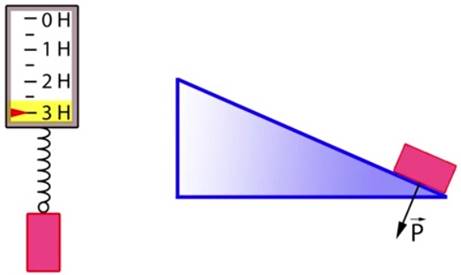
Рис. 1
Далее будем стараться перемещать каретку по наклонной плоскости, заметим при этом показания динамометра, который покажет силу тяги прикладываемой к каретке. При равномерном перемещении сила тяги равна 1,8Н. Узнаем путь каретки, он составляет 0,38 м, высота на которую каретку подняли 0,18 м (рис.2).
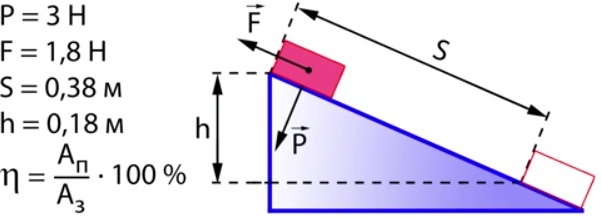
Рис. 2
Рассчитываем полезную и затраченную работу. Мы подняли груз весом P на высоту h – это полезная работа: ![]() .
.
Сила тяги и путь пройденный кареткой – это затраченная работа: ![]() .
.
Определим КПД: ![]() .
.
Задача
Условие: с помощью неподвижного блока груз массой m = 100 кг, подняли на высоту h = 5 м. Необходимо посчитать затраченную работу ![]() , если КПД этой установки
, если КПД этой установки ![]() = 70%.
= 70%.
Решение
В формулу расчета КПД запишем известные нам данные и преобразуем, разделив левую и правую часть на 100%.
![]()
![]()
![]()
Из этого выражения получим ![]() .
.
Чтобы рассчитать полезную работу, необходимо выяснить, что полезного совершалось в данной задаче. Груз массой 100 кг поднимали на высоту 5 м.
![]()
![]()
![]() – ускорение свободного падения.
– ускорение свободного падения.
Объединяем все полученные формулы вместе: ![]() .
.
Проверка единиц измерения: ![]() .
.
![]()
Ответ: приблизительное значение работы составляет 7143 Дж.
Заключение
Когда конструкторы создают различные механизмы, они стремятся увеличить КПД, подбирают смазочные материалы, материалы для изготовления изделия. Но есть еще способ увеличить КПД, необходимо уменьшать вес самого механизма.
Вычисление полезной работы через КПД
Определение
Коэффициентом полезного действия (при сокращённом написании КПД) именуют безразмерную физическую величину, характеризующую отношение энергии, которую система потратила с пользой для нас, к полному количеству полученной энергии.
Измерять КПД принято в процентах. Например, КПД 35%, означает, что почти две трети энергии пошли на ненужные траты, стали рассеянным в пустую теплом, были потрачены на истирание деталей машины, образование искр и т. п.
Важно. 35% совсем не плохой КПД. У паровозов первой половины 20 века он составлял всего 10%. Лишь одна десятая образующегося при сгорании топлива тепла шла на перемещение состава, остальное рассеивалось в атмосфере. Среднеэксплуатационный КПД у современных тепловозов 20-22%. КПД машин на бензиновом ДВС равен 25%. КПД дизеля – 33%. Хорошо на этом фоне выглядит КПД электромобилей. Он у них около 90%.
В формуле нахождения полезной работы да в физике в основном КПД обозначают буквой из греческого алфавита η (эта).
Полезная работа в физике и ненужные траты энергии
Прежде чем говорить о том, как найти полезную работу в физике, следует сказать о ней самой. Дело в том что полезная работа в физике – величина очень даже субъективная. Она напрямую связана с человеческим восприятием, с тем, чего нам нужно получить от системы. Поэтому часто, когда говорят о КПД, имеют в виду различные технические устройства, а не природные объекты.
Хотя технологии постоянно развиваются избежать значительных потерь энергии всё же не удаётся. Получается, что:
Aзатр > Aполез
Aзатр – затраченная работа, Aполез – полезная работа, та что идёт на осуществление нужного нам процесса.
Как бы мы ни пытались уменьшить ненужные потери энергии, полностью от них избавиться не получиться. Непреодолимой преградой для этого является первый закон термодинамики. Из него явственно следует, что КПД любого устройства и механизма ни при каких обстоятельствах не может быть больше единицы и даже стать равным ей.
Формула
Общая формула КПД:
[η = (Aполез/Aзатр) * 100%].
Мощность представляет собой работу, совершённую за единицу времени. В связи с этим КПД можно посчитать как отношение входной мощности системы к выходной. Т. е.
η = Pвх/Pвых.
Как найти полезную работу в физике используя формулы для разных физических процессов
Вид формул, как найти полезную работу в физике, зависит от природы физических явлений, использующихся для преобразования затраченной энергии в нужную.
Нет времени решать самому?
Наши эксперты помогут!
Как найти полезную работу в физике механической системы
Лучше всего это показать на конкретном примере. Допустим, нам требуется найти КПД процесса, при котором мальчик вкатывает санки весом 4 кг на горку длиной 12, высотой 2 м. Он прикладывает для этого силу, равную 15 Н.
Решение:
Напомним, что общая формула для КПД
η = (Aполез/Aзатр) * 100%
Aполез в нашем случае равна потенциальной энергии (Eп), которую нужно потратить на то, чтобы поднять санки на высоту, т. е. Aполез = m*g*h.
Затраченная мальчиком работа равна произведению силы на перемещение, т. е. Aзатр = F*S.
Подставляем в общую формулу для КПД
η = (m*g*h*100)/(F*S)
При подстановке численных значений получаем
η = 4*9,8*2/15*12 * 100% = 78,4/180 * 100% ≃ 43,6 %
Из этого примера ясно, чему равна полезная работа в физике механической системы, выраженная через КПД.
Формула
[Aполез = (η*F*S)/100]
Формула полезной работы в физике термодинамической системы
Именно по ней судят об эффективности тепловых машин. Допустим, нам нужно отыскать КПД тепловой машины, рабочее тело которой берёт от нагревателя 20кДж, а холодильнику отдаёт 10кДж.
Решение:
Тепловая машина работает следующим образом: нагреватель передаёт определённое количество теплоты рабочему телу, оно из-за этого расширяется, совершая тем самым механическую работу. Однако в последнюю переходит далеко не вся часть переданной тепловой энергии. Чтобы вернуть систему в исходное состояние и начать новый цикл приходится использовать холодильник.
Из выше сказанного можно сделать вывод, что Aполез равна разности энергии взятой от нагревателя и энергии, забранной холодильником, т. е.
Aполез = Qнагревателя – Qхолодильника
Затраченная работа равняется количеству той теплоты, которая была сообщена нагревателю.
Если всё это подставим в формулу для КПД, то получим
[eta=(text { Qнагревателя }-text { Qхолодильника })^{*} 100 / text { Qнагревателя }]
После подстановки численных значений будем иметь
η = (20 – 10)/20*100% = 50%
Теперь ясно, как определить полезную работу в физике термодинамической системы.
Формула
[eta=(text { Qнагревателя }-text { Qхолодильника })^{*} 100 / text { Qнагревателя }]
Формула полезной работы в физике электродинамической системы
Очень важный класс явлений. Каждый день все пользуются самыми разными электрическими устройствами: телевизором, компьютером, телефоном и т. д. Но мы рассмотрим случай попроще. Вычислим КПД электрического чайника. Допустим воде было передано 22176 Дж тепла за 2 мин. Напряжение в электросети стандартное 220 В. Сила тока равняется 1,4 А.
Решение:
Aполез будем считать работу, которая пошла на нагрев воды. Хотя она нам и дана из условия, формулу вспомнить всё равно не будет лишним.
- Q = cm(tконечная-tначальная)
- Q — количество теплоты [Дж]
- c — удельная теплоёмкость вещества [Дж/кг*˚C]
- m — масса [кг]
- tконечная — конечная температура [˚C]
- tначальная — начальная температура [˚C]
- Работа тока вычисляется по формуле
- A = (I^2)*Rt = (U^2)/R *t = UIt
- A — работа электрического тока [Дж]
- I — сила тока [А]
- U — напряжение [В]
- R — сопротивление [Ом]
- t — время [c]
В нашем примере она примет вид
η = Q/A *100% = Q/UIt *100%
Переводим минуты в секунды и, подставляя численные значения, получаем
η = 22176/220*1,4*120 *100% = 60%
Формула полезной работы электродинамической системы будет:
Формула
[Aполез = (η*U*I*t)/100%]
Второй закон Ньютона в импульсной форме позволяет определить, как меняется скорость тела по модулю и направлению, если в течение некоторого времени на него действует определенная сила:
![]()
Работа силы
В механике также важно уметь вычислять изменение скорости по модулю, если при перемещении тела на некоторый отрезок на него действует некоторая сила. Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуется величиной, зависящей как от сил, так и от перемещений. Эту величину в механике называют работой силы.
Работа силы обозначается буквой А. Это скалярная физическая величина. Единица измерения — Джоуль (Дж).
Работа силы равна произведению модуля силы, модуля перемещения и косинусу угла между ними:
![]()

Важно!
Механическая работа совершается, если:
- На тело действует сила.
- Под действием этой силы тело перемещается.
- Угол между вектором силы и вектором перемещения не равен 90 градусам (потому что косинус прямого угла равен нулю).
Внимание! Если к телу приложена сила, но под ее действием тело не начинает движение, механическая работа равна нулю.
Пример №1. Груз массой 1 кг под действием силы 30 Н, направленной вертикально вверх, поднимается на высоту 2 м. Определить работу, совершенной этой силой.
Так как перемещение и вектор силы имеют одно направление, косинус угла между ними равен единице. Отсюда:
![]()
Работа различных сил
Любая сила, под действием которой перемещается тело, совершает работу. Рассмотрим работу основных сил в таблице.
| Работа силы тяжести |
Модуль силы тяжести: Fтяж = mg Работа силы тяжести: A = mgs cosα |
| Работа силы трения скольжения |
Модуль силы трения скольжения: Fтр = μN = μmg Работа силы трения скольжения: A = μmgs cosα |
| Работа силы упругости |
Модуль силы упругости: Fупр = kx Работа силы упругости:
|
Работа силы упругости
Работа силы упругости не может быть определена стандартной формулой, так как она может применяться только для постоянной по модулю силы. Сила же упругости меняется по мере сжатия или растяжения пружины. Поэтому берется среднее значение, равное половине суммы сил упругости в начале и в конце сжатия (растяжения):

Нужно также учесть, что перемещение тела под действием силы упругости равно разности удлинения пружины в начале и конце:
s = x1 – x2
Перемещение и направление силы упругости всегда сонаправлены, поэтому угол между ними нулевой. А косинус нулевого угла равен 1. Отсюда работа силы упругости равна:

Работы силы трения покоя
Работы силы трения покоя всегда равна 0, так как под действием этой силы тело не сдвигается с места. Исключение составляет случай, когда покоящееся тело лежит на подвижном предмете, на который действует некоторая сила. Относительно системы координат, связанной с подвижным предметом, работа силы трения покоя будет нулевой. Но относительно системы отсчета, связанной с Землей, эта сила будет совершать работу, так как тело будет двигаться, оставаясь на поверхности движущегося предмета.

Пример №2. Груз массой 100 кг волоком перетащили на 10 м по плоскости, поверхность которой имеет коэффициент трения 0,4. Найти работу, совершенной силой трения скольжения.
A = μmgs cosα = 0,4∙100∙10∙10∙(–1) = –4000 (Дж) = –4 (кДж)
Знак работы силы
Знак работы силы определяется только косинусом угла между вектором силы и вектором перемещения:
- Если α = 0о, то cosα = 1.
- Если 0о < α < 90o, то cosα > 0.
- Если α = 90о, то cosα = 0.
- Если 90о < α < 180o, то cosα < 0.
- Если α = 180о, то cosα = –1.
Работа силы трения скольжения всегда отрицательна, так как сила трения скольжения направлена противоположно перемещению тела (угол равен 180о). Но в геоцентрической системе отсчета работа силы трения покоя будет отличной от нуля и выше нуля, если оно будет покоиться на движущемся предмете (см. рис. выше). В таком случае сила трения покоя будет направлена с перемещением относительно Земли в одну сторону (угол равен 0о). Это объясняется тем, что тело по инерции будет пытаться сохранить покой относительно Земли. Это значит, что направление возможного движения противоположно движению предмета, на котором лежит это тело. А сила трения покоя направлена противоположно направлению возможного движения.
Геометрический смысл работы
Графическое определение
Механическая работа численно равна площади фигуры, ограниченной графиком с осями OF и OX.

A = Sфиг
Мощность
Определение
Мощность — физическая величина, показывающая, какую работу совершает тело в единицу времени. Мощность обозначается буквой N. Единица измерения: Ватт (Вт). Численно мощность равна отношению работы A, совершенной телом за время t:

Рассмотрим частные случаи определения мощности в таблице.
Мощность при равномерном прямолинейном движении тела |
Работа при равномерном прямолинейном движении определяется формулой: A = Fтs Fт — сила тяги, s — перемещение тела под действием этой силы. Отсюда мощность равна:
|
Мощность при равномерном подъеме груза |
Когда груз поднимается, совершается работа, по модулю равная работе силе тяжести. За перемещение в этом случае можно взять высоту. Поэтому:
|
Мгновенная мощность при неравномерном движении |
Выше мы уже получили, что мощность при постоянной скорости равна произведению этой скорости на силу тяги. Но если скорость постоянно меняется, можно вычислить мгновенную мощность. Она равна произведению силы тяги на мгновенную скорость:
|
Мощность силы трения при равномерном движении по горизонтали |
Мощность силы трения отрицательна так же, как и работа. Это связано с тем, что угол между векторами силы трения и перемещения равен 180о (косинус равен –1). Учтем, что сила трения скольжения равна произведению силы нормальной реакции опоры на коэффициент трения:
|
Пример №3. Машина равномерно поднимает груз массой 10 кг на высоту 20 м за 40 с. Чему равна ее мощность?
Коэффициент полезного действия
Не вся работа, совершаемая телами, может быть полезной. В реальном мире на тела действует несколько сил, препятствующих совершению работы другой силой. К примеру, чтобы переместить груз на некоторое расстояние, нужно совершить работу гораздо большую, чем можно получить при расчете по формулам выше.
Определения:
- Работа затраченная — полная работа силы, совершенной над телом (или телом).
- Работа полезная — часть полной работы силы, которая вызывает непосредственно перемещение тела.
- Коэффициент полезного действия (КПД) — процентное отношение полезной работы к работе затраченной. КПД обозначается буквой «эта» — η. Единицы измерения эта величина не имеет. Она показывает эффективность работы механизма или другой системы, совершающей работу, в процентах.
КПД определяется формулой:

Работа может определяться как произведение мощности на время, в течение которого совершалась работа:
A = Nt
Поэтому формулу для вычисления КПД можно записать в следующем виде:

Частые случаи определения КПД рассмотрим в таблице ниже:
Устройство |
Работа полезная и полная |
КПД |
| Неподвижный блок, рычаг |
Aполезн = mgh Асоверш. |
 |
| Наклонная плоскость |
Aполезн = mgh Асоверш. = Fl l — совершенный путь (длина наклонной плоскости). |
 |
Пример №4. Определите полезную мощность двигателя, если его КПД равен 40%, а его мощность по паспорту равна 100 кВт.
В данном случае необязательно переводить единицы измерения в СИ. Но в таком случае ответ мы тоже получим в кВт. Из этой формулы выразим полезную мощность:
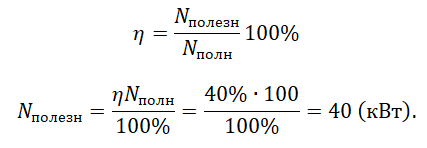
Задание EF17557
Какую мощность развивает сила тяги трактора, перемещая прицеп со скоростью 18 км/ч, если она составляет 16,5 кН?
Ответ:
а) 916 Вт
б) 3300 Вт
в) 82500 Вт
г) 297000 Вт
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Записать формулу для расчета мощности.
3.Выполнить общее решение задачи.
4.Подставить известные данные и выполнить вычисления.
Решение
Запишем исходные данные:
• Сила тяги, перемещающая прицеп, равна: Fт = 16,5 кН.
• Скорость перемещения прицепа под действием силы тяги: v = 18 км/ч.
Переведем единицы измерения в СИ:
16,5 кН = 16,5∙103 Н
18 км/ч = 18000/3600 м/с = 5 м/с
Мощность равна отношению работы ко времени, в течение которого эта работа совершалась:
N=At
Но работа равна произведению силы, перемещения и косинуса угла между векторами силы и перемещения. В данном случае будем считать, что угол равен нулю, следовательно косинус — единице. Тогда работа равна:
A = Fs
Тогда мощность равна:
N=Fst=Fv=16,5·103·5=82500 (Вт)
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17574
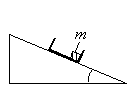 С вершины наклонной плоскости из состояния покоя скользит с ускорением лёгкая коробочка, в которой находится груз массой m (см. рисунок). Как изменятся время движения, ускорение и модуль работы силы трения, если с той же наклонной плоскости будет скользить та же коробочка с грузом массой m/2? Для каждой величины определите соответствующий характер изменения:
С вершины наклонной плоскости из состояния покоя скользит с ускорением лёгкая коробочка, в которой находится груз массой m (см. рисунок). Как изменятся время движения, ускорение и модуль работы силы трения, если с той же наклонной плоскости будет скользить та же коробочка с грузом массой m/2? Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
|
Время движения |
Ускорение |
Модуль работы силы трения |
Алгоритм решения
1.Установить наличие и характер зависимости кинематических характеристик движения от массы тела.
2.Вывести формулу для модуля работы силы трения.
3.Установить, как изменится модуль работы силы трения при уменьшении массы тела вдвое.
Решение
При скольжении с наклонной плоскости происходит равноускоренное движение. Положение тела в любой момент времени при таком движении можно определить с помощью кинематических уравнений:
x=xo+v0xt+axt22
y=yo+v0yt+ayt22
Из этих уравнений видно, что ускорение и время никак не зависят от массы тела. Следовательно, при уменьшении массы тела в 2 раза его время движения и ускорение не изменятся.
Чтобы выразить модуль работы силы трения, выберем такую систему отсчета, чтобы вектор силы трения был расположен вдоль оси Ox.Тогда сила трения будет равна:
Fтр = μmg
Известно, что работа определяется формулой:
A = Fs cosα
Тогда работа силы трения равна:
A = μmgs cosα
Вектор силы трения всегда направлен противоположно вектору перемещения. Поэтому косинус угла между ними равен –1. Но нас интересует только модуль работы. Поэтому будем считать, что он равен:
A = μmgs
Модуль работы силы трения и масса тела зависят прямо пропорционально. Следовательно, если массу тела уменьшить вдвое, то и модуль работы силы трения уменьшится вдвое.
Поэтому правильная последовательность цифр в ответе: 332.
Ответ: 332
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18646
В первой серии опытов брусок перемещают при помощи нити равномерно и прямолинейно вверх по наклонной плоскости. Во второй серии опытов на бруске закрепили груз, не меняя прочих условий.
Как изменятся при переходе от первой серии опытов ко второй сила натяжения нити и коэффициент трения между бруском и плоскостью?
Для каждой величины определите соответствующий характер её изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.
| Сила натяжения нити | Коэффициент трения |
Алгоритм решения
- Определить, какая величина изменилась во второй серии опытов.
- Определить, как зависит от этой величины сила натяжения нити.
- Определить, как зависит от этой величины коэффициент трения.
Решение
Когда к бруску подвесили груз, увеличилась масса. Когда тело на нити перемещается вверх прямолинейно и равномерно, сила натяжения нити определяется модулем силы тяжести:
T = mg
Эта формула показывает, что сила натяжения нити и масса тела зависят прямо пропорционально. Если, добавив к бруску груз, масса увеличится, то сила натяжения нити тоже увеличится.
Коэффициент трения — это величина, которая зависит только от материалов и типа поверхности. Поэтому увеличение массы тела на него никак не повлияют.
Верная последовательность цифр в ответе: 13.
Ответ: 13
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18271
Определите коэффициент полезного действия атомной электростанции, расходующей за неделю уран-235 23592U массой 1,4 кг, если её мощность равна 38 МВт. При делении одного ядра урана-235 выделяется энергия 200 МэВ.
Алгоритм решения
1.Записать исходные данные и перевести их в СИ.
2.Записать формулу для определения КПД атомной электростанции.
3.Решить задачу в общем виде.
4.Подставить известные данные и вычислить искомую величину.
5.Массовое число: A = 235.
6.Зарядовое число: Z = 92.
Решение
Запишем исходные данные:
• Энергия, выделяемая при делении одного ядра урана-235: Q0 = 200 МэВ.
• Масса урана-235: m = 1,4 кг.
• Время, в течение которого происходит деление: t = 1 неделя.
• Мощность атомной электростанции: N = 38 МВт.
Переведем все единицы измерения в СИ:
1 эВ = 1,6∙10–19 Дж
200 МэВ = 200∙106∙1,6∙10–19 Дж = 320∙10–13 Дж
1 неделя = 7∙24∙60∙60 с = 604,8∙103 с
38 МВт = 38∙106 Вт
КПД атомной электростанции есть отношение полезной работы к выделенной за это же время энергии:
η=AполезнQ100%
Полезную работу мы можем вычислить по формуле:
A=Nt
Выделенное количество теплоты мы можем рассчитать, вычислив количество атомов, содержащихся в 1,4 кг урана-235 и умножив их на энергию, выделяемую при делении одного такого атома.
Количество атомов равно произведению количество молей на постоянную Авогадро:
Nкол.атомов = νNA
Количество молей равно отношения массы вещества к его молярной массе, следовательно:
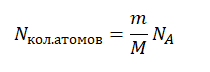
Молярная масса численно равна массовому числу в граммах на моль. Следовательно:
M = A (г/моль) = A∙10–3 (кг/моль)
Отсюда количество атомов равно:
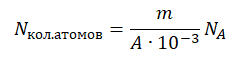
Энергия, выделенная всеми атомами, равна:
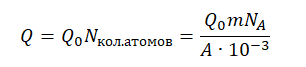
Теперь можем вычислить КПД:
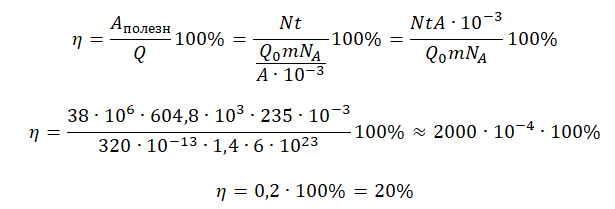
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 12k
Используя тот или иной механизм, мы совершаем работу, всегда превышающую ту, которая необходима для достижения поставленной цели. В соответствии с этим различают полную или затраченную работу Aз и полезную работу Aп. Если, например, наша цель — поднять груз массой m на высоту h, то полезная работа — это та, которая обусловлена лишь преодолением силы тяжести, действующей на груз. При равномерном подъеме груза, когда прикладываемая нами сила равна силе тяжести груза, эта работа может быть найдена следующим образом:
Aп = Fтh = mgh. (24.1)
Если же мы применяем для подъема груза блок или какой-либо другой механизм, то, кроме силы тяжести груза, нам приходится преодолевать еще и силу тяжести частей механизма, а также действующую в механизме силу трения. Например, используя подвижный блок, мы вынуждены будем совершать дополнительную работу по подъему самого блока с тросом и по преодолению силы трения в оси блока. Кроме того, выигрывая в силе, мы всегда проигрываем в пути (об этом подробнее будет рассказано ниже), что также влияет на работу. Все это приводит к тому, что затраченная нами работа оказывается больше полезной:
Aз > Aп
Полезная работа всегда составляет лишь некоторую часть полной работы, которую совершает человек, используя механизм.
Физическая величина, показывающая, какую долю составляет полезная работа от всей затраченной работы, называется коэффициентом полезного действия механизма.
Сокращенное обозначение коэффициента полезного действия — КПД.
Чтобы найти КПД механизма, надо полезную работу разделить на ту, которая была затрачена при использовании данного механизма.
Коэффициент полезного действия часто выражают в процентах и обозначают греческой буквой η (читается «эта»):
η =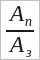 * 100% (24.2)
* 100% (24.2)
Поскольку числитель Aп в этой формуле всегда меньше знаменателя Aз, то КПД всегда оказывается меньше 1 (или 100%).
Конструируя механизмы, стремятся увеличить их КПД. Для этого уменьшают трение в осях механизмов и их массу. В тех случаях, когда трение ничтожно мало и используемые механизмы имеют массу, пренебрежимо малую по сравнению с массой поднимаемого груза, коэффициент полезного действия оказывается лишь немного меньше 1. В этом случае затраченную работу можно считать примерно равной полезной работе:
Aз ≈ Aп (24.3)
Следует помнить, что выигрыша в работе с помощью простого механизма получить нельзя.
Поскольку каждую из работ в равенстве (24.3) можно выразить в виде произведения соответствующей силы на пройденный путь, то это равенство можно переписать так:
F1s1 ≈ F2s2 (24.4)
Отсюда следует, что,
выигрывая с помощью механизма в силе, мы во столько же раз проигрываем в пути, и наоборот.
Этот закон называют «золотым правилом» механики. Его автором является древнегреческий ученый Герон Александрийский, живший в I в. н. э.
«Золотое правило» механики является приближенным законом, так как в нем не учитывается работа по преодолению трения и силы тяжести частей используемых приспособлений. Тем не менее оно бывает очень полезным при анализе работы любого простого механизма.
Так, например, благодаря этому правилу мы сразу можем сказать, что рабочему, изображенному на рисунке 47, при двукратном выигрыше в силе для подъема груза на 10 см придется опустить противоположный конец рычага на 20 см. То же самое будет и в случае, изображенном на рисунке 58. Когда рука человека, держащего веревку, опустится на 20 см, груз, прикрепленный к подвижному блоку, поднимется лишь на 10 см.
1. Почему затраченная при использовании механизмов работа оказывается все время больше полезной работы? 2. Что называют коэффициентом полезного действия механизма? 3. Может ли КПД механизма быть равным 1 (или 100%)? Почему? 4. Каким образом увеличивают КПД? 5. В чем заключается «золотое правило» механики? Кто его автор? 6. Приведите примеры проявления «золотого правила» механики при использовании различных простых механизмов.