Оценка погрешностей измерений при выполнении лабораторных работ по физике
Выполнение лабораторных
работ связано с измерением различных
физических величин и последующей
обработкой полученных результатов.
Поскольку не существует абсолютно
точных приборов и других средств
измерения, следовательно, не бывает
и абсолютно точных результатов измерения.
Погрешности возникают при любых
измерениях, и только правильная оценка
погрешностей проведенных измерений и
расчетов позволяет выяснить степень
достоверности полученных результатов.
Абсолютная погрешность измерения
Рисунок
1
Предположим, что
диаметр стержня, измеренный штангенциркулем,
оказался равным 14 мм. Можно ли быть
уверенным, что он пройдет в “идеальное”
отверстие того же диаметра? Если бы этот
вопрос был поставлен чисто ”теоретически“,
то ответ был бы утвердительным, но на
практике может получиться иначе. Диаметр
стержня был определен с помощью реального
измерительного прибора, следовательно,
с некоторой погрешностью. Значит 14 мм
– это приближенное
значение диаметра
– Xпр.
Определить его истинное значение
невозможно, можно только указать
некоторые границы достоверности
полученного приближенного результата,
внутри которых находится истинное
значение диаметра нашего стержня. Эта
граница называется границей
абсолютной погрешности
и обозначается ΔX
(её часто называют просто абсолютной
погрешностью).
Поэтому наш стержень может пройти в
отверстие, а так же может и не пройти в
него: все зависит от того, в каком месте
интервала [Xпр
– ΔX,
Xпр
+ ΔX]
находится
истинное значение диаметра нашего
стержня. На рисунке 1 показан случай,
когда стержень в отверстие не пройдет.
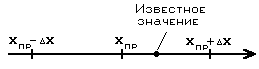
Итак, абсолютная
погрешность показывает, насколько
неизвестное экспериментатору истинное
значение измеряемой величины может
отличаться от измеренного значения.
Результат измерения
с учетом абсолютной погрешности
записывают так:
Относительная погрешность измерения
Значение абсолютной
погрешности все же не позволяет в полной
мере оценить качество наших измерений.
Если, например, в результате измерений
установлено, что длина стола с учетом
абсолютной погрешности равна (100±
1) см, а толщина
его крышки равна (2
± 1) см, то качество
измерений в первом случае выше (хотя
граница абсолютной погрешности измерений
в обоих случаях одинакова). Качество
измерений характеризуется относительной
погрешностью ε,
равной отношению абсолютной погрешности
ΔX к значению
величины Xпр,
получаемой в результате измерения:
.
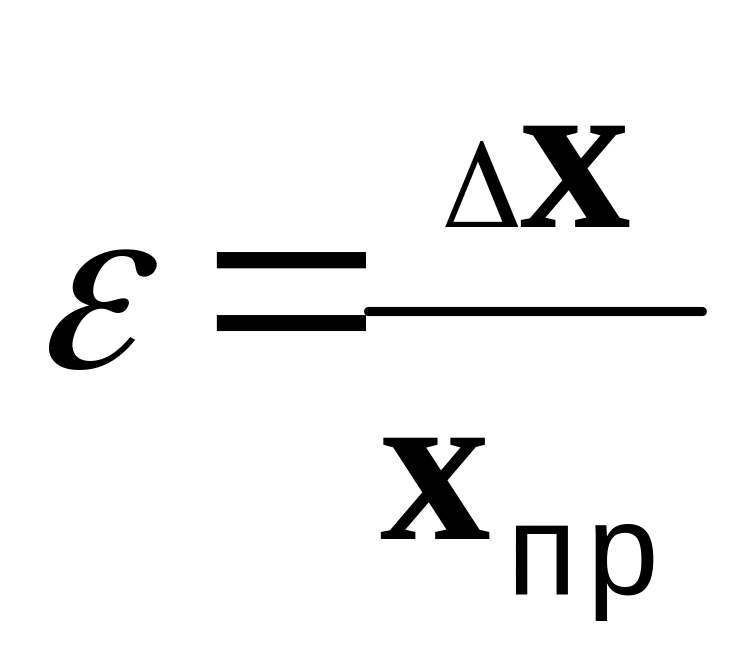
При выполнении
лабораторных работ выделяют следующие
виды погрешностей:
погрешности прямых измерений; погрешности
косвенных измерений; случайные погрешности
и систематические погрешности.
Погрешности прямых измерений
Прямое измерение
– это такое
измерение, при котором его результат
определяется непосредственно в процессе
считывания со шкалы прибора. В нашем
первом примере с определением диаметра
стержня речь шла как раз о таком измерении.
Погрешность прямого измерения обозначается
значком Δ. Если вы умеете правильно
пользоваться измерительным прибором,
то погрешность прямого измерения зависит
только от его качества и равна сумме
инструментальной
погрешности
прибора (Δ и)
и погрешности
отсчета (Δ 9).
Таким образом: Δ = Δ и
+ Δ о
Инструментальная
погрешность
измерительного прибора (Δи)
определяется на заводе-изготовителе.
Абсолютные инструментальные погрешности
измерительных приборов, чаще всего
используемых для проведения лабораторных
работ, приведены в таблице 1.
Таблица
1
|
Средства измерения |
Предел измерения |
Цена деления |
Инструментальная погрешность |
|
Линейка ученическая |
До 30 см |
1 мм |
|
|
Линейка чертежная |
До 50 см |
1 мм |
0,2 |
|
Линейка инструментальная |
До 30 см |
1 мм |
0,1 |
|
Линейка демонстрационная |
100 см |
1 см |
0,5 |
|
Лента измерительная |
150 см |
0,5 см |
0,25 |
|
Измерительный |
до 250 мл |
1 мл |
1 |
|
Штангенциркуль |
150 мм |
0,1 мм |
0,05 |
|
Микрометр |
25 мм |
0,01 мм |
0,005 |
|
Динамометр учебный |
4 Н |
0,1 Н |
0,05 |
|
Секундомер электронный |
100 с |
0,01 с |
0,01 |
|
Барометр-анероид |
720-780 мм.рт.ст |
1 мм.рт.ст. |
3 |
|
Термометр спиртовой |
0-100оС |
1оС |
1оС |
|
Термометр ртутный |
До 250оС |
1оС |
0,5оС |
|
Амперметр школьный |
2 А |
0,1 А |
0,05 |
|
Вольтметр школьный |
6 В |
0,2 В |
0,15 |
Погрешность отсчета
измерительного прибора (Δ
о)
связана с тем, что указатель прибора
не всегда точно совпадает с делениями
шкалы. В этом случае погрешность отсчета
не превосходит половины цены деления
шкалы.
Поэтому абсолютную
погрешность прямого измерения находят
по формуле
.,
где с – цена деления шкалы измерительного
прибора.
Учитывать погрешность
отсчета надо только в тех случаях, когда
указатель прибора при измерении находится
между нанесенными на шкалу прибора
делениями. Не имеет смысла учитывать,
погрешности отсчета у цифровых
измерительных приборов.
Одновременно
учитывать обе составляющие погрешности
прямого измерения следует лишь в том
случае, если их значения близки друг к
другу. Любым из
этих слагаемых можно пренебречь, если
оно не превосходит одной трети или
одной четверти второго. В этом состоит
так называемое правило “ничтожных
погрешностей“.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вычисление погрешностей измерений
Выполнение лабораторных работ связано с измерением физических величин, т. е. определением значений величин опытным путём с помощью измерительных приборов (средств измерения), и обработкой результатов измерений.
Различают прямые и косвенные измерения. При этом результат любого измерения является приблизительным, т. е. содержит погрешность измерения. Точность измерения физической величины характеризуют абсолютная и относительная погрешности.
Прямое измерение — определение значения физической величины непосредственно с помощью измерительного прибора.
Абсолютную погрешность прямых измерений определяют суммой абсолютной инструментальной погрешности и абсолютной погрешности отсчёта Δx = Δиx + Δоx при условии, что случайная погрешность и погрешность вычисления или отсутствуют, или незначительны и ими можно пренебречь.
Абсолютная инструментальная погрешность Δиx связана с классом точности прибора. Абсолютные инструментальные погрешности некоторых средств измерений представлены в таблице 1.
| Средства измерений | Диапазон измерений | Абсолютная инструментальная погрешность |
| Линейки: металлические деревянные пластмассовые |
150, 300, 500 мм 400, 500, 750 мм 200, 250, 300 мм |
0,1 мм 0,5 мм 1 мм |
| Лента измерительная | 150 см | 0,5 см |
| Мензурки 2-го класса | 100, 200, 250 см3 | 5 см3 |
| Амперметр школьный | 2 А | 0,05 А |
| Миллиамперметр | от 0 до Imax | 4 % максимального предела измерений Imax |
| Вольтметр школьный | 6 В | 0,15 В |
| Термометр лабораторный | 100 °С | 1 °С |
| Барометр-анероид | 720–780 мм рт. ст. | 3 мм рт. ст. |
| Штангенциркули с ценой деления 0,1; 0,05 мм | 155, 250, 350 мм | 0,1; 0,05 мм в соответствии с ценой деления нониуса |
| Микрометры с ценой деления 0,01 мм | 0–25, 25–50, 50–75 мм | 0,004 мм |
Абсолютная погрешность отсчёта Δоx связана с дискретностью шкалы прибора. Если величину измеряют с точностью до целого деления шкалы прибора, то погрешность отсчёта принимают равной цене деления. Если при измерении значение величины округляют до половины деления шкалы, то погрешность отсчёта принимают равной половине цены деления.
Абсолютная погрешность определяет значение интервала, в котором лежит истинное значение измеренной величины:
Относительную погрешность прямого измерения определяют отношением абсолютной погрешности к значению измеряемой величины:
Относительная погрешность характеризует точность измерения: чем она меньше, тем точность измерения выше.
Косвенное измерение — определение значения физической величины с использованием формулы, связывающей её с другими величинами, измеренными непосредственно с помощью приборов.
Одним из методов определения погрешности косвенных измерений является метод границ погрешностей. Формулы для вычисления абсолютных и относительных погрешностей косвенных измерений методом границ погрешностей представлены в таблице 2.
| Вид функции y | Абсолютная погрешность Δy | Относительная погрешность |
| x1 + x2 | Δx1 + Δx2 | |
| x1 − x2 | Δx1 + Δx2 | |
| Cx | CΔx | |
| x1x2 | |x1| Δx2 + |x2| Δx1 | |
| xn | |n||x|n−1Δx | |
| lnx | ||
| sinx | |cosx| Δx | |
| cosx | |sinx| Δx | |tgx| Δx |
| tgx |
Абсолютную погрешность табличных величин и фундаментальных физических постоянных определяют как половину единицы последнего разряда значения величины.
Лабораторная работа 1
Определение абсолютной и относительной погрешностей
прямых измерений
Цель: научиться определять абсолютную и относительную погрешности прямых измерений и представлять результат измерений в интервальной форме.
Оборудование: металлический шарик на нитке длиной =1 м, секундомер, штатив со стержнем, треугольник (рис. 1).
Краткие теоретические сведения
Прямым называется измерение, при котором значение искомой величины находится непосредственно по шкале прибора. Результат любого измерения содержит погрешность.
Систематическая погрешность связана в основном с несовершенством измерительного прибора и округлениями при отсчетах и вычислениях. При повторении измерений систематическая погрешность остается неизменной.
Случайная погрешность — это погрешность, которая от одного измерения к другому изменяется непредсказуемым образом. Для определения случайной погрешности необходимо провести серию повторных измерений.
Абсолютная погрешность ΔА физической величины А равна:
ΔА = ΔА пр+ А отс + ΔАсл (1) , где
ΔА пр – абсолютная погрешность прибора (указывается для каждого прибора или берется из таблицы)
А отс –абсолютная погрешность отсчета (половина цены деления шкалы прибора)
ΔАсл – абсолютная случайная погрешность ( как вычисляется эта погршеность будет рассмотрено в ходе выполнения работы)
ΔАсист = ΔА пр+ А отсч
Абсолютная погрешность определяет значение интервала, в котором лежит истинное значение измеренной величины:
А=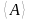 
А
Относительную погрешность прямого измерения определяют отношением абсолютной погрешности к значению измеряемой величины:
А = 
*100%
Относительная погрешность характеризует точность измерения: чем она меньше, тем точность измерения выше.
Окончательный результат записывается в интервальной форме:
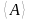
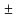А= А
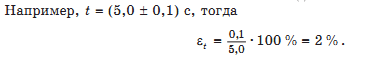
П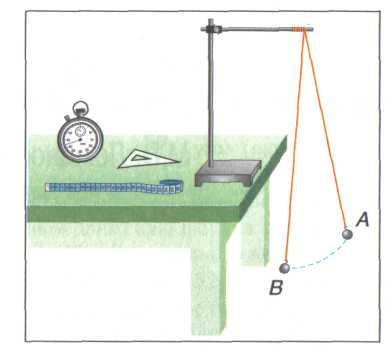
орядок выполнения работы
1. К стержню штатива прикрепите нить с шариком (см. рис. 1). Отведите шарик в сторону (точку А) так, чтобы нить составила с вертикалью угол а = 30° (определяется треугольником). Отпустите шарик и, одновременно нажав на кнопку секундомера, измерьте минимальный промежуток времени, через который шарик снова окажется в точке А.
2. Повторите опыт не менее 5 раз.
3. Вычислите среднее значение промежутка времени:
4. Вычислите абсолютную случайную погрешность при каждом измерении и
среднее значение Δtсл при пяти измерениях:
1)
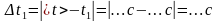
2) 
…
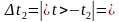3) 
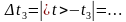
4) 
…
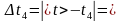5) 
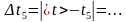
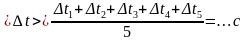
5. Определите абсолютную погрешность прямого измерения промежукта времени:
∆tпр=∆tсл.+∆tпр+∆tотсч
6. Вычислите относительную погрешность прямого измерения промежутка времени:
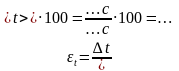
7. Запишите окончательный результат в интервальной форме:
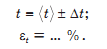
Контрольные вопросы
1. Приведите примеры прямых и косвенных измерений.
2. Почему нельзя абсолютно точно измерить прибором физическую величину?
Проще пареной репы.
Пусть мы измеряем физические величины A, B, и C
После этого по какой-то формуле вычисляем D
например D = AB/(C-B) + B^2
Как наити погрешность для D
1) Надо определить погрешность для каждой из измеряемых величин
Рассматриваем вариант, когда измерение проходит в один замер (для школьных работ характерно)
Обозначим
А – измеренное значение величины
dA – абсолютная погрешность измерения А
(сигма) % = dA/A 100% – относительная погрешность
Величина dA складывается из двух величин (погрешность снятия показаний) + (инструментальная погрешность)
dA = dA1 + dA2
dA1 = половине самого мелкого деления прибора. Например, у миллиметровой линейки это будет dA1=0,5 мм
dA2 – это погрешность самого прибора (инструментальная погрешность)
Она указывается на самом приборе в виде относительной погрешности в %. Внимательно посмотрите на “циферблат прибора – там будет стоять цифра (% часто не пишут) или найдите в паспорте к нему. Берем диапазон измерений прибора и умножаем на % точности. Если шкала от 0 до 600 – диапазон 600, если шкала от 400 до 600 – диапазон 200/ Пусть точность прибора 2,5%, а вся шкала измерений от 0 до 400 “баранов”, тогда абсолютная инструментальная погр.
dA2 = 400 * 2,5/100 = 10 баранов
Если на приборе не указана точность – это означает, что dA2 можно не учитывать при расчете и
dA = dA1
Именно так поступаем при измерении линейкой
dA = dA1 = 0,5 mm
Итак определились с абс. погрешностью, вычисляем относительную.
Например, линейкой измерили расстояние, получили замер L=330 мм.
dL = 0,5 mm – абсолютная погр.
(сигма) % = dL/L 100% = 0,5 100/330 %=0,15 % – относительная погрешность
2) Так разобрались со всеми измеряемыми величинами. Начинаем расчет по формуле. Правила просты
формула D = A + B
(отн. погр. )
dD/D = (dA + dB)/(A + B)
формула D = A – B
dD/D = (dA + dB)/(A – B)
формула D = ABC D=AB/C – любое умножение и деление
dD/D = dA/A + dB/B + dC/C
т, е. просто складываем относительнае погрешности
Частный случай последнего возведение в степень и извлечение корня
D = A^n
dD/D = ndA/A
в куб – n=3 dD/D = 3dA/A
корень кубический n=1/3 dD/D = 1/3 dA/A
Например, линейкой измеряем стороны прямоугольника
сторона 1 = 100 мм
абс. погр 0,5 мм
отн. погр. = 0.5/100 * 100% = 0,5%
сторона 2 = 80 мм
абс. погр 0,5 мм
отн. погр. = 0.5/80 * 100% = 0,625% = 0,6% (округляем до десятых – это обязательно, максимум до сотых%, тысячные ни в коем случае не оставляем)
Расчеты
а) сумма длин 180 мм
отн. погр. = (0,5 + 0,5)/180 *100% = 10/18 = 0,56 %
сумма длин = 180 мм плюс/минус 1 мм
б) разность длин 100-80=20
отн. погр. = (0,5 + 0,5)/20 *100% = 5,0 %
разность длин =20 плюс/минус 1 мм
в) площадь 100*80=8000 мм2
отн. погр. = 0,5% + 0,6% = 1,1%
это означает, что площадь = 8000 плюс/минус 88 мм2
д) отношение длин 100/80=1,25
отн. погр. = 0,5% + 0,6% = 1,1%
L1/L2 = 1,25 плюс/минус 0,01
