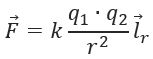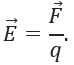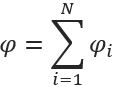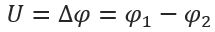Времена, когда ток обнаруживался с помощью личных ощущений ученых, пропускавших его через себя, давно миновали. Теперь для этого применяют специальные приборы, называемые амперметрами.
Амперметр — это прибор, служащий для измерения силы тока. Что понимают под силой тока?
Обратимся к рисунку 21, б. На нем выделено поперечное сечение проводника, через которое проходят заряженные частицы при наличии в проводнике электрического тока. В металлическом проводнике этими частицами являются свободные электроны. В процессе своего движения вдоль проводника электроны переносят некоторый заряд. Чем больше электронов и чем быстрее они движутся, тем больший заряд будет ими перенесен за одно и то же время.
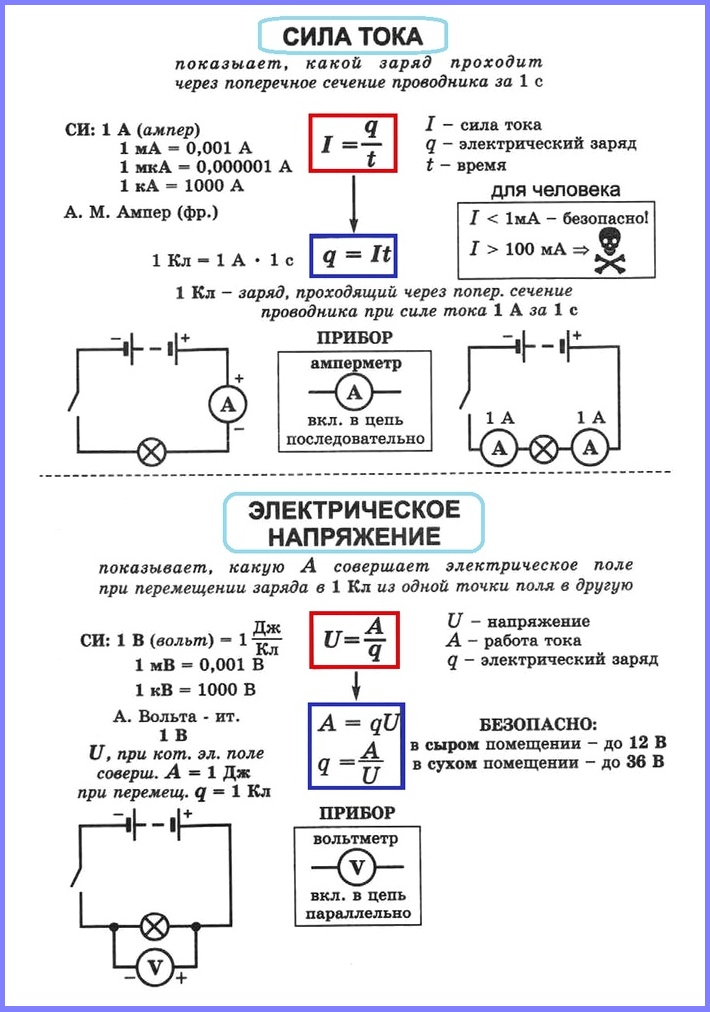
Силой тока называется физическая величина, показывающая, какой заряд проходит через поперечное сечение проводника за 1 с.
Пусть, например, за время t = 2 с через поперечное сечение проводника носители тока переносят заряд q = 4 Кл. Заряд, переносимый ими за 1 с, будет в 2 раза меньше. Разделив 4 Кл на 2 с, получим 2 Кл/с. Это и есть сила тока. Обозначается она буквой I:
I — сила тока.
Итак, чтобы найти силу тока I, надо электрический заряд q, прошедший через поперечное сечение проводника за время t, разделить на это время:
I = q/t (10.1)
Единица силы тока называется ампером (А) в честь французского ученого А. М. Ампера (1775—1836). В основу определения этой единицы положено магнитное действие тока, и мы на нем останавливаться не будем.
Если сила тока I известна, то можно найти заряд q, проходящий через сечение проводника за время t. Для этого надо силу тока умножить на время:
q = It. (10.2)
Полученное выражение позволяет определить единицу электрического заряда — кулон (Кл):
1 Кл = 1 А · 1 с = 1 А·с.
1 Кл — это заряд, который проходит за 1 с через поперечное сечение проводника при силе тока 1 А.
Помимо ампера на практике часто применяются и другие (кратные и дольные) единицы силы тока, например миллиампер (мА) и микроампер (мкА):
1 мА = 0,001 А, 1 мкА = 0,000001 А.
Как уже говорилось, измеряют силу тока с помощью амперметров (а также милли- и микроамперметров). Демонстрационный гальванометр, о котором упоминалось выше, представляет собой обычный микроамперметр.
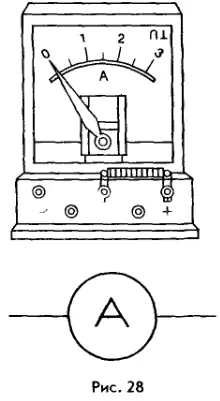
Существуют разные конструкции амперметров. Амперметр, предназначенный для демонстрационных опытов в школе, изображен на рисунке 28. На этом же рисунке приведено его условное обозначение (кружок с латинской буквой «А» внутри).
При включении в цепь амперметр, как и всякий другой измерительный прибор, не должен оказывать заметного влияния на измеряемую величину. Поэтому амперметр устроен так, что при его включении сила тока в цепи почти не изменяется.
В зависимости от назначения в технике используют амперметры с разной ценой деления. По шкале амперметра видно, на какую наибольшую силу тока он рассчитан. Включать его в цепь с большей силой тока нельзя, так как прибор может испортиться.
Для включения амперметра в цепь ее размыкают и свободные концы проводов присоединяют к клеммам (зажимам) прибора. При этом необходимо соблюдать следующие правила:
1) амперметр включают последовательно с тем элементом цепи, в котором измеряют силу тока;
2) клемму амперметра со знаком «+» следует соединять с тем проводом, который идет от положительного полюса источника тока, а клемму со знаком «–» — с тем проводом, который идет от отрицательного полюса источника тока.
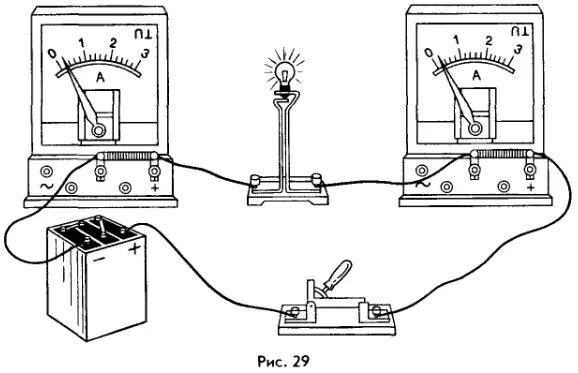
При включении амперметра в цепь не имеет значения, с какой стороны (слева или справа) от исследуемого элемента его подключать. В этом можно убедиться на опыте (рис. 29). Как видим, при измерении силы тока, проходящего через лампу, оба амперметра (и тот, что слева, и тот, что справа) показывают одно и то же значение.
??? 1. Что такое сила тока? Какой буквой она обозначается? 2. По какой формуле находится сила тока? 3. Как называется единица силы тока? Как она обозначается? 4. Как называется прибор для измерения силы тока? Как он обозначается на схемах? 5. Какими правилами следует руководствоваться при включении амперметра в цепь? 6. По какой формуле находится электрический заряд, проходящий через поперечное сечение проводника, если известны сила тока и время его прохождения?
Закон Кулона
Закон Кулона — это один из основных законов электростатики. Он определяет величину и направление силы взаимодействия между двумя неподвижными точечными зарядами.
Под точечным зарядом понимают заряженное тело, размер которого много меньше расстояния его возможного воздействия на другие тела. В таком случае ни форма, ни размеры заряженных тел не влияют практически на взаимодействие между ними.
Закон Кулона экспериментально впервые был доказан приблизительно в 1773 г. Кавендишем, который использовал для этого сферический конденсатор. Он показал, что внутри заряженной сферы электрическое поле отсутствует. Это означало, что сила электростатического взаимодействия меняется обратно пропорционально квадрату расстояния, однако результаты Кавендиша не были опубликованы.
В 1785 г. закон был установлен Ш. О. Кулоном с помощью специальных крутильных весов.
Опыты Кулона позволили установить закон, поразительно напоминающий закон всемирного тяготения.
Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.
В аналитическом виде закон Кулона имеет вид:
$F=k{|q_1|·|q_2|}/{r^2}$
где $|q_1|$ и $|q_2|$ — модули зарядов; $r$ — расстояние между ними; $k$ — коэффициент пропорциональности, зависящий от выбора системы единиц. Сила взаимодействия направлена по прямой, соединяющей заряды, причем одноименные заряды отталкиваются, а разноименные — притягиваются.
Сила взаимодействия между зарядами зависит также от среды между заряженными телами.
В воздухе сила взаимодействия почти не отличается от таковой в вакууме. Закон Кулона выражает взаимодействие зарядов в вакууме.
Кулон — единица электрического заряда. Кулон (Кл) — единица СИ количества электричества (электрического заряда). Она является производной единицей и определяется через единицу силы тока 1 ампер (А), которая входит в число основных единиц СИ.
За единицу электрического заряда принимают заряд, проходящий через поперечное сечение проводника при силе тока $1$А за $1$с.
То есть $1$ Кл$= 1А·с$.
Заряд в $1$ Кл очень велик. Сила взаимодействия двух точечных зарядов по $1$ Кл каждый, расположенных на расстоянии $1$ км друг от друга, чуть меньше силы, с которой земной шар притягивает груз массой $1$ т. Сообщить такой заряд небольшому телу невозможно (отталкиваясь друг от друга, заряженные частицы не могут удержаться в теле). А вот в проводнике (который в целом электронейтрален) привести в движение такой заряд просто (ток в $1$ А вполне обычный ток, протекающий по проводам в наших квартирах).
Коэффициент $k$ в законе Кулона при его записи в СИ выражается в $Н · м^2$ / $Кл^2$. Его численное значение, определенное экспериментально по силе взаимодействия двух известных зарядов, находящихся на заданном расстоянии, составляет:
$k=9·10^9H·м^2$/$Кл^2$
Часто его записывают в виде $k={1}/{4πε_0}$, где $ε_0=8.85×10^{-12}Кл^2$/$H·м^2$ – электрическая постоянная.
Электрическая емкость конденсатора
Электроемкость
Электроемкостью проводника $С$ называют численную величину заряда, которую нужно сообщить проводнику, чтобы изменить его потенциал на единицу:
$C={q}/{φ}$
Емкость характеризует способность проводника накапливать заряд. Она зависит от формы проводника, его линейных размеров и свойств среды, окружающей проводник.
Единицей емкости в СИ является фарада ($Ф$) — емкость проводника, в котором изменение заряда на $1$ кулон меняет его потенциал на $1$ вольт.
Электрический конденсатор
Электрический конденсатор (от лат. condensare, буквально сгущать, уплотнять) — устройство, предназначенное для получения электрической емкости заданной величины, способное накапливать и отдавать (перераспределять) электрические заряды.
Конденсатор — это система из двух или нескольких равномерно заряженных проводников с равными по величине зарядами, разделенных слоем диэлектрика. Проводники называются обкладками конденсатора. Как правило, расстояние между обкладками, равное толщине диэлектрика, намного меньше размеров самих обкладок, так что поле в конденсаторе практически все сосредоточено между его обкладками. Если обкладки являются плоскими пластинами, поле между ними однородно. Электроемкость плоского конденсатора определяется по формуле:
$C={q}/{U}={ε_{0}εS}/{d}$
где $q$ — заряд конденсатора, $U$ — напряжение между его обкладками, $S$ — площадь пластины, $d$ — расстояние между пластинами, $ε_{0}$ — электрическая постоянная, $ε$ — диэлектрическая проницаемость среды.
Под зарядом конденсатора понимают абсолютное значение заряда одной из пластин.
Энергия поля конденсатора
Энергия заряженного конденсатора выражается формулами
$E_n={qU}/{2}={q^2}/{2C}={CU^2}/{2}$
которые выводятся с учетом выражений для связи работы и напряжения и для емкости плоского конденсатора.
Энергия электрического поля. Объемная плотность энергии электрического поля (энергия поля в единице объема) напряженностью $Е$ выражается формулой:
$ω={εε_{0}E^2}/{2}$
где $ε$ — диэлектрическая проницаемость среды, $ε_0$ — электрическая постоянная.
Сила тока
Электрическим током называется упорядоченное (направленное) движение заряженных частиц.
Сила электрического тока — это величина ($I$), характеризующая упорядоченное движение электрических зарядов и численно равная количеству заряда $∆q$, протекающего через определенную поверхность $S$ (поперечное сечение проводника) за единицу времени:
$I={∆q}/{∆t}$
Итак, чтобы найти силу тока $I$, надо электрический заряд $∆q$, прошедший через поперечное сечение проводника за время $∆t$, разделить на это время.
Сила тока зависит от заряда, переносимого каждой частицей, скорости их направленного движения и площади поперечного сечения проводника.
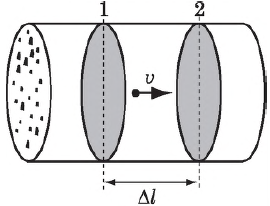
Рассмотрим проводник с площадью поперечного сечения $S$. Заряд каждой частицы $q_0$. В объеме проводника, ограниченном сечениями $1$ и $2$, содержится $nS∆l$ частиц, где $n$ — концентрация частиц. Их общий заряд $q=q_{0}nS∆l$. Если частицы движутся со средней скоростью $υ$, то за время $∆t={∆l}/{υ}$ все частицы, заключенные в рассматриваемом объеме, пройдут через поперечное сечение $2$. Сила тока, следовательно, равна:
$I={∆q}/{∆t}={q_{0}nS∆l·υ}/{∆l}=q_{0}nυS$
В СИ единица силы тока является основной и носит название ампер (А) в честь французского ученого А. М. Ампера (1755-1836).
Силу тока измеряют амперметром. Принцип устройства амперметра основан на магнитном действии тока.
Оценка скорости упорядоченного движения электронов в проводнике, проведенная по формуле для медного проводника с площадью поперечного сечения $1мм^2$, дает весьма незначительную величину — $∼0.1$ мм/с.
Закон Ома для участка цепи
Сила тока на участке цепи равна отношению напряжения на этом участке к его сопротивлению.
Закон Ома выражает связь между тремя величинами, характеризующими протекание электрического тока в цепи: силой тока $I$, напряжением $U$ и сопротивлением $R$.
Закон этот был установлен в 1827 г. немецким ученым Г. Омом и поэтому носит его имя. В приведенной формулировке он называется также законом Ома для участка цепи. Математически закон Ома записывается в виде следующей формулы:
$I={U}/{R}$
Зависимость силы тока от приложенной разности потенциалов на концах проводника называется вольт-амперной характеристикой (ВАХ) проводника.
Для любого проводника (твердого, жидкого или газообразного) существует своя ВАХ. Наиболее простой вид имеет вольт-амперная характеристика металлических проводников, заданная законом Ома $I={U}/{R}$, и растворов электролитов. Знание ВАХ играет большую роль при изучении тока.
Закон Ома — это основа всей электротехники. Из закона Ома $I={U}/{R}$ следует:
- сила тока на участке цепи с постоянным сопротивлением пропорциональна напряжению на концах участка;
- сила тока на участке цепи с неизменным напряжением обратно пропорциональна сопротивлению.
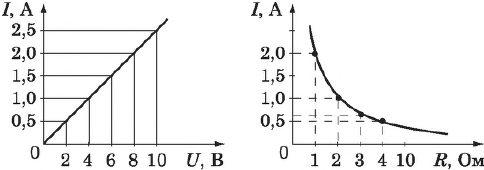
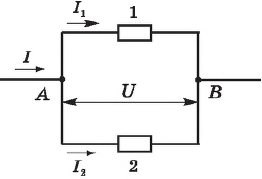
Эти зависимости легко проверить экспериментально. Полученные с использованием схемы, графики зависимости силы тока от напряжения при постоянном сопротивлении и силы тока от сопротивления представлены на рисунке. В первом случае использован источник тока с регулируемым выходным напряжением и постоянное сопротивление $R$, во втором — аккумулятор и переменное сопротивление (магазин сопротивлений).
Электрическое сопротивление
Электрическое сопротивление — это физическая величина, характеризующая противодействие проводника или электрической цепи электрическому току.
Электрическое сопротивление определяется как коэффициент пропорциональности $R$ между напряжением $U$ и силой постоянного тока $I$ в законе Ома для участка цепи.
Единица сопротивления называется омом (Ом) в честь немецкого ученого Г. Ома, который ввел это понятие в физику. Один ом ($1$ Ом) — это сопротивление такого проводника, в котором при напряжении $1$ В сила тока равна $1$ А.
Удельное сопротивление
Сопротивление однородного проводника постоянного сечения зависит от материла проводника, его длины $l$ и поперечного сечения $S$ и может быть определено по формуле:
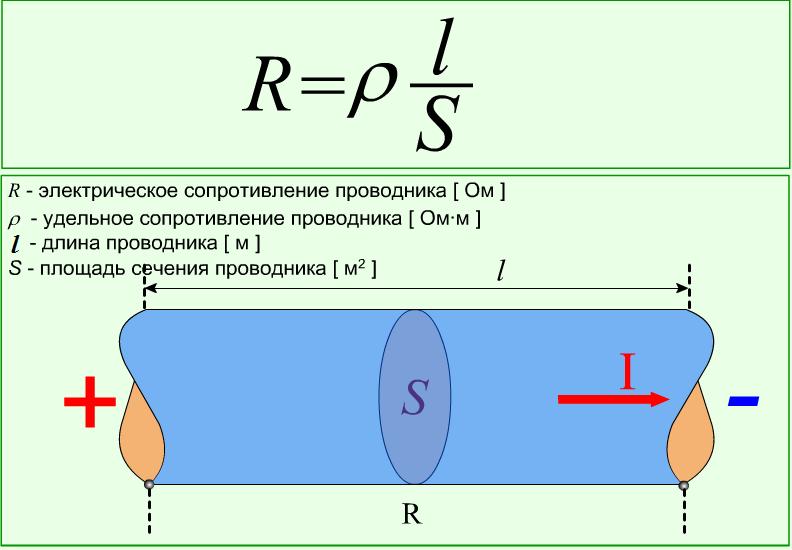
$R=ρ{l}/{S}$
где $ρ$ — удельное сопротивление вещества, из которого изготовлен проводник.
Удельное сопротивление вещества — это физическая величина, показывающая, каким сопротивлением обладает изготовленный из этого вещества проводник единичной длины и единичной площади поперечного сечения.
Из формулы $R=ρ{l}/{S}$ следует, что
$ρ={RS}/{l}$
Величина, обратная $ρ$, называется удельной проводимостью $σ$:
$σ={1}/{ρ}$
Так как в СИ единицей сопротивления является $1$ Ом, единицей площади $1м^2$, а единицей длины $1$ м, то единицей удельного сопротивления в СИ будет $1$ Ом$·м^2$/м, или $1$ Ом$·$м. Единица удельной проводимости в СИ — $Ом^{-1}м^{-1}$.
На практике площадь сечения тонких проводов часто выражают в квадратных миллиметрах (м$м^2$). В этом случае более удобной единицей удельного сопротивления является Ом$·$м$м^2$/м. Так как $1 мм^2 = 0.000001 м^2$, то $1$ Ом$·$м $м^2$/м$ = 10^{-6}$ Ом$·$м. Металлы обладают очень малым удельным сопротивлением — порядка ($1 ·10^{-2}$) Ом$·$м$м^2$/м, диэлектрики — в $10^{15}-10^{20}$ раз большим.
Зависимость сопротивления от температуры
С повышением температуры сопротивление металлов возрастает. Однако существуют сплавы, сопротивление которых почти не меняется при повышении температуры (например, константан, манганин и др.). Сопротивление же электролитов с повышением температуры уменьшается.
Температурным коэффициентом сопротивления проводника называется отношение величины изменения сопротивления проводника при нагревании на $1°$С к величине его сопротивления при $0°$С:
$α={R_t-R_0}/{R_0t}$
Зависимость удельного сопротивления проводников от температуры выражается формулой:
$ρ=ρ_0(1+αt)$
В общем случае $α$ зависит от температуры, но если интервал температур невелик, то температурный коэффициент можно считать постоянным. Для чистых металлов $α=({1}/{273})K^{-1}$. Для растворов электролитов $α < 0$. Например, для $10%$-го раствора поваренной соли $α=-0.02K^{-1}$. Для константана (сплава меди с никелем) $α=10^{-5}K^{-1}$.
Зависимость сопротивления проводника от температуры используется в термометрах сопротивления.
Параллельное и последовательное соединение проводников
Для параллельного соединения проводников справедливы следующие соотношения:
1) электрический ток, поступающий в точку $А$ разветвления проводников (она называется также узлом), равен сумме токов в каждом из элементов цепи:
$I=I_1+I_2;$
2) напряжение $U$ на концах проводников, соединенных параллельно, одно и то же:
$U=U_1=U_2;$
3) при параллельном соединении проводников складываются их обратные сопротивления:
${1}/{R}={1}/{R_1}+{1}/{R_2}, R={R_1·R_2}/{R_1+R_2};$
4) сила тока и сопротивление в проводниках связаны соотношением:
${I_1}/{I_2}={R_2}/{R_1}$
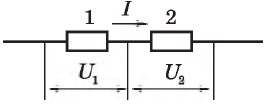
Для последовательного соединения проводников в цепи справедливы следующие соотношения:
1) для общего тока $I$:
$I=I_1=I_2,$
где $I_1$ и $I_2$ — ток в проводниках $1$ и $2$ соответственно; т. е. при последовательном соединении проводников сила тока на отдельных участках цепи одинакова;
2) общее напряжение $U$ на концах всего рассматриваемого участка равно сумме напряжений на отдельных его участках:
$U=U_1+U_2;$
3) полное сопротивление $R$ всего участка цепи равно сумме последовательно соединенных сопротивлений:
$R=R_1+R_2;$
4) также справедливо соотношение:
${U_1}/{U_2}={R_1}/{R_2}$
Работа электрического тока. Закон Джоуля-Ленца
Работа, совершаемая током, проходящим по некоторому участку цепи, согласно ($U=φ_1-φ_2={A}/{q}$) равна:
$A=qU$
где $А$ — работа тока; $q$ — электрический заряд, прошедший за данное время через рассматриваемый участок цепи. Подставляя в последнее равенство формулу $q=It$, получаем:
$A=IUt$
Работа электрического тока на участке цепи равна произведению напряжения на концах этого участка на силу тока и на время, в течение которого совершалась работа.
Закон Джоуля-Ленца
Закон Джоуля — Ленца гласит: количество теплоты, выделяемое в проводнике на участке электрической цепи с сопротивлением $R$ при протекании по нему постоянного тока $I$ в течение времени $t$ равно произведению квадрата тока на сопротивление и время:
$Q=I^2Rt$
Закон был установлен в 1841 г. английским физиком Дж. П. Джоулем, а в 1842 г. подтвержден точными опытами русского ученого Э. X. Ленца. Само же явление нагрева проводника при прохождении по нему тока было открыто еще в 1800 г. французским ученым А. Фуркруа, которому удалось раскалить железную спираль, пропустив через нее электрический ток.
Из закона Джоуля — Ленца следует, что при последовательном соединении проводников, поскольку ток в цепи всюду одинаков, максимальное количество тепла будет выделяться на проводнике с наибольшим сопротивлением. Это используется в технике, например, для распыления металлов.
При параллельном соединении все проводники находятся под одинаковым напряжением, но токи в них разные. Из формулы ($Q=I^2Rt$) следует, что, так как, согласно закону Ома $I={U}/{R}$, то
$Q={U^2t}/{R}$
Следовательно, на проводнике с меньшим сопротивлением будет выделяться больше тепла.
Если в формуле ($A=IUt$) выразить $U$ через $IR$, воспользовавшись законом Ома, получим закон Джоуля-Ленца. Это лишний раз подверждает тот факт, что работа тока расходуется на выделение тепла на активном сопротивлении в цепи.
Мощность электрического тока
Действие тока характеризуют не только работой $A$, но и мощностью $Р$. Мощность тока показывает, какую работу совершает ток за единицу времени. Если за время $t$ была совершена работа $А$, то мощность тока $P={A}/{t}$. Подставляя в это равенство выражение ($A=IUt$), получаем:
$P=IU$
Это выражение можно переписать в разных формах, воспользовавшись законом Ома для участка цепи:
$P=IU=I^{2R}={U^2}/{R}$
Из соотношения для ЭДС легко получить мощность источника тока:
$P_ε=εI$
В СИ работу выражают в джоулях (Дж), мощность — в ваттах (Вт), а время -в секундах (с). При этом
$1$Вт$=1$Дж/с, $1$Дж$=1$Вт$·$с.
Рассчитаем наибольшую допустимую мощность потребителей электроэнергии, которые могут одновременно работать в квартире. Так как в жилых зданиях сила тока в проводке не должна превышать $I=10$А, то при напряжении $U=220$В соответствующая электрическая мощность оказывается равной:
$Р=10А·220В=2200Вт=2.2кВт.$
Одновременное включение в сеть приборов с большей суммарной мощностью приведет к увеличению силы тока, и потому недопустимо.
В быту работу тока (или израсходованную на совершение этой работы электроэнергию) измеряют с помощью специального прибора, называемого электрическим счетчиком (счетчиком электроэнергии). При прохождении тока через этот счетчик внутри его начинает вращаться легкий алюминиевый диск. Скорость его вращения прямо пропорциональна силе тока и напряжению. Поэтому по числу оборотов, сделанных им за данное время, можно судить о работе, совершенной током за это время. Работа тока при этом выражается обычно в киловатт-часах ($кВт·ч$).
$1кВт·ч$ — это работа, совершаемая электрическим током мощностью $1кВт$ в течение $1ч$. Так как $1кВт=1000Вт$, а $1ч=3600с$, то $1кВт·ч=1000Вт·3600с=3600000 Дж$.
На этой странице вы узнаете
- Что общего у электрического тока с водой?
- В чем отличие сопротивления от удельного сопротивления?
- Почему нежелательно использовать телефон, подключенный к зарядке?
- Фамилия какого ученого стоит миллион?
«Все, кина не будет. Электричество кончилось». Наверное, никого не оставит равнодушным популярная фраза из широко известного фильма «Джентльмены удачи». Ведь действительно: бесит, когда сидишь за просмотром любимого сериальчика, вдруг — бамс! Вырубили свет, и зарядки ноута, как назло, не хватило. И не выработаешь электричество в домашних условиях, а жаль… Но вот понять, как оно работает — это мы сможем сделать в статье.

Электрический ток
В наше время трудно себе представить жизнь без электричества. Телевизор не посмотреть, телефон не зарядить, чай не попить… Ни один электроприбор в доме не будет работать без электричества. А объявление об отключении электроэнергии, вызывает тихий ужас.
Электричество — это форма энергии, которая существует в виде статических или подвижных электрических зарядов.
Поток. И то и другое представляет собой направленное движение частиц. Из чего состоит вода? Из молекул. Когда эти молекулы движутся в одном направлении, то они образуют поток воды, который течет, например, по трубам.
Так же и электрический ток. Он образуется потоком заряженных частиц, которые движутся по проводам.
Сформулируем определение:
Электрический ток — это упорядоченное движение заряженных частиц.
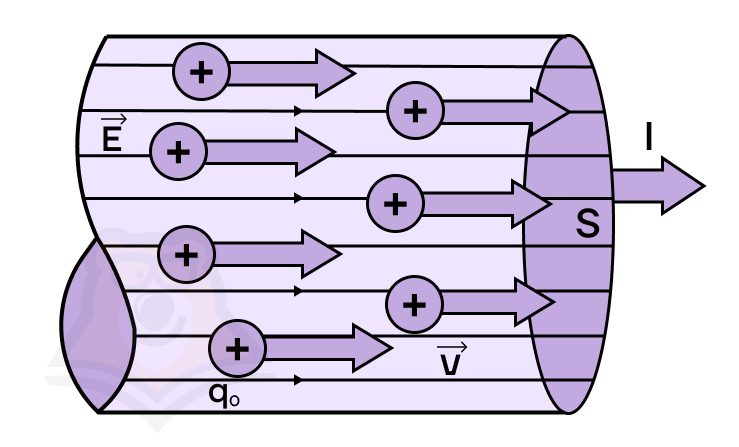
Чтобы электрический ток существовал, необходимо выполнение следующих условий:
- наличие свободных заряженных частиц;
- наличие электрического поля;
- наличие замкнутой электрической цепи.
Основными количественными характеристиками электрического тока являются сила тока и напряжение.
Напряжение
Чтобы внутри цепи существовал электрический ток, цепь должна быть замкнута и между концами участка цепи должно существовать напряжение.
Напряжение — скалярная (не имеющая направления) физическая величина, значение которой равно работе тока на участке цепи, совершаемой при переносе единичного электрического заряда из одной точки в другую.
U — напряжение (В),
A — работа тока на участке цепи (Дж),
q — электрический заряд (Кл).
Единица измерения U — В (Вольт) = (frac{Дж}{Кл})

Электрический ток – результат “труда” множества частиц. Они любят работать – не ленятся перемещаться из одного конца цепи в другой. И чем больше они будут работать, тем большее напряжение получится. Так запоминаем связь напряжения (U) с работой (A).
Услышав слова из известной песни Димы Билана «Это ты, это я, между нами молния, С электрическим разрядом 220 Вольт…» любой физик (и электрик) приобретает новую пару седых волосинок. Такое напряжение очень опасно для человека. Однако, 220 Вольт — это то самое напряжение в наших розетках!
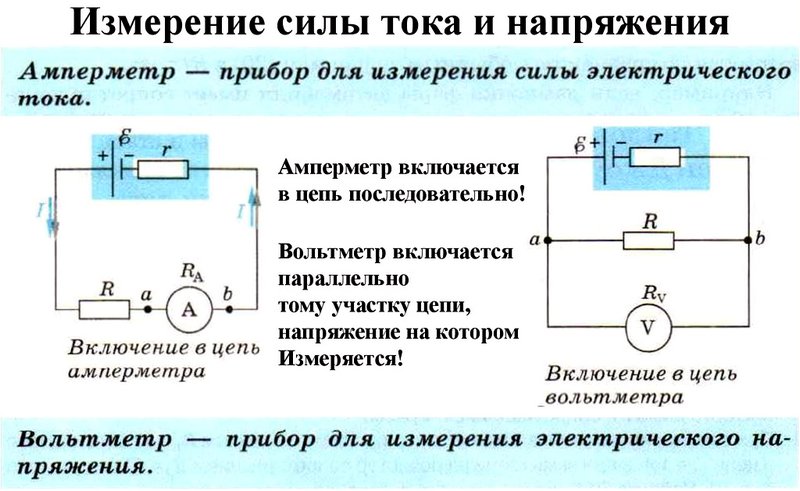
Прибор для измерения напряжения — вольтметр. Он включается в цепь параллельно. Пример подключения представлен на рисунке:
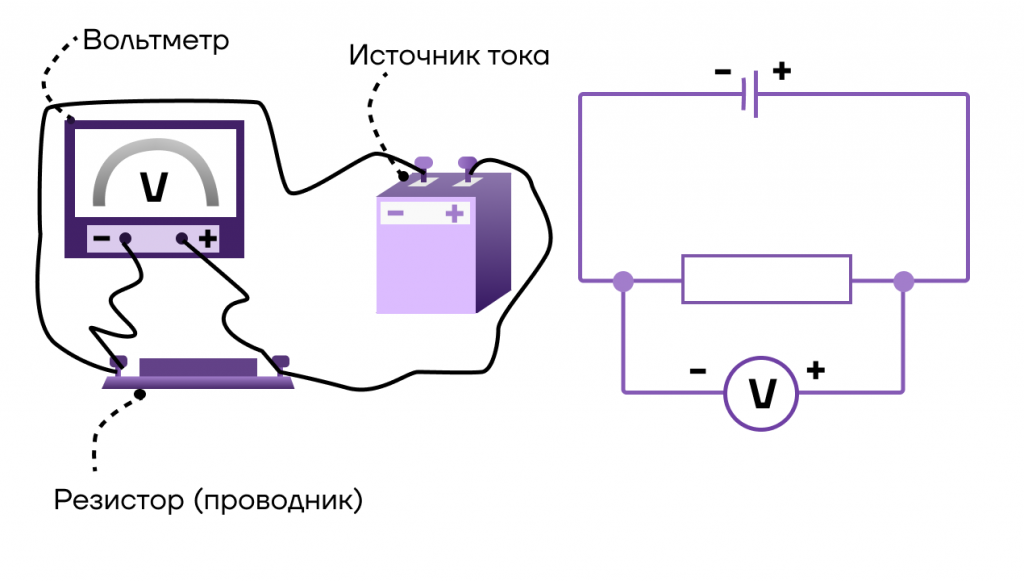
Сила тока
Это еще одна немаловажная характеристика электрического тока.
Сила тока — это физическая величина, показывающая, какой заряд переносится через рассматриваемую площадь поперечного сечения за единицу времени .
I — сила тока (А),
q — электрический заряд (Кл),
t — время (с).
Единица измерения I — А (ампер) = (frac{Кл}{с}).
Представим, что внутри проводника «бежит» в одном направлении огромное количество заряженных частиц. Так вот, чем больше общий заряд частиц, пробегающих через поперечное сечение проводника за единицу времени, тем больше будет значение силы тока. Это поможет вам запомнить зависимость силы тока (I) от электрического заряда (q).
Прибор для измерения силы тока — амперметр. Он включается в цепь последовательно. Пример подключения представлен на рисунке:
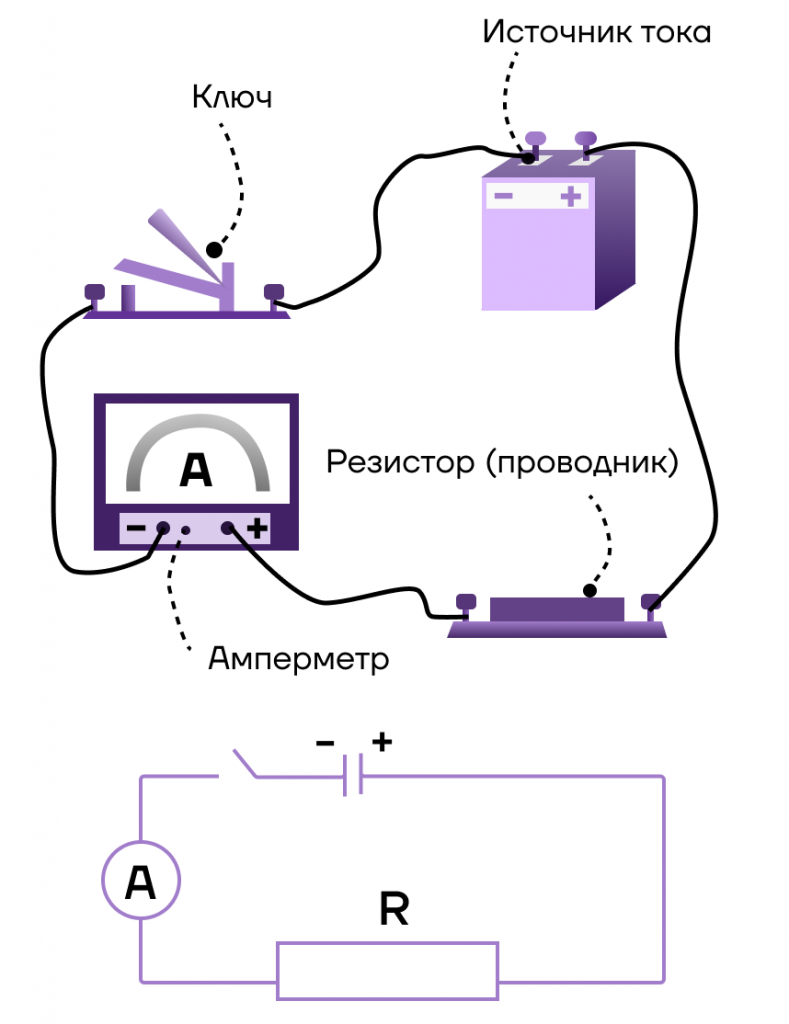
Направление тока совпадает с направлением движения положительно заряженных частиц.
Давайте разберемся, как можно определить направление тока в цепи на примере.
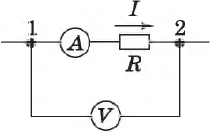
Задача. На рисунке изображена электрическая цепь с источником тока и сопротивлением R. Определите направление тока в данной цепи (по часовой стрелке/против часовой стрелки).
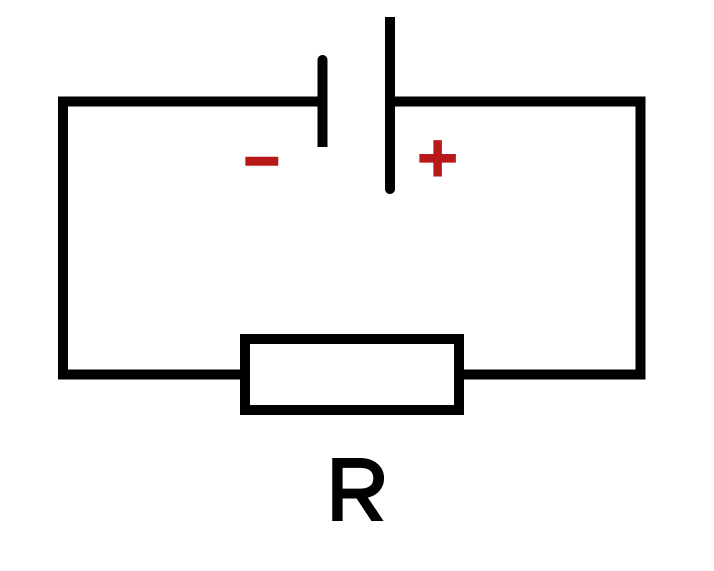
Решение:
Обратите внимание, «большая» пластина реостата расположена справа (именно она и направляет ток), а «маленькая» слева. Положительно заряженные частицы двигаются от катода к аноду (от положительно заряженной пластинки к отрицательно заряженной), а направление тока всегда совпадает с направлением положительно заряженных частиц. Значит, ток в цепи направлен по часовой стрелке.
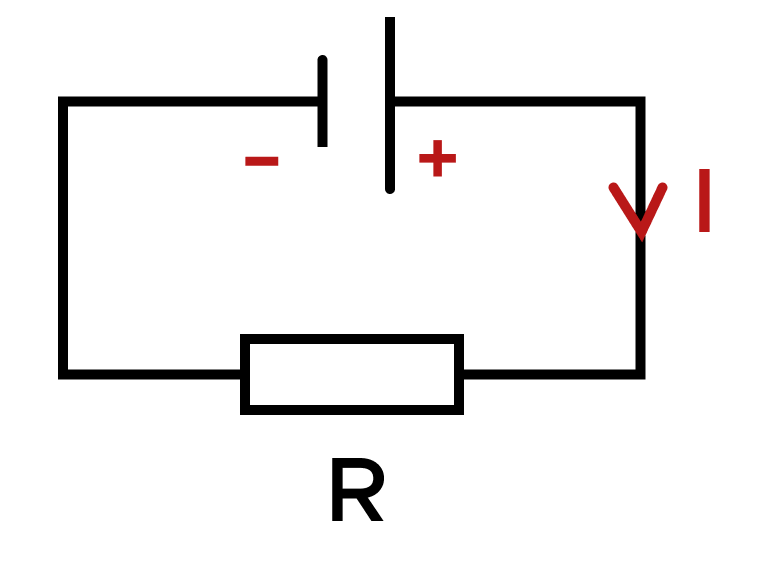
Ответ: по часовой стрелке
Электрическое сопротивление
Оно является электрической характеристикой проводника.
Сопротивление — физическая величина, характеризующая электрические свойства участка цепи.
R — сопротивление (Ом),
p — удельное сопротивление проводника,
l — длина проводника (м),
S — площадь поперечного сечения проводника (мм²).
Единица измерения R — Ом.
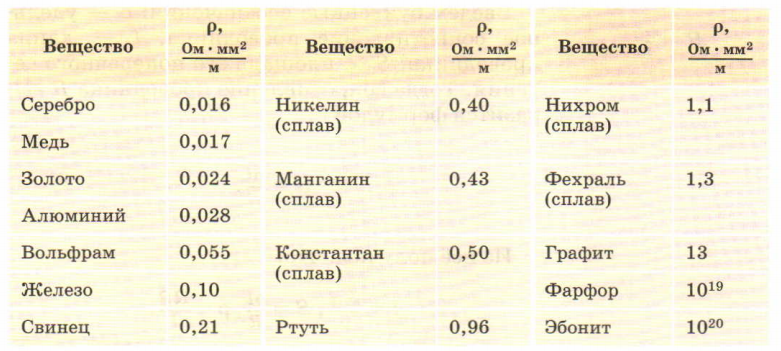
Удельное сопротивление проводника (p) можно посмотреть в специальной таблице в справочнике или в интернете. Для каждого материала будет свое значение. Мы приведем для примера лишь фрагмент такой таблицы.
Таблица удельных сопротивлений проводников
| Металл | Удельное сопротивление, Ом * (мм^2)/ м |
| Серебро | 0,0015 |
| Медь | 0,018 |
| Золото | 0,023 |
| Алюминий | 0,029 |
| Вольфрам | 0,055 |
| Железо | 0,098 |
Сопротивление — это внешнее свойство, зависящее от количества присутствующего материала, от геометрических характеристик проводника и от самого материала, из которого сделан проводник.
Удельное сопротивление — это внутреннее свойство проводника, которое не зависит от его размера, а зависит от химического состава вещества и температуры.
Условно можно сказать, что сопротивление — это свойство проводника, а удельное сопротивление — свойство материала.
Получается, что прежде всего на то, каким будет сопротивление, влияют размеры проводника, его форма, материал, из которого он сделан.
Удельное сопротивление проводника зависит также от температуры. Когда температура твердых тел увеличивается, то удельное сопротивление возрастает. А в растворах и расплавах — наоборот, уменьшается. В экзаменационных задачах случаи с изменением удельного сопротивления не рассматриваются, а вот в олимпиадных задачах такое встретить можно.
Давайте поразмышляем: что чему сопротивляется?
Причина электрического сопротивления кроется во взаимодействии зарядов разного знака при протекании тока по проводнику. Это взаимодействие можно сравнить с силой трения, стремящейся остановить движение заряженных частиц.
Чем сильнее взаимодействие свободных электронов с положительными ионами в узлах кристаллической решетки проводника, тем больше сопротивление проводника.
Проводник с определенным постоянным сопротивлением называется резистор.
Вернемся к сравнению электрического тока с водой: как молекулы воды из крана движутся сверху вниз, так и электрический ток имеет определенное направление — от катода к аноду. Электрический заряд условно в нашем примере аналогичен массе воды, а напряжение — напору воды из крана.
Закон Ома
Сила тока, напряжение и сопротивление связаны между собой соотношением, которое называется закон Ома:
I — сила тока (А),
U — напряжение (В),
R — сопротивление (Ом).
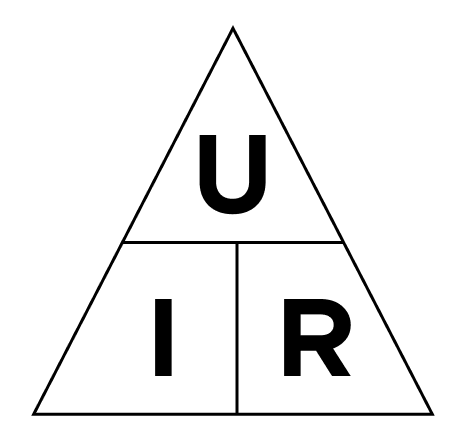
Для упрощенного понимания закона Ома можно использовать данный треугольник. Чтобы вспомнить формулу для нахождения той или иной величины, нужно ее закрыть рукой. Если оставшиеся открытыми величины стоят бок о бок, то они перемножаются друг с другом (U=IR). А если одна величина стоит выше другой, то в таком случае мы делим их друг на друга (I=U/R или R=U/I)
Данный закон справедлив для участка цепи, на который не действуют сторонние силы.
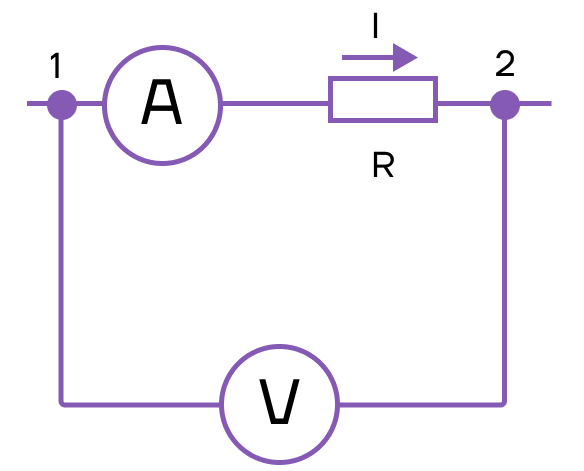
Разберем задачу из контрольно-измерительных материалов ЕГЭ (номер 12).
Ниже на рисунке приведена схема электрической цепи, в которой провода можно считать идеальными. Определите сопротивление резистора, если показания амперметра 0,2 А, а вольтметра — 8 В.
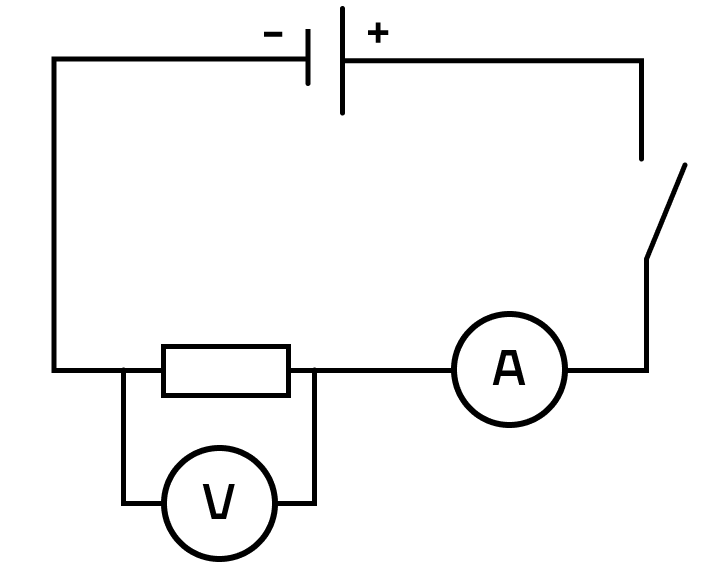
Решение:
Вольтметр подключен параллельно резистору. Следовательно, он показывает напряжение на резисторе U.
Амперметр подключен последовательно. Следовательно, он показывает силу тока I на всей цепи.
Чтобы найти сопротивление на резисторе, воспользуемся законом Ома:
I=(frac{U}{R}), где R — сопротивление резистора.
Выразим R и подставим значения:
R=(frac{U}{I})
R=(frac{8}{0,2})=40 (Ом)
Ответ: 40
Работа и мощность электрического тока
Вернемся к понятию работы. Мы говорили, при перемещении заряда по проводнику электрическое поле совершает работу (А):
A = qU
Если мы выразим заряд из формулы силы тока q=It, то получим, формулу для расчета работы электрического поля (А) при протекании постоянного тока (или просто работа тока):
A — работа электрического тока (Дж),
U — напряжение (В),
I — сила тока (А),
t — время прохождения тока (с).
Единица измерения А — Дж (Джоуль).
В быту ток совершает работу длительное время, поэтому при определении затраченной электрической энергии используют единицу измерения кВт * ч. Киловатт в час — это энергия, которая потребляется устройством мощностью 1 кВт в течении 1 часа. Учитывая, что 1 ч=3600 с, получим:
1 кВт*ч = 1000 Вт * 3600 с = 3600000 Дж = 3600 кДж
Если же работу тока рассчитать за единицу времени, то мы получим мощность постоянного электрического тока.
Мощность — величина, обозначающая интенсивность передачи электрической энергии.
P — мощность (Вт),
A — работа электрического тока (Дж),
t — время прохождения тока (с).
Единица измерения P — Вт (Ватт).
Средняя мощность тока равна:
(P = frac{A}{t} = frac{qU}{t} = IU = frac{U^2}{R} = I^2R)
Теперь мы знаем все про мощность и работу тока, а значит, нужно отработать это на практике. Тем более что такие задачи встречаются в ЕГЭ (номер 12).
Задача.
Какую работу совершит электрический ток в электродвигателе вентилятора за 20 мин., если сила тока в цепи 0,2 А, а напряжение 12 В?
Решение.
Вспомним формулу для работы тока A=U*I*t , где U=12 В — напряжение в электродвигателе, I=0,2 A — сила тока, t=20 мин=1200 с — время.
Все данные нам уже известны, поэтому можем подставить их в формулу для работы тока и получить ответ.
A=12*0,2*1200=2880 Дж
Ответ: 2880 Дж
Мощность электроприбора всегда указывается в документации, прилагающейся к нему. Кроме того, нередко ее пишут на самом приборе. Давайте посмотрим на утюг, или стиральную машину дома. Мы увидим, что утюг имеет мощность 1000 Вт, а обычная энергосберегающая лампочка, всего 40 Вт (на то она и сберегающая). Чем больше мощность прибора, тем больше энергии он будет потреблять. Примеры мощностей различных приборов представлены на рисунке.
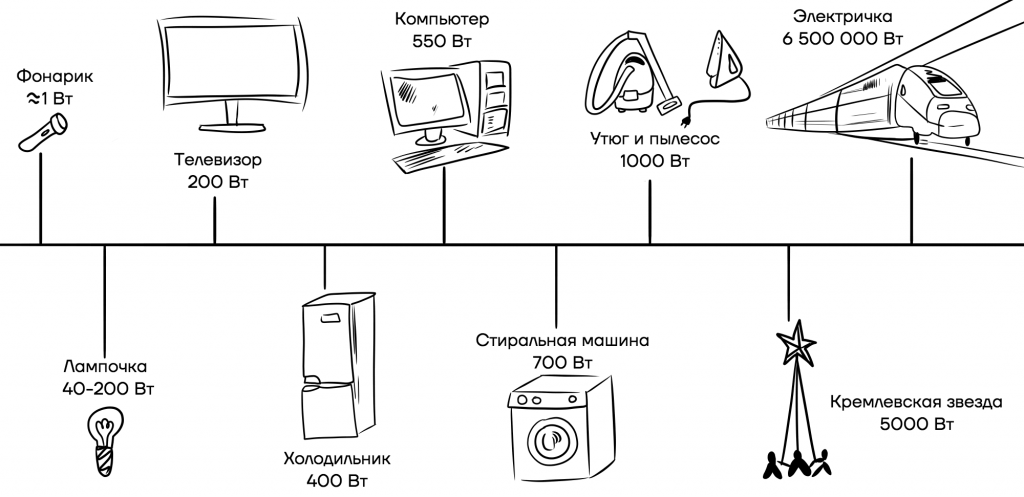
Закон Джоуля — Ленца
Теперь же свяжем работу тока и теплоту, которая выделяется на проводнике за некоторое время t.
Когда приборы подключены в сеть, мы можем заметить, что они нагреваются. Очень часто это наблюдается, когда телефон подключен на зарядку, а мы продолжаем по нему звонить, использовать интернет и прочее. Это плохо влияет на телефон: перегрев батареи и корпуса могут быстрее привести девайс в негодность.

Почему так происходит?
Электрический ток оказывает тепловое действие на проводник. Количество теплоты, которое при этом выделяется, будет рассчитываться по закону Джоуля — Ленца:
Количество теплоты, выделяемое за время в проводнике с током, пропорционально произведению квадрата силы тока на этом участке и сопротивления проводника:
Q — количество теплоты (Дж),
I — работа электрического тока (Дж),
R — сопротивление (Ом),
t — время прохождения тока (с).
Единица измерения Q — Дж (Джоуль).
В электронагревательных приборах используются проводники с высоким сопротивлением, что обеспечивает выделение тепла на определенном участке.
Так, проволоку из нихрома (сплав никеля с хромом) применяют в электронагревательных элементах, работающих при температуре до 1000 ℃ (резисторах, например). Нихром относится к классу сплавов с высоким электрическим сопротивлением, что определяет его применение в качестве электрических нагревателей. Этот сплав используется также в печах обжига и сушки и различных аппаратах теплового воздействия, например, в фенах, паяльниках или обогревателях.

Кто первый ввел понятие «электрический ток» в науку? Ответ: Андре-Мари Ампер.
Такой был финальный вопрос (ценой в 1 000 000) в игре «Кто хочет стать миллионером?» от 20 января 2018 г. Но участники не смогли ответить на него, и мечту получить свой миллион не исполнили.

Еще немного про электричество…
- Постоянный электрический ток используется в работе двигателей электротранспорта, схемах автомобилей, электронике и др.
- Электричество есть и в нашем организме. Мышечные клетки сердца при сокращении производят электроэнергию, эти импульсы можно измерить с помощью электрокардиограммы (ЭКГ).
- Бенджамин Франклин (да-да, президент Америки) провел множество опытов в 18 веке и создал громоотвод. Также он является человеком, который вывел закон сохранения электрического заряда.
- В древности люди считали, что, если молния ударила в курган, значит, там зарыто сокровище.
Термины
Источник тока — устройство, разделяющее положительные и отрицательные заряды.
Сторонние силы — силы неэлектрического происхождения, вызывающие разделение зарядов в источнике тока.
Фактчек
- Сила тока — это физическая величина, показывающая, какой заряд переносится через рассматриваемую площадь поперечного сечения за единицу времени: (I = frac{q}{t})
- Напряжение — скалярная физическая величина, равная отношению полной работы кулоновских и сторонних сил А при перемещении положительного заряда на участке цепи к значению этого заряда: (U = frac{A}{q})
- Сопротивление — физическая величина, характеризующая электрические свойства участка цепи: (R = frac{pl}{S})
- Мощность — величина, обозначающая интенсивность передачи электрической энергии: (P = frac{A}{t})
- Закон Ома: сила тока в однородном участке цепи прямо пропорциональна напряжению при постоянном сопротивлении и обратно пропорциональна сопротивлению участка при постоянном напряжении: (I = frac{U}{R}).
- Закон Джоуля— Ленца: количество теплоты Q, выделяемое за время t в проводнике с током, пропорционально произведению квадрата силы тока I на этом участке и сопротивления R проводника: Q = I2Rt.
- Работа электрического поля при протекании постоянного тока (или просто работа тока): А = UIt.
Проверь себя
Задание 1.
Упорядоченное движение заряженных частиц — это:
- электрическое поле
- электрический ток
- электрическая мощность
- работа тока
Задание 2.
Удельное сопротивление проводника:
- зависит от температуры
- не зависит от температуры
- зависит от силы протекающего через проводник тока
- не зависит от напряжения
Задание 3.
Формула для расчета силы тока:
- I = Ut
- I = UIt
- I = I2Rt
- (I = frac{q}{t})
Задание 4.
Что такое мощность электрического тока:
- работа за единицу времени
- отношение заряда к единице времени
- произведение силы тока на сопротивление
- тепло, выделяемое на резисторе
Задание 5.
Причина электрического сопротивления:
- во взаимодействии зарядов одинакового знака
- в отсутствии взаимодействия между зарядами
- во взаимодействии зарядов разного знака
- в передаче тепла
Ответы: 1.— 2; 2. — 1; 3.— 4; 4.— 1; 5. — 3.
Закон Кулона, конденсатор, сила тока, закон Ома, закон Джоуля – Ленца
Теория к заданию 14 из ЕГЭ по физике
Закон Кулона
Закон Кулона — это один из основных законов электростатики. Он определяет величину и направление силы взаимодействия между двумя неподвижными точечными зарядами.
Под точечным зарядом понимают заряженное тело, размер которого много меньше расстояния его возможного воздействия на другие тела. В таком случае ни форма, ни размеры заряженных тел не влияют практически на взаимодействие между ними.
Закон Кулона экспериментально впервые был доказан приблизительно в 1773 г. Кавендишем, который использовал для этого сферический конденсатор. Он показал, что внутри заряженной сферы электрическое поле отсутствует. Это означало, что сила электростатического взаимодействия меняется обратно пропорционально квадрату расстояния, однако результаты Кавендиша не были опубликованы.
В 1785 г. закон был установлен Ш. О. Кулоном с помощью специальных крутильных весов.
Опыты Кулона позволили установить закон, поразительно напоминающий закон всемирного тяготения.
Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.
В аналитическом виде закон Кулона имеет вид:
где $|q_1|$ и $|q_2|$ — модули зарядов; $r$ — расстояние между ними; $k$ — коэффициент пропорциональности, зависящий от выбора системы единиц. Сила взаимодействия направлена по прямой, соединяющей заряды, причем одноименные заряды отталкиваются, а разноименные — притягиваются.
Сила взаимодействия между зарядами зависит также от среды между заряженными телами.
В воздухе сила взаимодействия почти не отличается от таковой в вакууме. Закон Кулона выражает взаимодействие зарядов в вакууме.
Кулон — единица электрического заряда. Кулон (Кл) — единица СИ количества электричества (электрического заряда). Она является производной единицей и определяется через единицу силы тока 1 ампер (А), которая входит в число основных единиц СИ.
За единицу электрического заряда принимают заряд, проходящий через поперечное сечение проводника при силе тока $1$А за $1$с.
Заряд в $1$ Кл очень велик. Сила взаимодействия двух точечных зарядов по $1$ Кл каждый, расположенных на расстоянии $1$ км друг от друга, чуть меньше силы, с которой земной шар притягивает груз массой $1$ т. Сообщить такой заряд небольшому телу невозможно (отталкиваясь друг от друга, заряженные частицы не могут удержаться в теле). А вот в проводнике (который в целом электронейтрален) привести в движение такой заряд просто (ток в $1$ А вполне обычный ток, протекающий по проводам в наших квартирах).
Коэффициент $k$ в законе Кулона при его записи в СИ выражается в $Н · м^2$ / $Кл^2$. Его численное значение, определенное экспериментально по силе взаимодействия двух известных зарядов, находящихся на заданном расстоянии, составляет:
Часто его записывают в виде $k=<1>/<4πε_0>$, где $ε_0=8.85×10^<-12>Кл^2$/$H·м^2$ — электрическая постоянная.
Электрическая емкость конденсатора
Электроемкость
Электроемкостью проводника $С$ называют численную величину заряда, которую нужно сообщить проводнику, чтобы изменить его потенциал на единицу:
Емкость характеризует способность проводника накапливать заряд. Она зависит от формы проводника, его линейных размеров и свойств среды, окружающей проводник.
Единицей емкости в СИ является фарада ($Ф$) — емкость проводника, в котором изменение заряда на $1$ кулон меняет его потенциал на $1$ вольт.
Электрический конденсатор
Электрический конденсатор (от лат. condensare, буквально сгущать, уплотнять) — устройство, предназначенное для получения электрической емкости заданной величины, способное накапливать и отдавать (перераспределять) электрические заряды.
Конденсатор — это система из двух или нескольких равномерно заряженных проводников с равными по величине зарядами, разделенных слоем диэлектрика. Проводники называются обкладками конденсатора. Как правило, расстояние между обкладками, равное толщине диэлектрика, намного меньше размеров самих обкладок, так что поле в конденсаторе практически все сосредоточено между его обкладками. Если обкладки являются плоскими пластинами, поле между ними однородно. Электроемкость плоского конденсатора определяется по формуле:
где $q$ — заряд конденсатора, $U$ — напряжение между его обкладками, $S$ — площадь пластины, $d$ — расстояние между пластинами, $ε_<0>$ — электрическая постоянная, $ε$ — диэлектрическая проницаемость среды.
Под зарядом конденсатора понимают абсолютное значение заряда одной из пластин.
Энергия поля конденсатора
Энергия заряженного конденсатора выражается формулами
которые выводятся с учетом выражений для связи работы и напряжения и для емкости плоского конденсатора.
Энергия электрического поля. Объемная плотность энергии электрического поля (энергия поля в единице объема) напряженностью $Е$ выражается формулой:
где $ε$ — диэлектрическая проницаемость среды, $ε_0$ — электрическая постоянная.
Сила тока
Электрическим током называется упорядоченное (направленное) движение заряженных частиц.
Сила электрического тока — это величина ($I$), характеризующая упорядоченное движение электрических зарядов и численно равная количеству заряда $∆q$, протекающего через определенную поверхность $S$ (поперечное сечение проводника) за единицу времени:
Итак, чтобы найти силу тока $I$, надо электрический заряд $∆q$, прошедший через поперечное сечение проводника за время $∆t$, разделить на это время.
Сила тока зависит от заряда, переносимого каждой частицей, скорости их направленного движения и площади поперечного сечения проводника.
Рассмотрим проводник с площадью поперечного сечения $S$. Заряд каждой частицы $q_0$. В объеме проводника, ограниченном сечениями $1$ и $2$, содержится $nS∆l$ частиц, где $n$ — концентрация частиц. Их общий заряд $q=q_<0>nS∆l$. Если частицы движутся со средней скоростью $υ$, то за время $∆t=<∆l>/<υ>$ все частицы, заключенные в рассматриваемом объеме, пройдут через поперечное сечение $2$. Сила тока, следовательно, равна:
В СИ единица силы тока является основной и носит название ампер (А) в честь французского ученого А. М. Ампера (1755-1836).
Силу тока измеряют амперметром. Принцип устройства амперметра основан на магнитном действии тока.
Оценка скорости упорядоченного движения электронов в проводнике, проведенная по формуле для медного проводника с площадью поперечного сечения $1мм^2$, дает весьма незначительную величину — $∼0.1$ мм/с.
Закон Ома для участка цепи
Сила тока на участке цепи равна отношению напряжения на этом участке к его сопротивлению.
Закон Ома выражает связь между тремя величинами, характеризующими протекание электрического тока в цепи: силой тока $I$, напряжением $U$ и сопротивлением $R$.
Закон этот был установлен в 1827 г. немецким ученым Г. Омом и поэтому носит его имя. В приведенной формулировке он называется также законом Ома для участка цепи. Математически закон Ома записывается в виде следующей формулы:
Зависимость силы тока от приложенной разности потенциалов на концах проводника называется вольт-амперной характеристикой (ВАХ) проводника.
Для любого проводника (твердого, жидкого или газообразного) существует своя ВАХ. Наиболее простой вид имеет вольт-амперная характеристика металлических проводников, заданная законом Ома $I=/$, и растворов электролитов. Знание ВАХ играет большую роль при изучении тока.
Закон Ома — это основа всей электротехники. Из закона Ома $I=/$ следует:
- сила тока на участке цепи с постоянным сопротивлением пропорциональна напряжению на концах участка;
- сила тока на участке цепи с неизменным напряжением обратно пропорциональна сопротивлению.
Эти зависимости легко проверить экспериментально. Полученные с использованием схемы, графики зависимости силы тока от напряжения при постоянном сопротивлении и силы тока от сопротивления представлены на рисунке. В первом случае использован источник тока с регулируемым выходным напряжением и постоянное сопротивление $R$, во втором — аккумулятор и переменное сопротивление (магазин сопротивлений).
Электрическое сопротивление
Электрическое сопротивление — это физическая величина, характеризующая противодействие проводника или электрической цепи электрическому току.
Электрическое сопротивление определяется как коэффициент пропорциональности $R$ между напряжением $U$ и силой постоянного тока $I$ в законе Ома для участка цепи.
Единица сопротивления называется омом (Ом) в честь немецкого ученого Г. Ома, который ввел это понятие в физику. Один ом ($1$ Ом) — это сопротивление такого проводника, в котором при напряжении $1$ В сила тока равна $1$ А.
Удельное сопротивление
Сопротивление однородного проводника постоянного сечения зависит от материла проводника, его длины $l$ и поперечного сечения $S$ и может быть определено по формуле:
где $ρ$ — удельное сопротивление вещества, из которого изготовлен проводник.
Удельное сопротивление вещества — это физическая величина, показывающая, каким сопротивлением обладает изготовленный из этого вещества проводник единичной длины и единичной площади поперечного сечения.
Из формулы $R=ρ/$ следует, что
Величина, обратная $ρ$, называется удельной проводимостью $σ$:
Так как в СИ единицей сопротивления является $1$ Ом, единицей площади $1м^2$, а единицей длины $1$ м, то единицей удельного сопротивления в СИ будет $1$ Ом$·м^2$/м, или $1$ Ом$·$м. Единица удельной проводимости в СИ — $Ом^<-1>м^<-1>$.
На практике площадь сечения тонких проводов часто выражают в квадратных миллиметрах (м$м^2$). В этом случае более удобной единицей удельного сопротивления является Ом$·$м$м^2$/м. Так как $1 мм^2 = 0.000001 м^2$, то $1$ Ом$·$м $м^2$/м$ = 10^<-6>$ Ом$·$м. Металлы обладают очень малым удельным сопротивлением — порядка ($1 ·10^<-2>$) Ом$·$м$м^2$/м, диэлектрики — в $10^<15>-10^<20>$ раз большим.
Зависимость сопротивления от температуры
С повышением температуры сопротивление металлов возрастает. Однако существуют сплавы, сопротивление которых почти не меняется при повышении температуры (например, константан, манганин и др.). Сопротивление же электролитов с повышением температуры уменьшается.
Температурным коэффициентом сопротивления проводника называется отношение величины изменения сопротивления проводника при нагревании на $1°$С к величине его сопротивления при $0°$С:
Зависимость удельного сопротивления проводников от температуры выражается формулой:
В общем случае $α$ зависит от температуры, но если интервал температур невелик, то температурный коэффициент можно считать постоянным. Для чистых металлов $α=(<1>/<273>)K^<-1>$. Для растворов электролитов $α
Источник
Электрический заряд, напряжение, напряженность, потенциал
Любой физический объект в окружающем нас мире состоит из огромного количества элементарных частиц, обладающих зарядами. Элементарная частица протон имеет элементарный электрический заряд, которому приписывают (условно) положительный знак, элементарная частица электрон имеет элементарный отрицательный заряд.
Электрический заряд
Под электрическим зарядом понимают физическую величину, которая характеризует способность тел (объектов) вступать в электрическое взаимодействие. Электрический заряд обозначается через q (иногда для обозначения используют заглавную букву Q) и в Международной системе единиц (СИ) измеряется в Кулонах, [Кл].
Электрический заряд – дискретная величина, кратная элементарному электрическому заряду одного электрона (по модулю) e = 1,60217*10 -9 Кл.
С физической точки зрения 1 кулон [Кл] соответствует электрическому заряду, проходящему через поперечное сечение проводника при силе тока 1 Ампер за 1 секунду.
Заряды существуют в двух видах: положительные (+) и отрицательные (-). Одноименные заряды отталкиваются, а разноименные – притягиваются.
Сила взаимодействия зарядов направлена вдоль прямой, соединяющей их, пропорциональна величине зарядов и обратно пропорциональна квадрату расстояния между ними (рисунок 1).
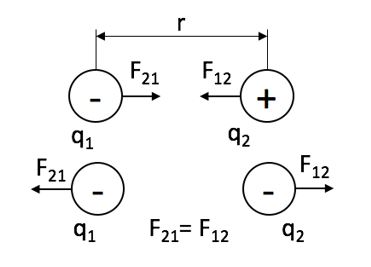
где k – коэффициент пропорциональности, зависящий от выбора системы единиц;

Силу взаимодействия двух зарядов 
Если объект (система) не обменивается зарядами с окружающей средой, его называют электрически изолированным. В такой системе сумма электрических зарядов (положительных и отрицательных) не меняется со временем, то есть наблюдается закон сохранения заряда.
Большинство тел в природе электрически нейтральны, так как содержат заряды обоих типов в одинаковом количестве. Положительные и отрицательные заряды попарно нейтрализуют действие друг друга. Для перехода тела в заряженное состояние необходимо пространственно перераспределить в нем заряды, сконцентрировав одноименные заряды в одной области тела. Это возможно сделать, например, при помощи трения или взаимодействия с другим заряженным объектом (рисунок 2).

Электрический заряд порождает в окружающем его пространстве непрерывную материю, называемую электрическим полем. Благодаря электрическому полю заряды имеют возможность взаимодействовать между собой. В электротехнике электрическое поле характеризуется двумя величинами: напряженностью (силовая характеристика) и потенциалом (энергетическая характеристика).
Напряженность электрического поля
Напряженность электрического поля – это векторная физическая количественная характеристика электрического поля. Ее величина показывает силу, которая действует на пробный точечный единичный положительный заряд, помещенный в некоторую точку электрического поля.
Под точечным зарядом понимают упрощенную модель положительного заряда, в которой его формой и размером можно пренебречь.
Вектор напряженности 


Величина напряженности поля в точке А определяется согласно формуле
где r – расстояние от заряда q до точки А, k – коэффициент пропорциональности, зависящий от выбора системы единиц.
Электрическое поле графически изображается линиями напряженности электрического поля, которые условно принято обозначать исходящими из положительно заряженных элементов и входящими в отрицательно заряженные заряды (рисунок 4).
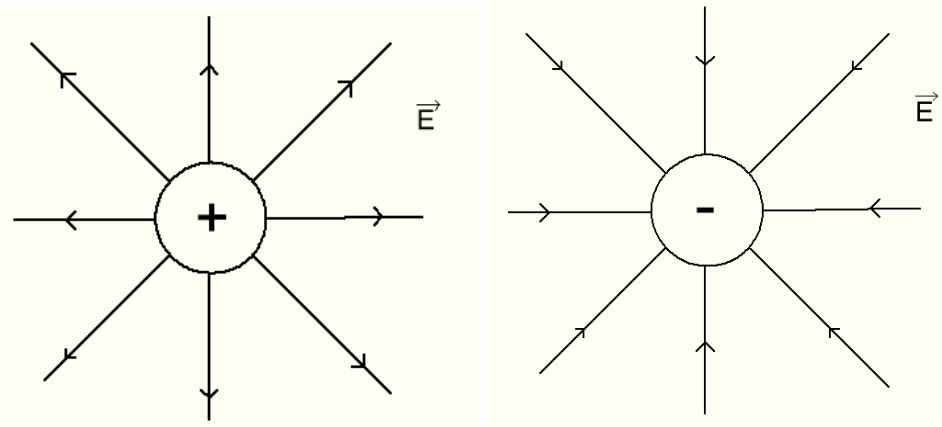

Рис. 4. Распределение линий напряженности для изолированных (а) и взаимодействующих (б) зарядов
Потенциал, напряжение
Физическую величину, равную отношению потенциальной энергии W электрического заряда в электростатическом поле к величине самого заряда q, называют потенциалом φ электрического поля
Потенциал – это скалярная величина, которая показывает, какую работу способно затратить поле, чтобы переместить единичный пробный положительный заряд в бесконечно удалённую точку. Единицей измерения электрического потенциала является вольт, [В].
При этом важно отметить, что работа сил электростатического поля при перемещении заряда из одной точки электрического поля в другую не зависит от формы траектории перемещения, а зависит только от начального и конечного положения заряда, а также от его величины.
Если имеется некоторая система, состоящая из N точечных зарядов, то потенциал ее электрического поля φ будет равен алгебраической сумме потенциалов полей каждого входящего в него заряда, то есть
Напряжение электрического поля – это разность потенциалов между двумя точками этого поля (рисунок 5).
Напряжение (U) — это работа (А) совершаемая силой поля по перемещению заряженных частиц между двумя точками поля.
U = A/q [Дж/Кл] или [В]

Напряжение является относительной величиной, то есть всегда определяется относительно некоторого уровня. Нулевой уровень выбирается произвольно и не влияет на итоговое значение напряжения, так как соответствует разности потенциалов в двух точках (то есть изменению потенциальной энергии). Для простоты расчетов в качестве нулевого уровня в большинстве случаев принимают потенциал заземленного проводника или земли.
Как уже было отмечено ранее электрическое напряжение – это разность потенциалов двух точек, следовательно его значение определяется по формуле
В системе СИ за единицу измерения напряжения принимается вольт, [В]. Физически величина напряжения, равная 1 вольту, соответствует работе 1 джоуль при перемещении заряда в 1 кулон.
Источник
Содержание
- Физика сила тока как найти заряд
- Электрическое поле
- 1.1. Электрический заряд. Закон Кулона
- Физика сила тока как найти заряд
- Амперметр
- Напряжение
- Вольтметр
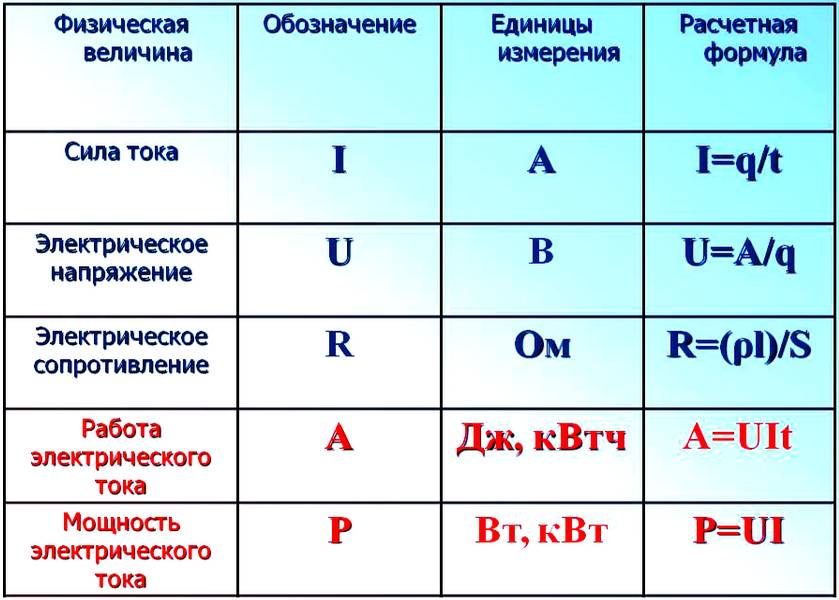
- Формулы и определения.
- Закон Кулона, конденсатор, сила тока, закон Ома, закон Джоуля – Ленца
- Теория к заданию 14 из ЕГЭ по физике
- Закон Кулона
- Электрическая емкость конденсатора
- Электроемкость
- Электрический конденсатор
- Энергия поля конденсатора
- Сила тока
- Закон Ома для участка цепи
- Электрическое сопротивление
- Удельное сопротивление
- Зависимость сопротивления от температуры
- Сила тока
- Сила тока с точки зрения гидравлики
- Что такое сила тока?
- Формула силы тока
- Сила тока и сопротивление
- Сила тока в проводнике
- Как измерить силу тока?
Физика сила тока как найти заряд
Многие физические явления, наблюдаемые в природе и окружающей нас жизни, не могут быть объяснены только на основе законов механики, молекулярно-кинетической теории и термодинамики. В этих явлениях проявляются силы, действующие между телами на расстоянии, причем эти силы не зависят от масс взаимодействующих тел и, следовательно, не являются гравитационными. Эти силы называют электромагнитными силами .
О существовании электромагнитных сил знали еще древние греки. Но систематическое, количественное изучение физических явлений, в которых проявляется электромагнитное взаимодействие тел, началось только в конце XVIII века. Трудами многих ученых в XIX веке завершилось создание стройной науки, изучающей электрические и магнитные явления. Эта наука, которая является одним из важнейших разделов физики, получила название электродинамики .
Основными объектами изучения в электродинамике являются электрические и магнитные поля, создаваемые электрическими зарядами и токами.
Электрическое поле
1.1. Электрический заряд. Закон Кулона
Подобно понятию гравитационной массы тела в механике Ньютона, понятие заряда в электродинамике является первичным, основным понятием.
Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.
Электрический заряд обычно обозначается буквами или .
Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы:
Существует два рода электрических зарядов, условно названных положительными и отрицательными.
Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.
Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.
Одним из фундаментальных законов природы является экспериментально установленный закон сохранения электрического заряда .
Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака.
С современной точки зрения, носителями зарядов являются элементарные частицы. Все обычные тела состоят из атомов, в состав которых входят положительно заряженные протоны, отрицательно заряженные электроны и нейтральные частицы – нейтроны. Протоны и нейтроны входят в состав атомных ядер, электроны образуют электронную оболочку атомов. Электрические заряды протона и электрона по модулю в точности одинаковы и равны элементарному заряду .
В нейтральном атоме число протонов в ядре равно числу электронов в оболочке. Это число называется атомным номером . Атом данного вещества может потерять один или несколько электронов или приобрести лишний электрон. В этих случаях нейтральный атом превращается в положительно или отрицательно заряженный ион.
Заряд может передаваться от одного тела к другому только порциями, содержащими целое число элементарных зарядов. Таким образом, электрический заряд тела – дискретная величина:
Физические величины, которые могут принимать только дискретный ряд значений, называются квантованными . Элементарный заряд является квантом (наименьшей порцией) электрического заряда. Следует отметить, что в современной физике элементарных частиц предполагается существование так называемых кварков – частиц с дробным зарядом и Однако, в свободном состоянии кварки до сих пор наблюдать не удалось.
В обычных лабораторных опытах для обнаружения и измерения электрических зарядов используется электрометр – прибор, состоящий из металлического стержня и стрелки, которая может вращаться вокруг горизонтальной оси (рис. 1.1.1). Стержень со стрелкой изолирован от металлического корпуса. При соприкосновении заряженного тела со стержнем электрометра, электрические заряды одного знака распределяются по стержню и стрелке. Силы электрического отталкивания вызывают поворот стрелки на некоторый угол, по которому можно судить о заряде, переданном стержню электрометра.
Электрометр является достаточно грубым прибором; он не позволяет исследовать силы взаимодействия зарядов. Впервые закон взаимодействия неподвижных зарядов был открыт французским физиком Ш. Кулоном в 1785 г. В своих опытах Кулон измерял силы притяжения и отталкивания заряженных шариков с помощью сконструированного им прибора – крутильных весов (рис. 1.1.2), отличавшихся чрезвычайно высокой чувствительностью. Так, например, коромысло весов поворачивалось на 1° под действием силы порядка .
Идея измерений основывалась на блестящей догадке Кулона о том, что если заряженный шарик привести в контакт с точно таким же незаряженным, то заряд первого разделится между ними поровну. Таким образом, был указан способ изменять заряд шарика в два, три и т. д. раз. В опытах Кулона измерялось взаимодействие между шариками, размеры которых много меньше расстояния между ними. Такие заряженные тела принято называть точечными зарядами .
Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь.
На основании многочисленных опытов Кулон установил следующий закон:
Силы взаимодействия подчиняются третьему закону Ньютона: Они являются силами отталкивания при одинаковых знаках зарядов и силами притяжения при разных знаках (рис. 1.1.3). Взаимодействие неподвижных электрических зарядов называют электростатическим или кулоновским взаимодействием. Раздел электродинамики, изучающий кулоновское взаимодействие, называют электростатикой .
Закон Кулона справедлив для точечных заряженных тел. Практически закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними.
Коэффициент пропорциональности в законе Кулона зависит от выбора системы единиц. В Международной системе СИ за единицу заряда принят кулон (Кл).
Кулон – это заряд, проходящий за 1 с через поперечное сечение проводника при силе тока 1 А. Единица силы тока (ампер) в СИ является наряду с единицами длины, времени и массы основной единицей измерения .
В системе СИ элементарный заряд равен:
Опыт показывает, что силы кулоновского взаимодействия подчиняются принципу суперпозиции.
Если заряженное тело взаимодействует одновременно с несколькими заряженными телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел.
Рис. 1.1.4 поясняет принцип суперпозиции на примере электростатического взаимодействия трех заряженных тел.
Принцип суперпозиции является фундаментальным законом природы. Однако, его применение требует определенной осторожности, в том случае, когда речь идет о взаимодействии заряженных тел конечных размеров (например, двух проводящих заряженных шаров 1 и 2). Если к системе из двух заряженных шаров поднсти третий заряженный шар, то взаимодействие между 1 и 2 изменится из-за перераспределения зарядов .
Принцип суперпозиции утверждает, что при заданном (фиксированном) распределении зарядов на всех телах силы электростатического взаимодействия между любыми двумя телами не зависят от наличия других заряженных тел.
Источник
Физика сила тока как найти заряд
Характеристикой тока в цепи служит величина, называемая силой тока ( I ). Сила тока – физическая величина, характеризующая скорость прохождения заряда через проводник и равная отношению заряда q, прошедшeгo через пoперeчное сечение проводника за промежуток времени t, к этому промежутку времени: I = q/t . Единица измерения силы тока – 1 ампер (1 А).
Определение единицы силы тока основано на магнитном действии тока, в частности на взаимодействии параллельных проводников, по которым идёт электрический ток. Такие проводники притягиваются, если ток по ним идёт в одном направлении, и отталкиваются, если направление тока в них противоположное.
За единицу силы тока принимают такую силу тока, при которой отрезки параллельных проводников длиной 1 м, находящиеся на расстоянии 1 м друг от друга, взаимодействуют с силой 2*10 -7 Н. Эта единица и называется ампером (1 А).
Зная формулу силы тока, можно получить единицу электрического заряда: 1 Кл = 1А * 1с.
Амперметр
Прибор, с помощью которого измеряют силу тока в цепи, называется амперметром. Его работа основана на магнитном действии тока. Основные части амперметра магнит и катушка. При прохождении по катушке электрического тока она в результате взаимодействия с магнитом, поворачивается и поворачивает соединённую с ней стрелку. Чем больше сила тока, проходящего через катушку, тем сильнее она взаимодействует с магнитом, тем больше угол поворота стрелки. Амперметр включается в цепь последовательно с тем прибором, силу тока в котором нужно измерить, и потому он имеет малое внутреннее сопротивление, которое практически не влияет на сопротивление цепи и на силу тока в цепи.
У клемм амперметра стоят знаки «+» и «—», при включении амперметра в цепь клемма со знаком «+» присоединяется к положительному пoлюсу источника тока, а клемма со знаком «—» к отрицательному пoлюсу истoчникa тока.
Напряжение
Источник тока создаёт электрическое поле, которое приводит в движение электрические заряды. Характеристикой источника тока служит величина, называемая напряжением. Чем оно больше, тем сильнее созданное им поле. Напряжение характеризует работу, которую совершает электрическое поле по перемещению электрического заряда.
Напряжение ( U ) — это физическая величина, равную отношению работы (А) электрического поля по перемещению электрического заряда к заряду (q): U = A/q .
Возможно другое определение понятия напряжения. Если числитель и знаменатель в формуле напряжения умножить на время движения заряда (t), то получим: U = At/qt. В числителе этой дроби стоит мощность тока (Р), а в знаменателе — сила тока (I). Получается формула: U = Р/I , т.е. напряжение — это физическая величина, равная отношению мощности электрического тока к силе тока в цепи.
Единица напряжения: [U] = 1 Дж/1 Кл = 1 В (один вольт).
Вольтметр
Напряжение измеряют вольтметром. Он имеет такое же устройство, что и амперметр и такой же принцип действия, но он подключается параллельно тому участку цепи, напряжение на котором хотят. Внутреннее сопротивление вольтметра достаточно большое, соответственно проходящий через него ток мал по сравнению с током в цепи.
У клемм вольтметра стоят знаки «+» и «—», при включении вольтметра в цепь клeмма со знаком «+» присоединяется к положительному полюсу источника тока, а клеммa со знаком «—» к отрицательному полюсу источника тока.
Формулы и определения.
1. Все проводники, используемые в электрических цепях, имеют условные обозначения для изображения на схемах и могут образовывать последовательные, параллельные и смешанные соединения.
2. Мощность тока – физическая величинa, хаpактеpизующая скорость превращения электрической энергии в другие её виды. Единица для измерения – 1 ватт (1 Вт). Измерительный прибор – ваттметр.
3. Сила тока – физическaя вeличина, характеpизующaя скоpость прохождения заряда через проводник и равная отношению заряда, пpoшедшего через попеpeчное сечение проводника, ко времени перемещения. Единица – 1 ампер (1 А). Измерительный прибор – амперметр (подключают последовательно).
4. Электрическое напряжение – физическaя вeличина, характеризующая электрическое поле, создающее ток, и равная отношению мощности тока к его силе. Единица – 1 вольт (1 В). Измерительный прибор – вольтметр (подключают параллельно)
5. Работа тока – физичeская величинa, хаpактеpизующая количество электроэнергии, превратившейся в другие виды энергии. Единица – 1 джоуль (1 Дж). Измерительный прибор – электрический счётчик, использующий единицу 1 киловатт-час (1 кВт·ч).
Конспект урока «Сила тока. Напряжение».
Источник
Закон Кулона, конденсатор, сила тока, закон Ома, закон Джоуля – Ленца
Теория к заданию 14 из ЕГЭ по физике
Закон Кулона
Закон Кулона — это один из основных законов электростатики. Он определяет величину и направление силы взаимодействия между двумя неподвижными точечными зарядами.
Под точечным зарядом понимают заряженное тело, размер которого много меньше расстояния его возможного воздействия на другие тела. В таком случае ни форма, ни размеры заряженных тел не влияют практически на взаимодействие между ними.
Закон Кулона экспериментально впервые был доказан приблизительно в 1773 г. Кавендишем, который использовал для этого сферический конденсатор. Он показал, что внутри заряженной сферы электрическое поле отсутствует. Это означало, что сила электростатического взаимодействия меняется обратно пропорционально квадрату расстояния, однако результаты Кавендиша не были опубликованы.
В 1785 г. закон был установлен Ш. О. Кулоном с помощью специальных крутильных весов.
Опыты Кулона позволили установить закон, поразительно напоминающий закон всемирного тяготения.
Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.
В аналитическом виде закон Кулона имеет вид:
где $|q_1|$ и $|q_2|$ — модули зарядов; $r$ — расстояние между ними; $k$ — коэффициент пропорциональности, зависящий от выбора системы единиц. Сила взаимодействия направлена по прямой, соединяющей заряды, причем одноименные заряды отталкиваются, а разноименные — притягиваются.
Сила взаимодействия между зарядами зависит также от среды между заряженными телами.
В воздухе сила взаимодействия почти не отличается от таковой в вакууме. Закон Кулона выражает взаимодействие зарядов в вакууме.
Кулон — единица электрического заряда. Кулон (Кл) — единица СИ количества электричества (электрического заряда). Она является производной единицей и определяется через единицу силы тока 1 ампер (А), которая входит в число основных единиц СИ.
За единицу электрического заряда принимают заряд, проходящий через поперечное сечение проводника при силе тока $1$А за $1$с.
То есть $1$ Кл$= 1А·с$.
Заряд в $1$ Кл очень велик. Сила взаимодействия двух точечных зарядов по $1$ Кл каждый, расположенных на расстоянии $1$ км друг от друга, чуть меньше силы, с которой земной шар притягивает груз массой $1$ т. Сообщить такой заряд небольшому телу невозможно (отталкиваясь друг от друга, заряженные частицы не могут удержаться в теле). А вот в проводнике (который в целом электронейтрален) привести в движение такой заряд просто (ток в $1$ А вполне обычный ток, протекающий по проводам в наших квартирах).
Коэффициент $k$ в законе Кулона при его записи в СИ выражается в $Н · м^2$ / $Кл^2$. Его численное значение, определенное экспериментально по силе взаимодействия двух известных зарядов, находящихся на заданном расстоянии, составляет:
Часто его записывают в виде $k=<1>/<4πε_0>$, где $ε_0=8.85×10^<-12>Кл^2$/$H·м^2$ — электрическая постоянная.
Электрическая емкость конденсатора
Электроемкость
Электроемкостью проводника $С$ называют численную величину заряда, которую нужно сообщить проводнику, чтобы изменить его потенциал на единицу:
Емкость характеризует способность проводника накапливать заряд. Она зависит от формы проводника, его линейных размеров и свойств среды, окружающей проводник.
Единицей емкости в СИ является фарада ($Ф$) — емкость проводника, в котором изменение заряда на $1$ кулон меняет его потенциал на $1$ вольт.
Электрический конденсатор
Электрический конденсатор (от лат. condensare, буквально сгущать, уплотнять) — устройство, предназначенное для получения электрической емкости заданной величины, способное накапливать и отдавать (перераспределять) электрические заряды.
Конденсатор — это система из двух или нескольких равномерно заряженных проводников с равными по величине зарядами, разделенных слоем диэлектрика. Проводники называются обкладками конденсатора. Как правило, расстояние между обкладками, равное толщине диэлектрика, намного меньше размеров самих обкладок, так что поле в конденсаторе практически все сосредоточено между его обкладками. Если обкладки являются плоскими пластинами, поле между ними однородно. Электроемкость плоского конденсатора определяется по формуле:
где $q$ — заряд конденсатора, $U$ — напряжение между его обкладками, $S$ — площадь пластины, $d$ — расстояние между пластинами, $ε_<0>$ — электрическая постоянная, $ε$ — диэлектрическая проницаемость среды.
Под зарядом конденсатора понимают абсолютное значение заряда одной из пластин.
Энергия поля конденсатора
Энергия заряженного конденсатора выражается формулами
которые выводятся с учетом выражений для связи работы и напряжения и для емкости плоского конденсатора.
Энергия электрического поля. Объемная плотность энергии электрического поля (энергия поля в единице объема) напряженностью $Е$ выражается формулой:
где $ε$ — диэлектрическая проницаемость среды, $ε_0$ — электрическая постоянная.
Сила тока
Электрическим током называется упорядоченное (направленное) движение заряженных частиц.
Сила электрического тока — это величина ($I$), характеризующая упорядоченное движение электрических зарядов и численно равная количеству заряда $∆q$, протекающего через определенную поверхность $S$ (поперечное сечение проводника) за единицу времени:
Итак, чтобы найти силу тока $I$, надо электрический заряд $∆q$, прошедший через поперечное сечение проводника за время $∆t$, разделить на это время.
Сила тока зависит от заряда, переносимого каждой частицей, скорости их направленного движения и площади поперечного сечения проводника.
Рассмотрим проводник с площадью поперечного сечения $S$. Заряд каждой частицы $q_0$. В объеме проводника, ограниченном сечениями $1$ и $2$, содержится $nS∆l$ частиц, где $n$ — концентрация частиц. Их общий заряд $q=q_<0>nS∆l$. Если частицы движутся со средней скоростью $υ$, то за время $∆t=<∆l>/<υ>$ все частицы, заключенные в рассматриваемом объеме, пройдут через поперечное сечение $2$. Сила тока, следовательно, равна:
В СИ единица силы тока является основной и носит название ампер (А) в честь французского ученого А. М. Ампера (1755-1836).
Силу тока измеряют амперметром. Принцип устройства амперметра основан на магнитном действии тока.
Оценка скорости упорядоченного движения электронов в проводнике, проведенная по формуле для медного проводника с площадью поперечного сечения $1мм^2$, дает весьма незначительную величину — $∼0.1$ мм/с.
Закон Ома для участка цепи
Сила тока на участке цепи равна отношению напряжения на этом участке к его сопротивлению.
Закон Ома выражает связь между тремя величинами, характеризующими протекание электрического тока в цепи: силой тока $I$, напряжением $U$ и сопротивлением $R$.
Закон этот был установлен в 1827 г. немецким ученым Г. Омом и поэтому носит его имя. В приведенной формулировке он называется также законом Ома для участка цепи. Математически закон Ома записывается в виде следующей формулы:
Зависимость силы тока от приложенной разности потенциалов на концах проводника называется вольт-амперной характеристикой (ВАХ) проводника.
Для любого проводника (твердого, жидкого или газообразного) существует своя ВАХ. Наиболее простой вид имеет вольт-амперная характеристика металлических проводников, заданная законом Ома $I=/$, и растворов электролитов. Знание ВАХ играет большую роль при изучении тока.
Закон Ома — это основа всей электротехники. Из закона Ома $I=/$ следует:
- сила тока на участке цепи с постоянным сопротивлением пропорциональна напряжению на концах участка;
- сила тока на участке цепи с неизменным напряжением обратно пропорциональна сопротивлению.
Эти зависимости легко проверить экспериментально. Полученные с использованием схемы, графики зависимости силы тока от напряжения при постоянном сопротивлении и силы тока от сопротивления представлены на рисунке. В первом случае использован источник тока с регулируемым выходным напряжением и постоянное сопротивление $R$, во втором — аккумулятор и переменное сопротивление (магазин сопротивлений).
Электрическое сопротивление
Электрическое сопротивление — это физическая величина, характеризующая противодействие проводника или электрической цепи электрическому току.
Электрическое сопротивление определяется как коэффициент пропорциональности $R$ между напряжением $U$ и силой постоянного тока $I$ в законе Ома для участка цепи.
Единица сопротивления называется омом (Ом) в честь немецкого ученого Г. Ома, который ввел это понятие в физику. Один ом ($1$ Ом) — это сопротивление такого проводника, в котором при напряжении $1$ В сила тока равна $1$ А.
Удельное сопротивление
Сопротивление однородного проводника постоянного сечения зависит от материла проводника, его длины $l$ и поперечного сечения $S$ и может быть определено по формуле:
где $ρ$ — удельное сопротивление вещества, из которого изготовлен проводник.
Удельное сопротивление вещества — это физическая величина, показывающая, каким сопротивлением обладает изготовленный из этого вещества проводник единичной длины и единичной площади поперечного сечения.
Из формулы $R=ρ/$ следует, что
Величина, обратная $ρ$, называется удельной проводимостью $σ$:
Так как в СИ единицей сопротивления является $1$ Ом, единицей площади $1м^2$, а единицей длины $1$ м, то единицей удельного сопротивления в СИ будет $1$ Ом$·м^2$/м, или $1$ Ом$·$м. Единица удельной проводимости в СИ — $Ом^<-1>м^<-1>$.
На практике площадь сечения тонких проводов часто выражают в квадратных миллиметрах (м$м^2$). В этом случае более удобной единицей удельного сопротивления является Ом$·$м$м^2$/м. Так как $1 мм^2 = 0.000001 м^2$, то $1$ Ом$·$м $м^2$/м$ = 10^<-6>$ Ом$·$м. Металлы обладают очень малым удельным сопротивлением — порядка ($1 ·10^<-2>$) Ом$·$м$м^2$/м, диэлектрики — в $10^<15>-10^<20>$ раз большим.
Зависимость сопротивления от температуры
С повышением температуры сопротивление металлов возрастает. Однако существуют сплавы, сопротивление которых почти не меняется при повышении температуры (например, константан, манганин и др.). Сопротивление же электролитов с повышением температуры уменьшается.
Температурным коэффициентом сопротивления проводника называется отношение величины изменения сопротивления проводника при нагревании на $1°$С к величине его сопротивления при $0°$С:
Зависимость удельного сопротивления проводников от температуры выражается формулой:
В общем случае $α$ зависит от температуры, но если интервал температур невелик, то температурный коэффициент можно считать постоянным. Для чистых металлов $α=(<1>/<273>)K^<-1>$. Для растворов электролитов $α
- Русский язык
- Математика (профильная)
- Обществознание
- Физика
- История
- Биология
- Химия
- Литература
- Информатика
- Задания ЕГЭ
- Тесты
- Варианты
- Теория
- Банк заданий
- Перевод баллов
- Сочинение ЕГЭ
- Отзывы
Источник
Сила тока
Сила тока с точки зрения гидравлики
Думаю, вы не раз слышали такое словосочетание, как “сила тока“. А для чего нужна сила? Ну как для чего? Чтобы совершать полезную или бесполезную работу. Главное, чтобы что-то делать. Каждый из нас обладает какой-либо силой. У кого-то сила такая, что он может одним ударом разбить кирпич в пух и в прах, а другой не сможет поднять даже соломинку. Так вот, дорогие мои читатели, электрический ток тоже обладает силой.
Представьте себе шланг, с помощью которого вы поливаете свой огород
Давайте теперь проведем аналогию. Пусть шланг – это провод, а вода в нем – электрический ток. Мы чуть-чуть приоткрыли краник и вода сразу же побежала по шлангу. Медленно, но все-таки побежала. Сила струи очень слабая.
А давайте теперь откроем краник на полную катушку. В результате струя хлынет с такой силой, что можно даже полить соседский огород.
В обоих случаях диаметр шланга одинаков.
А теперь представьте, что вы наполняете ведро. Напором воды из какого шланга вы его быстрее наполните? Разумеется из зеленого, где напор воды очень сильный. Но почему так происходит? Все дело в том, что объем воды за равный промежуток времени из желтого и зеленого шланга выйдет тоже разный. Или иными словами, из зеленого шланга количество молекул воды выбежит намного больше, чем из желтого за равный период времени.
Разберем еще один интересный пример. Давайте допустим, что у нас есть большая труба, и к ней заварены две другие, но одна в два раза меньше диаметром, чем другая.
Из какой трубы объем воды будет выходить больше за секунду времени? Разумеется с той, которая толще в диаметре, потому что площадь поперечного сечения S2 большой трубы больше, чем площадь поперечного сечения S1 малой трубы. Следовательно, сила потока через большую трубу будет больше, чем через малую, так как объем воды, который протекает через поперечное сечение трубы S2, будет в два раза больше, чем через тонкую трубу.
Что такое сила тока?
Итак, теперь давайте все что мы тут пописали про водичку применим к электронике. Провод – это шланг. Тонкий провод – это тонкий в диаметре шланг, толстый провод – это толстый в диаметре шланг, можно сказать – труба. Молекулы воды – это электроны. Следовательно, толстый провод при одинаковом напряжении можно протащить больше электронов, чем тонкий. И вот здесь мы подходим вплотную к самой терминологии силы тока.
Все это выглядит примерно вот так. Здесь я нарисовал круглый проводок, “разрезал” его и получил ту самую площадь поперечного сечения. Именно через нее и бегут электроны.
За период времени берут 1 секунду.
Формула силы тока
Формула для чайников будет выглядеть вот так:
I – собственно сила тока, Амперы
N – количество электронов
t – период времени, за которое эти электроны пробегут через поперечное сечение проводника, секунды
Более правильная (официальная) формула выглядит вот так:

Δq – это заряд за какой-то определенный промежуток времени, Кулон
Δt – тот самый промежуток времени, секунды
I – сила тока, Амперы
В чем прикол этих двух формул? Дело все в том, что электрон обладает зарядом приблизительно 1,6 · 10 -19 Кулон. Поэтому, чтобы сила тока была в проводе (проводнике) была 1 Ампер, нам надо, чтобы через поперечное сечение прошел заряд в 1 Кулон = 6,24151⋅10 18 электронов. 1 Кулон = 1 Ампер · 1 секунду.
Итак, теперь можно официально сказать, что если через поперечное сечение проводника за 1 секунду пролетят 6,24151⋅10 18 электронов, то сила тока в таком проводнике будет равна 1 Ампер! Все! Ничего не надо больше придумывать! Так и скажите своему преподавателю по физике).
Если преподу не понравится ваш ответ, то скажите типа что-то этого:
Сила тока – это физическая величина, равная отношению количества заряда прошедшего через поверхность (читаем как через площадь поперечного сечения) за какое-то время. Измеряется как Кулон/секунда. Чтобы сэкономить время и по другим морально-эстетическим нормам, Кулон/секунду договорились называть Ампером, в честь французского ученого-физика.
Сила тока и сопротивление
Давайте еще раз глянем на шланг с водой и зададим себе вопросы. От чего зависит поток воды? Первое, что приходит в голову – это давление. Почему молекулы воды движутся в рисунке ниже слева-направо? Потому, что давление слева, больше чем справа. Чем больше давление, тем быстрее побежит водичка по шлангу – это элементарно.
Теперь такой вопрос: как можно увеличить количество электронов через площадь поперечного сечения?
Первое, что приходит на ум – это увеличить давление. В этом случае скорость потока воды увеличится, но ее много не увеличишь, так как шланг порвется как грелка в пасти Тузика.
Второе – это поставить шланг бОльшим диаметром. В этом случае у нас количество молекул воды через поперечное сечение будет проходить больше, чем в тонком шланге:
Все те же самые умозаключения можно применить и к обыкновенному проводу. Чем он больше в диаметре, тем больше он сможет “протащить” через себя силу тока. Чем меньше в диаметре, то желательно меньше его нагружать, иначе его “порвет”, то есть он тупо сгорит. Именно этот принцип заложен в плавких предохранителях. Внутри такого предохранителя тонкий проводок. Его толщина зависит от того, на какую силу тока он рассчитан.
Как только сила тока через тонкий проводок предохранителя превысит силу тока, на которую рассчитан предохранитель, то плавкий проводок перегорает и размыкает цепь. Через перегоревший предохранитель ток уже течь не может, так как проводок в предохранителе в обрыве.
сгоревший плавкий предохранитель
Поэтому, силовые кабели, через которые “бегут” сотни и тысячи ампер, берут большого диаметра и стараются делать из меди, так как ее удельное сопротивление очень мало.
Сила тока в проводнике
Очень часто можно увидеть задачки по физике с вопросом: какая сила тока в проводнике? Проводник, он же провод, может иметь различные параметры: диаметр, он же площадь поперечного сечения; материал, из которого сделан провод; длина, которая играет также важную роль.
Да и вообще, сопротивление проводника рассчитывается по формуле:
формула сопротивления проводника
Таблица с удельным сопротивлением из разных материалов выглядит вот так.
таблица с удельным сопротивлением веществ
Для того, чтобы найти силу тока в проводнике, мы должны воспользоваться законом Ома для участка цепи. Выглядит он вот так:

Задача
У нас есть медный провод длиной в 1 метр и его площадь поперечного сечения составляет 1 мм 2 . Какая сила тока будет течь в этом проводнике (проводе), если на его концы подать напряжение в 1 Вольт?
задача на силу тока в проводнике

Как измерить силу тока?
Для того, чтобы измерить значение силы тока, мы должны использовать специальные приборы – амперметры. В настоящее время силу тока можно измерить с помощью цифрового мультиметра, который может измерять и силу тока, и напряжение и сопротивление и еще много чего. Для того, чтобы измерить силу тока, мы должны вставить наш прибор в разрыв цепи вот таким образом.
Более подробно как это сделать, можете прочитать в этой статье.
Также советую посмотреть обучающее видео, где очень умный преподаватель объясняет простым языком, что такое “сила тока”.
Источник