Формула как найти диаметр основания цилиндра

Онлайн калькулятор для цилиндра позволяет по известным данным вычислить:

• объем цилиндра,
• площадь основания, площадь боковой поверхности и  площадь полной поверхности цилиндра,
• элементы: радиус, диаметр и высоту.

Калькулятор для цилиндра: комментарий

Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью (называемой боковой поверхностью цилиндра) и не более чем двумя поверхностями (основаниями цилиндра).

Обозначения для цилиндра:
R – радиус, D – диаметр,
V – объем,
Sо – площадь основания, Sб – площадь боковой поверхности, S – площадь полной поверхности,
h – высота прямого кругового цилиндра (h1 и h2 — минимальная  и максимальная высота)
π – число Пи которое всегда примерно равно 3,14.

Прямой круговой цилиндр

Круговым называется цилиндр, если его направляющая является окружностью. Прямым называется цилиндр, если его образующая перпендикулярна основаниям.

Формулы для прямого кругового цилиндра:

Найти объем цилиндра, если известны:

• радиус и высота цилиндра: V=πR²h
• диаметр и высота цилиндра: V=πD²/4h
• площадь и высота цилиндра: V=Sоh

Площадь(Sб) боковой поверхности прямого кругового цилиндра

Так как боковая поверхность представляет собой прямоугольник, то площадь боковой поверхности цилиндра определяется по формуле: Sб=2πR⋅h

Площадь(Sо) основания цилиндра

Основание цилиндра —круг, поэтому площадь одного основания находится по формуле площади круга: Sо=πR².

Площадь(S)  полной поверхности прямого кругового цилиндра

Площадь полной поверхности цилиндра определяется по формуле: S=2πRh+2πR²=2πR(h+R)

Формулы нахождения радиуса и диаметра по:

• высоте и объему: R=√(V/πh), D=2*√(V/πh)
• площади боковой поверхности и высоте: R=Sб/2πh, D=2*Sб/2πh
• площади основания и высоте: R=√(Sо/π), R=2*√(Sо/π)

Формулы нахождения высоты по:

• радиусу и объему: h=V/πR²
• площади боковой поверхности и радиусу: h=Sб/2πR
• площади полной поверхности и радиусу: h=S/2πR-R

Скошенный цилиндр

Прямой круговой цилиндр со скошенным основанием (скошенный цилиндр) определяется радиусом основания R, минимальной высотой h1 и максимальной высотой h2.

Формулы для скошенного цилиндра:

• Объем скошенного цилиндра: V=πR²(h1+h2)²
• Площадь(Sб) боковой поверхности скошенного цилиндра: Sб=πR(h1+h2)
• Площадь(Sо) оснований скошенного цилиндра: Sо=πR²+πR √(R2+((h1−h2)/2)²)
• Площадь(S) полной поверхности скошенного цилиндра  
  S=Sб+Sо= πR(h1+h2)+ πR²+πR √ (R²+((h1−h2)/2)²)  = πR[(h1+h2)+ R+√ (R²+((h1−h2)/2)²) ]

Список всех онлайн-конвертеров на странице «Калькуляторы«.

На этой странице вы узнаете

• Как вода в кружке иллюстрирует сечение цилиндра?
• Как лист бумаги превратить в цилиндр?

Что общего у джентльмена 19 века, Вилли Вонка из «Чарли и шоколадная фабрика», Шерлока Холмса в экранизации «Безобразная невеста» и некоторых сценических костюмов? Цилиндр! О нем, вернее о фигуре цилиндра и поговорим в статье.

Понятие цилиндра

Сейчас мы говорим про мужской головной убор, который был популярен в 19 веке и стал достаточно узнаваем в массовой культуре. Оказывается, в математике также существует цилиндр. И они похожи по форме.

Цилиндр — тело вращения, полученное при вращении прямоугольника вокруг одной из его сторон. 

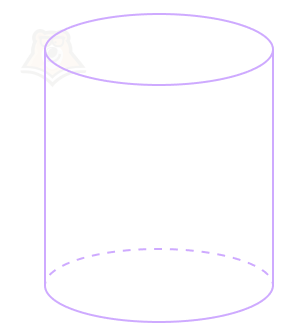
Возможно, для уточнения некоторых терминов вам захочется заглянуть в статью «Тела вращения». 

Если посмотреть на форму шляпы, то она действительно будет похожа на геометрическую фигуру.  Встретить цилиндр можно и в наше время. Обычная кружка является цилиндром.

Прямая, вокруг которой мы крутили прямоугольник, чтобы получить цилиндр, — это ось цилиндра. 

Также, как у Земли есть ось вращения, она есть и у цилиндра. 

Наша кружка стоит на круглом дне. Это дно, как и самый верх кружки, будут называться основаниями цилиндра. 

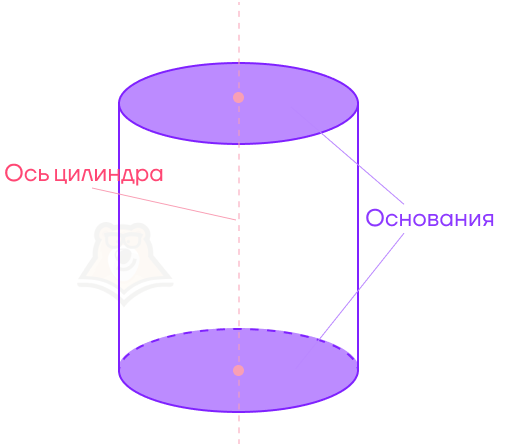
Снова посмотрим на стенки кружки. В цилиндре эта поверхность будет называться цилиндрической поверхностью. Ее также могут называть боковой поверхностью цилиндра. 

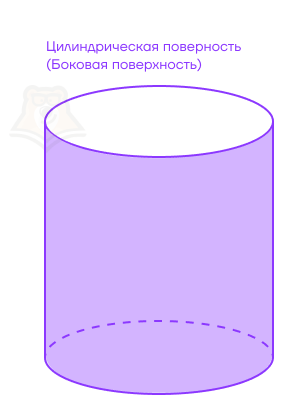
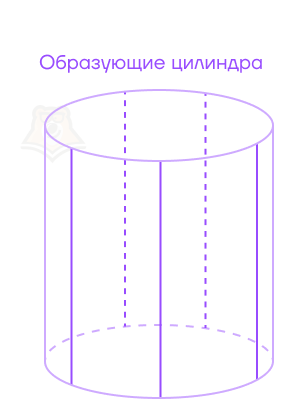
Представим, что наша кружка раскрашена вертикальными линиями. Эти линии будут лежать на цилиндрической поверхности и перпендикулярны основаниям. У них есть название:

Образующая цилиндра — отрезок, соединяющий точки окружностей основания и перпендикулярный плоскостям оснований. 

Все образующие, — а в цилиндре их очень-очень много, —лежат только на цилиндрической поверхности. Эта поверхность и состоит из множества образующих. 

Узнаем ширину кружки. Для этого нужно измерить радиус дна. Этот же радиус будет радиусом основания, а в цилиндре он называется радиусом цилиндра. 

Теперь найдем высоту кружки. Для этого нужно измерить расстояние от дна до самого верха кружки. 

В математике это будет расстоянием между плоскостями, а ищется оно как длина перпендикуляра, опущенного из одной плоскости на другую. Подробнее про это можно прочесть в статье «Расстояния между фигурами». 

Высота цилиндра — перпендикуляр, опущенный из плоскости одного основания на плоскость второго основания. 

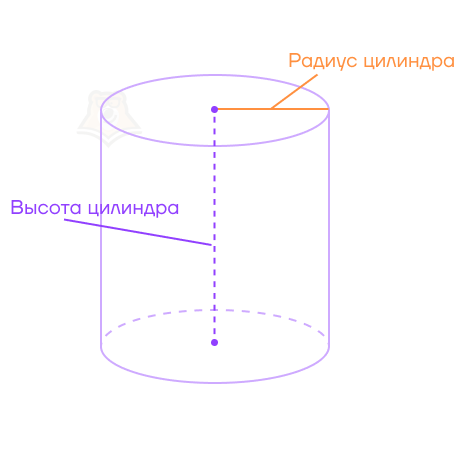
Свойства цилиндра

Рассмотрим, какими свойствами обладает цилиндр. 

Свойство 1. Основания цилиндра равны и параллельны. 

Это всегда два равных круга, лежащих в параллельных плоскостях. 

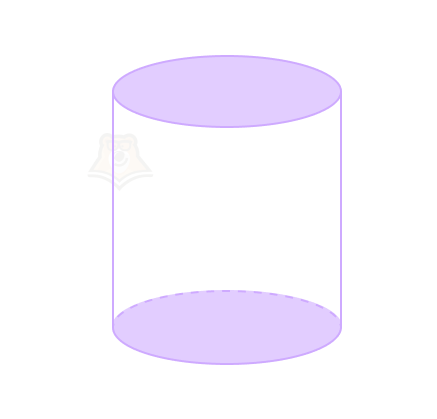
Свойство 2. Образующие цилиндра равны и параллельны. 

Поскольку все образующие перпендикулярны основаниям, то они параллельны между собой по свойству прямой и перпендикулярной ей плоскости. Подробнее про это свойство можно прочесть в статье «Углы в пространстве». 

А равны они потому, что являются перпендикуляром к основаниям, то есть равны высоте цилиндра.

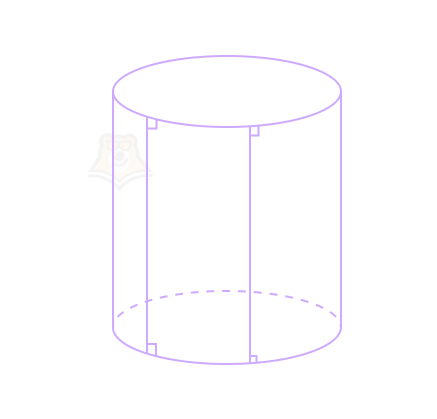
Свойство 3. Сечение цилиндра, проходящее через ось цилиндра, является прямоугольником. Такое сечение в цилиндре будет называться осевым сечением цилиндра. 

Например, если разрезать тортик по диаметру, то место среза как раз будет прямоугольником. 

Подробности про сечения фигур можно найти в статье «Сечения». 

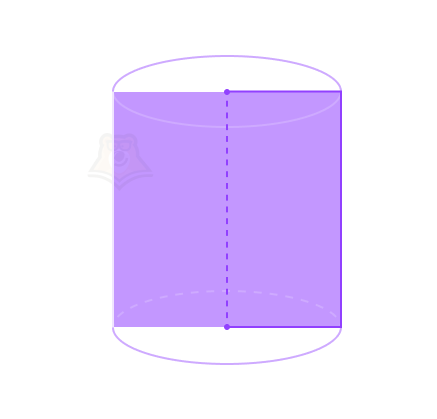
Свойство 4. Сечение цилиндра, проходящее параллельно оси цилиндра и перпендикулярно его основаниям, будет являться прямоугольником. 

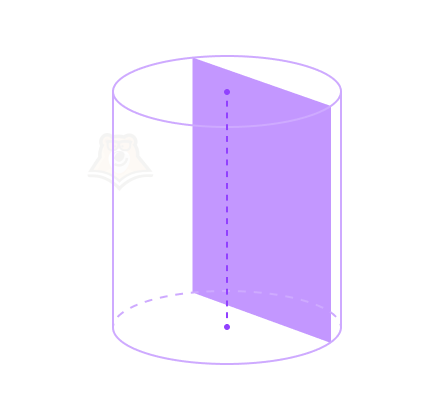
Свойство 5. Сечение цилиндра, перпендикулярное оси цилиндра, является кругом с радиусом, равным радиусу цилиндра. Такое сечение в цилиндре называется перпендикулярным сечением цилиндра. 

Заметим, что все вышеописанные свойства относятся к прямому цилиндру. 

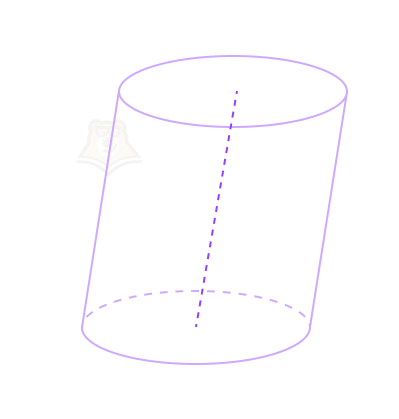
Цилиндр также может быть наклонным. В этом случае ось цилиндра и его образующие не будут перпендикулярны основаниям. 

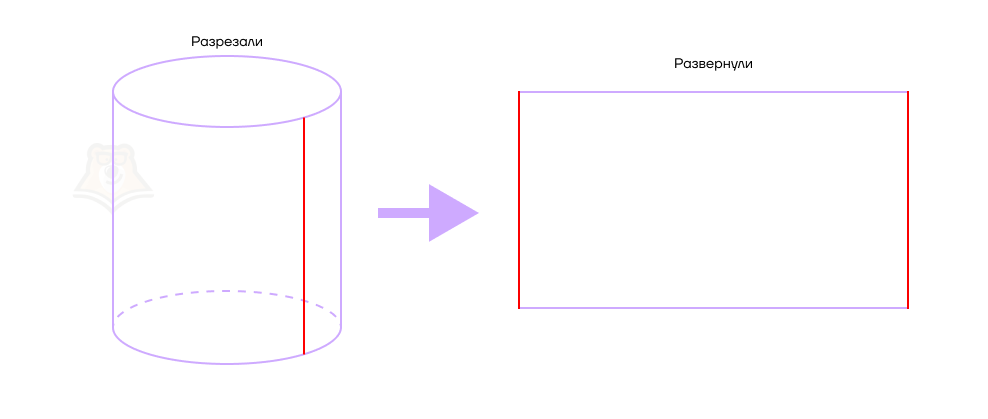
Если мы разрежем поверхность цилиндра по одной из его образующих и как бы “развернем” ее, у нас получится прямоугольник. 

Это также легко увидеть, если вспомнить художников с тубусами. Тубус имеет форму цилиндра, и свернутый прямоугольный лист принимает такую же форму. 

Развертка боковой поверхности цилиндра — прямоугольник, одна сторона которого равна высоте цилиндра, а вторая — длине окружности его основания. 

Формулы цилиндра

А если это прямоугольник, то мы знаем, как найти его площадь. Нам нужно умножить его длину на высоту. Так мы получаем площадь боковой поверхности цилиндра. 

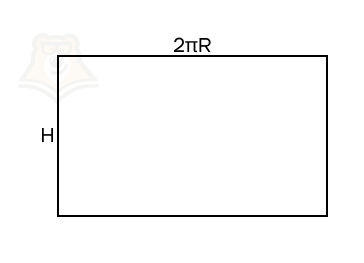
(S_{бок.} = 2 pi RH)

В этой формуле 2R — длина окружности основания, где R — его радиус, а Н — образующая (или высота) цилиндра. Подробнее про площадь прямоугольника и длину окружности (а также про площадь круга) можно прочесть в статьях «Параллелограмм» и «Окружность и круг». 

Мы нашли площадь боковой поверхности. Как же теперь найти площадь полной поверхности?

Для этого нужно сложить площади боковой поверхности и оснований. Следовательно, мы получаем следующую формулу. 

(S = S_{бок.} + 2S_{осн.} = 2 pi RH+2 pi R^2 = 2 pi R(H + R))

Допустим, мы решили сделать чашку очень вкусного чая, но чтобы правильно его заварить нам нужно знать точный объем воды. Для этого вычислим объем цилиндра. Воспользуемся следующей формулой:

(V = S_{осн.}H = pi R^2H)

В этой формуле R — радиус цилиндра, Н — высота. 

Часто формулу объема можно применить для решения жизненных задач. Например, чтобы найти объем детали, погруженной в воду. 

Пример 1. В цилиндрическом сосуде налито 1650 см³ жидкости. В этот сосуд опустили деталь. При этом уровень жидкости увеличился в 1,2 раза. Найдите объем детали. Ответ выразите в см³. 

Решение. 

Шаг 1. Выразим высоту жидкости в первый и второй раз. Пусть вначале уровень жидкости был равен х, значит после того, как в нее опустили деталь, он стал равен 1,2х. 

Шаг 2. Вспомним физику и заметим, что объем жидкости в сосуде после того, как в него опустили деталь, будет равен сумме объемов жидкости и детали: V = V_ж + V_д. 

Шаг 3. С помощью объема жидкости выразим площадь основания сосуда:

V_ж = S_осн.H
1650 = S_осн.x
(S_{осн} = frac{1650}{x})

Шаг 4. Подставим площадь основания в формулу объема жидкости после того, как в нее опустили деталь:

(V = S_{осн.}H = frac{1650}{x} * 1,2x = 1980)

Шаг 5. Тогда объем детали будет равен:

V_д = V — V_ж
V_д = 1980 — 1650 =330 

Ответ: 330 см³

Фактчек

• Цилиндр — тело вращения, полученное при вращении прямоугольника вокруг одной из его сторон. Цилиндр может быть прямым и наклонным. В наклонном цилиндре ось не перпендикулярна основаниям цилиндра. 
• Цилиндр состоит из двух оснований и цилиндрической поверхности (боковой поверхности цилиндра). Основания имеют форму кругов, равны между собой и лежат в параллельных плоскостях. Развертка боковой поверхности имеет форму прямоугольника. 
• Образующая цилиндра — отрезок, соединяющий точки окружностей основания и перпендикулярный плоскостям оснований. В прямом цилиндре образующая равна высоте цилиндра. Образующие равны и параллельны друг другу, а также образуют боковую поверхность цилиндра. 
• Осевое сечение цилиндра проходит через его ось и является прямоугольником. Любое сечение, параллельное осевому, также будет являться прямоугольником. Перпендикулярное сечение проходит перпендикулярно оси цилиндра и параллельно его основаниям. Перпендикулярное сечение имеет форму круга. 

Проверь себя

Задание 1. 
Что такое образующая цилиндра?

1. Ось вращения, с помощью которой получен цилиндр.
2. Диаметр оснований цилиндра.
3. Любой перпендикуляр, проведенный от одного основания к другому.
4. Отрезок, соединяющий точки окружности основания. 

Задание 2. 
Площадь боковой поверхности цилиндра равняется 44. Его радиус равен 8. Найдите высоту цилиндра. 

1. 2,75
2. 5,5
3. (2,75 pi)
4. 2

Задание 3. 
Площадь основания цилиндра равна 16. Его высота равна 4. Найдите площадь полной поверхности цилиндра. 

1. 64
2. (64 pi)
3. 32
4. (32 pi)

Задание 4. 
Объем цилиндра равен 28, а его высота равняется 7. Найдите диаметр основания.

1. 4
2. 2
3. 16
4. 8

Ответы: 1. – 4 2. – 1 3. – 2  4. – 1

12(B13). Найти диаметр основания цилиндра, если дана боковая поверхность (вар. 49)

Площадь боковой поверхности цилиндра равна 56π, а высота равна 7. Найдите диаметр основания.

Что представляет из себя боковая поверхность цилиндра? Разрежем его мысленно по образующей. 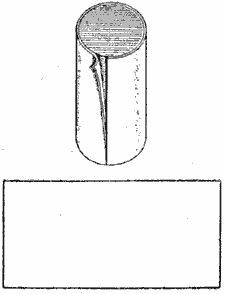При этом получим обыкновенный прямоугольник. Одно из его измерений – высота цилиндра. Второе измерение – длина окружности основания цилиндра. Она равна 2π·R = π·(2R) = π·D. 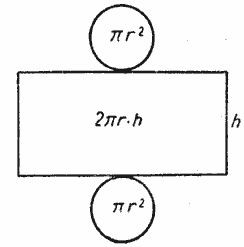На рисунке изображена полная развёртка цилиндра, но нас интересует только прямоугольник. Площадь прямоугольника (боковая поверхность) равна (π·D)·Н. По условию она равна 56π. Получаем (π·D)·Н = 56π. Отсюда D·Н = 56. Учтём теперь, что по условию высота равна 7. D·7 = 56. Отсюда находим диаметр D = 8. Ответ: 8 Можно поступить и так. В формулу боковой поверхности цилиндра S_бок. = 2π·R·H подставить площадь 56π и высоту 7, получим 56π = 2πR·7, 56 = 2R·7, 8 = 2R = D.

Автор: Ольга Себедаш Просмотров: 41586

Комментарии к этой задаче:

Комментарий добавил(а): Артур
Дата: 2014-06-03

А общее формула нахождение диаметра цилиндра? Она имеет лишь такое произведение? Или есть иное?

C помощью нашего Онлайн-калькулятора для расчета объема цилиндра Вы можете быстро и точно рассчитать объем цилиндра. Для того, чтобы вычислить объем цилиндра, сначала выберите формулу, по которой Вы собираетесь произвести расчет. Объем цилиндра (в зависимости от исходных данных) можно вычислить двумя способами: 1. через высоту и радиус основания; 2. через высоту и площадь основания. Затем введите значения исходных данных для расчета (значение высоты цилиндра, значение радиуса основания цилиндра (или значение площади основания цилиндра) и нажмите кнопку “Рассчитать”. Также Вы можете указать точность полученного результата, т.е. количество знаков после запятой, до которого будет округлен рассчитанный объем цилиндра.

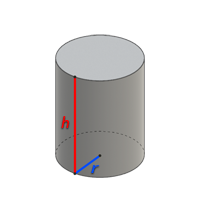
Цилиндр – это геометрическое тело, которое ограничено двумя параллельными поверхностями, пересекающими цилиндрическую поверхность. Цилиндрическая поверхность называется боковой поверхностью цилиндра. Две параллельные поверхности называются основаниями цилиндра.

Объем цилиндра можно вычислить по двум формулам:

1. через высоту цилиндра и радиус основания;
2. через высоту цилиндра и площадь основания.

Свойства

Через диаметр цилиндра можно рассчитать его радиус и периметр основания цилиндра. Радиус будет равен половине диаметра, а периметр – его произведению на число π. r=D/2 P=πD

Зная диаметр и высоту цилиндра, можно узнать площадь, объем, диагональ цилиндра и остальные параметры. Площадь боковой поверхности цилиндра представляет собой площадь прямоугольника, сторонами которого являются периметр основания цилиндра и его высота. Чтобы затем найти площадь полной поверхности цилиндра через диаметр и высоту, нужно к площади боковой поверхности добавить площадь верхнего и нижнего оснований, каждое из которых равно произведению числа π на четверть квадрата диаметра. S_(б.п.)=hP=πDh S_(п.п.)=S_(б.п.)+2S_(осн.)=πDh+(πD^2)/2=πD/2(2h+D) P=πD

Объем цилиндра представляет собой площадь его основания, умноженную на высоту. Чтобы найти объем цилиндра через диаметр и высоту, нужно умножить квадрат диаметра на четверть числа π и на высоту. V=(πD^2 h)/4 P=πD

Диагональ цилиндра находится из прямоугольного треугольника, в котором она является гипотенузой, а катеты представлены высотой и диаметром цилиндра. По теореме Пифагора диагональ цилиндра через высоту и диаметр цилиндра равна квадратному корню из суммы их квадратов. (рис. 25.1) d=√(h^2+D^2 ) P=πD

Чтобы найти радиус сферы вписанной в цилиндр, если его диаметр равен высоте, нужно разделить диаметр цилиндра либо высоту на два, так как радиус вписанной сферы равен радиусу цилиндра. (рис.25.2) r_1=h/2=D/2 P=πD

Радиус сферы, описанной вокруг цилиндра, при соблюдении тех же условий (равенство диаметра цилиндра и его высоты) равен половине диагонали цилиндра.(рис.25.3) R=d/2=√(h^2+D^2 )/2