Формула как найти массу солнца

Как вычислить массу солнца?

Андрей Галиновский

Знаток

(407),
закрыт

10 лет назад

1 Задача! Расстояние от Земли до Солнца 1,496 * 10^11 м. ^ – степень! Период обращения Земли вокруг Солнца = 365,26 суток. Определите массу солнца!
2 Задача! Фобос – спутник планеты Марс. Фобос обращается вокруг Марса по орбите радиусом 9400км. Период его обращения 7 ч 39 мин. НАйдите массу планеты Марс!
Если нет время решать напишите просто формулу к первой и второй задаче!

Простая и надежная методика измерения массы космических тел – как узнать сколько весит Солнце, зная лишь силу притяжения между космическими телами

Как можно измерить вес (точнее, массу) Солнца, если даже реальный размер нашей “домашней звезды” настолько велик, что просто не укладывается в голове? Наверняка тут должен быть какой-то секрет… И подумав так, вы будете правы и не правы одновременно.

С одной стороны, никакого секрета в деле измерения массы любого небесного тела сколько угодно большого размера, конечно же нет. С другой стороны, без определенных хитростей тут, конечно, не обойтись.

Давайте сразу условимся – говоря, что  “нам нужно определить массу Солнца”, мы имеем ввиду “определить количество вещества входящего в состав Солнца”.

Для начала измерим массу Земли

Переформулировав задачу таким образом, мы сразу же получим зацепки ведущие к решению. Первым делом нам нужно определить величину силы притяжения возникающей между любыми двумя массами.

Принцип этого определения следующий:

Представьте себе очень при очень чувствительные равноплечие весы с двумя чашками. В каждой чашке (А и Б) пускай лежит некий груз имеющий совершенно одинаковую массу. Весы в таком случае, будут прибывать в полном равновесии.

Теперь мы берем третье тело (В) масса которого нам также известна, и помещаем его под тело А. Взаимное притяжение между А и В, ожидаемо заставляет чашку весов А опуститься вниз. Для сохранения равновесия нам срочно необходимо добавить к массе Б очень небольшую, но опять же вполне измеримую массу Г.

А вот теперь самое интересное: поскольку сила, с которой вся Земля притягивает тело Г, равна взаимному притяжению между А и В, можно без труда определить массу Земли, которая оказывается равной 6,59 х 10²¹ тонн.

А теперь измерим массу Солнца!

Земля по своей орбите движется примерно так, как если бы невидимая нить соединяла ее с Солнцем. Действительно, гравитационное притяжение подобно натяжению нити, так что Земля все время движется к Солнцу, вместо того чтобы «улететь» по прямой линии, что будет, если эта “нить” вдруг оборвется. Можно сказать, что, двигаясь вокруг Солнца, Земля все время «падает» на него.

Этому “падению” соответствует отклонение ее орбиты от прямой линии, составляющее около 3 мм в секунду. Еще со времен Галилея известно, что на поверхности Земли в первую секунду своего падения всякое тело проходит 4,9 м. Расстояния 3 мм и 4,9 м прямо пропорциональны соответствующим гравитационным ускорениям, т. е. силам, действующим на единичную
массу со стороны Солнца на расстоянии Земли и Земли на ее поверхности.

Отсюда, зная, что гравитационное ускорение прямо пропорционально массе и обратно пропорционально квадрату расстояния от центра тела, можно легко вычислить, что масса Солнца в 329 390 раз больше массы Земли.

Воспользовавшись значением массы Земли, полученным выше, находим, что масса Солнца составляет 2.24 х 10²⁷  тонн. Полностью это немыслимое число можно записать, как 2 240 000 000 000 000 000 000 000 000 тонн.

Теперь уже можно вычислить и среднюю плотность Солнца, т. е. его массу, поделенную на массу воды, занимающей тот же объем.

Поскольку один кубический сантиметр воды весит один грамм, мы просто должны разделить массу Солнца (в граммах) на его объем (в кубических сантиметрах). Получим в результате число 1,42.

Иными словами, в среднем некоторый объем солнечного вещества должен весить приблизительно столько же, сколько ком битумного угля, занимающего такой же объем.

Естественно, “среднее значение” на то и среднее, чтоб представлять некую золотую середину между солнечным ядром (где плотность вещества в 10 раз превышает плотность стали) и веществом солнечной короны (где плотность падает почти до величины космического вакуума). Тем не менее, в общем и целом данная методика расчетов абсолютно верна и может с успехом применяться при расчете массы любого небесного тела – хоть астероида, хоть звезды.

На любое тело действуют две силы или две “скорости” – сила тяготения (маленький объект падает на большой) и, собственно, скорость, с которой этот объект летит “прямо”.

Первая картинка из гугла с какой-то там задачи вполне подходит для пояснения.

Если скорость большая – то тело совершает дугу и улетает. Как делают кометы.

То есть, вот она летела-летела, начала притягиваться, но поскольку летела слишком быстро, не успела упасть, а сделала дугу и улетела дальше.

Если сила тяготения большая – то тело просто падает.

А вот если оно летает по кругу – значит, эти две силы равны между собой. Земля пытается улететь, но её по чуть-чуть притягивает к себе Солнце, постоянно изменяя её траекторию вплоть до замкнутого состояния.

Центростремительная сила вычисляется по формуле F=ma. Где массу Земли мы знаем (вычислили по ходу развития науки), а ускорение – вычисляется из того, что Земля делает один оборот за год.

И, как я уже объяснил выше, эта сила должна быть равна силе тяготения. Ну а тяготение рассчитывается исходя из массы двух тел. И зная массу Земли, расстояние до Солнца, и силу, которая на Землю действует, мы спокойно можем вычислить массу Солнца.

Для расчёта в наше время хватает буквально школьного уровня знаний.

По примерно такой же методике вычисляется и масса любых других объектов – спутников, вращающихся вокруг планеты, других планет, вращающихся вокруг звёзд, самих звёзд, взаимодействующих друг с другом и так далее.

3,1 K

Характеристики планет Солнечной системы были известны еще в средневековье, во времена Кеплера и Галилея. То есть, массу планет приблизительно можно было определить даже простыми методами и инструментами. В современной астрономии есть несколько методов расчета характеристик планет, звезд, скоплений и галактик.

Интересный факт: 99,9% всей массы Солнечной системы сосредоточена в самом Солнце. На все планеты вместе взятые приходится не более 0,01%. При этом из этих 0,01%, в свою очередь, 99% массы приходится на газовые гиганты (в том числе 90% только на Юпитер и Сатурн).

Рассчитываем массу Земли и Луны

Чтобы измерить массу планет солнечной системы, проще всего в первую очередь найти значения для Земли. Как мы помним, ускорение свободного падения определяется по формуле F=mg, где m – масса тела, а F – действующая на него сила.

Параллельно вспоминаем универсальный закон всемирного тяготения Ньютона:

Сопоставив эти две формулы, и зная значение гравитационной постоянной 6,67430(15)·10−11 м³/(кг·с²), можно рассчитать массу Земли. Ускорение свободного падения на Земле мы знаем, 9,8 м/с2, радиус планеты тоже. Подставив все данные на выходе получим приблизительно 5,97 х 10²⁴ кг.

Зная массу Земли, мы легко рассчитает параметры по другим объектам Солнечной системы – Луна, планеты, Солнце и так далее. С Луной вообще все довольно просто. Здесь достаточно учесть, что расстояния от центров тел до центра масс соотносятся обратно их массам. Подставив эти цифры для Земли и ее спутника получим массу Луны 7.36 × 10²² килограмма.

Перейдем теперь к методикам измерения массы планет земной группы – Меркурий, Венера, Марс. После чего рассмотрим газовые гиганты, и в самом конце – экзопланеты, звезды и галактики.

Общие методики определения масс планет

Наиболее классический способ, как узнать массу планет – расчет при помощи формул третьего закона Кеплера. Он гласит, что квадраты периодов обращения планет соотносятся так же, как кубы больших полуосей орбит. Ньютон немного уточнил этот закон, внеся в формулу массы небесных тел. На выходе получилась такая формула –

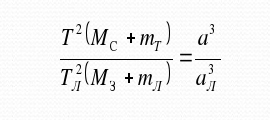
Таким способом можно найти массу всех планет Солнечной системы и самого Солнца.И периоды обращения, и большие полуоси орбит планет Солнечной системы легко измеряются астрономическими методиками, доступными даже без сложных инструментов. А так как массу Земли мы уже рассчитали, можно все цифры подставить в формулу и найти конечный результат.

В отношении же экзопланет и других звезд (но только двойных) в астрономии обычно применяется метод анализа видимых возмущений и колебаний. Он основан на том факте, что все массивные тела “возмущают” орбиты друг друга.

Такими расчетами были открыты планеты Нептун и Плутон, еще до их визуального обнаружения, как говорят “на кончике пера”.

Значения масс планет Солнечной системы

Итак, мы разобрались с общими методиками расчета масс разных небесных тел и посчитали значения для Луны, Земли и Галактики. Давайте теперь составим рейтинг планет нашей системы по их массе.

Возглавляет рейтинг с наибольшей массой планет Солнечной системы – Юпитер, которому не хватило одного порядка чтобы наша система стала двойной. Еще чуть-чуть и у нас могло быть два Солнца, второе вместо Юпитера. Итак, масса этого газового гиганта равняется 1,9 × 10²⁷ кг.

Интересно, что Юпитер – единственная планета нашей системы, центр масс вращения с Солнцем которой расположен вне поверхности звезды. Он отстоит примерно на 7% расстояния между ними от поверхности Солнца.

Вторая по массе планета – Сатурн, его масса 5,7 × 10²⁶ кг. Следующим идет Нептун – 1 × 10²⁶. Четвёртая по массе планета, газовый гигант Уран, масса которого – 8,7 × 10²⁵ кг.

Далее идут планеты земной группы, каменистые тела, в отличие от газовых гигантов с их большим радиусом и относительно малой плотностью.

Самой тяжелой из этой группы является наша планета, ее массу мы уже рассчитали. Далее идет Венера, масса этой планеты равняется 4,9 × 10²⁴ кг. После нее в рейтинге идет Марс, он почти в 10 раз легче – 6,4 × 10²³кг. И замыкает его, как планета самой маленькой массы, Меркурий – 3,3 × 10²³кг. Что интересно, Меркурий даже легче, чем два спутника в Солнечной системе – Ганимед и Каллисто.

Определение масс звезд и галактик

Для того чтобы найти характеристики одинарных звездных систем применяется гравиметрический метод. Его суть в измерении гравитационного красного смещения света звезды. Оно измеряется по формуле ∆V=0,635 M/R, где M и R – масса и радиус звезды, соответственно.

Косвенно можно также вычислить массу звезды по видимому спектру и светимости. Сначала определяется ее класс светимости по диаграмме Герцшпрунга-Рассела, а потом вычисляется зависимость масса/светимость. Такой способ не подходит для белых карликов и нейтронных звезд.

Масса галактик вычисляется в основном по скорости вращения ее звезд (или просто по относительной скорости звезд, если это не спиральная галактика). Все тот же всемирный закон тяготения Ньютона нам гласит, что центробежную силу звезд в галактике можно выразить в формуле:

Только в этот раз в формулу мы подставляем расстояние от Солнца до центра нашей галактики и его массу. Так можно рассчитать массу Млечного Пути, которая равняется 2,2 × 10⁴⁴г.

Не забываем, что эта цифра – это масса галактики без учета звезд, орбиты которых располагаются вне орбиты вращения Солнца. Поэтому для более точных расчетов берутся самые внешние звезды рукавов спиральных галактик.

Для эллиптических галактик способ нахождения массы схож, только там берется зависимость между угловым размером, скоростью движения звезд и общей массой.

From Wikipedia, the free encyclopedia

Solar mass
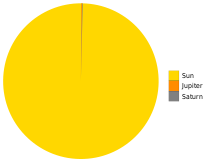
The Sun contains 99.86% of the mass of the Solar System. Bodies lighter than Saturn are not visible at this scale.
General information
Unit system	astronomy
Unit of	mass
Symbol	M☉
In SI base units	(1.98847±0.00007)×1030 kg[1]

The solar mass (M_☉) is a standard unit of mass in astronomy, equal to approximately 2×10³⁰ kg. It is often used to indicate the masses of other stars, as well as stellar clusters, nebulae, galaxies and black holes. It is approximately equal to the mass of the Sun. This equates to about two nonillion (short scale), two quintillion (long scale) kilograms or 2000 quettagrams:

M_☉ = (1.98847±0.00007)×10³⁰ kg

The solar mass is about 333000 times the mass of Earth (M_Earth), or 1047 times the mass of Jupiter (M_J).

History of measurement[edit]

The value of the gravitational constant was first derived from measurements that were made by Henry Cavendish in 1798 with a torsion balance.^[2] The value he obtained differs by only 1% from the modern value, but was not as precise.^[3] The diurnal parallax of the Sun was accurately measured during the transits of Venus in 1761 and 1769,^[4] yielding a value of 9″ (9 arcseconds, compared to the present value of 8.794148″). From the value of the diurnal parallax, one can determine the distance to the Sun from the geometry of Earth.^[5][6]

The first known estimate of the solar mass was by Isaac Newton.^[7] In his work Principia (1687), he estimated that the ratio of the mass of Earth to the Sun was about 1⁄28700. Later he determined that his value was based upon a faulty value for the solar parallax, which he had used to estimate the distance to the Sun. He corrected his estimated ratio to 1⁄169282 in the third edition of the Principia. The current value for the solar parallax is smaller still, yielding an estimated mass ratio of 1⁄332946.^[8]

As a unit of measurement, the solar mass came into use before the AU and the gravitational constant were precisely measured. This is because the relative mass of another planet in the Solar System or the combined mass of two binary stars can be calculated in units of Solar mass directly from the orbital radius and orbital period of the planet or stars using Kepler’s third law.

Calculation[edit]

The mass of the Sun cannot be measured directly, and is instead calculated from other measurable factors, using the equation for the orbital period of a small body orbiting a central mass.^[9] Based on the length of the year, the distance from Earth to the Sun (an astronomical unit or AU), and the gravitational constant (G), the mass of the Sun is given by solving Kepler’s third law:^[10][11]

The value of G is difficult to measure and is only known with limited accuracy (see Cavendish experiment). The value of G times the mass of an object, called the standard gravitational parameter, is known for the Sun and several planets to a much higher accuracy than G alone.^[12] As a result, the solar mass is used as the standard mass in the astronomical system of units.

Variation[edit]

The Sun is losing mass because of fusion reactions occurring within its core, leading to the emission of electromagnetic energy, neutrinos and by the ejection of matter with the solar wind. It is expelling about (2–3)×10⁻¹⁴ M_☉/year.^[13] The mass loss rate will increase when the Sun enters the red giant stage, climbing to (7–9)×10⁻¹⁴ M_☉/year when it reaches the tip of the red-giant branch. This will rise to 10⁻⁶ M_☉/year on the asymptotic giant branch, before peaking at a rate of 10⁻⁵ to 10⁻⁴ M_☉/year as the Sun generates a planetary nebula. By the time the Sun becomes a degenerate white dwarf, it will have lost 46% of its starting mass.^[14]

The mass of the Sun has been decreasing since the time it formed. This occurs through two processes in nearly equal amounts. First, in the Sun’s core, hydrogen is converted into helium through nuclear fusion, in particular the p–p chain, and this reaction converts some mass into energy in the form of gamma ray photons. Most of this energy eventually radiates away from the Sun. Second, high-energy protons and electrons in the atmosphere of the Sun are ejected directly into outer space as the solar wind and coronal mass ejections.^{[citation needed]}

The original mass of the Sun at the time it reached the main sequence remains uncertain.^[15] The early Sun had much higher mass-loss rates than at present, and it may have lost anywhere from 1–7% of its natal mass over the course of its main-sequence lifetime.^[16] The Sun gains a very small amount of mass through the impact of asteroids and comets. However, as the Sun already contains 99.86% of the Solar System’s total mass, these impacts cannot offset the mass lost by radiation and ejection.^{[citation needed]}

[edit]

One solar mass, M_☉, can be converted to related units:^[17]

• 27068510 M_L (Lunar mass)
• 332946 M_Earth (Earth mass)
• 1047.35 M_J (Jupiter mass)
• 1988.55 quettagrams (1.98855 ronnatonnes)

It is also frequently useful in general relativity to express mass in units of length or time.

• M_☉ G / c² ≈ 1.48 km (half the Schwarzschild radius of the Sun)
• M_☉ G / c³ ≈ 4.93 μs

The solar mass parameter (G·M_☉), as listed by the IAU Division I Working Group, has the following estimates:^[18]

• 1.32712442099(10)×10²⁰ m³s⁻² (TCG-compatible)
• 1.32712440041(10)×10²⁰ m³s⁻² (TDB-compatible)

See also[edit]

• Chandrasekhar limit
• Gaussian gravitational constant
• Orders of magnitude (mass)
• Stellar mass
• Sun

References[edit]