Формула как найти периметр основания призмы

На этой странице вы узнаете

• Чем упаковка стикеров похожа на призму?
• Как можно попасть в призму в реальной жизни?
• Как сложить игральные кости из листа бумаги?
• Как найти объем воды в аквариуме? 

Слышали такое выражение «смотреть сквозь призму чего-либо»? Оно значит ситуацию, в которой мы воспринимаем что-либо под влиянием каких-то убеждений или представлений. Замысловато, конечно… Возможно, потому что и сама призма — непростое понятие. Давайте разберемся с ней с точки зрения математики.

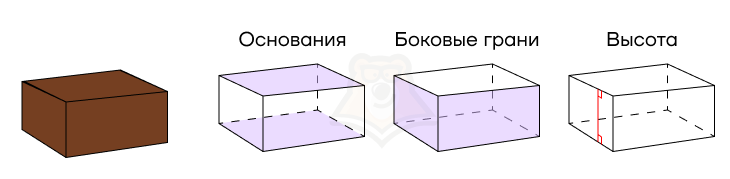
Определение призмы

Многие из нас пользуются стикерами. Для записи своих дел, для закладок, для пометок при ведении конспектов. Даже если мы ими не пользуемся, то наверняка видели их в магазинах или у родственников и друзей. 

Один такой стикер можно принять за плоскость. Теперь вспомним, как выглядит упаковка с ними. Много-много стикеров накладываются друг на друга и получается небольшая объемная фигура, сверху и снизу которой лежат два абсолютно одинаковых листа. При этом сразу заметим, что нижний и верхний стикеры будут параллельны друг другу. 

На самом деле, упаковка со стикерами является не чем иным, как призмой! 

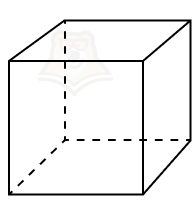
Призма — это многогранник, в котором две грани являются равными многоугольниками и лежат в параллельных плоскостях, а все остальные — параллелограммами. 

Определение может показаться немного запутанным, но в нем нет ничего страшного. Разберемся, поближе взглянув на составные призмы. 

Строение призмы

Представим себе обычную коробку. Ее дно и крышка равны между собой и лежат в параллельных плоскостях. Это и есть равные многоугольники. Также их называют основаниями призмы. 

Посмотрим на стенки коробки. Они являются параллелограммами, просто с прямыми углами. Подробнее про параллелограммы можно прочитать в статье «Параллелограмм». Эти параллелограммы называются боковыми гранями призмы. 

Возьмем линейку и измерим расстояние между основаниями призмы. Для этого из любой точки одного основания проведем перпендикуляр к другому. 

Подробнее про расстояния между плоскостями можно узнать в статьях «Углы в пространстве» и «Расстояния между фигурами». 

Может возникнуть вопрос, что мы сейчас нашли? Мы нашли высоту призмы. 

Высота призмы — перпендикуляр, опущенный из любой точки одного основания на другое основание призмы. 

В задачах намного удобнее опускать перпендикуляр не из произвольной точки, а из вершины призмы. 

Рассмотрим элементы призмы. 

Ребро — это линия пересечения двух плоскостей. 

Представим, что вместо картонных стенок в нашей коробке ткань, которую нам нужно натянуть на каркас так, чтобы коробка не изменилась. В этом случае все прямые этого каркаса и будут ребрами.

Ребра бывают двух видов: 

• ребра оснований,
• боковые ребра. 

Отличить их также легко: ребра основания являются стороной многоугольника, который в нем лежит, в то время как боковые ребра не принадлежат основаниям. 

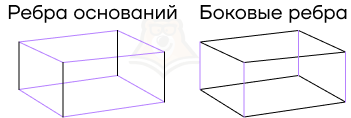
У боковых ребер есть одно очень важное свойство: они равны между собой и параллельны. 

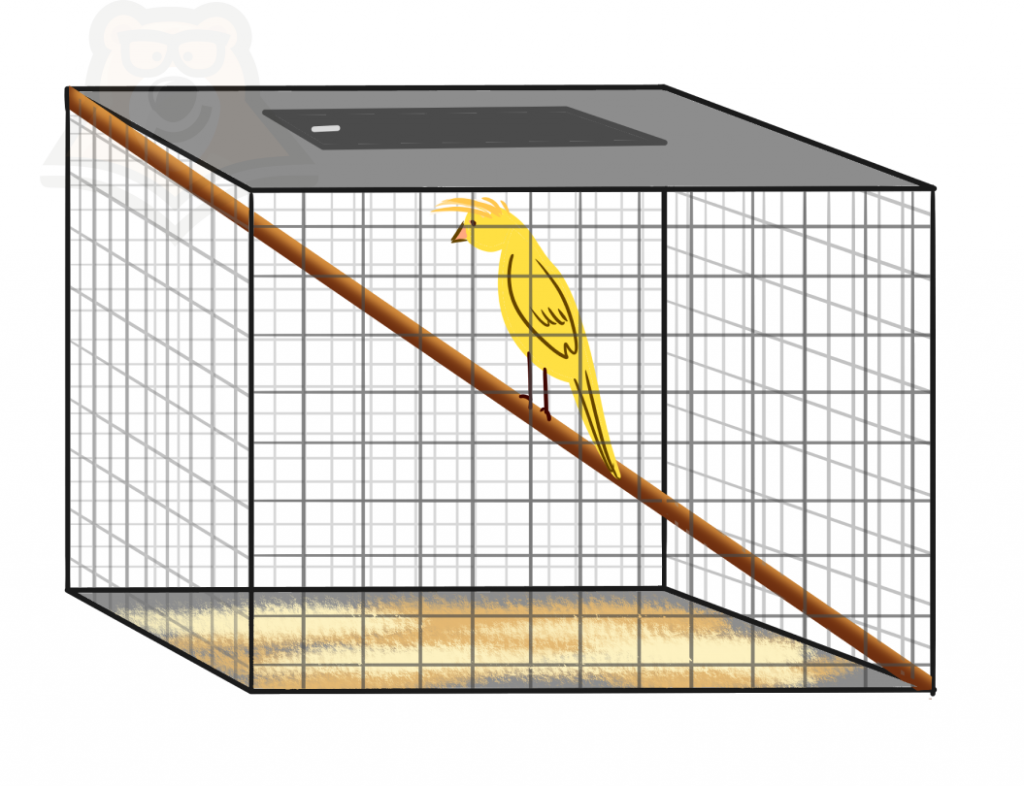
Диагональ призмы — отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. 

Например, мы можем взять клетку попугая и от угла до угла сделать ему жердочку, чтобы птичке было весело жить. Эта жердочка и будет диагональю призмы. 

Виды призм

Вернемся к рассуждениям о том, чем упаковка стикеров похожа на призму. Например, куб и параллелепипед будут отличаться. А если в основании призмы будет лежать треугольник или шестиугольник? Или двадцатиугольник? Разделим призмы на несколько видов.

Мы рассмотрим две классификации. 

В первом случае будем рассматривать призмы по фигурам, которые лежат в основании. В многоугольнике может быть множество сторон, а значит, и в основании призмы может быть треугольник, четырехугольник, шестиугольник, десятиугольник и так далее. 

В зависимости от фигуры в основании призмы могут называться по-разному. Вот три основных, которые чаще всего встречаются при решении заданий:

• треугольная призма,

• четырехугольная призма,

• шестиугольная призма. 

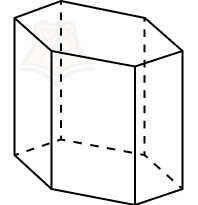
Аналогичным образом можно дать название любой призме, например, десятиугольная призма или стоугольная призма. 

В определении призмы сказано, что в боковых гранях лежат параллелограммы. До этого мы чертили только прямоугольники, но в боковых гранях могут лежать не только они. 

С этим связана вторая классификация призм. По этому признаку призмы делятся всего на два вида:

• прямые,
• наклонные. 

Разберемся в них чуть подробнее. 

Прямая призма — призма, боковые ребра которой перпендикулярны основаниям. 

В этом случае боковые ребра и ребра оснований действительно образовывают прямоугольник. 

Наклонная призма — призма, боковые ребра которой находятся под углом к основаниям. 

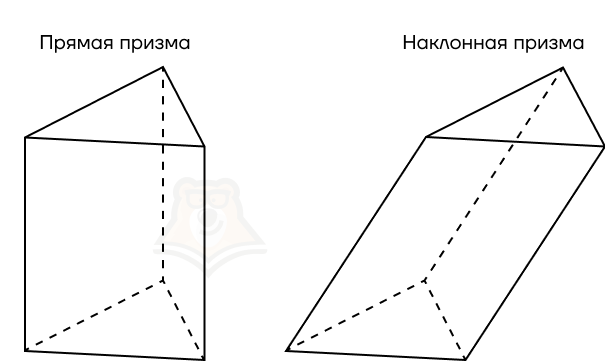
Где мы можем найти прямые и наклонные призмы? Оказывается, в архитектуре. Обычный жилой дом типовой застройки будет прямой призмой. А вот примером наклонной призмы может служить комплекс зданий “Ворота Европы” в Мадриде. 

Чуть подробнее остановимся на прямых призмах. Они встречаются достаточно часто и обладают несколькими важными свойствами. 

Посмотрите на свою комнату. Если по плану квартиры она будет многоугольником, то вы как бы сидите в призме. Теперь ответим на вопрос: как найти высоту комнаты? 

Простой ответ: померить по стене. А если посмотреть на угол, то можно заметить, что ребро призмы совпадает с высотой. Таким образом, мы получаем первое свойство прямых призм. 

Свойство 1. Высота прямой призмы совпадает с её боковым ребром. 

Посмотрим на стены комнаты, на их форму. Они все являются прямоугольниками, верно? 

Свойство 2. Все боковые грани прямой призмы — прямоугольники. 

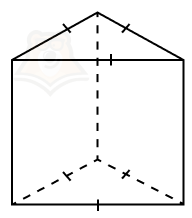
Если мы в основании прямой призмы разместим правильный многоугольник, у нас получится правильная призма.

Правильная призма — прямая призма, в основании которой лежит правильный многоугольник. 

Например,  в правильной треугольной призме будет лежать равносторонний треугольник, а в правильной шестиугольной призме — правильный шестиугольник. 

Определение параллелепипеда

Еще одной разновидностью прямоугольной призмы является параллелепипед. 

Параллелепипед — это четырехугольная призма, все грани которой являются параллелограммами. 

Параллелепипеды встречаются повсюду: коробки, мебель, комнаты, здания, склады, магазины. Поэтому изучить их не составит труда. 

Свойство параллелепипеда, видимое невооруженным глазом: противоположные грани параллелепипеда равны. Как пример, вспомним ту же комнату: потолок и пол равны, так же как и стены, находящиеся напротив друг друга. 

Нельзя не упомянуть про одно очень важное свойство параллелепипеда: 

• Все его диагонали пересекаются в одной точке и этой точкой делятся пополам. Это свойство справедливо для всех видов параллелепипеда. 

Какие бывают параллелепипеды? 

Параллелепипеды также бывают прямыми и наклонными. В этих случаях все определения такие же, как и для всех остальных призм. 

Прямой параллелепипед

Рассмотрим несколько интересных свойств прямого параллелепипеда. 

1 свойство. Боковые ребра прямого параллелепипеда перпендикулярны основаниям. 

2 свойство. Высота прямоугольного параллелепипеда равна длине его бокового ребра. 

3 свойство. Боковые грани, которые лежат напротив друг друга, равны между собой и являются прямоугольниками. 

Прямые параллелепипеды можно разделить еще на два вида:

• Прямой параллелепипед: в основании лежит параллелограмм;

• Прямоугольный параллелепипед: в основании лежит прямоугольник. 

Рассмотрим свойства прямоугольного параллелепипеда. 

1 свойство. Все грани прямоугольного параллелепипеда являются прямоугольниками. 

2 свойство. Все углы в прямоугольном параллелепипеде, образованные двумя гранями, равны 90°. 

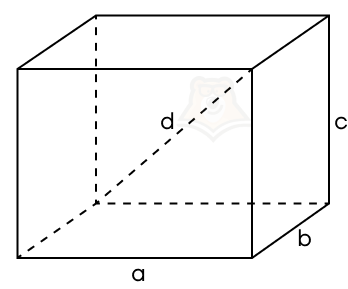
3 свойство. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин его ширины, длины и высоты. 

Таким образом, мы получаем важную формулу для параллелепипеда. 

d² = a² + b² + c²

Пример 1. Дан прямоугольный параллелепипед. Два ребра, выходящие из одной его вершины, равны (sqrt{35}) и (sqrt{46}). Диагональ параллелепипеда равна 15. Найдите третье ребро параллелепипеда. 

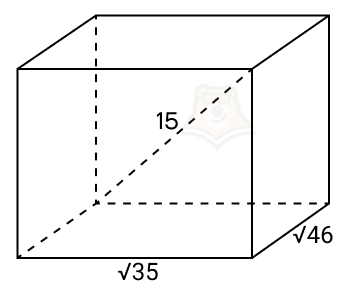
Решение. Пусть третье ребро параллелепипеда равняется х. Получаем уравнение:

(15^2 = (sqrt{35})^2 + (sqrt{46})^2 + x^2)
225 = 35 + 46 + x²
x² = 144
x = 12

Ответ: 12. 

У прямоугольного параллелепипеда существует еще несколько видов. Прямоугольные параллелепипеды делятся на:

• Произвольный прямоугольный параллелепипед. В основании может лежать прямоугольник. 

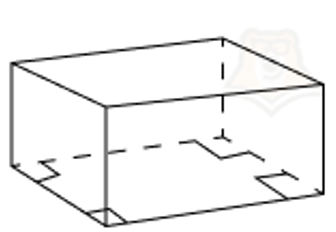
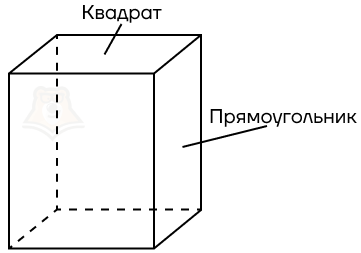
• Правильный прямоугольный параллелепипед. В основании лежит правильный четырехугольник, то есть квадрат. 
  При этом боковые ребра не равны ребрам основания. Следовательно, в основаниях будут лежать квадраты, а в боковых гранях прямоугольники. 

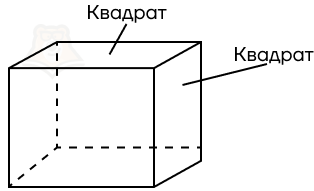
• Куб. В основании лежит квадрат, а боковые ребра равны ребрам основания. 
  В кубе все ребра равны, а все его грани будут квадратом. 

Таким образом, мы рассмотрели все виды параллелепипеда. 

Формулы для призмы

Однако ни одна задача не может быть решена без формул. Поэтому необходимо рассмотреть несколько основных формул, которые могут встретиться не только в задачах, но и в жизни. 

Немного вспомним моделирование, а именно развертку кубика. Мы знаем, что из листа бумаги без труда можно сложить кубик, если правильно его вычертить. 

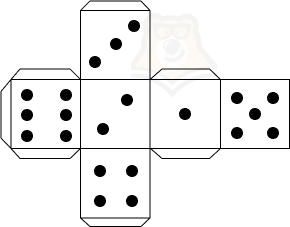
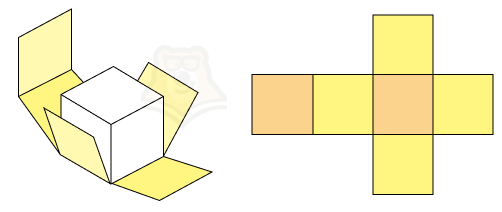
На рисунке оранжевым показаны основания, а желтым боковые грани нашего будущего кубика. А теперь представим, что нам нужно найти площадь боковой поверхности. Как это сделать?

Нужно найти площади желтых квадратиков и сложить их. 

Площадь боковой поверхности призмы — сумма площадей всех боковых ее граней. 

Единой формулы тут нет, поскольку призмы могут очень сильно отличаться друг от друга. В произвольных призмах придется считать площадь каждой боковой грани, а уже после их складывать. 

Но есть один фокус! Правда, он работает только для прямой призмы. Если по условию дана прямая призма, то можно воспользоваться формулой 

S_бок. = P * h

В этой формуле Р — периметр основания, h — высота призмы, которая совпадает с высотой боковой грани. 

Пример 1. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равняется 2, а высота 10. 

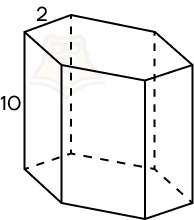
Решение. 

Шаг 1. Поскольку правильная призма по определению прямая, мы можем воспользоваться формулой S = Ph. 

Шаг 2. В основании правильной призмы лежит правильный шестиугольник, следовательно, периметр основания будет равен 6 * 2 = 12. 

Шаг 3. Осталось найти только площадь боковой поверхности. Подставляем данные в формулу и получаем: S = 12 * 10 = 120. 

Ответ: 120. 

Пример 2. Дана прямая треугольная призма, в основании которой лежит прямоугольный треугольник с катетами 12 и 5. Высота призмы равна 13. Найдите площадь ее боковой поверхности. 

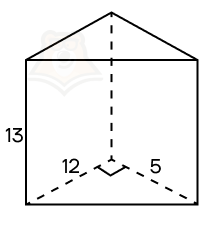
Решение. 

Шаг 1. Поскольку призма прямая, можно воспользоваться формулой S = Ph. 

Шаг 2. Найдем периметр основания. Для этого необходимо найти гипотенузу треугольника. Воспользуемся теоремой Пифагора: (sqrt{12^2 + 5^2} = sqrt{144 + 25} = sqrt{169} = 13). 

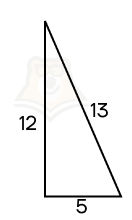
Шаг 3. Найдем периметр основания: P = 12 + 5 + 13 = 30. 

Шаг 4. Осталось найти только площадь боковой поверхности. Подставляем данные в формулу и получаем: S = 30 * 13 = 390. 

Ответ: 390. 

Мы научились находить площадь боковой поверхности. А как найти всю площадь призмы? Вспомним нашу развертку с кубиком. Чтобы найти всю площадь кубика, нужно найти площадь всех квадратов, из которых он состоит. То есть и площадь боковой поверхности, и площадь оснований. 

Площадь полной поверхности призмы — сумма площадей всех граней. 

Следовательно, нам нужно сложить площади всех боковых граней и дважды площадь основания. Получаем следующую формулу. 

S = S_бок + 2S_осн

Вспомним обычный хлеб, черный или белый. Его форма очень приближена к параллелепипеду. Тогда его корочка будет площадью полной поверхности параллелепипеда. А все что внутри, то есть мякиш, можно принять за объем. 

Пример 3. Дана прямая призма, в основании которой лежит ромб с диагоналями 12 и 16. Боковое ребро призмы равно 25. Найдите площадь поверхности призмы. 

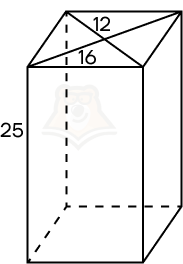
Решение. 

Шаг 1. Найдем площадь основания. Площадь ромба можно найти по формуле (frac{1}{2} * D_1 * D_2). Следовательно, площадь ромба равна (frac{1}{2} * 12 * 16 = 96). 

Шаг 2. Заметим, что диагонали ромба образуют четыре равных прямоугольных треугольника. Следовательно, чтобы найти сторону ромба, достаточно рассмотреть прямоугольный треугольник с катетами 6 и 8. По теореме Пифагора сторона ромба будет равна (sqrt{6^2 + 8^2} = sqrt{36 + 64} = sqrt{100} = 10).

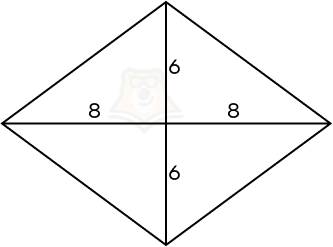
Шаг 3. Периметр ромба будет равен 4 * 10 = 40. Тогда площадь боковой поверхности равна 40 * 25 = 1000. 

Шаг 4. Площадь полной поверхности будет равняться 1000 + 2 * 96 = 1000 + 192 = 1192.

Ответ: 1192

Пример 4. Площадь поверхности правильной четырехугольной призмы равняется 1980. Сторона основания равна 5. Найдите боковое ребро этой призмы. 

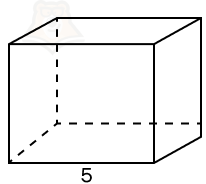
Решение. 

Шаг 1. Воспользуемся формулой S = S_бок + 2S_осн. Площадь основания будет равняться площади квадрата, то есть 5 * 5 = 25. 

Шаг 2. Подставим известные величины в формулу: 

1980 = S_бок + 2 * 25
S_бок = 1930

Шаг 3. Площадь боковой поверхности равна произведению периметра основания на высоту призмы. Периметр равен 5 * 4 = 20. Тогда получаем уравнение:

20h = 1930
h = 96,5

Шаг 4. Поскольку по условию дана правильная призма, то высота совпадает с боковым ребром. Следовательно, боковое ребро равняется 96,5.

Ответ: 96,5. 

Теперь рассмотрим, как найти объем призмы. Допустим, мы налили в прямоугольный аквариум немного воды. Как определить, сколько воды мы налили?

Для этого достаточно воспользоваться формулой объема призмы. 

V = S_осн. * h

Эта формула общая, однако для каждой призмы она может принять свой вид в зависимости от того, какую формулу нужно использовать для поиска площади основания или высоты. 

Например, чтобы найти объем воды в аквариуме, необходимо длину умножить на ширину и на высоту, а значит формула принимает вид V = abh. 

Пример 5. Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 12 и 15. Боковое ребро призмы равно 4. Найдите объем этой призмы. 

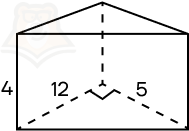
Решение. 

Шаг 1. Для начала найдем площадь основания. В этом случае мы можем воспользоваться формулой (frac{1}{2}ab). Площадь равна (frac{1}{2} * 12 * 15 = 90).

Шаг 2. Воспользуемся формулой объема призмы и подставим известные величины: 

V = 90 * 4 = 360.

Ответ: 360. 

Пример 6. Дан сосуд, в основании которого лежит правильный треугольник. В этот сосуд налили 3000 см³ воды. Высота жидкости оказалась равной 10 см. После этого в сосуд опустили шарик и высота изменилась с 10 см на 14 см. Найдите объем шарика. 

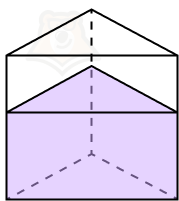
Решение. Немного вспомним физику, а именно тот факт, что объем вытесненной жидкости равен объему тела. Значит, чтобы найти объем шарика, необходимо найти насколько изменился объем воды. 

Шаг 1. Найдем площадь основания сосуда. Для этого немного преобразуем формулу объема: 
(S = frac{V}{h})
Тогда:
(S = frac{3000}{10} = 300)

Шаг 2. А теперь найдем объем после того, как в воду погрузили шарик. Он будет равен 300 * 14 = 4200. 

Шаг 3. Объем вытесненной жидкости равен 4200 — 3000 = 1200.

Ответ: 1200. 

Мы рассмотрели основные формулы, которые применяются для решения задач. Стоит заметить, что они универсальны, и в каждой задаче их рационально преобразовывать под ситуацию. 

Фактчек 

• Призма — это многогранник, в котором две грани являются равными многоугольниками и лежат в параллельных плоскостях, а все остальные — параллелограммами. Равные многоугольники называются основаниями призмы, а остальные стороны — боковыми гранями. В призме есть ребра — линии пересечения двух ее граней. Ребра как бы образуют каркас призмы. 
• Призмы можно разделить на несколько видов по тому, какая фигура лежит в основании: треугольник, четырехугольник, шестиугольник или любой другой многоугольник. Призмы бывают прямые и наклонные. В прямых призмах боковые ребра перпендикулярны основанию, а в наклонных — нет. Правильная призма — прямая призма, в основании которой лежит правильный многоугольник. 
• Параллелепипед — это четырехугольная призма, все грани которой являются параллелограммами. Параллелепипеды бывают наклонными и прямыми. Прямые параллелепипеды включают в себя прямоугольные параллелепипеды, которые, в свою очередь, делятся на произвольные, правильные и кубы. 
• В призме можно найти площадь боковой поверхности, площадь полной поверхности и объем. Для каждого из этих случаев необходимо пользоваться формулами. 

Проверь себя

Задание 1.
Что такое диагональ призмы?

1. Отрезок, соединяющий две соседние вершины в призме.
2. Отрезок, соединяющий противоположные углы в боковой грани призмы.
3. Отрезок, соединяющий противоположные углы в основании призмы.
4. Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.  

Задание 2.
Что такое прямая призма?

1. Призма, боковые ребра которой перпендикулярны основаниям.
2. Призма, боковые ребра которой расположены под острым углом относительно основания.
3. Призма, боковые ребра которой расположены под тупым углом относительно основания.
4. Призма, в основании которой лежит прямоугольник.

Задание 3.
Как найти высоту прямой призмы?

1. Высоту нужно найти с помощью оснований.
2. Высота совпадает с боковым ребром.
3. Необходимо найти расстояние между двумя вершинами, не принадлежащими одной грани.
4. В прямой призме невозможно найти высоту. 

Задание 4.
Какая фигура лежит в основании прямоугольного параллелепипеда?

1. Параллелограмм с острыми углами.
2. Ромб с острыми углами.
3. Трапеция.
4. Прямоугольник. 

Задание 5. 
Как найти площадь полной поверхности призмы?

1. Нужно найти сумму площадей всех боковых граней.
2. Нужно сложить площадь боковой поверхности и площадь основания.
3. Нужно сложить площадь боковой поверхности и удвоенную площадь основания.
4. Нужно сложить площади оснований. 

Ответы: 1. — 4 2. — 1 3. — 2 4. — 4 5. — 3

You can see prisms in both math class and throughout your everyday life. A brick is a rectangular prism. A carton of orange juice is a type of prism. A tissue box is a rectangular prism. Barns are a type of pentagonal prism. The pentagon is a pentagonal prism. A fish tank is a rectangular prism. This list goes on and on.

Prisms by definition are solid objects with identical end shapes, identical cross sections and flat side faces (no curves). And while most math problems and real world examples regarding prism calculations have to do with a volume formula or a surface area formula, there’s one calculation that you need to understand first before you can do that: ​the perimeter of a prism​.

What Is a Prism?

The general definition of a prism is a 3-dimensional solid shape that has the following characteristics:

The name of the prism comes from the shape of the two ends, which are known as the bases. This can be any shape (besides curves or circles). For example, a prism with triangular bases is called a triangular prism. A prism with rectangular bases is called a rectangular prism. This list goes on.

Looking at the characteristics of prisms, this eliminates spheres, cylinders and cones as prisms because they have curved faces. This also eliminates pyramids because they don’t have identical base shapes or identical cross sections throughout.

Perimeter of Prism

When talking about the perimeter of the prism, you’re actually referring to the perimeter of the base shape. The perimeter of the base of a prism is the same as the perimeter along any cross section of the prism since all cross sections are the same along the length of the prism.

Perimeter measures the sum of the lengths of any polygon. So for each prism type, you’d find the sum of the lengths of whatever shape is the base, and that would be the perimeter of the prism.

The formula for finding the perimeter of a triangular prism, for example, would be the sum of the three lengths of the triangle that makes up the base, or:

text{Perimeter of triangle } = a + b + c

where ​a​, ​b​ and ​c​ are the three lengths of the triangle.

This would be the perimeter of a rectangular prism formula:

text{ Perimeter of rectangle } = 2l + 2w

where ​l​ is the length of the rectangle and ​w​ is the width.

Apply standard perimeter calculations to the base shape of the prism, and that gives you the perimeter.

Why Would You Need to Calculate the Perimeter of a Prism?

Finding the perimeter of a prism doesn’t seem too complex once you understand what’s being asked. However, the perimeter is an important calculation that factors into surface area and volume formulas for some prisms.

For example, this is the formula for finding the surface area of a right prism (a right prism has identical bases and sides that are all rectangular):

text{Surface Area } = 2b + ph

where ​b​ is equal to area of the base, p is equal to the perimeter of the base and ​h​ is equal to the height of the prism. You can see that perimeter essential for finding the surface area.

Example Problem: Perimeter of a Rectangular Prism

Let’s say you’re given a problem with a right rectangular prism and you’re asked to find the perimeter. You’re given the following values:

Length = 75 cm

Width = 10 cm

Height = 5 cm

To find the perimeter, use the formula for finding the perimeter of a rectangular prism since the name tells you the base is a rectangle:

begin{aligned} text{Perimeter } &= 2l + 2w \ &= 2(75 text{ cm}) + 2(10 text{ cm} ) \ &= 150 text{ cm} + 20 text{ cm} \ &= 170 text{ cm} end{aligned}

You can then go on to find the surface area because you’re given the height, you have the perimeter of the base and it’s given that this prism is a ​right​ prism.

The area of the base is equal to length × width (as it always is for a rectangle), which is:

begin{aligned} text{ Area of base } &= 75 text{ cm} × 10 text{ cm} \ &= 750 text{ cm}^2 end{aligned}

Now you have all the values for a surface area calculation:

begin{aligned} text{ Surface Area } &= 2b + ph \ &= 2(750 text{ cm}^2) + 170 text{ cm}(5 text{ cm}) \ &= 1500 text{ cm}^2 + 850 text{ cm}^2 \ &= 2350 text{ cm}^2 end{aligned}

Вы можете увидеть призмы как на уроке математики, так и на протяжении всей вашей повседневной жизни. Кирпич – это прямоугольная призма. Упаковка апельсинового сока – это тип призмы. Коробка из ткани представляет собой прямоугольную призму. Амбары представляют собой тип пятиугольной призмы. Пентагон – это пятиугольная призма. Аквариум представляет собой прямоугольную призму. Этот список можно продолжать и продолжать.

Призмы по определению – это сплошные объекты с одинаковыми концевыми формами, одинаковыми сечениями и плоскими боковыми гранями (без кривых) И хотя большинство математических задач и примеров из реальной жизни, касающихся вычислений призмы, связаны с формулой объема или формулой площади поверхности, прежде чем вы сможете это сделать, вам нужно сначала понять один расчет: периметр призмы.

Что такое призма?

Общее определение призмы – это трехмерная сплошная форма, которая имеет следующие характеристики:

• Это многогранник (то есть это сплошная фигура).
• Поперечное сечение объекта является одинаковым по всей длине объекта.
• Это параллелограмм (четырехсторонняя форма, в которой противоположные стороны параллельны друг другу).
• Грани объекта плоские (без изогнутых граней).
• Две концевые формы идентичны.

Название призмы происходит от формы двух концов, которые известны как основания. Это может быть любая форма (кроме кривых или кругов). Например, призма с треугольными основаниями называется треугольной призмой. Призма с прямоугольными основаниями называется прямоугольной призмой. Этот список можно продолжить.

Рассматривая характеристики призм, это исключает сферы, цилиндры и конусы как призмы, потому что они имеют изогнутые грани. Это также устраняет пирамиды, потому что они не имеют одинаковых основных форм или идентичных поперечных сечений повсюду.

Периметр призмы

Говоря о периметре призмы, вы на самом деле имеете в виду периметр базовой формы. Периметр основания призмы такой же, как периметр вдоль любого поперечного сечения призмы, поскольку все поперечные сечения одинаковы по всей длине призмы.

Периметр измеряет сумму длин любого многоугольника. Таким образом, для каждого типа призмы вы найдете сумму длин любой формы, являющейся основанием, и это будет периметр призмы.

Например, формула для нахождения периметра треугольной призмы будет суммой трех длин треугольника, составляющего основание, или:

Периметр треугольника = a + b + c, где a , b и c – три длины треугольника.

Это будет периметр формулы прямоугольной призмы:

Периметр прямоугольника: 2l + 2w, где l – длина прямоугольника, а w – ширина.

Примените стандартные расчеты периметра к базовой форме призмы, и это даст вам периметр.

Зачем вам нужно рассчитывать периметр призмы?

Поиск периметра призмы не кажется слишком сложным, если вы понимаете, о чем идет речь. Однако периметр является важным расчетом, который учитывает формулы площади и объема поверхности для некоторых призм.

Например, это формула для определения площади поверхности правой призмы (правая призма имеет идентичные основания и стороны, которые все прямоугольные):

Площадь поверхности = 2b + ph

где b равно площади основания, p равно периметру основания, а h равно высоте призмы. Вы можете видеть этот периметр, необходимый для определения площади поверхности.

Пример задачи: периметр прямоугольной призмы

Допустим, у вас есть проблема с правильной прямоугольной призмой, и вас попросили найти периметр. Вам даны следующие значения:

Длина = 75 см

Ширина = 10 см

Высота = 5 см

Чтобы найти периметр, используйте формулу для нахождения периметра прямоугольной призмы, поскольку имя говорит о том, что основание представляет собой прямоугольник:

Периметр = 2l + 2w = 2 (75 см) + 2 (10 см) = 150 см + 20 см = 170 см

Затем вы можете продолжить, чтобы найти площадь поверхности, потому что у вас есть высота, у вас есть периметр основания, и это считается, что эта призма является правой призмой.

Площадь основания равна длине × ширине (как всегда для прямоугольника), которая равна:

Площадь основания = 75 см × 10 см = 750 см ²

Теперь у вас есть все значения для расчета площади поверхности:

Площадь поверхности = 2b + ph = 2 (750 см ²) + 170 см (5 см) = 1500 см ² + 850 см = 2350 см ²

Как найти периметр призмы 🚩 периметр призмы формула 🚩 Математика

Опыт отслеживания политических настроений активной части общества через социальные сети уже имеется на Западе. Так, в США в Twitter ведется сервис микроблогов, сравнивающий количество положительных и отрицательных отзывов о том или ином участнике предвыборной компании с общим количеством опубликованных записей. Каждую неделю анализу подвергается порядка двух миллионов записей о Бараке Обаме или Митте Ромни.

Разработчиками системы, подобной западной, – терминала «Призма» является компания «Медиология». Она утверждает, что возможности разработки достаточно высоки – в режиме реального времени можно обрабатывать информацию, поступающую одновременно от 60 миллионов источников. «Призма» способна отслеживать динамику изменения во времени количества положительных или отрицательных отзывов на то или иное событие, учитывая при этом искусственные накрутки, возникающие в результате атак ботов.

Темы, выбираемые для статистических выборок, настраиваются в ручном режиме. В информации, просочившейся из Управления внутренней политики администрации Президента, утверждается, что терминал, установленный там, позволяет отслеживать ход дискуссий в социальных сетях и блогах на LiveJournal, Twitter, YouTube. Источник в администрации Президента, который Forbes называет надежным, утверждает, что к наблюдению за блогами относятся очень серьезно, терминал установлен непосредственно в кабинете руководителя Управления Вячеслава Володина.

На сайте разработчиков утверждается, что с помощью терминала «Призма» возможно производить мониторинг активности пользователей и определять тот градус соцмедиа активности, который может привести к росту политической и социальной напряженности. Система отслеживает увеличение протестных и экстремистских настроений, дискуссий об увеличении уровня цен, проблем ЖКХ, обсуждения вопросов, связанных с зарплатами и пенсиями, коррупцией, уровнем медицинского обслуживания и др.

Этот интерес властей к тому, что волнует интернет-пользователей, которых с каждым годом становится все больше, конечно, радует. Остается только открытым вопрос, насколько они смогут правильно воспользоваться получаемой информацией, и насколько власть будет готова решать те проблемы, которые ставит перед ней часть населения страны, пользующаяся социальными сетями.

www.kakprosto.ru

Треугольная призма все формулы и примеры задач

Треугольная призма — это трехмерное тело, образованное соединением прямоугольников и треугольников. В этом уроке вы узнаете, как найти размер внутри (объем) и снаружи (площадь поверхности) треугольной призмы.

Определение

Треугольная призма — это пятигранник, образованный двумя параллельными плоскостями, в которых расположены два треугольника, образующих две грани призмы, и оставшиеся три грани — параллелограммы, образованные со-сторонами треугольников.

Элементы треугольной призмы

Треугольники ABC и A₁B₁C₁ являются основаниями призмы.

Четырехугольники A₁B₁BA, B₁BCC₁ и A₁C₁CA являются боковыми гранями призмы.

Стороны граней являются ребрами призмы (A₁B₁, A₁C₁, C₁B₁, AA₁, CC₁, BB₁, AB, BC, AC), всего у треугольной призмы 9 граней.

Высотой призмы называется отрезок перпендикуляра, который соединяет две грани призмы (на рисунке это h).

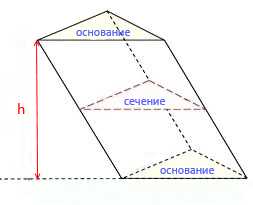
Диагональю призмы называется отрезок, который имеет концы в двух вершинах призмы, не принадлежащих одной грани. У треугольной призмы такой диагонали провести нельзя.

Площадь основания — это площадь треугольной грани призмы.

Площадь боковой поверхности призмы — это сумма площадей четырехугольных граней призмы.

Виды треугольных призм

Треугольная призма бывает двух видов: прямая и наклонная.

У прямой призмы боковые грани прямоугольники, а у наклонной боковые грани — параллелограммы (см. рис.)

Прямая треугольная призма

Призма, боковые ребра которой перпендикулярны плоскостям оснований, называется прямой.

Наклонная треугольная призма

Призма, боковые ребра которой являются наклонными к плоскостям оснований, называется наклонной.

Основные формулы для расчета треугольной призмы

Объем треугольной призмы

Чтобы найти объем треугольной призмы, надо площадь ее основания умножить на высоту призмы.

 Объем призмы = площадь основания х высота

или

V=S_осн ^. h

Площадь боковой поверхности призмы

Чтобы найти площадь боковой поверхности треугольной призмы, надо периметр ее основания умножить на высоту.

Площадь боковой поверхности треугольной призмы = периметр основания х высота

или

S_бок=P_осн^.h 

Площадь полной поверхности призмы

Чтобы найти площадь полной поверхности призмы, надо сложить ее площади оснований и площадь боковой поверхности.

так как S_бок=P_осн^.h, то получим:

S_{полн.пов.}=P_осн^.h+2S_осн

Правильная призма — прямая призма, основанием которой является правильный многоугольник.

Свойства призмы:

Верхнее и нижнее основания призмы – это равные многоугольники.

Боковые грани призмы имеют вид параллелограмма.
Боковые ребра призмы параллельные и равны.

Совет: при расчете треугольной призмы вы должны обратить внимание на используемые единицы. Например, если площадь основания указана в см², то высота должна быть выражена в сантиметрах, а объем — в см³ . Если площадь основания в мм², то высота должна быть выражена в мм, а объем в мм³ и т. д.

Пример призмы

В этом примере:
— ABC и DEF составляют треугольные основания призмы
— ABED, BCFE и ACFD являются прямоугольными боковыми гранями
— Боковые края DA, EB и FC соответствуют высоте призмы.
— Точки A, B, C, D, E, F являются вершинами призмы.

Задачи на расчет треугольной призмы

Задача 1. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Решение: Объем прямой призмы равен V = Sh, где S — площадь основания, а h — боковое ребро. Площадь основания в данном случае это площадь прямоугольного треугольника (его площадь равна половине площади прямоугольника со сторонами 6 и 8). Таким образом, объём равен:

V = 1/2  · 6 · 8 · 5 = 120.

Задача 2.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.

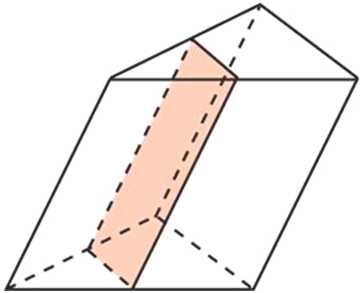
Решение: 

Объём призмы равен произведению площади основания на высоту: V = S_осн ·h.

Треугольник, лежащий в основании исходной призмы подобен треугольнику, лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию (линейные размеры большего треугольника в два раза больше линейных размеров меньшего). Известно, что площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть S

2 = S₁k² = S₁2² = 4S₁.

Площадь основания всей призмы больше площади основания отсечённой призмы в 4 раза. Высоты обеих призм одинаковы, поэтому объем всей призмы в 4 раза больше объема отсечённой призмы.

Таким образом, искомый объём равен 20.

novstudent.ru

Основанием прямой треугольной призмы

Для вас ещё несколько несложных задачек на решение призмы. Рассмотрим прямую призму с прямоугольным треугольником в основании. Ставится вопрос о нахождении объёма или площади поверхности. Формула объёма призмы:

Формула площади поверхности призмы (общая):

*У прямой призмы боковая поверхность состоит из прямоугольников и равна она произведению периметра основания и высоты призмы. Необходимо помнить формулу площади треугольника. В данном случае, имеем прямоугольный треугольник – его площадь равна половине произведения катетов. Рассмотрим задачи:

Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 10 и 15, боковое ребро равно 5. Найдите объем призмы.

Площадь основания это площадь прямоугольного треугольника. Она равна половине площади прямоугольника со сторонами 10 и 15).

Таким образом,  искомый объём равен:

Ответ: 375

Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 20 и 8. Объем призмы равен 400. Найдите ее боковое ребро.

Задача обратная предыдущей.

Объем  призмы:

Площадь основания это площадь прямоугольного треугольника:

Таким образом

Ответ: 5

Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 12, высота призмы равна 8. Найдите площадь ее поверхности.

Площадь поверхности призмы складывается из площадей всех граней – это два равных по площади основания и боковая поверхность.

Для того, чтобы найти площади всех граней необходимо найти третью сторону основания призмы (гипотенузу прямоугольного треугольника).

По теореме Пифагора:

Теперь мы можем найти площадь основания и площадь боковой поверхности. Площадь основания равна:

Площадь боковой поверхности призмы с периметром основания  равна:

*Можно обойтись без формулы и просто сложить площади трёх прямоугольников:

Полная площадь поверхности призмы:

Ответ: 300

27082.  Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.

Посмотреть решение

27132. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.

Посмотреть решение

27151. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.

На этом всё. Успеха вам!

С уважением, Александр. 

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

matematikalegko.ru

Призма [wiki.eduVdom.com]

Призма — многогранник, две параллельные грани которого (основания) n−угольники, а остальные n граней (боковые) — параллелограммы. Очевидно, что все боковые ребра призмы равны, и в основаниях — равные n−угольники с соответственно параллельными сторонами.

Призма является многогранником.

Боковыми ребрами называются отрезки, соединяющие соответствующие вершины оснований.

Высотой призмы называется расстояние между плоскостями ее оснований.

Призма называется прямой, если ее боковое ребро перпендикулярно плоскости основания.
См.Рис.1

Рис.1

Призма называется наклонной, если боковое ребро призмы не перпендикулярно плоскости основания.
См.Рис.2

Рис.2

Правильная призма — прямая призма, основания которой являютя правильными многоугольниками.

Площадь полной поверхности призмы — сумма площадей всех её граней. Площадь полной поверхности (Sполн) выражается через площадь боковой поверхности (


Sбок) и площадь основания призмы формулой: Sполн=Sбок+2Sосн .

Площадь боковой поверхности призмы (Sбок) — сумма площадей её боковых граней.

Имеют место формулы : Sбок = Pl; V = Sосн · H , где S_бок — площадь боковой поверхности призмы, P — периметр перпендикулярного сечения, l — длина бокового ребра, V — объем, S_осн — площадь основания, H — высота призмы.

Теорема о площади боковой поверхности прямой призмы. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

Сечение, образованное плоскостью, перпендикулярной к боковому ребру призмы, называется нормальным (ортогональным) сечением призмы.

Призма называется параллелепипедом, если её основания — параллелограммы.

---

---

Пример 1. Найдите объём многогранника, вершинами которого являются точки A, B, C, A₁, B₁, C₁ правильный шестиугольник призмы ABCDEFA₁B₁C₁D₁E₁F₁ , площадь основания которой равна 6, а боковое ребро равно 3.

Видео-решение.

---

Пример №2

---

Пример №3

---

Пример №4

---

---

www.wiki.eduvdom.com

Призма. Формулы и свойства призмы

Определение.

Призма — это многогранная объемная фигура, которая состоит из двух одинаковых плоских многоугольников (основ), находящихся в двух параллельных плоскостях, а другие грани (боковые грани) — параллелограммы, что имеют общие стороны с этими многоугольниками.

Определение. Основы призмы — две грани, которые являются равными параллельными плоскими многоугольниками (ABCEF, GMNJK).

Определение. Боковые грани призмы — все остальные грани за исключением основ.

Определение. Боковая поверхность призмы — совокупность всех боковых граней призмы.

Определение. Поверхность призмы — это совокупность поверхностей двух оснований и боковой поверхности.

Определение. Боковое ребро призмы — общая сторона двух боковых граней.

Определение. Высота — это перпендикуляр, который соединяет две основы призмы под прямым углом.

Определение. Диагональ основания призмы — это отрезок, соединяющий две не соседние вершины, принадлежащие этой же основе.

Определение. Диагональ боковой грани призмы — это отрезок, соединяющий две противоположные вершины, лежащие на одной боковой грани однако принадлежат различным основам.

Определение. Диагональ призмы (AN) — это отрезок, соединяющий две вершины, лежащие на разных основаниях, но не лежат на одной боковой стороне.

Определение. Диагональное сечение — это пересечение призмы плоскостью, проходящей через диагональ основания призмы и боковое ребро. Треугольная призма (в основе призмы треугольники) не имеет диагональных сечений.

Определение. Перпендикулярное сечение — это пересечение призмы плоскостью, пересекающей боковые ребра призмы под прямым углом.

Определение. Прямая призма — это призма, в которой все боковые грани перпендикулярны к основанию. Высота равна длине бокового ребра.

Определение. Наклонная призма — это призма, в которой боковые грани не перпендикулярны к основанию.

Определение. Правильная призма — это призма, в которой основы являются правильными многоугольниками. Правильная призма может быть, как прямой, так и наклонной.

Определение. Усечённая призма — это призма, в которой две основы не параллельны (рис. 2). Усечённая призма может быть, как прямой, так наклонной.

Объём призмы

Формула. Объём призмы через площадь основания и высоту:

V = S_оснH

Формула. Объём наклонной призмы через площадь перпендикулярного сечения и длину бокового ребра:

V = S_пL

Формула.
Объём правильной прямой призмы через высоту (h), длину стороны (a) и количество сторон (n):

Площадь поверхности призмы

Формула. Площадь боковой поверхности призмы через периметр основания и высоту:

S_b = P·h

Формула. Площадь поверхности призмы через площадь основания, периметр основания и высоту:

S = 2S_oсн + P·h

Формула.
Площадь поверхности правильной призмы через высоту (h), длину стороны (a) и количество сторон (n):

Основные свойства призмы

Основы призмы — равные многоугольники.

Боковые грани призмы — параллелограммы.

Боковые ребра призмы параллельны и равны между собой.

Перпендикулярное сечение перпендикулярно всем боковым ребрам и боковым граням.

Высота прямой призмы равна длине бокового ребра.

Высота наклонной призмы всегда меньше длины ребра.

В прямой призме гранями могут быть прямоугольниками или квадратами.

ru.onlinemschool.com

Призма /qualihelpy

Многогранник, две грани которого равные -угольники, лежащие в параллельных плоскостях, а остальные  граней – параллелограммы, называют -угольной призмой. Два -угольника называют основаниями призмы, а параллелограммы – боковыми гранями. Стороны граней называют ребрами призмы, а концы ребер – вершинами призмы. 

На рисунке 9.41 изображена пятиугольная призма, на рисунке 9.42 – треугольная, а на рисунке 9.43 – четырехугольная. 

На рисунке 9.42 треугольники и – основания призмы , параллелограммы , , – боковые грани, отрезки , , – боковые ребра, отрезки ,  , , , , – ребра оснований, точки  ,  ,  ,  ,  ,  – вершины призмы.Две вершины призмы, не принадлежащие одной грани, называют противоположными. Например, на рисунке 9.43 вершины  и  – противоположные. Диагональю призмы называют отрезок, соединяющий две противоположные вершины (например, диагональ  на рисунке 9.41). 

Треугольная призма не имеет противоположных граней, не имеет противоположных вершин и не имеет диагоналей.

Прямой призмой называют призму, боковые ребра которой перпендикулярны плоскостям ее оснований (рис. 9.42). Боковые грани прямой призмы – прямоугольники.

Наклонной призмой называют призму, боковые ребра которой являются наклонными к плоскостям ее оснований (рис. 9.41 и 9.43). Боковые грани наклонной призмы – параллелограммы (некоторые боковые грани могут быть и прямоугольниками).

Высотой призмы называют перпендикуляр, заключенный между основаниями призмы. Высота  прямой призмы равна длине ее бокового ребра (рис. 9.42), высота  наклонной призмы – не равна (рис. 9.41 и 9.43).Диагональным сечением призмы называют сечение, содержащее диагональ призмы. На рисунке 9.44 построены диагональные сечения  и  четырехугольной призмы .

Параллелепипедом называют призму, основание которой – параллелограмм (рис. 9.44). 

Прямым параллелепипедом называют параллелепипед, боковые ребра которого перпендикулярны плоскостям его оснований (рис. 9.45). 

Прямоугольным параллелепипедом называют прямой параллелепипед, основанием которого является прямоугольник. На рисунке 9.46 изображен прямоугольный параллелепипед.

Свойство диагонали прямоугольного параллелепипеда: квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений: 

  , (9.1)где  ,  ,  – длины ребер, выходящих из одной вершины,  – диагональ параллелепипеда. 

Объем прямоугольного параллелепипеда находят по формуле: 

 . (9.2)

Кубом называют прямоугольный параллелепипед с равными ребрами. Все грани куба – квадраты (рис. 9.47).

Объем прямой призмы высоты  и периметром основания  находят по формуле:   . (9.6)

Площадь поверхности прямой призмы находят по формуле: 

 . (9.7)Площадь боковой поверхности прямой призмы высоты  и периметром основания  находят по формуле: . (9.8)

Объем наклонной призмы можно вычислить по формуле:

  . (9.9) 

Площадь поверхности наклонной призмы можно вычислить по формуле:  

 , (9.10)

а также по формулам:

  , (9.9.1)  , (9.10.1) где   сечение, перпендикулярное ребру   (рис. 9.48).

Правильной призмой называют прямую призму, основанием которой является правильный многоугольник. 

helpy.quali.me

Как найти площадь сечения призмы

24 апреля 2012

Автор КакПросто!

Призма — это многогранник, основанием которого служат равные многоугольники, боковыми гранями — параллелограммы. Для того чтобы найти площадь сечения призмы, необходимо знать, какое сечение рассматривается в задании. Различают перпендикулярное и диагональное сечение.

Статьи по теме:

Инструкция

Способ расчета площади сечения также зависит от данных, которые уже имеются в задаче. Кроме этого, решение определяется тем, что лежит в основании призмы. Если необходимо найти диагональное сечение призмы, найдите длину диагонали, которая равна корню из суммы (основания сторон в квадрате). Например, если основания сторон прямоугольника равны 3 см и 4 см, соответственно, длина диагонали равна корню из (4х4+3х3)= 5 см. Площадь диагонального сечения найдите по формуле: диагональ основания умножить на высоту. Если в основании призмы находится треугольник, для вычисления площади сечения призмы используйте формулу: 1/2 часть основания треугольника умножить на высоту. В случае, если в основании находится круг, площадь сечения призмы найдите умножением числа «пи» на радиус заданной фигуры в квадрате.

Различают следующие виды призм — правильные и прямые. Если необходимо найти сечение правильной призмы, вам нужно знать длину только одной из сторон многоугольника, ведь в основании лежит квадрат, у которого все стороны равны. Найдите диагональ квадрата, которая равна произведению его стороны на корень из двух. После этого перемножив диагональ и высоту, вы получите площадь сечения правильной призмы.

Призма имеет свои свойства. Так, площадь боковой поверхности произвольной призмы вычисляется по формуле, где — периметр перпендикулярного сечения, — длина бокового ребра. При этом перпендикулярное сечение перпендикулярно ко всем боковым ребрам призмы, а его углы — это линейные углы двугранных углов при соответствующих боковых ребрах. Перпендикулярное сечение перпендикулярно и ко всем боковым граням.

Источники:

• диагональное сечение призмы

Совет полезен?

Статьи по теме:

Не получили ответ на свой вопрос?
Спросите нашего эксперта:

www.kakprosto.ru