Формула как найти периметр правильного треугольника

Формула как найти периметр правильного треугольника

Содержание:

  • Формула
  • Примеры вычисления периметра равностороннего треугольника

Формула

Чтобы найти периметр равностороннего треугольника, надо длину его стороны умножить на три.

Периметр равностороннего треугольника – это сумма длин его сторон. У равностороннего треугольника
все стороны равны. Поэтому чтобы найти периметр равностороннего треугольника
$ABC$, со стороной
$a$ нужно воспользоваться формулой

$$P_{Delta A B C}=a+a+a=3 a$$

Примеры вычисления периметра равностороннего треугольника

Пример

Задание. Найти периметр треугольника
$ABC$ со стороной, равной 5 дм.

Решение. Воспользуемся формулой для нахождения периметра равностороннего треугольника:

$$P_{Delta A B C}=3a$$

Тогда искомый периметр равен:

$P_{Delta A B C}=3 cdot 5=15$ (дм)

Ответ. $P_{Delta A B C}=15$ (дм)

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Периметр равностороннего треугольника
$ABC$ равен
27 см. Найти длины его стороны.

Решение. Периметр равностороннего треугольника вычисляется по формуле:

$$P_{Delta A B C}=3 a$$

Подставим в нее заданное значение периметра и выразим из полученного уравнения искомую длину
$a$:

$27=3 a Rightarrow a=27: 3=9$ (см)

Ответ. $a=9$ (см)

Читать дальше: как найти периметр круга.

Источник

Периметр правильного треугольника


Периметр правильного треугольника

4.6

Средняя оценка: 4.6

Всего получено оценок: 165.

4.6

Средняя оценка: 4.6

Всего получено оценок: 165.

Правильный треугольник особенно выделяется на фоне других фигур. Любой параметр такого треугольника может быть определен из длины стороны. Особенной простотой отличается нахождение периметра.

Определения

Для начала вспомним несколько определений, которые потребуются для того, чтобы решать задачи на нахождение периметра правильного треугольника:

  • Правильным треугольником является треугольник, все стороны которого равны, а каждый из углов составляет 60 градусов.
  • Правильный треугольник является частным случаем равнобедренного, поэтому любая высота правильного треугольника будет являться биссектрисой и медианой.
  • Некоторые формулы для произвольного треугольника при применении к правильному треугольнику можно значительно упростить с помощью теоремы Пифагора.

Периметр треугольника

Что такое периметр? Это сумма длин всех сторон.

Формула периметра одинакова для любой фигуры. Это всегда сумма длин всех сторон.

Различные фигуры

Рис. 1. Различные фигуры.

Конкретно для правильного треугольника, нужно вспомнить, что все стороны этой фигуры равны между собой. Сторон у треугольника 3, а значит, формула периметра выглядит следующим образом:

$$P=3a$$

Пример

Сложную задачу на нахождение периметра правильного треугольника придумать нелегко. Поэтому решим интересную, но простую задачу на заданную тематику. В процессе решения рассмотрим применение теоремы Пифагора для решения задач с правильным треугольником.

Площадь правильного треугольника АВС равняется $9sqrt{3}$

Рисунок к задаче

Рис. 2. Рисунок к задаче.

Любую характеристику правильного треугольника можно найти, если есть хотя бы одна из длин. Неважно, будет это сторона, площадь, периметр, медиана или биссектриса. Любой длины будет достаточно для решения задачи.

Вспомним формулу площади треугольника и упростим ее для правильного треугольника.

Площадь треугольника находится как половина произведения основания на высоту, проведенную к этому основанию.

В правильном треугольнике АВС проведем медиану АМ, которая совпадет с высотой и биссектрисой. Тогда треугольник АВМ будет прямоугольным. По теореме Пифагора найдем АМ.

Сумма углов треугольника

Рис. 3. Сумма углов треугольника.

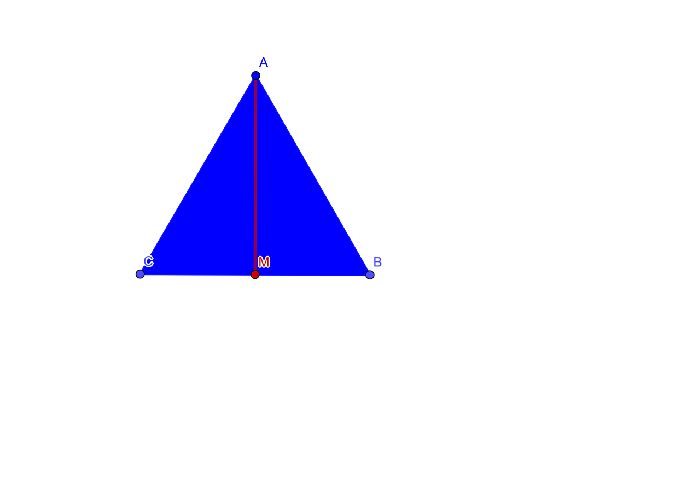
$$АМ=sqrt{AB^2-BM^2}= sqrt{а^2-{аover{2}}^2}= sqrt{а^2-{{а^2}over{4}}}=sqrt{{3a^2}over{4}}$$

Подставим значение АМ в формулу площади:

$$S={1over{2}}*a*h={1over{2}}*a*a*{sqrt{3}over{2}}=a^2*{sqrt{3}over{4}}$$

Из этой формулы выразим значение стороны:

$$a=sqrt{4Sover{sqrt{3}}}=sqrt{{4*{9over{sqrt{3}}}}over{sqrt{3}}}=6$$

Теперь найти периметр не составит проблем.

$$P=3a=3*6=18$$

Заключение

Что мы узнали?

Мы привели формулу периметра правильного треугольника. На примере показали, как можно найти площадь правильного треугольника через площадь. На том же примере показали примерный ход решения любой задачи на решение правильного треугольника.

Тест по теме

Доска почёта

Доска почёта

Чтобы попасть сюда – пройдите тест.

  • chashkova-tatyan чашкова

    5/5

  • Анна Ножеева

    5/5

  • Данила Салин

    5/5

Оценка статьи

4.6

Средняя оценка: 4.6

Всего получено оценок: 165.

А какая ваша оценка?

Источник

Чтобы найти периметр равностороннего треугольника(или найти периметр правильного треугольника), нужно знать его сторону.

В общем случае для нахождения периметра треугольника используют формулу

    [P = a + b + c]

perimetr ravnostoronnego treugolnika

Поскольку в равностороннем треугольнике все три стороны равны, формула упрощается:

    [P = a + a + a = 3 cdot a]

Таким образом, формула периметра равностороннего треугольника:

    [P = 3a]

(а — длина его стороны).

Примеры.

1) Найти периметр равностороннего треугольника, сторона которого равна 10 см.

Решение:

По формуле Р=3а имеем: Р=3∙10=30 (см).

2) Периметр равностороннего треугольника равен 21 см. Найти его сторону.

Решение:

Р=3а, значит, а=Р:3. Таким образом, длина стороны треугольника равна а=21:3= 7 (см).

perimetr pravilnogo treugolnika 3) Найти периметр правильного треугольника АВС, если АВ=25 см.

Решение:

По формуле P=3a, P=3∙АВ=3∙25=75 (см).

Источник

Правильный (равносторонний, или равноугольный) треугольник — это правильный многоугольник с тремя сторонами, простейший из правильных многоугольников. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.

Содержание

  • 1 Свойства
  • 2 Правильный сферический треугольник
  • 3 Теоремы о равностороннем треугольнике или содержащие его
  • 4 См. также
  • 5 Примечания

Свойства[править | править код]

Правильный тетраэдр состоит из четырёх правильных треугольников.

Пусть a — сторона правильного треугольника, R — радиус описанной окружности, r — радиус вписанной окружности.

  • Радиус вписанной окружности правильного треугольника, выраженный через его сторону:
r = frac{sqrt 3}{6} a
  • Радиус описанной окружности правильного треугольника, выраженный через его сторону:
R = frac{sqrt 3}{3} a
  • Периметр правильного треугольника:
P = 3a = 3 sqrt 3 R = 6 sqrt 3 r
  • Высоты, медианы и биссектрисы правильного треугольника:
h = m = l = frac{sqrt 3}{2} a
  • Площадь правильного треугольника рассчитывается по формулам:
S={frac {{sqrt 3}}{4}}a^{2}={frac {3{sqrt 3}}{4}}R^{2}=3{sqrt 3}r^{2}={frac {{sqrt 3}}{36}}P^{2}
  • Радиус описанной окружности равен двойному радиусу вписанной окружности:
R = 2r
  • Правильными треугольниками можно замостить плоскость.
  • В правильном треугольнике окружность девяти точек совпадает с вписанной окружностью.

Правильный сферический треугольник[править | править код]

Для любого значения в интервале от 60 до 180 градусов существует правильный сферический треугольник с равными этому значению углами.

Теоремы о равностороннем треугольнике или содержащие его[править | править код]

  • Задача Наполеона
  • Прямая Симсона одно из свойств
  • Теорема Вивиани
  • Теорема Морли
  • Теорема Наполеона
  • Теорема Помпею
  • Теоремы Тебо 2 и 3
  • Точки Аполлония
  • Точки Торричелли

См. также[править | править код]

  • Замечательные прямые треугольника
  • Замечательные точки треугольника
  • Равнобедренный треугольник
  • Теорема Чевы
  • Треугольник
  • Треугольник Рёло

Примечания[править | править код]

Перейти к шаблону «Символ Шлефли» 

Символ Шлефли
Многоугольники
  • {1}
  • {2}
  • {3}
  • {4}
  • {5}
  • {6}
  • {7}
  • {8}
  • {9}
  • {10}
  • {11}
  • {12}
  • {14}
  • {15}
  • {17}
  • {18}
  • {20}
  • {30}
  • {51}[de]
  • {257}
  • {65537}
  • {4294967295}
  • {∞}
Звёздчатые многоугольники
  • {5/2}
  • {6/2}
  • {7/2}
  • {7/3}
  • {8/2}
  • {8/3}
  • {9/2}
  • {9/3}
  • {9/4}
Паркеты на плоскости
  • {3,6}
  • {4,4}
  • {6,3}
Правильные многогранники
и сферические паркеты
  • {2,n}
  • {3,3}
  • {4,3}
  • {3,4}
  • {5,3}
  • {3,5}
  • {n,2}
Многогранники Кеплера — Пуансо
  • {5/2,5}
  • {5,5/2}
  • {5/2,3}
  • {3,5/2}
Соты

{4,3,4}
Четырёхмерные многогранники
  • {3,3,3}
  • {4,3,3}
  • {3,3,4}
  • {3,4,3}
  • {5,3,3}
  • {3,3,5}
Источник

Периметр Правильного Треугольника: Определение и Формулы

Обновлено 14.01.2022

Правильный треугольник — это треугольник, у которого
все стороны и углы равны.

Правильный треугольник, также называют равносторонним
и равноугольным. Все углы в таких треугольника имеют
градусную меру в 60 градусов.

Периметр правильного треугольника — это периметр
треугольника,  у которого все стороны и углы равны.

Периметр в правильном треугольнике, можно найти с
помощью площади, длины сторон, радиуса и так далее.

Формула периметра
правильного треугольника

  1. Формула периметра правильного треугольника, через сторону:

    [ P = 3a ]

  2. Формула периметра правильного треугольника, через радиус вписанной окружности:

    [ P=6sqrt{3}r ]

  3. Формула периметра правильного треугольника, через радиус описанной окружности:

    [ P = 3sqrt{3}R ]

  4. Формула периметра правильного треугольника, через площадь:

    [ P = sqrt{frac{S}{frac{sqrt{3}}{36} }} ]

    С помощью этих формул можно найти периметр через площадь,
    сторону, радиус вписанной и описанной окружностей.

Источник

Добавить комментарий