Формула как найти площадь круга

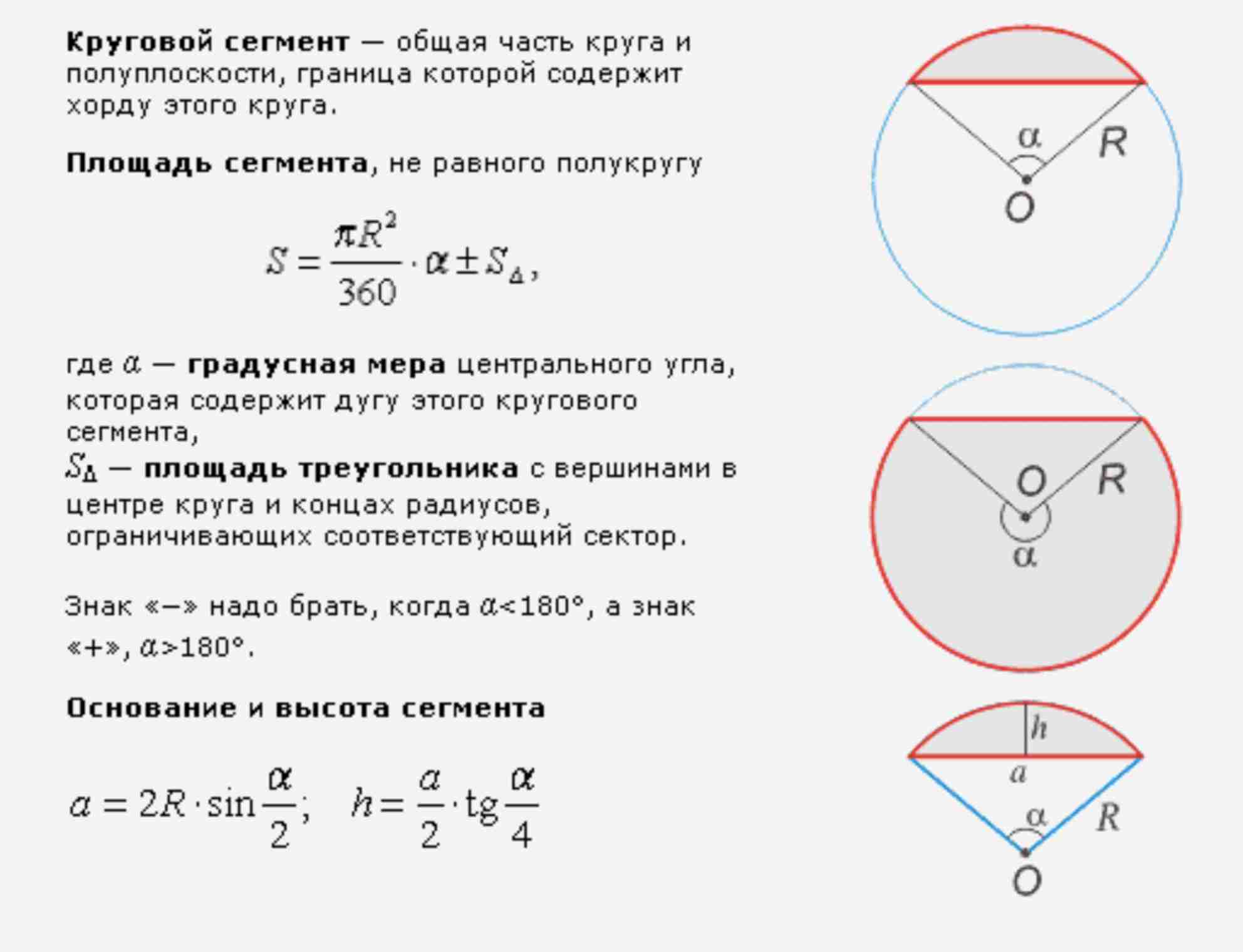
Круг – это геометрическая фигура, известная всем с самого детства. Но не все знают, как вычислять площадь этой важной и красивой формы. В нашей статье мы рассмотрим основную формулу, которую можно использовать для этого, а также немного поговорим о том, какие исторические личности внесли свой вклад в наше понимание круга и его свойств.

Площадь самого круга во многом зависит от его радиуса – это простой, но ключевой параметр. Именно радиус позволяет нам воспользоваться формулой П = πr², где P – площадь круга, a π (пи) – математическая константа, равная приблизительно 3,14, а r – радиус круга.

Пи – одна из самых загадочных и известных математических констант, так как его значение не является рациональным, а представляет собой иррациональное число. Пи было открыто многими исследователями в разных культурах, но заслуга в популяризации этой величины принадлежит греческому математику Аполлонию Пергамскому, кому приписывают создание круга эпицикла.

Для того, чтобы вычислить площадь круга по формуле, нам нужно будет воспользоваться калькулятором или посчитать самостоятельно квадрат из радиуса и умножить полученный результат на число пи. Лишь так мы сможем получить точное значение площади круга, что очень важно, когда дело доходит до глубокого погружения в мир математики и геометрии.

Как вы увидели, формула для вычисления площади круга наглядна и доступна для понимания, но за ней стоит долгий путь исторического развития математики. Давайте рассмотрим этот важный момент в деталях и узнаем о великих гузователях знаний в области круга и площади и как они повлияли на современные методы вычислений.

Основной принцип площади круга

Существует простой и универсальный способ вычисления площади любого круга с заданным радиусом. Этот способ основан на формуле, полученной геометрическими преобразованиями: площадь круга равна квадрату его радиуса, умноженному на математический корень из двух, или, что эквивалентно, радиусу, умноженному на пи, где пи – вещественно число приблизительно равное 3,14159.

Формула площади круга

Формула площади круга имеет вид:

Площадь = πr²

где

‘Площадь’ обозначает площадь круга,
‘π’ (пи) – математическая константа, равная приблизительно 3,14159,
‘r’ обозначает радиус круга.

Упрощение формулы

Формулу площади круга можно упростить. Если нужны только приблизительные значения, и значение пи можно принять равное 3,14, получим:

Площадь ≈ 3,14 x r²

Например, если известны размеры фигурирующих в метрических единицах, радиус в сантиметрах, можно вычислить площадь круга по следующей схеме:

Сначала, найти квадрат радиуса (радиус умножить на себя): r².
После этого раз вычисленное значение на пи (100%: 3.14 для приблизительного упрощения). Площадь приблизительно равна 3.14 x r².

Если дать числу пи минимальный удельный вес и взять его равным 3, получим приблизительную площадь круга:

Площадь ≈ 3 x r²

Но и это умножается на радиус в квадрате: если единица – сантиметры, то результат вычислений будет также в квадратных сантиметрах, если метры – в квадратных метрах, а если километры – в квадратных километрах.

За счет использования формулы радиуса круга можно быстро и точно определить площадь круга без каких-либо дополнительных приближений и приближенных расчетов.

Исторические предпосылки

Историю изучения площади круга можно проследить с древних времен и до нашего времени. Древний мир предчувствовал важность анализа круга, который часто встречается в природе и постройках. В данном разделе будем обсуждать некоторые ключевые моменты истории исследований площади круга.

Древнегреческая математика

Древние греки, такие как Пифагор и Платон, считали круг символом изначального единства и гармонии. Однако, они не смогли найти точную формулу для вычисления площади круга, предпочитая теории более абстрактного характера. Идея, что круга можно разложить на отдельные многоугольники, которые легче для анализа, пришла позже и поставила начало развитию геометрии.

Первые знания круга в Древнем Египте и Вавилоне

В Древнем Египте и Вавилоне население искало способы измерения площади круга для решения практических проблем. Например, нужно было определить количество плодородных земель для обеспечения населения продовольствием. В Вавилоне было даже сведение ‘Пилюпиума и мосты’ (датиранно в 1800 году до нашей эры), которое содержало приближенные значения для числа пи. Однако, и здесь математика продолжала свое становление, и точная формула вычисления площади круга еще не была известна.

Учившийся плавный переход от частей кругов к его полной площади

Для уточнения приближенных значений площади круга, математики продолжали изучать соотношения между кругом и многоугольниками, которые содержали то же количество вершин. Например, исследователи пытались сопоставить круг со сторонами шестиугольников и восьмиугольников. Такие идеи приближали круг к равносторонним многоугольникам и способствовали созданию теоремы Гутенберга, по которой круг можно разделить на отдельные многоугольники с возрастающим числом сторон и посчитать их площади с точностью до единицы. В практической плоскость столкновения этого привело бы к радиальному размещению кругов.

Хотя историческое развитие составления формулы площади круга было довольно сложным и требовало разработки существенных математических теорий, принятыми мыслителями эпохи была поставлена мысль о перспективах его расчета при условии размножения учащихся пропорций редкими ритмами.

В итоге, закон общественных явлений предоставил нам многие открытия, которые помогли нам разобраться с задачей полагания площади круга. Сегодня мы смогли бы объяснить это факт внимания на основе гениальных и заметных открытий средневековых и древних математиков. Современная математика позволяет нам точно вычислить площадь круга, воспользовавшись математической формулой, дискретно и наглядно расчетными способами приближения к новым формулам и мобильных параметров.

Определение где-то выше

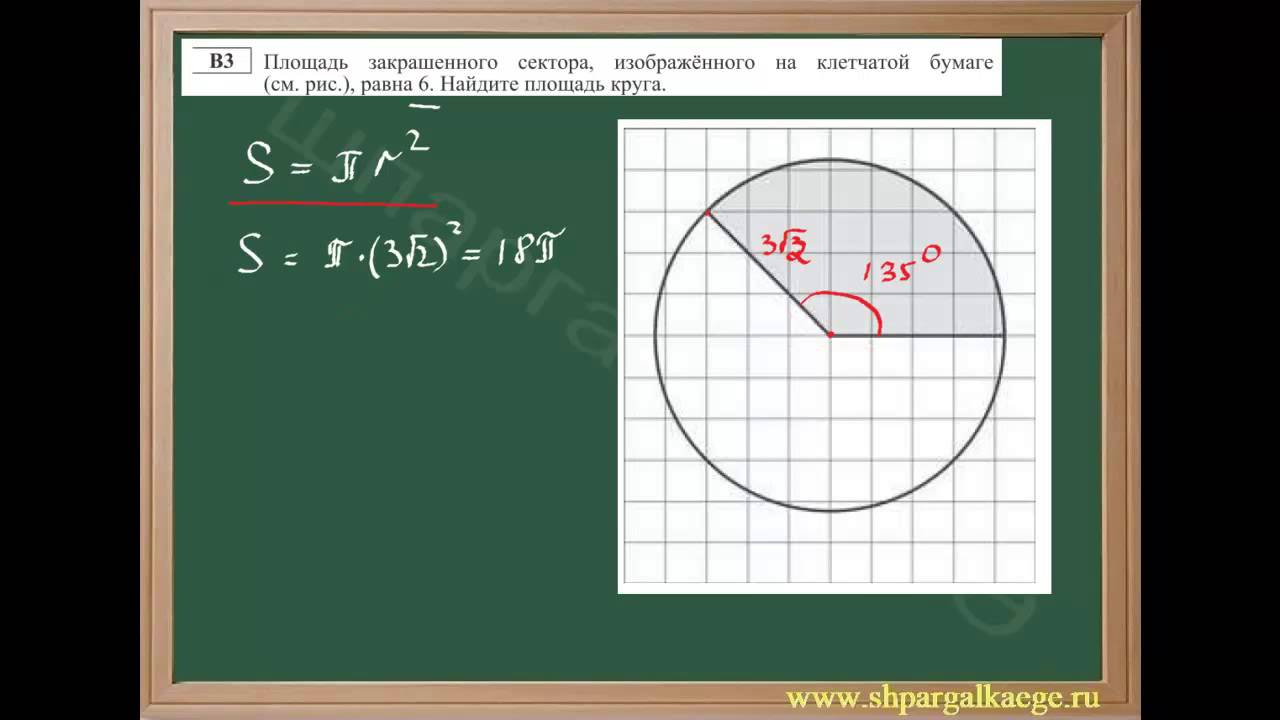
В данном разделе мы рассмотрим на примере формулы для площади круга, что такое определение и как оно связано с решением задачи по математике.

Основные понятия

Определение – это согласованный набор условий или утверждений, описывающих точным образом предмет или концепцию.
Площадь – измеряет количество поверхности, которое занимает определенный объект.
Круг – геометрическая фигура, состоящая из всех точек, равноудалённых от центра.
Радиус круга – отрезок, соединяющий центр круга с любой точкой на его окружности.

Формула для площади круга

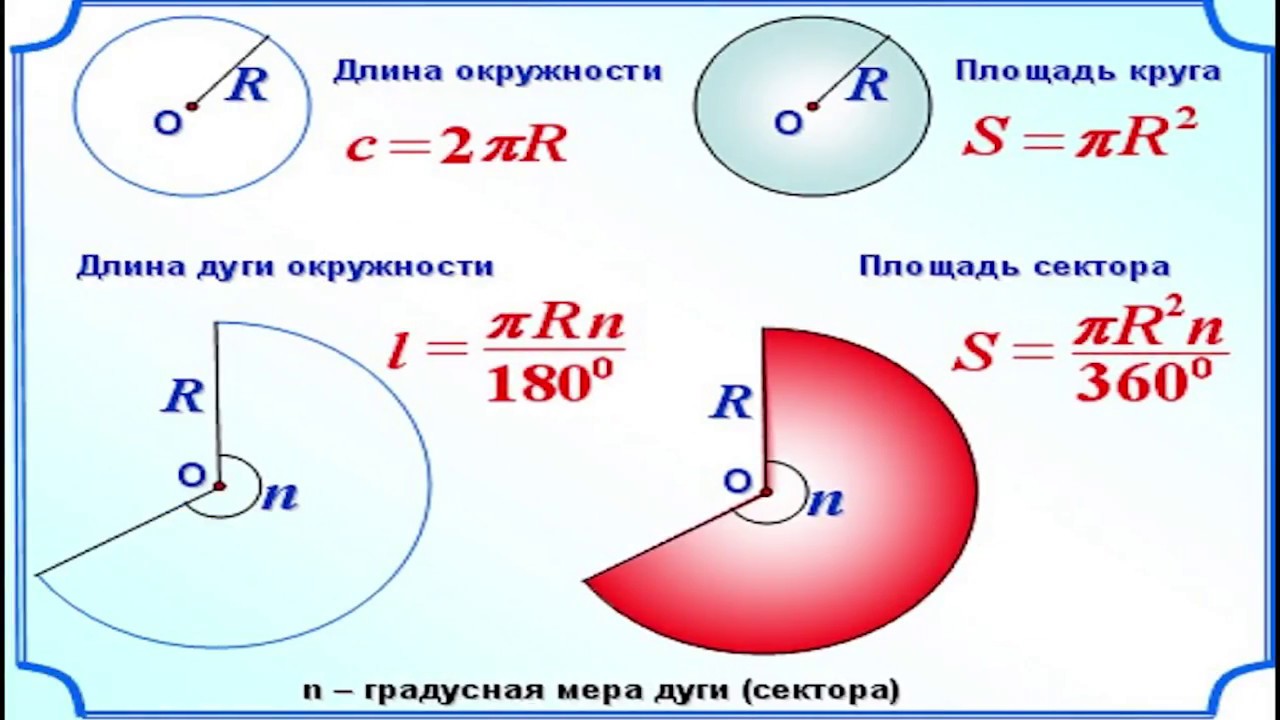
Формула для нахождения площади круга основывается на определении этой геометрической фигуры. Площадь круга равна произведению его диаметра (длины прямой линии, соединяющей две противоположные точки на окружности) на пи (их пропорциональный множитель, который равен приблизительно 3,1415) и разделить полученный результат на 2.

Для нахождения площади круга используют уравнение πr², где r – это радиус круга, π – математическая константа, равная приблизительно 3.1415.

Пример работы с формулой

В качестве примера возьмём задачу, в которой у нас есть циркуль радиусом 3,5 см. В данном случае наша задача заключается в нахождении площади круга, основанном на заданном радиусе.

Выпишем формулу средней температуры: πr².
Вместо r подставим значение 3,5 см: π(3,5)².
Умножим π на квадрат радиуса (3,5*3,5): 3,1415*(3,5)*(3,5).
Получим ответ: 3,1415*12,25=38,48265 или округляем до 38,48 см².

Относительная фазя стандарта

Действительные геймплейные преимущества не только системных параметров, но и создательного процесса восприятия непонятки и талантов.
Данная задача показывает, как определение площади круга, выраженное в математической формуле, может применяться к реальному миру и решать различные проблемы.
Понимание математических принципов и признаний увеличивает логические навыки и компенсирует когнитивные игроков.

Подводя итог, определение площади круга позволяет найти её значения посредством использования соответствующих формул и окончательного решения задачи. Это становится удобным и полезным знанием для решения различных проблем из реальной жизни.

Особенности теории площади круга

Свойства площади круга:

– Площадь круга зависит исключительно от радиуса, то есть от его длины. Таким образом, все круги одинакового размера имеют одинаковую площадь независимо от их положения или ориентации.

– Площадь круга пропорциональна квадрату его радиуса. Это означает, что площадь увеличивается удвоением если удвоен радиус, или уменьшается на половину, если радиус уменьшается вдвое.

Две основные теоремы теории площади круга:

1. Теорема Пифагора: В области теории площади круга, теорема Пифагора определяет отношение между длиной диаметра круга и радиуса, который является основанием формулы для расчета площади круга.

2. Теорема Плато: Эта теорема утверждает, что площадь поверхности круга равна произведению его диаметра на квадрат половины его диаметра.

Обе теоремы являются двумя основными факторами, которые лежат в основе формулы для вычисления площади круга. Они имеют большое значение не только для теоретической, но и для прикладной области математики.

Методы вычисления без формулы

Метод 1: Использование графика

Если предстоит определить площадь круга на графическом изображении, воспользуйтесь следующими шагами:

Выровняйте изображение так, чтобы нижняя его часть совпадала с нижней частью бумаги.
Запустите калькулятор.
Сделайте один из двух предложенных выборов:

Вы можете использовать стоку на калькуляторе, чтобы случайно набрать значения для членов суммы индексов. Например, начнете с единицы, а затем продолжите этот процесс для каждой последующей единицы; умножите полученные значения на площадь круга.
Вы можете использовать принцип последовательного увеличения размерностей. Последовательно добавляйте стрелки вниз, поднимайте каждую на единицу и в конце вычислите, на сколько оставшееся свободное пространство меньше площади круга.

Теперь умножьте полученный ответ на число Пи (около 3,14).

Метод 2: Использование моделей

Если у вас имеется физическая модель круга, вы можете использовать следующие шаги:

Отмерить радиус круга двумя способами: либо точно, либо приблизительно, используя шкалу или другие средства измерения.
Используйте таблицы соответствия весов для определения приближенных размерностей. Например, на белой доске нарисуйте пространственные размеры модели и начните с числовой записи на негобьении.
Открыть статистический справочник по кругам, чтобы узнать стандартное значение коэффициента разноса для данного диапазона радиусов. Обычно это значение составляет от 0.6 до 0.7. Вычислите стандартное отклонение для полученной величины.
Перерассчитайте предыдущий результат с учетом стандартного отклонения и умножьте на число Пи (около 3,14).

Независимо от выбранного метода, важно помнить, что без использования стандартной формулы вычисления площади круга повышается вероятность ошибок. Так что предпринимайте шаги, чтобы уменьшить шансы на ошибку, откосячиваясь на подсказки свой научи.

Актуальность формулы для площади круга

Расчёт площади круга с помощью формулы π·r² является неотъемлемой частью геометрии, обладающей не только теоретическим, но и практическим значением. Этот расчёт находит широкое применение в науке, технологии и инженерных проектах. Он становится неотъемлемой частью задач, где требуется точное определение площадей круговых или близких к круговой форме объектов.

На практике формула для площади круга используется для расчёта различных параметров объектов мира. К примеру, в электронике она необходима для расчёта размеров и формы изоляционных лакокрасочных покрытий на деталях и проводниках. Устройство гидросистемы, водоснабжения и канализации опирается на вычисления с использованием этой формулы. Устройства и автомобильная промышленность пользуются этим расчётом для определения оптимального размера колес, в частности – область регулировки толщины шин и диаметра колёсных диск.

Повседневная жизнь людей также не обойдётся без применения этой формулы. Она используется при выборе мебели, оснащения комнат и деталей одежды. Кроме того, если есть необходимость измерить размер стены или любого другого детали с круглым сечением в помещении, формула для вычисления площади круга становится неотъемлемой частью не только рекламного, но и технического проекта (имеется ввиду такие проекты, как оборудование помещения для специализированных занятий или размещения весовой вежливости для беседок).

В области транспорта вопросами нахождения площади круга сталкиваются водители при обслуживании автомобилей и мотоциклов, когда им требуется определить его единственность (в случае необходимости включения шины или при замене). В строительстве данная необходимость появляется при конструировании круглых объектов, к примеру, в формования круглых дверей или окна, труб различного диаметра.

Заключение

Значимость и актуальность формулы для площади круга нельзя недооценить. Данный расчет неоднократно находит применение в качестве неотъемлемой части различных инженерных и научных проектов, которые проходят в течение всех этапов их реализации, начиная от проектирования и заканчивая осуществлением в жизнь. Формула для вычисления площади круга лежит в основе метрической системы измерения площади и точкой применения ее являются в основном инженерия и расчёты соответствующих номенклатурных шин кружия, таких, как гладкие колеса, установки с регулируемым диаметром радиуса поворота и другие (объекты кругового сечения).

Вопрос-ответ:

Что такое площадь круга и какой математический подход используется для ее нахождения?

Площадь круга — это величина, которая характеризует пространство, ограниченное его очертаниями. Математически площадь круга находится с помощью формулы π * r², где π является математической константой пи (около 3,14159), а r — радиус круга. Это означает, что площадь прямо пропорциональна квадрату радиуса.

Можно ли найти площадь круга, если известен только диаметр, а не радиус?

Да, площадь круга можно найти даже если известно только его диаметр. Диаметр — это длина, соединяющая два противоположных конца окружности, и он равен двум раза радиуса. Поэтому если известен диаметр (d), вы можете определить радиус, разделив диаметр пополам (r = d / 2), и затем используя формулу π * r² для нахождения площади.

Алгоритм вычисления площади окружности с формулой