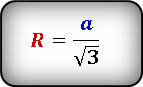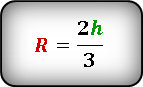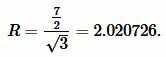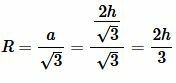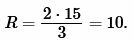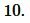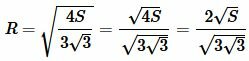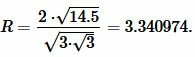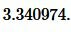Формула как найти радиус в равностороннем треугольнике

Радиус описанной окружности равностороннего треугольника

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, описанной около произвольного (любого), прямоугольного или равностороннего треугольника. Также разберем примеры решения задач для закрепления представленного теоретического материала.

Формулы вычисления радиуса описанной окружности

Произвольный треугольник

Радиус окружности, описанной вокруг любого треугольника, рассчитывается по формуле:

где a, b, c – стороны треугольника, S – его площадь.

Прямоугольный треугольник

Радиус окружности, описанной около прямоугольного треугольника, равен половине его гипотенузы или высоте, проведенной к гипотенузе.

Равносторонний треугольник

Радиус описанной около правильного треугольника окружности вычисляется по формуле:

где a – сторона треугольника.

Примеры задач

Задание 1
Дан треугольник со сторонами 4, 6 и 9 см. Найдите радиус описанной около него окружности.

Решение
Для начала нам необходимо найти площадь треугольника. Т.к. нам известны длины всех его сторон, можно применить формулу Герона:

Теперь мы можем воспользоваться первой формулой из перечисленных выше для расчета радиуса круга:

Задание 2
Дан треугольник, у которого известны две стороны из трех: 6 и 8 см. Найдите радиус описанной вокруг него окружности.

Решение
Треугольник со сторонами 6 и 8 см может быть только прямоугольным, причем известные по условиям задачи стороны являются его катетами. Таким образом, мы можем найти гипотенузу фигуры, воспользовавшись теоремой Пифагора:

Как мы знаем, радиус круга, описанного вокруг прямоугольного треугольника, равняется половине его гипотенузы, следовательно: R = 10 : 2 = 5.

Радиус описанной окружности около равностороннего треугольника онлайн

С помощю этого онлайн калькулятора можно найти радиус описанной окружности около любого треугольника, в том числе радиус окружности около равностороннего треугольника. Для нахождения радиуса окружности описанной около треугольника введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.

Открыть онлайн калькулятор

1. Радиус окружности описанной около равностороннего треугольника, если известна сторона a

Пусть известна сторона a равностороннего треугольника. Найдем радиус описанной окружности около треугольника. На странице Радиус окружности описанной около треугольника вычисляется из формулы:

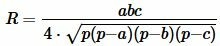(1)

где p вычисляется из формулы:

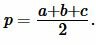(2)

Учитывая, что у нас треугольник равносторонний, т.е. a=b=c, имеем:

( small p= frac<large 3a><large 2>, )

(3)

( small p-a=p-b=p-c= frac< large a>< large 2>. )

(4)

Подставляя (3),(4) в (1) и учитывая, что a=b=c, получим:

( small R=frac<large a^3><large 4 cdot sqrt<frac<3><2>a left( frac <2>right)^3>> ) ( small =frac<large a^3><large 4 cdot sqrt< frac<3a^4><16>>> ) ( small =frac<large a>< large sqrt< 3>> )

( small R=frac<large a>< large sqrt< 3>>=frac<large a sqrt<3>>< large 3>. )

(5)

Пример 1. Известна сторона ( small a=frac<7> <2>) равностороннего треугольника. Найти радиус окружности описанной около треугольника.

Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (5).

Подставим значение ( small a=frac<7> <2>) в (5):

Ответ:

2. Радиус окружности описанной около равностороннего треугольника, если известна высота треугольника

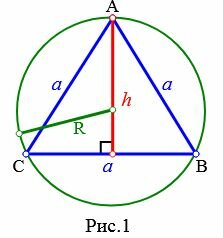
Пусть известна высота h равностороннего треугольник (Рис.1):

Найдем радиус описанной окружности около равностороннего треугольника. Из теоремы синусов имеем:

( small frac<large a>< large sin 90°>=frac<large h >< large sin C>. )

(6)

Уситывая, что сумма углов треугольника равна 180° и что у равностороннего треугольника все углы равны, имеем: ( small angle A= angle B=angle C=60°. ) Тогда из (6) получим:

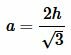(7)

Подставляя (7) в (5), получим:

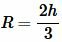(8)

Пример 2. Высота равностороннего треугольника равна:( small h=15 .) Найти радиус окружности описанной около равностороннего треугольника.

Решение. Для нахождения радиуса окружности описанной около равностороннего треугольника воспользуемся формулой (8). Подставим значения ( small h=15 ) в (8):

Ответ:

3. Радиус окружности описанной около равностороннего треугольника, если известна площадь треугольника

Пусть известна площадьS равностороннего треугольника. Найдем радиус окружности, описанной около треугольника. На странице Площадь равностороннего треугольника онлайн была выведена формула площади равностороннего треугольника по радиусу описанной окружности:

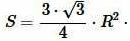(9)

В формуле (9) найдем R:

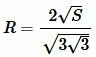(10)

Пример 3. Площадь равностороннего треугольника равна:( small S=14.5 .) Найти радиус окружности описанной около равностороннего треугольника.

Решение. Для нахождения радиуса окружности описанной около равностороннего треугольника воспользуемся формулой (10). Подставим значения ( small S=14.5 ) в (10):

Ответ:

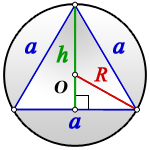
Радиус описанной окружности равностороннего треугольника

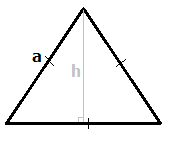
– сторона треугольника

– высота

– радиус описанной окружности

Формула радиуса описанной окружности равностороннего треугольника через его сторону:

Калькулятор – вычислить, найти радиус описанной окружности равностороннего треугольника по стороне

Формула радиуса описанной окружности равностороннего треугольника через высоту:

Калькулятор – вычислить, найти радиус описанной окружности равностороннего треугольника по стороне

Нахождение радиуса описанной вокруг треугольника окружности

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, описанной около произвольного (любого), прямоугольного или равностороннего треугольника. Также разберем примеры решения задач для закрепления представленного теоретического материала.

Формулы вычисления радиуса описанной окружности

Произвольный треугольник

Радиус окружности, описанной вокруг любого треугольника, рассчитывается по формуле:

где a, b, c – стороны треугольника, S – его площадь.

Прямоугольный треугольник

Радиус окружности, описанной около прямоугольного треугольника, равен половине его гипотенузы или высоте, проведенной к гипотенузе.

Равносторонний треугольник

Радиус описанной около правильного треугольника окружности вычисляется по формуле:

где a – сторона треугольника.

Примеры задач

Задание 1
Дан треугольник со сторонами 4, 6 и 9 см. Найдите радиус описанной около него окружности.

Решение
Для начала нам необходимо найти площадь треугольника. Т.к. нам известны длины всех его сторон, можно применить формулу Герона:

Теперь мы можем воспользоваться первой формулой из перечисленных выше для расчета радиуса круга:

Задание 2
Дан треугольник, у которого известны две стороны из трех: 6 и 8 см. Найдите радиус описанной вокруг него окружности.

Решение
Треугольник со сторонами 6 и 8 см может быть только прямоугольным, причем известные по условиям задачи стороны являются его катетами. Таким образом, мы можем найти гипотенузу фигуры, воспользовавшись теоремой Пифагора:

Как мы знаем, радиус круга, описанного вокруг прямоугольного треугольника, равняется половине его гипотенузы, следовательно: R = 10 : 2 = 5.

[spoiler title=”источники:”]

http://www-formula.ru/2011-09-22-04-51-34

[/spoiler]

Равносторонний треугольник – это треугольник, у которого все стороны равны.

Другие виды треугольников:

• прямоугольные треугольники;
• равнобедренные треугольники.

Любой равносторонний треугольник характеризуется стороной a (см. рисунок). При решении задач могут понадобиться высота h, радиусы вписанной (r) и описанной (R) окружности. Именно эти характеристики используются в формулах равностороннего треугольника при вычислении площади, периметра, а также радиусов вписанной и описанной окружностей.

Формула радиуса вписанной окружности для равностороннего треугольника

Радиус вписанной окружности r можно вычислить, зная сторону равностороннего треугольника:

r = a/(2√3)

Формула радиуса описанной окружности для равностороннего треугольника

Радиус описанной окружности R можно вычислить, зная сторону равностороннего треугольника:

R = a/(√3)

Формула периметра равностороннего треугольника

Периметр P равностороннего треугольника можно получить, зная его сторону:

P = 3a

Формулы площади равностороннего треугольника

p>При вычислении площади равностороннего треугольника можно использовать формулы, которые применяются для вычисления площади произвольного треугольника, так как равносторонний треугольник является частным случаем произвольного треугольника.

Площадь равностороннего треугольника S можно вычислить, зная его сторону a:

S = (√3 ⋅ a²)/4

Площадь равностороннего треугольника S также можно вычислить, зная его высоту h:

S = h²/√3

Если в задаче присутствует окружность, вписанная в треугольник, площадь равностороннего треугольника можно вычислить через радиус окружности r:

S = 3√3 ⋅ r²

Если в задаче присутствует окружность, описанная вокруг треугольника, площадь равностороннего треугольника можно вычислить через радиус окружности R:

S = (3√3 ⋅ R²)/4

Свойства равностороннего треугольника

Свойство 1. В равностороннем треугольнике все углы равны между собой и равны ({{60}^{o }})

Естественно, не правда ли? Три одинаковых угла, в сумме ({{180}^{o }}), значит, каждый по ({{60}^{o }})

Свойство 2. В равностороннем треугольнике точки пересечения высот, биссектрис, медиан и серединных перпендикуляров совпадают – оказываются одной и той же точкой. И эта точка называется центром треугольника (равностороннего!).

Почему так? А посмотрим-ка на равносторонний треугольник.

Он является равнобедренным, какую бы его сторону ни принять за основание – так сказать, со всех сторон равнобедренный.

Значит, любая высота в равностороннем треугольнике является также и биссектрисой, и медианой, и серединным перпендикуляром!

В равностороннем треугольнике оказалось не (12) особенных линий, как во всяком обычном треугольнике, а всего три!

Итак, ещё раз:

Центр равностороннего треугольника является центром вписанной и описанной окружности, а также точкой пересечения высот и медиан.

Свойство 3. В равностороннем треугольнике радиус описанной окружности в два раза больше, чем радиус вписанной. (R=2cdot r)

Уже должно быть очевидно, отчего так.

Посмотри на рисунок: точка( O) – центр треугольника.

Значит, (OB) – радиус описанной окружности (обозначили его (R)), а (OK) – радиус вписанной окружности (обозначим (r)).

Но ведь точка (O) – ещё и точка пересечения медиан! Вспоминаем, что медианы точкой пересечения делятся в отношении (2:1), считая от вершины.

Поэтому (OB=2cdot OK), то есть (R=2cdot r).

Свойство 4. В равностороннем треугольнике длины всех элементов «хорошо» выражаются через длину стороны.

Давай удостоверимся в этом.