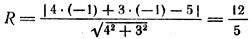Формула как найти точку центра окружности - Сайт, где вы сможете решить свои вопросы

Как найти координаты центр окружности??

Инструкция
1
Аналитически окружность задается уравнением вида (x-x0)²+(y-y0)²=R², где x0 и y0 − координаты центра окружности, R − ее радиус. Итак, центр окружности (x0;y0) здесь задан в явном виде.
2
Пример. Установите центр фигуры, заданной в декартовой системе координат уравнением (x-2)²+(y-5)²=25.
Решение. Данное уравнение является уравнением окружности. Ее центр имеет координаты (2;5). Радиус такой окружности равен 5.
3
Уравнение x²+y²=R² соответствует окружности с центром в начале координат, то есть, в точке (0;0). Уравнение (x-x0)²+y²=R² означает, что центр окружности имеет координаты (x0;0) и лежит на оси абсцисс. Вид уравнения x²+(y-y0)²=R² говорит о расположении центра с координатами (0;y0) на оси ординат.
4
Общее уравнение окружности в аналитической геометрии запишется как: x²+y²+Ax+By+C=0. Чтобы привести такое уравнение к выше обозначенному виду, надо сгруппировать члены и выделить полные квадраты: [x²+2(A/2)x+(A/2)²]+[y²+2(B/2)y+(B/2)²]+C-(A/2)²-(B/2)²=0. Для выделения полных квадратов, как можно заметить, требуется добавлять дополнительные величины: (A/2)² и (B/2)². Чтобы знак равенства сохранялся, эти же величины надо вычесть. Прибавление и вычитание одного и того же числа не меняет уравнения.
5
Таким образом, получается: [x+(A/2)]²+[y+(B/2)]²=(A/2)²+(B/2)²-C. Из этого уравнения уже видно, что x0=-A/2, y0=-B/2, R=√[(A/2)²+(B/2)²-C]. Кстати, выражение для радиуса можно упростить. Домножьте обе части равенства R=√[(A/2)²+(B/2)²-C] на 2. Тогда: 2R=√[A²+B²-4C]. Отсюда R=1/2·√[A²+B²-4C].
6
Окружность не может быть графиком функции в декартовой системе координат, так как, по определению, в функции каждому x соответствует единственное значение y, а для окружности таких «игреков» будет два. Чтобы убедиться в этом, проведите перпендикуляр к оси Ox, пересекающий окружность. Вы увидите, что точек пересечения две.
7
Но окружность можно представить как объединение двух функций: y=y0±√[R²-(x-x0)²]. Здесь x0 и y0, соответственно, представляют собой искомые координаты центра окружности. При совпадении центра окружности с началом координат объединение функций принимает вид: y=√[R²-x²].

Как найти координаты окружности формула

Как найти координаты центр окружности??

Формула окружности в системе координат

Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой центром.

Если точка С — центр окружности, R — ее радиус, а М — произвольная точка окружности, то по определению окружности

Равенство (1) есть уравнение окружности радиуса R с центром в точке С.

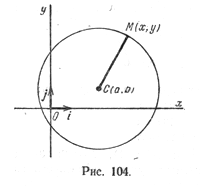
Пусть на плоскости задана прямоугольная декартова система координат (рис. 104) и точка С(а; b) — центр окружности радиуса R. Пусть М(х; у) — произвольная точка этой окружности.

Так как |СМ| = ( sqrt ), то уравнение (1) можно записать так:

(x — a) 2 + (у — b) 2 = R 2 (2)

Уравнение (2) называют общим уравнением окружности или уравнением окружности радиуса R с центром в точке (а; b). Например, уравнение

есть уравнение окружности радиуса R = 5 с центром в точке (1; —3).

Если центр окружности совпадает с началом координат, то уравнение (2) принимает вид

Уравнение (3) называют каноническим уравнением окружности.

Задача 1. Написать уравнение окружности радиуса R = 7 с центром в начале координат.

Непосредственной подстановкой значения радиуса в уравнение (3) получим

Задача 2. Написать уравнение окружности радиуса R = 9 с центром в точке С(3; —6).

Подставив значение координат точки С и значение радиуса в формулу (2), получим

(х — 3) 2 + (у — (—6)) 2 = 81 или (х — 3) 2 + (у + 6) 2 = 81.

Задача 3. Найти центр и радиус окружности

Сравнивая данное уравнение с общим уравнением окружности (2), видим, что а = —3, b = 5, R = 10. Следовательно, С(—3; 5), R = 10.

Задача 4. Доказать, что уравнение

является уравнением окружности. Найти ее центр и радиус.

Преобразуем левую часть данного уравнения:

Это уравнение представляет собой уравнение окружности с центром в точке (—2; 1); радиус окружности равен 3.

Задача 5. Написать уравнение окружности с центром в точке С(—1; —1), касающейся прямой АВ, если A (2; —1), B(— 1; 3).

Напишем уравнение прямой АВ:

или 4х + 3y —5 = 0.

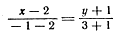
Так как окружность касается данной прямой, то радиус, проведенный в точку касания, перпендикулярен этой прямой. Для отыскания радиуса необходимо найти расстояние от точки С(—1; —1) — центра окружности до прямой 4х + 3y —5 = 0:

Напишем уравнение искомой окружности

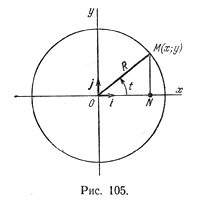
Пусть в прямоугольной системе координат дана окружность x 2 + у 2 = R 2 . Рассмотрим ее произвольную точку М(х; у) (рис. 105).

Пусть радиус-вектор OM > точки М образует угол величины t с положительным направлением оси Ох, тогда абсцисса и ордината точки М изменяются в зависимости от t

(0 2 = 3 cos 2 t, у 2 = 3 sin 2 t. Складывая эти равенства почленно, получаем

Числовая ось

Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.

Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .

Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .

Прямоугольная декартова система координат на плоскости

Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).

Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.

Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA₁ и AA₂ на прямые Ox и Oy соответственно (рис.3).

Определение 4 . Абсциссой точки A называют координату точки A₁ на числовой оси Ox , ординатой точки A называют координату точки A₂ на числовой оси Oy .

Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).

Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .

Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).

Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.

Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .

Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.

Формула для расстояния между двумя точками координатной плоскости

Утверждение 1 . Расстояние между двумя точками координатной плоскости

вычисляется по формуле

Доказательство . Рассмотрим рисунок 6.

| A₁A₂| 2 =
= ( x₂ – x₁) 2 + ( y₂ – y₁) 2 .

(1)

что и требовалось доказать.

Уравнение окружности на координатной плоскости

Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:

Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A (x ; y ) .

Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид

Определение: замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра О), лежащей в той же плоскости, что и кривая.

Определения связанные с окружностью

Хорда: отрезок, соединяющий две точки окружности.

Диаметр: хорда, проходящая через центр окружности. Диаметром окружности также называют длину этой хорды.

Пи ( ): Число 3, 141 592 653 589 793 . , равное отношению длины окружности к диаметру.

Радиус: отрезок, соединяющий центр окружности с какой-либо ее точкой (а так же длина этого отрезка).

Сектор круга: фигура, ограниченная двумя радиусами и дугой, на которую они опираются.

Касательная к окружности: прямая, перпендикулярная радиусу окружности, проведенная в точку касания.

Диаметр = 2 x радиус окружности

Длина окружности = x диаметр = 2 x радиус

Площадь круга :
площадь = r 2

Длина дуги окружности: (с центральным углом )
если выражен в градусах, то длина = x ( /180) x r
если выражен в радианах, то длина = r x

Площадь сектора окружности: (с центральным углом q )
если выражен в градусах, то площадь = ( /360) x r 2
если выражен в радианах, то площадь = ( /2) x r 2

Уравнение окружности: (в декартовых координатах)

для окружности с центром в точке (x , y ) и радиусом ( r ):

Уравнение окружности: (в полярных координатах)
для окружности с центром в точке (0, 0): r ( ) = радиус

для окружности с центром с полярными координатами: ( c , a ) и радиусом a :
r 2 – 2 cr cos ( – a ) + c 2 = a 2

Окружность на координатной плоскости

Окружность на плоскости — это множество точек на плоскости равноудаленных от точки центра. На рисунке данная точка обозначена C.

Окружность радиуса R с центром в начале координат представляется уравнением:

Окружность радиуса R с центром в точке C(a;b) представляется уравнением:

Расстояние от центра окружности С(a;b) до точки M(x;y) называется радиусом окружности R (на рисунке красная линия ).
Это уравнение можно записать в виде:

Если уравнение помножить на любое число A, то получим

Примечание
Окружность относится к линии второго порядка, так как представляется уравнением второй степени.

Необходимые условия для этого:
1. Отсутствие в уравнение второй степени члена с произведением xy;
2. Коэффициенты при x 2 и y 2 были равны в уравнение вида:

3. Если выполняется неравенство

Как найти радиус и центр окружности

Уравнение Ax 2 +Bx+Ay 2 +Cy+D=0 если оно удовлетворяет примечаниям (1, 2 и 3), то тогда (a;b) и радиус R окружности можно найти по формулам:

Пример 1
Уравнение 5x 2 -10x+5y 2 +20y-20=0
Здесь
A=5, B=-10, C=20, D=-20
Оно удовлетворяет примечаниям 1, 2 и выполняется неравенство

Решая, получаем что центр есть (1;-2), а радиус R=3

Анимационный график окружности

Пример 2
Уравнение второй степени x 2 +4xy+y 2 =1 не является окружностью, так как в нём есть член 4xy.

Пример 3
Уравнение второй степени 4x 2 +9y 2 =36 не представляет окружность, так как в нём коэффициенты при x 2 и y 2 не равны.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.3 / 5. Количество оценок: 4

Уравнение окружности по трем точкам

Калькулятор расчета онлайн уравнения окружности по трем заданным точкам, а также нахождение координат точки центра и радиус окружности.

Уравнение окружности

r 2 = (x — h) 2 + (y — k) 2

h,k — координаты центра Окружности
x,y — координаты точки окружности
r — радиус

Пример

Найдите координаты точки центра окружности, радиус и уравнение окружности, если известны координаты трех точек A (2,2), B (2,4) и C (5,5)

Решение :

Подставляем координаты точек в формулу

(2 — h) 2 + (2 — k) 2 = r 2
(2 — h) 2 + (4 — k) 2 = r 2
(5 — h) 2 + (5 — k) 2 = r 2

Шаг :2

Найдем значение k упрощая 1 и 2 уравнения

(2 — h) 2 + (2 — k) 2 = (2 — h) 2 + (4 — k) 2
4 — 4h + h 2 + 4 — 4k + k 2 = 4 — 4h + h 2 +16 — 8k + k 2
8 — 4k = 20 — 8k
k= 3

Шаг :3

Найдем значение h упрощая уравнения 2 и 3

(2 — h) 2 + (2 — k) 2 = (5 — h) 2 + (5 — k) 2
4 — 4h + h 2 + 4 — 4k + k 2 = 25 — 10h + h 2 + 25 — 10k + k 2
8 — 4k — 4h = 50 — 10h — 10k
6k + 6h = 42

Подставив значение k=3 в уравнение

Получаем координаты точки центра (h,k) = ( 4,3 )

Шаг :4

Подставим значения h,k в формулу

r 2 = (x — h) 2 + (y — k) 2
r 2 = (2 — 4) 2 + (2 — 3) 2
r 2 = (-2) 2 + (-1) 2
r 2 = 5
r = 2.24

Шаг :5

Подставим значения h, k в уравнение окружности

(x — h) 2 + (y — k) 2

Уравнение окружности = (x — 4) 2 + (y — 3) 2

[spoiler title=”источники:”]

http://b4.cooksy.ru/articles/kak-nayti-koordinaty-okruzhnosti-formula

http://wpcalc.com/uravnenie-okruzhnosti-po-trem-tochkam/

[/spoiler]

Источник

Если окружность задана уравнением вида

$[{(x - a)^2} + {(y - b)^2} = {R^2},]$

найти центр (a;b) и радиус R такой окружности несложно.

Примеры.

Определить по уравнению окружности координаты её центра и радиуса:

$[1){(x - 3)^2} + {(y - 7)^2} = 4;]$

$[2){(x + 2)^2} + {(y - 5)^2} = 1;]$

$[3){x^2} + {(y + 3)^2} = 9;]$

$[4){(x - 6)^2} + {y^2} = 5;]$

$[5){x^2} + {y^2} = 11.]$

Решение:

$[1){(x - 3)^2} + {(y - 7)^2} = 4;]$

a=3, b=7, R²=4.

Таким образом, центр данной окружности — точка (3;7), радиус R=2.

$[2){(x + 2)^2} + {(y - 5)^2} = 1;]$

a=-2, b=5, R²=1. Окружность с центром в точке (-2;5) и радиусом 1.

$[3){x^2} + {(y + 3)^2} = 9;]$

a=0, b=-3, R²=9.

Центр окружности — (0;-3), радиус R=3.

$[4){(x - 6)^2} + {y^2} = 5;]$

a=6, b=0, R²=5.

Центр — в точке (6;0), радиус R=√5.

$[5){x^2} + {y^2} = 11.]$

Это уравнение задаёт окружность с центром в начале координат. Центр — O(0;0), радиус R=√11.

Чтобы найти центр и радиус окружности, заданной уравнением вида

$[{x^2} + {y^2} - 2ax - 2by + c = 0,]$

нужно дополнить его до полных квадратов, чтобы привести к привычному виду.

Для этого сначала сгруппируем слагаемые

$[({x^2} - 2ax) + ({y^2} - 2by) + c = 0,]$

затем прибавим и вычтем квадрат второго слагаемого из формулы квадрата разности (2ax- удвоенное произведение первого слагаемого на второе. Первое — x, второе — a)

$[({x^2} - 2ax + {a^2}) - {a^2} + ({y^2} - 2by + {b^2}) - {b^2} + c = 0.]$

Отсюда

$[{(x - a)^2} + {(y - b)^2} + c - {a^2} - {b^2} = 0,]$

$[{(x - a)^2} + {(y - b)^2} = {a^2} + {b^2} - c.]$

При a²+b²-c>0 это уравнение задаёт окружность с радиусом

$[R = sqrt {{a^2} + {b^2} - c} .]$

При a²+b²-c=0 уравнению удовлетворяют координаты единственной точки (a;b).

При a²+b²-c<0 нет ни одной точки, удовлетворяющей этому уравнению.

Примеры.

Найти координаты центра и радиус окружности:

$[1){x^2} + {y^2} + 10x - 6y - 15 = 0;]$

$[2){x^2} + {y^2} - 5x + 4 = 0;]$

$[3)3{x^2} + 3{y^2} - 4x - 9y + 4 = 0.]$

Решение:

$[1){x^2} + {y^2} + 10x - 6y - 15 = 0]$

Группируем слагаемые

$[({x^2} + 10x) + ({y^2} - 6y) - 15 = 0]$

Выделяем в уравнении полные квадраты. В первых скобках удвоенное слагаемое 10x представляем как 10x=2·a·5 (чтобы получить 2ab для формулы a²+2ab+b²=(a+b)²). Получается, что b=5. Если прибавить и вычесть b², результат не изменится:

$[{x^2} + 10x = ({x^2} + 2 cdot x cdot 5 + {5^2}) - {5^2}.]$

Аналогично

$[{y^2} - 6y = ({y^2} - 2 cdot y cdot 3 + {3^2}) - {3^2}.]$

Таким образом,

$[({x^2} + 2 cdot x cdot 5 + {5^2}) - {5^2} + ({y^2} - 2 cdot y cdot 3 + {3^2}) - {3^2} - 15 = 0]$

$[{(x + 5)^2} + {(y - 3)^2} - 25 - 9 - 15 = 0]$

$[{(x + 5)^2} + {(y - 3)^2} = 49]$

Центром этой окружности является точка (-5;3), радиус R=7.

$[2){x^2} + {y^2} - 5x + 4 = 0]$

$[({x^2} - 5x) + {y^2} + 4 = 0]$

$[({x^2} - 2 cdot x cdot 2,5 + {2,5^2}) - {2,5^2} + {y^2} + 4 = 0]$

$[{(x - 2,5)^2} + {y^2} + 4 - 6,25 = 0]$

$[{(x - 2,5)^2} + {y^2} = 2,25]$

Центр окружности — точка (2,5;0), радиус R=1,5.

$[3)3{x^2} + 3{y^2} - 4x - 9y + 4 = 0]$

Разделим обе части уравнения на 3:

$[{x^2} + {y^2} - frac{4}{3}x - 3y + frac{4}{3} = 0]$

Далее — аналогично

$[({x^2} - frac{4}{3}x) + ({y^2} - 3y) + frac{4}{3} = 0]$

$[({x^2} - 2 cdot x cdot frac{2}{3} + {(frac{2}{3})^2}) - {(frac{2}{3})^2} + ({y^2} - 2 cdot y cdot frac{3}{2} + {(frac{3}{2})^2}) - ]$

$[ - {(frac{3}{2})^2} + frac{4}{3} = 0]$

$[{(x - frac{2}{3})^2} + {(y - frac{3}{2})^2} - frac{{{4^{backslash 4}}}}{9} - frac{{{9^{backslash 9}}}}{4} + frac{{{4^{backslash 12}}}}{3} = 0]$

$[{(x - frac{2}{3})^2} + {(y - frac{3}{2})^2} = frac{{49}}{{36}}]$

Центр этой окружности лежит в точке

$[(frac{2}{3};frac{3}{2}),R = frac{7}{6}.]$

Источник

РМ

Рафаел Махмудов

Источник

Как найти координаты центра окружности

Окружность − геометрическое место точек плоскости, равноудаленных от центра на некоторое расстояние, называемое радиусом. Если задана нулевая точка отсчета, единичный отрезок и направление координатных осей, центр окружности будет характеризоваться определенными координатами. Как правило, окружность рассматривают в декартовой прямоугольной системе координат.

Инструкция

Аналитически окружность задается уравнением вида (x-x0)²+(y-y0)²=R², где x0 и y0 − координаты центра окружности, R − ее радиус. Итак, центр окружности (x0;y0) здесь задан в явном виде.

Пример. Установите центр фигуры, заданной в декартовой системе координат уравнением (x-2)²+(y-5)²=25.Решение. Данное уравнение является уравнением окружности. Ее центр имеет координаты (2;5). Радиус такой окружности равен 5.

Уравнение x²+y²=R² соответствует окружности с центром в начале координат, то есть, в точке (0;0). Уравнение (x-x0)²+y²=R² означает, что центр окружности имеет координаты (x0;0) и лежит на оси абсцисс. Вид уравнения x²+(y-y0)²=R² говорит о расположении центра с координатами (0;y0) на оси ординат.

Общее уравнение окружности в аналитической геометрии запишется как: x²+y²+Ax+By+C=0. Чтобы привести такое уравнение к выше обозначенному виду, надо сгруппировать члены и выделить полные квадраты: [x²+2(A/2)x+(A/2)²]+[y²+2(B/2)y+(B/2)²]+C-(A/2)²-(B/2)²=0. Для выделения полных квадратов, как можно заметить, требуется добавлять дополнительные величины: (A/2)² и (B/2)². Чтобы знак равенства сохранялся, эти же величины надо вычесть. Прибавление и вычитание одного и того же числа не меняет уравнения.

Таким образом, получается: [x+(A/2)]²+[y+(B/2)]²=(A/2)²+(B/2)²-C. Из этого уравнения уже видно, что x0=-A/2, y0=-B/2, R=√[(A/2)²+(B/2)²-C]. Кстати, выражение для радиуса можно упростить. Домножьте обе части равенства R=√[(A/2)²+(B/2)²-C] на 2. Тогда: 2R=√[A²+B²-4C]. Отсюда R=1/2·√[A²+B²-4C].

Окружность не может быть графиком функции в декартовой системе координат, так как, по определению, в функции каждому x соответствует единственное значение y, а для окружности таких «игреков» будет два. Чтобы убедиться в этом, проведите перпендикуляр к оси Ox, пересекающий окружность. Вы увидите, что точек пересечения две.

Но окружность можно представить как объединение двух функций: y=y0±√[R²-(x-x0)²]. Здесь x0 и y0, соответственно, представляют собой искомые координаты центра окружности. При совпадении центра окружности с началом координат объединение функций принимает вид: y=√[R²-x²].

Обратите внимание

Две окружности, имеющие центром точку с одними и теми же координатами, называются концентрическими. Если они заданы уравнениями (x-x0)²+(y-y0)²=R² и (x-x0′)²+(y-y0′)²=R’², тогда x0=x0′, y0=y0′. В общем уравнении для концентрических окружностей A1=A2 и B1=B2.

Полезный совет

Кстати, в физике окружность может рассматриваться как тонкое однородное кольцо. Центр этого кольца будет являться центром масс (или центром инерции) такого тела. Если кольцо имеет массу m и радиус r, а через центр перпендикулярно плоскости кольца провести ось, то момент инерции кольца относительно оси будет равен mr². Момент инерции принципиально важен при рассмотрении вращательного движения тела.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Download Article

Finding the center of a circle can help you perform basic geometric tasks like finding the circumference or area. There are several ways to find the center point! You can draw crossed lines, you can draw overlapping circles, or you can use a straightedge and ruler.

Things You Should Know

Measure out and draw a set of crossed lines inside of a circle to pinpoint the center.
Sketch two separate sets of overlapping circles to identify the exact center point.
Draw a square snugly around the circle. Sketch an “X” between all 4 corners of the square to find the circle’s center.

1
Draw a circle. Use a compass, or trace any circular object. The size of the circle does not matter. If you’re finding the center of an existing circle, then you don’t need to draw a new circle.
- A geometry compass is a tool specifically designed to draw and measure circles. Buy one in a school or office supply store!^[1]
2
Sketch a chord between two points. A chord is a straight line segment that links any two points along the edge of a curve.^[2] Name the chord AB.
- Consider using a pencil to sketch your lines. This way, you can erase the marks once you’ve found the center. Draw with a light touch so that it’ll be easier to erase.
Advertisement
3

Draw a second chord. This line should be parallel and equal in length to the first chord that you drew. Name this new chord CD.^[3]
4

Make another line between A and C. This third chord (AC) should stretch through the center of the circle – but you will need to draw one more line to find the exact center point.
5

Join B and D. Draw one final chord (BD) across the circle between Point B and Point D. This new line should cross over the third chord (AC) that you drew.
6

Find the center. If you have drawn straight and accurate lines, then the center of the circle lies at the intersection of the crossed lines AC and BD.^[4] Mark the center point with a pen or pencil. If you only want the center point marked, then erase the four chords that you drew.

1

Draw a chord between two points. Use a ruler or straightedge to draw a straight line inside the circle, from one edge to another. The points that you use don’t matter. Label the two points A and B.
2
Use a compass to draw two overlapping circles. The circles should be the exact same size. Make A the center of one circle, and B the center of the other. Space the two circles so that they overlap like a Venn diagram.
- Draw these circles in pencil, not pen. The process will be simpler if you are able to erase these circles later on.
3

Draw a vertical line through the two points at which the circles intersect. There will be a point at the top and a point at the bottom of the “Venn diagram” space created between the overlap of the circles. Use a ruler to make sure that the line protrudes straight through these points. Finally, label the two points (C and D) at which this new line crosses the rim of the original circle. This line marks the diameter of the original circle.
4

Erase the two overlapping circles. This should clear up your work space for the next step of the process. Now, you should have a circle with two perpendicular lines running through it. Do not erase the center points (A and B) of these circles! You will be drawing two new circles.
5

Sketch two new circles. Use your compass to draw two equal circles: one with the point C at its center, and one with the point D. These circles, too, should overlap like a Venn diagram. Remember: C and D are the points at which the vertical line intersects the main circle.
6

Draw a line through the points at which these new circles intersect. This straight, horizontal line should cut through the overlap space of the two new circles. This line is the second diameter of your original circle, and it should be exactly perpendicular to the first diameter line.
7

Find the center. The intersection point of the two straight diameter lines is the exact center of the circle! Mark this center point for reference. If you want to clean up the page, feel free to erase the diameter lines and the non-original circles.

1

Draw two straight, intersecting tangent lines onto the circle. The lines can be completely random. However, the process will be easier if you make them roughly square or rectangular.^[5]
2

Translate both of the lines to the other side of the circle. You will end up with four tangent lines forming a parallelogram or a rough rectangle.
3

Draw the diagonals of the parallelogram. The point where these diagonal lines intersect is the circle’s center.
4

Check the accuracy of the center with a compass. The center should be on target as long as you didn’t slip while translating the lines or when drawing the diagonals. Feel free to erase the parallelogram and diagonal lines.

Practice Problems and Answers

Add New Question

Question

How do you find the center of a circle if you’re only given the equation?

David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.

Academic Tutor

Expert Answer
Question

How do you find the center of the circle if you’re only given the endpoints of the diameter?

David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.

Academic Tutor

Expert Answer
Question

In the first method, what do I do if the chords are of different lengths?

It’s not easy to construct parallel chords of equal length. In practice, it would be a process of trial and error until you get the chords you need. But the real goal here is to find the center of a circle, and here’s a way to do it without worrying about equal and parallel chords: (1) draw any two or more chords; (2) perpendicularly bisect each chord (using either a compass or a ruler and right triangle; (3) the perpendicular bisectors will intersect at the circle’s center.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

You can also find the center of a circle by mathematically “completing the square.”^[6] This is useful if you are given a circle equation, but you aren’t working with a physical circle.
Try using graph paper instead of blank or ruled paper. It might help to have the perpendicular lines and boxes for guidance.
If you have right angled square, place the corner anywhere along the circumference. Draw the 2 lines that intersect the circumference. Draw a line between those 2 points. Repeat on any other point on the circle. Where the lines intersect is the centrepoint.

A straightedge is not the same as a ruler. A straightedge can be any straight and even surface, but a ruler shows measurements. You can turn a straightedge into a functional ruler by marking it with inch or centimeter increments.
In order to find the true center of a circle, you must use a geometric compass and a straightedge.

Things You’ll Need

Pencil
Paper
Straightedge
Geometric compass
Grid paper

References

About This Article

Article SummaryX

To find the center of a circle, start by drawing a straight line between 2 points on the circle. Don’t worry about trying to draw the straight line so it’s in the center — anywhere on the circle will do. Then, draw a second straight line that’s parallel to the first line on the opposite side of the circle. Next, draw a diagonal line from the first end of the first line to the opposite end of the second line. Repeat with the other two ends so that you’ve drawn an “X.” The point where the lines intersect is the center of the circle! If you want to learn how to draw overlapping circles to find the center, keep reading the article!

Did this summary help you?

Thanks to all authors for creating a page that has been read 755,194 times.

Reader Success Stories

“I had a circular piece of wood that was a circular tabletop that I wanted to use for something else. I needed to…” more

Did this article help you?

Источник

Как найти координаты центр окружности??

Как найти координаты окружности формула

Как найти координаты центр окружности??

Формула окружности в системе координат

Числовая ось

Прямоугольная декартова система координат на плоскости

Формула для расстояния между двумя точками координатной плоскости

Уравнение окружности на координатной плоскости

Окружность на координатной плоскости

Окружность радиуса R с центром в начале координат представляется уравнением:

Как найти радиус и центр окружности

Уравнение окружности по трем точкам

Уравнение окружности

Пример

Решение :

Шаг :2

Шаг :3

Шаг :4

Шаг :5

Как найти координаты центра окружности

Things You Should Know

Practice Problems and Answers

Things You’ll Need

References

About This Article

Reader Success Stories

Did this article help you?

Вам также может понравиться

Как составить отчетность в росстат

Как найти клад в озере

Как найти человеку хобби

Добавить комментарий Отменить ответ