Формула как найти время через ускорение

Прямолинейное равноускоренное движение — это прямолинейное движение, при котором скорость тела изменяется (увеличивается или уменьшается) на одну и ту же величину за равные промежутки времени.

Ускорение — физическая величина, характеризующая быстроту изменения скорости тела. То есть, показывает, на какую величину изменяется скорость за единицу времени.

Примеры равноускоренного движения:

• разгон самолета перед взлетом;
• падающая с крыши сосулька;
• торможение лыжника на горном склоне;
• разгоняющийся на склоне сноубордист;
• свободное падение в результате прыжка с парашютом;
• камень брошенный под углом к горизонту;

Равномерное прямолинейное движение является частным случаем равноускоренного движения, при котором ускорение равно нулю.

Равноускоренное движение: формулы

Формула для скорости при равноускоренном движении:

где: V_к — конечная скорость тела,
V_н — начальная скорость тела,
a=const — ускорение (a>0 при ускорении, a<0 при замедлении)
t — время.

Формула для ускорения при равноускоренном движении:

Во время движения тела ускорение остается постоянным.

Задача 1

Кирилл ехал на велосипеде со скоростью 6 м/с, затем начал разгоняться на горке. Чему будет равна его скорость через 10 секунд, если ускорение равно 0,5 м/с?
Решение. Vн=6м/с, ускорение a=0,5м/с, время разгона t=10 секунд.
Получаем: Vн= 6 + 0,5 · 10 = 11 м/с.
Ответ: за 10с Кирилл разгонится до скорости 11 м/с.

Формула расстояния при равноускоренном движении

• Если известны  время, скорость начальная и скорость конечная

• Если известны время, скорость начальная и ускорение

где: S — путь, пройденный за время t,
Vн — начальная скорость,
Vк — конечная скорость,
a — ускорение тела,
t — время.

В случае равноускоренного движения с неизвестным временем движения, но с заданными начальной и конечной скоростями пройденный путь можно найти с помощью следующей формулы:

где S — путь, пройденный за время t ,
V0 — начальная скорость,
V — скорость в момент времени t,
a — ускорение тела.

Задача 2

Таксист получил заказ и начал движение с ускорением 0,1 м/с2. На каком расстоянии от начала движения его скорость станет равной 15м/с?
Решение. Так как таксист начал движение, начальная скорость равна нулю (Vн=0), Vк=15м/с, ускорение a=0,1м/с2.
Получаем: ​
S = 15^2 — 0^2 =1125 м.
Ответ: на расстоянии 1 125 м от начала движения скорость такси станет равной 15 м/с.

Перемещение при равноускоренном движении

Важно напомнить разницу между путем и перемещением тела.

• Путь — длина траектории. Если тело движется в любом направлении, то его путь увеличивается. Путь — всегда положительное значение.
• Перемещение — вектор, соединяющий начальное и конечное положение тела. Проекция перемещения может принимать отрицательное значение.

Например, если путник прошел в одну сторону расстояние S1, а обратно — S2, то: путь тела равен S1 + S2, а перемещение равно S1 − S2. В некоторых задачах путь и перемещение могут совпадать, но не всегда.

Равноускоренное движение: графически

График зависимости ускорения от времени:
Во время движения тела ускорение остается постоянным.

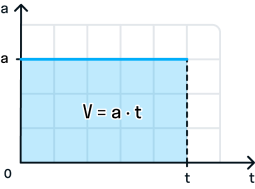
Взаимосвязь скорости, времени и расстояния:
На рисунке показан график,  в котором скорость равномерно увеличивается.
С помощью графика скорости можно определить ускорение тела как тангенс угла наклона графика к оси времени.

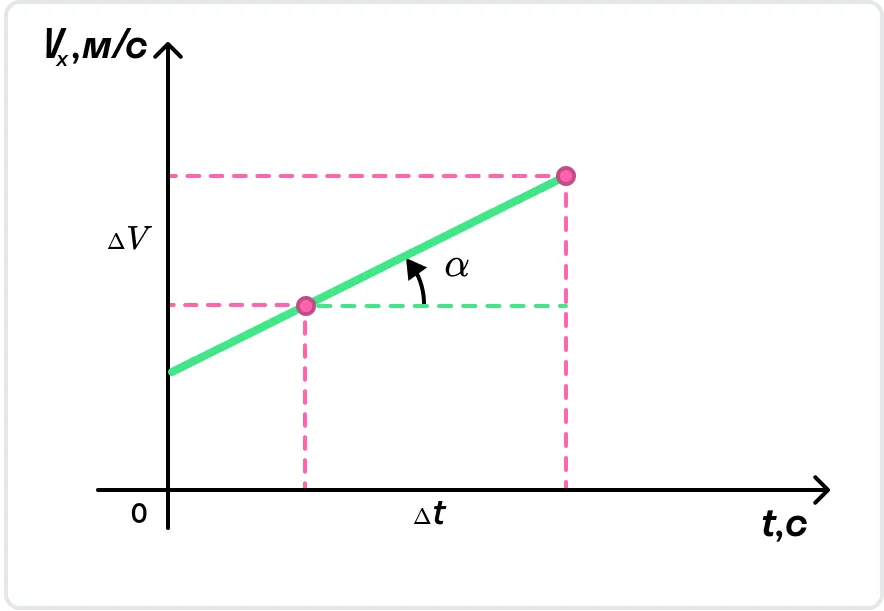
Из графика скорости получим формулу пути при равноускоренном движении тела.

Пройденный телом путь при равноускоренном движении численно равен площади фигуры под графиком зависимости скорости от времени. Вычислим площадь трапеции как сумму площадей прямоугольника V_нt и треугольника at²/2. Получим: S = V_нt + at²/2.​

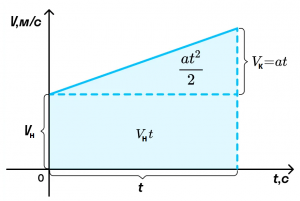
Математически зависимость координаты от времени при равноускоренном движении представляет собой квадратичную функцию, ее график — парабола.

Задача 3

Лыжник подъехал со скоростью 3 м/с к спуску длиной 36 м и съехал с него за несколько секунд, при этом его конечная скорость составила 15 м/с. Определите местонахождение лыжника спустя 2с после начала движения из начала координат.

Дано:
Vн = 3 м/с, начальная координата (t) равна нулю,
Vк = 15м/с, 
a —  скорость лыжника увеличивается, поэтому ускорение — положительное число,
S = 36м — путь с горы,
t — 2с.

Решение:
Найдем ускорение из формулы пути при равноускоренном движении: 2аS = V_к²−V_н² 
Получим:  а = (V_к²−V_н² )/2S = (225-9)/(2*36) = 3 м/с2.
Составим уравнение движения лыжника исходя из формулы: S = V_нt + at²/2.
Получаем: x(t) =  3t + 1,5t² 
По уравнению определим координату лыжника в момент времени t = 2с:
Получаем: x(2) =  3*2 + 1,5*2² =6+6=12 м.

Ответ: через 2 с после начала движения координата лыжника будет равна 12 м.

Для того, чтобы проверить правильность решения задач на равноускоренное движение, воспользуйтесь калькулятором равноускоренного движения.

Для того, чтобы перевести единицы измерения, воспользуйтесь конвертерами единиц измерения:

• Конвертер единиц измерения расстояния (длины)
• Конвертер единиц измерения скорости
• Конвертер единиц измерения времени

«Формула времени. Решение задач»

Скорость, время и расстояние — физические величины, взаимосвязаны процессом движения. Виды движений: 1) равномерное (прямолинейное, криволинейное и по окружности), 2) равноускоренное (с постоянным ускорением), 3) гармоническое. Для каждого вида движения своя формула времени.

Время обозначается как t. Единица измерения времени – с (секунды).

Самая простая формула при равномерном прямолинейном движении. Время, необходимое для прохождения пути равняется частному от деления пути на скорость равномерного прямолинейного движения: t = S / v.

При равноускоренном движении время равняется частному от деления разницы конечной и начальной скорости на ускорение: t = (v — v₀) / a  или частному от деления пути на разность конечной и начальной скорости: t = S / (v — v₀).

Решение задач через формулу времени

Задача № 1.

Конькобежец может развивать скорость до 13 м/с. За какое время он пробежит дистанцию длиной 2,6 км?

 Ответ: 200 с.

---

Задача № 2.

Двигаясь с ускорением 5 м/с² скорость космической ракеты увеличилась на 100 м/с. За какое время произошло такое изменение скорости?

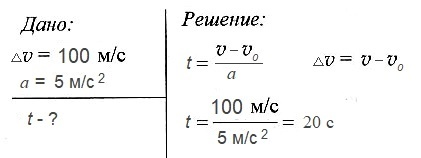 Ответ: 20 с.

---

Задача № 3.

Пункты А и В находятся на берегу реки на некотором расстоянии друг от друга. Моторная лодка проходит расстояние АВ вниз по течению реки за время t₁ = 3 ч, а плот то же расстояние – за время t₀ =12 ч. Какое время t₂ затратит моторная лодка на обратный путь?

Решение. Обозначим расстояние между пунктами А и В через L, скорость моторной лодки относительно воды через v_л , а скорость течения через v_т. Тогда t₀ = L / v_т ,  t₁ = L / (v_л +  v_т) ,  t₂ = L / (v_л —  v_т) . Исключая из записанной системы уравнений L, v_л и  v_т
находим 

Ответ: 6 ч.

---

Конспект урока «Формула времени. Решение задач».

Следующая тема: «».

Равноускоренное движение

Равноускоренное движение – это движение, при котором вектор ускорения не меняется по модулю и направлению (в случае равнозамедленного движения модуль скорости равномерно меняется). Примеры такого движения: велосипед, который катится с горки; камень брошенный под углом к горизонту. Равномерное движение, в отличие от неравномерного, – частный случай ускоренного в равной степени движения с ускорением, равным нулю.

Рассмотрим случай свободного падения (тело брошено под углом к горизонту) более подробно с вычислением. Такое движение можно рассчитать и представить в виде суммы движений относительно вертикальной и горизонтальной осей.

Как найти ускорение в физике? Нахождение ускорения в физике происходит с учетом того, что в любой точке траектории на тело действует ускорение свободного падения g→, которое не меняется по величине и всегда направлено в одну сторону. 

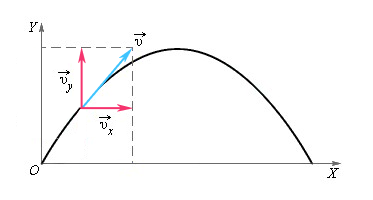
Вдоль оси X движение равномерное и прямолинейное, а вдоль оси Y – движение равноускоренное и прямолинейное. Будем рассматривать определенные проекции векторов скорости и ускорения на оси.

Формулы для равноускоренного движения

Формула для скорости (формула ускорения) при равноускоренном движении:

v=v0+at.

Здесь v0 – начальная скорость тела, a=const – ускорение.

Покажем на графике, что при равноускоренном движении зависимость v(t) имеет вид прямой линии. Вот небольшой тест.

​​​​​​​

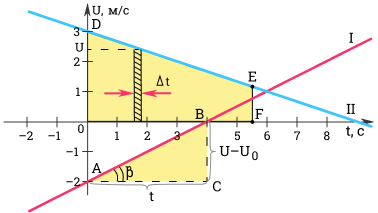
Как найти ускорение? Ускорение можно определить по углу наклона графика скорости. На рисунке выше модуль ускорения равен отношению сторон треугольника ABC. Вот как выглядит формула ускорения в физике.

a=v-v0t=BCAC

Чем больше угол β, тем больше наклон (крутизна) графика по отношению к оси времени. Соответственно, тем больше ускорение тела.

Для первого графика: v0=-2 мс; a=0,5 мс2.

Для второго графика: v0=3 мс; a=-13 мс2.

По данному графику физик может также вычислить (произвести определение) перемещение тела за время t. Как это сделать?

Выделим на графике малый отрезок времени ∆t. Будем считать, что он настолько мал, что движение за время ∆t можно считать равномерным движением со скоростью, равной скорости тела в середине промежутка ∆t. Тогда, перемещение ∆s за время ∆t будет равно ∆s=v∆t.

Разобьем все время t на бесконечно малые промежутки ∆t. Перемещение s за время t равно площади трапеции ODEF.

s=OD+EF2OF=v0+v2t=2v0+(v-v0)2t.

Мы знаем, что v-v0=at, поэтому окончательная формула или расчет для перемещения тела примет вид:

s=v0t+at22

Для того чтобы найти координату тела в данный момент времени, нужно к начальной координате тела добавить перемещение (расстояние). Изменение координаты в зависимости от времени выражает закон равноускоренного движения.

Какова будет формула пути при равноускоренном движении? В этом случае путь изменяется согласно квадратной зависимости: 8=v0t + at²/2.

Закон равноускоренного движения

y=y0+v0t+at22.

Еще одна распространенная задача кинематики, которая возникает при анализе равноускоренного движения – находить координаты при заданных значениях начальной и конечной скоростей и ускорения.

Исключая из записанных выше уравнений t и решая их, получаем:

s=v2-v022a.

По известным начальной скорости, ускорению и перемещению может находиться конечная скорость тела:

v=v02+2as.

При v0=0 s=v22a и v=2as

Величины v, v0, a, y0, s, входящие в выражения, являются алгебраическими величинами. Они могут принимать как положительные, так и отрицательные значения – это будет зависеть от характера движения и направления координатных осей в условиях конкретной задачи.

Равноускоренное движение: формулы, примеры

Равноускоренное движение

Равноускоренное движение – это движение, при котором вектор ускорения не меняется по модулю и направлению. Примеры такого движения: велосипед, который катится с горки; камень брошенный под углом к горизонту. Равномерное движение – частный случай равноускоренного движения с ускорением, равным нулю.

Рассмотрим случай свободного падения (тело брошено под уголом к горизонту) более подробно. Такое движение можно представить в виде суммы движений относительно вертикальной и горизонтальной осей.

В любой точке траектории на тело действует ускорение свободного падения g → , которое не меняется по величине и всегда направлено в одну сторону.

Вдоль оси X движение равномерное и прямолинейное, а вдоль оси Y – равноускоренное и прямолинейное. Будем рассматривать проекции векторов скорости и ускорения на оси.

Формулы для равноускоренного движения

Формула для скорости при равноускоренном движении:

Здесь v 0 – начальная скорость тела, a = c o n s t – ускорение.

Покажем на графике, что при равноускоренном движении зависимость v ( t ) имеет вид прямой линии.

​​​​​​​

Ускорение можно определить по углу наклона графика скорости. На рисунке выше модуль ускорения равен отношению сторон треугольника ABC.

a = v – v 0 t = B C A C

Чем больше угол β , тем больше наклон (крутизна) графика по отношению к оси времени. Соответственно, тем больше ускорение тела.

Для первого графика: v 0 = – 2 м с ; a = 0 , 5 м с 2 .

Для второго графика: v 0 = 3 м с ; a = – 1 3 м с 2 .

По данному графику можно также вычислить перемещение тела за время t . Как это сделать?

Выделим на графике малый отрезок времени ∆ t . Будем считать, что он настолько мал, что движение за время ∆ t можно считать равномерным движением со скоростью, равной скорости тела в середине промежутка ∆ t . Тогда, перемещение ∆ s за время ∆ t будет равно ∆ s = v ∆ t .

Разобьем все время t на бесконечно малые промежутки ∆ t . Перемещение s за время t равно площади трапеции O D E F .

s = O D + E F 2 O F = v 0 + v 2 t = 2 v 0 + ( v – v 0 ) 2 t .

Мы знаем, что v – v 0 = a t , поэтому окончательная формула для перемещения тела примет вид:

s = v 0 t + a t 2 2

Для того, чтобы найти координату тела в данный момент времени, нужно к начальной координате тела добавить перемещение. Изменение координаты в зависимости от времени выражает закон равноускоренного движения.

Закон равноускоренного движения

y = y 0 + v 0 t + a t 2 2 .

Еще одна распространенная задача кинематики, которая возникает при анализе равноускоренного движения – нахождение координаты при заданных значениях начальной и конечной скоростей и ускорения.

Исключая из записанных выше уравнений t и решая их, получаем:

s = v 2 – v 0 2 2 a .

По известным начальной скорости, ускорению и перемещению можно найти конечную скорость тела:

v = v 0 2 + 2 a s .

При v 0 = 0 s = v 2 2 a и v = 2 a s

Величины v , v 0 , a , y 0 , s , входящие в выражения, являются алгебраическими величинами. В зависимости от характера движения и направления координатных осей в условиях конкретной задачи они могут принимать как положительные, так и отрицательные значения.

Время, скорость, расстояние

О чем эта статья:

Расстояние

Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.

Расстояние — это длина от одного пункта до другого.

• Например: расстояние от дома до школы 3 км, от Москвы до Петербурга 705 км.

Расстояние обозначается латинской буквой s.

Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).

Формула пути

Чтобы найти расстояние, нужно умножить скорость на время движения:

s = v × t

Скорость

Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.

Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.

Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.

Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.

Формула скорости

Чтобы найти скорость, нужно разделить путь на время:

v = s : t

Показатели скорости чаще всего выражаются в м/сек или км/час.

Скорость сближения — это расстояние, на которое сблизились два объекта за единицу времени. Чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, надо сложить скорости этих объектов.

Скорость удаления — расстояние, на которое отдалились друг от друга два объекта за единицу времени.

Чтобы найти скорость удаления объектов, которые движутся в противоположных направлениях, нужно сложить скорости этих объектов.

Чтобы найти скорость удаления при движении с отставанием или скорость сближения при движении вдогонку, нужно из большей скорости вычесть меньшую.

Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.

Время

Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.

Время — это продолжительность каких-то действий, событий.

• Например: от метро до дома — 10 минут, от дома до дачи — 2 часа.

Время движения обозначается латинской буквой t.

Чаще всего вам будут встречаться такие единицы времени, как секунды, минуты и часы.

Формула времени

Чтобы найти время, нужно разделить расстояние на скорость:

t = s : v

Эта формула пригодится, если нужно узнать, за какое время тело преодолеет то или иное расстояние.

Взаимосвязь скорости, времени, расстояния

Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.

Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.

Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес-браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?

Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров в минуту на 15 минут, мы определим расстояние от дома до магазина:

s = v × t = 50 × 15 = 750 (м)

Ответ: мы прошли 750 метров.

Если известно время и расстояние, то можно найти скорость: v = s : t.

Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние между двором и площадкой — 100 метров. Первый школьник добежал за 25 секунд, второй за 50 секунд. Кто добежал быстрее?

Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников — это расстояние, которое они пробегают за 1 секунду.

Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:

Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).

В нашей задаче расстояние дано в метрах, а время в секундах. Значит, будем измерять скорость в метрах в секунду (м/с).

100 м : 25 с = 4 м/с

Так мы узнали, что скорость движения первого школьника 4 метра в секунду.

Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:

Значит, скорость движения второго школьника составляет 2 метра в секунду.

Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.

Скорость первого школьника больше. Значит, он добежал до спортивной площадки быстрее.

Ответ: первый школьник добежал быстрее.

Если известны скорость и расстояние, то можно найти время: t = s : v.

Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?

Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?

Чтобы ответить на этот вопрос, нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое дойдем до стадиона:

t = s : v = 500 : 100 = 5 (мин)

Ответ: от школы до стадиона мы дойдем за 5 минут.

Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.

Формулы равномерного и равноускоренного движения

Равномерное движение

Формула скорости движения при равномерном движении: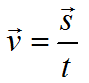

v=const
a=0
v — скорость, м/с
s — перемещение, м
t — время, с
Формула перемещения при равномерном движении: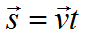

Координата вычисляются через кинематическое уравнение равномерного прямолинейного движения по формуле: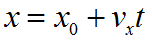

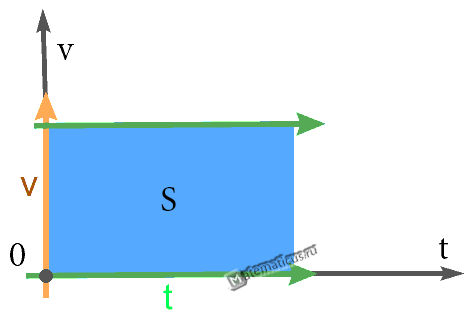
График — Равномерного прямолинейного движения

Равноускоренное движение

Формула скорости при равноускоренном движении: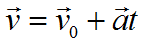

a=const
v₀ — начальная скорость, м/с
a — ускорение, м/с 2
Формула для нахождения перемещения при равноускоренном движении: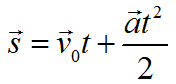

или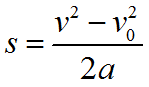

Уравнение равноускоренного движения в проекции на оси координат: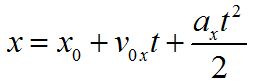

Формула для определения ускорения при равноускоренном прямолинейном движении: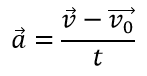

v₀ — начальная скорость, м/с
v — мгновенная скорость, м/с
Формула для определения средней скорости движения: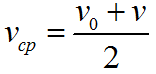

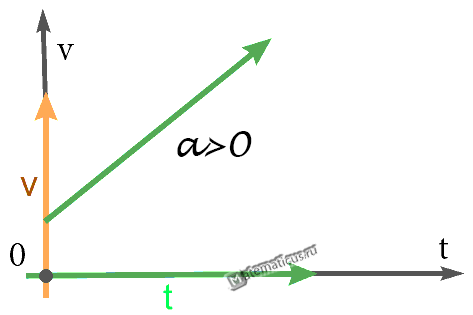
График — Равноускоренное движение при a>0

Равнозамедленное движение

Формула скорости при равнозамедленном движении: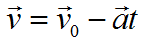

Формула перемещения при равнозамедленном движении: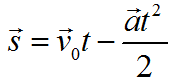

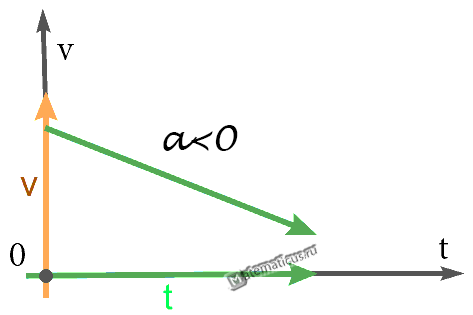
График — Равнозамедленное движение при a 2
Формула для вычисления скорости при свободном падении тела: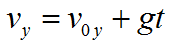

Формула для вычисления перемещения при свободном падении тела: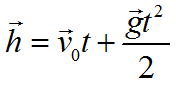


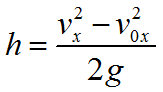
Формула координаты при свободном падении тела: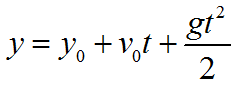

Формула высоты с которой тело свободно падает: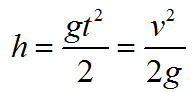

Формула для определения скорости тела в конце свободного падения: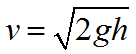

Время свободного падения тела равно: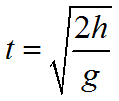

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.7 / 5. Количество оценок: 45

[spoiler title=”источники:”]

http://skysmart.ru/articles/mathematic/vremya-skorost-rasstoyanie

[/spoiler]