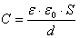Формула как найти заряд на обкладках конденсатора

Одним из важных элементов электрической цепи является конденсатор, формулы для которого позволяют рассчитать и подобрать наиболее подходящий вариант. Основная функция данного устройства заключается в накоплении определенного количества электроэнергии. Простейшая система включает в себя два электрода или обкладки, разделенные между собой диэлектриком.

В чем измеряется емкость конденсатора

Одной из важнейших характеристик конденсатора является его емкость. Данный параметр определяется количеством электроэнергии, накапливаемой этим прибором. Накопление происходит в виде электронов. Их количество, помещающееся в конденсаторе, определяет величину емкости конкретного устройства.

Для измерения емкости применяется единица – фарада. Емкость конденсатора в 1 фараду соответствует электрическому заряду в 1 кулон, а на обкладках разность потенциалов равна 1 вольту. Эта классическая формулировка не подходит для практических расчетов, поскольку в конденсаторе собираются не заряды, а электроны. Емкость любого конденсатора находится в прямой зависимости от объема электронов, способных накапливаться при нормальном рабочем режиме.

Для обозначения емкости все равно используется фарада, а количественные параметры определяются по формуле: С = Q / U, где С означает емкость, Q – заряд в кулонах, а U является напряжением. Таким образом, просматривается взаимная связь заряда и напряжения, оказывающих влияние на способность конденсатора к накоплению и удержанию определенного количества электричества.

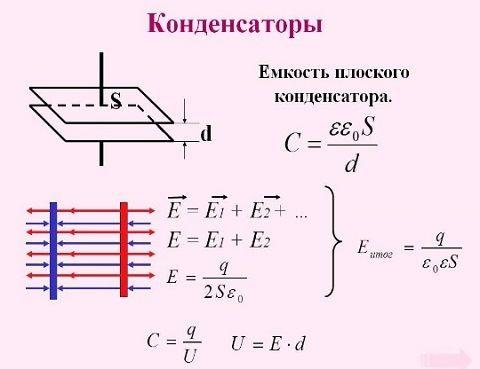
Для расчетов емкости плоского конденсатора используется формула:
в которой ε = 8,854187817 х 10^-12 ф/м представляет собой постоянную величину. Прочие величины: ε – является диэлектрической проницаемостью диэлектрика, находящегося между обкладками, S – означает площадь обкладки, а d – зазор между обкладками.

Формула энергии конденсатора

С емкостью самым тесным образом связана другая величина, известная как энергия заряженного конденсатора. После зарядки любого конденсатора, в нем образуется определенное количество энергии, которое в дальнейшем выделяется в процессе разрядки. С этой потенциальной энергией вступают во взаимодействие обкладки конденсатора. В них образуются разноименные заряды, притягивающиеся друг к другу.

В процессе зарядки происходит расходование энергии внешнего источника для разделения зарядов с положительным и отрицательным значением, которые, затем располагаются на обкладках конденсатора. Поэтому в соответствии с законом сохранения энергии, она не исчезает бесследно, а остается внутри конденсатора в виде электрического поля, сосредоточенного между пластинами. Разноименные заряды образуют взаимодействие и последующее притяжение обкладок между собой.

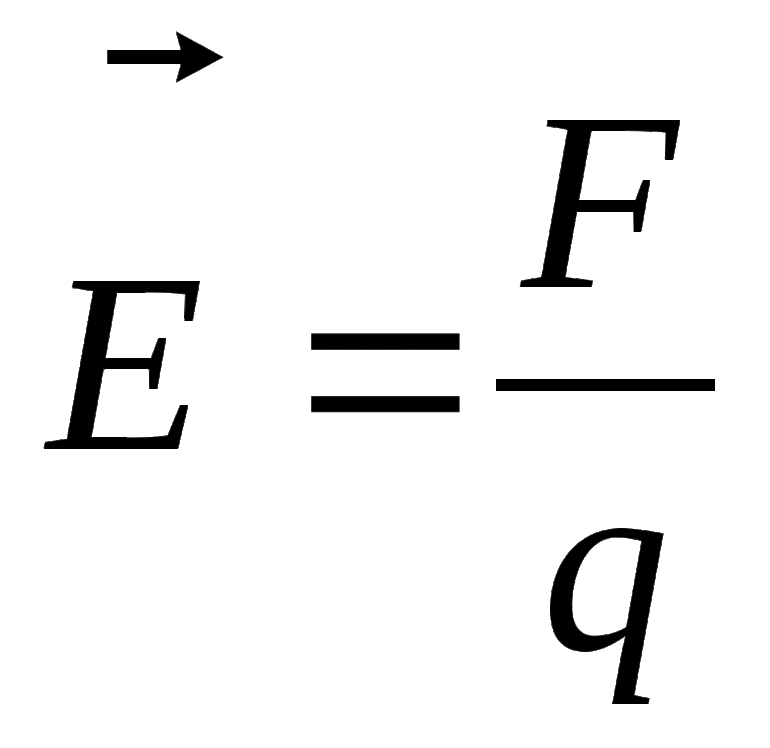
Каждая пластина конденсатора под действием заряда создает напряженность электрического поля, равную Е/2. Общее поле будет складываться из обоих полей, возникающих в каждой обкладке с одинаковыми зарядами, имеющими противоположные значения.

Таким образом, энергия конденсатора выражается формулой: W=q(E/2)d. В свою очередь, напряжение выражается с помощью понятий напряженности и расстояния и представляется в виде формулы U=Ed. Это значение, подставленное в первую формулу, отображает энергию конденсатора в таком виде: W=qU/2. Для получения окончательного результата необходимо использовать определение емкости: C=q/U, и в конце концов энергия заряженного конденсатора будет выглядеть следующим образом: W_эл = CU²/2.

Формула заряда конденсатора

Для выполнения зарядки, конденсатор должен быть подключен к цепи постоянного тока. С этой целью может использоваться генератор. У каждого генератора имеется внутреннее сопротивление. При замыкании цепи происходит зарядка конденсатора. Между его обкладками появляется напряжение, равное электродвижущей силе генератора: U_c = E.

Обкладка, подключенная к положительному полюсу генератора, заряжается положительно (+q), а другая обкладка получает равнозначный заряд с отрицательной величиной (- q). Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.

В процессе зарядки одна из обкладок конденсатора приобретает, а другая теряет определенное количество электронов. Они переносятся по внешней цепи под влиянием электродвижущей силы генератора. Такое перемещение является электрическим током, известным еще как зарядный емкостной ток (Iзар).

Течение зарядного тока в цепи происходит практически за тысячные доли секунды, до того момента, пока напряжение конденсатора не станет равным электродвижущей силе генератора. Напряжение увеличивается плавно, а потом постепенно замедляется. Далее значение напряжения конденсатора будет постоянным. Во время зарядки по цепи течет зарядный ток. В самом начале он достигает максимальной величины, так как напряжение конденсатора имеет нулевое значение. Согласно закона Ома I_зар = Е/R_i, поскольку к сопротивлению Ri приложена вся ЭДС генератора.

Формула тока утечки конденсатора

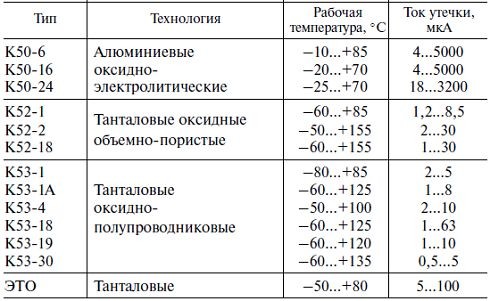
Ток утечки конденсатора вполне можно сравнить с воздействием подключенного к нему резистора с каким-либо сопротивлением R. Ток утечки тесно связан с типом конденсатора и качеством используемого диэлектрика. Кроме того, важным фактором становится конструкция корпуса и степень его загрязненности.

Некоторые конденсаторы имеют негерметичный корпус, что приводит к проникновению влаги из воздуха и возрастанию тока утечки. В первую очередь это касается устройств, где в качестве диэлектрика использована промасленная бумага. Значительные токи утечки возникают из-за снижения электрического сопротивления изоляции. В результате нарушается основная функция конденсатора – способность получать и сохранять заряд электрического тока.

Основная формула для расчета выглядит следующим образом: I_ут = U/R_d, где I_ут, – это ток утечки, U – напряжение, прилагаемое к конденсатору, а R_d – сопротивление изоляции.

Наряду с резисторами одними из наиболее часто используемых электронных компонентов являются конденсаторы. И в этой статье мы разберемся, из чего они состоят, как работают и для чего применяются 👍 В первую очередь, рассмотрим устройство и принцип работы, а затем плавно перейдем к основным свойствам и характеристикам – заряду, энергии и, конечно же, емкости конденсатора.

Плоский конденсатор.

Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин:

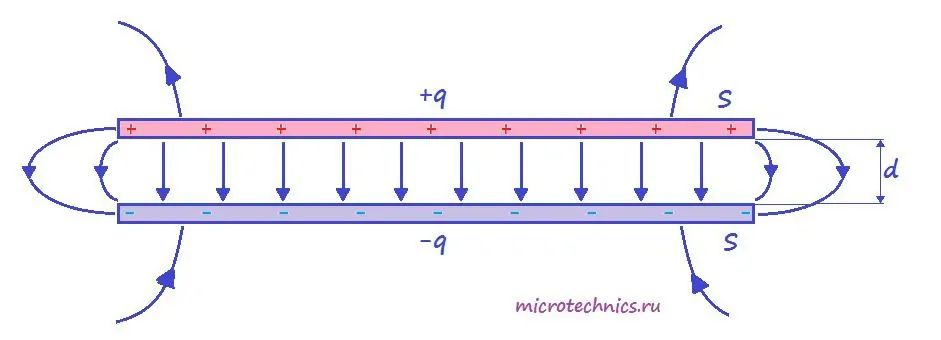
Такое устройство называется плоским конденсатором, а пластины – обкладками конденсатора. Стоит уточнить, что здесь мы рассматриваем уже заряженный конденсатор (сам процесс зарядки мы изучим чуть позже), то есть на обкладках сосредоточен определенный заряд. Причем наибольший интерес представляет тот случай, когда заряды пластин конденсатора одинаковы по модулю и противоположны по знаку (как на рисунке).

А поскольку на обкладках сосредоточен заряд, между ними возникает электрическое поле. Поле плоского конденсатора, в основном, сосредоточено между пластинами, однако, в окружающем пространстве также возникает электрическое поле, которое называют полем рассеяния. Очень часто его влиянием в задачах пренебрегают, но забывать о нем не стоит.

Для определения величины этого поля рассмотрим еще одно схематическое изображение плоского конденсатора:

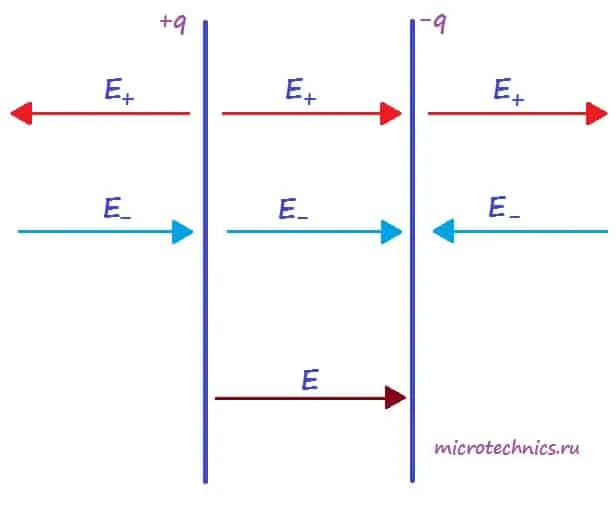
Каждая из обкладок конденсатора в отдельности создает электрическое поле:

• положительно заряженная пластина (+q) создает поле, напряженность которого равна E_{+}
• отрицательно заряженная пластина (-q) создает поле, напряженность которого равна E_{-}

Выражение для напряженности поля равномерно заряженной пластины выглядит следующим образом:

E_{пл} = frac{sigma}{2varepsilon_0thinspacevarepsilon}

Здесь sigma– это поверхностная плотность заряда: sigma = frac{q}{S}, а varepsilon – диэлектрическая проницаемость диэлектрика, расположенного между обкладками конденсатора. Поскольку площадь пластин конденсатора у нас одинаковая, как и величина заряда, то и модули напряженности электрического поля, равны между собой:

E_+ = E_- = frac{q}{2varepsilon_0thinspacevarepsilon S}

Но направления векторов разные – внутри конденсатора вектора направлены в одну сторону, а вне – в противоположные. Таким образом, внутри обкладок результирующее поле определяется следующим образом:

E = E_+ + E_- = frac{q}{2varepsilon_0thinspacevarepsilon S} + frac{q}{2varepsilon_0thinspacevarepsilon S} = frac{q}{varepsilon_0thinspacevarepsilon S}

Соответственно, вне конденсатора (слева и справа от обкладок) поля пластин компенсируют друг друга и результирующая напряженность равна 0.

Процессы зарядки и разрядки конденсаторов.

С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. На принципиальных электрических схемах конденсатор обозначают следующим образом:

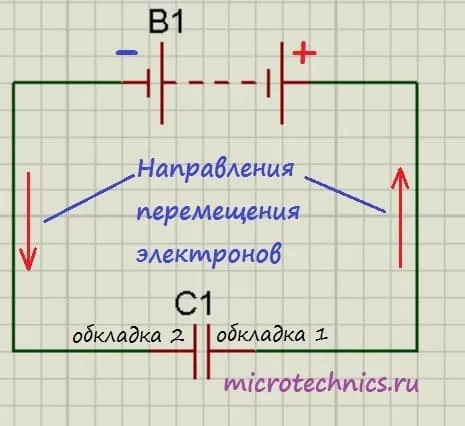
Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что будет происходить?

Свободные электроны с первой обкладки конденсатора устремятся к положительному полюсу источника. Из-за этого на обкладке возникнет недостаток отрицательно заряженных частиц, и она станет положительно заряженной. В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора. В результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной.

Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную разность потенциалов. Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока. После этого процесс зарядки закончится, и перемещение электронов по цепи прекратится.

При отключении от источника конденсатор может на протяжении длительного времени сохранять накопленные заряды. Соответственно, заряженный конденсатор является источником электрической энергии, это означает, что он может отдавать энергию во внешнюю цепь. Давайте создадим простейшую цепь, просто соединив обкладки конденсатора друг с другом:

В данном случае по цепи начнет протекать ток разряда конденсатора, а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Именно так происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию. Как видите, здесь нет ничего сложного.

Емкость и энергия конденсатора.

Важнейшей характеристикой является электрическая емкость конденсатора. Это физическая величина, которая определяется как отношение заряда q одного из проводников к разности потенциалов между проводниками:

C = frac{q}{Deltavarphi} = frac{q}{U}

Емкость конденсатора изменяется в Фарадах, но величина 1 Ф является неимоверно большой, поэтому чаще всего используются микрофарады (мкФ), нанофарады (нФ) и пикофарады (пФ). А поскольку мы уже вывели формулу для расчета напряженности, то давайте выразим напряжение на конденсаторе следующим образом:

U = Ed = frac{qd}{varepsilon_0thinspacevarepsilon S}

Здесь у нас d – это расстояние между пластинами конденсатора, а q – заряд конденсатора. Подставим эту формулу в выражение для емкости:

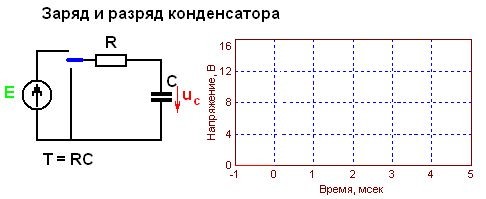
C = frac{qvarepsilon_0thinspacevarepsilon S}{qd} = frac{varepsilon_0thinspacevarepsilon S}{d}

Если в качестве диэлектрика выступает воздух, то во всех формулах можно подставить varepsilon = 1. Для запасенной же энергии конденсатора справедливы следующие выражения:

W = frac{CU^2}{2} = frac{qU}{2} = frac{q^2}{2C}

Помимо емкости конденсаторы характеризуются еще одним параметром, а именно величиной напряжения, которое может выдержать его диэлектрик. При слишком больших значениях напряжения электроны диэлектрика отрываются от атомов, и диэлектрик начинает проводить ток. Это явление называется пробоем конденсатора, и в результате обкладки оказываются замкнутыми друг с другом. Собственно, характеристикой, которая часто используется при работе с конденсаторами является не напряжение пробоя, а рабочее напряжение. Это такая величина напряжения, при которой конденсатор может работать неограниченно долгое время, и пробоя не произойдет.

Итак, резюмируем – сегодня рассмотрели основные свойства конденсаторов, их устройство и характеристики, так что на этом заканчиваем статью, а в следующей мы будем обсуждать различные варианты соединений и маркировку.

Общие сведения

Слово «конденсатор» переводится с латинского как «сгущение». Поэтому устройство, позволяющее получить однородное электрическое поле, и было названо эти термином. В физике существует чёткое определение такого прибора. Согласно ему, конденсатором называется система из двух плоских проводников расстояние между которыми гораздо меньше их размеров. Первым таким устройством стала «Лейденская банка».

В 1745 году голландец Питерван Мушенбрук и его ученик Кюнеус в городе Лейдене собрали прибор в форме банки предназначенный для хранения и накапливания зарядов. Устройство содержало следующие компоненты:

• стеклянный цилиндр;
• внешнюю и внутреннюю оболочки;
• деревянную пробку;
• проволочный проводник.

Оболочки покрывали сосуд примерно на две трети и были выполнены из листового олова. Через пробку обеспечивающую герметичность банки проходил металлический стержень. Касаясь подводника заряженным телом, учёный передавал заряды в ёмкость. При соприкосновении электроны перемещались на проводник и накапливались на электроде. В итоге одна обкладка конденсатора заряжалась положительно, а другая — отрицательно.

Как оказалось, такая конструкция была способна накапливать запас электричества. Изобретение первого конденсатора привело к более глубокому изучению природы электричества. С его помощью стало возможным разобраться в поведении диэлектриков и проводников, понять механизм разделения зарядов.

С физической точки зрения, в устройстве проходят следующие процессы. Две разделённые пластины заряжаются частицами с разным знаком. Вектор напряжённости положительно заряженного проводника направлен от него во все стороны. При этом силовые линии, которые создаются между обкладками не зависят от расстояния, одинаковые по модулю и направлению. Поэтому с внешней стороны отрицательной пластины создаётся такое же поле, но с линиями входящими в неё.

Так как заряды на электродах одинаковые, то напряжённость поля внутри обкладок равняется E = E1 * E2 = 2E1 = 2E2. Снаружи силовые линии направлены друг на друга, поэтому суммарное значение энергии за пластинами равняется нулю.

Таким образом, конденсатор не только позволяет создавать внутри него однородное поле, но и блокировать его снаружи. Следовательно, такое устройство может набрать довольно высокое значение заряда.

Электрическая ёмкость

Способность устройства накапливать заряд прежде всего зависит от его ёмкости. Найти её величину можно разделив заряд, сосредоточенный на пластинах, на разность потенциалов между ними: C = q / U. Полученный результат измеряется в фарадах [F]. Так, ёмкость в 1 фарад будет равняться значению заряда в 1 кулон создавшему напряжение на выводах конденсатора 1 вольт. Кулон — это довольно большая величина. Поэтому на практике при различных расчётах приходится иметь дело с микрофарадами (µF), нанофарадами (nF) и пикофарадами (pF).

После создания «Лейденской банки» учёные провели ряд экспериментов, направленных на увеличение количества запасаемой энергии устройством. Так было обнаружено, что если между обкладками конденсатора поместить диэлектрик, то он не только предотвращает замыкание проводников, но и влияет на ёмкость.

Пусть имеется устройство пластины которого имеют площадь S. Между обкладками размещён непроводник тока, характеризующийся диэлектрической проницаемостью ε. Это коэффициент, показывающий во сколько раз напряжённость в однородном поле меньше чем создаваемое значение теми же зарядами в вакууме.

Можно предположить, что положительный заряд будет скапливаться на левой пластине, а отрицательный на правой. Чтобы найти ёмкость конденсатора нужно воспользоваться следующей последовательностью действий:

1. Найти напряжённость поля в середине устройства. Для этого каждую обкладку нужно представить, как бесконечно однородно заряженную плоскость. Тогда: E1 = σ / (2 * ε * ε0). Так как поля внутри складываются, то расчётная формула примет вид: E = σ / (ε * ε0).
2. Определить поверхностную плотность зарядов. Это величина, показывающая чему равняется отношение заряда к площади, по которой он распределён: σ = q / S.
3. Выразить напряжение между пластинами через заряд. Между обкладками поле однородное. Значит, напряжение можно найти умножением напряжённости на расстояние: U = E * d. Тогда, пользуясь полученными формулами для E и σ, можно записать: U = (q * d) / (ε * ε0 * S).
4. Вычислить электрическую ёмкость, подставив выражения в формулу: C = q / U. В результате получится: C = (ε * ε0 * S) / d.

Таким образом, чем больше площадь пластин, тем выше ёмкость конденсатора. Отсюда следует, что будет больше накоплен заряд. При этом его величина зависит и от расстояния между пластинами. Если d уменьшается, то ёмкость увеличивается.

Энергия устройства

Зарядить конденсатор мгновенно невозможно. Для этого процесса требуется определённое время. Это явление используется в радиотехнике. Так, с помощью конденсатора сглаживаются импульсные всплески. В первом приближении конденсатор похож на аккумулятор. Но при этом он отличается от него принципом накопления энергии, ёмкостью и скоростью заряда разряда. При подключении источника питания к выводам обкладок устройства конденсатор накапливает на них заряд.~

Работу устройства можно объяснить по аналогии с протеканием воды. Пусть имеется сосуд с жидкостью площадью поперечного сечения S. По сути, это эквивалент ёмкости. Тогда вода это будет заряд, а высота водяного столба — напряжение. Получается, что энергия — это произведение зарядов на высоту. Но если аккумулятор можно представить как сосуд, в котором имеется тонкий шланг (вывод) и по которому вытекает вода (заряд), то в конденсаторе его диаметр трубки будет равен размеру всей банки. То есть устройство может мгновенно отдать весь накопленный заряд.

При подаче напряжения на обкладки происходит электризация диэлектрика. В результате происходит смещение и на пластины передаётся энергия. На одной из них возникнет избыток электронов, и она условно зарядится отрицательно, а на второй недостаток — проводник станет положительным. Поэтому в формуле, определяющей заряд на обкладках конденсатора, большое значение имеет диэлектрическая проницаемость непроводящего ток вещества.

Между обкладками возникает сила. Величина действующей со стороны первой равняется F = ε1 * q, а со стороны второй F = ε2 * q. Таким образом, можно записать: F = ε1 * q = ε2 * q = E / 2 * q. При увеличении расстояние между обкладками от нулевого до d, будет выполняться работа: A = F * d. Она направлена на преодоление силы взаимодействия между заряженными проводниками.

То есть: A = E / 2 * q * d. Исходя из того, что ε = U/d будет верно записать: А = 1 / 2 q * U. Значит, механическая работа A в соответствии с законом сохранения энергии будет равна количеству зарядов, запасённых в электрическом поле конденсатора: Wэ = C * U² / 2.

Следует отметить, что при подаче переменного сигнала внутри диэлектрика происходит постоянная смена знаков заряда. В итоге происходит нагревание, что приводит конденсатор к выходу из строя. Характеризуется это явление тангенсом угла диэлектрических потерь. Определяется он как отношение затраченной мощности к реактивной.

Заряд и разряд

Процесс зарядки конденсатора не может быть мгновенным. Его время зависит от силы тока и электроёмкости. При подключении источника питания на одном проводнике собираются электроны, а на другом — остаются протоны. Так как между обкладками находится диэлектрик, то заряженные частицы не могут перейти на противоположную сторону. Но вместе с тем, электроны поступают от источника напряжения на пластины, поэтому ток в цепи всё же есть.

В начале периода зарядки разность потенциалов между обкладками равняется нулю. Как только на пластины переходят заряженные частицы, возникает напряжение. Происходит это из-за диэлектрика, который не даёт притягивающимся друг к другу зарядам перейти на другую сторону. В момент заряда конденсатора на его обкладках много свободного места. Электрический ток в этот момент не встречает сопротивления, и его величина достигает максимального значения. По мере разделения заряженных частиц сила тока снижается. Это происходит до тех пор, пока не исчезнет свободное место на обкладках конденсатора.

То время, которое проходит между начальным состоянием и полного заряда, называют переходным периодом заряда конденсатора. В его конце прекращается рост напряжения, и оно становится равным значению, выдаваемому источником питания. Если нарисовать зависимости тока и напряжения заряда от времени на графике, то можно будет увидеть, что их изменения проходят зеркально по отношению друг к другу.

Формула, по которой можно рассчитать, как происходит заряд конденсатора выглядит так: I = C * V / t, где:

• I — сила тока;
• С — ёмкость конденсатора;
• V / t — изменение напряжения за время.

Как только источник питания будет отключён, то вся энергия, запасённая конденсатором, будет отдана в нагрузку. Фактически устройство само на этом моменте превращается в источник питания. Электроны из-за силы притяжения существующей между разноимёнными частицами, начнут перемещаться в сторону положительно заряженной обкладки.

В начальный момент подключения нагрузки, напряжение на конденсаторе равно тому, что выдавал источник питания.

Но в тот момент, когда в цепи появится ток, конденсатор начнёт отдавать энергию, а напряжение на его выводах станет падать. Следовательно, сила тока тоже снизится. При этом время зарядки и разрядки конденсатора определяется двумя параметрами — ёмкостью и сопротивлением цепи.

Для учащихся (для лучшего понимания физики).

Вспомним основное из предыдущей статьи.

Плоский конденсатор представляет собой устройство, состоящее из двух металлических пластин (обкладок), между которыми находится диэлектрик.

На практике конденсаторы нашли очень широкое применение благодаря их способности накапливать на обкладках значительные электрические заряды. При этом между обкладками возникает разность потенциалов (напряжение).

Конденсаторы характеризуются электрической ёмкостью С:

Ёмкость конденсатора численно равна отношению заряда на одной из обкладок к напряжению между обкладками

или

ёмкость конденсатора численно равна заряду, который надо сообщить обкладке конденсатора, чтобы повысить напряжение между обкладками на единицу напряжения.

Надо помнить, что заряд конденсатора и его напряжение зависят друг от друга, а ёмкость конденсатора не зависит ни от заряда, ни от напряжения, она только численно равна их отношению.

Ёмкость плоского конденсатора зависит лишь от его размеров (от площади пластин, расстояния между ними) и от диэлектрической проницаемости среды между обкладками:

Заряжаются конденсаторы от источников постоянного тока (см. статью “Зарядка конденсатора. Зарядный и разрядный ток проводимости”

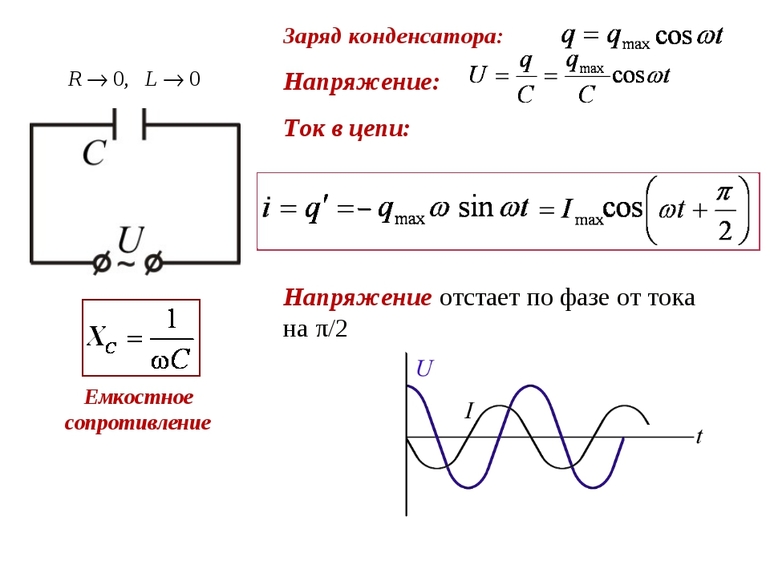
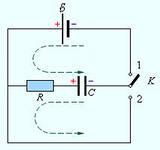
На рисунке ниже показана электрическая цепь, состоящая из источника постоянного напряжения, конденсатора и сопротивления:

В момент замыкания ключа К возникший в цепи ток (рисунок справа) имеет максимальное значение, так как разность потенциалов между полюсом источника и обкладкой конденсатора (она не была заряжена) максимальна.

По мере роста заряда на обкладке ток в цепи уменьшается, обращаясь в нуль в момент, когда напряжение на конденсаторе станет равным напряжению на клеммах источника:

Если заряженный конденсатор отключить от источника (следующий рисунок) и замкнуть его обкладки через сопротивление, то по цепи пойдёт разрядный ток, направленный в сторону обратную зарядному току.

Ниже на одном рисунке показаны кривые зависимости зарядного и разрядного тока от времени, из которого видно, что и зарядный, и разрядный токи имеют максимальные значения в моменты замыкания цепей.

При разрядке конденсатор является источником электрической энергии, отдаваемой во внешнюю цепь.

Чтобы энергия конденсаторов постоянно пополнялась, их включают в электрические цепи, содержащие источники постоянного тока. Такие цепи называют ещё конденсаторными цепями.

Дальше рассмотрим некоторые задачи на расчёт таких цепей. Расчёт сводится, как правило, к нахождению заряда конденсаторов или напряжения на конденсаторах.

Задача.

При решении задач на конденсаторные цепи можно кроме способов, применённых при решении рассмотренных выше задач, пользоваться первым, вторым, третьим и четвёртым правилами.

Сейчас на примере качественного решения следующей задачи рассмотрим перечисленные правила.

Задача

Найти заряд каждого конденсатора в изображённой на рисунке цепи, если известны ЭДС источников постоянного тока и ёмкости конденсаторов.

Сначала подумаем, какие обкладки конденсаторов заряжены положительно, а какие – отрицательно.

Левая обкладка первого конденсатора и правая обкладка третьего конденсатора заряжены отрицательно, так как они соединены с отрицательными полюсами источников. По этой же причине верхняя обкладка второго конденсатора заряжена положительно. Другие обкладки конденсаторов имеют противоположные знаки.

Первое правило

Если в цепи есть точки, в которых сходятся провода обкладок конденсаторов, не соединённых с источником, то их общий заряд равен нулю.

В нашей задаче такой точкой является точка В.

Второе правило

В цепи находим точки равного потенциала и соединяем их в узлы. Потенциал одного из узлов принимаем за нуль. Заряд каждого конденсатора выражаем через его ёмкость и разность потенциалов (напряжение).

Наша цепь содержит два узла А и В. Примем потенциал узла В за нуль.

Третье правило

Для любого замкнутого контура в конденсаторной цепи алгебраическая сумма ЭДС, входящих в контур, равна алгебраической сумме напряжений на конденсаторах в контурах.

В статье “Как найти заряды конденсаторов в цепи …” всё это проделано для нашей задачи и получен ответ.

Все четыре правила расчёта конденсаторных цепей подробно с примерами рассмотрены в статье Занятии 54 и следующих за ней четырёх статьях.

Итак, пользуясь изложенными здесь методами и правилами можно решать сложные задачи на расчёт цепей постоянного тока, содержащих конденсаторы.

К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Спасибо.

Для школьников предлагаются подборки материала по темам:

!. Механика. Кинематика. Равномерное прямолинейное движение.

2. Равнопеременное прямолинейное движение.

Предыдущая запись: Ёмкость уединённого проводника. Ёмкость конденсатора. Почему диэлектрик повышает ёмкость конденсатора?

Следующая запись: Явление электростатической индукции в задачах.

Ссылки на занятия до электростатики даны в Занятии 1 .

Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .

Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.

Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70 .

1. Конденсаторы.

Емкостью обладают
не только отдельные проводники, но и
системы проводников. Система, состоящая
из двух проводников, разделенных слоем
диэлектрика, называется конденсатором.
Проводники в этом случае называются
обкладками конденсатора. Заряды на
обкладках имеют противоположные знаки,
но по модулю – одинаковы. Практически
все поле конденсатора сосредоточено
между обкладками и.

Емкостью конденсатора
называется величина

С=
,

(1)

где q
– абсолютная величина заряда одной из
обкладок, U
– разность потенциалов (напряжение)
между обкладками.

В зависимости от
формы обкладок, конденсаторы бывают
плоскими, сферическими, цилиндрическими.

Найдем емкость
плоского конденсатора, обкладки которого
имеют площадь S,
расположены на расстоянии d,
а пространство между обкладками заполнено
диэлектриком с диэлектрической
проницаемостью ε.

Если поверхностная
плотность заряда на обкладках равна σ
(σ=
),
то напряженность поля конденсатора
(поле считается однородным) равна:

Е=

=

Разность потенциалов
между обкладками связана с напряженностью
поля: Е =
, откуда получим U=Ed
=

=

Используя формулу
( 1 ), получим для емкости плоского
конденсатора выражение:

С
=
(2)

1. Соединение конденсаторов.

Используются два
основных вида соединения: последовательное
и параллельное.

При параллельном
соединении (рис 1), общая емкость батареи
равна сумме емкостей всех конденсаторов:

С_общ.=
С₁
+С₂+С₃+…=ΣС_i
. (3)

При последовательном
соединении (рис.2) величина, обратная
общей емкости, равна сумме величин,
обратных емкостям всех конденсаторов:

.
(4)

Если последовательно
соединены n
конденсаторов с одинаковой емкостью
С, то общая емкость: С_общ.=

Рис. 1.Параллельное
соединение. Рис. 2.Последовательное
соединение

1. Энергия конденсатора.

Если процесс
зарядки конденсатора является медленным
(квазистационарным), то можно считать,
что в каждый момент времени потенциал
любой из обкладок конденсатора во всех
точках одинаков. При увеличении заряда
на величину dq
совершается работа
,
где u
– мгновенное значение напряжения между
обкладками конденсатора. Учитывая, что
,
получаем:
.
Если емкость не зависит от напряжения,
то эта работа идет на увеличение энергии
конденсатора. Интегрируя данное
выражение, получим:

,

где W
– энергия конденсатора, U
– напряжение между обкладками заряженного
конденсатора.

Используя связь
между зарядом, емкостью конденсатора
и напряжением, можно представить
выражение для энергии заряженного
конденсатора в других видах:

.

(5)

1. Квазистационарные токи. Процессы зарядки и разрядки конденсатора.

При зарядке или
разрядке конденсатора в цепи конденсатора
течет ток. Если изменения тока происходят
очень медленно, то есть за время
установления электрического равновесия
в цепи изменения токов и э.д.с. малы, то
для определения их мгновенных значений
можно использовать законы постоянного
тока. Такие медленно меняющиеся токи
называют квазистационарными.

Так как скорость
установления электрического равновесия
велика, под понятие квазистационарных
токов подпадают и довольно быстрые в
обычном понимании процессы: переменный
ток, многие электрические колебания,
используемые в радиотехнике.
Квазистационарными являются и токи
зарядки или разрядки конденсатора.

Рассмотрим
электрическую цепь, общее сопротивление
которой обозначим R.
Цепь содержит конденсатор емкостью C,
подключенный к источнику питания с
э.д.с. ε (рис. 3).

Рис. 3. Процессы
зарядки и разрядки конденсатора.

Зарядка
конденсатора.
Применяя к контуру εRC1ε
второе правило Кирхгофа, получим:

,

где I,
U
– мгновенные значения силы тока и
напряжения на конденсаторе (направление
обхода контура указано стрелкой).

Учитывая, что
,
,
можно привести уравнение к одной
переменной:

.

Введем новую
переменную:
.
Тогда уравнение запишется:

.

Разделив переменные
и проинтегрировав, получим:
.

Для определения
постоянной А используем начальные
условия:

t=0,
U=0,
u=
– ε.
Тогда получим: А= – ε.
Возвращаясь к переменной
,
получим окончательно для напряжения
на конденсаторе выражение:

.

(6)

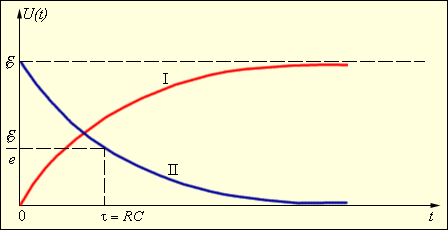
С течением времени
напряжение на конденсаторе растет,
асимптотически приближаясь к э.д.с.
источника (рис.4, I.).

Разрядка
конденсатора. Для
контура CR2C
по второму правилу Кирхгофа: RI=U.
Используем также:

,
и

(ток течет в обратном направлении).

Приведя к переменной
U,
получим:

.
Интегрируя, получим:
.

Постоянную
интегрирования B
определим из начальных условий: t=0,
U=ε.
Тогда получим: В=ε.

Для напряжения на
конденсаторе получим окончательно:

.

(7)

С течением времени
напряжение падает, приближаясь к 0 (рис.
4, II).

Рис. 4. Графики
зарядки (I)
и разрядки (II)
конденсатора.

1. Постоянная
   времени.
   Характер протекания процессов зарядки
   и разрядки конденсатора (установление
   электрического равновесия) зависит от
   величины:

,

(8)

которая имеет
размерность времени и называется
постоянной времени электрической цепи.
Постоянная времени показывает, через
какое время после начала разрядки
конденсатора напряжение уменьшается
в e
раз (е=2,71).

Теория метода

Прологарифмируем
выражение (7):

(учли,
что RC=τ).

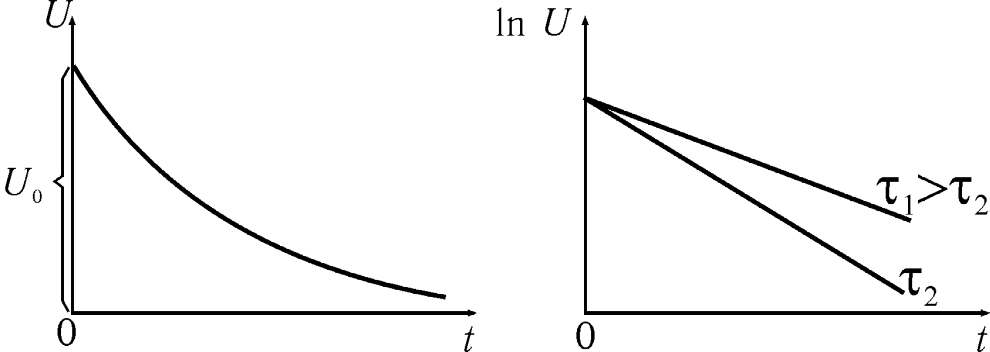
График зависимости
lnU
от t
(линейная зависимость) выражается прямой
линией (рис.5), пересекающей ось y
(lnU)
в точке с координатами (0; lnε).
Угловой коэффициент К этого графика и
будет определять постоянную времени
цепи:
,
откуда:

.

(9)

Рис. 5. Зависимость
натурального логарифма напряжения от
времени при разрядке конденсатора

Используя формулы:


и
,
можно
получить, что для одного и того же
интервала времени
:

.

Отсюда:
.

(10)

Экспериментальная
установка

Установка состоит
из основного блока – измерительного
модуля, имеющего клеммы для подключения
дополнительных элементов, источника
питания, цифрового мультиметра и набора
минимодулей с различными значениями
сопротивления и емкости.

Для выполнения
работы собирается электрическая цепь
в соответствии со схемой, изображенной
на верхней панели модуля. В гнезда «R₁»
подключается минимодуль с номиналом
1Мом, в гнезда «R₂»
– минимодуль
с номиналом 100Ом. Параметры исследуемого
конденсатора, подключаемого в гнезда
«С», задаются преподавателем. В гнезда
подключения амперметра устанавливается
перемычка. В гнезда вольтметра подключается
цифровой мультиметр в режиме вольтметра.

Следует отметить,
что сопротивления резисторов заряда-разряда
(минимодулей) R
и цифрового вольтметра R_V
образуют делитель напряжения, что
приводит к тому, что фактически
максимальное напряжение на конденсаторе
будет равно не ε, а
,

где r₀–
сопротивление источника питания.
Соответствующие поправки необходимо
будет вносить и при вычислении постоянной
времени. Однако, если входное сопротивление
вольтметра (10⁷Ом)
значительно превышает сопротивление
резисторов, и сопротивление источника
мало, то данными поправками можно
пренебречь.

Порядок выполнения
работы

1. Собрать электрическую
   цепь с заданным преподавателем значением
   емкости. Тумблер (переключатель
   заряда-разряда) установить в среднее
   положение (стоп). Переключатель предела
   измерения цифрового мультиметра
   установить в положение «20В» (режим
   измерения постоянного напряжения).

2. Подключить модуль
   к сети переменного тока (клавиша
   включения на задней панели модуля) и
   установить выходное напряжение
   ,
   заданное преподавателем (6,5В-15В). Включить
   цифровой мультиметр. Нажатием кнопки
   «Сброс» подготовить модуль к началу
   измерений.

3. Тумблер перевести
   в положение «Заряд». При этом запускается
   секундомер, и начинает меняться
   напряжение на конденсаторе (показания
   вольтметра). Довести напряжение на
   конденсаторе до значения примерно
   0,8ε.

4. Сбросить показания
   секундомера нажатием кнопки «Сброс».
   Перевести тумблер в положение «Разряд»
   и измерять напряжения на конденсаторе
   при его разрядке с интервалом времени
   5с. Занести данные в таблицу 1.

5. Подключить в цепь
   конденсатор с неизвестным значением
   емкости и повторить измерения по п. 4.
   Данные занести в таблицу 2.

6. Подключить в цепь
   конденсатор и резистор с другим известным
   значением емкости. Повторить измерения
   по п. 4. Данные занести в таблицу 3.

7. Нажать кнопку
   «Сброс». Выключить источник питания и
   мультиметр. Отключить от сети измерительный
   модуль и отсоединить от него дополнительные
   элементы.

Таблица
1

Таблица
2

Таблица
3

Обработка
результатов измерения

По результатам
измерений студенты выполняют одно из
следующих заданий (по указанию
преподавателя).

Задание 1.
Построение кривых разрядки конденсаторов
и экспериментальное подтверждение
закона, описывающего данный процесс.

1. Используя данные,
   взятые из таблиц 1 и 3, постройте графики
   зависимости напряжения от времени при
   разрядке конденсаторов С₁и
   С₂.
   Проанализируйте их, сравните с
   теоретическими (рис. 4).

2. Постройте графики
   разрядки конденсаторов С₁и
   С₂
   в осях (lnU,
   t).
   Проанализируйте их, сравните с
   теоретическими (рис. 5).

3. Определите по
   графикам угловые коэффициенты К₁и
   К_2.
   Среднее значение углового коэффициента
   находится как отношение, определяющее
   тангенс угла наклона прямой:

.

1. Случайные
   погрешности графическим методом можно
   оценить по отклонению опытных точек
   относительно проведенной прямой.
   Относительная погрешность углового
   коэффициента может быть найдена согласно
   формуле:

,

где δ(lnU)
– отклонение (в проекции на ось lnU)
от прямой линии наиболее удаленной
опытной точки,

– интервал, на котором сделаны измерения.

1. По значениям
   угловых коэффициентов определите
   постоянные времени τ₁
   и τ₂,
   используя формулу (9). Сравните полученные
   значения со значениями постоянной
   времени, рассчитанными по формуле (8).

2. Посчитайте
   относительные и абсолютные погрешности
   для постоянной времени:
   
   ,
   .

3. Сделайте выводы
   о соответствии экспериментальных
   графиков экспоненциальному виду
   зависимости напряжения от времени, и
   о влиянии постоянной времени на
   протекание процессов зарядки и разрядки
   конденсатора.

Задание 2.
Определение неизвестной емкости
конденсатора.

1. Используя данные,
   взятые из таблиц 1 и 2, постройте графики
   зависимости напряжения от времени при
   разрядке конденсаторов С₁
   и С_х.
   Проанализируйте их, сравните с
   теоретическими (рис. 4).

2. Постройте графики
   разрядки конденсаторов С₁
   и С_х
   в осях (lnU,
   t).
   Сравните их и сделайте вывод о соотношении
   постоянных времени (см. рис.5).

3. Определите по
   формуле (10) неизвестную емкость, используя
   графики и данные таблиц 1 и 2.

4. Найдите относительные
   погрешности угловых коэффициентов ε_К1
   и ε_кх
   (см. п.4
   задания 1).

5. Определите
   относительную и абсолютную погрешности
   емкости:

,
.

1. Сравните полученное
   значение С_х
   со значением,
   измеренным при помощи цифрового
   мультиметра в режиме измерения емкости.
   Сделайте вывод.

Дополнительное
задание.

Рассчитайте энергию
заряженного конденсатора, используя
формулу (5).

Контрольные
вопросы

1. Что представляет
   собой конденсатор? Что называется
   емкостью конденсатора?

2. Докажите, что
   электрическое поле плоского конденсатора
   сосредоточено между его обкладками.

2. Сколько надо
взять конденсаторов емкостью 2мкФ и как
их соединить,

чтобы получить
общую емкость 5 мкФ?

1. Как можно найти
   энергию заряженного конденсатора?

2. Какие токи
   называются квазистационарными? Почему
   токи зарядки и разрядки конденсатора
   можно отнести к квазистационарным?

3. По какому закону
   изменяется напряжение на конденсаторе
   в процессах а) зарядки и б) разрядки?

4. Что показывает
   постоянная времени цепи? От чего она
   зависит?

5. Зачем в данной
   работе строится график зависимости
   lnU
   от t?

6. Как в данной работе
   определяется постоянная времени
   электрической цепи?

ЛИТЕРАТУРА

1.Трофимова Т.И.
Курс физики. / Т.И. Трофимова. – М.: Высшая
школа, 2006-2009 г. г. – 544с.

2 Савельев И.В. Курс
физики. В 3-х томах. Том 2. Электричество.
Колебания и волны. Волновая оптика. Изд.
3-е, стереотип. / И.В. Савельев – М.: Лань,
2007. – 480 с.

3. Грабовский Р. И.
Курс физики / Р.И. Грабовский – СПб:
издательство «Лань», 2012. – 608с.

4 Зисман Г. А., Тодес
О. М. Курс общей физики. В 3-х томах. Том
2. Электричество и магнетизм / Г.А. Зисман,
О.М. Тодес – СПб: «Лань», 2007. – 352 c.

Концевой
титул

Учебное
издание

Составитель:

Плотникова
Ольга
Васильевна

Соседние файлы в папке 12-02-2015_08-16-01

• #
• #
• #
• #
• #
• #
• #
• #
• #